MPBSE Class 12 Physics Atomic Nucleus Question And Answers

Mpbse Class 12 Physics Atomic Nucleus Solutions

Question 1. The Q -the value of a nuclear reaction A + b → C + d is defined by Q = [m_A + m_b-m_C-m_d]c², where the masses refer to nuclear rest masses. Determine from the given data whether the following reactions are exothermic or endothermic

1. \({ }_1^1 \mathrm{H}+{ }_1^3 \mathrm{H} \rightarrow{ }_1^2 \mathrm{H}+{ }_1^2 \mathrm{H}\)

2. \({ }_6^{12} \mathrm{C}+{ }_6^{12} \mathrm{C} \rightarrow{ }_{10}^{20} \mathrm{Ne}+{ }_2^4 \mathrm{He}\)

Atomic masses are given to be

\(m\left({ }_1^1 \mathrm{H}\right)=1.007825 \mathrm{u}, m\left({ }_1^2 \mathrm{H}\right)=2.014102 \mathrm{u}\)

\(m\left({ }_1^3 \mathrm{H}\right)=3.016049 \mathrm{u}, m\left({ }_1^{12} \mathrm{C}\right)=12.000000 \mathrm{u}\)

\(m\left({ }_{10}^{20} \mathrm{Ne}\right)=19.992439 \mathrm{u}, \quad m\left({ }_2^4 \mathrm{He}\right)=4.002603 \mathrm{u}\)

Answer:

1. \({ }_1^1 \mathrm{H}+{ }_1^3 \mathrm{H} \rightarrow{ }_1^2 \mathrm{H}+{ }_1^2 \mathrm{H}\)

Q= \(m_{\mathrm{N}}\left({}_1^1\mathrm{H}\right)+m_{\mathrm{N}}\left({ }_1^3 \mathrm{H}\right)m_{\mathrm{N}}\left({ }_1^2 \mathrm{H}\right)-m_{\mathrm{N}}\left({ }_1^2 \mathrm{H}\right)\)

= \(m\left({ }_1^1 \mathrm{H}\right)-m_e+m\left({ }_1^3 \mathrm{H}\right)-m_e-m\left({ }_1^2 \mathrm{H}\right)\) + \(m_em\left({}_1^2\mathrm{H}\right)+m_e\)

= \(m\left({ }_1^1 \mathrm{H}\right)+m\left({ }_1^3 \mathrm{H}\right)-m\left({ }_1^2 \mathrm{H}\right)-m\left({ }_1^2 \mathrm{H}\right)\)

1.007825 + 3.016049-2 × 2.014102

= -0.00433 ×  931.5 MeV = -4.03 MeV

∴ Q < 0, the reaction is endothermic

2. \({ }_6^{12} \mathrm{C}+{ }_6^{12} \mathrm{C} \rightarrow{ }_{10}^{20} \mathrm{Ne}+{ }_2^4 \mathrm{He}\)

Q = \(2 m_{\mathrm{N}}\left({ }_6^{12} \mathrm{C}\right)-m_{\mathrm{N}}\left({ }_{10}^{20} \mathrm{Ne}\right)-m_{\mathrm{N}}\left({ }_2^4 \mathrm{He}\right)\)

= \(=2 m\left({ }_6^{12} \mathrm{C}\right)-12 m_e-m\left({ }_{10}^{20} \mathrm{Ne}\right)+10 m_e\) \(-m\left({ }_2^4 \mathrm{He}\right)+2 m_e\)

= [2 × 12.000000-19.992439-4.002603] × 931.5 MeV

= 0.004958 × 931.5 MeV = 4.62 MeV

Q > 0; so, the reaction is exothermic.

Mpbse Class 12 Physics Atomic Nucleus Solutions

Question 2. Is the fission of  ⁵⁶Fe₂₆ nucleus into two equal fragments,  ²⁸Al₁₃ energetically possible? Argue by working out the Q of the process. Given, m ( ⁵⁶Fe₂₆ ) = 55.93494 u and m(²⁸Al₁₃) = 27.98191 u
Answer:

If possible, let the reaction be \({ }_{26}^{56} \mathrm{Fe} \rightarrow{ }_{13}^{28} \mathrm{Al}+{ }_{13}^{28} \mathrm{Al}\)

Q -value of the process = \(m\left({ }_{26}^{56} \mathrm{Fe}\right)-2 m\left({ }_{13}^{28} \mathrm{Al}\right)\)

55.934944-2 × 27.98191

= -0.02888 × 931.5 MeV

= -26.90 MeV

Since the Q -value is negative, fission is not possible

Question 3. The fission properties of ²³⁹Pu₉₄ are very similar to those of ²³⁵U₉₂ The average energy released per fission is 180 MeV. How much energy, in MeV, is released if all the atoms in ²³⁹Pu₉₄1 kg of pure undergo fission?
Answer:

Number of nuclei in 1 kg of ²³⁹Pu₉₄

= \(\frac{6.023 \times 10^{23}}{239} \times 1000.0\)

= 2.52 × 10 ²⁴

The energy released per fission = 180 MeV

Total energy released = 2.52 x 10²⁴ × 180 MeV

= 4.54 × 10²⁶ MeV

Atomic Nucleus Class 12 Questions And Answers

Question 4. A 1000 MW fission reactor consumes half of its fuel in 5y. How much ²³⁵U₉₂ did it contain initially? Assume that the reactor was active 80% of the time and all the energy generated arises from the fission of ²³⁵U₉₂ and that this nuclide is consumed by the fission process.
Answer:

Energy generated per gram of ²³⁵U₉₂

= \(\frac{6.023 \times 10^{23}}{235} \times 200 \times 1.6 \times 10^{-13} \mathrm{~J} \cdot \mathrm{g}^{-1}\)

Energy generated in 5 y

Power × Time × 80%

(1000 × 10⁶) × (5 × 365 × 24 × 60 × 60) × 80% J

Amount of spent

= \(\frac{\left(1000 \times 10^6\right) \times(5 \times 365 \times 24 \times 60 \times 60)}{6.023 \times 10^{23} \times 200 \times 1.6 \times 10^{-13}} \mathrm{x} \times 235\)

= 1538 kg

Initial mass of ²³⁵U₉₂  = 2 × 1538 kg = 3076 kg

Question 5. How long an electric lamp of 100 W can be kept glowing by fusion of 2.0 kg of deuterium? The fusion reaction can be taken as = \({ }_1^2 \mathrm{H}+{ }_1^2\mathrm{H}\rightarrow{}_2^3\mathrm{He}+\mathrm{n}+3.2 \mathrm{MeV}\)
Answer:

Number of nuclei in 2 kg of ²H₁

= \(\frac{6.023 \times 10^{23} \times 2000}{2}=6.023 \times 10^{26}\)

Energy generated by the fusion of these nuclei

E = \(\frac{3.2 \times 6.023 \times 10^{26}}{2} \mathrm{MeV}\)

Power of the bulb = 100 W

Let the bulb = 100 W

Energy spent = \(\frac{100 \times t}{1.6 \times 10^{-13}} \mathrm{MeV}\)

∴ \(\frac{100 t}{1.6 \times 10^{-13}}=\frac{3.2 \times 6.023}{2} \times 10^{23}\)

t = \(\frac{3.2 \times 6.023 \times 10^{23} \times 1.6 \times 10^{-13}}{2 \times 100}\)

– 1.54 × 10 12 s

= 4.89 × 104 y

Nuclear Physics Class 12 Important Questions

Question 6. A source contains two phosphorus radionuclides  ³²P₁₅ (T_1/2 = 14.3 d) and ³³P₁₅ (T_1/2 = 25.3 d). Initially, 10% of the decay comes from ³³P₁₅. How long one must wait until 90% do so. 33 32
Answer:

Let i R₀₁ and R₀₂ be the initial activities of ³³P₁₅ and ³²P₁₅ respectively and R₁ and R₂ be their activities at any instant t. According to the first observation

R₀₁ = 10% (R₀₁ +R₀₂)

R₀₂ =  9 R₀₁ ……………………………. (1)

Again, R₁ = 90% (R₁ + R₂)

Or, \(\frac{R_2}{R_{02}}=\frac{1}{81} \frac{R_1}{R_{01}}\) ……………………………. (1)

Combining equation (1) and (2)

⇒ \(\frac{R_2}{R_{02}}=\frac{1}{81} \frac{R_1}{R_{01}}\)

Or, \(\frac{R_{02} e^{-\lambda_2 t}}{R_{02}}=\frac{1}{81} \times \frac{R_{01} e^{-\lambda_1 t}}{R_{01}}\)

Or, \(81 e^{-\lambda_2 t}=e^{-\lambda_1 t}\)

⇒ \(\left(\lambda_2-\lambda_1\right) t=\dot{2} .303 \log 81\)

t = \(\frac{2.303 \log 81}{\frac{0.693}{14.3}-\frac{0.693}{25.3}}\)

Since Or, λ = 0.693T_½

= 208 . 5 d

Question 7. Under certain circumstances, a nucleus can decay by = 231.1 MeV emitting a particle more massive than an a -particle. Consider the following decay processes

1. \({ }_{88}^{223} \mathrm{Ra} \rightarrow{ }_{82}^{209} \mathrm{~Pb}+{ }_6^{14} \mathrm{C}\)

2. \({ }_{88}^{223} \mathrm{Ra} \rightarrow{ }_{86}^{219} \mathrm{Rn}+{ }_2^4 \mathrm{He}\)

Calculate the Q -values for these two decays and determine that both are energetically possible. 

m( ²²³Ra₈₈ ) = 223.01850 u, m( ²⁰⁹Ra₈₂ ) = 208.98107 u,

m(²¹⁹Ra₈₆ ) = 219.00948 u, m(¹⁴C₆) = 14.00324 u and m(⁴He₂) = 4.00260 u

Answer:

1. \({ }_{88}^{223} \mathrm{Ra} \rightarrow{ }_{82}^{209} \mathrm{~Pb}+{ }_6^{14} \mathrm{C}+Q\)

= \(\left[m_{\mathrm{N}}\left({ }_{88}^{223} \mathrm{Ra}\right)-m_{\mathrm{N}}\left({ }_{82}^{209} \mathrm{~Pb}\right)-m_{\mathrm{N}}\left({ }_6^{14} \mathrm{C}\right)\right]\) x 931.2 MeV

= \(\left[m_{88}^{223} \mathrm{Ra}-m\left({ }_{82}^{209} \mathrm{~Pb}\right)-m\left({ }_6^{14} \mathrm{C}\right)\right] \times 931.2 \mathrm{MeV}\)

31. 8 MeV

∴ Q > 0: so, the decay is possible

2. \({ }_{88}^{223} \mathrm{Ra} \rightarrow{ }_{86}^{219} \mathrm{Rn}+{ }_2^4 \mathrm{He}+Q^{\prime}\)

Q’ = 5.98 MeV [by similar calculation as above]

∴ Q’ > 0; so, this decay is also possible.

Nuclear Physics Class 12 Important Questions

Question 8. Consider the fission of ²³⁸U₉₂ by fast neutrons. In one fission event, no neutrons are emitted and the final stable end products, after the beta decay of the primary fragments, are¹⁴⁰Ce₅₈ and ⁹⁹Ru₄₄ Calculate Q for this fission process
Given

\(m\left({ }_{92}^{238} \mathrm{U}\right)=238.05079 \mathrm{u}, m\left({ }_{58}^{140} \mathrm{Ce}\right)=139.90543 \mathrm{u}\)

\(m\left({ }_{44}^{99} \dot{\mathrm{Ru}}\right)=98.90594 \mathrm{u}, \dot{m}_n=1.008667 \mathrm{u}\)

Answer:

The fission reaction is

⇒ \({ }_{92}^{238} \mathrm{U}+{ }_0^1 \mathrm{n}{\beta}{ }_{58}^{140} \mathrm{Ce}+{ }_{44}^{99}\mathrm{Ru}+Q\)

∴ Q = \(\left[m\left({}_{92}^{238}\mathrm{U}\right)+m\left({ }_0^1\mathrm{n}\right)m\left({}_{58}^{140}\mathrm{Ce}\right)-m\left({ }_{44}^{99} \mathrm{Ru}\right)\right] \mathrm{u}\)

= \([238.05079+1.00867-139.90543-98.90594]\)

= 23 1.1 MeV

Question 9. Suppose India had a target of producing by 2020 AD, 200, 000 MW of electric power, 10% of which was to be obtained from nuclear power plants. Suppose we are given that, on average, the efficiency of utilization (i.e., conversion to electric energy) of thermal energy produced in a reactor was 25%. How much amount of fissionable uranium did our country need per year by 2020? Take the heat per fission of ²³⁵U₉₂ to be about 200 MeV. Avogadro’s number = 6.023 × 10 mol^-1. Nuclear power target = 10% of total generation
Answer:

Nuclear power target = 10% of total generation

= 10% × 2 × 10¹¹ W

= 2 × 10¹⁰ W

Efficiency, η = 25%

∴ Total power generated by the nuclear reactor

= \(\frac{2 \times 10^{10}}{25 \%} \mathrm{~W}=8 \times 10^{10} \mathrm{~W}\)

∴ Generated heat by the reactor in 2020

H = 8 × 10¹⁰ × 366 × 24 × 60 ×60 J

∴ Number of fission required for generation of this heat,

N = \(\frac{H}{200 \times 1.6 \times 10^{-13}}\)

If m g of  ²³⁵U₉₂ contains this number of nuclei, then,

m = \(\frac{N \times 235}{6.023 \times 10^{23}} \mathrm{~g}\)

= \(\frac{8 \times 10^{10} \times 366 \times 24 \times 60 \times 60 \times 235}{200 \times 1.6 \times 10^{-13} \times 6.023 \times 10^{23}} \mathrm{~g}\)

= 3.084 × 10⁴  kg

Structure Of Atomic Nucleus Class 12 Questions

Question 10. Calculate and compare the energy released by

1. Fusion of: 1.0 kg of hydrogen deep within the sun and
2. The fission oqc of 1.0 kg of ²³⁵U in a fission reactor.

Answer: 

1. Equation of fusion reaction,

4 ¹H → ⁴He₂ + 2 ⁰e₊₁ + 26 MeV

∴ 26 MeV of energy is released on a combination of four H nuclei.

Number of nuclei in 1 kg of hydrogen

= 6.023 × 1023 × 1000

Energy released,

E_H = 6.023  × 1026 ×  26 MeV

2. Fission of one  nucleus releases 200 MeV of energy

Number of nuclei in 1 kg of ²³⁵U₉₂ = \(\frac{6.023 \times 10^{23} \times 1000}{235}\)

∴ Energy released,

E_U = \(\frac{6.023 \times 10^{23} \times 1000 \times 20}{235}\)

= 5.12 × 10²⁶ MeV

∴ \(\frac{E_{\mathrm{H}}}{E_{\mathrm{U}}}=\frac{3.913 \times 10^{27}}{5.12 \times 10^{26}}\)

= 7.6

Question 11. The half-life of a radioactive substance is 30 days. The number of atoms in the substance is 10¹². How many disintegrations of atoms per second does occur?
Answer:

T = 30 d =30 × 24 × 60 × 60 s

⇒ \(\lambda=\frac{0.693}{T}\)

= \(=\frac{0.693}{30 \times 24 \times 60 \times 60}\)

= 2.67 × 10^-7(approx)

If t = 1 s, t = 2.67 × 10^-7

Hence, e^λt  = 1.000000267(approx)

N = N₀e^λt  = \(\)

= 9.99999733 × 10¹¹ (approx)

∴ Number of atoms disintegrated per second

= N₀ – N = 2.67 ×  10 5 (approx)

Question 12. Draw a plot of the potential energy of a pair of nucleons as a function of their separations. Mark the region where the nuclear force is (1) attractive and (il) repulsive. Write any two characteristic features of nuclear forces
Answer:

The required plot

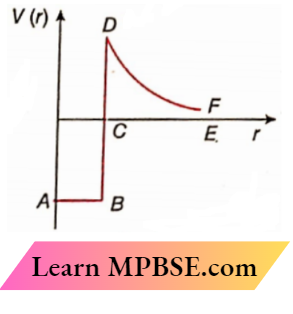
In region AB, nuclear force is attractive.

The nuclear force is not repulsive. The repulsive force corresponding to the region DF is the repulsive coulomb force between protons

Structure Of Atomic Nucleus Class 12 Questions

Question 13.

1. Draw the Plot of binding energy per nucleon (B.E./A ) as a function of mass number A . Write two important conclusions that can be drawn regarding the nature of
   nuclear force
   
2. Use this graph to explain the release of energy in both the processes of nuclear fusion and fission.
3. Write the basic nuclear process of neutrons undergoing β-decay. Why is the detection of neutrinos found very difficult?

Answer:

1.

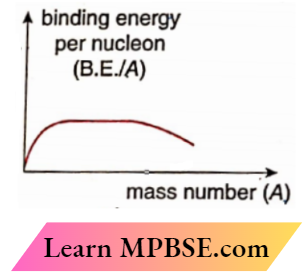
1. Two conclusions from the plot: the nuclear force is
2. Short-range and
3. Charge independent

2. Mass of a nucleus (M) = mass of its nucleons- binding energy (B)

So, M decreases with an increase in B.

Now, we consider nuclear fission: 1 → 2 + 3.

From mass-energy equivalence,

M₁ = M₂ + M₃+ energy release (Q)

or, Q = M₁ – M₂ – M₃

Q is positive, i.e., energy is released if

M₁ > M₂ – M₃,i.e., B₁ < B₂ – BM₃

or A₁e₁<A₂e₂ + A₃e₃

Where A₁A₂, A₃ are mass numbers A₁ = A₂ + A₃) and e₁ , e₂ , e₃ are binding energy per nucleon. From the plot, we see that this condition is satisfied for high A₁, where both e₂ and e₃ are higher than e₁ of the large nucleus 1.

The fission of a large nucleus releases energy. On the other hand, for low A nuclei, e_2, and e₃ will be less than the e₁ of the larger nucleus 1. So, energy will be released rather in the opposite process: 2 + 3 → 1. Therefore, a fusion of small nuclei releases energy

3. It is very difficult to detect neutrinos or antineutrinos experimentally because they have neither any charge nor any mass.

Question 14. Define the activity of a radioactive sample. Write its SI unit. A radioactive sample has the activity of 10000 disintegrations per second (DPS) after 20 hours. After the next 10 hours its activity reduces to 5000 dps. Find out its half-life and initial

The activity of a radioactive sample is defined as the rate of disintegration of the sample. It is also called the count rate. Its SI unit is becquerel (Bq).

1 Bq = 1 decays/s

We know A = A₈ e^-λt

5000 = 10000e^-λt

Or, e^λt = \(\frac{10000}{5000}\)

= 2

Taking logs on both sides we get

λt = log 2

Or, λ = \(\frac{\log 2}{t}\)

Now half-life T = \(=\frac{0.693}{\lambda}=\frac{0.693 \times t}{\log 2}=\frac{0.693 \times 600}{\log 2}\)

= 1381. 26 min 23 h

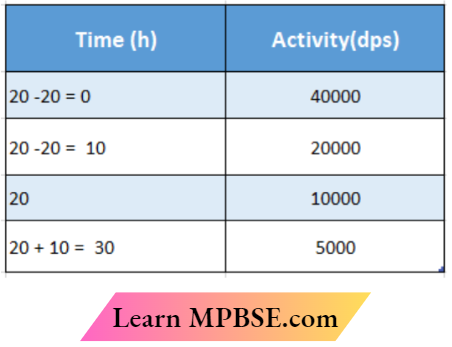
In this table, the last two values are the given values. Prom these values, the first two values have been calculated,

Atomic Nucleus Class 12 Questions And Answers

Question 15.

1. A radioactive nucleus ‘A ‘ undergoes a series of decays as given below:

The mass number and atomic number of A₂ are 176 and 71 respectively. Determine the mass and atomic numbers of A4 and A.

2. Write the basic nuclear processes underlying α and β decays

Answer:

1. When β^– decay occurs

When β⁺  decay occurs

In the case of β^–   decay, the mass number of A is 180 and its atomic number is 72. In the case of β⁺ decay, the mass number of A is 100 and its atomic number is 74. In both cases, the mass number of A₄   Is 172 and its atomic number is 69.

Question 16. Explain the processes of nuclear fission and nuclear fusion by using the plot of binding energy per nucleon (BE/A) versus the mass number A

Nuclear fission:

The binding energy per nucleon for heavier nuclei is approximately 7.6 MeV, but for lighter nuclei, it is roughly 8.4 MeV. The heavier nuclei exhibit reduced stability, leading to the fission of the heavier nucleus into lighter nuclei, which therefore releases energy. This process is referred to as nuclear fission.

Nuclear fusion:

The binding energy per nucleon for nuclei with mass number A < 12 is minimal, rendering them less stable. Consequently, two such nuclei can amalgamate to create a somewhat heavier nucleus, which possesses a greater binding energy per nucleon.

Consequently, energy is liberated in this process, referred to as nuclear fusion.

Atomic Nucleus Class 12 Questions And Answers

Question 17. A radioactive isotope has a half-life of 10 years. How long will it take for the activity to reduce to 3.125%?
Answer:

Activity A = λN

Given A = 3. 125 % of \(\frac{3.125 A_0}{100}=\frac{A_0}{32}\)

Or, \(\frac{A}{A_0}=\left(\frac{1}{2}\right)^5\)

∴ \(\frac{N}{N_0}=\left(\frac{1}{2}\right)^5\)

So the activity will reduce to 3.125% after 5 half-lives. Hence required time =5 × 10 = 50 years