MPBSE Class 12 Physics Electric Current and Ohm’s Law Shunt Notes

Mpbse Class 12 Physics Ohm’s Law Solutions

Current Electricity

Electric Current and Ohm’s Law Shunt

For every electrical instrument, the current flowing through it has a maximum permissible limit.

If the current exceeds the limit, there is a possibility of damage to the instrument.

To protect sensitive instruments like galvanometers and ammeters against possible damages due to heavy current passing through them, an alternative passage is provided as an inbuilt device within these instruments such that a major part of the main current in the circuit passes through this alternative route and a very small part through the instrument.

This alternative passage which is nothing but a low resistance connected in parallel with the instrument is called a shunt.

The arrangement of a shunt where a low resistance S (shunt) is connected in parallel with a galvanometer of resistance G.

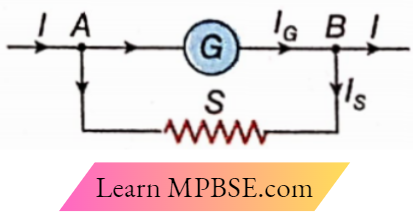
Let I be the main current, IG be the current through the galvanometer, and Is be the current through the shunt.

So, \(I=I_G+I_S\)

Now the equivalent resistance of the combination of the galvanometer and the shunt = \(\frac{G S}{G+S}\)

So, \(V_A-V_B=I \cdot \frac{G S}{G+S}\)

∴ \(I_G=\frac{V_A-V_B}{G}=I \cdot \frac{S}{S+G}\)…(2)

Mpbse Class 12 Physics Ohm’s Law Solutions

and \(I_S=\frac{V_A-V_B}{S}\)

= \(I \cdot \frac{G}{S+G}\) ….(3)

From equations (2) and (3) we get \(\frac{I_G}{I_S}=\frac{S}{G}\)

Particularly, if S << G, then IG << Is.

The ratio of the main current and the current passing through the galvanometer is known as the multiplying factor or power of a shunt, denoted by n

∴ \(\frac{I}{I_G}=n \quad \text { or, } \frac{S}{G+S}=\frac{1}{n} \text { [from equation (2)] }\)

or, \(\frac{S}{G}=\frac{1}{n-1} \quad \text { or, } S=\frac{G}{n-1}\)…(4)

Thus the shunt resistance can be adjusted according to the demand of n depending on G.

The shunt has another utility. With the help of the shunt, the galvanometer can almost accurately record the current flowing through the circuit. When a high-resistance galvanometer is connected to a circuit, the current drops considerably.

But with a shunt which is used in parallel, the equivalent resistance is reduced even below S. So, the main current of the circuit remains practically unchanged. Therefore, it becomes possible to measure the main current almost correctly.

Current Electricity Electric Current and Ohm’s Law Shunt Numerical Examples

Example 1. To reduce the action of a galvanometer by 25 times, a shunt is added to it. If the galvanometer resistance is 1000 ft, what is the resistance of the shunt? An ammeter is used to measure the current and a voltmeter
Solution:

⇒ \(I_G=I \cdot \frac{S}{S+G} \quad \text { or, } \frac{I_G}{I}=\frac{S}{S+G}\)

According to the question \(\frac{I_G}{I}=\frac{1}{25}\)

∴ \(\frac{1}{25}=\frac{S}{S+G} \quad \text { or, } 25 S=S+G \quad \text { or, } 24 S=1000\)

or, \(S=\frac{1000}{24}=41.67 \Omega\)

Example 2. If a shunt of 1Ω Is connected to a galvanometer of resistance 99Ω, what fraction of the main current will flow through the galvanometer?
Solution:

The galvanometer resistance G and the shunt resistance S are connected in parallel. So the galvanometer current

⇒ \(I_G=I \cdot \frac{S}{S+G} \quad[I=\text { main current }]\)

or, \(\frac{I_G}{I}=\frac{S}{S+G}=\frac{1}{1+99}=\frac{1}{100}=1 \%\)

i.e., 1% of the main current will flow through the galvanometer.

Ohm’S Law Class 12 Notes

Example 3. A battery of internal resistance zero is connected to a galvanometer of resistance 80Ω and a resistance of 20Ω in series. A current flows through the galvanometer. If a shunt of 1Ω resistance is connected to the galvanometer, show that the current that will now flow through the galvanometer becomes \(\frac{1}{17}\) of the previous current.
Solution:

The main current before adding the shunt to the circuit is

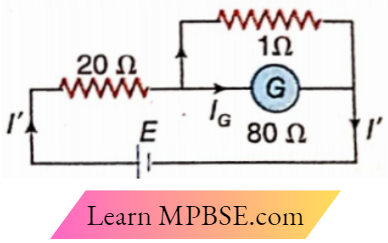
⇒ \(I=\frac{E}{80+20}=\frac{E}{100}\)

After adding the shunt the main current is

⇒ \(I^{\prime}=\frac{E}{\frac{80 \times 1}{80+1}+20}=\frac{E \times 81}{80+20 \times 81}\)

So, \(I_G=I^{\prime} \cdot \frac{S}{S+G}=I^{\prime} \cdot \frac{1}{80+1}=I^{\prime} \times \frac{1}{81}=\frac{E}{80+20 \times 81}\)

∴ \(\frac{I_G}{I}=\frac{E}{80+20 \times 81} \times \frac{100}{E}=\frac{100}{20(4+81)}=\frac{100}{20 \times 85}=\frac{1}{17}\)

i.e., \(I_G=\frac{1}{17} I\)

Connection of Ammeter and Voltmeter in a Circuit:

An ammeter is used to measure the current and a voltmeter is used to measure the potential difference between any two points of a circuit.

Milliammeters and ammeters are used to measure small currents while millivoltmeters and microvoltmeters are used to measure small potential differences.

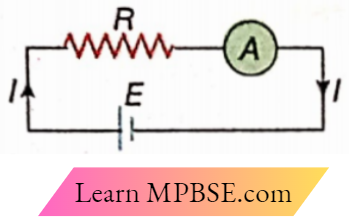
Connection of ammeter:

An ammeter is connected an electrical circuit, so that it may give the reading of the current when the circuit current passes through it. The main current decreases a little due to the resistance of the ammeter. To overcome this disadvantage a low-resistance ammeter should be used

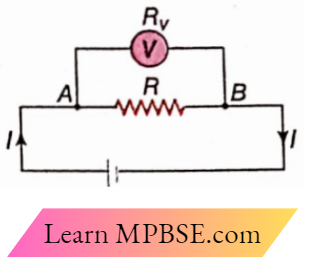
Connection of voltmeter: A voltmeter of resistance Rv is inserted in a parallel connection between the two points of the circuit across which the potentia difference is to be measured. The potential difference across the voltmeter is recorded as that between the two points. But there is a difficulty in this arrangement. Before inserting the voltmeter the resistance between the points A and B was R.

After joining the voltmeter, the resistance between points A and B is equal to the equivalent resistance of R and Rv, which is always less than R.

Electric Current Class 12 Physics Notes

So, the main current increases i.e., the potential difference between A and B also increases. Hence it is desirable that Rv should be much greater than R.

In that case, the equivalent resistance becomes almost equal to R and the slight increase of the potential difference can be ignored. So, the voltmeter is an instrument having a very high resistance and is connected in parallel in an electrical circuit.

Current Electricity

Electric Current and Ohm’s Law Numerical Examples

Example 1. The internal resistance of a battery of 100 V is 5fl. j When the emf of the battery is measured by a voltmeter 20% error is found. What is the resistance of the voltmeter?
Solution:

Suppose, the resistance of the voltmeter is R. Its reading is the potential difference of the external circuit.

According to the question, voltmeter reading =IR = 80% of 100 V = 80 V

∴ Lost volt =Ir = 100-80 = 20 V

∴ \(\frac{I R}{I r}=\frac{80}{20} \quad \text { or, } \frac{R}{r}=4\)

or, R = 4r

= 4 x 5

= 20Ω

Electric Current Class 12 Physics Notes

Example 2. In a supply line of 100 V, there is a resistance of 1000Ω. In between one terminal of the resistance and its point, a voltmeter is connected which gives a reading of 40 V. Determine the resistance of the voltmeter
Solution:

Suppose, the resistance of the voltmeter is R. I C is the midpoint of the resistance AB.

So, resistance of each portion AC and BC = \(\frac{1000}{2}\)

= 500Ω

Since the reading of the voltmeter = 40 V,

∴ V_A – V_C = 40V,

SO V_C– V_B = 100 – 40

= 60V

Now, the main current of the circuit,

⇒ \(I=\frac{V_C-V_B}{\text { resistance of } B C}=\frac{60}{500}=0.12 \mathrm{~A}\)

Again, current in the resistance AC,

⇒ \(I^{\prime}=\frac{V_A-V_C}{\text { resistance of } A C}\)

= \(\frac{40}{500}\)

= 0.08A

So, current in the voltmeter

IV = I-V

= 0.12 – 0.08

= 0.04 A

Therefore, the resistance of the voltmeter,

⇒ \(R=\frac{V_A-V_C}{I_V}=\frac{40}{0.04}=1000 \Omega\)

Shunt In Electric Circuits Class 12

Example 3. When a voltmeter of resistance 100Ω is connected. with an electric cell, the reading of the voltmeter Is 2 V. When the cell is connected with a resistance of 15Ω, an ammeter of resistance 1Ω gives the reading of 0.1 A. Determine the emf of the cell.
Solution:

In the first circuit

⇒ \(\text { current, } I_1=\frac{\text { reading of the voltmeter }}{\text { resistance of the voltmeter }}=\frac{2}{100}=0.02 \mathrm{~A}\)

If the die emf of the cell is E and the internal resistance is r then,

lost volt = I₁r

= 0.02r

i.e., E = 2 + 0.02r…(1)

Now, in the second circuit

⇒ \(\text { current, } I_2=\frac{E}{r+15+1}\)

or, \(0.1=\frac{E}{r+16}\)

or, E = 0.1r + 1.6…(2)

From the equations (1) and (2) we have,

2 + 0.02r = 0.1r+ 1.6

or, 0.08r = 0.4

or, \(r=\frac{0.4}{0.08}=5 \Omega\)

So, from (1), E = 2 + 0.02 x 5

= 2 + 0.1

= 2.1V