MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas

Point

A point determines a location and has no length, breadth or height. It is denoted by a single capital letter like P, Q, R etc. We can mark unlimited points on a plane.

•P

•Q

•R

The above points will be read as point P, point Q and point R.

e.g.

• The tip of a compass.
• The sharpened end of a pencil etc.

Example 1. Tip of an ice-cream cone gives us an idea of a point. Identify such few situations in your daily life and write them.

Solution. Such few situations in our daily life are as follows:

(1) The corners of a room

(2) Finger tip

(3) The location of a place on map

(4) A satellite in the space

(5) Moon from longer distance

Read and Learn More MP Board Class 6 Maths Solutions

Line Segment

A line segment is the shortest distance between two points which has a definite length.

The line segment joining points A and B is denoted by \(\overline{A B}\) or \(\overline{B A}\). These points A and B are called the end points of the line segment \(\overline{A B}\).

e.g. The edge of a box, a tubelight, the edge of a postcard, etc.

Mp Board Class 6 Maths Chapter 4 Solutions

Example 2. Name any five line segments in the following figure:

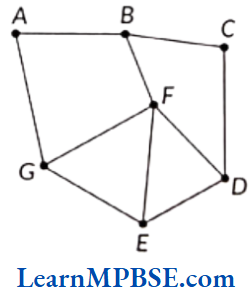
Solution. The five line segments in the figure are

\(\overline{A B}\),\(\overline{B C}\),\(\overline{C D}\),\(\overline{D E}\) and \(\overline{F G}\)

Example 3. Name the line segments in the given figure. Is P, the end point of each line segment?

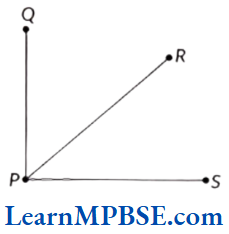
Solution. The line segment in the given figure are as follows: (1) \(\overline{P Q}\) (or \(\overline{Q P}\))

(2) \(\overline{P R}\) (or \(\overline{R P}\))

(iii) \(\overline{P S}\) (or \(\overline{S R}\))

Yes, from the figure, it is clear that point P is the end point of each line segment.

Line

A line is obtained when a line segment \(\overline{A B}\) is extended on both sides indefinitely and denoted by \(\overleftrightarrow{A B}\). Sometimes it is denoted by a single letter as 1, m.

In other words, two points are enough to fix a line.

i.e. Exactly one line can be drawn through the two given points.

A line has length only. It has neither width nor thickness. An endless line can be drawn on a paper by using two arrow heads one at each end of the portion of the line which indicates that it extends in both directions, indefinitely.

Example 4. Name the line given in all possible ways, choosing only two letters at a time from the three given letters.

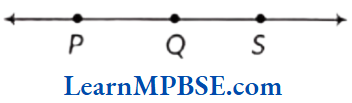
Solution. Name of lines in all possible ways are as follows:

(1) By taking P, all possible ways are \(\overleftrightarrow{P Q}\) and \(\overleftrightarrow{P S}\).

(2) By taking Q, all possible ways are \(\overleftrightarrow{Q P}\) and \(\overleftrightarrow{Q S}\).

(3) By taking S, all possible ways are \(\overleftrightarrow{S Q}\) and \(\overleftrightarrow{S P}\).

Intersecting Lines

If two lines have one common point, then they are called intersecting lines. The point at which lines meet is called the point of intersection.

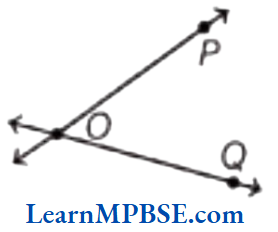
In the figure, lines, l1 and l2 are intersecting lines, which intersects at point O.

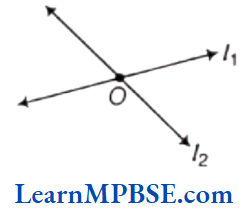
e.g. Two adjacent edges of a notebook, the english alphabet X, crossing roads etc.

Class 6 Maths Chapter 4 Mp Board Solutions

Example 5. Find

(1) two lines can intersect at how many points ?

(2) how many lines can intersect at one point?

Solution. (1) By the definition of intersecting lines, if two lines have one common point, then they are called intersecting lines. So, two lines can intersect at only one point.

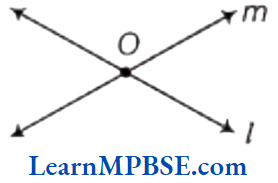
Here, l and m have only one intersecting point i.e. O.

(2) There are infinite number of lines that can intersect at one point.

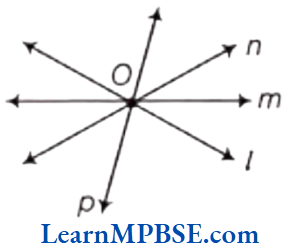
Here, lines l, m, nand p have one common point O, which is there intersecting point.

Note it The number of lines intersect at one point are infinite.

Parallel Lines

Two lines in a plane which are at equal distance from each other and never meet at any point or cross each other even if extended in any direction, are called parallel lines.

In the above figure, lines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) does not intersect each other and the common difference between them is always constant. Hence, \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are parallel to each other and are called parallel lines which can be denoted as \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{C D}\)

e.g. The opposite edges of ruler (or scale), the railway lines etc.

Mp Board Class 6 Maths Book Pdf

Example 6. From the following figure, find the

(1) pairs of intersecting lines.

(2) parallel lines.

(3) point of Intersection.

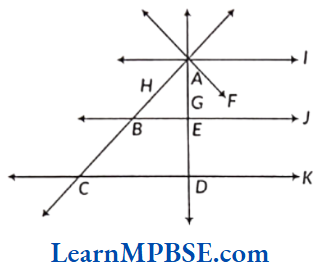
Solution. (1) Pairs of intersecting lines, F and G, F and H, F and I, G and I, H and I, G and H, J and H, J and G, K and G, K and H.

(2) Parallel lines are J ∥ I, J ∥ K, I ∥ K

(3) Point of intersection are A, B, E, C and D.

Ray

A ray is a portion of a line which starts at a point (called as starting point or initial point) and going in one direction endlessly.

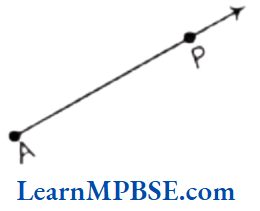
In the above figure, \(\overrightarrow{A P}\) is a ray whose starting point is A and P is a point on the path of the ray. Here, the arrow indicates that the ray \(\overrightarrow{A P}\) is endless in the direction from A to P.

e.g. Beam of light from a lighthouse, ray of light from a torch, Sun rays etc.

Example 7. Identify the rays from the following figure.

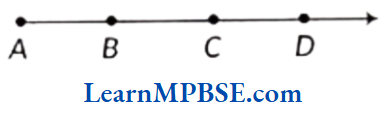
Solution. The rays are \(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D}, \overrightarrow{B C}, \overrightarrow{B D} \text { and } \overrightarrow{C D}\).

Mp Board Class 6 Maths Important Questions

Example 8. From the given figure answer the following.

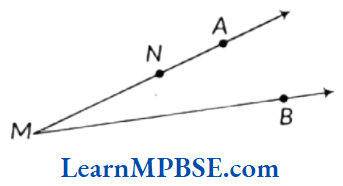
(1) Identify the rays and name them.

(2) Is M, a starting point of each of these rays?

Solution. (1) In the given figure, there are four rays namely \(\overrightarrow{M N}\), \(\overrightarrow{M A}\), \(\overrightarrow{N A}\) and \(\overrightarrow{M B}\).

(2) No, M is not the starting point of each of these rays. M is starting point of \(\overrightarrow{M N}\), \(\overrightarrow{M A}\), \(\overrightarrow{M B}\) and for \(\overrightarrow{N A}\), M is not the starting point.

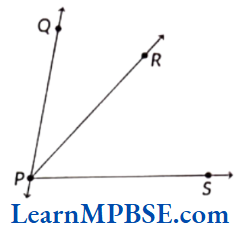
Example 9. In the given figure, name all the rays with initial points as P, Q and R, respectively.

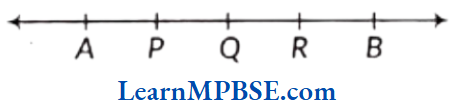
(1) Is ray \(\overrightarrow{P Q}\) different from ray \(\overrightarrow{P R}\)

(2) Is ray \(\overrightarrow{R A}\) different from ray \(\overrightarrow{R B}\).

Solution. \(\overrightarrow{P A}, \overrightarrow{P Q}, \overrightarrow{P R}, \overrightarrow{P B}, \overrightarrow{Q A}, \overrightarrow{Q P}, \overrightarrow{Q R}, \overrightarrow{Q B}, \overrightarrow{R A}, \overrightarrow{R P}, \overrightarrow{R Q}, \overrightarrow{R B}\)

(1) No

(2) Yes

Example 10. By using following figure, write

(1) all the points.

(2) a line.

(3) two rays with initial point Q.

(4) two line segments.

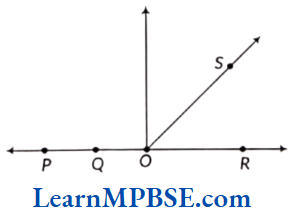
Solution. From the given figure,

(1) all the given points are P, Q, O, R and S.

(2) a line is \(\overleftrightarrow{P R}\)

(3) two rays with initial point Q is \(\overrightarrow{Q P}\) and \(\overrightarrow{Q O}\).

(4) two line segments are \(\overline{O Q} \text { and } \overline{O S}\).

Class 6 Maths Chapter 4 Exercise Solutions

Example 11. Use the following figure to name

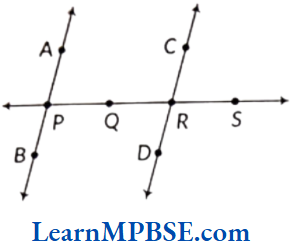
(1) Line containing point R.

(2) Line passing through point Q.

(3) Line on which C lies.

(4) Pair of intersecting lines.

Solution. (1) Here, two lines contain point R, one of them is \(\overleftrightarrow{P S}\).

(2) Here, line passing through point Q is \(\overleftrightarrow{P S}\).

(3) C lies on \(\overleftrightarrow{C D}\).

(4) Two pairs of intersecting lines are \(\overleftrightarrow{P S}\), \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P S}\), \(\overleftrightarrow{C D}\).

Example 12. Draw a rough figure and label suitably in each of the following cases.

(1) Point P, Q, R lies on \(\overline{A B}\).

(2) \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P Q}\) intersect at M.

(3) A line \(\overleftrightarrow{A B}\) which does not contain O.

(4) \(\overleftrightarrow{P Q}\) \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{P S}\) meet at P.

Solution. A rough figure in each of the cases is given below.

(1) Point P, Q, R lies on \(\overline{A B}\).

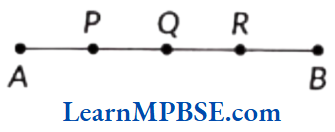
(2) \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P Q}\) intersect at M.

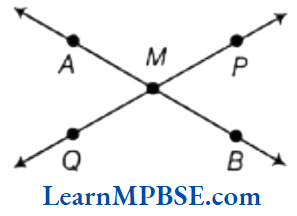
(3) A line \(\overleftrightarrow{A B}\) which does not contain O.

(4) \(\overleftrightarrow{P Q}\) \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{P S}\) meet at P.

Mp Board Class 6 Maths Chapter 4 Solutions

Example 13. From the figure, name

(1) All pairs of parallel lines.

(2) All pairs of intersecting lines.

(3) Lines whose point of intersection is P.

(4) Lines whose point of intersection is C.

(5) Lines whose point of intersection is R.

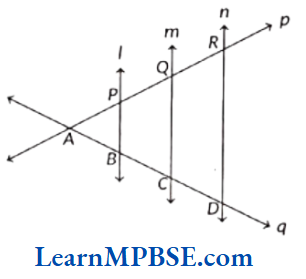
Solution. (1) l ∥ m, l ∥ n, m ∥ n

(2) p and q, p and l, p and m, p and n,q and l, q and m,q and n

(3) l and p

(4) q and m

(5) p and n

Example 14. Consider the following figure of line \(\overleftrightarrow{X Y}\). Say whether following statements are true or false in context of the given figure.

(1) Point Y does not lie on \(\overleftrightarrow{A C}\).

(2) A and C are the end points of line segment \(\overleftrightarrow{A Y}\).

(3) X and Y lies on the extended portion of \(\overleftrightarrow{A C}\).

(4) Point B lies outside of \(\overleftrightarrow{X Y}\).

Solution.

(1) False, because Y lies on the extended portion of \(\overleftrightarrow{A C}\).

(2) False, because it is clear from the figure that point C is between A and Y.

(3) True, it is clear from the figure that point X and Y lie on the extended portion of \(\overleftrightarrow{A C}\).

(4) False, point B lies between \(\overleftrightarrow{X Y}\).

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Curves and Polygons

Curve

Any drawing on the paper done without lifting the pencil from the paper and without use of ruler is called a curve. In this sense, a line is also called a curve.

e.g.

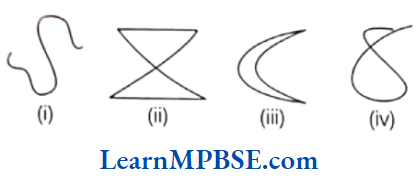
There are mainly three types of curves which are given below:

(1) Simple curve If a curve does not cross itself, is called a simple curve.

e.g.

(2) Open curve If a curve does not cut itself, is called an open curve.

In other words, when the end point of a curve are not joined, is called an open curve.

e.g.

(3) Closed curve If a curve cuts itself, is called a closed curve.

In other words, when the end points of a curve are joined, then it is called a closed curve.

e.g.

Position in a Figure

In a closed curve, there are three positions, which are as follows:

• Interior (inside) of the curve
• Boundary (on) of the curve
• Exterior (outside) of the curve

In the figure below, A is in the interior, B is on the curve and C is in the exterior.

The interior of a curve together with its boundary is called its region.

Example 1. Classify the following curves as

(1) Open

(2) Closed

Solution. (1) (a) and (c) are open curves.

(2) (b) and (d) are closed curves.

Example 2. Look at the alphabets given below and answer the questions.

P X S B C D V F

Which of the above letters are made of

(1) straight lines only?

(2) curves only?

(3) both straight line and curves?

Solution. (1) Straight lines only : X V F

(2) Curves only : S C

(3) Both straight line and curves : P B D

Class 6 Maths Chapter 4 Mp Board Solutions

Example 3. Consider the given figure and answer the following questions.

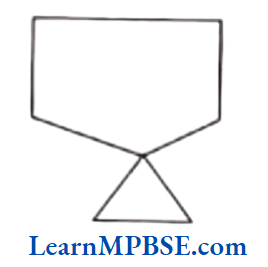
(1) Is it curve ?

(2) Is it closed?

Solution. Since, any drawn figure made without lifting the pencil from the paper is called a curve and if its ends points are joined, it is called a closed curve.

(1) Yes, it is a curve.

(2) Yes, it is closed curve.

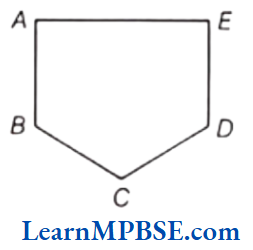
Polygon

A simple closed curve made up of line segments is called a polygon.

e.g.

A polygon has finite number of sides.

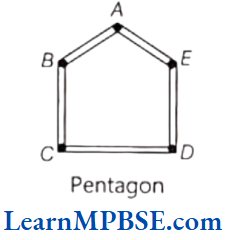
In the given figure, ABCDE is a polygon.

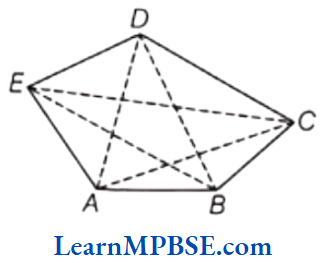
(1) Sides The line segments, forming a polygon are called its sides. In polygon ABCDE, AB, BC, CD, DE and EA are its sides.

(2) Vertex The meeting point of a pair of sides is called its vertex. In polygon ABCDE, A, B, C, D and E are its vertices.

(3) Adjacent sides Any two sides with a common end point (vertex) are called the adjacent sides of the polygon.

In polygon ABCDE, one pair of adjacent sides is AB and BC (where, B is a common vertex).

(4) Adjacent vertices The end points of the same side of a polygon are called the adjacent vertices.

In polygon ABCDE, A and B, B and C, C and D, D and E, E and A are adjacent vertices.

(5) Diagonals A diagonal is a line segment joining any two non-consecutive vertices.

In polygon ABCDE, AC, AD, BD, BE and CE are diagonals.

Note It No two line segments with a common ends points are coincident.

Example 4. Identify the polygons from the following figures:

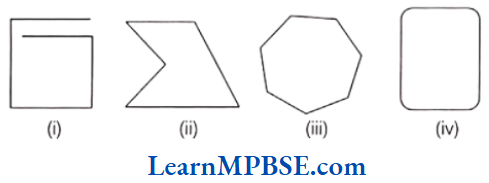
Solution. (1) The given figure is not closed. Hence, it is not a polygon.

(2) The given figure is closed. Hence, it is a polygon.

(3) The given figure is closed. Hence, it is a polygon.

(4) In the given figure, two sides are arc. Hence, it is not a polygon.

Mp Board Class 6 Maths Book Pdf

Example 5. Draw a polygon with four line segments and write its

(1) vertices

(2) sides

(3) diagonals

Solution. (1) Vertices of polygon PQRS are P, Q, R and S.

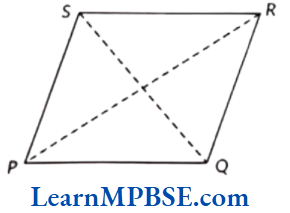
(2) Sides are PQ, QR, RS and SP.

(3) Diagonals are PR and QS.

Example 6. Illustrate, if possible, each one of the following with a rough diagram:

(1) A polygon with five sides.

(2) A polygon with two sides.

Solution. (1) The following figure is shows a polygon with five sides.

(2) It is not possible, because a polygon of two sides cannot be drawn. A minimum of three sides are required to form a polygon.

Example 7. In the given figure, write the

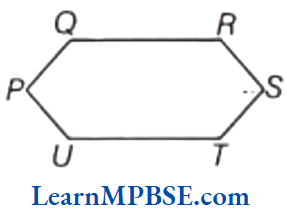
(1) number of sides.

(2) number of vertices.

Solution. (1) The following figure is drawn by joining the sides PQ, QR, RS, ST, TU and UP.

∴ Number of sides = 6

(2) Vertices in the given figure are P, Q, R, S, T and U.

∴ Number of vertices = 6

Mp Board Class 6 Maths Important Questions

Example 8. From the following figure, P answer the following question.

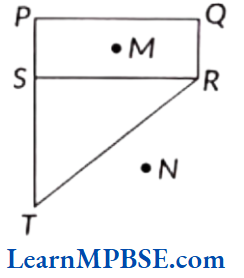
(1) Is PQRTS a polygon ?

(2) Is M lies in the exterior of the polygon?

(3) Is N lies in the interior of the polygon?

Solution. (i) Yes, since PQRTS is a simple closed curve entirely made of line segments, therefore it is a polygon.

(2) No, M lies in the interior of the polygon.

(3) No, N lies in the exterior of the polygon.

Example 9. Name the points which are inside the figure, on the figure and outside the figure.

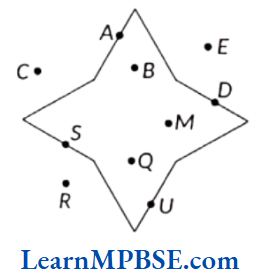
Solution. Points in the interior of figure: B, M and Q

Points on the figure: A, D, U and S;

Points on the exterior of the figure: C, E and R.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Angles

An angle is made up of two rays starting from a common starting/initial point. The two rays forming the angle are called the arms or sides of the angle and the common initial point is the vertex of the angle.

In the given figure, AOB is an angle and it is denoted by ∠AOB or ∠BOA or ∠O.

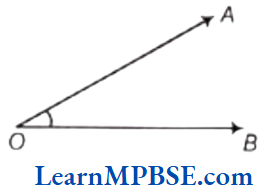
Here, OA and OB are arms or sides of angle and O is the vertex of the angle.

(1) In specifying the angle, the vertex is always written as the middle letter.

(2) An angle leads to three divisions of a region i.e. on the angle, the interior of the angle and the exterior of the angle.

In this diagram, point X is in the interior of the angle. Point P, point S and point R are on the angle and point Y is in the exterior of the angle.

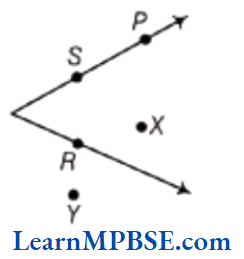
Example 1. Write the name of angles in the given figure.

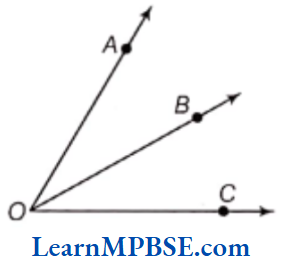
Solution. Here, angles are ∠AOB, ∠BOC and ∠AOC.

Class 6 Maths Chapter 4 Solutions

Example 2. Name the vertex and the arms of ∠PQR, given in the figure below.

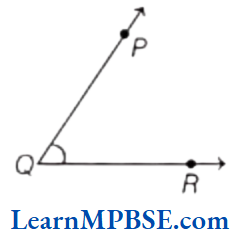
Solution. Q is the vertex, PQ and QR are the arms of angle ∠PQR

Example 3. Name the angles in the given figure.

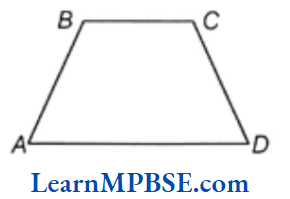
Solution. We know that an angle is made up of two rays starting from a common initial point. So, the angles in given figure are as follow:

(1) ∠A or ∠BAD

(2) ∠B or ∠ABC

(3) ∠C or ∠BCD

(4) ∠D or ∠CDA

Basic Geometrical Ideas Class 6 

Example 4. Draw rough diagrams of two angles for the conditions which are possible.

(1) One point in common.

(2) Three points in common.

(3) Four points in common.

Solution. (1) In the diagram, ∠POQ and ∠ROS have point O in common.

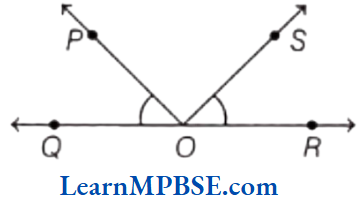
(2) In the diagram, ∠POR and ∠ROS have points O, Q and R in common.

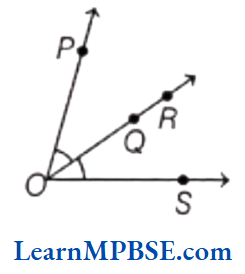
(3) In the diagram, ∠POR and ∠QOR have points O, R, S and T common.

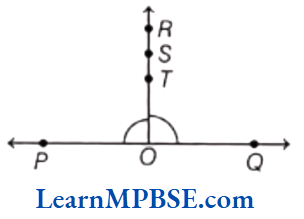
Example 5. Draw rough diagrams of two angles such that they have one ray in common.

Solution. Here, ∠ABC and ∠DBA have ray \(\overrightarrow{B A}\) in common.

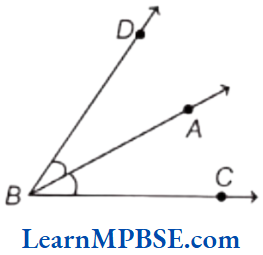
Example 6. Write the alternate name of the angle ∠SRQ in the given figure.

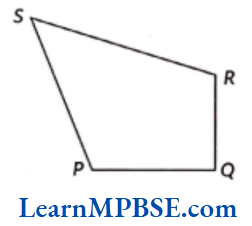
Solution. The alternate name for the angle ∠SRQ is ∠R

Basic Geometrical Ideas Class 6 

Example 7. In the following figure, how many angles are there? Name them.

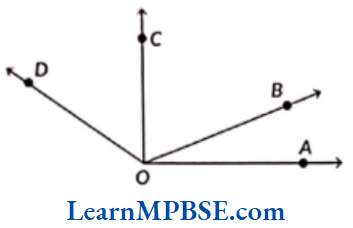
Solution. There are 6 angles i.e. ∠BOA, ∠COA, ∠DOA, ∠BOC, ∠BOD and ∠COD.

Example 8. How many angles does a polygon of six sides has?

Solution. Angles are formed when corners are formed. Following figure is the polygon with six sides.

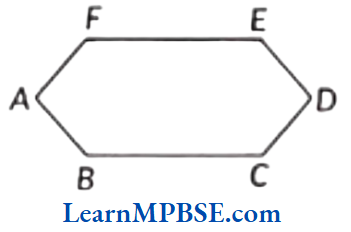
Here, six corners are formed.

So, the polygon with six sides has 6 angles.

Note it The number of angles in a polygon is equal to the number of sides of the polygon.

Example 9. Name each of the following angles in different ways.

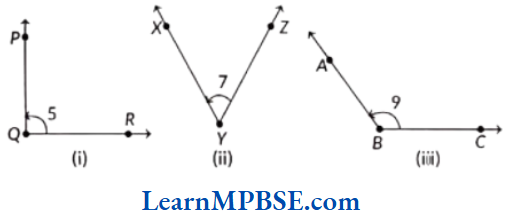
Solution. (1) ∠RQP or ∠PQR or ∠Q or ∠5

(2) ∠ZYX or ∠XYZ or ∠Y or ∠7

(3) ∠CBA or ∠ABC or ∠B or ∠9

Class 6 Maths Chapter 4 Exercise Solutions

Example 10. In figure, write another name for

(1) ∠1

(2) ∠2

(3) ∠3

(4) ∠4

(5) ∠5

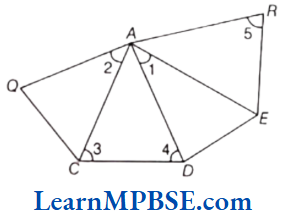
Solution.

(1) ∠1 → ∠DAE or ∠EAD

(2) ∠2 → ∠QAC or ∠CAQ

(3) ∠3 → ∠ACD or ∠DCA

(4) ∠4 → ∠ADC or ∠CDA

(5) ∠5 → ∠ARE or ∠ERA

Example 11. In the given diagram, name the point(s).

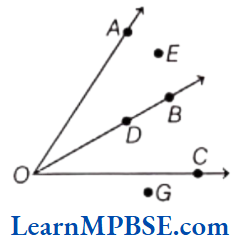
(1) In the interior of ∠AOB

(2) In the exterior of ∠BOC

(3) On ∠AOB

Solution. (1) In the given figure, point E lies between the sides OA and OB. So, it is in the interior of ∠AOB.

(2) In the given figure, points E, A and G are in the exterior of ∠BOC.

(3) In the given figure, point A, O, D and B lies on the sides OB and OA of ∠AOB, so these points are on ∠AOB.

Question 1. With a sharp tip of the pencil, mark four points on a paper and name them by the letters A, C, P, H. Try to name these points in different ways. One such way could be this

Solution. We can give the name to these given points in different ways as follows:

Question 2. A star in the sky also gives us an idea of a point. Identify atleast five such situations in your daily life.

Solution. Five situations of a point in our daily life are as follow:

(1) Tip of an ice cream cone.

(2) An edge of a table.

(3) Corner of a room.

(4) Corner of a desk.

(5) Corner of a paper.

Question 3. Name the line segments in the figure. Is A, the end point of each line segment?

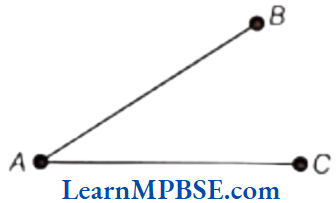
Solution. We know that the shortest distance between two points is called a line segment.

The line segment joining two points A and B is denoted by \(\overline{A B} \text { or } \overline{B A}\). The line segment in the given figure are as follows:

(1) \(\overline{A B}\) (or \(\overline{B A}\))

(2) \(\overline{A C}\) (or \(\overline{C A}\))

Yes, from the figure, it is clear that point A is the end point of each line segment.

MP Board Class 6 Chapter 4 Maths

Question 4. Take a sheet of paper. Make two folds (and crease them) to represent a pair of intersecting lines and discuss.

(1) Can two lines intersect in more than one point?

(2) Can more than two lines intersect in one point?

Solution. We know that if two lines have one common point, then they are called intersecting lines. By making two folds of a sheet of paper and crease them, we get the following figures.

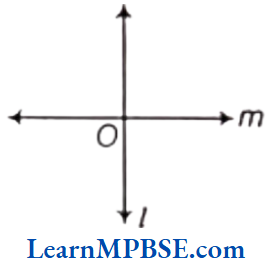
(1) From figure, it is clear that line l and m intersect at one point O (say) only. So, two lines cannot intersect in more than one point.

(2) Now, we again fold the paper diagonally (i.e. fold the paper three times) and crease them. We get the following figure.

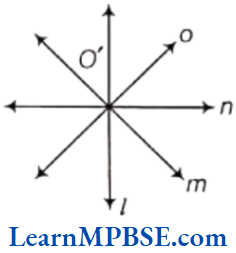
In the figure, four lines l, m, n and o are intersecting at one point O’ (say) only. So, it is clear from the above figure, that more than two lines intersect in one point.

Question 5. (i) Name the rays given in this picture.

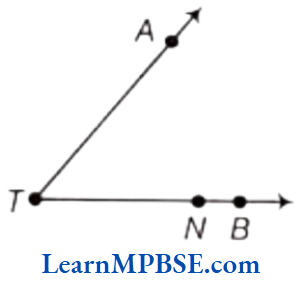
(2) Is T a starting point of each of these rays?

Solution. We know that a ray is a part of a line which starts at one point and goes endlessly in a direction.

(1) In the given figure, there are four rays namely \(\overrightarrow{T A}\), \(\overrightarrow{T N}\), \(\overrightarrow{N B}\) and \(\overrightarrow{T B}\).

(2) No, T is not a starting point of each of these rays. T is a starting point of \(\overrightarrow{T A}\), \(\overrightarrow{T B}\) and \(\overrightarrow{T N}\) only but not of \(\overrightarrow{N B}\).

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Exercise 4.1

Question 1. Use the figure to name

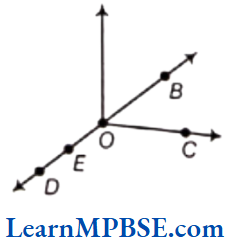
(1) five points.

(2) a line.

(3) four rays.

(4) five line segments.

Solution. From the given figure,

(1) Five points are B, C, D, E, and O.

(2) A line is \(\overleftrightarrow{B D}\) (or \(\overleftrightarrow{D B}\)).

(3) Four rays are \(\overrightarrow{O B}\), \(\overrightarrow{O C}\), \(\overrightarrow{O E}\) and \(\overrightarrow{O D}\).

(4) Five line segments in the given figure are \(\overline{O B}\), \(\overline{O C}\), \(\overline{O E}\), \(\overline{O D}\) and \(\overline{D E}\)

Note Two points are enough to fix a line. Hence, we can say that two points determine a line.

Question 2. Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given letters.

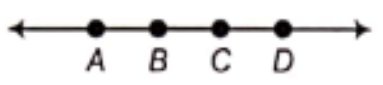
Solution. We know that a line is a line segment which can extend indefinitely in both directions. Name of lines in all possible ways are as follow:

(1) By taking A, all possible ways are \(\overleftrightarrow{A B}\), \(\overleftrightarrow{A C}\) and \(\overleftrightarrow{A D}\).

(2) By taking B, all possible ways are \(\overleftrightarrow{B C}\), \(\overleftrightarrow{B D}\) and \(\overleftrightarrow{B A}\).

(3) By taking C, all possible ways are \(\overleftrightarrow{C D}\), \(\overleftrightarrow{C A}\) and \(\overleftrightarrow{C B}\).

(4) By taking D, all possible ways are \(\overleftrightarrow{D A}\), \(\overleftrightarrow{D B}\) and \(\overleftrightarrow{D C}\).

Class 6 Maths Chapter 4 Mp Board Solutions

Question 3. Use the figure to name

(1) line containing point E

(2) line passing through A.

(3) line on which O lies.

(4) two pairs of intersecting lines.

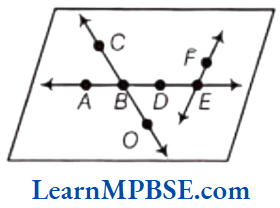
Solution. (1) Here, two lines contain point E, one of them is \(\overleftrightarrow{A E}\).

(2) Here, one line is passing through A, i.e. \(\overleftrightarrow{A E}\).

(3) Line on which O lies, is \(\overleftrightarrow{C O}\) or \(\overleftrightarrow{O C}\).

(4) There are two pairs of intersecting lines i.e. \(\overleftrightarrow{C O}\), \(\overleftrightarrow{A E}\) and \(\overleftrightarrow{A E}\), \(\overleftrightarrow{E F}\).

Question 4. How many lines can pass through

(1) one given point?

(2) two given points?

Solution. (1) Infinite number of lines can pass through one given point.

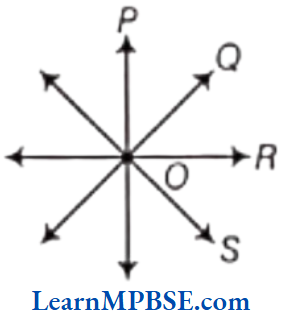
Let there be a point O on a surface. Now, we can draw infinite lines through it.

(2) Exactly one and only one line can pass through two given points (say A and B)

i.e

Question 5. Draw a rough figure and label suitably in each of the following cases.

(1) Point P lies on \(\overline{A B}\).

(2) \(\overleftrightarrow{X Y}\) and \(\overleftrightarrow{P Q}\) intersect at M.

(3) Line l contains E and F but not D.

(4) \(\overleftrightarrow{O P}\) and \(\overleftrightarrow{O Q}\) meet at 0.

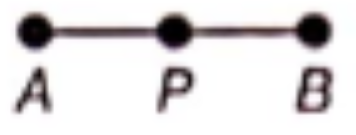
Solution. A rough figure in each of the cases is given below

(1) Point P lies on \(\overline{A B}\).

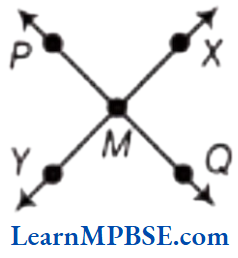
(2) \(\overleftrightarrow{X Y}\) and \(\overleftrightarrow{P Q}\) intersect at M.

(3) Line l contains E and F but not D.

(4) \(\overleftrightarrow{O P}\) and \(\overleftrightarrow{O Q}\) meet at O.

Class 6 Maths Chapter 4 Mp Board Solutions

Question 6. Consider the following figure of line \(\overleftrightarrow{M N}\). Say whether following statements are true or false in context of the given figure.

(1) Q, M, O, N, Pare points on the line \(\overleftrightarrow{M N}\).

(2) M, O, N are points on a line segment \(\overline{M N}\).

(3) M and N are end points of line segment \(\overline{M N}\).

(4) O and N are end points of line segment \(\overline{O P}\).

(5) M is one of the end points of line segment \(\overline{Q O}\).

(6) M is point on ray \(\overrightarrow{O P}\).

(7) Ray \(\overrightarrow{O P}\) is different from ray \(\overrightarrow{Q P}\).

(8) Ray \(\overrightarrow{O P}\) is same as ray \(\overrightarrow{O M}\).

(9) Ray OM is not opposite to ray \(\overrightarrow{O P}\).

(10) O is not an initial point of \(\overrightarrow{O P}\).

(11) N is the initial point of \(\overrightarrow{N P}\) and \(\overrightarrow{N M}\).

Solution.

(1) True, because points M, O and N lie on the line \(\overleftrightarrow{M N}\) and points Q, Plie on the extended portion of \(\overleftrightarrow{M N}\) on both sides.

(2) True, because points M, O, N lie on the line segment \(\overline{M N}\).

(3) True, because M to N is the shortest route of line segment \(\overline{M N}\).

(4) False, because it is clear from figure that point Nis between O and P.

(5) False, because it is clear from figure that point Mis between Qand O.

(6) False, because M is outside from ray OP.

(7) True, because all the rays have their own existence.

(8) False, because rays \(\overrightarrow{O P}\) and \(\overrightarrow{O M}\) are in opposite directions.

(9) False, because it is clear from figure that rays OM and OP are opposite.

(10) False, because it is clear from figure that point O is the initial point of \(\overrightarrow{O P}\).

(11) True, because it is clear from figure that ray \(\overrightarrow{N P}\) and \(\overrightarrow{N M}\) start from point N.

Question 7. Try to form a polygon with

(1) Five matchsticks.

(2) Four matchsticks.

(3) Three matchsticks.

(4) Two matchsticks.

In which case was it not possible? Why?

Solution. We know that if a closed simple figure is made up entirely of line segments, then it is called a polygon.

(1) Polygon with five matchsticks

(2) Polygon with four matchsticks.

(3) Polygon with three matchsticks

(4) We know that a polygon is a closed plane figure, bounded by line segments. So, with the help of two matchsticks, it is not possible to make a closed plane figure. Hence, no polygon is formed by two matchsticks.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical ideas Exercise 4.2

Question 1. Classify the following curves as (1) Open or (2) Closed.

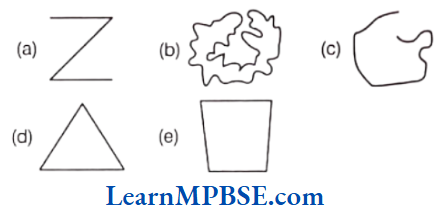
TIPS A simple curve is one, that does not cross itself. Besides, when the ends of a curve are joined, it is called a closed curve. If its ends are not joined, it is called an open curve.

Solution. (1) (a) and (c) are open curves.

(2) (b), (d) and (e) are closed curves.

Question 2. Draw rough diagram to illustrate the following:

(1) Open curve

(2) Closed curve

Solution. (1) The curve given below is an open curve, since its ends are not joined

(2) The curve given below is a closed curve, since its ends are joined

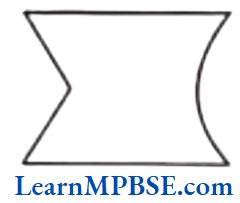
Question 3. Draw any polygon and shade its interior.

TIPS We know that a simple closed figure made up entirely of line segments is called a polygon and in a closed curve, the interior is inside of the curve.

Solution. ABCD is a polygon, where interior is shaded as given below:

Question 4. Consider the given figure and answer the questions.

(1) Is it a curve?

(2) Is it closed?

TIPS Any drawing drawn without lifting the pencil from the paper is called a curve. A curve is said to be a closed curve, if its ends are joined.

Solution. (1) Yes, it is a curve.

(2) Yes, it is closed.

Mp Board Class 6 Maths Important Questions

Question 5. Illustrate, if possible, each one of the following with a rough diagram:

(1) A closed curve that is not a polygon.

(2) An open curve made up entirely of line segments.

(3) A polygon with two sides.

Solution. (1) The following figure shows a closed curve, but not a polygon, because a polygon is made by line segments only.

(2) The following figure shows an open curve made up entirely of line segments.

(3) It is not possible, because a polygon of two sides cannot be drawn.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Exercise 4.3

Question 1. Name the angles in the given figure.

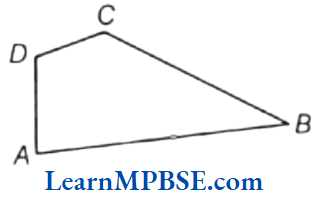
Solution. We know that an angle is made up of two rays starting from a common initial point. So, the angles in given figure are as follow:

(1) ∠A or ∠DAB

(2) ∠B or ∠ABC

(3) ∠C or ∠DCB

(4) ∠D or ∠ADC

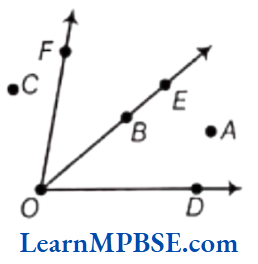
Question 2 In the given diagram, name the point(s).

(1) In the interior of ∠DOE

(2) In the exterior of ∠EOF.

(3) On ∠EOF.

Solution. (1) In given figure, point A lies between the sides OD and OE.

So, it is in the interior of ∠DOE.

(2) In given figure, points C, A and D are in the exterior of ∠EOF.

(3) In given figure, point E, B, O and Flie on the sides OE and OF of ∠EOF.

So, these points are on ZEOF

Mp Board Class 6 Maths Important Questions

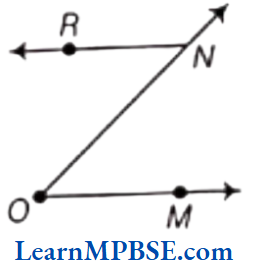
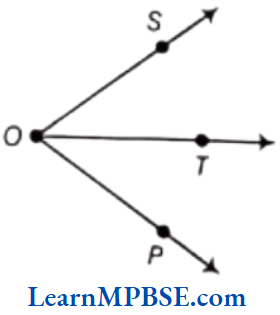
Question 3. Draw rough diagrams of two angles such that they have

(1) One point in common.

(2) Two points in common.

(3) Three points in common.

(4) Four points in common.

(5) One ray in common.

Solution. (1) The diagram is shown as below:

Here, ∠ROQ and ∠QOP have one point O in common.

(2) The diagram is shown as below:

Here, ∠MON and ∠ONR have two points O and N in common.

(3) The diagram is shown as below:

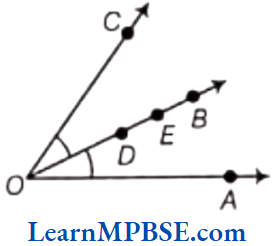
Here, ∠AOB and ∠BOC have three points B, E and D in common.

(4) The diagram is shown as below:

Here, ∠AOP and ∠AOQ have four points O, A, B and C in common.

(5) In the figure given below, ZSOT and ZPOT have one ray \(\overrightarrow{O T}\) in common.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Multiple Choice Questions

Question 1. How many points are marked in the following figure?

1. 1
2. 2
3. 3
4. 4

Answer. 4. 4

Question 2. Number of line segments in figure is

1. 5
2. 10
3. 15
4. 20

Answer. 2. 10

Question 3. Which of the following has two end points?

1. Ray
2. Line
3. Line segment
4. None of these

Answer. 3. Line segment

Question 4. A line segment has two end points and a line has …. end points.

1. 1
2. 2
3. 0
4. None of these

Answer. 3. 0

Question 5. Number of lines which can be drawn from one point

1. One
2. Two
3. Infinite
4. Five

Answer. 3. Infinite

Class 6 Maths Chapter 4 Exercise Solutions

Question 6. If two lines intersect each other, then the common point between them is known as ……

1. contact
2. collinear points
3. intersection point
4. concurrence

Answer. 3. intersection point

Question 7. Which of these is an example for a pair of the parallel lines?

1. Corner of a room
2. Railway track
3. Sides of a triangle
4. Surface of a ball

Answer. 2. Railway track

Question 8. A curve which does not cut itself called

1. Open Curve
2. Closed Curve
3. Both (a) and (b)
4. None of these

Answer. 1. Open Curve

Question 9. The number of interior points of the following figure is

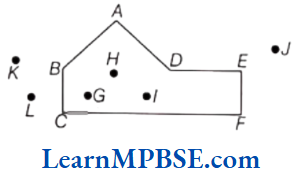
1. 5
2. 3
3. 2
4. 4

Answer. 2. 3

Question 10. The least number of line segment required to make a polygon is

1. 1
2. 2
3. 3
4. 5

Answer. 3. 3

Question 11. In the given figure, JLKM is polygon.

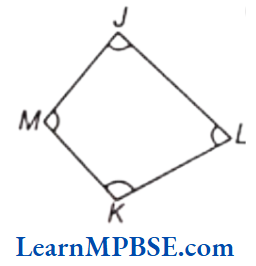
Which of the following is true for the polygon JLKM?

1. ∠J is adjacent to ∠K.
2. ∠J is opposite to ∠M.
3. Side JL is opposite to side MK.
4. Side KL is adjacent to side JM.

Answer. 3. Side JL is opposite to side MK.

Class 6 Geometry Concepts

Question 12. The number of diagonals of the following figure is

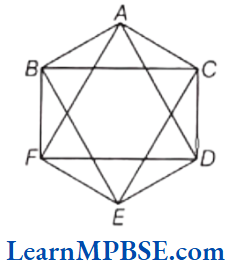
5

2

6

9

Answer. 3. 6

Question 13. Which of the following are the diagonals of the given polygon?

1. AD and BE
2. AF and FE
3. BC and ED
4. AB and ED

Answer. 1. AD and BE

Question 14. In the given figure, ∠XYZ cannot be written as

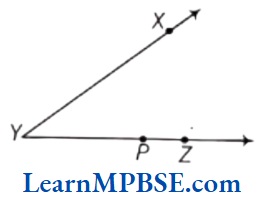
1. ∠Y
2. ∠ZXY
3. ∠ZYX
4. ∠XYP

Answer. 2. ∠ZXY

Question 15. The number of angles in the given figure are

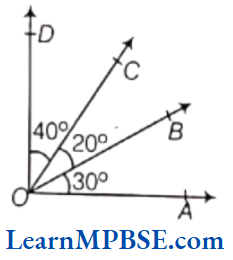
1. 3
2. 4
3. 5
4. 6

Answer. 4.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Assertion-Reason Type Question

Question 1. Assertion (A) Sharper the tip, thinner will be the dot.

Reason (R) A point determines a location.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 2. Assertion (A) A line contains a countless number of points.

Reason (R) Line extends indefinitely in both directions.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 3. Assertion (A) A ray PQ can be written as PQ.

Reason (R) A ray has one end point and extends without limit in one direction only.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Fill in the Blanks

Question 1. Two lines intersect at ……….point.

Solution. One

Question 2. In the given figure, points lying in the interior of the polygon are……….., that in the exterior of the polygon are……….and that on the polygon itself are………….

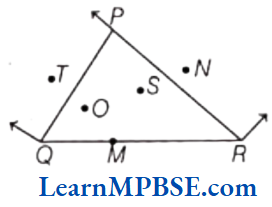
Solution. O and S, T and N; P, Q, R, M

Class 6 Maths Chapter 4 Exercise Solutions

Question 3. The number of common points in the two angles marked in the given figure is …..

Solution. Two

Question 4. The common part between the two angles BAC and DAB in figure is ……

Solution. AB

Question 5. The number of common points in the two angles marked in the given figure is

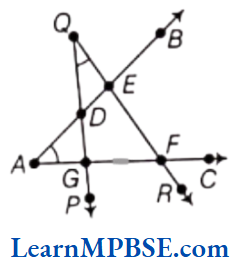
Solution. Four

Chapter 4 Basic Geometrical Ideas True/False

Question 1. A curve is said to be closed, if its end are not joined.

Solution. False

Question 2. Two parallel lines meet each other at some point.

Solution. False

Question 3. Two non-parallel line segments will always intersect.

Solution. False

Question 4. An angle is made up of two rays starting from a common initial point.

Solution. True

Question 5. Two adjacent angles have exactly one common arm.

Solution. True

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Match the Columns

Question 1. Match the item of Column A in Column B with their respective value.

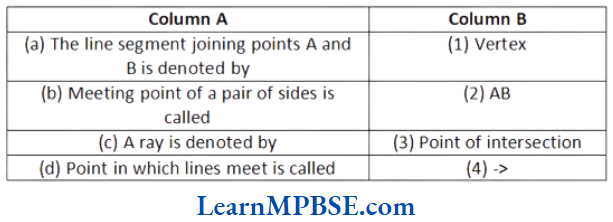
Solution. (a) → (2), (b) → (1), (c) → (4), (d) → (3)

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Case Based Questions

Question 1. Joy learns the art of knitting from his grandmother.

On the basis of the given information, answer the following questions.

(1) Which of the following pictures can be an example of a line segment?

(2) Which of the following is an open curve?

(3) Why is the below figure not considered a polygon?

(4) How many lines can pass through a point?

Solution. (1) (b) Option (b) is the example of a line segment.

(2) (b) An open curve does not cut itself.

(3) Since, a polygon is entirely made up of line segments. Therefore, the following figure is not considered a polygon because it is formed by two line segment and an arc.

(4) By observing the following figure we can say that many lines or infinite number of lines can pass through a point.

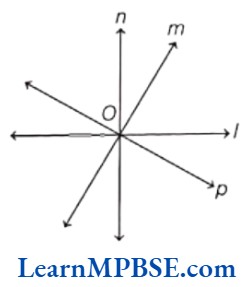
Question 2. Ankit marks five points by folding a rectangular paper sheet as shown below.

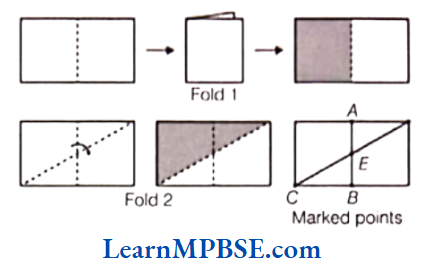
On the basis of the given information, answer the following questions.

(1) Choose the right word and fill in the blank. CE is an example of

(a) A ray

(b) An angle

(c) A point

(d) A line segment

(2) Which of the following is not true for both a ray and a line?

(a) They have end points.

(b) They have start points.

(c) They have no thickness.

(d) They can have infinite length.

(3) Fill in the blank with the correct word.

A line segment is a ….. of a line.

Solution. (1) (d) A line segment

(2) (a) A ray is a portion of a line, which starts at a point and goes endlessly in one direction, and a line obtained, when a line segment is extended on both sides indefinitely. Therefore, both does not have end points.

(3) A line segment is part or section of a line.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Very Short Answer Type Questions

Question 1. Use the follwoing figure to name:

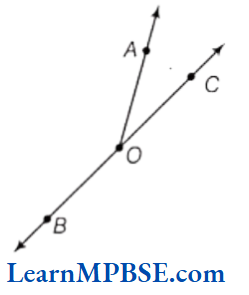
(1) all the points.

(2) two rays

Solution. (1) The points are O, A, B and C.

(2) Two rays are \(\overrightarrow{O A} \text { and } \overrightarrow{O C}\)

Question 2. Name all the line segments in given figure.

Solution. All the line segments are \(\overline{P Q}, \overline{P R}, \overline{P S}, \overline{Q R}, \overline{Q S} \text { and } \overline{R S} \text {. }\)

Mp Board Class 6 Maths Chapter 4 Solutions

Question 3. Name the line segments shown in the figure given below.

Solution. The line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E} \text { and } \overline{A E}\)

Question 4. Consider the following figure and write the name of

(1) a ray which contains point A.

(2) a ray which contains point B.

Solution. (1) Ray, which contains point A is \(\overrightarrow{P A}\).

(2) Ray, which contains point B is \(\overrightarrow{Q B}\).

Question 5. Draw two curves that are open.

Solution. The open curves are

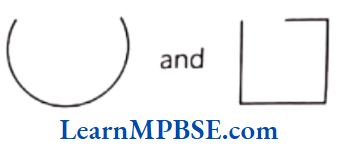
Question 6. Draw two curves that are closed.

Solution. The closed curves are

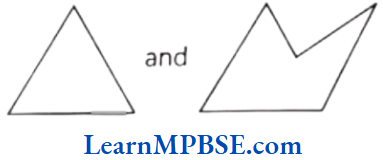
Question 7. Write all exterior and interior points of the given figure.

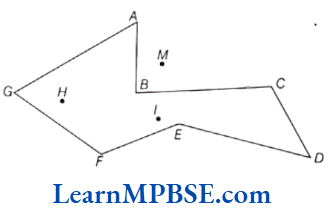
Solution. Here, interior points are H, I and exterior point is M.

Class 6 Geometry Concepts

Question 8. Name the vertices in given figure.

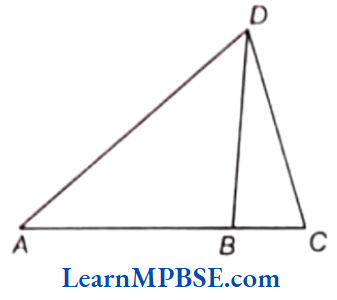
Solution. The vertices in the above figure are A, B, C and D.

Question 9. Write vertex of opposite side of AB and BC of the given figure.

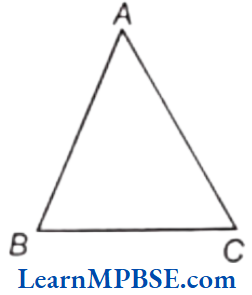
Solution. Vertex of opposite side of AB is C and of BC is A.

Question 10. Write all vertices of the given figure.

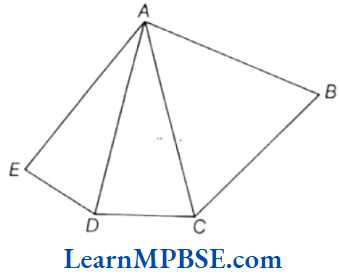
Solution. In the given figure, vertices are A,B,C,D and E.

Question 11. The number of common points in the two angles marked in the given figure is ….

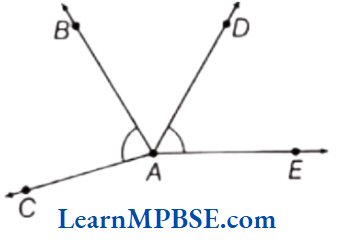
Solution. The common point in ∠BAC and ∠DAE is point A.

Mp Board Class 6 Maths Chapter 4 Solutions

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Short Answer Type Questions

Question 1. How many lines can pass through

(1) one given point?

(2) two given points?

Solution. (1) Through one given point, infinite number of lines can be drawn.

(2) Through two given points, only one line can be drawn.

Question 2. Identify parallel line segments in each of the figure given below.

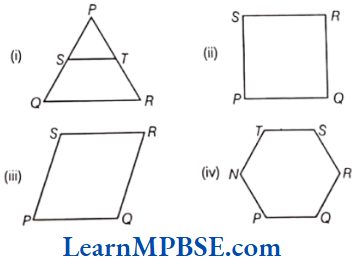
Solution. Parallel lines in the above figures are

(1) ST and QR.

(2) PQ and SR, SP and QR.

(3) PQ and SR, QR and SP.

(4) PQ and TS, QR and TN, SR and NP.

Class 6 Geometry Concepts

Question 3. Name the vertices and the line segments in the given figure.

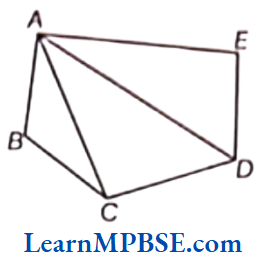
Solution. The vertices of the figure are A, B, C,D, E and the line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{E A}, \overline{A C}, \overline{A D}\)

Question 4. What is common in the following figures (1) and (2)?

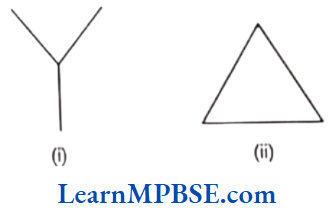
Is figure (1) is a triangle? If not, why?

Solution. In the given figures (1) and (2), both have three line segments. Figure (1) is not a triangle, because it is not a closed curve.

Question 5. Is PQRS a figure of polygon?

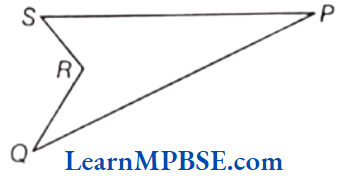
Solution. Yes, it is a polygon, because it is a simple closed curve made up of line segments only.

Question 6. In the given figure, list the points which

(1) are in the interior of ∠AOB.

(2) are in exterior of ∠AOB.

(3) lie on ∠AOB.

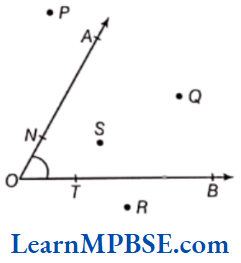
Solution. (1) The interior points of ∠AOB are S and Q.

(2) The exterior points of ∠AOB are P and R.

(3) The points, which lie on ∠AOB are A, O, B, T and N.

Mp Board Class 6 Maths Chapter 4 Solutions

Question 7. In the given figure, name the points, which are

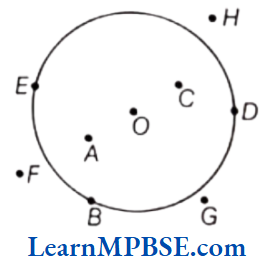
(1) in its exterior.

(2) in its interior.

(3) on the figure

Solution. (1) The points which lie in the exterior are F, G and H.

(2) Interior points are A, O and C.

(3) The points which lie on the figure are B, D and E.

Question 8. In the given figure, write

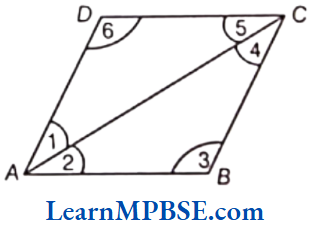
(1) name of the vertex of ∠3.

(2) name of the common arm of ∠1 and ∠2.

(3) name the vertex of ∠4.

Solution. (1) The vertex of ∠3 is B.

(2) Common arm of ∠1 and ∠2 is AC.

(3) The vertex of ∠4 is C.

Polygons and Curves for Class 6

Question 9. Write down six angles involved in the given figure.

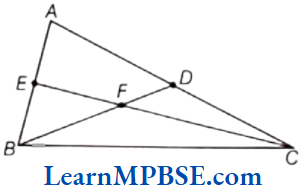
Solution. Six angles involved in the above figure are ∠ABC, ∠BCA, ∠CAB, ∠AEC, ∠ABD and ∠DBC.

Question 10. In the following figure, name the angles using three letters.

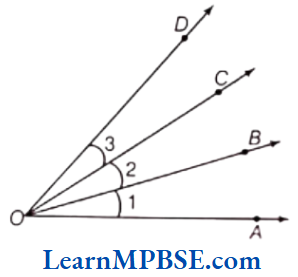
(1) ∠1 (2) ∠2 (3) ∠3

Solution. Here, we can write the name of angles with the help of given figure:

(1) ∠1 = ∠AOB (2) ∠2 = ∠BOC (3) ∠3 = ∠COD

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometric Ideas Long Answer Type Questions

Question 1. Name the points and then the line segments in each of the following figures.

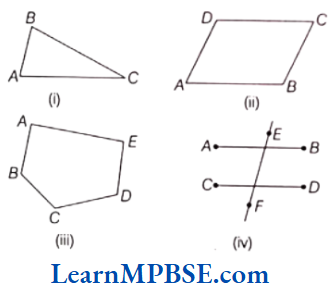
Solution. (1) The points are A, B, C and line segments are \(\overline{P Q}, \overline{R S}, \overline{P S}\).

(2) The points are A, B, C, D and line segments are \(\overline{A B}, \overline{B C}, \overline{C D} \text { and } \overline{A D}\).

(3) The points are A, B, C, D, E and line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{A E}\).

(4) The points are A, B, C, D, E, F and line segments are \(\overline{A B}, \overline{C D}, \overline{E F}\).

Polygons and Curves for Class 6

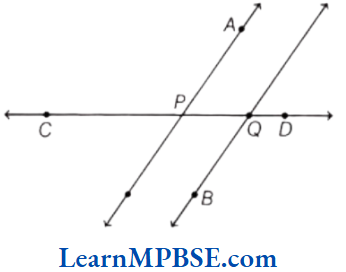
Question 2. In the given figure, write

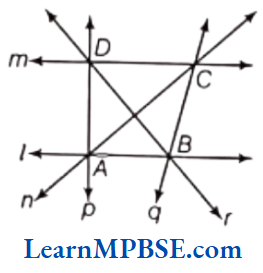
(1) parallel lines.

(2) point of intersection of the line l and n.

(3) point of intersection of the line q and r.

(4) point of intersection of the line m and r.

(5) point of intersection of the line p and m.

Solution. (1) The lines / and m are parallel lines.

(2) Point of intersection of the lines / and n is A.

(3) Point of intersection of the lines q and r is B.

(4) Point of intersection of the lines m and r is D.

(5) Point of intersection of the lines p and m is D.

Question 3. Sohan wants to show gratitude toward his teacher by giving a card made by him. He has three pieces of paper pasted one above the other as shown in the figure. These pieces are arranged in a way that AB ∥ HC ∥ GD ∥ FE.

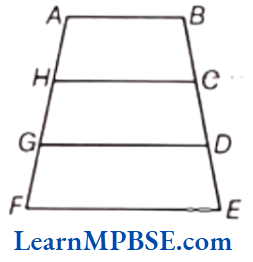
He wants to decorate the card by putting up a coloured paper on non-parallel sides of the card.

(1) Write the non-parallel sides of the card.

(2) which value is depicted by the Sohan?

Solution. (1) Non-parallel sides are AF and BE.

(2) Respect to teacher, happiness, beauty, and knowledge.

Polygons and Curves for Class 6

Question 4. Look at the following figure and answer the following questions.

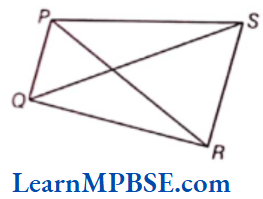
(1) Name the four sides of figure made by joining PQRS.

(2) Name the four pairs of adjacent sides.

(3) Name two pairs of opposite sides.

(4) Name a pair of diagonal.

Solution. (1) Four sides of figure PQRS are \(\overline{P Q}, \overline{R S}, \overline{P S} \text { and } \overline{Q R}\).

(2) Four pairs of adjacent sides are PQ and QR, QR and RS, RS and SP, SP and PQ.

(3) Two pairs of opposite sides are QR and PS, PQ and SR.

(4) Pair of diagonal is PR and QS.

Circle Basics Class 6 Solutions

Question 5. Look at figure and mark a point

(1) A, which is in the interior of both ∠1 and ∠2.

(2) B, which is in the interior of only ∠1.

(3) C in the interior of ∠1.

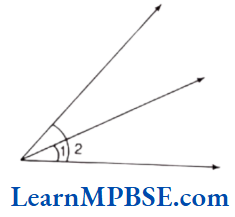
Now, state whether points B and C lie in the interior of ∠2 also.

Solution.

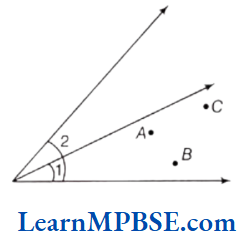
Yes, it is clear from the figure, that the points B and C lie in the interior of ∠2 also.