MP Board Class 6 Maths Solutions For Chapter 6 Integers

Chapter 6 Integers and Number Line

Natural Numbers Natural numbers are counting numbers i.e. 1, 2, 3,…

Whole Numbers If we include 0 (zero) with natural numbers, then they are called as whole numbers. Negative Numbers The numbers which are less than 0 are called negative numbers. To differentiate these negative numbers from whole numbers, we use a (-) minus sign attached to the number. This indicates that numbers with negative sign are less than zero.

e.g. 1 is less than zero is written as 1, 2 is less than zero is written as -2 etc.

Sign with Numbers

In our day-to-day life, we see some situations in which some numbers carry a negative sign and some carry positive sign. These situations are represented by appropriate signs i.e. ‘+’ sign and ‘-‘ sign.

e.g. Profit is represented by ‘+’ sign and loss is represented by ‘-‘ sign.

Example 1. Write the opposite of each of the following:

(1) Profit of 50.

(2) Deposit of 1000.

(3) 50 km towards South.

Solution. The opposite of each, is

(1) loss of ₹ 50.

(2) withdraw of ₹ 1000.

(3) 50 km towards North.

Read and Learn More MP Board Class 6 Maths Solutions

Example 2. Write the following numbers with appropriate signs:

(1) 200 m below sea level.

(2) 20°C below 0°C temperature.

(3) 25°C above 0°C temperature.

(4) A deposit of 50.

(5) Any four numbers less than 0.

Solution. (1) 200 m below sea level means – 200 m.

(2) 20°C below 0°C temperature means -20°C.

(3) 25°C above 0°C temperature means + 25°C.

(4) A deposit of 50 means + ₹ 50.

(5) Every negative integer is less than zero and every positive integer is greater than zero.

∴ Numbers less than zero are -1, -2, -3 and -4.

Integers

If we put the whole numbers and the negative numbers together, the new collection of numbers will look like …-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, .., and this collection of numbers is known as integers.

Here, 1, 2, 3,… are said to be positive integers and -1, -2, -3, … are said to be negative integers.

Note It Zero is an integer which is neither positive nor negative. One more than given number gives its successor and one less than that of given number gives its predecessor.

Representation of Integers on a Number Line

To represent integers on a number line, draw a line and mark the points at equal distance on it, as shown in the figure given below. Mark a point as zero on it. Points to the right of zero are positive integers marked as +1, +2, +3 etc or simply 1, 2, 3 etc. Points to the left of zero are negative integers marked as -1, -2, -3, etc.

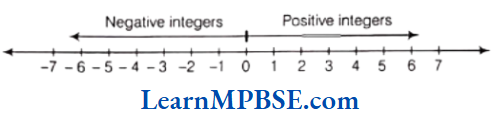
Mp Board Class 6 Book Solutions

Example 3. Represent the following numbers on the number line

(1)-2

(2) +6

(3) – 5

(4) -1

(5) +5

Solution. Draw a line and mark some points at equal distance on it. Mark a point as zero on it. Points to the right of zero are positive integers and are marked as +1, +2, +3 or simply by 1, 2, 3 etc. Points to the left of zero are negative integers and are marked by-1, -2, -3, etc.

(1) Representation of -2 To mark-2 on the number line, we move 2 points to the left of zero as shown in figure. A

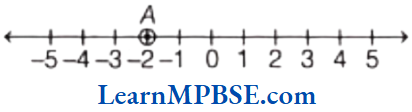
In the above figure, point A represents – 2.

(2) Representation of 6 To mark +6 on the number line, we move 6 points to the right of zero as shown in the figure.

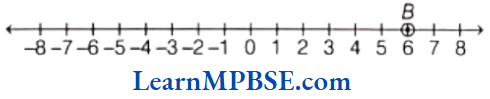
In the above figure, point B represents + 6.

(3) Representation of -5 To mark-5 on the number line, we move 5 points to the left of zero as shown in figure.

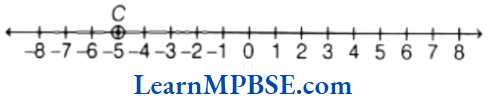
In the above figure, point C represents-5.

(4) Representation of -1 To mark-1 on the number line, we move 1 point to the left of zero as shown in figure.

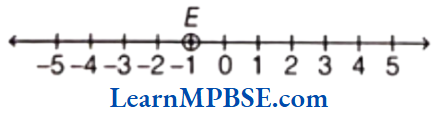
In the above figure, point E represents – 1.

(5) Representation of + 5 To mark + 5 on the number line, we move 5 points to the right of zero as shown in figure.

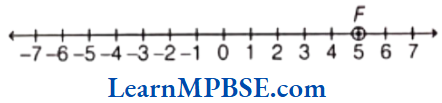
In the above figure, point F represents + 5.

Example 4. The given figure is a horizontal line representing integers. Observe it and locate the following points.

(1) If point D is +7, then which point is – 7

(2) Find that the point G is a negative or a positive integer.

(3) Write the integers of points F and C.

(4) Which point marked on this number line has the greatest value?

(5) Arrange all the points in increasing order of value.

Solution.

(1) From the figure, it is clear that + 7 is on point D, then for getting-7, we should move left of zero.

After moving 7 steps left of zero, we reach at the point H.

So, point H represents-7.

(2) The point G is left of zero. So, G is a negative integer.

(3) The integers for point F is -3 and for point C is 5.

(4) The point D has the greatest value i.e. 7.

(5) We know that on a number line, the number increases as we move to right. So, increasing order of value of all points is given here.

H, G, FE, O, A, B, C, D

Mp Board Class 6 Book Solutions

Example 5. Given below are the temperatures in some cities.

(1) Write the temperature of these cities in the form of integers.

(2) Which is the coolest city out of these cities?

(3) Give the names of cities, where temperature is above 5°C.

(4) Plot the temperature of cities on the number line.

Solution. (1) The temperature of Shimla is -10°C.

The temperature of Leh is -15 °C.

The temperature of Delhi is + 25 °C.

The temperature of Nagpur is + 30°C.

(2) After checking the temperature of all places, we can say that the Leh (-15°C) is the coolest place.

(3) Delhi (25°C) and Nagpur (30°C) are the cities, where temperature is above 5 °C.

(4)

Example 6. In the given following pairs which number is to the right of the other on the number line?

(1) 3,8

(2) -4, -9

(3) 0, -4

(4) -13, 8

Solution.

(1)

Here, 3 and 8 both are on the right of zero but 8 is farther from zero in comparison of 3. So, number 8 is right of number 3.

(2)

Here, -4 and -9 both are on the left of zero, but – 4 is nearer to zero in comparison of-9. So, -4 is right of

(3)

Here, 0 is right of -4.

(4) Here, -13 is left of zero and 8 is right of zero. So, 8 is right of -13.

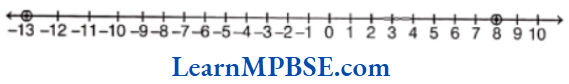
Ordering of Integers

On the number line, the number increases as we move to the right and decreases as we move to the left.

Therefore, -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 and so on.

Note it The greater the positive integer, the lesser is its opposite.

e.g. 7 > 4 but -7 < -4.

Mp Board Class 6 Book Solutions

Example 7. Compare the following pairs of numbers using > or <.

(1) 0 – -6

(2)-1 – -12

(3) 5 – -5

(4) 11 – 17

Solution.

(1) We know that -6 is to the left of 0 (zero) on number line. So,0 > -6

(2) We know that-1 is to the right of-12 on the number line. So -1 > -12

(3) We know that 5 is to right of-5. So, 5 > -5

(4) We Know that 17 is to right of 11. So, 11 < 17

Example 8. Write five negative integers

(1) greater than 30.

(2) less than -15.

Solution.

(1) When we move on the number line to the right, then the value of integer increases.

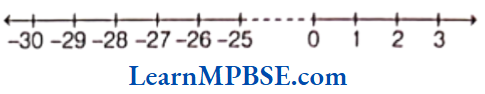
So, from the above figure, we get the five negative integers greater than 30 are 29,-28,-27,-26 and – 25.

(2) When we move on the number line to the left, then the value of integer decreases.

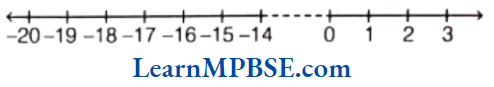
So, from the above figure, we get the five negative integers less than -15 and -16,-17, -18,-19 and – 20.

Example 9. Write all the integers between

(1) 0 and -9

(2) -15 and -5

and write them in the decreasing order.

Solution. (1) Integers 0 and -9 are shown on the number line as below.

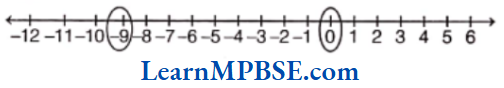
From the above number line, it is clear that integers between 0 and -9 are-1,-2,-3,-4,-5, -6, -7 and – 8.

Now, decreasing order of these integers is

-1 > -2 > -3 > -4 > -5 > -6 > -7 > -8

(2) Integers-15 and -5 are shown on the number line as below.

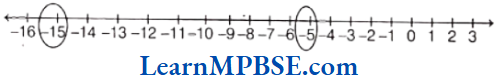
From the above number line, it is clear that integers between 15 and -5 are -14,-13,-12,-11,-10,-9, -8,-7,-6

Now, decreasing order of these integers is

-6 > -7 > -8 > -9 > -10 > -11 > -12 > -13 > -14

Example 10. For the following statements, write true (T) or false (F). If the statement is false, correct the statement.

(1)-6 is to the right of -12 on a number line.

(2)-70 is to the right of 30 on a number line.

(3) Smallest positive integer is 1.

(4)-24 is greater than -23.

Solution. (1) True, because on the number line going to the right, value of integer increases. Here, – 6 is greater than -12. So,-6 is to the right of-12 on the number line.

(2) False, because on the number line going to the left. value of integer decreases. Here, – 70 is less than 30. So,-70 is to the left of- 30 on the number line.

(3) True, because on the number line 1 is situated on the left of all positive integers. So, it is the smallest positive integer.

(4) False, because – 23 is on the right of – 24 on the number line. So, 23 is greater than – 24.

Mp Board Class 6 Maths Solutions

Example 11. Draw a number line and answer the following:

(1) Which number will we reach, if we move 5 numbers to the left of -1?

(2) Which number will we reach, if we move 4 numbers to the right 2?

(3) If we are at 6 on the number line, in which direction should we move to reach -11?

(4) If we are at 9 on the number line, in which direction should we move to reach – 3?

Solution. (1)

On the number line, starting from -1 and moving 5 points towards left (each step being equal to 1 unit), we will reach at -6.

(2)

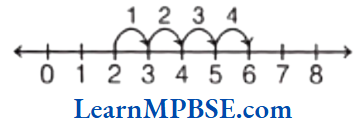
On the number line, starting from 2 and moving 4 points towards right (each step being equal to 1 unit), we will reach at 6.

(3) Here,-6-11. So, -11 is on the left of -6.

Hence, if we are at -6 on the number line, then move to the left from 6 to reach at -11.

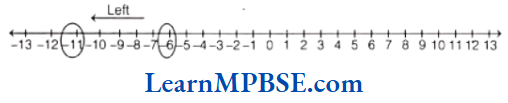
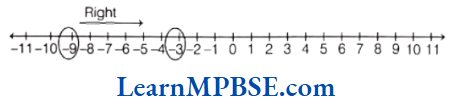
(4) Here, -3>9. So, – 3 is on the right of -9.

Hence, if we are at -9 on the number line, then move to the right from-9 to reach at – 3.

Example 12. Write the following numbers (integers) in increasing and decreasing order with using sign < and >’.

(1) 0,5, 10, 6, -3, 9

(2) 8, 6, 136, 32, -80, 120, 1

(3) 9, 8, 4, -3, -2, 1, 10

(4) 99, 98, 97, 97, 4, 1, 90

Solution. (1) Given numbers are 0, -5, 10,6,-3,9.

Increasing order is -5 < -3 < 0 < 6 < 9 < 10.

Decreasing order is 10 > 9 > 6 > 0 > -3 > -5.

(2) Given numbers are 8, 6,-136, 32, -80, 120, 1.

Increasing order is -136 < -80 < 1 < 6 < 8 < 32 < 120

Decreasing order is 120 > 32 > 8 > 6 > 1 > -80 > -136.

(3) Given numbers are 9, 8, 4, 3, 2, 1, 10.

Increasing order is -3 < -2 < 1 < 4 < 8 < 9 < 10.

Decreasing order is 10 > 9 > 8 > 4 > 1 > -2 > -3

(4) Given numbers are – 99, 98, -97, 97, 4, 1, 90.

Increasing order is -99 < -97 < 1 < 4 < 90 < 97 < 98.

Decreasing order is 98 > 97 > 90 > 4 > 1 > -97 > -99.

Chapter 6 Integers Addition of Integers

To add two positive integers, we simply add them and to add two negative integers, we firstly add them and then put negative sign before the sum.
e.g. (+3) + (+2) = +5

and (-2) + (-3) = -(2+3) = -5

When we have one positive and one negative integer, then we must subtract but answer will take the sign of the integer which has greater value to it.

e.g. (-3) + (+2) = -3 + 2 = -1

Note it The sum of two positive integers is always a positive integer and the sum of two negative integers is always a negative integer.

MP Board Class 6 Maths Solutions

Example 1. Write the answer of the following

(1) (+11) + (+6)

(2) (+17) + (+37)

(3) (-23) + (-7)

(4) (-9) + (-16)

Solution. (1) (+11) + (+6) = +(11 + 6) = 17

(2) (+17) + (+37) = +(17 + 37) = 54

(3) (-23) + (-7) = -(23 + 7) = -30

(4) (-9) + (-16) = -(9 + 16) = -25

Example 2. Find the answer of the following.

(1) (-8) + (+9)

(2) (-11) + (+16)

(3) (+11) + (-17)

(4) (+23) + (-6)

Solution. (1) (-8) + (+9) = (-8) + (+8) + (+1) [∵ 8 + 1 = 9]

= 0 + (+1) [∵ (-8) + (+8) = 0]

= +1

(2) (-11) + (+16) = (-11) + (+11) + (+5) [∵ 11 + 5 = 16]

= 0 + (+5) [∵ (-11) + (+11) = 0]

= +5

(3) (+11) + (-17) = (+11) + (-11-6) [-17 = -11-6]

= (+11) + (-11) + (-6)

= 0 + (-6) [∵ (+11) + (-11) = 0]

= -6

(4) (+23) + (-6) = (+17) + (+6) + (-6) [∵ 23 = 17 + 6]

= (+17) + 0

= +17

Example 3. Find the sum of

(1) 257 and -107

(2) -18 and 18

(3) -214, 65 and 104

(4) -40, -180 and 250

Solution. (1) We have, 257 + (-107)

= (+150) + (+107) + (-107) [∵ 257 = 150 + 107]

= (+150) + 0 = 150 [∵ (+107) + (-107) = 0]

(2) We have, -18 + (+18) = 0

(3) We have, -214 + 65 + 104

= -214 + 169

= (-169) + (-45) + 169

[∵ 214 = 169 + 45 = -214 = (-169) + (-45)]

= (-169) + 169 + (-45)

= 0 + (-45) = -45 [∵ (-169) + 169 = 0]

(4) We have, (-40) + (-180) + 250

= -(40+180) + 250 = (-220) + 250 [∵ 250 = 220 + 30]

= (-220) + (+220) + (+0) [∵ (-220) + (220) = 0]

= 0 + 30 = 30

MP Board Class 6 Maths Solutions

Example 4. Find the sum of

(1) (-8) + (-11) + (6) + (17)

(2) (36) + (-4) + (-70) + (-8)

(3) (-26) + (14) + (-1) + (16)

(4) (-14) + (-16) + (7) + (18)

Solution. (1) We have, (-8) + (-11) + (6) + (17)

= -(8+11) + 6 + 17 [∵ 23 = 19 + 4]

= (-19) + 23

= (-19) + (+19) + (+4) [∵ (-19) + (19) = 0]

= 0 + (+4) = 4

(2) We have, (36) + (-4) + (-70) + (-8)

= (36) – (4+70+8) = (36) – (82)

[∵ 82 = 36 + 46 ⇒ -82 = (-36) + (-46)]

= (36) + (-36) + (-46) [∵ (36) + (-36) = 0]

= 0 + (-46) = -46

(3) We have, (-26) + (14) + (-1) + (16)

= -(26+1) + (14) + (16) = (-27) + (30)

= (-27) + (+27) + (3) [∵ 30 = 27 + 3]

= 0 + 3 = 3 [∵ (-27) + (+27) = 0]

(4) We have, (-14) + (-16) + (7) + (18)

= -(14+16) + (7) + (18)

= (-30) + 25

= (-25) + (-5) + 25 [∵ 30 = 25 + 5 ⇒ -30 = (-25) + (-5)]

= (-25) + (+25) + (-5)

= 0 + (-5) [∵ (-25) + (+25) = 0]

= -5

Addition of Integers with the help of Number line

Firstly, draw the number line and represent first integer on it. Then, to add a positive integer number in first integer, we move right to the first integer and to add a negative integer, we move left to the first integer.

e.g. To add 6 and 2, we start from 6 and go to 2 steps to the right of 6 and reach at 8.

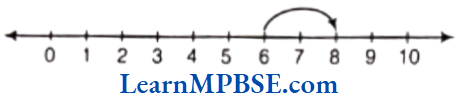
So, 6 + 2 = 8

Mp Board Class 6 Maths Solutions

Example 5. Find the solution of the following using number line.

(1) (-2) + 6

(2) (-6) + 2

(3) (-2) + (-9)

(4) (-3) + 7 + (-5)

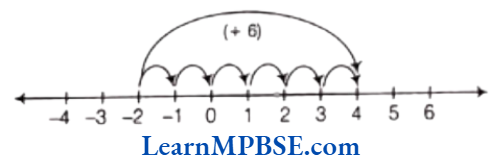
Solution. (1) First, mark at -2 on the number line. Now, move 6 steps to the right of it. We reach at the point +4.

∴ -2 + 6 = +4

(2) First, mark at -6 on the number line. Now, move 2 steps to the right of it. We reach at point-4.

Hence, -6 + 2 = -4

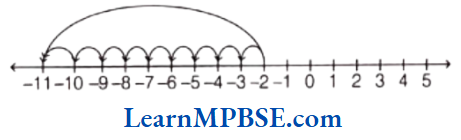
(3) First, mark at -2 on the number line. Now, move 9 steps to the left of it. We reach at point-11.

∴ (-2) + (-9) = -11

(4) First, mark at-3 on the number line. Now, first move 7 steps to the right of it and then move 5 steps to the left of +4. We reach at the point -1.

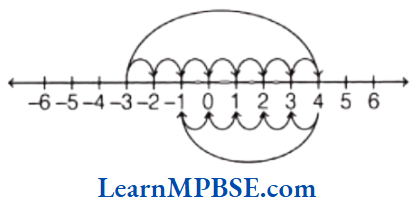
∴ -3 + (+7) + (-5) = -1

Example 6. Using the number line, write the integer which is

(1) 2 more than -1

(2) 5 less than 2.

Solution. (1) First, mark at -1 on the number line and move 2 steps to the right, we reach at point 1.

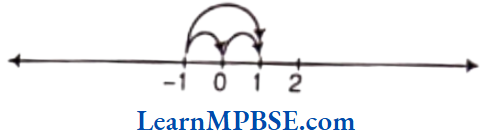
(2) First, mark at 2, on the number line and move 5 steps to the left, we reach at point -3.

Note it To find a number more than the given number, we move to the right of that given number and to find a number less than the given number, we move to the left of that number.

Example 7. A boy walked 6 km towards East, then he comes 9 km towards West. Find his position from the beginning point.

Solution. Let O be the beginning point of boy. East direction can be taken as positive and West as negative.

Then, walking 6 km towards East can be taken as + 6 km.

Walking 9 km towards West can be taken as – 9 km.

The final position = +6-9=-3km

Here, the negative sign shows that he is in West direction with respect to his beginning point.

∴ The boy’s final position is 3 km to the West with respect to his beginning point.

Chapter 6 Integers Subtraction of Integers

To subtract an integer from another integer, we add the additive inverse of the integer that is being subtracted from the other integer.

e.g. (-10) – (-4) = (-10) + Additive inverse of -4

= -10 + 4 = -6

i.e. subtraction of an integer is the same as the addition of its additive inverse.

Additive Inverse

Numbers such as 4 and -4, 2 and -2 when added to each other give the sum zero. They are called additive inverse of each other.

If two numbers when added to each other give the sum zero, then they are called additive inverse of each other. e.g. 3+(-3)=0. So, 3 is additive inverse of -3 and -3 is additive inverse of 3.

Class 6 Maths Chapter 6 Solutions Mp Board

Example 1. Find the value of the following:

(1)-20 – (-5)

(2) 39 – 16

Solution. (1) -20 – (-5) = -20 + Additive inverse of -5

We have one negative and one positive value. So, we will subtract and take sign of greater value.

= -20 + 5 = -15

(2) 39 – 16 = 39 + Additive inverse of 16

We have one negative and one positive value. So, we will subtract and take sign of greater value.

= 39 + (-16) = 23

Example 2. Find

(1) (-9) + (-7) – (-80)

(2) (-14) + 31 – 9 – 1

Solution. (1) We have, (-9) + (-7) – (-80)

= -(9+7) + Additive inverse of-80 = -16 + 80 = 64

(2) We have, (-14) + 31 – 9 – 1 = (-14) + 31 – 10

= (-14) + 31 + Additive inverse of 10

= (-14) + 31 + (-10)

= -14 – 10 + 31 = 24 + 31 = 7

Example 3. Subtract the following

(1)-8 from 13

(2) – 12 from – 7

Solution. (1) 13 – (-8) = 13+ Additive inverse of – 8

= 13 + 8 = 21

(2) -7 – (-12) = -7+ Additive inverse of -12

= -7 + 12 = 5

Example 4. Subtract -15 from the sum of 15 and 25.

Solution. The sum of 15 and 25 = 15 + 25 = 40

Now, subtract -15 from 40

40 – (-15) = 40 + Additive inverse of -15

= 40 + 15 = 55

Example 5. The sum of two integers is -33. If one of them is 8. Find the other.

Solution. Other integer = Sum of two integers – The given integer

= -33 – (-8) = 33+ Additive inverse of -8

= -33 + 8 = 25

Example 6. Fill in the blanks with >, < or = Sign.

(1) (-5) + (-7)…… (-5) – (-7)

(2) (-31) – (-15)……(-41) + (-16)

(3) 30 – (-10)…….45 + (-2)

(4) (-44) – (-21) ……..(-10) – (-35)

Solution. (1) We have. (-5) + (-7)……..(-5) – (-7)

LHS = (-5) + (-7) = -12

RHS = (-5) – (-7) = (-5) + Additive inverse of -7

= -5 + 7 = 2

Since, -12 is a negative integer and 2 is a positive integer.

∴ 12 < 2

(2) We have, (-31) – (-15) ………. (-41) + (-16)

LHS = -31 – (-15) = -31 + Additive inverse -15

= 31 + 15 = -16

RHS = (-41) + (-16) = -57

Here, both are negative integers but-57 is the left of -16

∴ -16 > -57

(3) We have, 30 – (-10) …….. 45 + (-2)

LHS = 30 – (-10) = 30 + Additive inverse of -10

= 30 + 10 = 40

RHS = 45 + (-2) = 43

Here, both are positive integers but 43 is right to the 40.

∴ 40 < 43

(4) We have, (-44) – (-21) ……. (-10) – (-35)

LHS = (44) – (-21) = -44 + Additive inverse of – 21

= -44 + 21 = -23

RHS = (-10) – (-35) = -10 + Additive inverse of -35

= -10 + 35 = 25

Since, 23 is a negative integers and 25 is a positive integer.

∴ -23 < 25

Example 7. Fill in the blanks.

(1) (-6)+ …. = 0

(2) 16 + …. = 0

(3) 14 + (-14) = …..

(4) -4 + … = -14

Solution. (1) We have, (-6) + … = 0

⇒ (-6) + 6 = 0 [∴ additive inverse of-6 is 6]

(2) We have, 16+…=0

⇒ 16 + (-16) = 0 [∴ additive inverse of-16 is 16]

(3) We have, 14 + (-14) = ….

⇒ 14 + (-14) = 0 [∴ 14 and 14 are additive inverse of each other]

(4) We have, (-4) + … = -14

Here, the sum of two integers is not zero, so here we cannot write additive inverse of -4.

⇒ -4+ …. = -14

⇒ -4 +… (4+10)

⇒ -4 + …. (-4) + (-10)

So, on comparing both sides, we get -10 to fill the blank space.

∴ (-4) + (-10) = -14

Subtraction of Integers With the Help of Number Line

Firstly, draw the number line and represent first integer on it. Then, to subtract a positive integer from first integer, we move left to the first integer and to subtract a negative integer, we move right to the first integer.

e.g. To subtract 3 from 5, we move 3 steps to the left of 5 and reach at 2.

So, 5 – 3 = 2

and to subtract-4 from 3, we move 4 steps to the right of 3 and reach at 7.

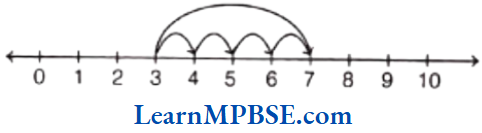
So, 3 – (-4) = 7

Class 6 Maths Chapter 6 Solutions Mp Board

Example 8. Find the value of the following using the number line

(1) 6 – 2

(2) 2 – 3

(3) 6 – (-3)

(4) -4 – (-2)

Solution. (1) We have, 6 – 2 = 4

(2) We have, 2 – 3 = -1

(3) We have, 6 – (-3) = 6 + Additive inverse of -3

= 6 + 3 = 9

(4) We have, -4 – (-2) = -4 + Additive inverse of -2.

= -4 + 2 = -2

Question 1. Suppose David and Mohan have started walking from zero position in opposite directions. Let the steps to the right of zero be represented by ‘+’ sign and to the left of zero be represented by sign. If Mohan moves 5 steps to the right of zero, it can be represented as +5 and if David moves 5 steps to the left of zero, it can be represented as -5. Now, represent the following positions with + sign or – sign.

(1) 8 steps to the left of zero.

(2) 7 steps to the right of zero.

(3) 11 steps to the right of zero.

(4) 6 steps to the left of zero.

Solution. We know that on the number line, all numbers to the right of 0 are positive integers and all numbers to the left of 0 are negative integers.

Thus, the representation of numbers on the number line is as follows

(1) 8 steps to the left of zero is represented by -8.

(2) 7 steps to the right of zero is represented by +7.

(3) 11 steps to the right of zero is represented by +11.

(4) 6 steps to the left of zero is represented by -6.

Question 2. Write the succeeding number of the following.

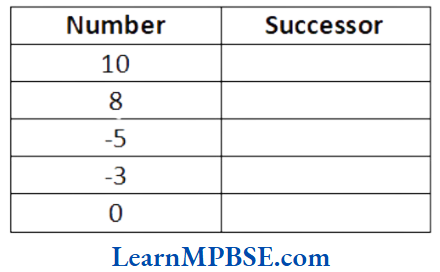
Solution. We know that one more than given number gives a successor. So, the succeeding numbers of given numbers are given as below:

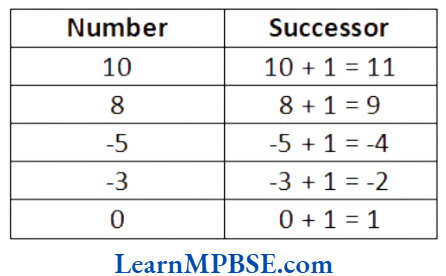
Class 6 Maths Chapter 6 Solutions Mp Board

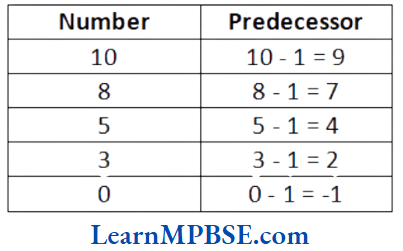
Question 3. Write the preceding number of the following.

Solution. We know that one less than a given number gives a predecessor. So, the preceding numbers of the given numbers are given as below:

Question 4. Write the following numbers with appropriate signs:

(1) 100 m below sea level.

(2) 25°C above 0°C temperature.

(3) 15°C below 0°C temperature.

(4) Any five numbers less than 0.

Solution.

(1) We can write 100 m below sea level as -100 m, because below sea level represents – sign and above sea level represents ‘+’ sign.

(2) We can write 25°C above 0°C temperature as +25°C, because temperature above 0°C is denoted by ‘+’ sign and temperature below 0°C is denoted by ‘-‘ sign.

(3) We can write 15°C below 0°C temperature as -15°C, because temperature above 0°C is denoted by ‘+’ sign and temperature below 0°C is denoted by ”sign.

(4) Every negative integer is less than zero and every positive integer is greater than zero.

∴ Numbers less than 0 are -1, -2, -3, -4, -5 …

Question 5. Mark -3, 7, -4, -8, -1 and +3 on the number line.

Solution. Draw a line and mark some points at equal distance on it as shown in the figure given below. Mark a point on it as zero. Points to the right of zero are positive integers and marked by +1, +2, +3 etc. or simply by 1, 2, 3 etc and points to the left of zero are negative integers and marked by-1,-2,-3 etc.

Now, -3 is a negative integer (since, -3 has negative sign). So, move 3 points to the left of zero and represent it by point C.

7 is a positive integer (since, + 7 has positive sign). So, move 7 points to the right of zero and represent it by point F.

To mark – 4 on this line, move 4 points to the left of zero and represent it by point B.

To mark – 8 on this line, move 8 points to the left of zero and represent it by point A.

To mark – 1 on this line, move 1 point to the left of zero and represent it by point D.

To mark 3 on this line, move 3 points to the right of zero and represent it by point E.

Thus, we get the following representation of these integers on the number line

Question 6. Compare the following pairs of numbers using > or <.

(1) 0 … -8

(2) -1 … -15

(3) 5 … -5

(4) 11 … 15

(5) 0 … 6

(6) -20 … 2

From the above exercise, Rohini arrived at the following conclusions:

(a) Every positive integer is larger than every negative integer.

(b) Zero is less than every positive integer.

(c) Zero is larger than every negative integer.

(d) Zero is neither a negative integer nor a positive integer.

(e) Farther a number from zero on the right, larger is its value.

(f) Farther a number from zero on the left, smaller is its value.

Do you agree with her? Give examples.

Solution. (1) We have,

0 … -8

Since, 0 is to the right of -8.

∴ 0 > -8

(2) We have,

-1 … -15

Since, 1 is to the right of -15.

∴ -1 > -15

(3) We have,

5 … -5

Since, 5 is to the right of -5.

∴ 5 > -5

(4) We have,

11 … 15

Since, 11 is to the left of 15.

∴ 11 < 15

(5) We have,

0 … 6

Since, 0 is to the left of 6.

∴ 0 < 6

(6) We have,

-20 … 2

Since, 20 is to the left of 2.

∴ -20 < 2
Yes, I agree with Rohini. Some examples are as follow

(a) Every positive integer is larger than every negative integer. e.g. 5 > -2.

(b) Zero is less than every positive integer. e.g. 0 < 3.

(c) Zero is larger than every negative integer.

e.g. 0 > -4.

(d) Zero is neither a negative integer nor a positive integer, because 0 has neither + sign nor ‘-‘ sign.

(e) Farther a number from zero, on the right side, larger is its value, because on number line, every integer on the right from zero is greater than zero. e.g. 5 > 0.

(f) Farther a number from zero, on the left side, smaller is its value because on number line, every integer on the left from zero is smaller than zero. e.g. -8 < 0.

Chapter 6 Integers Exercise 6.1

Question 1. Write opposites of the following:

(1) Increase in weight

(2) 30 km North

(3) 80 m East

(4) Loss of 700

(5) 100 m above sea level

Solution.

(1) Opposite of increase in weight is decrease in weight.

(2) Opposite of 30 km North is 30 km South.

(3) Opposite of 80 m East is 80 m West.

(4) Opposite of loss of 700 is profit of 700.

(5) Opposite of 100 m above sea level is 100 m below sea level.

Question 2. Represent the following numbers as Integers with appropriate signs.

(1) An aeroplane is flying at a height of two thousand metre above the ground.

(2) A submarine is moving at a depth, eight hundred metre below the sea level.

(3) A deposit of rupees two hundred.

(4) Withdrawal of rupees seven hundred.

Solution.

(1) An aeroplane is flying at a height of two thousand metre above the ground can be written as +2000 m because height above the ground is taken as positive.

(2) A submarine is moving at a depth of eight hundred metre below the sea level can be written as -800 m, because depth below the sea level is taken as negative.

(3) A deposit of rupees two hundred can be written as + 200, because deposit is represented with + sign.

(4) Withdrawal of rupees seven hundred can be written as-700, because withdrawal is represented with- sign.

Mp Board Maths Chapter 6 Solutions

Question 3. Represent the following numbers on a number line :

(1) +5

(2) -10

Solution. Draw a line and mark some points at equal distance on it. Mark a point as zero on it. Points to the right of zero are positive integers and are marked by +1, +2, +3 or simply by 1, 2, 3 etc. Points to the left of zero are negative integers and are marked by-1,-2,-3 etc.

(1) Representation of +5 To mark +5 on the number line, we move 5 points to the right of zero as shown in the figure.

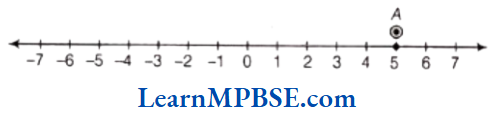
In the above figure, Point A represents +5.

(2) Representation of -10 To mark-10 on the number line, we move 10 points to the left of zero as shown in the figure.

In the above figure, Point B represents -10.

Question 4. Adjacent figure is a vertical number line, representing integers. Observe it and locate the following points.

(1) If Point D is +8, then which point is -8?

(2) Is Point G, a negative integer or a positive integer?

(3) Write integers for points B and E

(4) Which point marked on this number line has the least value?

(5) Arrange all the points in decreasing order of value?

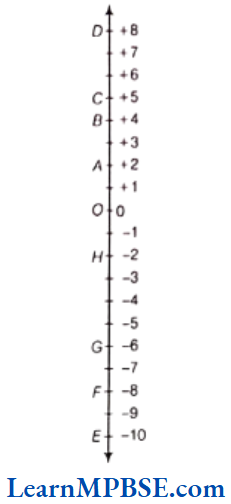
Solution. (1) Now, from the figure, it is clear that +8 is on Point D, then for getting -8, we should move below to 0.

After moving 8 steps below 0, we reach at point F. So, Point Frepresents – 8.

(2) We know that points lie above zero are positive F-8 integers and lie below zero are negative integers.

Here, we see that point G lies below zero.

So, G is a negative integer.

(3) On the given number line, point B lies above zero and point E lies below zero.

So, it is clear that point B is a positive integer and point E is a negative integer. Now, counting from 0, the distance of B is +4 units, because it is on right of zero and counting from 0, the distance of Eis-10 units because it is on left of zero.

∴ Integer B = +4 and integer E = -10

(4) Here, we see that the distance of point E is far from 0 and below from 0 and we know that on vertical number line below from 0 the value of integers are negative. Hence, the Point E has least value.

(5) We know that on a number line the number decreases as we move to left. Here, vertical number line is given to us, so the number decreases as we move to down. So, decreasing order of values of all points is given here.

Question 5. Following is the list of temperatures of five places in India on a particular day of the year.

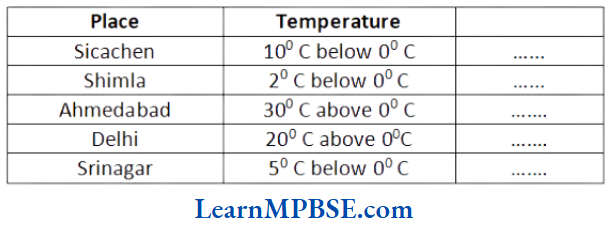
(1) Write the temperatures of these places in the form of integers in the blank column.

(2) Following is the number line representing the temperature in degree celsius.

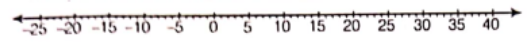
Plot the name of the city against its temperature.

(3) Which is the coolest place?

(4) Write the names of the places, where temperature are above 10°C.

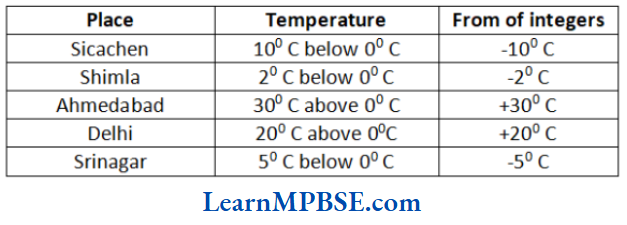
Solution.

(1)

(2) The name of city against its temperature on the number line is given below

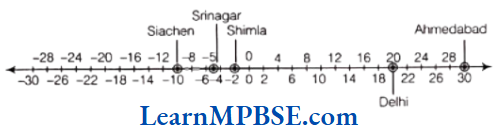
(3) After checking the temperature of all places, we can say that the Siachin (-10°) is the coolest place.

(4) Delhi (+20°C) and Ahmedabad (+30°C) are the places, where temperature is above 10°C.

Mp Board Maths Chapter 6 Solutions

Question 6. In each of the following pairs which number is to the right of the other on the number line?

(1) 2, 9

(2)-3, -8

Solution

(1)

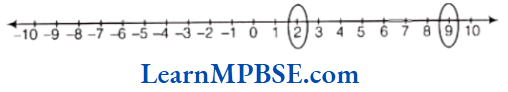
Here, 2 and 9 both are on the right of zero but 9 is farther from zero in comparison of 2. So, number 9 is right of number 2.

(2)

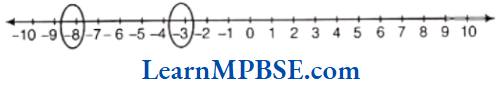
Here, -3 and -8 both are on the left of zero but-3 is near to the zero in comparison of -8. So, -3 is to the right of -8.

Question 7. Write all the integers between the given pairs (write them in the increasing order).

(1) 0 and -7

(2)-4 and 4

Solution. (1) Integers 0 and -7 are on the number line are shown as below:

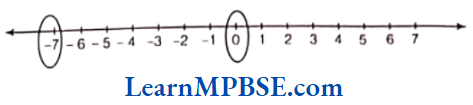
From the above figure, it is clear that integers between 0 and -7 are-1, -2, -3, -4, -5 and -6.

Now, increasing order of these integers is -6 < -5 < -4 < -3 < -2 < -1 because we are moving to the right from -7 to 0.

(2) Integers-4 and 4 on number line are shown as below

From the above figure, it is clear that integers between -4 and 4 are -3, -2, -1, 0, 1, 2 and 3.

Now, increasing order of these integers is -3 < -2 < -1 < 0 < 1 < 2 < 3 because we are moving to the right from -4 to 4.

Question 8. Write four negative integers greater than -20.

Solution. When we move on the number line to the right, then the value of integer increases.

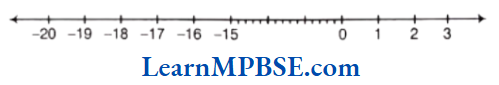
So, from the above figure, we get four negative integers greater than -20 are -19,-18, -17 and -16.

Mp Board Maths Chapter 6 Solutions

Question 9. For the following statements, write True (T) or False (F). If the statement is false, correct the statement.

(1) -8 is to the right of -10 on a number line.

(2) -100 is to the right of -50 on a number line.

(3) Smallest negative integer is -1.

(4) -26 is greater than -25.

Solution.

(1) True, because on the number line going to the right, value of integer is increases. Here, -8 is greater to -10, so-8 is to the right of-10 on number line.

(2) False, because on the number line going to the left, value of integer is decreases. Here, -100 is less than -50. So, -100 is to the left of -50 on number line.

(3) False, because on the number line -1 is situated on the right of all negative integers. So, it is the greatest negative integer.

(4) False, because on the number line -25 is on the right of-26. So.-25 is greater than -26.

Question 10. Draw a number line and answer the following

(1) Which number will we reach, if we move 4 numbers to the right of -2?

(2) Which number will we reach, if we move 5 numbers to the left of 1?

(3) If we are at -8 on the number line, in which direction should we move to reach -13?

(4) If we are at -6 on the number line, in which direction should we move to reach -1?

Solution. (1)

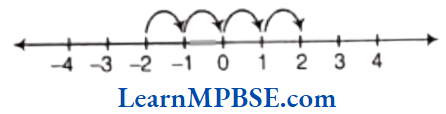
On the number line, starting from -2 and moving 4 points towards right (each step being equal to 1 unit), we will reach at 2.

(2)

On the number line, starting from 1 and moving 5 points towards left (each step being equal to 1 unit), we will reach at-4.

(3) Here, -8 – 13. So, -13 is on the left of -8. Hence, if we are at -8 on the number line, then move to the left from-8 to reach at -13.

(4)

Here, -1 – 6. So, -1 is on the right of -6. Hence, if we are at -6 on the number line, then move to the right from -6 to reach at -1.

Question 11. Find the answers of the following additions:

(1) (-11) + (-12)

(2) (+10) + (+4)

(3) (-32) + (-25)

(4) (+23) + (+40)

Solution. (1) (-11) + (-12) = (11+12) = -23

(2) (+10) + (+4) = +(10 +4) = +14

(3) (-32) + (-25) = (32+25) = -57

(4) (+23) + (+40) + (23+40) = +63

Question 12. Find the solution of the following:

(1) (-7) + (+8)

(2) (-9) + (+13)

(3) (+7) + (-10)

(4) (+12) + (-7)

Solution.

(1) (-7) + (+8) = (-7) + (+7) + (+1) [∴ 7 + 1 = 8]

= 0 + (+1) = +1 [∴ (-7) + (+7) = 0]

(2) (-9) + (+13) = (-9) + (+9) + (+4) [∴ 9 + 4 = 13]

= 0 + (+4) = +4 [∴ (-9) + (+9) = 0]

(3) (+7) + (-10) = (+7) + (-7) + (-3) [∴ -10 = – 7 – 3]

= 0 + (-3) = -3 [∴ (+7) + (-7) = 0]

(4) (+12) + (-7) = (+5) + (+7) + (-7) [∴ 12 = 5 + 7]

= (+5) + 0 = +5 [∴ (+7) + (-7) = 0]

Mp Board Maths Chapter 6 Solutions

Question 13. Find the solution of the following additions using a number line:

(1) (-2) + 6

(2) (-6) + 2

Make two such questions and solve them using the number line.

Solution. (1)

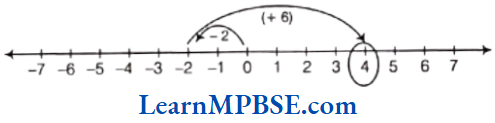
Firstly, draw a number line. Here, -2 is a negative integer and 6 is a positive integer. Then, we first move 2 steps to the left of 0 reaching at -2, then we move 6 steps to the right of-2 and reach at 4.

Thus, (-2) + 6 + 4.

(2)

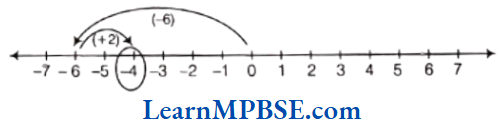
Firstly, draw a number line. Here, -6 is a negative integer and 2 is a positive integer. Then, we first move 6 steps to the left of 0 reaching at -6, then we move 2 steps to the right of-6 and reach at-4.

Thus, (-6) + 2 = -4.

Two such questions are as follow

(a) (-3) + 5

(b) 5 + (-1)

(a) We have, (-3) + 5

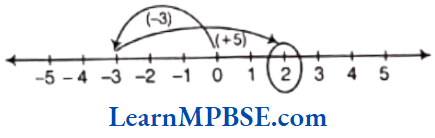
Here, we first move 3 steps to the left of 0 reaching at-3, then we move 5 steps to the right of-3 and reach at 2. Thus, (-3)+5=+2.

(b) We have, 5 + (-1)

Here, we first move 5 steps to the right of zero (0) reaching at 5, then we move 1 step to the left of 5 and reach at 4.

Thus, 5 + (-1) = 4.

Chapter 6 Integers Exercise 6.2

Question 1. Using the number line write the Integer which is

(1) 3 more than 5

(2) 5 more than -5

(3) 6 less than 2

(4) 3 less than -2

Solution. (1) To get the integer 3 more than 5, we start from 5 and move 3 steps to the right of 5 and reach at 8, as shown in the figure given below

Hence, 3 more than 5 is 8.

(2) To get the integer 5 more than -5, we start from -5 and move 5 steps to the right of -5 and reach at 0, as shown in the figure given below

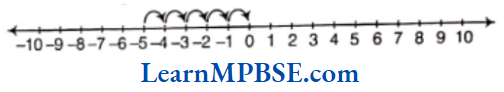
Hence, 5 more than -5 is 0.

(3) To get the integer 6 less than 2, we start from 2 and move 6 steps to the left of 2 and reach at-4, as shown in the figure given below

Hence, 6 less than 2 is -4.

(4) To get the integer 3 less than -2, we start from -2 and moves 3 steps to the left of-2 and reach at-5, as shown in the figure given below

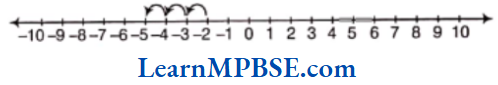
Hence, 3 less than -2 is -5.

Question 2. Use number line and add the following integers :

(1)9 + (-6)

(2) 5 + (-11)

Solution. (1) We have, 9 + (-6)

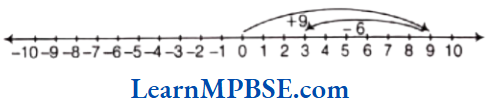
Firstly, draw a number line, then we move 9 steps to the right of 0 and reach at 9. Now, we move 6 steps to the left of 9 [-6 is a negative integer] and reach at 3, as shown in the above figure. Hence, 9 + (-6) = 3

(2) We have, 5 + (-11)

Firstly, draw the number line, then we move 5 steps to the right of 0 and reach at 5. Now, we move 11 steps to the left of 5 [-11 is a negative integer] and reach at -6, as shown in the above figure. Hence, 5 + (-11) = -6.

Class 6 Mp Board Maths Question Answers

Question 3. Find the sum:

(1) (-7) + (-9) + 4 + 16

(2) (37) + (-2) + (-65) + (-8)

Solution.

(1) We have, (-7) + (-9) + 4 + 16 = -(7 + 9) + 4 + 16

= -16 + 20 = -16 + (+16) + (+4) [∴ 20 = 16 + 4]

= 0 + (+4) = (+4) [∴ (-16) + (+16) = 0]

(2) We have, (37) + (-2) + (-65) + (-8)

= 37 – (2 + 65 + 8) = 37 – 75 = 37 – 37 – 38 [∴ 75 = 37 + 38 ⇒ -75 = -37 – 38]

= 0 – 38 = -38 [∴ -37 + 37 = 0]

Chapter 6 Integers Exercise 6.3

Question 1. Find

(1) 35 – (20)

(2) 72 – (90)

(3) (-15) – (-18)

(4) (-20) – (13)

Solution.

(1) We have, 35 – (20) = 35 + Additive inverse of 20

= 35 + (-20)

= 15 + 20 + (-20) [∴35 = 20 + 15]

= 15 + 0 = 15 [∴ 20 + (-20) = 0]

(2) We have, 72 – 90 = 72 + Additive inverse of 90

= 72 + (-90) = 72 + (-72) + (-18)

[∴ 90 = 72 + 18 ⇒ -90 = -72 + (-18)]

= 0 + (-18) = -18 [∴ 72 + (-72) = 0]

(3) We have, (-15) – (-18) = -15 + Additive inverse of -18

= -15 + 18

= (-15) + (15) + (3) [18 = 15 + 3]

= 0 + 3 = 3 [∴ (-15) + (15) = 0]

(4) We have, (-20) – (13) = (-20) + Additive inverse of 13

= (-20) + (-13) = (20+13)

= -33

Class 6 Mp Board Maths Question Answers

Question 2. Fill in the blanks with >, < or = Sign.

(1) (-3) + (-6) ______ (-3) – (-6)

(2) (-21) – (-10) ______ (-31) + (-11)

(3) 45 – (-11) ______ 57 + (-4)

Solution. (1) We have, (-3) + (-6) ______ (-3) – (-6)

LHS = (-3) + (-6) = -9

RHS = (-3) – (-6) = (-3) + Additive inverse of (-6)

= -3 + 6 = 3

Since, -9 is a negative integer and 3 is a positive integer.

∴ -9 < 3

(2) We have, (-21) – (-10) ______ (-31) + (-11)

LHS = (-21) – (-10) = -21 + Additive inverse of -10

= -21 + 10 = -11

RHS = (-31) + (-11) = -42

Here, both are negative integers but -42 is to the left of -11.

∴ -11 > -42

(3) We have, 45 – (-11) ______ 57 + (-4)

LHS = 45 – (-11) = 45 + 11 [∴ additive inverse of -11 is 11]

= 56

Here, both are positive integers but 56 is to the right of 53.

∴ 56 > 53

Question 3. Fill in the blanks.

(1) (-8) + ______ = 0

(2) 13 + ______ = 0

(3) 12 + (-12) = ______

(4) (-4) + ______ = -12

(5) ______ – 15 = -10

Solution. (1) We have, (-8) + ______ = 0

(-8) + 8 = 0 [∴ additive inverse of -8 is 8]

(2) We have, 13 + ______ = 0

13 + (-13) = 0 [∴ additive inverse of -13 is 13]

(3) We have, 12 + (-12) = 12 + (-12) = 0

[∴ 12 and -12 are additive inverse of each other]

(4) We have, (-4) + ______ = -12

Here, the sum of two integers is not zero, so here we cannot write additive inverse of -4.

-4 + ______ = -12

⇒ -4 + ______ = -(4+8)

⇒ -4 + ______ = (-4) + (-8)

So, on comparing both sides, we get -8 to fill the blank space.

Thus, (-4) + (-8) = -12

(5) We have, ______ – 15 = -10

⇒ ______ – (10+5) = -10

⇒ ______ -10 – 5 = -10

To get RHS = -10, we need to add additive inverse of -5 i.e. 5 in RHS.

so, + 5 – 10 – 5 = -10

Hence, +5 – 15 = -10

Class 6 Mp Board Maths Question Answers

Question 4. Find

(1) (-7) – 8 (-25)

(2) (-13) + 32 – 8 – 1

(3) (-7) + (-8) + (-90)

(4) 50 – (-40) – (-2)

Solution. (-7) – 8 – (-25) = (-7) + (-8) + 25

[∴ additive inverse of -25 is 25]

= -15 + 25

= -15 + 15 + 10 [∴ 25 = 15 + 10]

= 0 + 10 = 10 [∴ -15 + 15 = 0]

(2) (-13) + 32 – 8 – 1 = (-13) + 32 – 9

= -13 + 32 + Additive inverse of 9

= (-13) + 32 + (-9) = -13 – 9 + 32

= -22 + 32 [∴ 32 = 22 + 10]

= -22 + 22 + 10 = 0 + 10 = 10 [∴ -22 + 22 = 0]

(3) (-7) + (-8) + (-90) = -15 + (-90) = -105

(4) 50 – (-40) – (-2)

= 50 + Additive inverse of (-40) + Additive of (-2)

= 50 + 40 + 2 = 92

Chapter 6 Integers Multiple Choice Questions

Question 1. The predecessor of the integer -1 is

1. 0
2. 2
3. -2
4. 1

Answer. 3. -2

Question 2. The successor of the predecessor of -20 is

1. -20
2. -10
3. -19
4. -21

Answer. 1. -20

Question 3. An integer with positive sign (+) is always greater than

1. 3
2. 2
3. 1
4. 0

Answer. 4. 0

Class 6 Mp Board Maths Question Answers

Question 4. The statement ‘When an integer is added to itself, the sum is greater than the integer’ is

1. always true
2. never true
3. true only when the integer is positive
4. true for non-negative integers

Answer. 4. true for non-negative integers

Question 5. Every integer less than 0 has the sign

1. ÷
2. x
3. +
4. None of these

Answer. 4. None of these

Question 6. The integer 5 units to the right of 0 on the number line is

1. +5
2. -5
3. +4
4. -4

Answer. 1. +5

Question 7. Number of integers lying between -2 and 2 is

1. 3
2. 4
3. 2
4. 1

Answer. 1. 3

Question 8. Number of whole numbers lying between -7 and 6 is

1. 2
2. 4
3. 5
4. 6

Answer. 4. 6

Question 9. The least integer lying between -10 and -16 is

1. -13
2. -12
3. -15
4. -11

Answer. 3. -15

Question 10. Amulya and Amar visited two places A and B, respectively in Kashmir and recorded the minimum temperatures on a particular day as -4°C at A and -1°C at B. Which of the following statement is true?

A is cooler than B.

B is cooler than A.

There is a difference of 2°C in the temperature.

The temperature at A is 4°C higher than that at B.

Answer.  1. A is cooler than B.

Question 11. When a negative integer is subtracted from another negative integer, the sign of the result

1. is always negative.
2. is always positive.
3. is never negative.
4. depends on the numerical value of the integers.

Answer. 4. depends on the numerical value of the integers.

Question 12. Which of the following shows the maximum rise in temperature?

1. 0°C to 10°C
2. -4°C to 8°C
3. -15°C to -8°C
4. -7°C to 0°C

Answer. 2. -4°C to 8°C

Question 13. The additive inverse of a negative integer

1. is always negative.
2. is always positive.
3. is the same integer.
4. zero.

Answer. 2. is always positive

Question 14. On the number line, the integer 47 is located

1. to the left of 0
2. to the right of 49
3. to the right of 41
4. to the left of -47

Answer. 3. to the right of 41

Question 15. In which of the following pair of integers, the first integer is not on the left of the other integer on the number line?

1. (-3, -4)
2. (-1, 10)
3. (-6, 0)
4. (-5, 3)

Answer. 1. (-3, -4)

Chapter 6 Integers Assertion-Reason

Question 1. Assertion (A) The preceding number of the number 1 is -1.

Reason (R) Preceding number is the number which comes before a number.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (d) (A) is false but (R) is true.

Question 2. Assertion (A) Sum of two positive number is always negative.

Reason (R) The addition is taking two or more numbers and adding them.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (d) (A) is false but (R) is true.

Chapter 6 Integers Fill in the Blanks

Question 1. On the number line, -15 is to the ….. of zero.

Answer. Left

Question 2. The number of integers lying between -5 and 5 is …..

Answer. 9

Question 3. ….. – 3040 = -7910

Answer. -4870

Question 4. The additive inverse of -1 is ……

Answer. 1

Question 5. The additive inverse of 0 is ……

Answer. 0

Mp Board Class 6 Book Solutions

Chapter 6 Integers True/False

Question 1. Every positive integer is greater than every negative integer.

Answer. True

Question 2. The sum of any two negative integers is always smaller than both the integers.

Answer. True

Question 3. The sum of any two negative integers is always greater than both the integers

Answer. False

MP Board Class 6 Chapter 5 Maths

Question 4. The sum of any two positive integers is greater than both the integers.

Answer. True

Question 5. The difference between an integer and its additive inverse is always even.

Answer. True

Chapter 6 Integers Match the Columns

Question 1. Match the Column A with Column B.

Solution. (1) → (b), (2) → (e), (3) → (d), (4) → (a), (5) → (b)

Chapter 6 Integers Case Based Questions

Question 1. The leavel of the surface of oceans or seas is called the sea level. Land and hills are raised and are at some height from the sea level.

City A is 10 m below sea level, city B is 28 m below sea level and city C is 14 m above sea level.

(1) Which of the three cities is at the highest elevation from the sea level?

(2) Aditi uses the following rules to represent the elevation of different locations.

The sea level is considered to be zero elevation.

Below sea level is shown using the ‘-‘ sign.

Above sea level is shown using the ‘+’ sign.

e.g. the elevation of City A is shown as -10. what would be the elevation of city B?

(3) The elevation of city D is 1 m above the elevation of city B. What is the elevation of city D?

(4) A submarine at the depth of 45 m rises to 20 m below sea level. What is the depth of the submarine after rising?

(5) A diver at the depth of 60 m spotted a seaweed 23 m below him. What is the depth of the seaweed from the sea level?

(6) 8 – 8 = 0

Which of the following is true for the numbers shown above?

(a) -8 is a multiplicative inverse of 8.

(b) -8 is a multiplicative identity of 8.

(c) -8 is the additive identity of 8.

(d) -8 is the additive inverse of 8.

Solution. (1) Let’s consider the sea level be 0.

City A is 10 m below sea level is -10.

City B is 28 m below sea level is – 28.

City C is 14 m above sea level is +14.

Hence, City C is at the highest elevation from the sea level.

(2)-28 is the elevation for City B.

(3) City B is 28 m below sea level is – 28.

Add 1 m to the elevation of city B i.e.-28

– 28 m +1 m = -27m

Hence, – 27 m is the elevation for City D.

(4) Given, a submarine at the depth of 45 m rises to 20 m below sea level.

Depth of a submarine at 45 m is + 45.

20 m below sea level is – 20.

Add the depth rises below sea level

+45 m + (-20 m) = +25 m

Hence, the depth of the submarine after rising is 25 m.

(5) Given, a diver at the depth of 60 m spotted a seaweed 23 m below him.

∴ 60 + 23 = 83

Hence, 83 m is the depth of the seaweed from the sea level.

(6) (d) Given, 8 – 8 = 0

⇒ 8 + (-8) = 0

Hence, -8 is the additive inverse of 8.

Mp Board Class 6 Book Solutions

Question 2. The figure shows the position of the satellite above earth.

PR is the line joining the satellite and the centre of earth. P is the position of the satellite, Q is a point on the surface of earth and R is the centre of earth.

The distance between P and Q is 1300 km and the distance between the centre of earth and the satellite is 7671 km.

(1) What is the distance between the points Q and R?

(a) 1300 km

(b) 6371 km

(c) 7671 km

(d) 8971 km

(2) Shobhit marks Q as zero and the direction from Q to P is positive. What is the distance of R with reference to P?

Solution. (1) (b) Distance between Q and R

= Distance between P and R – Distance between P and Q

⇒ QR = PR – PQ

⇒ QR = 7671 – 1300 = 6371 km

(2) Shobhit marks Q as zero and the direction from Q to P is positive.

Thus, distance from Q to P is +1300 km.

The distance from P to R is 7671 km.

Q is zero and below Q are negative values.

Hence,-7671 km is the distance of R with reference to P.

Question 3. The picture below shows the control panel of a lift in a mall.

MP Board Class 6 Chapter 5 Maths

O is the ground floor. The two-wheeler parking area -1 is at basement level 1 and the car parking area -2 is at basement level 2.

(1) Ahmed enters the lift at floor 3 and exits at the two-wheeler parking area. How many floors did the lift go down?

(2) Meera entered the lift at the car parking floor. She pressed ‘6’ on the control panel of the lift. How many floors up does she want to go?

Solution. (1) Ahmed enters the lift at floor 3 and exists at the two-wheeler parking area.

Ahmed travels in lift from

3 → 2,2 → 1,1 → 0,0 → 1

Hence, 4 floors lift go down.

(2) Meera entered the lift at the car parking floor. She pressed 6 on the control panel of the lift car parking floor is -2.

Meera starts from -2.

-2 → -1,-1 → -0, 0 → -1, 1 → 2, 2 → -3, 3 → -4, 4 → -5,5 → -6

Hence, 8 floors lift goes up.

Chapter 6 Integers Very Short Answer Type Questions

Question 1. Write the following numbers with appropriate sign

(1) 100 m below sea level.

(2) 15° C below 0°C temperature.

Solution. (1) 100 m below sea level means -100 m.

(2) 15°C below 0°C temperature means- 15°C.

Question 2. Write the integer which is 2 less than its additive inverse.

Solution. 1 because 1 – 2 = -1.

Question 3. Write additive inverse of -121.

Solution. Additive inverse of -121 is + 121.

Question 4. Find the value of 10+(-5).

Solution. Here, 10 + (-5) = 10 – 5 = 5

Question 5. Write two distinct integers whose sum is equal to one of the integers.

Solution. Any two integers with one of them as 0 i.e. 4 and 0.

Chapter 6 Integers Short Answer Type Questions

Question 1. Represent the following using integers with proper sign

(1) 35 km above sea level

(2) A loss of ₹ 400

Solution. Given, statements can be represented using integer

(1) +35 (2)-400

Question 2. How many integers are there between -8 and -2?

Solution. The integers -7,-6, -5,-4 and -3 lie between -8 and -2. So, there are 5 integers between -8 and -2.

Mp Board Class 6 Book Solutions

Question 3. Find the sum of the pairs of integers.

(1) -6, -5

(2) +4, -3

Solution. (1)-6, -5 both have negative signs.

So, -6 + (-5) = -(6+5) = -11

(2) +4 and -3 have opposite sign.

So, 4 + (-3) = 4 – 3 = 1

Question 4. Find the sum of -3 and -4 using the number line.

Solution. To add -3 and -4. Mark-3 on the number line. Move 4 steps to left of-3, we reach at -7.

∴ -3 + (-4) = -7

Question 5. Write two integers whose sum is less than both the integers.

Solution. For the required integers, we can take any two negative integers.

So, the required integers can be -5, and -7.

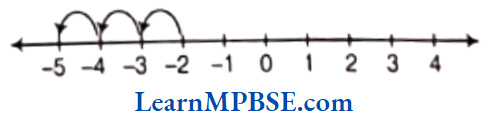
Question 6. Write four pairs of integers which are at the same distance from 2 on the number line?

Solution. We draw a number line.

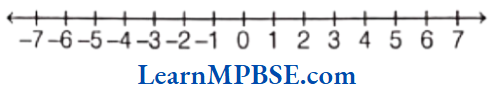
Now, four pairs are (0, 4), (-1,5), (- 3,7) and (1, 3).

Mp Board Class 6 Maths Solutions

Question 7. Write the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 in this order and insert ‘+’ or ‘-‘ between them to get the result.

(1) 7

(2) -5

Solution. (1) To get the sum =7

0 – 1 + 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9

= 2 + 3 + 5 + 7 + 9 – (1 + 4 + 6 + 8) = 26 – 19 = 7

(2) To get the sum = -5

0 – 1 – 2 + 3 + 4 – 5 + 6 + 7 – 8 – 9

= 3 + 4 + 6 + 7 – (1 + 2 + 5 + 8 + 9)

= 20 – 25 = -5

Question 8. The sum of two integers is 35. If one of the integer is -12, find the other integer.

Solution. Given, sum is 35. The other integer is obtained by subtracting-12 from 35. So, the required integer

= 35 – (-12) = 35 + 12 = 47.

Question 9. Subtract

(1) 5 from -6

(2) -3 from -6

Solution. (1) The additive inverse of 5 is -5.

So, -6 – 5 – 6 + (-5) = -(6+5) = -11

(2) The additive inverse of -3 is +3.

So, -6 – (-3) = -6 + 3 = -3

Mp Board Class 6 Maths Solutions

Question 10. Subtract using the number line.

(1) 3 form -2

(2) -5 from -3

Solution. (1) Move 3 steps from -2 on the left, we reach at -5.

So, -2 – 3 = -5

(2) Move 5 steps from -3 on the right, we reach at 2.

So, -3 – (-5) = -3 + 5 = 2.

Chapter 6 Integers Long Answer Type Questions

Question 1. Complete each of the following

(1) 30 + (-50) + (-20)

(2) 40 + (-10) + (-15)

(3) 45 – (-5) + 10

(4) 60 – 10 + 5 – (-5)

(5) 16 + (-13) + (-10)

(6) 0 + 5 – (-6) + (-7)

Solution. According to the rules of addition and subtraction of integers.

(1) 30 + (-50) + (-20) = 30 – (50+20) = 30 – 70 = -40

(2) 40 + (-10) + (-15) = 40 – (10+15) = 40 – 25 = 15

(3) 45 – (-5) + 10 = 45 + 5 + 10 = 60

(4) 60 – 10 + 5 – (-5) = 60 + 5 + 5 – 10 = 70 – 10 = 60

(5) 16 + (-13) + (-10) = 16 – (13+10) = 16 – 23 = -7

(6) 0 + 5 – (-6) + (-7) = 0 + 5 + 6 – 7 ⇒ 11 – 7 = 4

Mp Board Class 6 Maths Solutions

Question 2. If we denote the height of a place above sea level by a positive integer and depth below the sea level by a negative integer, write the following using integers with the appropriate signs:

(1) 200 m above sea level

(2) 100 m below sea level

(3) 10 m above sea level

(4) Sea level

Solution. (1) 200 m above sea level = +200 m

(2) 100 m below sea level = -100 m

(3) 10 m above sea level = +10 m

(4) Sea level = 0

Question 3. Write six distinct integers whose sum is 7.

Solution. Let the six integers be 1, 2, -2, 3, -3 and 6.

Now, sum of the above integers

= 1 + 2 + (-2) + 3 + (-3) + 6

We can arrange the numbers, so that the positive integers and the negative integers are grouped together.

We have, 1 + 2 + 3 + 6 + (-2) + (-3) = 12 – 2 – 3

= 12 – 5 = 7

Hence, the required integers are 1, 2, -2, 3, -3 and 6.

Class 6 Maths Chapter 6 Solutions Mp Board

Question 4. Write the integer which is 4 more than its additive inverse.

Solution. Firstly, draw a number line.

Let +1 be an integer and its additive inverse is -1. From the number line, we see that +1 is 2 more than its additive inverse. So, we reject this integer.

Again, let +2 be an integer, its additive inverse is -2.

From the number line, we see that +2 is 4 more than its additive inverse.

Hence, the required integer is 2.

Question 5. Temperature of a place at 12:00 noon was +5°C. Temperature increased by 3°C in first hour and decreased by 1°C in the second hour. What was the temperature at 2:00 pm?

Solution. Given, initial temperature at 12:00 noon was +5°C.

Since, the temperature increased by 3°C in first hour.

∴ Temperature at 1:00 pm = 5°C + 3°C = 8°C

Also, the temperature decreased by 1°C in the second hour.

∴ Temperature at 2:00 pm = 8°C – 1°C = 7°C

Hence, the temperature at 2:00 pm is 7°C.