MP Board Class 6 Maths Solutions For Chapter 8 Decimals

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Comparison of Decimals

For comparing decimals, we follow the steps given below:

(1) We first convert them into like decimals i.e. having a same number of decimal points and then compare the whole part, where the decimal number having a greater whole part will be greater.

e.g. In 1.09 and 2.09, the whole parts are 1 and 2, respectively.

And 2 is greater than 1.

So, 2.09 is greater than 1.09.

(2) If the whole part is the same for both, then compare the tenths part and decimal having greater tenths part will be greater.

In 1.09 and 1.19, the whole part is the same.

But the tenth part of 1.09 is smaller than the enth part of 1.19.

So, 1.19 is greater than 1.09.

(3) If tenth part is also same, then compare the hundredths part and so on.

e.g. In 1.09 and 1.093, converting them into like decimals, we get 1.090 and 1.093.

Here, the whole part, tenths part and hundredths part are same but thousandths part of 1.093 is greater.

So, 1.093 is greater than 1.09.

Read and Learn More MP Board Class 6 Maths Solutions

Note it Without changing the value of a decimal, the number of decimal places can be increased simply by adding zeroes to the extreme right of its decimal parts.

Example 1. Which is greater?

(1) 2.03 or 3.07

(2) 2.09 or 2.19

(3) 3.12 or 3.15

(4) 0.05 or 0.02

(5) 1.7 or 1.72

(6) 2.7 or 2.70

(7) 22.63 or 22.84

(8) 112.316 or 112.314

(9) 6.3 or 3.6

(10) 0.70 or 0.7

Solution. (1) We have, 2.03 and 3.07

On comparing whole parts, we get

2 < 3

∴ Hence, 2.03 < 307

(2) We have, 2.09 and 2.19

Here, whole part of both numbers are same.

So, on comparing the tenths part, we get

0 < 1

Hence, 2.09 < 2.19

(3) We have, 3.12 and 3.15

Here, whole part and tenths part of both numbers are same.

So, on comparing the hundredths part, we get

2 < 5

Hence, 312 < 315

(4) We have, 0.05 and 0.02

Here, whole part and tenths part of both numbers are same.

So, on comparing the hundredths part, we get

5 > 2

Hence, 0.05 > 0.02

(5) We have, 1.7 and 1.72

By converting them into like decimals, we get

1.70 and 1.72

Here, whole part and tenths of both numbers are same.

So, on comparing the hundredths part, we get

0 < 2

Hence, 1.7 < 1.72

(6) We have, 2.7 and 2.70

By converting them into like decimals, we get

2.70 and 2.70

Here, both the given numbers are same.

Hence, 2.7 = 2.70

(7) We have, 22.63 and 22.84

Here, whole part of both numbers are same.

So, on comparing the tenths part, we get

6 < 8

Hence, 22.63 < 22.84

(8) We have, 112.316 and 112.314

Here, whole part, tenths part and hundredth part are same.

So, on comparing the thousandths part, we get

6 > 4

Hence, 112.316 > 112.314

(9) We have, 6.3 and 3.6

On comparing the whole part of 6.3 and 3.6, we get

6 > 3

Hence, 6.3 > 3.6

(10) We have, 0.70 and 0.7

By converting them into like decimals, we get 0.70 and 0.70

Here, both the given numbers are same.

Hence, 0.70 = 0.7

MP Board Class 6 Maths Solutions For Example 2. Arrange the following decimal numbers in ascending order 36.4, 6.02, 6.2, 4.93, 3.793.

Solution. The given decimal numbers are 36.4, 6.02, 6.2, 4.93 and 3.793

By converting them into like decimals, we get 36.400, 6.020, 6.200, 4.930 and 3.793

On comparing these like decimal numbers, we find that 3.793 < 4.930 < 6.020 < 6.200 < 36.400

Thus, 3.793 < 4.93 < 6.02 < 6.2 < 36.4

Hence, the given decimals numbers in ascending order are as follows: 3.793, 4.93, 6.02, 6.2, 36.4.

Mp Board Class 6 Book Solutions

Example 3. Arrange the following decimal numbers in descending order 3.6, 49.26, 0.23, 0.244 and 3.108.

Solution. The given decimal numbers are 3.6, 49.26, 0.23, 0.244 and 3.108

By converting them into like decimals, we get 3.600, 49.260, 0.230, 0.244 and 3.108

On comparing these like decimal numbers, we find that 49.260 > 3.600 > 3.108 > 0.244 > 0.230

Thus, 49.26 > 3.6 > 3.108 > 0.244 > 0.23

Hence, the given decimal numbers in descending order are as follows: 49.26, 3.6, 3.108, 0.244, 0.23.

Example 4. Compare the following figures

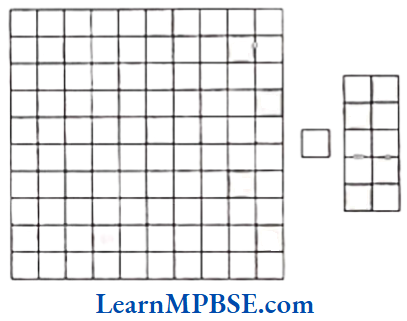
Solution. In the figure of left side, we have 12 shaded parts out of 100.

∴ \(\frac{12}{100}=0.12\)

In the right side figure, we have 4 shaded parts out of 10.

∴ \(\frac{4}{10}=0.4\)

Hence, 0.12 < 0.4.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Using Decimals

Decimals are used in numerous ways in our day to day life. e.g. In representing money, length, weight etc.

Money

We know that 100 paise = ₹ 1

∴ \(1 \text { paisa }=₹ \frac{1}{100}=₹ 0.01\)

So, the convert paise (money) into rupee, multiple paise by \(\frac{1}{100}\).

Example 1. Express as rupees using decimal.

(1) 65 paise

(2) 105 paise

(3) 20 rupees 27 paise

(4) 27 rupees and 7 paise in decimal.

Solution.

(1) \(65 \text { paise }=₹ \frac{65}{100}=₹ 0.65\)

(2) \(105 \text { paise }=(100+5) \text { paise }=₹\left(\frac{100}{100}+\frac{5}{100}\right)=₹ 1.05\)

(3) We have, \(₹ 20+27 \text { paise }=₹ 20+₹\left(27 \times \frac{1}{100}\right)\)

= ₹ (20 + 0.27) = ₹ 20.27

(4) We have, \(₹ 27+7 \text { paise }=₹ 27+₹\left(7 \times \frac{1}{100}\right)\)

= ₹ (27 + 0.07) = ₹ 27.07

Example 2. If Sohan gave 950 paise to shopkeeper, then how much money in rupees did he gave to shopkeeper?

Solution. Given, Sohan gave money to shopkeeper = 950 paise

We know that 1 paisa = ₹ \(\frac{1}{100}\)

∴ \(950 \text { paise }=₹ 950 \times \frac{1}{100}=₹ \frac{950}{100}=₹ 9.50\)

Hence, Sohan gave ₹ 9.50 to shopkeeper.

Length

We know that 100 cm = 1m

∴ 1 cm = \(\frac{1}{100} \mathrm{~m}=0.01 \mathrm{~m}\)

So, to convert centimetre into metre, multiply centimetre by \(\frac{1}{100}\).

Also, 1000 m = 1 km

∴ \(1 \mathrm{~m}=\frac{1}{1000} \mathrm{~km}=0.001 \mathrm{~km}\)

So, to convert metre into kilometre, multiply metre by 1/1000

Also, 10 mm = 1 cm

∴ \(1 \mathrm{~mm}=\frac{1}{10} \mathrm{~cm}=0.1 \mathrm{~cm}\)

So, to convert milimetre into centimetre, multiply milimetre by 1/10.

Mp Board Class 6 Book Solutions

Example 3. Express as metres using decimals.

(1) 17 cm

(2) 4 cm

(3) 3 m 48 cm

(4) 309 cm

Solution. (1) We know that 100 cm = 1 m

⇒ \(1 \mathrm{~cm}=\frac{1}{100} \mathrm{~m}\)

∴ \(17 \mathrm{~cm}=17 \times \frac{1}{100} \mathrm{~m}=\frac{17}{100} \mathrm{~m}=0.17 \mathrm{~m}\)

(2) We know that

\(1 \mathrm{~cm}=\frac{1}{100} \mathrm{~m}\)

∴ \(4 \mathrm{~cm}=4 \times \frac{1}{100} \mathrm{~m}=\frac{4}{100} \mathrm{~m}=0.04 \mathrm{~m}\)

(3) We know that 1 cm = \(\frac{1}{100}\) m

∴ 3 m 48 cm = \(3 \mathrm{~m}+48 \mathrm{~cm}=3 \mathrm{~m}+48 \times \frac{1}{100} \mathrm{~m}\)

= \(3 m+\frac{48}{100} m=3 m+0.48 m\)

= (3 + 0.48)m = 3.48 m

(4) We know that

\(1 \mathrm{~cm}=\frac{1}{100} \mathrm{~m}\)

∴ \(309 \mathrm{~cm}=309 \times \frac{1}{100} \mathrm{~m}\)

= \(\frac{309}{100} \mathrm{~m}=3.09 \mathrm{~m}\)

Example 4. Express as centimetres using decimals.

(1) 7 mm

(2) 70 mm

(3) 8 cm 4 mm

(4) 198 mm

Solution. (1) We know that

10 mm = 1cm

⇒ \(1 \mathrm{~mm}=\frac{1}{10} \mathrm{~cm}\)

∴ \(7 \mathrm{~mm}=7 \times \frac{1}{10} \mathrm{~cm}=\frac{7}{10} \mathrm{~cm}=0.7 \mathrm{~cm}\)

(2) We know that

1mm = \(\frac{1}{10}\) cm

∴ \(70 \mathrm{~mm}=70 \times \frac{1}{10} \mathrm{~cm}=\frac{70}{10} \mathrm{~cm}=7 \mathrm{~cm}\)

(3) We know that

1mm = \(\frac{1}{10}\) cm

∴ \(8 \mathrm{~cm} 4 \mathrm{~mm}=8 \mathrm{~cm}+4 \mathrm{~mm}=8 \mathrm{~cm}+\left(4 \times \frac{1}{10}\right) \mathrm{cm}\)

= \(8 \mathrm{~cm}+\frac{4}{10} \mathrm{~cm}=8 \mathrm{~cm}+0.4 \mathrm{~cm}\)

= (8 + 0.4)cm = 8.4 cm

(4) We know that

1mm = \(\frac{1}{10}\) cm

∴ \(198 \mathrm{~mm}=198 \times \frac{1}{10} \mathrm{~cm}=\frac{198}{10} \mathrm{~cm}=19.8 \mathrm{~cm}\)

Mp Board Class 6 Book Solutions

Example 5. Express as kilometers using decimals.

(1) 98 m

(2) 7 m

(3) 6843 m

(4) 15 km 7 m

Solution. (1) We know that

1000 m = 1 km

⇒ \(1 \mathrm{~m}=\frac{1}{1000} \mathrm{~km}\)

∴ \(98 \mathrm{~m}=98 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{98}{1000}=0.098 \mathrm{~km}\)

(2) We know that

l m = \(\frac{1}{1000}\) km

∴ \(7 \mathrm{~m}=7 \times \frac{1}{1000} \mathrm{~km}=\frac{7}{1000} \mathrm{~km}=0.007 \mathrm{~km}\)

(3) We know that

1 m = \(\frac{1}{1000}\) km

∴ \(6843 \mathrm{~m}=6843 \times \frac{1}{1000} \mathrm{~km}=\frac{6843}{1000} \mathrm{~km}\)

= 6.843 km

(4) We know that

1m = \(\frac{1}{1000}\) km

∴ \(15 \mathrm{~km} 7 \mathrm{~m}=15 \mathrm{~km}+7 \mathrm{~m}=15 \mathrm{~km}+7 \times \frac{1}{1000} \mathrm{~km}\)

= \(15 \mathrm{~km}+\frac{7}{1000} \mathrm{~km}=15 \mathrm{~km}+0.007 \mathrm{~km}\)

= (15 + 0.007) km = 15.007 km

Example 6. Express the following using decimals.

1. 6 mm in cm
2. 60 m in km using decimals

Solution. (1) We know that 10 mm = 1 cm

1 mm = \(\frac{1}{10}\) cm

⇒ \(6 \mathrm{~mm}=\frac{6}{10} \mathrm{~cm}=0.6 \mathrm{~cm}\)

(2) We know that 1000 m = 1km

1 m = \(\frac{1}{1000}\) km

⇒ \(60 \mathrm{~m}=\frac{60}{1000} \mathrm{~km}=0.060 \mathrm{~km}\)

Example 7. How can we write 946 mm in metres?

Solution. We know that

1 mm = \(\frac{1}{10}\) cm

and 1 cm = \(\frac{1}{100}\) m

∴ 946 mm = \(946 \times \frac{1}{10} \mathrm{~cm}\)

= \(\frac{946}{10} \mathrm{~cm}=94.6 \mathrm{~cm}\)

= \(94.6 \times \frac{1}{100} \mathrm{~m}=\frac{94.6}{100} \mathrm{~m}=0.946 \mathrm{~m}\)

Weight

We know that 1000 g = 1kg

⇒ 1 g = \(\frac{1}{1000}\) kg

So, to convert gram into kilogram, multiply gram by \(\frac{1}{1000}\)

e.g. \(452 \mathrm{~g}=\frac{452}{1000}=0.452 \mathrm{~kg}\)

MP Board Class 6 Maths Solutions For Example 8. Express as kilograms using decimals.

(1) 6 g

(2) 120 g

(3) 2645 g

(4) 8 kg 9 g

Solution. (1) We know that

1000 g = 1kg

⇒ \(1 \mathrm{~g}=\frac{\mathrm{l}}{1000} \mathrm{~kg}\)

∴ \(6 \mathrm{~g}=6 \times \frac{1}{1000} \mathrm{~kg}=\frac{6}{1000} \mathrm{~kg}=0.006 \mathrm{~kg}\)

(2) We know that

1 g = \(\frac{1}{1000}\) kg

∴ \(120 \mathrm{~g}=120 \times \frac{1}{1000} \mathrm{~kg}\)

= \(\frac{120}{1000} \mathrm{~kg}=0.12 \mathrm{~kg}\)

(3) We know that

1 g = \(\frac{1}{1000}\) kg

∴ \(2645 \mathrm{~g}=2645 \times \frac{1}{1000} \mathrm{~kg}\)

= \(\frac{2645}{1000}\) kg

= 2.645 kg

(4) We know that

1 g = \(\frac{1}{1000}\) kg

∴ 8 kg 9 g = 8 kg + 9 g

= \(8 \mathrm{~kg}+9 \times \frac{1}{1000} \mathrm{~kg}\)

= \(8 \mathrm{~kg}+\frac{9}{1000} \mathrm{~kg}\)

= 8 kg + 0.009 kg

= (8 + 0.009) kg

= 8.009 kg

Mp Board Class 6 Book Solutions

Example 9. Ramesh bought 3 kg 560 g onions that means he bought 3.560 kg onion. State whether the given statement is true or false?

Solution. Weight of onions = 3 kg 560 g

∴ 3 kg 560 g = 3kg + 560 g [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(3 \mathrm{~kg}+560 \times \frac{1}{1000} \mathrm{~kg}\)

= 3 kg + 0.560 kg

= (3 + 0.560) kg

= 3.560 kg

Hence, the given statement is true.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Addition of Numbers with Decimals

To add the numbers with decimals, we follow the steps given below

(1) Firstly, convert the given decimals into like decimals.

(2) Write the numbers according to the place value chart or arrange in columns in such a way that the digits of same place are arranged in same columns.

(3) Now, add the numbers in column from the right, the same way as we carry the regular addition.

Example 1. Find the sum in each of the following

(1) 0.37 +0.46

(2) 0.6+0.09

(3) 0.79+0.65

(4) 2.34+161

Solution. (1) We have, 0.37 + 0.46

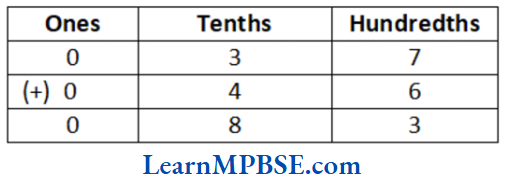
∴ 0.37 + 0.46 = 0.83

(2) We have, 0.6 + 0.09

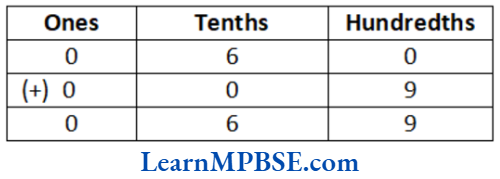
∴ 0.6 + 0.09 = 1.44

(3) We have, 0.79 + 0.65

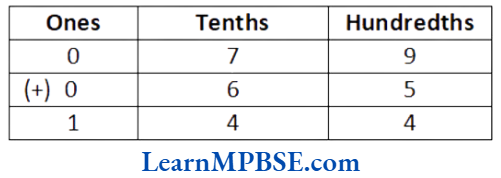
∴ 0.79 + 0.65 = 1.44

(4) We have, 2.34 + 1.61

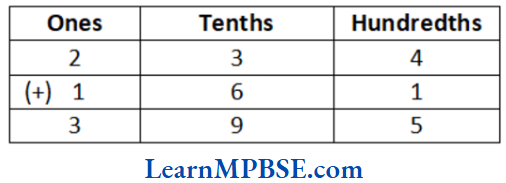
∴ 2.34 + 1.61 = 3.95

Mp Board Class 6 Maths Solutions

Example 2. Find the sum in each of the following

(1) 280.64 + 25.5 + 28

(2) 270.24 + 12.52 + 1.5

(3) 0.006 + 7.3 + 26.08

(4) 0.61 + 19.314 + 7

Solution. (1) Here, 280.64 + 255 + 28 can be written as

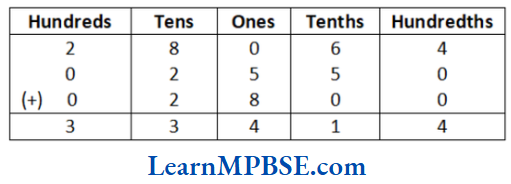
∴ 280.64 + 25.5 + 28 = 334.14

(2) Here, 270.24 +12.52 +1.5 can be written as Hundreds

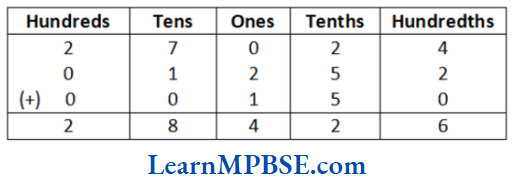
∴ 270.24 + 12.52 + 1.50 = 284.26

(3) We have, 0.006 + 7.3 + 26.08

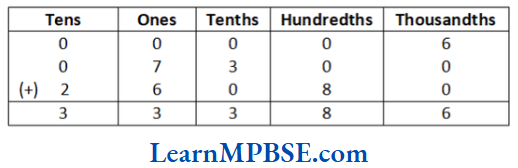
∴ 0.006 + 7.3 + 26.08 = 33.386

(4) We have, 0.61 + 19.314 + 7

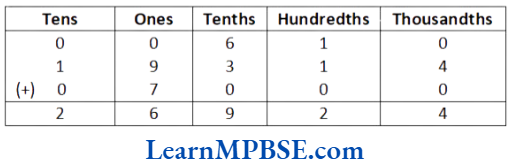
∴ 0.61 + 19.314 + 7 = 26924

Class 6 Maths Chapter 8 Solutions 

Example 3. Mahesh spent 30.55 for the Mathematics book and 20.54 for the Science book. Find the total amount spent by Mahesh.

Solution. Money spent for Mathematics book = ₹ 30.55

and money spent for Science book = ₹ 20.54

∴ Total amount spent = ₹ 30.55 + ₹ 20.54

= 30.55 + 20.54 = 51.09

Hence, the total amount spent by Mahesh is * 51.09.

Mp Board Class 6 Maths Solutions

Example 4. Sohan’s grandmother gave him? 15.50 and his grandfather gave him 23.60, then find the total amount given to Sohan from his grandmother and grandfather.

Solution. Money given to Sohan by his grandmother = ₹ 15.50

and money given to Sohan by his grandfather = ₹ 23.60

∴ Total money = ₹ 15.50 + ₹ 23.60

= 15.50 + 23.60 = 39.10

Hence, the total money given to Sohan by his grandmother and grandfather is ₹ 39.10.

Example 5. Shobhit bought 3 m 20 cm cloth for his shirt and 1 m 50 cm for his pant. Then, find the total length of cloth bought by him.

Solution. Shobhit bought cloth for his shirt = 3m 20 cm

= \(3 \mathrm{~m}+20 \mathrm{~cm}=3 \mathrm{~m}+20 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= 3m + 0.20 m = (3 + 0.20) m = 3.20 m

Shobhit bought cloth for his pants=1 m 50 cm

= \(1 \mathrm{~m}+50 \mathrm{~cm}=1 \mathrm{~m}+50 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= 1m + 0.50 m = (1 + 0.50) m = 1.50 m

∴ The total length of cloth bought by Shobhit is

= 3.20 + 1.50 = 4.70 m

Hence, the total length of cloth brought by Shobit is 4.70 m.

Class 6 Maths Chapter 8 Solutions Mp Board

Example 6. Seema travelled 16 km 475 m by train, 5 km 70 m by bus and 700 m by rickshaw in order to reach a hill station. How much distance travelled by her to reach the hill station?

Solution. Distance travelled by train = 16 km 475 m

= 16 km + 475 m

= \(16 \mathrm{~km}+475 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(16 \mathrm{~km}+\frac{475}{1000} \mathrm{~km}\)

= 16 km + 0.475 km

= (16 + 0.475) km = 16.475 km

Distance travelled by bus = 5 km 70 m = 5 km + 70 m

= \(5 \mathrm{~km}+70 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(5 \mathrm{~km}+\frac{70}{1000} \mathrm{~km}=5 \mathrm{~km}+0.070 \mathrm{~km}\)

= (5 + 0.070) km = 5.070 km

Distance travelled by rickshaw = \(700 \mathrm{~m}=700 \times \frac{1}{1000} \mathrm{~km}\)

[∴ 1 m = \(\frac{1}{1000}\) km]

= \(\frac{700}{1000} \mathrm{~km}=0.700 \mathrm{~km}\)

∴ Total distance travelled by Seema

= 16.475 + 5.070 + 0.700 = 22.245

Hence, the total distance travelled by Seema is 22.245 km.

Example 7. Shaurya bought 5 kg 80 g apples, 8 kg 400 g grapes and 3 kg 340 g mangoes. Find the total weight of all the fruits he bought.

Solution. Weight of apples purchased by Shaurya

= 5 kg 80 g = 5 kg + 80 g

= \(5 \mathrm{~kg}+80 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(5 \mathrm{~kg}+\frac{80}{1000} \mathrm{~kg}=5 \mathrm{~kg}+0.080 \mathrm{~kg}\)

= (5 + 0.080) kg = 5.080 kg

Weight of grapes purchased by Shaurya

= 8 kg 400 g = 8 kg + 400 g

= \(8 \mathrm{~kg}+400 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(8 \mathrm{~kg}+\frac{400}{1000} \mathrm{~kg}=8 \mathrm{~kg}+0.400 \mathrm{~kg}\)

= (8 + 0.400) kg = 8.400 kg

Weight of mangoes purchased by Shaurya

= 3 kg 340 g = 3 kg + 340 g

= \(3 \mathrm{~kg}+340 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(3 \mathrm{~kg}+\frac{340}{1000} \mathrm{~kg}=3 \mathrm{~kg}+0.340 \mathrm{~kg}\)

= (3 + 0.340) kg = 3.340 kg

∴ Total weight of his purchases

= 5.080 + 8.400 + 3.340 = 16.820

Hence, the total weight of all of his purchases is 16.820 kg.

Class 6 Maths Chapter 8 Solutions Mp Board

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Subtraction of Decimals

To subtract the decimal number, we follow the steps given below

(1) Firstly, convert the given decimals into like decimals.

(2) Write the smaller number below the larger number in column form in such a way that the decimal points of both the numbers are in the same column and the digits of the same place are arranged in same column.

(3) Subtract as we do in case of whole numbers.

(4) Put the decimal point directly under the decimal points of the given numbers.

Note It Sometimes while subtracting decimals, we may need to regroup we did in addition.

Example 1. Subtract

(1) 0.95 from 2.29

(2) 23.75 from 2725

(3) 302.56 m from 416.44 m

(4) 1.416 kg from 3.209 kg

Solution. (1) We have, 2.29 – 0.95

At tenths place subtraction cannot done so grouped it.

∴ 2.29 – 0.95 = 1.34

(2) We have, ₹ 27.25 – ₹ 23.75

At tenths place subtraction cannot done so regrouped it.

∴ ₹ 27.25 – ₹ 23.75 = ₹ (27.25 – 23.75) = ₹ 3.50

(3) We have, 416.44 m – 302.56 m

At tenths place subtraction cannot done so regrouped it.

∴ 416.44 m – 302.56 m = (416.44 – 302.56) m = 113.88 m

(4) We have, 3.209 kg – 1.416 kg

At tenths place subtraction cannot done so regrouped it.

∴ 3.209 kg – 1.416 kg = (3.209 – 1.416) kg

Class 6 Maths Chapter 8 Solutions Mp Board

Example 2. Find the value of

(1) 8.146 – 5.38

(2) 19.09 – 11.36

(3) 11.5 – 4.49

(4) 13.7 – 9.198

Solution.

(1) We have, 8.146 – 5.38

= 8.146 – 5.380 = 2.766

∴ 8.146 – 5.380 = 2.766

(2) We have, 19.09 – 11.36

= 19.09 – 11.36 = 7.73

∴ 19.09 – 11.36 = 7.73

(3) We have, 11.50 – 4.49

= 11.50 – 4.49 = 7.01

∴ 11.50 – 4.49 = 7.01

(4) We have, 13.7 – 9.198

13.700 – 9.198 = 4.502

∴ 13.7 – 9.198 = 4.502

Example 3. By what amount should 48.76 be increased to get 97?

Solution. We subtract 48.76 from 97 in order to find the number that is to be added to 48.76 to get 97.

Converting into like decimals and then subtracting.

= 97.00 – 48.76 = 48.24

Hence, 48.24 should be increase in 48.76 to get 97.

Decimals Class 6 Maths Solutions

Example 4. What should be added to 29.6 to get 59?

Solution. We subtract 29.6 from 59 in order to find the number that should be added to 29.6 to make it 59.

Converting into like decimals and then subtracting.

= 59.0 – 29.6 = 29.4

Hence, 29.4 should be added to 29.6 to get 59.

Example 5. What should be subtracted from 179 to get 91.94?

Solution. We subtract 91.94 from 179 in order to find the number that should be subtracted from 179 to get 91.94.

Converting into like decimals and then subtracting.

= 179.00 – 91.94 = 87.06

Hence, 87.06 should be subtracted from 179 to get 91.94.

Example 6. Ramesh purchased a book worth ₹ 300.80 from a bookseller and gave him a ₹ 500. How much balance did he get back?

Solution. Total money paid = ₹ 500.00

Cost of the book = ₹ 300.80

∴ Balance = 500.00 – 300.80 = ₹ 199.20

Hence, the balance he will get back from bookseller is ₹ 199.20.

Example 7. Shiva bought a toy for 47.85. He gave ₹50 to the shopkeeper. How much money did he get back from the shopkeeper?

Solution.

Cost of toy bought by Shiva = ₹ 47.85

and money gave to shopkeeper = ₹ 50

∴ Money get back from shopkeeper = ₹ 50 – ₹ 47.85

= ₹ (50 – 47.85) = ₹ 2.15

Hence, the money get back from shopkeeper is ₹ 2.15.

Mp Board Maths Chapter 8 Solutions

Example 8. Reena had 10 m 5 cm long cloth. She cuts 3 m 65 cm length of cloth from this for making a cover of table. How much cloth is left with her?

Solution. Total length of cloth = 10 m 5 cm = 10m + 5 cm

= \(10 \mathrm{~m}+5 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(10 \mathrm{~m}+\frac{5}{100} \mathrm{~m}\)

= 10 m + 0.05 m

= (10 + 0.05) m

= 10.05 m

Length cut out for cover of table = 3 m 65 cm = 3m + 65 cm

= \(3 \mathrm{~m}+65 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(3 \mathrm{~m}+\frac{65}{100} \mathrm{~m}=3 \mathrm{~m}+0.65 \mathrm{~m}\)

= (3 + 0.65) m = 3.65 m

∴ Length of cloth left with Reena = 10.05 m – 3.65 m = (10.05 – 3.65) m = 6.40 m

Hence, 6.40 m cloth is left with her.

Example 9. Rohan’s school is at a distance of 6 km 450 m from his house. He travels 5 km 225 m by bus and rest on foot. How much distance does he travel on foot?

Solution. Distance of school from Rohan’s house = 6 km 450 m

= 6 km + 450 m

= \(6 \mathrm{~km}+450 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1m = \(\frac{1}{1000}\) km]

= \(6 \mathrm{~km}+\frac{450}{1000} \mathrm{~km}\)

= 6 km + 0.450 km

= (6 + 0.450) km = 6.450 km

and distance travelled by bus = 5 km 225 m

= 5 km + 225 m

= \(5 \mathrm{~km}+225 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1m = \(\frac{1}{1000}\) km]

= \(5 \mathrm{~km}+\frac{225}{1000} \mathrm{~km}\)

= 5 km + 0.225 km

= (5 + 0.225) km = 5.225 km

∴ Distance travelled on foot

= 6.450 km – 5.225 km

=(6.450 – 5.225) km = 1.225 km

Hence, Rohan travels 1.225 km on foot.

Example 10. Ashu bought fruits weight 20 kg. Out of this 6 kg 700 g is apples, 5 kg 25 g is mangoes and rest is grapes. Find the weight of the grapes.

Solution. Given, total weight of fruits = 20 kg

Weight of apples = 6 kg 700 g = 6 kg + 700 g

= \(6 \mathrm{~kg}+700 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(6 \mathrm{~kg}+700 \times \frac{1}{1000} \mathrm{~kg}\)

=6 kg + 0.700 kg

=(6 + 0.700) kg = 6.700 kg

Weight of mangoes = 5 kg 25 g = 5 kg + 25 g

= \(5 \mathrm{~kg}+25 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1g = \(\frac{1}{1000}\) kg]

= \(5 \mathrm{~kg}+\frac{25}{1000} \mathrm{~kg}=5 \mathrm{~kg}+0.025 \mathrm{~kg}\)

= (5 + 0.025) kg = 5.025 kg

∴ Total weight of apples and mangoes

= 6.700 kg + 5.025 kg = 11725 kg

Now, weight of grapes = Total weight of fruits – weight of apples and mangoes

= 20 kg – 11.725 kg = 8.275 kg

Hence, the weight of the grapes is 8.275 kg.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Exercise 8.1

Question 1. Which is greater?

(1) 0.3 or 0.4

(2) 0.07 or 0.02

(3) 1.5 or 1.50

Solution. (1) We have, 0.3 and 0.4

Here, whole part of both numbers are same.

Now, tenths part of 0.3 = 3

and tenths part of 0.4 = 4

Here, 4 is greater than 3.

∴ 0.4 > 0.3

Hence, 0.4 is greater than 0.3.

(2) We have, 0.07 and 0.02

Here, whole parts as well as tenths parts of both numbers are same i.e. 0.

Now, hundredths part of 0.07 = 7

and hundredths part of 0.02 = 2

Here, 7 is greater than 2 i.e.7 > 2

Hence, 0.07 is greater than 0.02.

(3) We have, 1.5 or 1.50

∴ \(1.5=1+\frac{5}{10}+\frac{0}{100} \text { and } 1.50=1+\frac{5}{10}+\frac{0}{100}\)

Here, whole parts, tenths parts as well as hundredths parts of both numbers are same.

∴ 1.5 = 150

Hence, both numbers are equal.

MP Board Class 6 Chapter 8 Maths 

Question 2. Write 2 rupees 5 paise and 2 rupees 50 paise in decimals.

Solution. We have, 2 rupees 5 paise = ₹ 2 + 5 paise

= \(₹ 2+₹\left(5 \times \frac{1}{100}\right)\)

= ₹ (2 + 0.05) = ₹ 2.05

and 2 rupees 50 paise = ₹ 2 + 50 paise

= \(₹ 2+₹\left(50 \times \frac{1}{100}\right)\)

= ₹ (2 + 0.50) = ₹ 2.50

Question 3. Can you write 4 mm in ‘cm’ using decimals?

Solution. Yes, we can write 4 mm in centimetres using decimals as follows

We know that 10 mm = 1 cm

⇒ \(1 \mathrm{~mm}=\frac{1}{10} \mathrm{~cm}\)

∴ \(4 \mathrm{~mm}=4 \times \frac{1}{10} \mathrm{~cm}=\frac{4}{10} \mathrm{~cm}=0.4 \mathrm{~cm}\)

Question 4. How will you write 7 cm 5 mm in ‘cm’ using decimals?

Solution. We know that 10 mm = 1 cm ⇒ 1mm = \(\frac{1}{10}\) cm

∴ \(7 \mathrm{~cm} 5 \mathrm{~mm}=7 \mathrm{~cm}+5 \mathrm{~mm}=7 \mathrm{~cm}+5 \times \frac{1}{10} \mathrm{~cm}\)

= \(7 \mathrm{~cm}+\frac{5}{10} \mathrm{~cm}=\left(7+\frac{5}{10}\right) \mathrm{cm}\)

= (7 + 0.5) cm = 7.5 cm

Mp Board Maths Chapter 8 Solutions

Question 5. Can you now write 52 m as ‘km’ using decimals? How will you write 340 m as ‘km’ using decimals? How will you write 2008 m in ‘km’?

Solution. Yes, we can write 52 m as ‘km’ using decimals as follows

We know that 1000 m = 1 km ⇒ 1 m = \(\frac{1}{1000}\) km

∴ \(52 \mathrm{~m}=52 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{52}{1000} \mathrm{~km}=0.052 \mathrm{~km}\)

To write 340 m as kilometres.

We know that 1 m = \(\frac{1}{1000}\) km

∴ \(340 \mathrm{~m}=340 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{340}{1000} \mathrm{~km}=0.340 \mathrm{~km}\)

To write 2008 m as kilometers.

We know that 1 m = \(\frac{1}{1000}\) km

∴ \(2008 \mathrm{~m}=2008 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{2008}{1000} \mathrm{~km}=2.008 \mathrm{~km}\)

Question 6. Can you now write 456 g as kg using decimals?

Solution. We know that

1000 g = 1 kg ⇒ \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)

∴ \(456 \mathrm{~g}=456 \times \frac{1}{1000} \mathrm{~kg}=\frac{456}{1000} \mathrm{~kg}=0.456 \mathrm{~kg}\)

Question 7. How will you write 2 kg 9 g in ‘kg’ using decimals?

Solution. We have, 2 kg 9 g = 2kg + 9g

= \(2 \mathrm{~kg}+9 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(2 \mathrm{~kg}+\frac{9}{1000} \mathrm{~kg}=2 \mathrm{~kg}+0.009 \mathrm{~kg}\)

= (2 + 0.009) kg = 2.009 kg

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Exercise 8.2

Question 1. Express as rupees using decimals.

(1) 5 paise

(2) 50 rupees 90 paise

Solution.

(1) We know that 1 paise = ₹ \(\frac{1}{100}\)

∴ \(5 \text { paise }=₹ 5 \times \frac{1}{100}=₹ \frac{5}{100}=₹ 0.05\)

(2) We know that 1 paise = ₹ \(\frac{1}{100}\)

∴ 50 rupees 90 paise = ₹ 50 + 90 paise

= \(₹ 50+₹ 90 \times \frac{1}{100}=₹ 50+₹ \frac{90}{100}\)

= ₹ 50 + ₹ 0.90 = ₹(50 + 0.90) = ₹ 50.90

Question 2. Express as metres using decimals.

(1) 15 cm

(2) 2 m 45 cm

(3) 419 cm

Solution. (1) We know that 100 cm = 1 m

⇒ 1 cm = \(\frac{1}{100}\) m

∴ \(15 \mathrm{~cm}=15 \times \frac{1}{100} \mathrm{~m}=\frac{15}{100} \mathrm{~m}=0.15 \mathrm{~m}\)

(2) We know that 1 cm = \(\frac{1}{100}\) m

∴ \(2 \mathrm{~m} 45 \mathrm{~cm}=2 \mathrm{~m}+45 \mathrm{~cm}=2 \mathrm{~m}+45 \times \frac{1}{100} \mathrm{~m}\)

= \(2 \mathrm{~m}+\frac{45}{100} \mathrm{~m}=2 \mathrm{~m}+0.45 \mathrm{~m}\)

= (2 + 0.45) m = 2.45 m

(3) We know that 1 cm = \(\frac{1}{100}\) m

∴ \(419 \mathrm{~cm}=419 \times \frac{1}{100} \mathrm{~m}=\frac{419}{100} \mathrm{~m}=4.19 \mathrm{~m}\)

Mp Board Maths Chapter 8 Solutions

Question 3. Express as centimeters using decimals.

(1) 5 mm

(2) 9 cm 8 mm

Solution. (1) We know that 1 mm = \(\frac{1}{10}\) cm

∴ \(5 \mathrm{~mm}=5 \times \frac{1}{10} \mathrm{~cm}=\frac{5}{10} \mathrm{~cm}=0.5 \mathrm{~cm}\)

(2) We know that 1 mm = \(\frac{1}{10}\) cm

∴ \(9 \mathrm{~cm} 8 \mathrm{~mm}=9 \mathrm{~cm}+8 \mathrm{~mm}=9 \mathrm{~cm}+8 \times \frac{1}{10} \mathrm{~cm}\)

= \(9 \mathrm{~cm}+\frac{8}{10} \mathrm{~cm}=\left(9+\frac{8}{10}\right) \mathrm{cm}\)

= (9 + 0.8) cm = 9.8 cm

Question 4. Express as kilometres using decimals.

(1) 8 m

(2) 88 m

(3) 8888 m

(4) 70 km 5 m

Solution. (1) We know that 1000 m = 1 km

⇒ 1 m = \(\frac{1}{1000}\) km

∴ \(8 \mathrm{~m}=8 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{8}{1000} \mathrm{~km}=0.008 \mathrm{~km}\)

(2) We know that 1 m = \(\frac{1}{1000}\) km

∴ \(88 \mathrm{~m}=88 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{88}{1000} \mathrm{~km}=0.088 \mathrm{~km}\)

(3) We know that 1 m = \(\frac{1}{1000}\) km

∴ \(8888 \mathrm{~m}=8888 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{8888}{1000} \mathrm{~km}=8.888 \mathrm{~km}\)

(4) We know that 1m = \(\frac{1}{1000}\) km

∴ 70 km 5 m = 70 km + 5 m

= \(70 \mathrm{~km}+5 \times \frac{1}{1000} \mathrm{~km}\)

= \(70 \mathrm{~km}+\frac{5}{1000} \mathrm{~km}\)

= (70 + 0.005) km = 70.005 km

Question 5. Find

(1) 0.29 + 0.36

(2) 0.7 + 0.08

Solution. (1) We have, 0.29 + 0.36

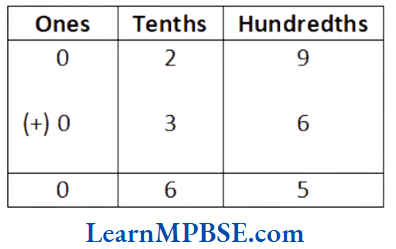
∴ 0.29 + 0.36 = 0.65

(2) We have, 0.7 + 0.08

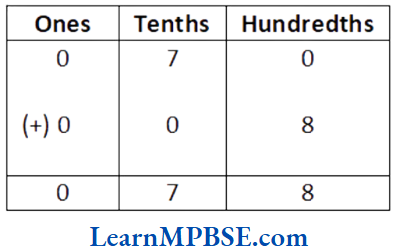
∴ 0.7 + 0.08 = 0.78

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Exercise 8.3

Question 1. Find the sum in each of the following.

(1) 0.007 + 8.5 + 30.08

(2) 15 + 0.632 + 13.8

Solution. (1) We have, 0.007 + 8.5 + 30.08

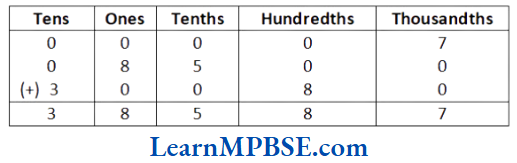
∴ 0.007 + 8.5 + 30.08 = 38.587

(2) We have, 15 + 0.632 + 13.8

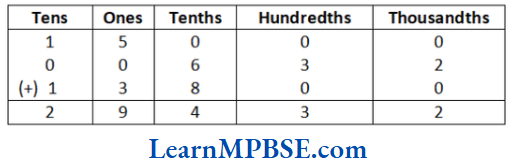
∴ 15 + 0.632 + 13.8 = 29.432

Mp Board Maths Chapter 8 Solutions

Question 2. Rashid spent 35.75 for Maths book and 32.60 for Science book. Find the total amount spent by Rashid.

Solution. Money spent by Rashid for Maths book = 35.75 and money spent by Rashid for Science book = 32.60

∴ Total money spent 35.75 + 32.60 = 68.35

Hence, the total money spent by Rashid is ₹ 68.35.

Question 3. Radhika’s mother gave her 10.50 and her father gave her 15.80. Find the total amount given to Radhika by the parents.

Solution. Money given to Radhika by her mother = 10.50 and money given to Radhika by her father= 15.80

∴ Total money = 10.50 + 15.80 = 26.30

Hence, the total money given to Radhika by her parents is ₹ 26.30.

Question 4. Nasreen bought 3 m 20 cm cloth for her shirt and 2 m 5 cm cloth for her trouser. Find the total length of cloth bought by her.

Solution. Cloth bought by Nasreen for her shirt = 3 m 20 cm

= 3 m + 20 cm

= \(3 \mathrm{~m}+20 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= 3m + 0.20 m = (3 + 0.20) m = 3.20 m

Cloth bought by Nasreen for her trouser

= 2m 5 cm = 2m + 5 cm

= \(2 \mathrm{~m}+5 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= 2m + 0.05 m = (2 + 0.05) m = 2.05 m

Total length of cloth 3.20 + 2.05 = 5.25

Hence, the total length of cloth bought by Nasreen is 5.25 m.

Question 5. Naresh walked 2 km 35 m in the morning and 1 km 7 m in the evening. How much distance did he walk in all?

Solution. Naresh walked in morning

= 2 km 35 m = 2 km + 35 m

= \(2 \mathrm{~km}+35 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(2 \mathrm{~km}+\frac{35}{1000} \mathrm{~km}=(2+0.035) \mathrm{km}=2.035 \mathrm{~km}\)

Naresh walked in evening

= 1 km 7 m = 1 km + 7 m

= \(1 \mathrm{~km}+7 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(1 \mathrm{~km}+\frac{7}{1000} \mathrm{~km}=(1+0.007) \mathrm{km}=1.007 \mathrm{~km}\)

∴ Total distance = 2.035 + 1.007 = 3.042

Hence, the total distance walked by Naresh is 3.042 km.

Class 6 Mp Board Maths Question Answers

Question 6. Sunita travelled 15 km 268 m by bus, 7 km 7 m by car and 500 m on foot in order to reach her school. How far is her school from her residence?

Solution. Distance travelled by bus

= 15 km 268 m = 15 km + 268 m

= \(15 \mathrm{~km}+268 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(15 \mathrm{~km}+\frac{268}{1000} \mathrm{~km}\)

= (15 + 0.268) km

= 15.268 km

Distance travelled by car = 7 km 7 m = 7 km + 7m

= \(7 \mathrm{~km}+7 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(7 \mathrm{~km}+\frac{7}{1000} \mathrm{~km}=7 \mathrm{~km}+0.007 \mathrm{~km}\)

= (7 + 0.007) km = 7.007 km

Distance travelled by foot

= \(500 \mathrm{~m}=500 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(\frac{500}{1000} \mathrm{~km}=0.500 \mathrm{~km}\)

∴ Total distance travelled by Sunita

15.268 + 7.007 +0.500 = 22.775

Hence, the total distance travelled by Sunita is 22.775 km.

Question 7. Ravi purchased 5 kg 400 g rice, 2 kg 20 g sugar and 10 kg 850 g flour. Find the total weight of his purchases.

Solution. Weight of rice purchased by Ravi

= 5 kg 400 g = 5 kg + 400 g

= \(5 \mathrm{~kg}+400 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(5 \mathrm{~kg}+\frac{400}{1000} \mathrm{~kg}=(5+0.400) \mathrm{kg}=5.400 \mathrm{~kg}\)

Weight of sugar purchased by Ravi

= 2 kg 20 g = 2kg + 20 g

= \(2 \mathrm{~kg}+20 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(2 \mathrm{~kg}+\frac{20}{1000} \mathrm{~kg}=(2+0.020) \mathrm{kg}=2.020 \mathrm{~kg}\)

Weight of flour purchased by Ravi

= 10 kg 850 g = 10 kg + 850 g

= \(10 \mathrm{~kg}+850 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(10 \mathrm{~kg}+\frac{850}{1000} \mathrm{~kg}=(10+0.850) \mathrm{kg}=10.850 \mathrm{~kg}\)

∴ Total weight of his purchases

5.400 + 2.020 + 10.850 = 18.270

Hence, the total weight of all his purchases is 18.270 kg.

Question 8. Subtract 1.85 from 5.46.

Solution. We have, 5.46 – 1.85

Now,

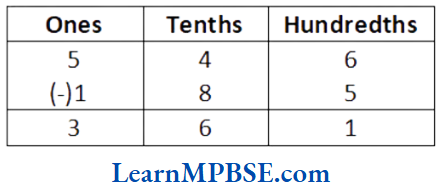
∴ 5.46 – 1.85 = 3.61

Class 6 Mp Board Maths Question Answers

Question 9. Subtract 5.25 from 8.28.

Solution. We have, 8.28 – 5.25

Now,

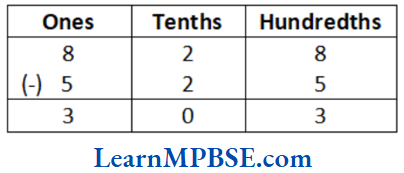
∴ 8.28 – 5.25 = 3.03

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Exercise 8.4

Question 1. Subtract.

(1) 18.25 from 20.75

(2) 202.54 m from 250 m

Solution. (1) We have, ₹ 20.75 – ₹ 18.25

Now,

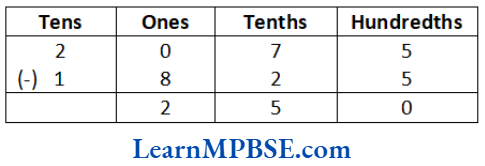
∴ ₹ 20.75 – ₹ 18.25 = ₹ (20.75 – 18.25) = ₹ 2.50

(2) We have, 250 m – 202.54 m

Now,

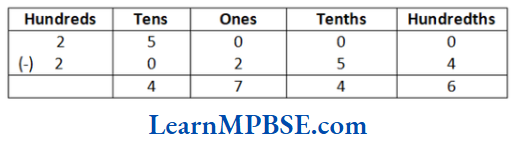
∴ 250 m 202.54 m = (250 – 202.54) m = 47.46 m

Question 2. Find the value of: 9.756 – 6.28

Solution. We have, 9.756 – 6.28

9.756 – 6.280 = 3.476

∴ 9.756 – 6.28 = 3.476

Question 3. Raju bought a book for ₹ 35.65. He gave ₹ 50 to the shopkeeper. How much money did he get back from the shopkeeper?

Solution. Cost of book bought by Raju = ₹ 35.65

and money given to shopkeeper = ₹ 50

∴ Money get back from shopkeeper = ₹ (50 – 35.65) = ₹ 14.35

Hence, the money get back from shopkeeper is ₹ 14.35.

Decimal Representation on Number Line

Question 4. Rani had ₹ 18.50. She bought one ice-cream for ₹ 11.75. How much money does she have now?

Solution. Total money Rani had = ₹ 18.50

and cost of ice-cream = ₹ 11.75

∴ Remaining money = ₹ (18.50 – 11.75) = ₹ 6.75

Hence, she have ₹ 6.75.

Question 5. Tina had 20 m 5 cm long cloth. She cuts 4 m 50 cm length of cloth from this for making a curtain. How much cloth is left with her?

Solution. Tina had length of cloth 20 m 5 cm = 20 m + 5 cm

= \(20 m+5 \times \frac{1}{100} m\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(20 \mathrm{~m}+\frac{5}{100} \mathrm{~m}\)

= (20 + 0.05) m = 20.05 m

and length of cloth cut by her = 4 m 50 cm

= 4m + 50 cm

= \(m+50 \times \frac{1}{100} m\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(4 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=(4+0.50) \mathrm{m}=4.50 \mathrm{~m}\)

∴ Length of cloth left with Tina 20.05 m-4.50 m

= (20.05 – 4.50) m = 15.55 m

Hence, 15.55 m cloth is left with her.

Class 6 Mp Board Maths Question Answers

Question 6. Namita travels 20 km 50 m everyday. Out of this she travels 10 km 200 m by bus and the rest by auto. How much distance does she travel by auto?

TIPS Firstly, write the distance travelled by Namita in kilometres using decimals. To find the distance travelled by auto, subtract distance travelled by bus from total distance travelled by Namita.

Solution.

Total distance travelled by Namita

= 20 km 50 m = 20 km + 50 m

= \(20 \mathrm{~km}+50 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(20 \mathrm{~km}+\frac{50}{1000} \mathrm{~km}\)

= (20 + 0.050) km = 20.050 km

and distance travelled by Namita by bus

= 10 km 200 m = 10 km + 200 m

= \(10 \mathrm{~km}+200 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(10 \mathrm{~km}+\frac{200}{1000} \mathrm{~km}\)

= 10 km + 0.200 km

= (10 + 0.200) km = 10.200 km

∴ Distance travelled by auto

= 20.050 km – 10.200 km

= (20.050 – 10.200) km

= 9.850 km

Hence, she travels 9.850 km by auto.

Question 7. Aakash bought vegetables weighing 10 kg. Out of this, 3 kg 500 g is onions, 2 kg 75 g is tomatoes and the rest is potatoes. What is the weight of the potatoes?

Tips Firstly, write the weight of all vegetables in kilograms using decimals, then add the weight of onions and tomatoes. To find the weight of potatoes, subtract this sum from total weight of vegetables.

Solution. Given, total weight of vegetables = 10 kg

Weight of onions = 3 kg 500 g = 3 kg + 500 g

= \(3 \mathrm{~kg}+500 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(3 \mathrm{~kg}+\frac{500}{1000} \mathrm{~kg}\)

= 3 kg +0.500 kg

= (3 + 0.500) kg = 3.500 kg

Weight of tomatoes = 2 kg 75 g = 2 kg + 75 g

= \(2 \mathrm{~kg}+\frac{75}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= 2 kg + 0.075 kg

= (2 + 0.075) kg = 2.075 kg

∴ Total weight of onions and tomatoes

= 3.500 kg + 2.075 kg

= (3.500 + 2.075) kg = 5.575 kg

Now, weight of potatoes = Total weight of vegetables – Weight of onions and tomatoes

= 10 kg – 5.575 kg = (10 – 5.575) kg

= 4.425 kg

Hence, the weight of potatoes is 4.425 kg.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Multiple Choice Questions

Question 1. Which is larger 3.1 or 3.044?

1. 3.044
2. 3.1
3. Both are equal
4. None of these

Answer. 2. 3.1

Question 2. Which of the following decimals is the smallest?

1. 0.37
2. 1.52
3. 0.087
4. 0.105

Solution. 3. 0.087

Question 3. Which of the following decimals is the greatest?

1. 0.182
2. 0.0928
3. 0.29
4. 0.038

Answer. 3. 0.29

Decimal Representation on Number Line

Question 4. 0.024 lies between

1. 0.2 and 0.3
2. 0.02 and 0.03
3. 0.03 and 0.029
4. 0.026 and 0.024

Answer. 2. 0.02 and 0.03

Question 5. To change milimetre in centimetre, we divide by

1. 10
2. 100
3. 1000
4. 10000

Answer. 1. 10

Question 6. 66 kg 15 g is equal to

1. 66.15 kg
2. 66.150 kg
3. 66.015 kg
4. 66.0019 kg

Answer. 3. 66.015 kg

Question 7. 555 m is equal to

1. 5 km
2. 0.555 km
3. 5.55 km
4. 55.5 km

Answer. 2. 0.555 km

Question 8. 2 cm 2 mm is equal to

1. 2.2 cm
2. 0.22 cm
3. 2.1 cm
4. 1.2 cm

Answer. 1. 2.2 cm

Question 9. 0.07 + 0.0008 is equal to

1. 0.15
2. 0.015
3. 0.078
4. 0.78

Answer. 3. 0.078

Question 10. \(1+\frac{1}{10}=\)

1. 0.11
2. 1.1
3. 1.01
4. 1.001

Answer. 2. 1.1

Question 11. 15.8 – 6.73 is equal to

1. 8.07
2. 9.07
3. 9.13
4. 9.25

Answer. 2. 9.07

Mp Board Class 6 Book Solutions

Question 12. By what amount should 36.45 be increased to get 87?

1. 36.45
2. 123.45
3. 50.55
4. None of these

Answer. 3. 50.55

Question 13. The value of 4.5 + 7.06 – 6.006 is

1. 5.54
2. 5.554
3. 5.0054
4. 5.054

Answer. 2. 5.554

Question 14. Simplify and mark the correct answer.

71.02 + 4.91 – 49.999

1. 25.931
2. 25.941
3. 20.941
4. 39.964

Answer. 1. 25.931

Question 15. 484.71 + 285.33 – 782.38 + 73.9 = ?

1. 61.56
2. 15.75
3. 19.78
4. 35.54

Answer. 1. 61.56

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Assertion – Reason

Question 1. Assertion (A) 31.47 < 31.478

Reason (R) If the whole part of two decimal numbers are equal, we compare their tenths part. If that too are equal, we move to hundredths and then thousandths.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (a) Both (A) and (R) are true and (R) is the correct explanation of (A).

Question 2. Assertion (A) 6005 m = 6.005 km

Reason (R) \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

Question 3. Assertion (A) 2.34 + 6.54 = 9.88

Reason (R) To add two decimal numbers, first check if they have the same number of digits to the right of the decimal point.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (d) (A) is false but (R) is true.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Fill in the Blanks

Question 1. 8.0999 is ….. than 8.1

Answer. Smaller

Question 2. The value of 545 g is equal to …. kg.

Answer. 0.545 kg

Question 3. 2 km 590 m is equal to ….. km.

Answer. 2.590 km

Question 4. The value of 50 coins of 50 paise = ₹ …..

Answer. 25

Mp Board Class 6 Book Solutions

Question 5. The value of 3.64 – 1.28 is ……

Answer. 2.36

MP Board Class 6 Maths Solutions For Chapter 8 Decimals True/False

Question 1. 4.51 is greater than 4.051.

Answer. True

Question 2. 36.096 is smaller than 45.064.

Answer. True

Question 3. 180 m 28 cm = 180.028 m

Answer. False

Question 4. 4.03 + 0.016 = 4.046

Answer. True

Question 5. 42.28 – 3.19 = 39.09

Answer. True

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Match the Columns

Question 1. Match the Column A with Column B.

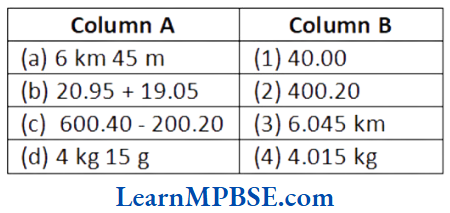
Solution. (a) → (3), (b) → (1), (c) → (2), (d) → (4)

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Case Based Type Questions

Question 1. Suraj provides laundry services to nearby areas. The charges for wash and fold are calculated per kilogram of the weight of the clothes.

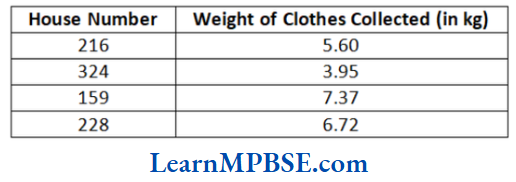
The table below shows the weight of the clothes for washing and folding from four houses.

(1) Which house will pay the most?

(a) House number 216

(b) House number 324

(c) House number 159

(d) House number 228

(2) What is the total weight of the clothes collected for washing and folding?

(3) Suraj collected 30.50 kg of clothes on Tuesday and 25.48 kg of clothes on Wednesday.

How many more kilograms of clothes were collected by Suraj on Tuesday than on Wednesday?

Solution. (1) (c) On comparing the whole part of 5.60, 3.95, 7.37 and 6.72, we get 7 > 6 > 5 > 3

∴ 7.37 is greater than the other number.

Hence, house number 159 pays the most.

(2) Weight of clothes collected for washing and folding are 5.60 kg, 3.95 kg, 7.37 kg and 6.72 kg.

∴ Total weight of cloths

= 5.60 kg + 3.95 kg + 7.37 kg + 6.72 kg = 23.64 kg

(3) Weight of clothes collected on Tuesday = 30.50 kg

Weight of clothes collected on Wednesday = 25.48 kg

∴ Difference in weight of clothes

= Weight of clothes collected on Tuesday – Weight of clothes collected on Wednesday

= 30.50 kg – 25.48 kg

= (30.50 – 25.48) kg

= 5.02 kg

Hence, Suraj collected 5.02 kg more clothes on Tuesday than on Wednesday.

Mp Board Class 6 Book Solutions

Question 2. The picture shows the nutritional information on a packet of cookies.

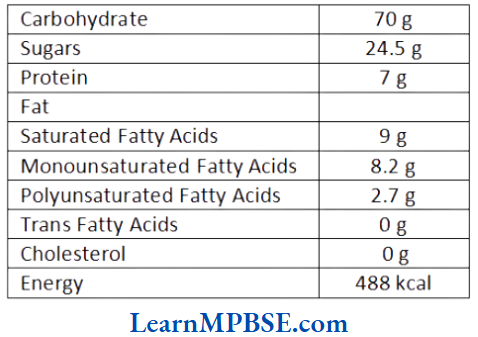
The cookies contain four types of fat.

(1) How much fat (in g) is in 100 g of cookies?

(2) Which fat content is the highest in the cookies?

(a) Saturated Fatty Acids.

(b) Monounsaturated Fatty Acids

(c) Polyunsaturated Fatty Acids

(3) The sugar content in the cookies is more than three times the protein content. Do you agree with this statement? Give reasons.

Solution. (1) To find out how much fat is in 100 g of cookies we need to add up the amount of each type of fat listed in the nutritional information.

∴ Fat Saturated Fatty Acids + Monounsaturated Fatty Acids + Polyunsaturated Fatty Acids + Trans Fatty Acids.

= 9 g + 8.2 g + 2.7 g + 0g = 199 g

(2) (a) We need to compare the amount of each type of fat 0 g < 2.7 g < 8.2 g < 9g

∴ Saturated Fatty acids is the highest type of fat content in the cookies.

(3) (b) From the nutritional, information, we see that the cookies contain 24.5 g of sugar and 7 g of protein per 100 g of cookies.

For compare these values, we have

7 + 7 + 7 = 3 x 7 = 21 < 24.5

(content of sugar in cookies)

\(=\frac{\text { Sugar }}{\text { Protein }}=\frac{24.5}{7}=3.5\)

This shows that the sugar content is more than 3 times the protein content.

∴ Yes, I agree that sugar content in the cookies is more than three times the protein content.

Question 3. Pulkit sets the car air-conditioner at 18.5° C when he starts the car. After a while, he increases the temperature to 21° C.

(1) How much is the increment in the temperature?

(2) Later, he increase the temperature to 24.5° C. What is the total change in temperature?

(3) 160.3 cm = …..

(a) 160 cm + 3 cm

(b) 160 cm + 3 mm

(c) 160 m + 3 cm

(d) 160 mm + 3 cm

(4) Ritesh’s height is 162.9 cm and Aarav’s height is 163.2 cm. What is the difference between their heights?

Solution. (1) Increment in Temperature = 21° C – 18.5°C = 25°C

(2) Total change in temperature = 24.5° C – 18.5°C = 6°C

(3) (b) We know that, 1 cm = 10 mm

Therefore, 160.3 cm = 160 cm + 0.3 cm

= 160 cm + 0.3 × 10 mm

= 160 cm + 3mm

(4) Given, Ritesh’s height=162.9 cm and Aarav’s height = 163.2 cm

∴ Difference between their heights

= 163.2 cm – 162.9 cm

= (163.2 – 162.9) cm

= 0.3 cm

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Very Short Answer Type Questions

Question 1. Which one is greater 1 or 0.98?

Solution. Here, we have 1 and 0.98

Since, whole of 1 is greater than whole of 0.98.

∴ 1 > 0.98

Question 2. Write ₹ 12 and 80 paise in rupees using decimal.

Solution. Given, 12 rupees and 80 paise = \(₹\left(12+\frac{80}{100}\right)=₹ 12.80\)

Question 3. Convert 5214 g to kg.

Solution. We know that 1 g = \(\frac{1}{1000} \mathrm{~kg}\)

∴ \(5214 \mathrm{~g}=\frac{5214}{1000} \mathrm{~kg}\)

= 5.214 kg

Mp Board Class 6 Maths Solutions

Question 4. Convert 12 mm into centimetres using decimals.

Solution. We have, 12 mm

\(12 \mathrm{~mm}=12 \times \frac{1}{10} \mathrm{~cm}=1.2 \mathrm{~cm}\)

Question 5. Find 0.09 + 0.731.

Solution. Here, 0.09 + 0.731 = 0.821

Question 6. Find 11.7 – 6.213.

Solution. Here, 11.7 – 6.213 = 5.487

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Short Answer Type Questions

Question 1. Arrange the following decimal numbers in ascending order 3.74, 2.791, 6.002, 6.2, 4.91

Solution. Given, decimal numbers are 3.74,2.791,6.002,6.2,491

By converting into like decimals, we get

3.740, 2.791, 6.002, 6.200, 4.910

On comparing these like decimals, we get

2.791 < 3.740 4.910 < 6.002 < 6.200

Thus, 2.791 < 3.74 < 4.91 < 6.002 < 6.2

Question 2. Arrange the following decimal numbers in descending order. 1.93, 4.001, 4.10, 19.21, 6.432

Solution. Given, decimal numbers are 1.93, 4.001, 4.10, 19.21, 6.432

By converting into like decimals, we get

1.930, 4.001, 4.100, 19.210, 6.432

On comparing these like decimals, we get

19.210 > 6.432 > 4.100 > 4.001 > 1.930

Thus, 19.21 > 6.432 > 4.10 > 4.001 > 1.93

Mp Board Class 6 Maths Solutions

Question 3. Express in kilometers, using decimals.

(1) 15 km 245 m

(2) 19 km 48 m

Solution. We know that 1000 m = 1 km

⇒ \(1 \mathrm{~m}=\frac{1}{1000} \mathrm{~km}\)

(1) \(15 \mathrm{~km} 245 \mathrm{~m}=15 \mathrm{~km}+\frac{245}{1000} \mathrm{~km}\)

= 15 km + 0.245 km = 15.245 km

(2) \(19 \mathrm{~km} 48 \mathrm{~m}=19 \mathrm{~km}+48 \mathrm{~m}=19 \mathrm{~km}+\frac{48}{1000} \mathrm{~km}\)

= 19 km + 0.048 km = 19.048 km

Question 4. Which one is greater?

1 metre 40 centimeters + 60 centimeters or 2.6 metres.

Solution. We know that

\(1 \mathrm{~cm}=\frac{1}{100} \mathrm{~m}\)

∴ 1 m 40 cm = 1 m + 40 cm = \(1 \mathrm{~m}+40 \times \frac{1}{100} \mathrm{~m}\)

= \(1 \mathrm{~m}+\frac{40}{100} \mathrm{~m}=1 \mathrm{~m}+0.40 \mathrm{~m}=1.40 \mathrm{~m}\)

and \(60 \mathrm{~cm}=60 \times \frac{1}{60} \mathrm{~m}=\frac{60}{100} \mathrm{~m}=0.60 \mathrm{~m}\)

Now, 1 m 40 cm + 60 cm = 1.40 m + 0.60 m = 2.0 m

So, we have to compare 2.0 m and 2.6 m

Here, whole part of both numbers are same.

So, compare the tenths part, we get

0 < 6

Here, 2.6 > 2.0.

Therefore, 2.6 metres is greater than

(1 m + 40 cm + 60 cm).

Question 5. Add 67.25, 249, 8.785, 9.8 and 0.23.

Solution. Converting the given decimals into like decimals, we get 67.250, 249.000, 8.785, 9.800 and 0.230

Here, 67.250 + 249.000 + 8.785 + 9.800 + 0.230 = 335.065

Question 6. During three days of a week, a rickshaw puller earns ₹ 40.20, ₹ 60.10 and ₹ 55, respectively. What is his total earning during these days?

Solution. Earning on 1st day = ₹ 40.20

Earning on 2nd day = ₹ 60.10

Earning on 3rd day = ₹ 55.00

∴ Total earning = ₹ 40.20 + ₹ 60.10 + ₹ 55.00 = ₹ 155.30

Question 7. Subtract

(1) ₹ 5.35 from ₹ 9.48

(2) 0.316 kg from 2.876 kg.

Solution. (1) ₹ 9.48 – ₹ 5.36

i.e. 9.48 – 5.36 = ₹ 4.12

(2) 2.876 kg – 0.316 kg

i.e. 2.876 – 0.316 = 2.560 kg

Mp Board Class 6 Maths Solutions

Question 8. What should be added to 25.5 to get 50?

Solution. We subtract 25.5 from 50 to get the required result.

∴ 50.0 – 25.5 = 24.5

So, 24.5 should be added to 25.5 to get 50.

Question 9. What should be subtracted from 117.47 to get 47.95?

Solution. To get the required number, we have

117.47 – 47.95 = 69.52

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Long Answer Type Questions

Question 1. Rajesh covers journey by car in 3 h. He covers a distance 60 km 320 m during first hour, 54 km 70 m during the second hour and 65 km 9 m during the third hour. What is the total distance covered in his journey?

Solution. We know that 1000 m = 1 km

∴ 1m = \(\frac{1}{1000} \mathrm{~km}\)

Now, distance covered during the first hour = 60.320 km

Distance covered during the second hour = 54.070 km

Distance covered during the third hour = 65.009 km

Total distance 60.320 km + 54.070 km + 65.009 km = 179.399 km

Hence, the total length of journey is 179.399 km.

Question 2. Sohan purchased a book, a pen and a notebook for ₹ 165.35, ₹ 70 and ₹ 20.50, respectively. How much money will he have to pay to the shopkeeper for these items?

Solution. Cost of a book = ₹ 165.35

Cost of a pen = ₹ 70.00

Cost of a notebook = ₹ 20.50

∴ Total cost = ₹ 165.35 + ₹ 70.00 + ₹ 20.50 = ₹ 255.85

Hence, the total money to be paid by Ramesh is ₹ 255.85.

Question 3. Reshma went to the market with ₹ 5000 cash. Out of this money she purchased one frock, one toy and one bag costing ₹ 1150.48, ₹ 540.52 and ₹ 2160.70, respectively. How much money is left with her?

Solution. Reshma has cash in hand = ₹ 5000

Cost of one frock = ₹ 1150.48

Cost of one toy = ₹ 540.52

Cost of one bag = ₹ 2160.70

∴ Total cost = ₹ 1150.48 + ₹ 540.52 + ₹ 2160.70

= ₹ 3851.70

∴ Balance = ₹ 5000.00 – ₹ 3851.70 = ₹ 1148.30

Hence, the money left with Reshma is ₹ 1148.30.

Question 4. Seema has ₹ 2000, she bought readymade garments for ₹ 987.50, medicines for ₹ 210.25, groceries for ₹ 530.25. She denoted ₹ 200 for charity. How much money is left with her?

Solution. Total money that Seema has = ₹ 2000.

Cost of readymade garments = ₹ 1987.50

Cost of medicines = ₹ 210.25

Cost of groceries = ₹ 530.25

Total cost = ₹ 987.50 + ₹ 210.25 + ₹ 530.25 = ₹ 1728

Money donate for charity = ₹ 200

Total money spent = ₹ 1728.00 + ₹ 200 = ₹ 1928.00

∴ Balance = ₹ 2000.00 – ₹ 1928.00 = ₹ 72.00

So, 72 are left with her.

Mp Board Class 6 Maths Solutions

Question 5. Alok purchased 1 kg 200 g potatoes, 250 g dhanina, 5 kg 300 g onion, 500 g palak and 2 kg 600 g tomatoes. Find the total weight of his purchases in kilograms.

Solution. Firstly, we convert all the weight in the same unit i.e. gram into kilogram and then find the total weight.

Given, weight of potatoes = 1 kg + 200 g = 1 kg + 200 g

= \(1 \mathrm{~kg}+\frac{200}{1000} \mathrm{~kg}\) [∴ \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)]

= 1kg + 0.200 kg = 1.200 kg

Weight of dhania = \(250 \mathrm{~g}=\frac{250}{1000} \mathrm{~kg}=0.250 \mathrm{~kg}\)

Weight of onion = 5 kg 300 g = 5 kg + 300 g

= \(5 \mathrm{~kg}+\frac{300}{1000} \mathrm{~kg}=5 \mathrm{~kg}+0.300 \mathrm{~kg}\)

= 5.300 kg

Weight of palak = 500 g = \(\frac{500}{1000} \mathrm{~kg}=0.500 \mathrm{~kg}\)

Weight of tomatoes = 2 kg 600 g = 2 kg + 600 g

= \(2 \mathrm{~kg}+\frac{600}{1000} \mathrm{~kg}\) [∴ \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)]

= 2kg + 0.600 kg = 2.600 kg

∴ Total weight of his purchases in kilograms = Weight of potatoes + Weight of dhania + Weight of onion + Weight of palak + Weight of tomatoes

= 1.200 kg + 0.250 kg + 5.300 kg + 0.500 kg + 2.600 kg

= [1200 +0.250 +5.300 + 0.500 + 2.600] kg

= 9.850

Hence, the total weight is 9.850 kg.