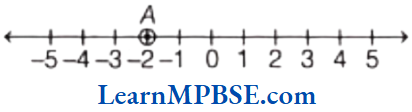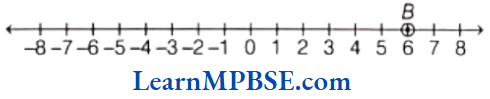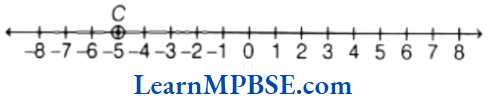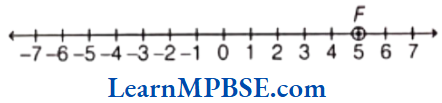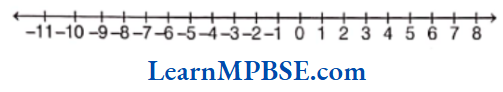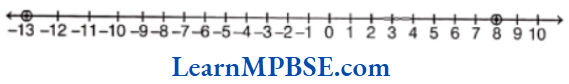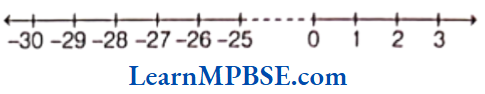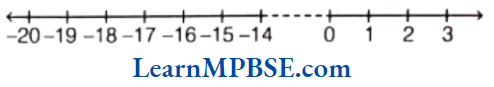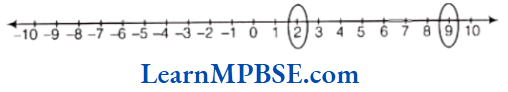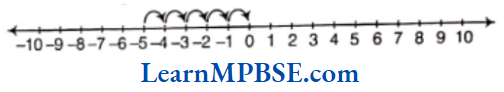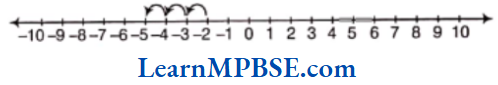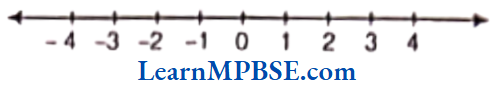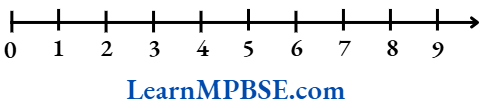tanuja

Chapter 7 Fraction and Its Representation

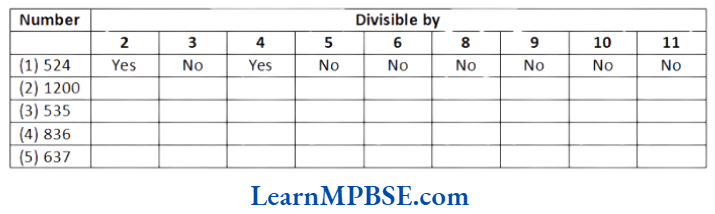
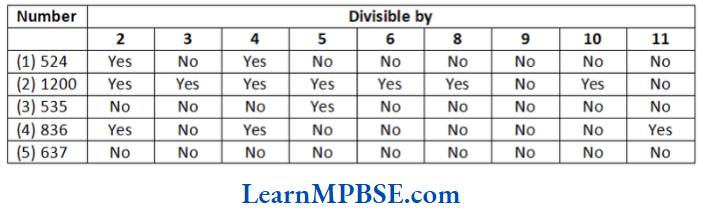
Fraction

A fraction is a number representing part of a whole. The whole may be a single object or a group of objects. It is defined as

Here, the denominator can never be zero.

e.g. (1) \(\frac{1}{5}\) is a fraction and it is read as one-fifth, which means that 1 part out of 5 equal parts in which the whole is divided. Also, here 1 is called, the numerator and 5 is called, the denominator.

(2) If we take a pizza and divide it equally among 4 persons, then each person will have \(\frac{1}{4}\) or written in word, one quarter of the pizza.

Read and Learn More MP Board Class 6 Maths Solutions

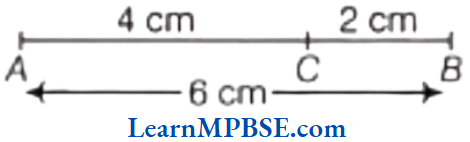
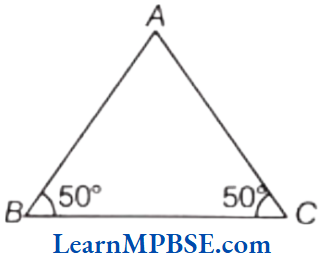
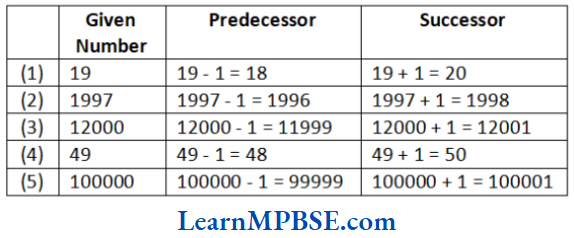
Example 1. What fraction of a day is 15 h?

Solution. We know that, one day = 24 h

∴ The required fraction = \(\frac{15 \mathrm{~h}}{24 \mathrm{~h}}=\frac{15}{24}\)

MP Board Class 6 Maths Solutions 

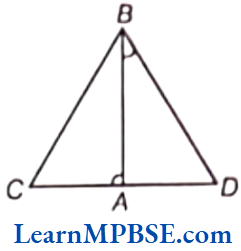
Example 2. Write the fraction representing the shaded portion.

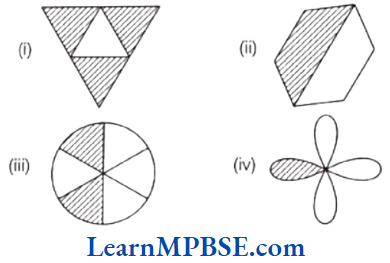
Solution. (1) Total number of equal parts = 4 and shaded parts = 3

∴ Fraction representing the shaded portion

(2) Total number of equal parts = 2 and shaded part = 1

∴ Fraction representing the shaded portion

(3) Total number of equal parts = 6 and shaded parts = 2

∴ Fraction representing the shaded portion

(4) Total number of equal parts = 4 and shaded part = 1

∴ Fraction representing the shaded portion

Example 3. Shade the part according to the given fraction.

Solution. The figures are shaded as per given fraction shown below

Example 4. Identify the error, if any.

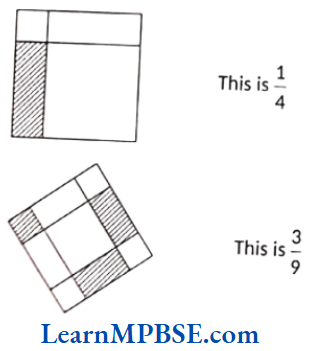
Solution. (1) In this given figure, four parts are not equal.

So, fraction is not equal to \(\frac{1}{4}\)

(2) In this given figure, all the nine parts are not equal.

Fraction is not equal to \(\frac{3}{9}\).

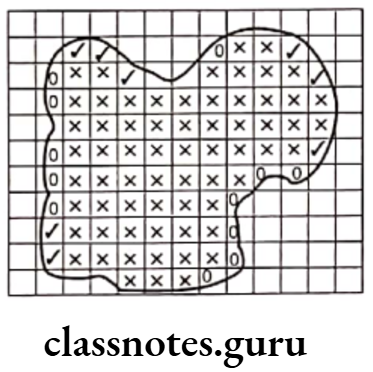
Example 5. What fraction of these boxes have a cross (x) In them?

Solution. Total number of boxes = 8,

Number of boxes having cross sign (x) = 3

∴ Required fraction

MP Board Class 6 Maths Solutions 

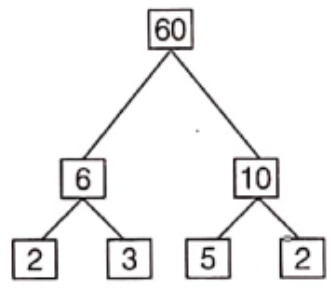
Example 6. Write the natural numbers from 113 to 125. What fraction of them are prime numbers?

Solution. Natural numbers from 113 to 125

= 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125.

Total natural numbers = 13

Prime number from 113 to 125 = 113

Total prime numbers = 1

∴ Required fraction \(=\frac{\text { Total prime numbers }}{\text { Total natural numbers }}=\frac{1}{13}\)

Example 7. Three girls Manisha, Sakshi and Shubhangini shared lunch at school. Manisha has brought two burgers, one is veg burger and one is non-veg. The other two girls forget to bring their lunch.

Manisha agreed to share her burgers so that each person will have an equal share of each burgers.

(1) How can Manisha divided her burgers so that each person has an equal share?

(2) What part of a burger will every girl receive?

Solution. Total number of burgers = 2,

Total number of girls = 3

(1) Here, Manisha has to divide 2 burgers into three person. So, she will divided each burger into three equal parts and give one part of each burger to each of them.

Thus, each person will get \(\frac{2}{3}\) burgers.

(2) One burger is to be divided among three girls.

Total number of parts = 6

Each gets 2 parts out of 6.

Then, the fraction = \(\frac{2}{6}\)

∴ Each girl will get = part of a burger.

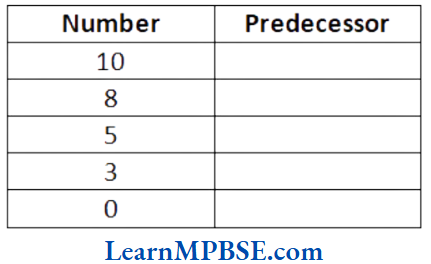
Chapter 7 Fractions Representation on Number Line and Types of Fraction

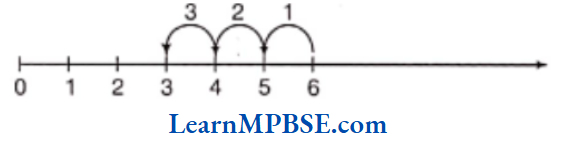
Fraction on the Number Line

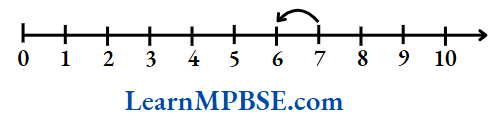
Every fraction has a point associated with it on the number line. For this, we will need to divide the gap of 0 to 1 into as many equal parts as in the denominator of that fraction.

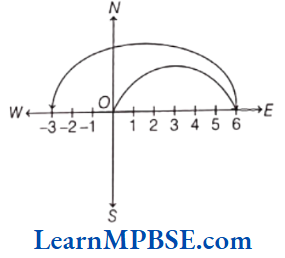
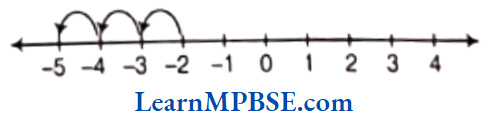
Suppose, we want to denote the fraction \(\frac{5}{7}\) on the number line. Now, take a line OP of unit length.

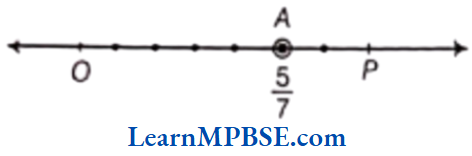
Divide line OP into seven equal parts and take 5 parts out of it to reach the point A. Then, the point A represents the number \(\frac{5}{7}\).

MP Board Class 6 Maths Solutions 

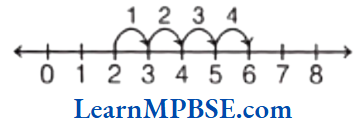
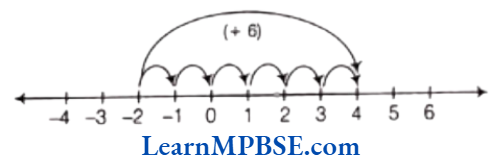
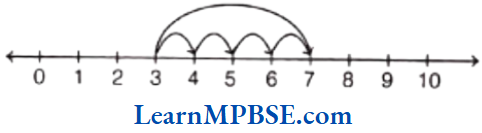
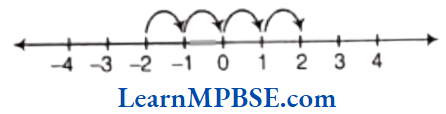
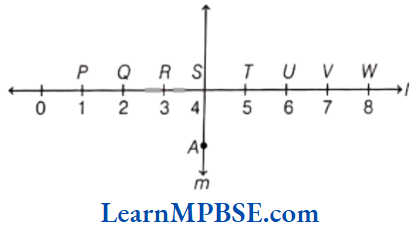
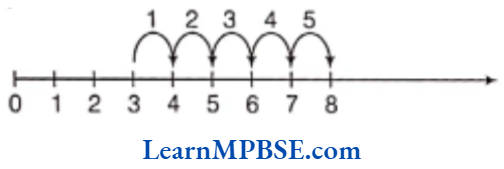
Example 1. Show \(\frac{4}{5}\) on a number line.

Solution. We know that \(\frac{4}{5}\) is greater than zero but less than 1. So, it will lie between 0 and 1.

Now, we have to show \(\frac{4}{5}\) on a number line.

So, we have to divide the length between 0 and 1 into 5 equal parts and take 4 parts out of it to reach point A.

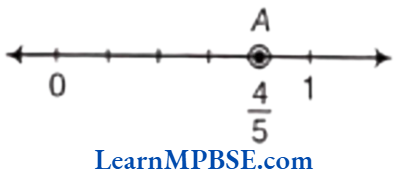
Then, the point A represents the number

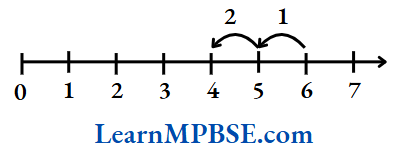
Example 2. Write the fraction denoted by point A

Solution. Point A is marked at fifth place out of 10.

Therefore, fraction is \(\frac{5}{10}\).

MP Board Class 6 Maths Solutions 

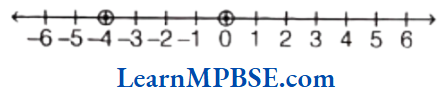
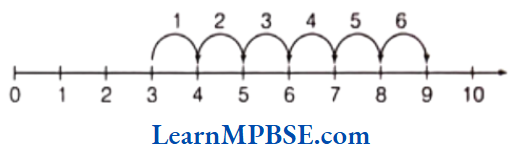
Example 3. Show \(\frac{2}{9}, \frac{5}{9}, \frac{0}{9} \text { and } \frac{9}{9}\) on a number line.

Solution. We know that, all given fractions are greater than or equal to zero but less than or equal to 1.

So, we have to divide the gap between 0 and 1 into nine equal parts, then each part shows \(\frac{1}{9}\) and 2 part shows \(\frac{2}{9}\), 5 part shows \(\frac{5}{9}\), 9 part shows \(\frac{9}{9}\)

Also, 0 shows \(\frac{0}{9}\).

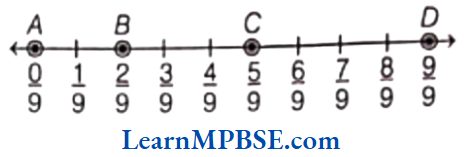
Hence, points A, B, C and D respectively represents the fraction \(\frac{0}{9}, \frac{2}{9}, \frac{5}{9} \text { and } \frac{9}{9} \text {. }\)

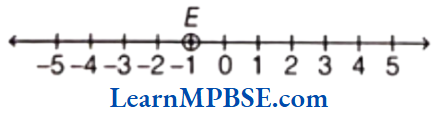
Example 4. Write five fraction between 0 and 1 that you can show and depict them on the number line.

Solution. As, we know that, we can show many fractions which are greater than 0 and less than 1

i.e. between 0 and 1.

Five fractions are \(\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6} \text { and } \frac{5}{6}\)

These fraction are shown on a number line as given below.

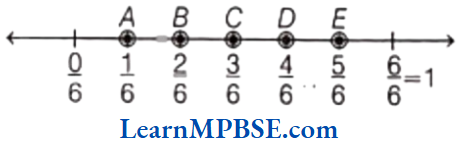
Hence, points A, B, C, D and E represent \(\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}\) and \(\frac{5}{6}\) respectively.

Note It Between two whole numbers, there lie infinite fractions.

Types of Fraction

Proper Fraction

A fraction whose numerator is always less than the denominator is called a proper fraction.

i.e. Numerator < Denominator.

e.g. \(\frac{9}{10}\), \(\frac{5}{8}\) are proper fractions. It is always less than 1. So, if 10’8 we represent a proper fraction on a number line, it will always lie to the left of 1.

MP Board Class 6 Maths Solutions 

Example 5. Choose the proper fraction from the following numbers.

\(6 \frac{1}{2}, \frac{8}{3}, \frac{2}{9}, 7 \frac{2}{3}\)

Solution. A fraction is proper fraction, if numerator is less than denominator.

Therefore, \(\frac{2}{9}\) is a proper fraction.

Example 6. Give a proper fraction:

(1) Whose numerator is 4 and denominator is 7.

(2) Whose denominator is 8 and numerator is 1.

(3) Whose numerator and denominator add upto 8. How many fractions of this kind can you make?

(4) Whose denominator is 3 more than numerator. (Give any five. How many more can you make?)

Solution. (1) Numerator = 4 and denominator = 7

∴ Required fraction = \(\frac{4}{7}\)

(2) Numerator = 1 and denominator = 8

∴ Required fraction = \(\frac{1}{8}\)

(3) Possible pairs of numerator and denominator which

add upto 8 are (0, 8), (1, 7), (2, 6), (3, 5).

Now, proper fractions = \(\frac{0}{8}, \frac{1}{7}, \frac{2}{6}, \frac{3}{5}\)

There are four fraction.

So, we can make four such fractions.

(4) There can be infinite number of fractions whose denominator is 3 more than the numerator.

Some of them \(\frac{0}{3}, \frac{1}{4}, \frac{2}{5}, \frac{3}{6}, \frac{4}{7} \ldots \ldots\) so on.

Improper Fraction

A fraction whose numerator is always greater than the denominator is called an improper fraction.

i.e. Numerator > denominator.

e.g. \(\frac{3}{2}\), \(\frac{18}{5}\) are improper fractions.

It is always greater than 1. So, if we represent an improper fraction on a number line, it will always lie to the right of 1.

MP Board Class 6 Maths Solutions 

Example 7. Write five improper fractions with denominator 8.

Solution. Five improper fractions with denominator 8 are \(\frac{9}{8}, \frac{10}{8}, \frac{11}{8}, \frac{12}{8}, \frac{13}{8}\)

Mixed Fraction

A fraction which is a combination of a whole number and a proper fraction (or part) is called a mixed fraction.

e.g. \(1 \frac{1}{4}\) is a mixed fraction. Here, I is a whole number and \(\frac{1}{4}\) is a proper fraction.

Example 8. Combine the following as a mixed fraction.

(1) 2 and one-third

(2) 5 and \(\frac{3}{5}\)

Solution. (1) We have, 2 and one-third.

Here, whole part = 2

and proper fraction part = One-third = \(\frac{1}{3}\)

∴ Mixed fraction = \(2 \frac{1}{3}\)

(2) We have, 5 and \(\frac{3}{5}\)

Here, whole part = 5 and proper fraction = \(\frac{3}{5}\)

∴ Mixed fraction = \(5 \frac{3}{5}\)

Conversion of an Improper Fraction into a Mixed Fraction

To express an improper fraction as a mixed fraction, firstly we divide the numerator by denominator to obtain the quotient and the remainder. Then,

Mixed fraction = \(\text { Quotient } \frac{\text { Remainder }}{\text { Divisor }}\)

e.g. Consider an improper fraction = \(\frac{17}{4}\)

Now, dividing numerator by denominator

i.e. 17 by 4, we get quotient = 4 and remainder = 1

Hence, mixed fraction = \(4 \frac{1}{4}\)

MP Board Class 6 Maths Solutions 

Example 9. Express the following as mixed fractions.

(1) \(\frac{19}{3}\)

(2) \(\frac{14}{4}\)

(3) \(\frac{17}{7}\)

(4) \(\frac{33}{9}\)

Solution. (1) We have, \(\frac{19}{3}\)

On dividing 19 by 3, we get quotient = 6 and remainder = 1.

Hence, mixed fraction = \(6 \frac{1}{3}\)

(2) We have, \(\frac{14}{4}\)

On dividing 14 by 4, we get quotient = 3 and remainder = 2

Hence, mixed fraction = \(3 \frac{2}{4}\)

(3) We have, \(\frac{17}{7}\)

On dividing 17 by 7, we get quotient = 2 and remainder = 3

Hence, mixed fraction = \(2 \frac{3}{7}\)

(4) We have \(\frac{33}{9}\)

On dividing 33 by 9, we get quotient = 3 and remainder = 6

Hence, mixed fraction = \(3 \frac{6}{9}\)

Conversion of a Mixed Fraction into an Improper Fraction

Multiply the whole number with denominator of the fraction and then add the numerator of the fraction. This gives the numerator of the required improper fraction. Its denominator is the same as the denominator of the fractional part of mixed fraction.

Improper fraction \(=\frac{\text { Whole part } \times \text { Denominator }+ \text { Numerator }}{\text { Denominator }}\)

MP Board Class 6 Maths Solutions 

Example 10. Express the following fractions as improper fractions.

(1) \(3 \frac{2}{5}\)

(2) \(2 \frac{3}{7}\)

(3) \(7 \frac{1}{4}\)

(4) \(3 \frac{1}{6}\)

(5) \(7 \frac{3}{8}\)

(6) \(11 \frac{3}{2}\)

Solution.

(1) We have, \(3 \frac{2}{5}=3+\frac{2}{5}=\frac{3 \times 5+2}{5}=\frac{17}{5}\)

(2) We have, \(2 \frac{3}{7}=2+\frac{3}{7}=\frac{2 \times 7+3}{7}=\frac{17}{7}\)

(3) We have, \(7 \frac{1}{4}=7+\frac{1}{4}=\frac{7 \times 4+1}{4}=\frac{29}{4}\)

(4) We have, \(3 \frac{1}{6}=3+\frac{1}{6}=\frac{3 \times 6+1}{6}=\frac{19}{6}\)

(5) We have, \(7 \frac{3}{8}=7+\frac{3}{8}=\frac{7 \times 8+3}{8}=\frac{59}{8}\)

(6) We have, \(11 \frac{3}{2}=11+\frac{3}{2}=\frac{22+3}{2}=\frac{25}{2}\)

Chapter 7 Fractions Equivalent Fraction and Simplest Form of a Fraction

Equivalent Fraction

Fractions having the same values are called equivalent fractions. To find an equivalent fraction of a given number, we multiply or divide the numerator and the denominator of the given fraction by the same non-zero number.

Example 1. Find five equivalent fractions of each of the following

(1) \(\frac{2}{3}\)

(2) \(\frac{1}{5}\)

Solution.

(1) Given, fraction is \(\frac{2}{3}\).

∴ \(\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{2 \times 3}{3 \times 3}=\frac{2 \times 4}{3 \times 4}=\frac{2 \times 5}{3 \times 5}=\frac{2 \times 6}{3 \times 6}\)

⇒ \(\frac{4}{6}=\frac{6}{9}=\frac{8}{12}=\frac{10}{15}=\frac{12}{18}\)

Hence, the five fractions equivalent to \(\frac{2}{3}\) are \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15} \text { and } \frac{12}{18}\).

(2) Given, fraction is \(\frac{1}{5}\).

⇒ \(\frac{2}{10}=\frac{3}{15}=\frac{4}{20}=\frac{5}{25}=\frac{6}{30}\)

Hence, the five fractions equivalent to \(\frac{1}{5}\) are \(\frac{2}{10}, \frac{3}{15}, \frac{4}{20}, \frac{5}{25} \text { and } \frac{6}{30} .\)

Example 2. Give example of four equivalent fractions.

Solution. Four equivalent fractions are \(\frac{1}{3}, \frac{2}{6}, \frac{3}{9}, \frac{4}{12},\) etc.

To Test Whether Two Given Fractions are Equivalent or not

We can check whether two fractions are equivalent or not by finding their cross product i.e. we multiply the numerator of first fraction with the denominator of second fraction and the denominator of first fraction with the numerator of sechond fraction. If the two products are equal, then the given fractions are equivalent, otherwise not.

Let \(\frac{a}{b}\) and \(\frac{c}{d}\) be two given fractions. Their cross multiplication shown as

(1) If ad = bc, then \(\frac{a}{b}\) and \(\frac{c}{d}\) are equivalent.

(2) If ad < bc, then \(\frac{a}{b}\) < \(\frac{c}{d}\)

(3) If ad > bc, then \(\frac{a}{b}\) > \(\frac{c}{d}\)

Class 6 Maths Chapter 7 Solutions

Example 3. Check whether the fractions \(\frac{5}{8}\) and \(\frac{15}{24}\) are equivalent or not.

Solution. Let \(\frac{a}{b}\) = \(\frac{5}{8}\), \(\frac{c}{d}\) = \(\frac{15}{24}\).

By Cross multiplication \(\frac{a}{b} \times \frac{c}{d}\)

We have \(\frac{5}{8} \times \frac{15}{24}\),

Here, ad = bc i.e. 5 x 24 = 15 x 8 = 120

So, \(\frac{5}{8}\) and \(\frac{15}{24}\) are equivalent.

Example 4. Identify the fractions in each. Are these fractions equivalent?

Solution. (1) Here, the total parts is 4, out of which 2 parts are shaded. So, required fraction = \(\frac{2}{4}\)

(2) Here, total parts are 6, out of which 3 parts are shaded. So, required fraction = \(\frac{3}{6}\)

Now, take \(\frac{2}{4}\) and \(\frac{3}{6}\). Here, 2 x 6 = 12 and 3 × 4 = 12

∴ 12 = 12,

∴ \(\frac{2}{4}\) and \(\frac{3}{6}\) are equivalent.

Example 5. Write a fraction equivalent to \(\frac{3}{5}\) with numerator 12.

Solution. Let D stands for denominator.

Given, numerator of an equivalent fraction = 12

\(\frac{12}{D}\) = \(\frac{3}{5}\) ⇒ D x 3 = 12 x 5 ⇒ D = \(\frac{12 \times 5}{3}=20\)

Hence, required equivalent fraction of \(\frac{3}{5}\) is \(\frac{12}{20}\).

Example 6. Write a fraction equivalent to with denominator 35.

Solution. Let N stands for numerator.

Given, denominator of an equivalent fraction = 35

\(\frac{N}{35}\) = \(\frac{5}{7}\) ⇒ N x 7 = 35 x 5 ⇒ N = \(\frac{35 \times 5}{7}\) = 25

Hence, required equivalent fraction of \(\frac{5}{7}\) is \(\frac{25}{35}\).

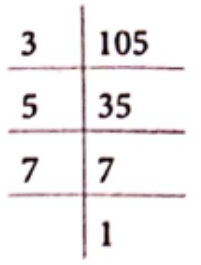
Simplest Form of a Fraction

A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1. i.e their HCF =1.

To find the equivalent fraction in the simplest form, firstly we find the HCF of the numerator and denominator and then divide both of them by their HCF.

Class 6 Maths Chapter 7 Solutions

Example 7. Write the simplest form of

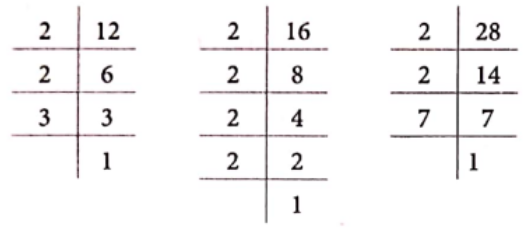
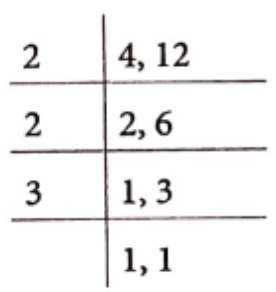
(1) \(\frac{28}{42}\)

(2) \(\frac{36}{49}\)

Solution. (1) We have, \(\frac{28}{42}\)

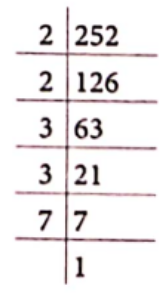
Now, factors of 28 = 2, 2, 7 and factors of 42 = 2, 3, 7 Common factors = 2 and 7

∴ HCF of 28 and 42 = 2 x 7 = 14

Then, \(\frac{28}{42}=\frac{28 \div 14}{42 \div 14}=\frac{2}{3}\)

Hence, fraction \(\frac{2}{3}\) is the simplest form of given fraction.

(2) Here, factors of 36 = 6, 6 and factors of 49 = 7, 7

∴ 36 and 49 have no common factor except 1.

Hence, fraction \(\frac{36}{49}\) is in simplest form.

Chapter 7 Fractions Like, Unlike and Comparing Fractions

Like and Unlike Fractions

Fractions having same denominator are called like fractions.

e.g. \(\frac{1}{7}, \frac{2}{7}, \frac{3}{7}\) etc.

While fractions having the different denominator are called unlike fractions.

e.g. \(\frac{2}{3}, \frac{1}{5}, \frac{2}{15}, \frac{7}{9}\) etc.

Conversion of Unlike Fraction into Like Fraction

Unlike fractions are converted into like fractions by converting each of them into their equivalent fractions having denominator equal to the LCM of all the denominators of all unlike fractions.

Example 1. Convert the fractions \(\frac{1}{2}\), \(\frac{2}{3}\) and \(\frac{5}{6}\) into like fractions.

Solution. The given fractions are \(\frac{1}{2}\), \(\frac{2}{3}\) and \(\frac{5}{6}\).

LCM of denominators 2, 3 and 6 = 6

We convert each of the fraction into an equivalent fraction with 6 as the denominator.

and \(\frac{5}{6}=\frac{5 \times 1}{6 \times 1}=\frac{5}{6}\)

The required like fractions are \(\frac{3}{6}\), \(\frac{4}{6}\) and \(\frac{5}{6}\).

Comparing Fractions

There are two methods of comparison of fractions which are given below

Comparison of Like Fractions

If two fractions have same denominator, then the fraction with the greater numerator is greater.

e.g. Between \(\frac{11}{20}\) and \(\frac{13}{20}\), the fraction \(\frac{13}{20}\) is grater.

Class 6 Maths Chapter 7 Solutions

Example 2. Which is the larger fraction?

(1) \(\frac{6}{10}\) or \(\frac{7}{10}\)

(2) \(\frac{12}{24}\) or \(\frac{13}{24}\)

Solution. We have, \(\frac{6}{10}\) or \(\frac{7}{10}\)

Here, denominators of both fractions are same and 7 > 6.

So, \(\frac{7}{10}\) > \(\frac{6}{10}\)

(2) We have, \(\frac{12}{24}\) or \(\frac{13}{24}\)

Here, denominator of both fractions are same and 13 > 12.

So, \(\frac{13}{24}\) > \(\frac{12}{24}\)

Example 3. Parul reads 20 pages of a novel containing 100 pages. Sachin reads \(\frac{2}{5}\) of the same book. Who read less?

Solution. Fraction of book read by Parul = \(\frac{20}{100}\) = \(\frac{1}{5}\)

Fraction of novel read by Sachin = \(\frac{2}{5}\)

Here, denominator of both fractions are same and 2 > 1.

∴ \(\frac{1}{5}\) < \(\frac{2}{5}\)

Hence, Parul reads less pages of the novel.

Example 4. Write the following in ascending and descending order.

(1) \(\frac{2}{9}, \frac{7}{9}, \frac{5}{9}\)

(2) \(\frac{1}{3}, \frac{11}{3}, \frac{4}{3}, \frac{7}{3}, \frac{5}{3}\)

Solution. (1) We have, \(\frac{2}{9}, \frac{7}{9}, \frac{5}{9}\)

Here, denominator of all fractions are same.

∴ Ascending order of numerator = 2 < 5 < 7

and descending order of numerator = 7 > 5 > 2

∴ Ascending order of fraction = \(\frac{2}{9}<\frac{5}{9}<\frac{7}{9}\)

and descending order of fraction = \(\frac{7}{9}>\frac{5}{9}>\frac{2}{9}\)

(2) Since, denominator of all fractions are same.

∴ Ascending order of fraction = \(\frac{1}{3}<\frac{4}{3}<\frac{5}{3}<\frac{7}{3}<\frac{11}{3}\)

and descending order of fraction = \(\frac{11}{3}>\frac{7}{3}>\frac{5}{3}>\frac{4}{3}>\frac{1}{3}\)

Class 6 Maths Chapter 7 Solutions

Example 5. Write shaded portion as fraction. Arrange them in ascending and descending order using correct sign,>’ between the fractions.

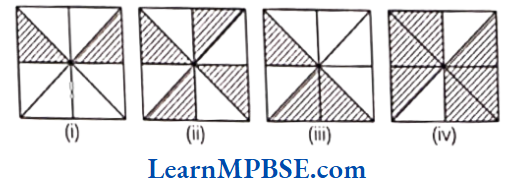
Solution. Here, total number of equal parts in all figures = 8

Shaded portion of figure (1) represents fraction = \(\frac{2}{8}\)

Shaded portion of figure (2) represents fraction = \(\frac{4}{8}\)

Shaded portion of figure (3) represents fraction = \(\frac{3}{8}\)

Shaded portion of figure (4) represents fraction = \(\frac{6}{8}\)

∴ Denominator of all fractions are same. So, we arrange them in ascending order and descending order according to their numerators.

∴ Ascending order of fractions \(\frac{2}{8}<\frac{3}{8}<\frac{4}{8}<\frac{6}{8}\)

[∴ fraction with small numerator will be smaller]

and descending order of fractions = \(\frac{6}{8}>\frac{4}{8}>\frac{3}{8}>\frac{2}{8}\)

[∴ fraction having greatest numerator will be greatest].

Comparison of Unlike Fractions

There are two types of comparison of unlike fractions.

Comparison of Unlike Fractions with Same Numerators

Among two fractions having same numerator, the one with the smaller denominator is the greater of the two.

e.g. \(\frac{7}{11}>\frac{7}{13} \text { and } \frac{11}{23}>\frac{11}{25}\)

MP Board Class 6 Chapter 7 Maths 

Example 6. Arrange the following in ascending and descending order.

\(\frac{2}{13}, \frac{2}{11}, \frac{2}{17}, \frac{2}{5}, \frac{2}{7}, \frac{2}{9}, \frac{2}{55}\)

Solution. Here, numerator of all fractions are same.

Descending order of denominators

= 55 > 17 > 13 > 11 > 9 > 7 > 5.

∴ Ascending order of fraction

= \(\frac{2}{55}<\frac{2}{17}<\frac{2}{13}<\frac{2}{11}<\frac{2}{9}<\frac{2}{7}<\frac{2}{5}\)

∴ [\(\frac{2}{55}\) has larger denominator, so it is smallest fraction].

and descending order of fractions.

= \(\frac{2}{5}>\frac{2}{7}>\frac{2}{9}>\frac{2}{11}>\frac{2}{13}>\frac{2}{17}>\frac{2}{55}\)

Example 7. Kanchan and Kiran are two friends. Kanchan get one-fifth of a bottle of apple juice and Kiran get one-fourth of a bottle of apple juice. Who gets more?

Solution. Here, we will compare one-fifth i.e. \(\frac{1}{5}\) and one-fourth i.e. \(\frac{1}{4}\).

Since \(\frac{1}{5}\) and \(\frac{1}{4}\) have same numerator, so the fraction with smaller denominator is greater.

Thus, \(\frac{1}{4}\) > \(\frac{1}{5}\)

Thus, Kiran gets more apple juice.

Comparison of Unlike Fractions with Different Numerators

If numerator and denominator both are different of given two fractions, then for comparing, we use the method of equivalent fractions i.e. we change the denominator of a fraction without changing its value.

MP Board Class 6 Chapter 7 Maths 

Example 8. Compare \(\frac{5}{6}\) and \(\frac{13}{15}\).

Solution. The given fractions are unlike, we should first get their equivalent fractions with a denominator, which is common multiple of 6 and 15 i.e 30.

Now, \(\frac{5 \times 5}{6 \times 5}=\frac{25}{30} \text { and } \frac{13 \times 2}{15 \times 2}=\frac{26}{30}\)

Since, \(\frac{26}{30}>\frac{25}{30}, \text { so } \frac{13}{15}>\frac{5}{6}\)

Example 9. Arrange the following in ascending and descending order.

\(\frac{2}{3}, \frac{1}{9}, \frac{5}{12} \text { and } \frac{7}{36}\)

Solution. We have, \(\frac{2}{3}, \frac{1}{9}, \frac{5}{12}, \frac{7}{36}\)

LCM of 3, 9, 12 and 36 = 3 x 3 x 4 = 36

So, we convert each of the given fraction into an equivalent fraction with denominator 36.

Clearly, \(\frac{24}{36}>\frac{15}{36}>\frac{7}{36}>\frac{4}{36}\)

Hence, \(\frac{2}{3}>\frac{5}{12}>\frac{7}{36}>\frac{1}{9}\)

∴ Ascending order is \(\frac{1}{9}<\frac{7}{36}<\frac{5}{12}<\frac{2}{3}\) and descending order is \(\frac{2}{3}>\frac{5}{12}>\frac{7}{36}>\frac{1}{9}\)

Example 10. Find answer to the following. Write and indicate how you solved them.

(1) is \(\frac{5}{4}\) equal to \(\frac{9}{5}\) ?

(2) is \(\frac{20}{16}\) equal to \(\frac{5}{4}\) ?

Solution. (1) LCM of 4 and 5 = 20

Now, \(\frac{5}{4}=\frac{5 \times 5}{4 \times 5}=\frac{25}{20}\)

and \(\frac{9}{5}=\frac{9 \times 4}{5 \times 4}=\frac{36}{20}\)

Thus, both fractions are like fractions but \(\frac{25}{20} \neq \frac{36}{20}\)

∴ \(\frac{5}{4}\) ≠ \(\frac{9}{5}\)

(2) LCM of 16 and 4 = 16

Now, \(\frac{20}{16}=\frac{20 \times 1}{16 \times 1}=\frac{20}{16}\)

and \(\frac{5}{4}=\frac{5 \times 4}{4 \times 4}=\frac{20}{16}\)

Thus, both fraction are like fractions and \(\frac{20}{16}\) = \(\frac{20}{16}\)

∴ \(\frac{20}{16}\) = \(\frac{5}{4}\)

MP Board Class 6 Chapter 7 Maths 

Example 11. Ravish takes \(2 \frac{1}{5}\) min to walk across the school ground. Rahul takes \(1 \frac{3}{4}\) min to do the same. Who takes less time and by what fraction?

Solution. Time taken by Ravish to walk across the school ground = \(2 \frac{1}{5}\) min = \(\frac{11}{5}\) min

Time taken by Rahul to walk across the school ground = \(1 \frac{3}{4}\) min = \(\frac{7}{4}\) min

The LCM of 5 and 4 = 20

∴ \(\frac{11}{5}=\frac{11 \times 4}{5 \times 4}=\frac{44}{20} \text { and } \frac{7}{4}=\frac{7 \times 5}{4 \times 5}=\frac{35}{20}\)

Now, \(\frac{35}{20}\) < \(\frac{44}{20}\)

∴ \(\frac{7}{4}\) < \(\frac{11}{5}\)

⇒ Rahul takes less time.

The difference between the time taken by Ravish and Rahul to walk across the school ground = \(\frac{11}{5}\) – \(\frac{7}{4}\)

= \(\frac{44-35}{20}=\frac{9}{20} \min\)

Thus, Rahul takes \(\frac{9}{20}\) min less than Ravish.

Example 12. Asha and Deepa have bookshelves of the same size partly filled with books. Asha’s shelf is \(\frac{5}{7}\) th full and Deepa’s shelf is \(\frac{3}{5}\) th full. Whose bookshelf is more full? By what fraction?

Solution. Here, we have to compare two unlike fractions.

Asha’s shelf = \(\frac{5}{7}\)th

Deepa’s shelf = \(\frac{3}{5}\)th

∴ LCM of 7 and 5 = 35

∴ \(\frac{5}{7}=\frac{5 \times 5}{7 \times 5}=\frac{25}{35} \text { and } \frac{3}{5}=\frac{3 \times 7}{5 \times 7}=\frac{21}{35}\)

∴ 25 > 21

∴ \(\frac{5}{7}\) > \(\frac{3}{5}\)

Hene, Asha’s bookshelf is filled more than Deepa’s bookshelf.

∴ Difference = \(\frac{5}{7}-\frac{3}{5}=\frac{25}{35}-\frac{21}{35}=\frac{4}{35}\)

Therefore, Asha’s bookshelf is more full by \(\frac{4}{35}\) th than Deepa’s bookshelf.

Chapter 7 Fractions Addition and Subtraction of Like Fractions

Addition of Like Fractions

To add like fractions, we add their numerators keeping denominator unchanged and then write it in simplest form.

Suppose, we have two like fractions \(\frac{a}{b}\) and \(\frac{c}{b}\) , then sum = \(\frac{a+c}{b}\)

∴ Sum of like fractions \(=\frac{\text { Sum of their numerators }}{\text { Common denominator }}\)

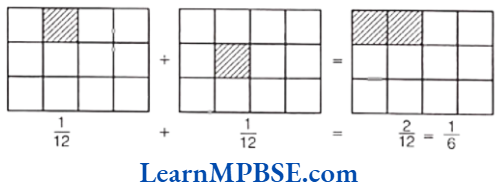
e.g. By pictorial representation

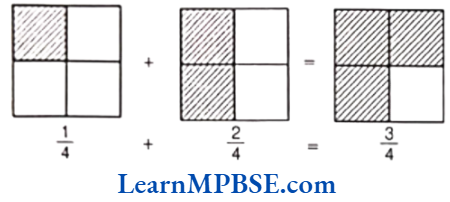
MP Board Class 6 Chapter 7 Maths 

Example 1. Add

(1) \(\frac{1}{8}+\frac{1}{8}\)

(2) \(\frac{2}{5}+\frac{3}{5}\)

Solution. (1) Let \(\frac{a}{b}\) = \(\frac{1}{8}\) and \(\frac{c}{b}\) = \(\frac{1}{8}\), then sum = \(\frac{a+c}{b}=\frac{1+1}{8}=\frac{2}{8}=\frac{1}{4}\)

Hence, the sum of \(\frac{1}{8}\) and \(\frac{1}{8}\) is \(\frac{1}{4}\).

(2) Let \(\frac{a}{b}\) = \(\frac{2}{5}\) and \(\frac{c}{b}\) = \(\frac{3}{5}\), then sum = \(\frac{a+c}{b}=\frac{2+3}{5}=\frac{5}{5}=1\)

Hence, the sum of \(\frac{2}{5}\) and \(\frac{3}{5}\) is 1.

Example 2. Add the shaded part of the fraction for the given figure.

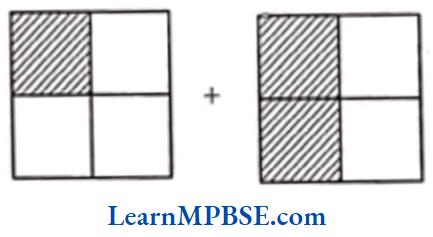
Solution. We have,

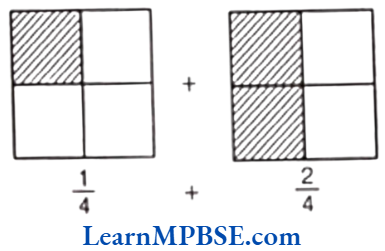
Then, pictorial representation of \(\frac{3}{4}\) is

MP Board Class 6 Chapter 7 Maths 

Example 3. Add these with the help of a diagram.

(1) \(\frac{2}{6}+\frac{3}{6}\)

(2) \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\)

Solution. (1) Here, draw two rectangles and divide them into 6 equal parts separately. In first rectangle, 2 parts out of 6 parts are shaded and in second rectangle, 3 parts out of 6 parts are shaded. On adding them, we get

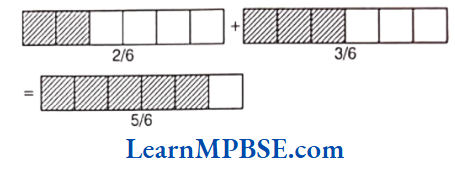
i.e. \(\frac{2}{6}+\frac{3}{6}=\frac{2+3}{6}=\frac{5}{6}\)

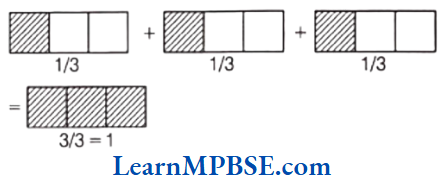
i.e. \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=\frac{1+1+1}{3}=\frac{3}{3}=1\)

Example 4. On her birthday Niharika divided a cake into 6 equal parts. She distributed 2 parts in her family and 3 parts in neighbourhood. How much cake did she distributed together?

Solution. Here, Niharika divided the cake into 6 equal parts, so each part will represent \(\frac{1}{6}\). She gave two parts in her family, i.e. \(\frac{2}{6}\) and she gave three parts in the neighbourhood, i.e. \(\frac{3}{6}\).

Part of cake she distributed = \(\frac{3}{6}+\frac{2}{6}\)

∴ Here, denominator of both fractions are same. So, we add numerator to find their sum.

i.e. \(\frac{3+2}{6}=\frac{5}{6}\)

Hence, she distributed \(\frac{5}{6}\) of the cake into her family and neighbourhood.

Subtraction of Like Fractions

To subtract like fractions, we subtract the smaller numerator from the greater numerator, keeping denominator unchanged and then write it in simplest form.

Suppose, we have two like fractions \(\frac{a}{b}\) and \(\frac{c}{b}\) (a > c), then

Difference = \(\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}\)

∴ Difference of like fractions \(=\frac{\text { Difference of their numerators }}{\text { Common denominator }}\)

MP Board Class 6 Chapter 7 Maths 

Example 5. Find the difference of \(\frac{7}{9}\) and \(\frac{2}{9}\)

Solution. Let \(\frac{a}{b}\) = \(\frac{7}{9}\) and \(\frac{c}{b}\) = \(\frac{2}{9}\)

Here, a > c i.e. 7 > 2

So, Difference \(\frac{\text { Difference of their numerators }}{\text { Common denominator }}=\frac{7-2}{9}=\frac{5}{9}\)

Example 6. Mohit was reading a book. He read one-third of book on Sunday. He read another one-third on Wednesday and the remaining on Friday. What fraction of the book did he read on Friday?

Solution. Book read by Mohit on Sunday = \(\frac{1}{3}\)

Book read by Mohit on Wednesday = \(\frac{1}{3}\)

∴ Book read by him on Friday = \(1-\frac{1}{3}-\frac{1}{3}=\frac{3}{3}-\frac{1}{3}-\frac{1}{3}\)

[∴ 1 and \(\frac{3}{3}\) are equivalent fractions]

= \(\frac{3-1-1}{3}=\frac{1}{3}\)

Hence, he read one-third of the book on Friday.

Example 7. Add the difference of \(\frac{7}{10}\) and \(\frac{2}{10}\) to \(\frac{8}{20}\)

Solution. Difference of \(\frac{7}{10}\) and \(\frac{2}{10}\) is equal to \(\frac{7}{10}\) – \(\frac{2}{10}\).

[Since, both are like fractions and 7 is greater than 2, so subtract \(\frac{2}{10}\) from \(\frac{7}{10}\)]

Now, \(\frac{7}{10}-\frac{2}{10}=\frac{7-2}{10}=\frac{5}{10} \text { or } \frac{1}{2}\)

Now, adding \(\frac{5}{10} \text { to } \frac{8}{20} \text { i.e. } \frac{5}{10}+\frac{8}{20}\)

Here, LCM of 10 and 20 are 20.

∴ \(\frac{5 \times 2}{10 \times 2}+\frac{8}{20}=\frac{10}{20}+\frac{8}{20}=\frac{18}{20}=\frac{9}{10}\)

MP Board Class 6 Chapter 7 Maths 

Chapter 7 Fractions Addition and Subtraction of Unlike and Mixed Fractions

Addition of Unlike Fractions

To add unlike fractions, we first convert them into equivalent fractions with the same denominator (which is LCM of denominators) and then add them as like fractions.

Example 1. Add the following

(1) \(\frac{2}{6}\) and \(\frac{3}{4}\)

(2) \(\frac{3}{7}\) and \(\frac{5}{8}\)

Solution. (1) We have, \(\frac{2}{6}+\frac{3}{4}\)

LCM of 6 and 4 = 12

∴ \(\frac{2}{6}+\frac{3}{4}=\frac{2 \times 2}{6 \times 2}+\frac{3 \times 3}{4 \times 3}=\frac{4}{12}+\frac{9}{12}=\frac{13}{12}\)

Hence, \(\frac{2}{6}+\frac{3}{4}=\frac{13}{12}\)

(2) We have,\( \frac{3}{7}+\frac{5}{8}\)

LCM of 7 and 8 = 56

∴ \(\frac{3}{7}+\frac{5}{8}=\frac{3 \times 8}{7 \times 8}+\frac{5 \times 7}{8 \times 7}=\frac{24}{56}+\frac{35}{56}=\frac{59}{56}\)

Hence, \(\frac{3}{7}+\frac{5}{8}=\frac{59}{56}\)

Example 2. Karishma bought \(\frac{3}{5}\) m of cloth for her college dress and her mother bought \(\frac{2}{7}\) m of cloth. What is the total length of the cloth they bought?

Solution. Given, cloth bought by Karishma = \(\frac{3}{5}\) m

and cloth bought by her mother = \(\frac{2}{7}\) m

∴ Total length of cloth bought by them = \(\left(\frac{3}{5}+\frac{2}{7}\right) \mathrm{m}\)

Now, LCM of 5 and 7 = 35

∴ \(\frac{3}{5}+\frac{2}{7}=\frac{3 \times 7}{5 \times 7}+\frac{2 \times 5}{7 \times 5}\)

= \(\frac{21}{35}+\frac{10}{35}=\frac{31}{35}\)

Hence, total length of cloth bought by them = \(\frac{31}{35}\)m.

Subtraction of Unlike Fractions

To subtract unlike fractions, we first convert them into equivalent fractions with the same denominator (which is LCM of denominators) and then subtract them as like fractions.

Example 3. Subtract the following

(1) \(\frac{2}{3}\) from \(\frac{4}{5}\)

(2) \(\frac{3}{7}\) from \(\frac{5}{9}\)

Solution. (1) We have, \(\frac{4}{5}-\frac{2}{3}\)

LCM of 5 and 3 = 15

∴ \(\frac{4}{5}-\frac{2}{3}=\frac{4 \times 3}{5 \times 3}-\frac{2 \times 5}{3 \times 5}=\frac{12}{15}-\frac{10}{15}=\frac{12-10}{15}=\frac{2}{15}\)

(2) We have, \(\frac{5}{9}-\frac{3}{7}\)

LCM of 9 and 7 = 63

∴ \(\frac{5}{9}-\frac{3}{7}=\frac{5 \times 7}{9 \times 7}-\frac{3 \times 9}{7 \times 9}=\frac{35}{63}-\frac{27}{63}=\frac{8}{63}\)

MP Board Class 6 Chapter 7 Maths 

Example 4. A thread \(\frac{5}{9}\) m long cut into two pieces. One piece was \(\frac{1}{3}\) m long. How long is the other piece?

Solution. Given, total length of a piece of thread = \(\frac{5}{9}\) m

Length of one piece of thread = \(\frac{1}{3}\) m

∴ Length of another piece = \(\left(\frac{5}{9}-\frac{1}{3}\right) \mathrm{m}\)

LCM of 9 and 3 = 9

∴ \(\frac{5}{9}-\frac{1}{3}=\frac{5 \times 1}{9 \times 1}-\frac{1 \times 3}{3 \times 3}\)

= \(\frac{5}{9}-\frac{3}{9}=\frac{2}{9}\)

Hence, the length of another piece of thread is \(\frac{2}{9}\) m.

Example 5. Two kid Vehan and Vijay have the glass of same size partly filled with milk. Vehan glass is \(\frac{5}{6}\)th full and Vijay’s glass is \(\frac{2}{5}\)th full. Whose glass is more full? By what fraction?

Solution. The portion of Vehan’s glass filled by milk = \(\frac{5}{6}\) part

and the portion of Vijay’s glass filled by milk = \(\frac{2}{5}\) part.

Now, LCM of 6 and 5 = 30

Equivalent fractions of \(\frac{5}{6}\) are

and equivalent fraction of \(\frac{2}{5}\) are

Here, equivalent fractions \(\frac{12}{30}\) and \(\frac{25}{30}\) have same denominator.

∴ 25 > 12

∴ \(\frac{25}{30}>\frac{12}{30} \text { i.e. } \frac{5}{6}>\frac{2}{5}\)

Now, \(\frac{5}{6}-\frac{2}{5}=\frac{25}{30}-\frac{12}{30}\)

Hence, Vehan’s glass is more full by fraction \(\frac{13}{30}\).

Example 6. Complete the addition and subtraction box.

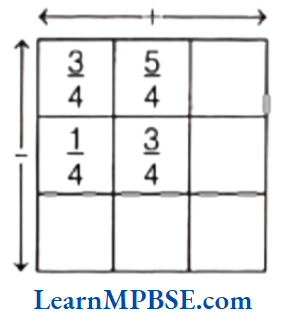
Solution. Here, \(\frac{3}{4}+\frac{5}{4}=\frac{3+5}{4}=\frac{8}{4}=2 \text { and } \frac{1}{4}+\frac{3}{4}=\frac{1+3}{4}=\frac{4}{4}=1\)

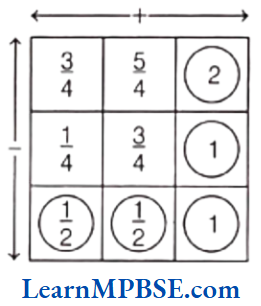
Now, \(\frac{3}{4}-\frac{1}{4}=\frac{3-1}{4}=\frac{2}{4}=\frac{1}{2}\)

and \(\frac{5}{4}-\frac{3}{4}=\frac{5-3}{4}=\frac{2}{4}=\frac{1}{2}\)

Also, we have 2 – 1 = 1

and \(\frac{1}{2}+\frac{1}{2}=\frac{1+1}{2}=\frac{2}{2}=1\)

Hence, the required complete box is shown above.

Addition and Subtraction of Mixed Fractions

Firstly, we convert both mixed fractions into improper fractions and then add them by converting into equivalent fractins with the same denominator.

To subtract mixed fractions, we subtract smaller whole part from greater whole part and then subtract corresponding fractional parts.

Mixed fractions cab be written either as a whole part plus a proper fraction or entirely as an improper fraction. One way to add (or subtract) mixed fractions is to do the operation separately for the whole parts and other way is to write the mixed fractions as improper fractions and then directly add (or subtract) them.

MP Board Class 6 Chapter 7 Maths 

Example 7. Add \(2 \frac{2}{5}\) and \(3 \frac{5}{6}\).

Solution. We have, \(2 \frac{2}{5}\) and \(3 \frac{5}{6}\)

To add mixed fractions, first convert both mixed fractions into improper fractions.

Now, \(2 \frac{2}{5}=\frac{12}{5} \text { and } 3 \frac{5}{6}=\frac{23}{6}\)

⇒ \(2 \frac{2}{5}+3 \frac{5}{6}=\frac{12}{5}+\frac{23}{6}\)

Now, converting them into equivalent fractions with the same denominator.

We have, \(\frac{12}{5}=\frac{12 \times 6}{5 \times 6}=\frac{72}{30} \text { and } \frac{23}{6}=\frac{23 \times 5}{6 \times 5}=\frac{115}{30}\) [LCM of 5 and 6 is 30]

∴ \(2 \frac{2}{5}+3 \frac{5}{6}=\frac{72}{30}+\frac{115}{30}=\frac{187}{30}=6 \frac{7}{30}\)

Example 8. Subtract \(3 \frac{5}{9}\) from \(5 \frac{1}{6}\).

Solution. We have, \(3 \frac{5}{9}\) and \(5 \frac{1}{6}\)

To subtract mixed fractions, first convert both mixed fractions into improper fractions.

∴ \(5 \frac{1}{6}-3 \frac{5}{9}=\frac{31}{6}-\frac{32}{9}\)

= \(\frac{31 \times 3}{6 \times 3}-\frac{32 \times 2}{9 \times 2}=\frac{93}{18}-\frac{64}{18}\)

= \(\frac{93-64}{18}=\frac{29}{18}\) [∴ LCM of 6 and 9 is 18]

⇒ \(5 \frac{1}{6}-3 \frac{5}{9}=1 \frac{11}{18}\)

Example 9. Simplify \(3 \frac{1}{3}+6 \frac{2}{3}-2 \frac{2}{3}\)

Solution. \(\left(3+\frac{1}{3}\right)+\left(6+\frac{2}{3}\right)-\left(2+\frac{2}{3}\right)\)

= \(\frac{(3 \times 3)+1}{3}+\frac{(6 \times 3)+2}{3}-\frac{(3 \times 2)+2}{3}\)

= \(\frac{10}{3}+\frac{20}{3}-\frac{8}{3}=\frac{10+20-8}{3}=\frac{30-8}{3}=\frac{22}{3}\)

Example 10. What should be added to \(7 \frac{4}{15}\) to get \(8 \frac{2}{5}\)

Solution. Let x be added to the \(7 \frac{4}{15}\),

i.e. \(7 \frac{4}{15}+x=8 \frac{2}{5}\)

⇒ \(\frac{109}{15}+x=\frac{42}{5}\)

⇒ \(x=\frac{42}{5}-\frac{109}{15}=\frac{126-109}{15}\)

[∴ LCM of 5 and 15 = 15]

∴ \(x=\frac{17}{15}=1 \frac{2}{15}\)

Example 11. Rahul was given \(1 \frac{1}{5}\) piece of bread and Garima was given \(1 \frac{1}{4}\) piece of bread. Find the total amount of bread was given to both of them.

Solution. Bread given to Rahul = \(1 \frac{1}{5}\) piece

Bread given to Garima = \(1 \frac{1}{4}\) piece.

Total bread given to both of them = \(1 \frac{1}{5}+1 \frac{1}{4}\)

= \(\frac{5 \times 1+1}{5}+\frac{4 \times 1+1}{4}=\frac{6}{5}+\frac{5}{4}\)

LCM of 5 and 4 = 20

∴ \(\frac{6}{5}+\frac{5}{4}=\frac{6 \times 4}{5 \times 4}+\frac{5 \times 5}{4 \times 5}=\frac{24}{20}+\frac{25}{20}=\frac{24+25}{20}=\frac{49}{20}\)

Hence, total bread given to both of them = \(\frac{49}{20}\)

MP Board Class 6 Chapter 7 Maths 

Example 12. Add the difference of \(1 \frac{3}{4}\) and \(\frac{4}{5}\) to the sum of \(\frac{3}{5}\) and \(\frac{2}{7}\).

Solution. We have, \(1 \frac{3}{4}-\frac{4}{5} \text { and } \frac{3}{5}+\frac{2}{7}\)

Now, \(\frac{7}{4}-\frac{4}{5}=\frac{35-16}{20}=\frac{19}{20} \text { and } \frac{3}{5}+\frac{2}{7}=\frac{21+10}{35}=\frac{31}{35}\)

Now, according to the question, \frac{19}{30}+\frac{31}{35}

∴ LCM of 20 and 35 = 140

∴ \(\frac{19 \times 7}{20 \times 7}+\frac{31 \times 4}{35 \times 4}=\frac{133}{140}+\frac{124}{140}=\frac{133+124}{140}=\frac{257}{140}=1 \frac{117}{140}\)

Example 13. Savita bought \(\frac{2}{5}\) m of ribbon and Kavita bought \(\frac{3}{4}\) m of the ribbon. What was the total length of the ribbon they bought?

Solution. The ribbon bought by Savita = \(\frac{2}{5}\) m

The ribbon bought by Kavita = \(\frac{3}{4}\) m

∴ Total ribbon bought by them = \(\frac{3}{4}+\frac{2}{5}\)

LCM of 4 and 5 = 20

∴ \(\frac{3}{4}+\frac{2}{5}=\frac{3 \times 5}{4 \times 5}+\frac{2 \times 4}{5 \times 4}=\frac{15}{20}+\frac{8}{20}=\frac{23}{20} \mathrm{~m}\)

Hence, total ribbon bought by both = \(\frac{23}{20}\) m

Chapter 7 Fractions Exercise 7.1

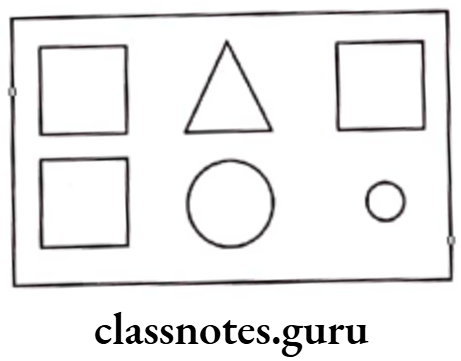
Question 1. Write the fraction representing the shaded portion.

Solution.

Total number of equal parts = 4;

Shaded parts = 2

∴ Fraction representing the shaded portion \(=\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{2}{4}=\frac{1}{2}\)

Types of Fractions Class 6

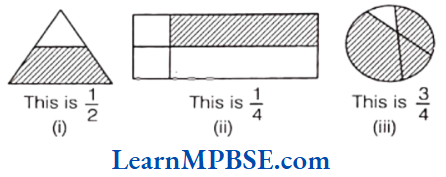
Question 2. Colour the part according to the given fraction.

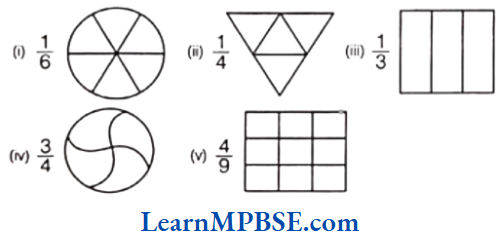
Solution. (1) Here, fraction 1/6 shows that out of 6 equal parts, 1 part is shaded. So, the required figure is shown alongside.

(2) Here, fraction 1/4 shows that out of 4 equal parts, 1 part is shaded. So, the required figure is shown alongside.

(3) Here, fraction 1/3 shows that out of 3 equal parts, 1 part is shaded. So, the required figure is shown alongside.

(4) Here, fraction 3/4 shows that out of 4 equal parts, 3 parts are shaded. So, the required figure is shown along side.

(5) Here, fraction \frac{4}{9} shows that out of 9 equal parts, 4 parts are shaded. So, the required figure is shown along side.

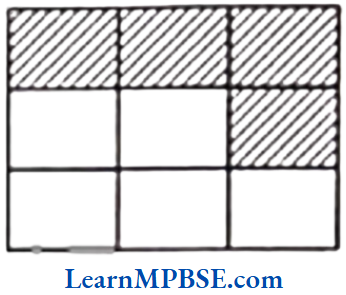
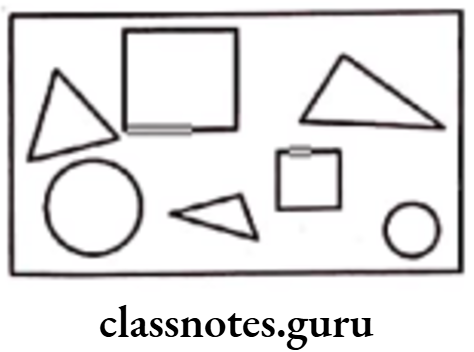
Question 3. Identify the error if any.

Solution. (1) In the given figure, shaded portion is not equal to unshaded portion. So, fraction is not equal to 1/2.

(2) In the given figure, four parts are not equal.

∴ Fraction is not equal to 1/4.

(3) In the given figure, four parts are not equal.

∴ Fraction is not equal to 3/4.

Types of Fractions Class 6

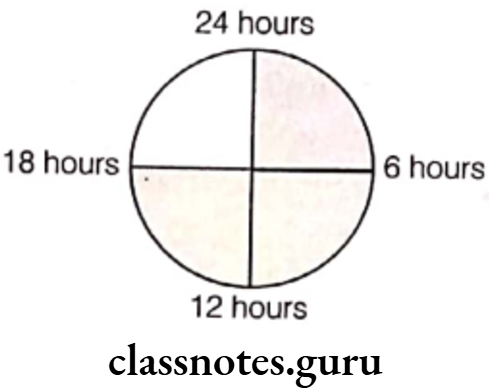
Question 4. What fraction of a day is 8 hours?

Solution. We know that total hours in a day = 24 h

∴ Required fraction \(=\frac{8 \mathrm{~h}}{24 \mathrm{~h}}=\frac{8}{24}=\frac{1}{3}\)

Question 5. What fraction of an hour is 40 minutes?

Solution. We know that total minutes in an hour = 60 min

∴ Required fraction \(=\frac{40 \mathrm{~min}}{60 \mathrm{~min}}=\frac{40}{60}=\frac{2}{3}\)

Question 6. Arya, Abhimanyu and Vivek shared lunch. Arya has brought two sandwiches, one made of vegetable and one of jam. The other two boys forgot to bring their lunch. Arya agreed to share his sandwiches, so that each person will have an equal share of each sandwich.

(1) How can Arya divide his sandwiches, so that each person has an equal share?

(2) What part of a sandwich will each boy receive?

Solution. Total number of sandwiches = 2

Total number of boys = 3

(1) Here, Arya has to divide 2 sandwiches into 3 persons. So, he will divide each sandwich into three equal parts and give one part of each sandwich to each of them.

Thus, each person gets 2/3 sandwiches.

(2) One sandwich is to be divided among three boys.

∴ Each boy will get = 1/3 part of a sandwich.

Types of Fractions Class 6

Question 7. Kanchan dyes dresses. She had to dye 30 dresses. She has so far finished 20 dresses. What fraction of dresses has she finished?

Solution. Total number of dresses to be dyed = 30

Number of dresses finished = 20

∴ Required fraction of finished dresses \(=\frac{\text { Number of dress finished }}{\text { Total number of dresses }}=\frac{20}{30}=\frac{2}{3}\)

Question 8. Write the natural numbers from 2 to 12. What fraction of them are prime numbers?

Solution. Natural numbers from 2 to 12=2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

Total natural numbers = 11

Prime numbers from 2 to 12 = 2, 3, 5, 7, 11

Total prime numbers = 5

∴ Required fraction \(=\frac{\text { Total prime numbers }}{\text { Total natural numbers }}=\frac{5}{11}\)

Question 9. What fraction of these circles have X in them?

Solution. Total number of circles = 8; Number of circles having X = 4

∴ Required fraction \(=\frac{\text { Number of circles having } X}{\text { Total number of circles }}\)

= \(\frac{4}{8}\) = \(\frac{1}{2}\)

Types of Fractions Class 6

Question 10. Kristin received a CD player for her birthday. She bought 3 CDs and received 5 others as gifts. What fraction of her total CDs did she buy and what fraction did she receive as gifts?

Solution. Number of CDs bought by Kristin = 3

Number of CDs recived as gifts = 5

∴ Total number of CDs = 3 + 5 = 8

Hence, the fraction of CDs bought by Kristin

and fraction of CDs, she received as gifts

Question 11. Show 3/5 on a number line.

Solution. We know that 3/5 is greater than zero but less than 1. So, it will lie between 0 and 1.

Since, we have to show 3/5, so we have to divide the gap between 0 and 1 into five equal parts. Then, each part shows 1/5 and 3 parts will show 3/5.

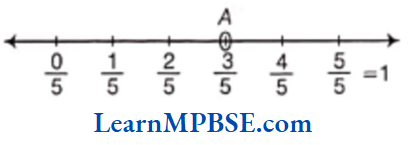
[also, \(\frac{0}{5}\) = 0]

Hence, point A represents 3/5.

Question 12. Show \(\frac{1}{10}\), \(\frac{0}{10}\), \(\frac{5}{10}\) and \(\frac{10}{10}\) on a number line.

Solution. We know that all given fractions are greater than or equal to zero but less than or equal to 1.

So, we have to divide the gap between 0 and 1 into ten equal parts, then each part shows \(\frac{1}{10}\) and 5 parts show \(\frac{5}{10}\), 10 parts show \(\frac{10}{10}\). Also, 0 shows \(\frac{0}{10}\)

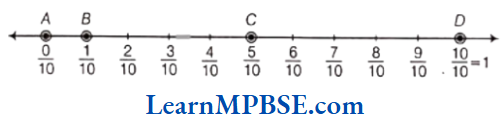
[also, \(\frac{0}{10}\) = 0]

Hence, points A, B, C and D represent the fractions \(\frac{0}{10}, \frac{1}{10}, \frac{5}{10} \text { and } \frac{10}{10}\) and respectively.

Types of Fractions Class 6

Question 13. Can you show any other fraction between 0 and 1? Write five more fractions that you can show and depict them on the number line.

Solution. Yes, we can show many other fractions which are greater than 0 and less than 1 i.e. between 0 and 1.

Five other fractions are \(\frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{4}{8} \text { and } \frac{5}{8}\)

These fractions are shown on a number line as given below

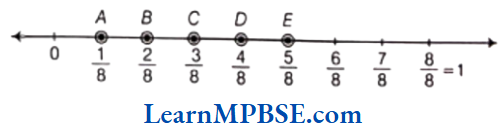
Here, points A, B, C, D and E represent \(\frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{4}{8} \text { and } \frac{5}{8}\) respectively.

Question 14. How many fractions lle between 0 and 1? Think, discuss and write your answer?

Solution. There are infinite number of points between 0 and 1 on the number line. So, there are infinite number of fractions lie between 0 and 1.

Question 15. Give a proper fraction,

(1) whose numerator is 5 and denominator is 7.

(2) whose denominator is 9 and numerator is 5.

(3) whose numerator and denominator add upto 10. How many fractions of this kind can you make?

(4) whose denominator is 4 more than the numerator.

Give any five. How many more can you make?

Solution. (1) Numerator = 5 and denominator = 7

∴ Required fraction = \(\frac{5}{7}\)

(2) Numerator = 5 and denominator = 9

∴ Required fraction = \(\frac{5}{9}\)

(3) Possible pairs of numerator and denominator which add upto 10 are (0,10), (1, 9), (2, 8), (3, 7) and (4, 6).

Now, proper fractions = \(\frac{0}{10}, \frac{1}{9}, \frac{2}{8}, \frac{3}{7} \text { and } \frac{4}{6}\)

There are five fractions. So, we can make five such fractions.

(4) There can be infinite number of fractions whose denominator is 4 more than the numerator. Some of them are \(\frac{0}{4}, \frac{1}{5}, \frac{2}{6}, \frac{3}{7} \text { and } \frac{4}{8}\)

Types of Fractions Class 6

Chapter 7 Fractions Exercise 7.2

Question 1. Draw number lines and locate the points on them.

(1) \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{3}{4}\), \(\frac{4}{4}\)

(2) \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\), \(\frac{7}{8}\)

(3) \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{8}{5}\), \(\frac{4}{5}\)

Solution. Here, fractions are \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{3}{4}\), \(\frac{4}{4}\). Also, \(\frac{1}{2}=\frac{1 \times 2}{2 \times 2}=\frac{2}{4}\)

Now, draw a number line, mark two points 0 and 1 on it. Divide the gap between 0 and 1 into four equal parts because denominator is 4, then each part will show \(\frac{1}{4}\). Also, 2 parts show \(\frac{2}{4}\), 3 parts show \(\frac{3}{4}\) and 4 parts show \(\frac{4}{4}\).

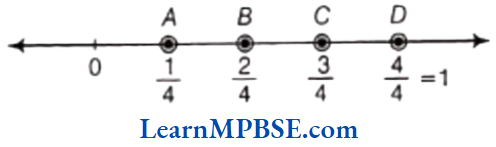
Hence, A, B, C and D represent \(\frac{1}{4}\), \(\frac{2}{4}\), \(\frac{3}{4}\) and \(\frac{4}{4}\) respectively.

Here, fractions are \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\) and \(\frac{7}{8}\).

Now, draw a number line, mark two points 0 and 1 on it. Divide the gap between 0 and 1 into eight equal parts because denominator is 8, then each part will show \(\frac{1}{8}\). Also, 2 parts show \(\frac{2}{8}\), 3 parts show \(\frac{3}{8}\) and 7 parts show \(\frac{7}{8}\).

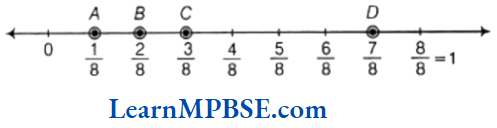
Hence, A, B, C and D represent \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\) and \(\frac{7}{8}\) respectively.

(3) Here, fractions are \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\) and \(\frac{8}{5}\).

Now, draw a number line, mark two points 0 and 1 on it. Divide the gap between 0 and 1 into five equal parts because denominator is 5, then each part will show \(\frac{1}{5}\).

Also, 2 parts show \(\frac{2}{5}\), 3 parts show \(\frac{3}{5}\), 4 parts show \(\frac{4}{5}\) and \(\frac{8}{5}\) lies between 2 and 2.

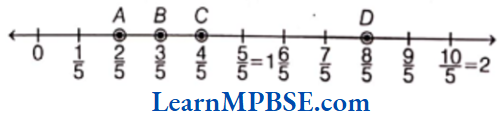
Hence, A, B, C and D represent \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\) and \(\frac{8}{5}\) respectively.

Question 2. Express the following as mixed fractions.

(1) \(\frac{20}{3}\)

(2) \(\frac{11}{5}\)

Solution. (1) We have, \(\frac{20}{3}\)

On dividing 20 by 3, we get quotient = 6, remainder = 2

∴ \(\frac{20}{3}\) = \(6 \frac{2}{3}\) i.e. 6 whole and \(\frac{2}{3}\) more

(2) We have, \(\frac{11}{5}\)

On dividing 11 by 5, we get quotient = 2, remainder = 1

∴ \(\frac{11}{5}\) = \(2 \frac{1}{5}\) i.e. 2 whole and \(\frac{1}{5}\) more

Types of Fractions Class 6

Question 3. Express the following as improper fractions.

(1) \(7 \frac{3}{4}\)

(2) \(5 \frac{6}{7}\)

(3) \(2 \frac{5}{6}\)

(4) \(10 \frac{3}{5}\)

(5) \(9 \frac{3}{7}\)

(6) \(8 \frac{4}{9}\)

Solution. (1) \(7 \frac{3}{4}=7+\frac{3}{4}=\frac{7 \times 4+3}{4}=\frac{31}{4}\)

(2) \(5 \frac{6}{7}=5+\frac{6}{7}=\frac{5 \times 7+6}{7}=\frac{41}{7}\)

(3) \(2 \frac{5}{6}=2+\frac{5}{6}=\frac{2 \times 6+5}{6}=\frac{17}{6}\)

(4) \(10 \frac{3}{5}=10+\frac{3}{5}=\frac{10 \times 5+3}{5}=\frac{53}{5}\)

(5) \(9 \frac{3}{7}=9+\frac{3}{7}=\frac{9 \times 7+3}{7}=\frac{66}{7}\)

(6) \(8 \frac{4}{9}=8+\frac{4}{9}=\frac{8 \times 9+4}{9}=\frac{76}{9}\)

Question 4. Are \(\frac{1}{3}\) and \(\frac{2}{7}\); \(\frac{2}{5}\) and \(\frac{2}{7}\); \(\frac{2}{9}\) and \(\frac{6}{27}\) equivalent? Give reason.

Solution. (1) \(\frac{1}{3}\) and \(\frac{2}{7}\)

Here, 1 x 7 = 7 and 3 x 2 = 6

∴ 7 ≠ 6, So \(\frac{1}{3}\) and \(\frac{2}{7}\) are not equivalent fractions.

(2) \(\frac{2}{5}\) and \(\frac{2}{7}\)

Here, 2 x 7 = 14 and 5 x 2 = 10

∴ 14 ≠ 10, so \(\frac{2}{5}\) and \(\frac{2}{7}\) are not equivalent fractions.

(3) \(\frac{2}{9}\) and \(\frac{6}{27}\)

Here, 2 x 27 = 54 and 9 x 6 = 54

∴ 54 = 54, so \(\frac{2}{9}\) and \(\frac{6}{27}\) are equivalent fractions.

Question 5. Give examples of four equivalent fractions.

Solution. Four equivalent fractions are \(\frac{1}{2}, \frac{2}{4}, \frac{3}{6}, \frac{4}{8},\) etc.

Comparing Fractions Class 6

Question 6. Find five equivalent fractions of each of the following.

(1) \(\frac{2}{3}\)

(2) \(\frac{1}{5}\)

Solution. (1) Five equivalent fractions of \(\frac{2}{3}\) are as follows.

Thus, five equivalent fractions of \(\frac{2}{3}\) are \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}\) and \(\frac{12}{18}\).

(2) Five equivalent fractions of \(\frac{1}{5}\) are as follows.

Thus, five equivalent fractions of \(\frac{1}{5}\) are \(\frac{2}{10}, \frac{3}{15}, \frac{4}{20}, \frac{5}{25}\) and \(\frac{6}{30}\).

Question 7. Write the simplest form of:

(1) \(\frac{15}{75}\)

(2) \(\frac{16}{72}\)

Solution. (1) We have, \(\frac{15}{75}\)

Now, factors of 15 = 3 x 5

and factors of 75 = 3 x 5 x 5

Common factors = 3 and 5

∴ HCF of 15 and 75 = 3 x 5 = 15

Then, \(\frac{15}{75}=\frac{15+15}{75+15}=\frac{1}{5}\)

Hence, fraction \(\frac{1}{5}\) is the simplest form of given fraction.

(2) We have, \(\frac{16}{72}\)

Now, factors of 16 = 2 x 2 x 2 x 2

and factors of 72 = 2 x 2 x 2 x 3 x 3

Common factors = 2, 2 and 2

∴ HCF of 16 and 72 = 2 x 2 x 2 = 8

Then, \(\frac{16}{72}=\frac{16 \div 8}{72 \div 8}=\frac{2}{9}\)

Hence, fraction \(\frac{2}{9}\) is the simplest form of given fraction.

Comparing Fractions Class 6

Question 8. Is \(\frac{49}{64}\) in its simplest form?

Solution. Here, factors of 49 = 7 x 7 and factors of 64 = 8 x 8

∴ 49 and 64 have no common factor except 1.

Hence, fraction \(\frac{49}{64}\) is in simplest form.

Chapter 7 Fractions Exercise 7.3

Question 1. Write the fractions. Are all these fractions equivalent?

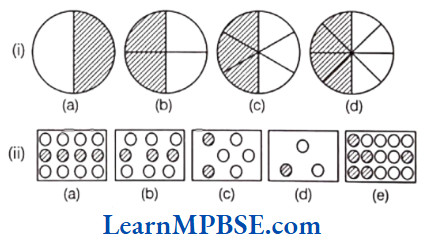
Solution. (1) (a) Total number of equal parts = 2

Number of shaded parts = 1

∴ Fraction of shaded portion \(=\frac{\text { Number of shaded parts }}{\text { Total number of equal paarts }}=\frac{1}{2}\)

(b) Total number of equal parts = 4;

Number of shaded parts = 2

∴ Fraction of shaded portion = \(\frac{2}{4}\)

(c) Total number of equal parts = 6;

Number of shaded parts = 3

∴ Fraction of shaded portion = \(\frac{3}{6}\)

(d) Total number of equal parts = 8;

Number of shaded parts = 4

∴ Fraction of shaded portion = \(\frac{4}{8}\)

Now, \(\frac{2}{4}=\frac{2+2}{4 \div 2}=\frac{1}{2}\) [∴ HCF of 2 and 4 is 2]

\(\frac{3}{6}=\frac{3 \div 3}{6+3}=\frac{1}{2}\) [∴ HCF of 3 and 6 is 3]

\(\frac{4}{8}=\frac{4 \div 4}{8 \div 4}=\frac{1}{2}\) [∴ HCF of 4 and 8 is 4]

Since, all fractions in simplest form are same.

∴ \(\frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\frac{4}{8}\) i.e. the fractions are equivalent.

(2) (a) Total number of equal parts = 12;

Number of shaded parts = 4

∴ Fraction of shaded portion = \(\frac{4}{12}\)

(b) Total number of equal parts = 9;

Number of shaded parts = 3

∴ Fraction of shaded portion = \(\frac{3}{9}\)

(c) Total number of equal parts = 6;

Number of shaded parts = 2

∴ Fraction of shaded portion = \(\frac{1}{3}\)

(d) Total number of equal parts = 3;

Number of shaded parts = 1

∴ Fraction of shaded portion = \(\frac{1}{3}\)

(e) Total number of equal parts = 15;

Number of shaded parts = 6

∴ Fraction of shaded portion = \(\frac{6}{15}\)

Now, \(\frac{4}{12}=\frac{4 \div 4}{12 \div 4}=\frac{1}{3}\) [∴ HCF of 4 and 12 is 4]

\(\frac{3}{9}=\frac{3+3}{9+3}=\frac{1}{3}\) [∴ HCF of 3 and 9 is 3]

\(\frac{2}{6}=\frac{2+2}{6+2}=\frac{1}{3}\) [∴ HCF of 2 and 6 is 2]

\(\frac{6}{15}=\frac{6+3}{15+3}=\frac{2}{5}\) [∴ HCF of 6 and 15 is 3]

Here, except \(\frac{6}{15}\) all the fractions in simplest form are same.

Question 2. Find the equivalent fraction of \(\frac{3}{5}\) having

(1) denominator 20

(2) numerator 9

Solution. Let N stands for the numerator and D stands for the denominator.

(1) Given, denominator of an equivalent fraction = 20

∴ \(\frac{N}{20}\) = \(\frac{3}{5}\) ⇒ N x 5 = 20 x 3

So, N x 5 = 4 x 5 x 3 [∴ 20 = 4 x 5]

⇒ N x 5 = 12 x 5

On comparing, we get N = 12

∴ Required equivalent fraction of \(\frac{3}{5}=\frac{N}{D}=\frac{12}{20}\)

(2) Given, numerator of an equivalent fraction = 9

∴ \(\frac{9}{D}\) = \(\frac{3}{5}\) ⇒ D x 3 = 9 x 5

So, D x 3 = 3 x 3 x 5 [∴ 9 = 3 x 3]

⇒ D x 3 = 15 x 3

On comparing, we get D = 15

∴ Required equivalent fraction of \(\frac{3}{5}=\frac{N}{D}=\frac{9}{15}\)

Comparing Fractions Class 6

Question 3. Check whether the given fractions are equivalent.

(1) \(\frac{5}{9}\), \(\frac{30}{54}\)

(2) \(\frac{3}{10}\), \(\frac{12}{50}\)

(3) \(\frac{7}{13}\), \(\frac{5}{11}\)

Solution.

(1) We have, \(\frac{5}{9}\) and \(\frac{30}{54}\)

Now, 5 x 54 = 270; 9 x 30 = 270 [by cross-product]

∴ 270 = 270

∴ \(\frac{5}{9}\) and \(\frac{30}{54}\) are equivalent fractions.

(2) We have, \(\frac{3}{10}\) and \(\frac{12}{50}\)

Now, 3 x 50 = 150; 10 x 12 = 120 [by cross-product]

But 150 ≠ 120

∴ \(\frac{3}{10}\) and \(\frac{12}{50}\) are not equivalent fractions.

(3) We have, \(\frac{7}{13}\) and \(\frac{5}{11}\)

Now, 7 x 11 = 77; 13 x 5 = 65 [by cross-product]

But 77 ≠ 65

∴ \(\frac{7}{13}\) and \(\frac{5}{11}\) are not equivalent fractions.

Question 4. Reduce the following fractions to simplest form.

(1) \(\frac{48}{60}\)

(2) \(\frac{150}{60}\)

Solution. (1) We have, \(\frac{48}{60}\)

Now, factors of 48 = 2, 2, 2, 2, 3

and factors of 60 = 2, 2, 3, 5

Common factors = 2, 2 and 3

HCF of 48 and 60 = 2 x 2 x 3 = 12

∴ \(\frac{48}{60}=\frac{48+12}{60+12}=\frac{4}{5}\)

Hence, the simplest form of the fraction \(\frac{48}{60}\) is \(\frac{4}{5}\).

(2) We have, \(\frac{150}{60}\)

Now, factors of 150 = 2, 3, 5, 5

and factors of 60 = 2, 2, 3, 5

Common factors = 2, 3 and 5

HCF of 150 and 60 = 2 x 3 x 5 = 30

∴ \(\frac{150}{60}=\frac{150+30}{60+30}=\frac{5}{2}\)

Hence, the simplest form of the fraction \(\frac{150}{60}\) is \(\frac{5}{2}\).

Comparing Fractions Class 6

Question 5. Ramesh had 20 pencils, Sheelu had 50 pencils and Jamaal had 80 pencils. After 4 months, Ramesh used up 10 pencils, Sheelu used up 25 pencils and Jamaal used up 40 pencils. What fraction did each used up? Check if each has used up an equal fraction of her/his pencils?

Solution. Here, the fraction of pencils used by Ramesh = \(\frac{10}{20}\)

Fraction of pencils used by Sheelu = \(\frac{25}{50}\)

Fraction of pencils used by Jamaal = \(\frac{40}{80}\)

Now, \(\frac{10}{20}=\frac{10 \div 10}{20 \div 10}=\frac{1}{2}\) [∴ HCF of 10 and 20 is 10]

\(\frac{25}{50}=\frac{25 \div 25}{50 \div 25}=\frac{1}{2}\) [∴ HCF of 25 and 50 is 25]

and \(\frac{40}{80}=\frac{40 \div 40}{80 \div 40}=\frac{1}{2}\) [∴ HCF of 40 and 80 is 40]

Thus, \(\frac{10}{20}=\frac{25}{50}=\frac{40}{80}=\frac{1}{2}\)

Question 6. You get one-fifth of a bottle of juice and your sister gets one-third of the same size of a bottle of juice. Who gets more?

Solution. Here, we will compare one-fifth i.e. \(\frac{1}{5}\) and one-third i.e. \(\frac{1}{3}\).

Since \(\frac{1}{5}\) and \(\frac{1}{3}\) have same numerator, so the fraction with smaller denominator is greater.

Thus, \(\frac{1}{3}\) > \(\frac{1}{5}\)

Thus, your sister gets more juice.

Question 7. Write these is ascending and also in descending order.

(1) \(\frac{1}{8}, \frac{5}{8}, \frac{3}{8}\)

Solution. (1) We have, \(\frac{1}{8}, \frac{5}{8}, \frac{3}{8}\)

Here, denominators of all fractions are same.

∴ Ascending order of numerators = 1 < 3 < 5

and descending order of numerators = 5 > 3 > 1

∴ Ascending order of fractions = \(\frac{1}{8}<\frac{3}{8}<\frac{5}{8}\)

and descending order of fractions = \(\frac{5}{8}>\frac{3}{8}>\frac{1}{8}\)

Question 8. Arrange the following in ascending and descending order.

(1) \(\frac{1}{12}, \frac{1}{23}, \frac{1}{5}, \frac{1}{7}, \frac{1}{50}, \frac{1}{9}, \frac{1}{17}\)

(2) \(\frac{3}{7}, \frac{3}{11}, \frac{3}{5}, \frac{3}{2}, \frac{3}{13}, \frac{3}{4}, \frac{3}{17}\)

(3) Write 3 more similar examples and arrange them in ascending and descending order.

Solution. (1) Here, numerators of all fractions are same.

Descending order of denominators = 50 > 23 > 17 > 12 > 9 > 7 > 5

∴ Ascending order of fractions = \(\frac{1}{50}<\frac{1}{23}<\frac{1}{17}<\frac{1}{12}<\frac{1}{9}<\frac{1}{7}<\frac{1}{5}\)

[∴ \(\frac{1}{50}\) has larger denominator, so it is smallest fraction]

and descending order of fractions = \(\frac{1}{5}>\frac{1}{7}>\frac{1}{9}>\frac{1}{12}>\frac{1}{17}>\frac{1}{23}>\frac{1}{50}\)

(2) Here, numerators of all fractions are same.

Descending order of denominators = 17 > 13 > 11 > 7 > 5 > 4 > 2

∴ Ascending order of fractions = \(\frac{3}{17}<\frac{3}{13}<\frac{3}{11}<\frac{3}{7}<\frac{3}{5}<\frac{3}{4}<\frac{3}{2}\)

and descending order of fractions = \(\frac{3}{2}>\frac{3}{4}>\frac{3}{5}>\frac{3}{7}>\frac{3}{11}>\frac{3}{13}>\frac{3}{17}\)

(3) Three more similar examples can be taken as

(a) \(\frac{2}{11}, \frac{2}{21}, \frac{2}{9}, \frac{2}{7}, \frac{2}{8}, \frac{2}{15}\)

Here, descending order of denominators = 21 > 15 > 11 > 9 > 8 > 7

∴ Ascending order of fractions = \(\frac{2}{21}<\frac{2}{15}<\frac{2}{11}<\frac{2}{9}<\frac{2}{8}<\frac{2}{7}\)

and descending order of fractions = \(\frac{2}{7}>\frac{2}{8}>\frac{2}{9}>\frac{2}{11}>\frac{2}{15}>\frac{2}{21}\)

(b) \(\frac{4}{5}, \frac{4}{6}, \frac{4}{13}, \frac{4}{2}, \frac{4}{9}, \frac{4}{11}\)

Here, descending order of denominators = 13 > 11 > 9 > 6 > 5 > 2

∴ Ascending order of fractions = \(\frac{4}{13}<\frac{4}{11}<\frac{4}{9}<\frac{4}{6}<\frac{4}{5}<\frac{4}{2}\)

and descending order of fractions = \(\frac{4}{2}>\frac{4}{5}>\frac{4}{6}>\frac{4}{9}>\frac{4}{11}>\frac{4}{13}\)

(c) \(\frac{7}{11}, \frac{7}{13}, \frac{7}{5}, \frac{7}{2}, \frac{7}{3}, \frac{7}{4}\)

Here, descending order of denominators = 13 > 11 > 5 > 4 > 3 > 2

∴ Ascending order of fractions = \(\frac{7}{13}<\frac{7}{11}<\frac{7}{5}<\frac{7}{4}<\frac{7}{3}<\frac{7}{2}\)

and descending order of fractions = \(\frac{7}{2}>\frac{7}{3}>\frac{7}{4}>\frac{7}{5}>\frac{7}{11}>\frac{7}{13}\)

Chapter 7 Fractions Exercise 7.4

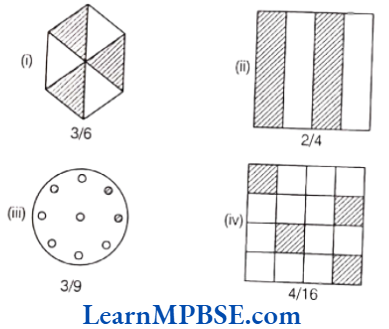
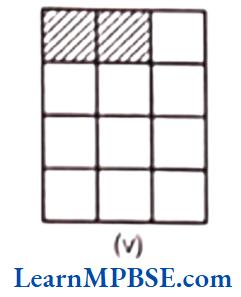
Question 1. Write shaded portion as fraction. Arrange them in ascending and descending order using correct sign ‘<‘, ‘=’, ‘>’ between the fractions.

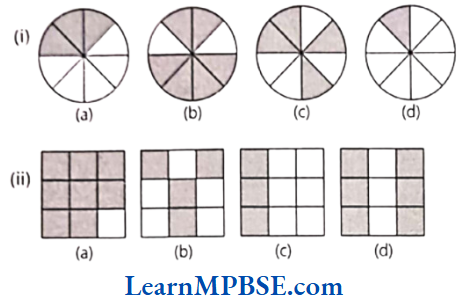
Solution. (1) Here, the total number of equal parts in all figures = 8

Shaded portion of figure (a) represents fraction = \(\frac{3}{8}\)

Shaded portion of figure (b) represents fraction = \(\frac{6}{8}\)

Shaded portion of figure (c) represents fraction = \(\frac{4}{8}\)

Shaded portion of figure (d) represents fraction = \(\frac{1}{8}\)

∴ Denominators of all fractions are same. So, we arrange them in ascending and descending order according to their numerators.

∴ Ascending order of fractions = \(\frac{1}{8}<\frac{3}{8}<\frac{4}{8}<\frac{6}{8}\)

[∴ fraction having small numerator will be smaller]

and descending order of fractions = \(\frac{6}{8}>\frac{4}{8}>\frac{3}{8}>\frac{1}{8}\)

[∴ fraction having greatest numerator will be greatest]

(2) Here, the total number of equal parts in all figures = 9

Shaded portion of figure (a) represents fraction = \(\frac{8}{9}\)

Shaded portion of figure (b) represents fraction = \(\frac{4}{9}\)

Shaded portion of figure (c) represents fraction = \(\frac{3}{9}\)

Shaded portion of figure (d) represents fraction = \(\frac{6}{9}\)

∴ Denominators of all fractions are same. So, we arrange them in ascending and descending order according to their numerators.

∴ Ascending order of fractions = \(\frac{3}{9}<\frac{4}{9}<\frac{6}{9}<\frac{8}{9}\)

and descending order of fractions = \(\frac{8}{9}>\frac{6}{9}>\frac{4}{9}>\frac{3}{9}\)

Comparing Fractions Class 6

Question 2. The following fractions represent just three different numbers. Separate them into three groups of equivalent fractions, by changing each one to its simplest form.

(1) \(\frac{2}{12}\)

(2) \(\frac{3}{15}\)

(3) \(\frac{8}{50}\)

(4) \(\frac{16}{100}\)

(5) \(\frac{10}{60}\)

(6) \(\frac{15}{75}\)

(7) \(\frac{12}{60}\)

(8) \(\frac{16}{96}\)

(9) \(\frac{12}{75}\)

(10) \(\frac{12}{72}\)

(11) \(\frac{3}{18}\)

(12) \(\frac{4}{25}\)

Solution. First, we have to convert all the fractions in its simplest form.

(1) We have, \(\frac{2}{12}\) ⇒ \(\frac{2 \div 2}{12 \div 2}=\frac{1}{6}\) [∴ HCF of 2 and 12 = 2]

(2) We have, \(\frac{3}{15}\) ⇒ \(\frac{3 \div 3}{15 \div 3}=\frac{1}{5}\) [∴ HCF of 3 and 15 = 3]

(3) We have, \(\frac{8}{50}\) ⇒ \(\frac{8 \div 2}{50 \div 2}=\frac{4}{25}\) [∴ HCF of 8 and 50 = 2]

(4) We have, \(\frac{16}{100}\) ⇒ \(\frac{16 \div 4}{100 \div 4}=\frac{4}{25}\) [∴ HCF of 16 and 100 = 4]

(5) We have, \(\frac{10}{60}\) ⇒ \(\frac{10+10}{60+10}=\frac{1}{6}\) [∴ HCF of a0 and 60 = 10]

(6) We have, \(\frac{15}{75}\) ⇒ \(\frac{15+15}{75+15}=\frac{1}{5}\) [∴ HCF of 15 and 75 = 15]

(7) We have, \(\frac{12}{60}\) ⇒ \(\frac{12+12}{60+12}=\frac{1}{5}\) [∴ HCF of 12 and 60 = 12]

(8) We have, \(\frac{16}{96}\) ⇒ \(\frac{16+16}{96+16}=\frac{1}{6}\) [∴ HCF of 16 and 96 = 16]

(9) We have, \(\frac{12}{75}\) ⇒ \(\frac{12 \div 3}{75+3}=\frac{4}{25}\) [∴ HCF of 12 and 75 = 3]

(10) We have, \(\frac{3}{18}\) ⇒ \(\frac{3 \div 3}{18 \div 3}=\frac{1}{6}\) [∴ HCF of 12 and 72 = 12]

(11) We have, \(\frac{3}{18}\) ⇒ \(\frac{3 \div 3}{18 \div 3}=\frac{1}{6}\) [∴ HCF of 3 and 18 = 3]

(12) We have, \(\frac{4}{25}\) ⇒ \(\frac{4 \div 1}{25 \div 1}=\frac{4}{25}\) [∴ HCF of 4 and 25 = 1]

Now, on grouping into three groups of equivalent fractions with the help of simplest form of fractions, we get

(a) \(\frac{2}{12}=\frac{10}{60}=\frac{16}{96}=\frac{12}{72}=\frac{3}{18}\)

[simplest form of each fraction = \(\frac{1}{6}\)]

(b) \(\frac{3}{15}=\frac{15}{75}=\frac{12}{60}\)

[simplest form of each fraction = \(\frac{1}{5}\)]

(c) \(\frac{8}{50}=\frac{16}{100}=\frac{12}{75}=\frac{4}{25}\)

[simplest form of each fraction = \(\frac{4}{25}\)]

Question 3. Find answers to the following. Write and indicate how you solved them.

(1) Is \(\frac{5}{9}\) equal to \(\frac{4}{5}\)?

(2) Is \(\frac{9}{16}\) equal to \(\frac{5}{9}\)?

Solution. LCM of 9 and 5 = 45

Now, \(\frac{5}{9}=\frac{5 \times 5}{9 \times 5}=\frac{25}{45} \text { and } \frac{4}{5}=\frac{4 \times 9}{5 \times 9}=\frac{36}{45}\)

Thus, both fractions are like fractions but \(\frac{25}{45} \neq \frac{36}{45}\)

∴ \(\frac{5}{9} \neq \frac{4}{5}\)

(2) LCM of 16 and 9 = 144

Now, \(\frac{9}{16}=\frac{9 \times 9}{16 \times 9}=\frac{81}{144} \text { and } \frac{5}{9}=\frac{5 \times 16}{9 \times 16}=\frac{80}{144}\)

Thus, both fractions are like fractions but \(\frac{81}{144} \neq \frac{80}{144}\)

∴ \(\frac{9}{16} \neq \frac{5}{9}\)

Comparing Fractions Class 6

Question 4. Ila reads 25 pages of a book containing 100 pages. Lalita reads \(\frac{2}{5}\) of the same book. Who read less?

Solution. Fraction of book read b Ila = \(\frac{25}{100}\)

= \(\frac{25+25}{100+25}=\frac{1}{4}\)

[∴ HCF of 25 and 100 = 25]

Fraction of book read by Lalita = \(\frac{2}{5}\)

For comparing \(\frac{1}{4}\) and \(\frac{2}{5}\)

We have, 1 x 5 = 5 and 4 x 2 = 8 [by cross-product]

∴ 5 < 8

∴ \(\frac{1}{4}\) < \(\frac{2}{5}\)

Hence, Ila reads less pages of a book.

Question 5. Rafiq exercised for \(\frac{3}{6}\) of an hour, while Rohit exercised for \(\frac{3}{4}\) of an hour. Who exercised for a longer time?

Solution. Rafiq exercised for \(\frac{3}{6}\) h. Rohit exercised for \(\frac{3}{4}\) h.

Now, we have to compare \(\frac{3}{6}\) and \(\frac{3}{4}\).

Here, numerator of both fractions are same.

We know that if two fractions have same numerator, then the fraction having less denominator will be greater.

∴ \(\frac{3}{4}>\frac{3}{6}\)

Hence, Rohit exercised for a longer time.

Comparing Fractions Class 6

Question 6. In a class A of 25 students, 20 passed with 60% or more marks; in another class B of 30 students, 24 passed with 60% or more marks. In which class, was a greater fraction of students getting with 60% or more marks?

Solution. Fraction of students who got 60% or more marks in class A

= \(\frac{20}{25}=\frac{20 \div 5}{25+5}=\frac{4}{5}\)

[∴ HCF of 20 and 25 = 5]

Fraction of students who got 60% or more marks in class B

= \(\frac{24}{30}=\frac{24+6}{30 \div 6}=\frac{4}{5}\)

[∴ HCF of 24 and 30 = 6]

∴ \(\frac{20}{25}=\frac{24}{30}=\frac{4}{5}\)

So, it is clear that an equal number of students got 60% or more marks in both the classes.

Question 7. My mother divided an apple into 4 equal parts. She gave me two parts and to my brother one part. How much apple did she give to both of us together?

Solution. Here, mother divided an apple into 4 equal parts, so each part will represents \(\frac{1}{4}\). She gave me two parts i.e. \(\frac{2}{4}\) apple and she gave to my brother one part i.e. \(\frac{1}{4}\) part.

Part of apple she gave to both of us = \(\frac{2}{4}+\frac{1}{4}\)

∴ Here, denominators of both fractions are same, so we add numerator to find their sum.

i.e. \(\frac{2+1}{4}=\frac{3}{4}\)

Hence, she gave \(\frac{3}{4}\) apple to both of us

Question 8. Mother asked Neelu and her brother to pick stones from the wheat. Neelu picked one-fourth of the total stones in it and her brother also picked up one-fourth of the stones. What fraction of the stones did both pick up together?

Solution. Neelu and her brother picked up \(\frac{1}{4}\) th of stones each from the wheat.

∴ Total stones picked up by both of them

= \(\frac{1}{4}+\frac{1}{4}=\frac{1+1}{4}=\frac{2}{4}=\frac{1}{2}\)

Hence, both together picked up \(\frac{1}{2}\) fraction of the stones.

Question 9. Sohan was putting covers on his notebooks. He put one-fourth of the covers on Monday. He put another one-fourth on Tuesday and the remaining on Wednesday. What fraction of the covers did he put on Wednesday?

Solution. Covers putting by Sohan on Monday = \(\frac{1}{4}\)

Covers putting by him on Tuesday = \(\frac{1}{4}\)

∴ Covers putting by him on Wednesday

= \(1-\frac{1}{4}-\frac{1}{4}=\frac{4}{4}-\frac{1}{4}-\frac{1}{4}\)

[∴ 1 and \(\frac{4}{4}\) are equivalent fractions]

= \(\frac{4-1-1}{4}=\frac{2}{4}=\frac{1}{2}\)

Hence, he put one-half of the covers on Wednesday.

Comparing Fractions Class 6

Question 10. Add with the help of a diagram.

(1) \(\frac{1}{8}+\frac{1}{8}\)

(2) \(\frac{2}{5}+\frac{3}{5}\)

Solution.

(1) Here, draw two rectangles and divide them into 8 equal parts out of which 1 part is shaded. On adding them, we get 2 parts shaded out of 8 equal parts. Thus,

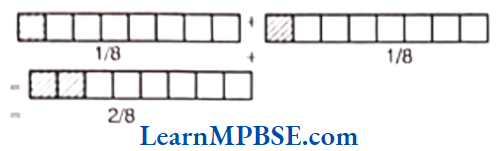
i.e. \(\frac{1}{8}+\frac{1}{8}=\frac{1+1}{8}=\frac{2}{8}=\frac{1}{4}\)

(2) Here, draw two rectangles and divide them into 5 equal parts separately. In first rectangle, 2 parts out of 5 parts are shaded and in second rectangle, 3 parts out of 5 parts are shaded. On adding them, we get all 5 parts shaded. Thus,

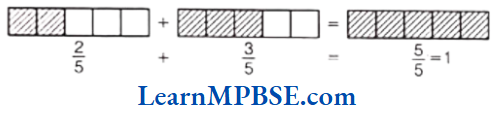
i.e. \(\frac{2}{5}+\frac{3}{5}=\frac{2+3}{5}=\frac{5}{5}=1\)

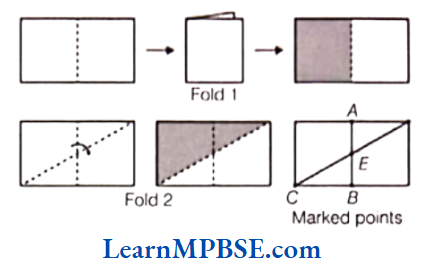
Question 11. Add \(\frac{1}{12}+\frac{1}{12}\). How will we show this pictorially? Using paper folding?

Solution. We have, \(\frac{1}{12}+\frac{1}{12}=\frac{1+1}{12}=\frac{2}{12}=\frac{1}{6}\)

Pictorially, it can be shown as

By folding paper, it can be shown in the following way Take a square piece of paper say ABCD.

Fold it by overlapping its edge AB and CD to get a figure.

Again, refold it by taking EF over C(A) D(B) to get a figure.

Now, reopen it, then we get the following figure

Now, fold it vertically at two places to obtain three equal vertical portion as shown in figure.

Shaded \(\frac{1}{12}\) portion twice,

We see that \(\frac{1}{12}+\frac{1}{12}=\frac{1+1}{12}=\frac{2}{12}=\frac{1}{6}\)

Question 12. Make 5 more examples of problems given in 1 and 2 above. Solve them with your friends.

Solution.

(1) \(\frac{1}{4}+\frac{1}{4}=\frac{1+1}{4}=\frac{2}{4}=\frac{1}{2}\)

[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]

(2) \(\frac{3}{6}+\frac{7}{6}+\frac{1}{6}=\frac{3+7+1}{6}=\frac{11}{6}\)

[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]

(3) \(\frac{5}{9}+\frac{8}{9}=\frac{5+8}{9}=\frac{13}{9}\)

[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]

(4) \(\frac{1}{10}+\frac{9}{10}=\frac{1+9}{10}=\frac{10}{10}=1\)

[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]

(5) \(\frac{11}{12}+\frac{4}{12}+\frac{5}{12}+\frac{6}{12}=\frac{11+4+5+6}{12}=\frac{26}{12}=\frac{13}{6}\)

[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]

Comparing Fractions Class 6

Question 13. Find the difference between \(\frac{7}{8}\) and \(\frac{3}{8}\).

Solution. Given, \(\frac{7}{8}\) and \(\frac{3}{8}\)

∴ Difference = \(\frac{7}{8}-\frac{3}{8}=\frac{7-3}{8}=\frac{4}{8}=\frac{1}{2}\)

Question 14. Mother made a gud patti in a round shape. She divided it into 5 parts. Seema ate one piece from it. If I eat another piece, then how much would be left?

Solution. Total number of equal parts of gud patti = 5

Gud patti eaten by Seema = \(\frac{1}{5}\); Gud patti eaten by me = \(\frac{1}{5}\)

Fraction of gud patti eaten by Seema and me

= \(\frac{1}{5}+\frac{1}{5}=\frac{1+1}{5}=\frac{2}{5}\)

∴ Fraction of gud patti left out = \(\frac{1}{1}-\frac{2}{5}=\frac{5-2}{5}=\frac{3}{5}\)

Hence, \(\frac{3}{5}\)th of the gud patti would be left.

Question 15. My elder sister divided the watermelon into 16 parts. I ate 7 out of them. My friend ate 4. How much did we eat between us? How much more of the watermelon did I eat than my friend? What portion of the watermelon remained?

Solution. Here, a watermelon is divided into 16 parts.

∴ Each part = \(\frac{1}{16}\)

I ate 7 parts out of 16 parts i.e. \(\frac{7}{16}\) part

My friend ate 4 parts out of 16 parts i.e. \(\frac{4}{16}\) part

Now, the part which we eat together

= \(\frac{7}{16}+\frac{4}{16}=\frac{7+4}{16}=\frac{11}{16} \text { part }\)

Now, difference between our parts = \(\frac{7}{16}-\frac{4}{16}=\frac{7-4}{16}=\frac{3}{16}\)

So, I ate \(\frac{3}{16}\) part of watermelon more than my friend.

Now, remaining part of the watermelon = \(1-\frac{11}{16}=\frac{16}{16}-\frac{11}{16}\)

[∴ \(\frac{16}{16}\) and 1 are equivalent fractions]

= \(\frac{16-11}{16}=\frac{5}{16}\)

Chapter 7 Fractions Exercise 7.5

Question 1. Write these fractions appropriately as additions or subtractions:

Solution. (1) In first figure, fraction for shaded portion = \(\frac{1}{5}\)

In second figure, fraction for shaded portion = \(\frac{2}{5}\)

and in third figure, fraction for shaded portion = \(\frac{3}{5}\)

Here, third figure represents more shaded portion than first and second figures.

So, \(\frac{1}{5}+\frac{2}{5}=\frac{1+2}{5}=\frac{3}{5}\)

∴ The given figure will be as follows

(2) In first figure, fraction for shaded portion = 1 or \(\frac{5}{5}\)

In second figure, fraction for shaded portion = \(\frac{3}{5}\)

and in third figure, fraction for shaded portion = \(\frac{2}{5}\)

Here, third figure represents less shaded portion than first and second figure.

So, \(1-\frac{3}{5}=\frac{5-3}{5}=\frac{2}{5}\)

∴ The given figure represented as follows

Question 2. Solve

1. \(\frac{1}{18}+\frac{1}{18}\)

2. \(\frac{8}{15}+\frac{3}{15}\)

3. \(\frac{7}{7}-\frac{5}{7}\)

4. \(\frac{1}{22}+\frac{21}{22}\)

5. \(\frac{12}{15}-\frac{7}{15}\)

6. \(\frac{5}{8}+\frac{3}{8}\)

7. \(1-\frac{2}{3}\)

8. \(\frac{1}{4}+\frac{0}{4}\)

9. \(3-\frac{12}{5}\)

Solution. (1) We have, \(\frac{1}{18}+\frac{1}{18}=\frac{1+1}{18}=\frac{2}{18}=\frac{1}{9}\) [simplest form]

(2) We have, \(\frac{8}{15}+\frac{3}{15}=\frac{8+3}{15}=\frac{11}{15}\) [simplest form]

(3) We have, \(\frac{7}{7}-\frac{5}{7}=\frac{7-5}{7}=\frac{2}{7}\) [simplest form]

(4) We have, \(\frac{1}{22}+\frac{21}{22}=\frac{1+21}{22}=\frac{22}{22}=1\) [simplest form]

(5) We have, \(\frac{12}{15}-\frac{7}{15}=\frac{12-7}{15}=\frac{5}{15}=\frac{1}{3}\) [simplest form]

(6) We have, \(\frac{5}{8}+\frac{3}{8}=\frac{5+3}{8}=\frac{8}{8}=1\) [simplest form]

(7) We have, \(1-\frac{2}{3}=\frac{3}{3}-\frac{2}{3}=\frac{3-2}{3}=\frac{1}{3}\)

[∴ 1 and \(\frac{3}{3}\) are (simplest form) equivalent fractions]

(8) We have, \(\frac{1}{4}+\frac{0}{4}=\frac{1+0}{4}=\frac{1}{4}\) [simplest form]

(9) We have, \(3-\frac{12}{5}=\frac{3}{1}-\frac{12}{5}=\frac{3 \times 5}{1 \times 5}-\frac{12}{5}\)

[converting \(\frac{3}{1}\) into like fraction by multiplying numerator and denominator by 5]

= \(\frac{15}{5}-\frac{12}{5}=\frac{15-12}{5}=\frac{3}{5}\) [simplest form]

Question 3. Shubham painted \(\frac{2}{3}\) of the wall space in his room. His sister Madhavi helped and painted \(\frac{1}{3}\) of the wall space. How much did they paint together?

Solution. Portion of the wall painted by Shubham = \(\frac{2}{3}\)

Portion of the wall painted by Madhavi = \(\frac{1}{3}\)

Portion of the wall painted by both = \(\frac{2}{3}+\frac{1}{3}=\frac{2+1}{3}=\frac{3}{3}=1\)

Hence, they painted complete wall together.

Comparing Fractions Class 6

Question 4. Javed was given \(\frac{5}{7}\) of a basket of oranges. What fraction of oranges was left in the basket?

Solution. Let full basket = 1 = \(\frac{7}{7}\)

Part of oranges given to Javed = \(\frac{5}{7}\)

∴ Part of oranges left in the basket = \(\frac{7}{7}-\frac{5}{7}=\frac{7-5}{7}=\frac{2}{7}\)

Hence, \(\frac{2}{7}\) part of oranges was left in the basket.

Question 5. Add \(\frac{2}{5}\) and \(\frac{3}{7}\)

Solution. We have, \(\frac{2}{5}+\frac{3}{7}\)

LCM of 5 and 7 = 35

∴ \(\frac{2}{5}+\frac{3}{7}=\frac{2 \times 7}{5 \times 7}+\frac{3 \times 5}{7 \times 5}=\frac{14}{35}+\frac{15}{35}=\frac{14+15}{35}=\frac{29}{35}\)

Hence, \(\frac{2}{5}+\frac{3}{7}=\frac{29}{35}\)

Question 6. Subtract \(\frac{2}{5}\) from \(\frac{5}{7}\).

Solution. We have, \(\frac{5}{7}-\frac{2}{5}\)

LCM of 5 and 7 = 35

∴ \(\frac{5}{7}-\frac{2}{5}=\frac{5 \times 5}{7 \times 5}-\frac{2 \times 7}{5 \times 7}=\frac{25}{35}-\frac{14}{35}=\frac{25-14}{35}=\frac{11}{35}\)

Hence, \(\frac{5}{7}-\frac{2}{5}=\frac{11}{35}\)

Chapter 7 Fractions Exercise 7.6

Question 1. Solve

1. \(\frac{2}{3}\) + \(\frac{1}{7}\)

2. \(\frac{3}{10}\) + \(\frac{7}{15}\)

3. \(1 \frac{1}{3}+3 \frac{2}{3}\)

4. \(\frac{16}{5}-\frac{7}{5}\)

5. \(\frac{4}{3}-\frac{1}{2}\)

Solution. (1) We have, \(\frac{2}{3}\) + \(\frac{1}{7}\) (LCM of 3 and 7 = 21)

∴ \(\frac{2}{3}+\frac{1}{7}=\frac{2 \times 7}{3 \times 7}+\frac{1 \times 3}{7 \times 3}=\frac{14}{21}+\frac{3}{21}=\frac{14+3}{21}=\frac{17}{21}\)

Hence, \(\frac{2}{3}+\frac{1}{7}=\frac{17}{21}\)

(2) We have, \(\frac{3}{10}\) + \(\frac{7}{15}\) (LCM of 10 and 15 = 30)

∴ \(\frac{3}{10}+\frac{7}{15}=\frac{3 \times 3}{10 \times 3}+\frac{7 \times 2}{15 \times 2}=\frac{9}{30}+\frac{14}{30}=\frac{9+14}{30}=\frac{23}{30}\)

Hence, \(\frac{3}{10}+\frac{7}{15}=\frac{23}{30}\)

(3) We have, \(1 \frac{1}{3}+3 \frac{2}{3}\)

= \(1+\frac{1}{3}+3+\frac{2}{3}\)

= \((1+3)+\left(\frac{1}{3}+\frac{2}{3}\right)=4+\frac{1}{3}+\frac{2}{3}\)

Now, \(\frac{1}{3}+\frac{2}{3}=\frac{1+2}{3}=\frac{3}{3}=1\)

∴ \(4+\frac{1}{3}+\frac{2}{3}=4+1=5\)

Hence, \(1 \frac{1}{3}+3 \frac{2}{3}=5\)

(4) We have, \(\frac{16}{5}-\frac{7}{5}\)

∴ \(\frac{16}{5}-\frac{7}{5}=\frac{16-7}{5}=\frac{9}{5}\)

Hence, \(\frac{16}{5}-\frac{7}{5}=\frac{9}{5}\)

(5) We have, \(\frac{4}{3}-\frac{1}{2}\)

LCM of 3 and 2 = 6

∴ \(\frac{4}{3}-\frac{1}{2}=\frac{4 \times 2}{3 \times 2}-\frac{1 \times 3}{2 \times 3}=\frac{8}{6}-\frac{3}{6}=\frac{8-3}{6}=\frac{5}{6}\)

Hence, \(\frac{4}{3}-\frac{1}{2}=\frac{5}{6}\)

Comparing Fractions Class 6

Question 2. Sarita bought \(\frac{2}{5}\) metre of ribbon and Lalita bought \(\frac{3}{4}\) metre of ribbon. What is the total length of the ribbon they bought?

Solution. Given, ribbon bought by Sarita = \(\frac{2}{5}\) m

and ribbon bought by Lalita = \(\frac{3}{4}\) m

∴ Total length of the ribbon bought buy them = \(\frac{2}{5}\) + \(\frac{3}{4}\)

Now, LCM of 5 and 4 = 20

∴ \(\frac{2}{5}+\frac{3}{4}=\frac{2 \times 4}{5 \times 4}+\frac{3 \times 5}{4 \times 5}=\frac{8}{20}+\frac{15}{20}=\frac{8+15}{20}=\frac{23}{20}\)

Hence, the total length of ribbon bought by them is \(\frac{23}{20}\) m.

Question 3. Naina was given \(1 \frac{1}{2}\) piece of cake and Najma was given \(1 \frac{1}{3}\) piece of cake. Find the total amount of cake was given to both of them.

Solution. Cake given to Naina = \(1 \frac{1}{2}\) piece

Cake given to Najma = \(1 \frac{1}{3}\) piece

Total cake given to both of them

LCM of 2 and 3 = 6

∴ \(\frac{3}{2}+\frac{4}{3}=\frac{3 \times 3}{2 \times 3}+\frac{4 \times 2}{3 \times 2}=\frac{9}{6}+\frac{8}{6}=\frac{9+8}{6}=\frac{17}{6}\)

Hence, the total cake given to both of them = \(\frac{17}{6}\) piece

Question 4. Complete the addition subtraction box.

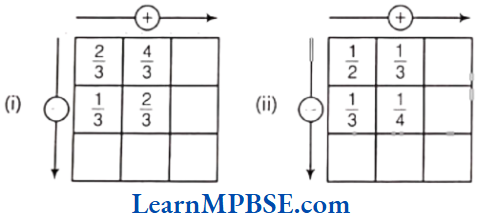
Solution. (1) Here, \(\frac{2}{3}+\frac{4}{3}=\frac{2+4}{3}=\frac{6}{3}=2 \text { and } \frac{1}{3}+\frac{2}{3}=\frac{1+2}{3}=\frac{3}{3}=1\)

Now, \(\frac{2}{3}-\frac{1}{3}=\frac{2-1}{3}=\frac{1}{3} \text { and } \frac{4}{3}-\frac{2}{3}=\frac{4-2}{3}=\frac{2}{3}\)

Also, we have 2 – 1 = 1 and \(\frac{1}{3}+\frac{2}{3}=\frac{1+2}{3}=\frac{3}{3}=1\)

Hence, the required complete box is

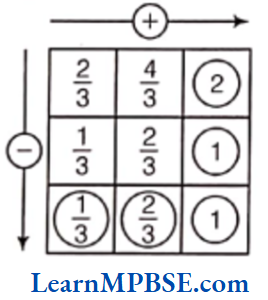
(2) Here, \(\frac{1}{2}+\frac{1}{3}=\frac{1 \times 3}{2 \times 3}+\frac{1 \times 2}{3 \times 2}=\frac{3}{6}+\frac{2}{6}=\frac{3+2}{6}=\frac{5}{6}\)

[∴ LCM of 2 and 3 = 6]

and \(\frac{1}{3}+\frac{1}{4}=\frac{1 \times 4}{3 \times 4}+\frac{1 \times 3}{4 \times 3}=\frac{4}{12}+\frac{3}{12}\)

= \(\frac{4+3}{12}=\frac{7}{12}\) [∴ LCM of 3 and 4 = 12]

Now, \(\frac{1}{2}-\frac{1}{3}=\frac{1 \times 3}{2 \times 3}-\frac{1 \times 2}{3 \times 2}\)

= \(\frac{3}{6}-\frac{2}{6}=\frac{3-2}{6}=\frac{1}{6}\)

[∴ LCM of 2 and 3 = 6]

and \(\frac{1}{3}-\frac{1}{4}=\frac{1 \times 4}{3 \times 4}-\frac{1 \times 3}{4 \times 3}\)

= \(\frac{4}{12}-\frac{3}{12}=\frac{4-3}{12}=\frac{1}{12}\)

[∴ LCM of 3 and 4 = 12]

Also, we have \(\frac{5}{6}-\frac{7}{12}=\frac{5 \times 2}{6 \times 2}-\frac{7 \times 1}{12 \times 1}\)

[∴ LCM of 6 and 12 = 12]

= \(\frac{10}{12}-\frac{7}{12}=\frac{10-7}{12}=\frac{3}{12}=\frac{1}{4}\)

[dividing numerator and denominator by 3]

and \(\frac{1}{6}+\frac{1}{12}=\frac{1 \times 2}{6 \times 2}+\frac{1 \times 1}{12 \times 1}\)

= \(\frac{2}{12}+\frac{1}{12}=\frac{2+1}{12}=\frac{3}{12}=\frac{1}{4}\)

[∴ LCM of 6 and 12 = 12]

[dividing numerator and denominator by 3]

Hence, the required complete box is

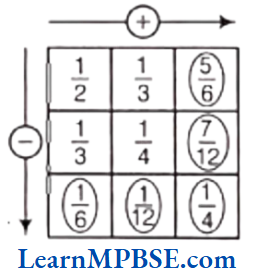
Question 5. A piece of wire \(\frac{7}{8}\) meter long broke into two pieces. One piece was \(\frac{1}{4}\) metre long. How long is the other piece?

Solution. Given, total length of a piece of wire = \(\frac{7}{8}\) m

Length of one piece of wire = \(\frac{1}{4}\) m

∴ Length of another piece = \(\left(\frac{7}{8}-\frac{1}{4}\right) \mathrm{m}\)

LCM of 8 and 4 = 8

∴ \(\frac{7}{8}-\frac{1}{4}=\frac{7 \times 1}{8 \times 1}-\frac{1 \times 2}{4 \times 2}\)

= \(\frac{7}{8}-\frac{2}{8}=\frac{7-2}{8}=\frac{5}{8}\)

Hence, the length of another piece of wire is \(\frac{5}{8}\) m.

Comparing Fractions Class 6

Question 6. Nandini’s house is \(\frac{9}{10}\) km from her school. She walked some distance and then took a bus for \(\frac{1}{2}\)km to reach the school. How far did she walk?

Solution. Given, distance of school from Nandini’s house = \(\frac{9}{10}\) km

Distance covered by Nandini by bus = \(\frac{1}{2}\) km

∴ Distance covered by Nandini by walking = \(\frac{9}{10}\) – \(\frac{1}{2}\)

LCM of 10 and 2 = 10

= \(\frac{9-5}{10}=\frac{4}{10}=\frac{2}{5} \mathrm{~km}\)

Hence, she walked \(\frac{2}{5}\) km.

Question 7. Asha and Samuel have bookshelves of the same size partly filled with books. Asha’s shelf is \(\frac{5}{6}\)th full and Samuel’s shelf is \(\frac{2}{5}\)th full. Whose bookshelf is more full ? By what fraction?

Solution. The protion of Asha’s shelf filled by books = \(\frac{5}{6}\) part

and the portion of Samuel’s shelf filled by books = \(\frac{2}{5}\) part

Now, LCM of 6 and 5 = 30

Equivalent fractions of \(\frac{5}{6}\) are \(\frac{5 \times 2}{6 \times 2}, \frac{5 \times 3}{6 \times 3}, \frac{5 \times 4}{6 \times 4}, \frac{5 \times 5}{6 \times 5}, \ldots\)

i.e. \(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}, \frac{25}{30}, \ldots\)

and equivalent fractions of \(\frac{2}{5}\) are

i.e. \(\frac{4}{10}, \frac{6}{15}, \frac{8}{20}, \frac{10}{25}, \frac{12}{30}, \ldots\)

Here, equivalent fractions \(\frac{12}{30}\) and \(\frac{25}{30}\) have same denominator.

∴ 25 > 12

∴ \(\frac{25}{30}>\frac{12}{30} \text { i.e. } \frac{5}{6}>\frac{2}{5}\)

Now, \(\frac{5}{6}-\frac{2}{5}=\frac{25}{30}-\frac{12}{30}=\frac{25-12}{30}=\frac{13}{30}\)

Hence, Asha’s book shelf is more full by fraction \(\frac{13}{30}\).

Question 8. Jaidev takes \(2 \frac{1}{5}\) minutes to walk across the school ground. Rahul takes \(\frac{7}{4}\) minutes to do the same. Who takes less time and by what fraction?

Solution. Time taken by Jaidev to walk across the school ground = \(2 \frac{1}{5} \min =\frac{11}{5} \min\)

and time taken by Rahul to walk across the school ground = \(\frac{7}{4}\) min

Now, equivalent fractions of \(\frac{11}{5}\) are

and equivalent fractions of \(\frac{7}{4} are \frac{7 \times 2}{4 \times 2}, \frac{7 \times 3}{4 \times 3}, \frac{7 \times 4}{4 \times 4}, \frac{7 \times 5}{4 \times 5},\)

i.e. \(\frac{14}{8}, \frac{21}{12}, \frac{28}{16}, \frac{35}{20}, \ldots\)

Here, equivalent fractions \(\frac{44}{20}\) and \(\frac{35}{20}\) have same denominators.

∴ 44 > 35

∴ \(\frac{44}{20}>\frac{35}{20} \text { i.e. } \frac{11}{5}>\frac{7}{4}\)

Now, \(\frac{11}{5}-\frac{7}{4}=\frac{44}{20}-\frac{35}{20}=\frac{44-35}{20}=\frac{9}{20}\)

Hence, Rahul takes less time by \(\frac{9}{20}\) min.

Chapter 7 Fractions Multiple Choice Questions

Question 1. The two consecutive integers between which the fraction \(\frac{5}{7}\) lies are

1. 5 and 6
2. 0 and 1
3. 5 and 7
4. 6 and 7

Answer. 2. 0 and 1

Question 2. How is the fractional number of “3 out of 7 of the fruits are apples” written ?

1. \(\frac{3}{7}\)
2. \(\frac{7}{3}\)
3. \(\frac{4}{7}\)
4. \(\frac{4}{3}\)

Answer. 1. \(\frac{3}{7}\)

Comparing Fractions Class 6

Question 3. \(\frac{21}{19}\) can be expressed in form

1. \(2 \frac{3}{19}\)
2. \(2 \frac{1}{19}\)
3. \(1 \frac{2}{19}\)
4. \(3 \frac{1}{19}\)

Answer. 3. \(1 \frac{1}{19}\)

Question 4. Raju scored 9 m arks in maths test. If the maximum marks of the test is 25, how is Raju’s score represented as a fraction?

1. \(\frac{1}{25}\)
2. \(\frac{16}{25}\)
3. \(\frac{9}{25}\)
4. \(\frac{25}{25}\)

Answer. 3. \(\frac{9}{25}\)

Question 5. The fraction which is not equal to \(\frac{4}{5}\) is

1. \(\frac{40}{50}\)
2. \(\frac{12}{15}\)
3. \(\frac{16}{20}\)
4. \(\frac{9}{15}\)

Answer. 4. \(\frac{9}{15}\)

Question 6. If \(\frac{3}{4}\) is equivalent to \(\frac{x}{24}\), then the value of x is

1. 15
2. 20
3. 16
4. 18

Answer. 4. 18

Question 7. Which option given an equivalent fraction of \(\frac{13}{25}\) ?

1. \(\frac{65}{50}\)
2. \(\frac{26}{75}\)
3. \(\frac{156}{300}\)
4. \(\frac{103}{205}\)

Answer. 3. \(\frac{156}{300}\)

Question 8. When \(\frac{1}{4}\) is written with denominator as 12, its numerator is

1. 3
2. 8
3. 24
4. 12

Answer. 1. 3

Comparing Fractions Class 6

Question 9. When \(\frac{1}{7}\) is written with denominator as 56, its numerator is

1. 3
2. 8
3. 24
4. 12

Answer. 2. 8

Question 10. Which of the following is not in the lowest form?

1. \(\frac{7}{5}\)
2. \(\frac{15}{20}\)
3. \(\frac{13}{33}\)
4. \(\frac{27}{28}\)

Answer. 2. \(\frac{15}{20}\)

Question 11. Which of the following fraction is smallest?

1. \(\frac{16}{23}\)
2. \(\frac{17}{23}\)
3. \(\frac{9}{23}\)
4. \(\frac{11}{23}\)

Answer. 3. \(\frac{9}{23}\)

Question 12. If \(\frac{5}{8}\) = \(\frac{20}{p}\), then value of p is

1. 23
2. 2
3. 32
4. 16

Answer. 3. 32

Question 13. If \(\frac{7}{9}\) = \(\frac{28}{p}\), then value of p is

1. 23
2. 2
3. 36
4. 16

Answer. 3. 36

Question 14. What are the fractions with the same denominator called?

1. Unit fractions
2. Unlike fractions
3. Like fractions
4. Improper fractions

Answer. 3. Like fractions

Question 15. The ascending order of the fractions \(\frac{14}{17}, \frac{10}{12}, \frac{6}{7}\) and \(\frac{18}{22}\) is

1. \(\frac{6}{7}, \frac{14}{17}, \frac{10}{12}, \frac{18}{22}\)
2. \(\frac{18}{22}, \frac{14}{17}, \frac{10}{12}, \frac{6}{7}\)
3. \(\frac{14}{17}, \frac{10}{12}, \frac{14}{17}, \frac{18}{22}\)
4. \(\frac{6}{7}, \frac{10}{12}, \frac{14}{17}, \frac{18}{22}\)

Answer. 2. \(\frac{18}{22}, \frac{14}{17}, \frac{10}{12}, \frac{6}{7}\)

Question 16. Sum of \(\frac{4}{17}\) and \(\frac{15}{17}\) is

1. \(2 \frac{1}{17}\)
2. \(1 \frac{2}{17}\)
3. \(3 \frac{1}{17}\)
4. \(3 \frac{2}{17}\)

Answer. 2. \(1 \frac{2}{17}\)

Question 17. On subtracting \(\frac{6}{13}\) from \(\frac{11}{13}\), the result is

1. \(\frac{5}{13}\)
2. \(\frac{2}{13}\)
3. \(\frac{3}{13}\)
4. \(\frac{8}{13}\)

Answer. 1. \(\frac{5}{13}\)

Comparing Fractions Class 6

Question 18. What should be added to \(\frac{11}{17}\) to make it \(\frac{15}{17}\) ?

1. \(\frac{26}{17}\)
2. 4
3. \(\frac{4}{17}\)
4. \(\frac{4}{34}\)

Answer. 3. \(\frac{4}{17}\)

Question 19. Choose the correct option for the sum of shaded parts of the given boxes.

1. \(\frac{2}{5}+\frac{2}{5}=\frac{4}{5}\)
2. \(\frac{2}{5}+\frac{1}{5}=\frac{3}{5}\)
3. \(\frac{2}{5}-\frac{1}{5}=\frac{1}{5}\)
4. \(\frac{3}{5}+\frac{1}{5}=\frac{4}{5}\)

Answer. 2. \(\frac{2}{5}+\frac{1}{5}=\frac{3}{5}\)

Chapter 7 Fractions Assertion – Reason

Question 1. Assertion (A) \(\frac{2}{7}\) is obtained when we divide a whole into seven equal parts and take two part.

Reason (R) A fraction is a number representing part of a whole.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true and R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 2. Assertion (A) The simplest form of \(\frac{12}{20}\) is \(\frac{3}{5}\)

Reason (R) A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true and R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 3. Assertion (A) \(\frac{4}{5}\) > \(\frac{6}{5}\)

Reason (R) For two fract ions with the same denominator, the fraction with greater numerator is greater.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true and R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (d) A is false but R is true.

Chapter 7 Fractions Fill in the Blanks

Question 1. A number representing a part of a ….. is called a fraction.

Answer. Whole

Question 2. 1 whole = …. tenths.

Answer. 10

Question 3. A fraction with numerator greater than the denominator is called an ….. fraction.

Answer. Improper

Question 4. \(\frac{21}{13}\) is an ….. fraction.

Answer. Improper

Question 5. \(13 \frac{5}{18}\) is a …… fraction.

Answer. Mixed

Comparing Fractions Class 6

Chapter 7 Fractions True/False

Question 1. If a whole of an object is divided into a number of equal parts, then each parts, then each part represents a fraction.

Answer. True

Question 2. The fraction represented by the shaded portion in the following figure is \(\frac{3}{8}\).

Answer. True

Question 3. The fraction represented by the unshaded portion in the following figure is \(\frac{5}{9}\).

Answer. False

Question 4. Ali divided one fruit cake equally among six persons. The part of the cake he gave to each person is \(\frac{1}{6}\).

Answer. True

Question 5. Sum of \(\frac{5}{12}\) and \(\frac{7}{12}\) is \(1 \frac{7}{12}\)

Answer. False

Chapter 7 Fractions Match the Columns

Question 1.

Solution. (i) → (d), (ii) → (a), (iii) → (e), (iv) → (b), (v) → (c)

Question 2.

Solution. (i) → (d), (ii) → (c), (iii) → (a), (iv) → (b)

Question 3.

Solution. (i) → (c), (ii) → (d), (iii) → (a), (iv) → (b)

Chapter 7 Fractions Case Based Questions

Question 1. Cross country is a running even in which runners completed a pre-decided distance.

It includes different activities in which runners cover different environments. A cross country running event of 11 km is as follows.

(1) What fraction of the total distance is the mud run?

(a) \(\frac{11}{1}\)

(b) \(\frac{1}{10}\)

(c) \(\frac{1}{11}\)

(d) 1

(2) What fraction of the total distance is the distance covered on paved and unpaved roads?

(a) \(\frac{3}{2}\)

(b) \(\frac{5}{5}\)

(c) \(\frac{5}{6}\)

(d) \(\frac{5}{11}\)

Solution. (1) (c) Total distance runner covers = 11km

Distance in mud run = 1 km

∴ Fraction of total distance in mud run \(=\frac{\text { Distance in mud run }}{\text { Total distance runner covers }}=\frac{1}{11}\)

(2) (d) Distance in paved road = 3 km.

Distance in unpaved road = 2 km.

∴ Total distance in both = \(\frac{3+2}{11}=\frac{5}{11}\)

Question 2. Katherine completed the cross country in 1 hr. She completed the run on the paved and unpaved roads in one-fourth of an hour while Juliana covered it in half an hour.

(1) In how many minutes did Katherine cover the distance on the paved and unpaved roads?

(a) 10 min

(b) 15 min

(c) 20 min

(d) 30 min

(2) How much more time (in hrs) was taken by Juliana than Katherine?

Solution. (1) (b) Katherine completed the cross country = 1hr

∴ Katherine covered the run on the paved and unpaved roads in one-fourth of an hour, which is equal to

Thus, Katherine coveres the distance on paved and unpaved roads in 15 min.

(2) Katherine completed the run on the paved and unpaved road = \(\frac{1}{4}\) of 1 h = \(\frac{1}{4}\) x 60 min = 15 min

While Juliana covered the run on the paved and unpaved road = \(\frac{1}{2}\) of 1 h = \(\frac{1}{2}\) x 60 min = 30 min

Thus, Juliana time – Katherine time

= (30 – 15) = 15 min

Thus, Juliana takes 15 min or \(\frac{1}{4}\) of an hour more than Katherine.

Question 3. Parul and two of her friends share a pizza equally among themselves.

(1) Parul says, ‘Here are three equal halves of the pizza.’ Is parul’s statement correct? Give reasons.

(2) Which fraction represents one part of the whole pizza?

(a) \(\frac{1}{2}\)

(b) \(\frac{1}{3}\)

(c) \(\frac{2}{3}\)

(d) 3

Later, three more friends join Parul. Parul divides the pizza again to have 6 parts.

(3) Does every one get an equal portion? Give reasons.

(4) Suggest a way to divide the pizza into six equal parts.

Solution. (1) No, Parul’s statement is not correct. Pizza is divided into three equal parts, which is not half of the pizza.

(2) (b) Pizza divided into 3 parts.

Therefore, one part of pizza = \(\frac{1}{3}\).

(3) Three more friends joined Parul means now remaining pizza is divided again.

So, everyone does not get an equal portion of pizza.

(4) Usually pizzas are circular. Therefore, total angle = 360°

To divide 360 into 6 parts divide 360 by 6

i.e. \(\frac{360^{\circ}}{6}=60^{\circ}\)

Now, measure 60° and cut the pizza into 6 equal parts.

Chapter 7 Fractions Very Short Answer Type Questions

Question 1. 3 mm is what fraction of a metre?

Solution. We know that 1 m = 1000 mm

3 mm = \(\frac{3}{1000}\) made

So, 3 mm is \(\frac{3}{1000}\) of a metre.

Question 2. Write \(\frac{2}{3}\) of 60 kg.

Solution. We have, \(\frac{2}{3}\) of 60 kg = \(\frac{2 \times 60}{3}=2 \times 20=40 \mathrm{~kg}\)

Question 3. What fraction of the week is 3 days?

Solution. We know that 1 week = 7 days 3

∴ 3 days = \(\frac{3}{7}\) week

So, 3 days are of a week.

Question 4. 30 seconds is what fraction of a minute?

Solution. We know that 1 min = 60 s

i.e. 60 s = 1 min

So, 30 sec are \(\frac{1}{2}\) of a minute.

Question 5. Name the fraction which are always less than 1.

Solution. We know that proper fractions are always less than 1.

Chapter 7 Fractions Short Answer Type Questions

Question 1. Write the natural numbers from 205 to 219. What fraction of them are odd numbers?

Solution. Natural numbers from 205 to 219 are 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219.

Total natural numbers = 15

Odd numbers = 8

∴ Required fraction = \(\frac{\text { Odd numbers }}{\text { Natural numbers }}=\frac{8}{15}\)

Question 2. What fraction of a kg is 650 gm?

Solution. We know that 1 kg = 1000 g

∴ \(650 \mathrm{gm}=\frac{650}{1000} \mathrm{~kg}=\frac{65}{100}\)

= \(\frac{65 \div 5}{100 \div 5}\) [∴ HCF of 65 and 100 is 5]

= \(\frac{13}{20}\)

So, 650 gm is \(\frac{13}{20}\) of a kg.

Question 3. Find the fraction that represents the number of natural numbers to total numbers of natural numbers to total numbers in the collection 0, 1, 2, 3, 4, 5. What fraction will it be for whole numbers?

Solution. Given collection is 0, 1, 2, 3, 4, 5.

Natural numbers = 1, 2, 3, 4, 5

∴ The fraction of natural numbers to the collection = \(\frac{5}{6}\)

Now, whole numbers = 0, 1, 2, 3, 4, 5

The fraction of whole numbers to the collection = \(\frac{6}{6}\) i.e. \(\frac{1}{1}\)

Question 4. Express the following as improper fraction.

(1) \(5 \frac{1}{4}\)

(2) \(7 \frac{2}{3}\)

Solution. (1) We have, \(5 \frac{1}{4}\)

Now, \(5 \frac{1}{4}=5+\frac{1}{4}=\frac{5 \times 4+1}{4}=\frac{21}{4}\)

(2) We have, \(7 \frac{2}{3}=7+\frac{2}{3}=\frac{7 \times 3+2}{3}=\frac{23}{3}\)

Question 5. Express the following as mixed fractions.

(1) \(\frac{15}{4}\)

(2) \(\frac{25}{6}\)

Solution. (1) We have, improper fraction = \(\frac{15}{4}\)

∴ \(\frac{15}{4}=3 \frac{3}{4}\)

(2) We have, improper fraction = \(\frac{25}{6}\)

∴ \(\frac{25}{6}=4 \frac{1}{6}\)

Question 6. Check whether the given fractions are equivalent.

(1) \(\frac{5}{7}\), \(\frac{9}{12}\)

(2) \(\frac{7}{5}\), \(\frac{21}{15}\)

Solution.

(1) We have, \(\frac{5}{7}\), \(\frac{9}{12}\) = \(\frac{5}{7}\) = \(\frac{9}{12}\)

⇒ 5 x 12 = 9 x 7

60 ≠ 63

So, \(\frac{5}{7}\), \(\frac{9}{12}\) are not equivalent fractions.

(2) We have, \(\frac{7}{5}\), \(\frac{21}{15}\) = \(\frac{7}{5}\) = \(\frac{21}{15}\)

⇒ 7 x 15 = 105, 21 x 5 = 105

So, \(\frac{7}{5}\), \(\frac{21}{15}\) are equivalent fractions.

Question 7. Write \(\frac{156}{60}\) in its lowest form.

Solution. We have, \(\frac{156}{60}\)

Now, we find the HCF of 156 and 60.

∴ HCF of 156 and 60 is 12.

So, \(\frac{156}{60}=\frac{156 \div 12}{60 \div 12}=\frac{13}{5}\)

Question 8. Compare \(4 \frac{2}{3} \text { and } 5 \frac{3}{7}\).

Solution. We have, \(4 \frac{2}{3} \text { and } 5 \frac{3}{7}\)

Now, \(4 \frac{2}{3}=\frac{4 \times 3+2}{3}=\frac{14}{3} \text { and } 5 \frac{3}{7}=\frac{5 \times 7+3}{7}=\frac{38}{7}\)

Now, let us compare \(\frac{14}{3}\) and \(\frac{38}{7}\) by cross-multiplication.

We have, \(\frac{14}{3}\) = \(\frac{38}{7}\)

14 x 7 = 98 and 38 x 3 = 114

∴ 114 > 98

∴ \(\frac{38}{7}\) > \(\frac{14}{3}\)

So, \(5 \frac{3}{7}>4 \frac{2}{3}\)

Question 9. Find the value of the following:

(1) \(\frac{6}{17}+\frac{3}{17}+\frac{11}{17}\)

(2) \(\frac{1}{2}+\frac{3}{4}+1 \frac{1}{3}\)

Solution.

(1) We have, \(\frac{6}{17}+\frac{3}{17}+\frac{11}{17}=\frac{6+3+11}{17}=\frac{20}{17}=1 \frac{3}{17}\)

(2) We have, \(\frac{1}{2}+\frac{3}{4}+1 \frac{1}{3}=\frac{1}{2}+\frac{3}{4}+\frac{4}{3}=\frac{6+9+16}{12}\)

[∴ LCM of 2, 4 and 3 is 12]

= \(\frac{31}{12}=2 \frac{7}{12}\)

Question 10. Neelam’s father needs \(1 \frac{3}{4}\) m of cloth for the skirt of Neelam’s new dress and \(\frac{1}{2}\) m for the scarf. How much cloth must he buy in all?

Solution. Cloth required for skirt = \(1 \frac{3}{4}\) m

Cloth required for scarf = \(\frac{1}{2}\) m

∴ Total cloth = \(\left(1 \frac{3}{4}+\frac{1}{2}\right) \mathrm{m}=\frac{7}{4}+\frac{1}{2}\)

\(\frac{7+2}{4}=\frac{9}{4}=2 \frac{1}{4} \mathrm{~m}\) [∴ LCM of 2 and 4 is 4]

So, he must buy \(2 \frac{1}{4}\) m cloth.

Question 11. Sunil purchased \(12 \frac{1}{2}\) L of juice on Monday and \(14 \frac{3}{4}\) L of lace for her new dress. How much lace is left with her?

Solution. Sunil purchased juice on Monday = \(12 \frac{1}{2}\) L

Juice purchased on Tuesday = \(14 \frac{3}{4}\) L

∴ Total juice purchased = \(12 \frac{1}{2}+14 \frac{3}{4}=\frac{25}{2}+\frac{59}{4}\)

= \(\frac{50+59}{4}=\frac{109}{4}=27 \frac{1}{4} \mathrm{~L}\)

So, he purchased \(27 \frac{1}{4}\) L of juice in two days.

Question 12. Simplify the following:

(1) \(6-\frac{3}{4}\)

(2) \(\frac{7}{12}-\frac{4}{15}\)

Solution. (1) We have, \(6-\frac{3}{4}=\frac{6}{1}-\frac{3}{4}=\frac{24-3}{4}=\frac{21}{4}=5 \frac{1}{4}\)

(2) We have, \(\frac{7}{12}-\frac{4}{15}=\frac{35-16}{60}=\frac{19}{60}\)

Question 13. A cup is \(\frac{1}{3}\) full of milk. What part of the cup is still to be filled by milk to make it full?

Solution. Given, cup is \(\frac{1}{3}\) full of milk.

∴ Required milk = \(1-\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}\)

Hence, \(\frac{2}{3}\) part of the cup is required to make it full.

Question 14. May bought \(3 \frac{1}{2} \mathrm{~m}\) of lace. She used \(1 \frac{3}{4} \mathrm{~m}\) of lace

Solution. Mary bought lace = \(3 \frac{1}{2} \mathrm{~m}\)

Lace used for new dress = \(1 \frac{3}{4} \mathrm{~m}\)

∴ Lace left with her = \(3 \frac{1}{2}-1 \frac{3}{4}=\frac{7}{2}-\frac{7}{4}=\frac{14-7}{4}=\frac{7}{4}=1 \frac{3}{4} m\)

So, \(1 \frac{3}{4} \mathrm{~m}\) lace is left with her.

Question 15. Nazima gave \(2 \frac{3}{4}\) L out of the \(5 \frac{1}{2} \mathrm{~L}\) of juice she purchased to her friends. How many litres of juice is left with her?

Solution. Quantity of juice Nazima has = \(5 \frac{1}{2} \mathrm{~L}\)

She gave \(2 \frac{3}{4}\) L out of this to her friends.

Now, juice left with her = \(5 \frac{1}{2}-2 \frac{3}{4}=\frac{11}{2}-\frac{11}{4}\)

= \(\frac{22-11}{4}=\frac{11}{4}=2 \frac{3}{4} \mathrm{~L}\)

So, \(2 \frac{3}{4} \mathrm{~L}\) of juice is left with her.

Chapter 7 Fractions Long Answer Type Questions

Question 1. It was estimated that because of people switching to Metro trains, about 33000 tonne of CNG, 3300 tonne of diesel and 21000 tonne of petrol was saved by the end of year 2007.

Find the fraction of

(1) the quantity of diesel saved to the quantity of petrol saved.

(2) the quantity of diesel saved to the quantity of CNG saved.

Solution. Given, quantity of CNG saved = 33000 tonne

Quantity of diesel saved = 3300 tonne

Quantity of petrol saved = 21000 tonne

(1) The fraction of the quantity of diesel saved to the quantity of petrol saved=

= \(\frac{3300}{21000}=\frac{33}{210}=\frac{33 \div 3}{210 \div 3}\)

[∴ HCF of 33 and 210 is 3]

= \(\frac{11}{70}\)

(2) The fraction of the quantity of diesel to the quantity of CNG saved

= \(\frac{3300}{33000}=\frac{33}{330}=\frac{33+33}{330+33}=\frac{1}{10}\)

Question 2. Poorvi cut a cake into 8 equal pieces. If she wanted to divide each of them into 3 equal pieces, what fraction of the whole cake would each small pieces be?

Solution. Number of pieces in which the cake cut = 8

Number of pieces each cut piece divided into = 3

∴ Total number of pieces = 8 x 3 = 24

Hence, each piece is represented by the fraction \(\frac{1}{24}\)

Question 3. The energy content of different foods are as follows:

Which food provides the least energy and which provides the maximum? Also, express the least energy as a fraction of the maximum energy.

Solution. In the given table, we see that the minimum value is 3.0J and maximum value is 5.3 J.

∴ Least energy provide by food = 3.0J i.e. Milk

Food which provide the maximum energy = 5.3J i.e. Rice Least energy 30 30

∴ Required fraction \(=\frac{\text { Least energy }}{\text { Maximum energy }}=\frac{3.0}{5.3}=\frac{30}{53}\)

Question 4. A rectangle is divided into certain number of equal parts. If 16 of the parts so formed represent the fraction \(\frac{1}{4}\), find the number of parts in which the rectangle has been divided.

Solution. Let a rectangle be divided into x equal parts.

Now, 16 of the parts represent \(\frac{1}{4}\)

∴ \(\frac{16}{x}=\frac{1}{4}\) ⇒ x = 16 x 4 ⇒ x = 64 parts

Hence, rectangle is divided into 64 equal parts.

Question 5. From school X out of 750 students, 250 were selected for an essay writing and from another school Y out of 1200 students, 300 were selected. From which school, more students were selected?

Solution. Total students in school X = 750

Selected students = 250

∴ Fraction of selected students to the total students

= \(\frac{250}{750}=\frac{1}{3}\) …(1)

Now, total students in school Y = 1200

Selected students = 300

∴ Fraction of selected students to the total students

= \(\frac{300}{1200}=\frac{1}{4}\) …(2)

From Eqs. (1) and (2), \(\frac{1}{3}\) > \(\frac{1}{4}\) [∴ 4 > 3]

Hence, from the school X more students were selected.

Question 6. The fish caught bu Neetu was of weight \(3 \frac{3}{4}\) kg and the fish caught by Narendra was of weight \(2 \frac{1}{2}\) kg. How much more was Neetu’s fish weight than that of Narendra?

Solution. Given, weight of fish caught by Neetu = \(3 \frac{3}{4} \mathrm{~kg}=\frac{15}{4} \mathrm{~kg}\)

and weight of the fish caught by Narendra = \(2 \frac{1}{2}=\frac{5}{2} \mathrm{~kg}\)

∴ Difference between their weights

= \(\frac{15}{4}-\frac{5}{2}=\frac{15}{4}-\frac{5 \times 2}{2 \times 2}\)

= \(\frac{15}{4}-\frac{10}{4}=\frac{15-10}{4}=\frac{5}{4} \mathrm{~kg}\)

Hence, Neetu’s fish weight is kg more than the Narendra’s fish weight.

Question 7. On an average, \(\frac{1}{10}\) of the food eaten is turned into organism’s own body and is available for the next level of consumer in a food chain. What fraction of the food eaten is not available for the next level?

Solution. Quantity of food eaten which turned into organism’s own body = \(\frac{1}{10}\) of the total food

Now, the quantity of food eaten which is not available

for the next level = \(1-\frac{1}{10}=\frac{10-1}{10}=\frac{9}{10}\)

Hence, the required fraction = \(\frac{9}{10}\)

Question 8. Mr. Rajan got a job at the age of 24 yr and he got retired from the job at the age of 60 yr. What fraction of his age till retirement was he in the job?

Solution. Given, Rajan’s age on the joining = 24 yr and retirement age = 60 yr

The number of years, he did the job

= Retirement age – Joining age

= 60 – 24 = 36 yr

∴ The fraction of his age till retirement, when he was in the job

= \(\frac{36 \div 12}{60 \div 12}=\frac{3}{5}\)

Hence, the required fraction is \(\frac{3}{5}\).

Question 9. Roma gave a wooden board of length \(150 \frac{1}{4}\)cm to a carpenter for making a shelf. The carpendter sawed off a piece of \(40 \frac{1}{5}\) cm from it. What is the length of the remaining piece?

Solution. Given, length of a wooden board = \(150 \frac{1}{4} \mathrm{~cm}=\frac{601}{4} \mathrm{~cm}\)

Carpenter sawed off a piece of wooden board = \(40 \frac{1}{5} \mathrm{~cm}=\frac{201}{5} \mathrm{~cm}\)

∴ Length of the remaining piece = \(\frac{601}{4}-\frac{201}{5}\)

∴ LCM of 4 and 5 = 20

∴ \(\frac{601}{4}-\frac{201}{5}=\frac{601 \times 5}{4 \times 5}-\frac{201 \times 4}{5 \times 4}\)

= \(\frac{3005}{20}-\frac{804}{20}\)

= \(\frac{3005-804}{20}=\frac{2201}{20} \mathrm{~cm}\)

Hence, the length of remaining piece is \(\frac{2201}{20}\) or \(110 \frac{1}{20}\) cm

Chapter 12 Ratio and Proportion Ratio

The comparison of two numbers or quantities by the method of division is known as the ratio of the numbers and it is denoted by symbol “:”

e.g. Let two numbers be a and b, where b 0, then the ratio of a and b is a:b.

The first term a is called the antecedent and the second term b is called the consequent.

Suppose, we have 5 pens and 9 toys. The ratio of number of pens to number of toys is 5:9 or 5 is to 9.

Ratio in Simplest Form

The ratio a : b is said to be in the simplest form or lowest form if the HCF of a and b is 1. A ratio in the simplest form is also called the ratio in the lowest term.

e.g. The ratio 11:18 is in the simplest form. Since, the HCF of 11 and 18 is 1. To convert a given ratio a: b to its simplest form, we divide each term by the HCF of a and b.

Example 1. Find the ratio of the following

(1) 21 to 84

(2) 30 min to 60 min

(3) 80 cm to 1.2 m

Solution. (1) Here, HCF of 21 and 84 = 21

∴ Ratio = \(\frac{21+21}{84+21}=\frac{1}{4}=1: 4\)

(2) Since, given quantities are in same unit.

∴ HCF of 30 and 60 = 30

∴ Ratio = \(\frac{30 \div 30}{50 \div 30}=\frac{1}{2}=1: 2\)

(3) Since, given quantities are not in the same unit.

Firstly, we have to convert them into same unit.

Read and Learn More MP Board Class 6 Maths Solutions

We know that 1 m = 100 cm

⇒ 1.2 m = 1.2 x 100 cm

= 120 cm

∴ Ratio of 80 cm to 1.2 m i.e. 80 cm to 120 cm = \(\frac{80}{120}\)

∴ HCF of 80 and 120 = 40

∴ Ratio = \(\frac{80 \div 40}{120 \div 40}=\frac{2}{3}\)

Hence, the required ratio is 2 : 3.

Note it Two quantities can be compared if they are expressed in the same unit and ratio has no unit.

Equivalent Ratio

We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.

e.g. 2:3 and 4:6 are equivalent ratios.

MP Board Class 6 Maths Solutions

Example 2. Give two equivalent ratios of 3 : 5.

Solution. Given, ratio = 3 : 5

Firstly, multiply the numerator and denominator with the same number.

Hence, two equivalent ratios of 3:5 are 6: 10 and 9: 15.

Note it A ratio does not change, if its numerator and denominator are multiplied or divided by the same non-zero number.

Example 3. Consider the statement : Ratio of the breadth to the length of a room is 1 : 2. Complete the following table that shows some possible breadths and lengths of the room.

Solution. Given, the ratio of the breadth to the length of a room = 1 : 1

Also given, breadth of room = 12 m

and length of room = 24 m

Then, the ratio of breadth and length = \(\frac{12}{24}\)

= \(\frac{1}{2}\) = 1 : 2

Now, for missing, we have 24 x 2 = 48

i.e. when we multiply 24 by 2, we get 48.

So to get first missing term, we multiply 12 by 2

∴ 12 x 2 = 24

Thus, the complete table is

Example 4. In a year, there are 55 holidays. What is the ratio of the number of holidays to the number of days in one year?

Solution. Given, number of holidays in one year = 55

We know that number of days in one year = 365

∴ Ratio of the number of holidays to the number of days in one year

\(= \frac{55 \div 5}{365 \div 5}=\frac{11}{73}\) [∴ HCF of 55 and 365 = 5]

Hence, the required ratio is 11 : 73.

MP Board Class 6 Maths Solutions

Example 5. Dhoni takes 1 h to reach playground from his house and Sehwag takes 20 min to reach playground from his house. Find the ratio of the time taken by Dhoni to the time taken by Sehwag.

Solution. Here, time taken by Dhoni is in hours and time taken by Sehwag is in minutes.

So, we have to convert time taken by both into the same unit.

∴ Time taken by Dhoni = 1 h = 1 x 60 min = 60 min [∴ 1h = 60 min]

and time taken by Sehwag = 20 min

∴ Ratio of the time taken by Dhoni to the time taken by Sehwag

= \(\frac{60+20}{20+20}=\frac{3}{1}=3: 1\) [∴ HCF of 60 and 20 = 20]

Hence, the required ratio is 3 : 1.

Example 6. Out of 40 students in a class, 10 like cricket, 20 like football and remaining like tennis. Find the ratio of

(1) the number of students liking cricket to the number of student liking tennis.

(2) the number of students liking football to the total number of student.

Solution. Given, the total number of students in a class = 40

Number of students who like cricket = 10

Number of students who like football = 20

Then, the number of students who like tennis = Total number of students -(Number of students who like football + Number of students who like cricket)

= 40 – (10 + 20) = 10

(1) Ratio of the number of students liking cricket to the number of student liking tennis

(2) Ratio of the number of students liking football to the total number of students

\(=\frac{20}{40}=\frac{20 \div 20}{40 \div 20}=\frac{1}{2}\) [HCF of 20 and 40 = 20]

= 1 : 2

Example 7. See the figure and find the ratio of

(1) the number of squares to the number of circles Inside the rectangle.

(2) the number of circles to the all shapes inside rectangle.

Solution. In the given figure, number of triangles = 1,

number of squares = 3 and number of circles = 2

∴ Total number of shapes = 1 + 3 + 2 = 6

(1) Required ratio of the number of squares to the number of circles

(2) Required ratio of the number of circles to the all shapes

\(=\frac{\text { Number of circles }}{\text { Total number of shapes }}=\frac{2}{6}=\frac{2+2}{6+2}\) [HCF of 2 and 6 = 6]

= \(\frac{1}{3}\) = 1 : 3

MP Board Class 6 Maths Solutions

Example 8. Distance travelled by Rakesh and Vishal in an hour are 8 km and 12 km, respectively. Find the ratio of the speed of Rakesh to the speed of Vishal.

Solution. We know that

Given, distance travelled by Rakesh in one hour = 8 km Distance 8

∴ Speed of Rakesh \(=\frac{\text { Distance }}{\text { Time }}=\frac{8}{1}=8 \mathrm{~km} / \mathrm{h}\)

and distance travelled by Vishal in one hour = 12 km

∴ Speed of Vishal = \(\frac{12}{1}\) km/h

∴ Ratio of the speed of Rakesh to the speed of Vishal

\(=\frac{\text { Speed of Rakesh }}{\text { Speed of Vishal }}=\frac{8}{12}=\frac{8 \div 4}{12 \div 4}=\frac{2}{3}=2: 3\) [∴ HCF of 8 and 12 = 4]

Example 9. Cost of 8 pens is 160 and cost of 6 pencils is 60. Find the ratio of the cost of a pen to the cost of a pencil.

Solution. Given, cost of 8 pens = ₹ 160

∴ Cost of 1 pen \(=\frac{\text { Total cost of pens }}{\text { Numbers of pens }}=\frac{160}{8}=₹ 20\)

Also given, cost of 6 pencils = ₹ 60

∴ Cost of 1 pencil \(=\frac{\text { Total cost of pencils }}{\text { Number of pencils }}=\frac{60}{6}=₹ 10\)

Hence, the required ratio \(=\frac{\text { Cost of } 1 \text { pen }}{\text { Cost of } 1 \text { pencil }}=\frac{20}{10}=\frac{2}{1}=2: 1\)

Example 10. Father wants to divide ₹ 42 between his sons Ritesh and Raj in the ratio of their ages. If the age of Ritesh is 16 yr and the age of Raj is 12 yr. Find how much Ritesh and Raj will get.

Solution. Given, Ritesh’s age=16 yr and Raj’s age = 12 yr

∴ Ratio of their ages \(=\frac{\text { Ritesh’s age }}{\text { Raj’s age }}=\frac{16}{12}=\frac{16 \div 4}{12 \div 4}=\frac{4}{3}=4: 3\)

[∴ HCF of 16 and 12 = 4]

Now, father wants to divide ₹ 42 between his sons in the ratio of their ages i.e.4 : 3.

∴ Sum of the parts of the ratio = 4 + 3 = 7

Amount which has to be divided = ₹ 42

Here, we can say that Ritesh gets 4 parts and Raj gets 3 parts out of every 7 parts.

∴ Ritesh’s share = \(\frac{4}{7}\) x 42 = ₹ 24

and Raj’s share = \(\frac{3}{7}\) x 42 = ₹ 18

Hence, Ritesh gets ₹ 24 and Raj gets ₹ 18.

Class 6 Maths Chapter 12 Solutions

Example 11. Present age of father is 36 yr and that of his son is 6 yr. Find the ratio of the

(1) present age of father to the present age of son.

(2) age of father to the age of son, when son was 4 yr old.

(3) age of father after 10 yr to the age of son after 10 yr.

Solution. Given, present age of father = 36 yr

and present age of son = 6 yr

(1) Required ratio \(=\frac{\text { Present age of father }}{\text { Present age of son }}\)

= \(\frac{36}{6}=\frac{36+6}{6 \div 6}\) [HCF of 36 and 6 = 6]

= \(\frac{6}{1}\) = 6 : 1

(2) When son’s age was 4 yr i.e. 2 yr back (because son’s present age is 6 yr), then father’s age

= 36 – 2 = 34 yr

∴ Required ratio \(=\frac{2 \mathrm{yr} \text { back father’s age }}{2 \mathrm{yr} \text { back son’s age }}\)

[∴ HCF of 34 and 4 = 2]

(3) After 10 yr, father’s and son’s age will be (36 + 10) yr and (6 + 10) yr, respectively, i.e. 46 yr and 16 yr.

∴ Required ratio \(=\frac{\text { Father’s age after } 10 \mathrm{yr}}{\text { Son’s age after } 10 \mathrm{yr}}\)

= \(\frac{46}{16}=\frac{46 \div 2}{16+2}=\frac{23}{8}=23: 8\)

[∴ HCF of 46 and 16 = 2]

Chapter 12 Ratio And Proportion

If the ratio of the first and second quantities is equal to the ratio of the third and fourth quantities, then the quantities are said to be in proportion and it is denoted by symbol ‘::’ or ‘=’.

Four numbers a, b, c and d are said to be in proportion, if a:bc:d and it is written as a:b::c:d, where a, b, c and d are respectively, known as first, second, third and fourth terms of the proportion.

First and fourth terms are called extreme terms or extremes, whereas second and third terms are called the middle terms or means.

Example 1. Are the ratios in proportion?

(1) 45 : 60 and 36 : 48

(2) 150 : 100 and 135 : 90

Solution. (1) ∴ Ratio of 45 to 60 = \(\frac{45}{60}=\frac{3}{4}=3: 4\)

and ratio of 36 to 48 = \(\frac{36}{48}=\frac{3}{4}=3: 4\)

∴ The ratio of 45 to 60 is equal to 36 to 48

So, 45 : 60 :: 36 : 48

Hence, 45 : 60 and 36 : 48 are in proportion.

(2) ∴ Ratio of 150 to 100 = \(\frac{150}{100}\) = 3 : 2

and ratio of 135 to 90 = \(\frac{135}{90}\) = 3 : 2

∴ The ratio of 150 to 100 is equal to 135 to 90.

So, 150 : 100 :: 135 : 90

Hence, 150, 100, 135 and 90 are in proportion.

Class 6 Maths Chapter 12 Solutions

Example 2. If 36 : 81 :: x : 63, then find the value of x.

Solution. Given, 36 : 81 :: x : 63

⇒ \(\frac{36}{81}=\frac{x}{63}\)

⇒ \(\frac{4}{9}=\frac{x}{63}\)

⇒ 9x = 4 x 63

⇒ \(x=\frac{4 \times 63}{9}\)

⇒ x = 4 x 7

Hence, the value of x is 28.

Example 3. Check whether the given ratios are equal i.e. they are in proportion. If yes, then write them in proper form.

(1) 1 : 4 and 5 : 20

(2) 2 : 7 and 8 : 28

(3) 3 : 11 and 4 : 21

(4) ₹ 4 to ₹ 7 and 16 to 28

Solution. (1) We have, 1 : 4 and 5 : 20

Here, \(5: 20=\frac{5}{20}=\frac{5+5}{20+5}=\frac{1}{4}=1: 4\)

[∴ HCF of 5 and 20 = 5]

i.e. 1:4 and 5:20 are in proportion.

Thus, the proper form is 1 : 4 :: 5 : 20.

(2) We have, 2 : 7 and 8 : 28

Here, \(8: 28=\frac{8}{28}=\frac{8 \div 4}{28+4}=\frac{2}{7}=2: 7\)

[∴ HCF of 8 and 28 = 47]

Therefore, 2 : 7 and 8 : 28 are in proportion.

Thus, the proper form is 2 : 7 :: 8 : 28.

(3) We have, 3 : 11 and 4 : 21

Here, \(3: 11=\frac{3}{11} \text { and } 4: 21=\frac{4}{21}\)

Here, 3 : 11 ≠ 4 : 21

Thus, 3:11 and 4:21 are not in proportion.

(4) We have, ₹ 4 : ₹ 7 = 4 : 7 and 16 : 28

Now, \(4: 7=\frac{4}{7} \text { and } 16: 28=\frac{16}{28}=\frac{16 \div 4}{28 \div 4}=\frac{4}{7}\)

[∴ HCF of 16 and 28 = 4]

Hence, 4 : 7 and 16 : 28 are in proportion.

Thus, the proper form is 4 : 7 :: 16 : 28.

Example 4. Determine whether the following are in proportion.

(1) 3, 9, 7,21

(2) 3, 55, 77, 17

Solution. (1) We have, 3, 9, 7, 21

∴ Ratio of 3 to 9 = \(\frac{3}{9}=\frac{3 \div 3}{9+3}\)

[∴ HCF of 3 and 9 = 3]

= \(\frac{1}{3}\) = 1 : 3

and ratio of 7 to 21 = \(\frac{7}{21}=\frac{7 \div 7}{21 \div 7}=\frac{1}{3}=1: 3\)

[∴ HCF of 7 and 21=7]

Therefore, 3, 9,7 and 21 are in proportion.

(2) We have, 3, 55, 77, 17

∴ Ratio of 3 to 55 = \(\frac{3}{55}\) and ratio of 77 to 17 = \(\frac{77}{17}\)

Here, 3 : 55 ≠ 77 : 17

Therefore, 3, 55, 77 and 17 are not in proportion.

Class 6 Maths Chapter 12 Solutions

Example 5. Write true (T) and false (F) against each of the following statements:

(1) 0.9 : 0.36 :: 12 : 48

(2) 20 m : 30 m :: 16 s : 24 s

Solution. (1) We have, 0.9 : 0.36 :: 12 : 48

Ratio of 0.9 to 0.36 = \(\frac{0.9}{0.36}=\frac{90}{36}=\frac{90 \div 18}{36+18}=\frac{5}{2}=5: 2\)

[∴ HCF of 90 and 36 = 18]

and ratio of 12 to 48 = \(\frac{12}{48}=\frac{12+12}{48+12}=\frac{1}{4}\)

[∴ HCF of 12 and 48 = 12]

Here, 0.9 : 0.36 ≠ 12 : 48

Hence, the given statement is false.

(2) We have, 20 : 30 :: 16 : 24

Ratio of 20 to 30 = \(\frac{20}{30}=\frac{20+10}{30+10}\)

[∴ HCF of 20 and 30 = 10]

\frac{2}{3} = 2 : 3

and ratio of 16 to 24 = \(\frac{16}{24}=\frac{16 \div 8}{24 \div 8}=\frac{2}{3}=2: 3\)

[∴ HCF of 16 and 24 = 8

Here, 20 : 30 = 16 : 24 = 2 : 3

Hence, the given statement is true.

Example 6. Are the following ratios form a proportion? Also, write the middle terms and extreme terms, where the ratios form a proportion.

(1) 50 cm : 1 m and 80 : 160

(2) 24 L : 60 L and 6 bottles : 15 bottles

Solution. (1) We have, 50 cm : 1 m

= 50 cm : 1 x 100 cm [∴ 1m = 100 cm]

= 50 cm : 100 cm

= \(\frac{50}{100}=\frac{50 \div 50}{100 \div 50}=\frac{1}{2}=1: 2\)

[∴ HCF of 50 and 100 = 50]

and ₹ 80 : ₹ 160 = 80 : 160 = \(\frac{80}{160}=\frac{80 \div 80}{160 \div 80}=\frac{1}{2}=1: 2\)

[∴ HCF of 80 and 160 = 80]

Here, 1 : 2 = 1 : 2

i.e. 50 cm : 1 m = ₹ 80 : ₹ 160

So, the ratios of 50 cm: 1m and 80: 160 are in proportion.

Hence, middle terms are 1 m and 80 and extreme terms are 50 cm and 160.

(2) We have, 24 L : 60 L and 6 bottles : 15 bottles

Now, 24 L to 60 L = \(\frac{24 \mathrm{~L}}{60 \mathrm{~L}}=\frac{24}{60}=\frac{24 \div 12}{60 \div 12}\)

[∴ HCF of 24 and 60 = 12]

= \(\frac{2}{5}\) = 2 : 5

and 6 bottles : 15 bottles = 6 : 15 = \(\frac{6}{15}=\frac{6 \div 3}{15 \div 3}\)

[∴ HCF of 6 and 25 = 3]

= \(\frac{2}{5}\) = 2 : 5

Here, 2:5 = 2:5

i.e. 24 L : 60 L and 6 bottles : 15 bottles are in proportion.

i.e. 24 L : 60 L :: 6 bottles : 15 bottles

Hence, middle terms of ratios are 60 L and 6 bottles and extreme terms of ratios are 24 L and 15 bottles.

Chapter 12 Ratio And Proportion Unitary method

A method in which first we find the value of one unit and then the value of required number of units is called unitary method.

e.g. If the cost of any number of article is given, then the cost of 1 article can be obtained by dividing the cost of given number of articles with the number of articles.

i.e. Cost of 1 article \(=\frac{\text { Cost of the given number of articles }}{\text { Number of articles }}\)

Now, with the help of 1 article, we find the any number of articles. Thus, in this method, the price of 1 article help us, in finding the price of any number of articles.

In unitary method, we follow the following trivial rules of variation:

(1) To get more, we multiply.

(2) To get less, we divide.

Example 1. If the cost of 15 mangoes is ₹90. Find the cost of 17 mangoes.

Solution. Given, the cost of 15 mangoes = ₹ 90

The cost of 1 mango = \(\frac{90}{15}\)

Now, the cost of 17 mangoes = 17 x 6 = ₹ 102

Hence, the cost of 17 mangoes is ₹ 102.

Class 6 Maths Chapter 12 Solutions

Example 2. The yield of wheat from 8 hectares of land is 360 quintals. Find the number of hectares of land required for a yield of 540 quintals.

Solution. Required area of land to yield 360 quintals wheat = 8 hectares

Required area of land to yield 1 quintal wheat = \(\frac{8}{360}\) hectares

Required area of land to yield 540 quintals wheat = \(540 \times \frac{8}{360}=\frac{3 \times 8}{2}=12 \text { hectares }\)

Example 3. If the cost of 5 m of ribbon is 500, then find the cost of 2m of ribbon.

Solution. Given, the cost of 5m of ribbon = ₹ 500

∴ Cost of 1 m of ribbon = \(\frac{500}{5}\) = ₹ 100

∴ Cost of 2m of ribbon = 100 × 2 = ₹ 200

Hence, the cost of 2m of ribbon is ₹ 200.

Example 4. Abhimanyu earns ₹ 2500 in 10 days. How much will he earn in 30 days?

Solution. Here, the number of days is known and money earn is unknown.

Given, Abhimanyu earns in 10 days = ₹ 2500

∴ Abhimanyu earns in 1 day = \(\frac{2500}{10}\) = ₹ 250

∴ Abhimanyu earns in 30 days = 250 x 30 = 7500

Hence, Abhimanyu earns ₹7500 in 30 days.

Example 5. During a rainy season, it has rained 369 mm in last 3 days, how many centimetres of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.

Solution. Here, the number of days is known and rainfall is unknown.

Given, rainfall in 3 days = 369 mm

∴ Rainfall in 1 day = \(\frac{369}{3}\) = 123 mm

∴ Rainfall in one full week i.e. 7 days = 123 × 7 mm = 861 mm

In centimetre, rainfall in one full week

= \(861 \times \frac{1}{10} \mathrm{~cm}=861 \mathrm{~cm}\) [∴ 1 mm = \(\frac{1}{10}\) cm]

Hence, 86.1 cm rain will fall in 7 days or one full week.

Example 6. The cost of 8 kg of sugar is ₹ 48.80.

(1) What will be the cost of 10 kg of sugar?

(2) What quantity of sugar can be purchased in ₹ 81?

Solution. (1) Here, the quantity of sugar is known and cost is unknown.

Given, the cost of 8 kg of sugar = ₹ 48.80

∴ Cost of 1 kg of sugar = \(\frac{48.80}{8}=₹ 6.10\)

∴ Cost of 10 kg of sugar = 6.10 x 10 = ₹ 61.0

Hence, the cost of 10 kg of sugar is ₹ 61.

(2) Here, the cost of sugar is known and quantity of sugar is unknown.

Given, in ₹ 48.80 quantity of sugar that can be purchased = 8 kg

∴ In ₹ 1, quantity of sugar that can be purchased = \(\frac{8}{48.80}=\frac{8 \times 10}{488}=\frac{80}{488} \mathrm{~kg}\)

∴ In ₹ 81, quantity of sugar that can be purchased = \(\frac{80}{188} \times 81=13.28 \mathrm{~kg}\)

Hence, 13.28 kg sugar can be purchased in ₹ 81.

Example 7. Venus pays ₹ 7000 as rent for 2 months. How much does she has to pay for a whole year, if the rent per month remains the same?

Solution. Given, rent paid for 2 months = ₹ 7000

∴ Rent paid for 1 month = \(\frac{7000}{2}=₹ 3500\)

∴ Rent paid for a whole year i.e. 12 months = 3500 × 12 = ₹ 42000

Hence, she has to pay ₹ 42000 for a whole year.

MP Board Class 6 Chapter 12 Maths

Example 8. The cost of 2 dozen bananas is ₹ 80. How many bananas can be purchased for ₹ 20?

Solution. We know that I dozen = 12 units

Given, in 80 the number of bananas that can be purchased = 2 dozen = 2 x 12 = 24

∴ In ₹ 1, the number of bananas that can be purchased

\(=\frac{24}{80}=\frac{24 \div 8}{80 \div 8}=\frac{3}{10}\) [∴ HCF of 24 and 80 = 8]

∴ In ₹ 20, the number of bananas that can be purchased

Example 9. A vehicle requires 120 L of petrol for covering a distance of 720 km. How much petrol will be required by the vehicle to cover a distance of 1850 km?

Solution. Given, petrol required for 720 km = 120 L

∴ Petrol required for 1 km = \(\frac{120}{720}=\frac{120+120}{720+120}=\frac{1}{6} L\)

∴ Petrol required for 1850 km = \(\frac{1}{6} \times 1850=308.33 \mathrm{~L}\)

Hence, 308.33 L petrol will be required by the vehicle to cover 1850 km.

Example 10. Arjun purchases 20 pens for ₹ 260 and Aryan purchases 8 pens for ₹ 96. Can you say who got the pens cheaper?

Solution. For Arjun, the cost of 20 pens = ₹ 260

∴ Cost of 1 pen = \(\frac{260}{20}=₹ 13\)

For Aryan, cost of 8 pens = ₹ 96

∴ Cost of 1 pen = \(\frac{96}{8}=₹ 12\)

Here, ₹ 12 < ₹ 13

Hence, Aryan got the pens cheaper.

Question 1. In a class, there are 20 boys and 40 girls. What is the ratio of the number of boys to the number of girls?

Solution. Here, number of boys = 20 and number of girls = 40

∴ Ratio of the number of boys to the number of girls

Hence, the required ratio is 1 : 2.

Question 2. Ravi walks 6 km in an hour while Roshan walks 4 km in an hour. What is the ratio of the distance covered by Ravi to the distance covered by Roshan?

Solution. Given, Ravi walks 6 km in an hour

i.e. distance covered by Ravi in one hour = 6 km

and Roshan walks 4 km in an hour

i.e. distance covered by Roshan in one hour = 4 km

∴ Ratio of the distance covered by Ravi to the distance covered by Roshan

Hence, the required ratio is 3 : 2.

MP Board Class 6 Chapter 12 Maths

Question 3. Saurabh takes 15 min to reach school from his house and Sachin takes one hour to reach school from his house. Find the ratio of the time taken by Saurabh to the time taken by Sachin.

Solution. Here, time taken by Saurabh is in minutes and time taken by Sachin is in hours. So, we have to convert time taken by both into the same unit.

∴ Time taken by Sachin = 1 h = 1 x 60 min = 60 min

[∴ 1 h = 60 min]

and time taken by Saurabh = 15 min

∴ Ratio of the time taken by Saurabh to the time taken by Sachin

[∴ HCF of 15 and 60 = 15]

= \(\frac{1}{4}\) = 1 : 4

Hence, the required ratio is 1:4.

Question 4. Cost of a toffee is 50 paise and cost of a chocolate is ₹ 10. Find the ratio of the cost of a toffee to the cost of a chocolate.

Solution. Here, cost of a toffee and a chocolate are not in the same unit. So, we have to convert both into the same unit.

∴ Cost of a toffee = 50 paise

and cost of a chocolate = ₹ 10 = 10 x 100 paise

= 1000 paise [∴ ₹ 1 = 100 paise]

∴ Ratio of the cost of a toffee to the cost of a chocolate

[∴ HCF of 50 and 1000 = 50]

= \(\frac{1}{20}\) = 1 : 20

Hence, the required ratio is 1 : 20.

Question 5. In a school, there were 73 holidays in one year. What is the ratio of the number of holidays to the number of days in one year?

Solution. Given, number of holidays in one year = 73

We know that number of days in one year = 365

∴ Ratio of the number of holidays to the number of days in one year

[∴ HCF of 73 and 365 = 73]

= \(\frac{1}{5}\) = 1 : 5

Hence, the required ratio is 1 : 5.

Chapter 12 Ratio And Proportion Exercise 12.1

Question 1. There are 20 girls and 15 boys in a class.

(1) What is the ratio of number of girls to the number of boys?

(2) What is the ratio of number of girls to the total number of students in the class?

Solution. Given, number of girls = 20 and number of boys = 15

∴ Total number of students in the class = 20 + 15 = 35

(1) Ratio of the number of girls to the number of boys

(2) Ratio of the number of girls to the total number of students in the class

= \(\frac{20+5}{35 \div 5}=\frac{4}{7}=4: 7\)

Question 2. Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of

(1) number of students liking football to the number of students liking tennis.

(2) number of students liking cricket to total number of students.

Solution. Given, the total number of students in a class = 30

Number of students who like football = 6

Number of students who like cricket = 12

Then, the number of students who like tennis

= Total number of students – (Number of students who like football + Number of students who like cricket)

= 30 – (6 + 12) = 30 – 18 = 12

(1) Ratio of the number of students liking football to the number of students liking tennis

= \(\frac{6}{12}=\frac{6 \div 6}{12 \div 6}=\frac{1}{2}=1: 2\)

(2) Ratio of the number of students liking cricket to the total number of students

MP Board Class 6 Chapter 12 Maths

Question 3. See the figure and find the ratio of

(1) number of triangles to the number of circles inside the rectangle.

(2) number of squares to all the figures inside the rectangle.

(3) number of circles to all the figures inside the rectangle.

Solution. In the given figure,

Number of triangles = 3; Number of squares = 2; Number of circles = 2

∴ Total number of shapes = 3 + 2 + 2 = 7

(1) Required ratio of the number of triangles to the number of circles

(2) Required ratio of the number of squares to all the shapes

(3) Required ratio of the number of circles to all the shapes

Question 4. Distances travelled by Hamid and Akhtar in an hour are 9 km and 12 km, respectively. Find the ratio of speed of Hamid to the speed of Akhtar.

Solution. Given, distance travelled by Hamid in one hour = 9 km

∴ Speed of Hamid = \(\frac{\text { Distance }}{\text { Time }}=\frac{9}{1}=9 \mathrm{~km} / \mathrm{h}\)

and distance travelled by Akhtar in one hour = 12 km

∴ Speed of Akhtar = \(\frac{12}{1}\) = 12 km/h

∴ Ratio of the speed of Hamid to the speed of Akhtar \(=\frac{\text { Speed of Hamid }}{\text { Speed of Akhtar }}=\frac{9}{12}=\frac{9 \div 3}{12 \div 3}=\frac{3}{4}=3: 4\)

MP Board Class 6 Chapter 12 Maths

Question 5. Find the ratio of the following.

(1) 81 to 108

Solution.

(1) Required ratio = \(\frac{81}{108}=\frac{81+27}{108+27}=\frac{3}{4}=3: 4\)

Question 6. Find the ratio of the following.

(1) 30 min to 1.5 h

(2) 40 cm to 1.5 m

(3) 55 paise to 1

(4) 500 mL to 2 L

Solution. (1) Here, we have to convert 1.5 h into min.

We know that 1 h = 60 min

∴ 1.5 h = 1.5 x 60 min = 90 min

∴ Required ratio = \(\frac{30}{90}=\frac{30 \div 30}{90 \div 30}=\frac{1}{3}=1: 3\)

(2) Here, we have to convert 1.5 m into cm.

We know that 1 m = 100 cm

∴ 1.5 m = 1.5 x 100 cm = 150 cm

∴ Required ratio = \(\frac{40}{150}=\frac{40 \div 10}{150+10}=\frac{4}{15}=4: 15\)

(3) Here, we have to convert ₹ 1 into paise.

We know that ₹ 1 = 100 paise

∴ Required ratio = \(\frac{55}{100}=\frac{55 \div 5}{100 \div 5}=\frac{11}{20}=11: 20\)

(4) Here, we have to convert L into mL.

We know that 1 L = 1000 mL

∴ 2 L = 2 x 1000 mL = 2000 mL

∴ Required ratio = \(\frac{500}{2000}=\frac{5}{20}=\frac{1}{4}=1: 4\)

Question 7. In a year, Seema earns ₹ 150000 and saves ₹ 50000. Find the ratio of

(1) money that Seema earns to the money she saves.

(2) money that she saves to the money she spends.

Solution. Given, money earned by Seema = ₹ 150000

and money saved by Seema = ₹ 50000

(1) Required ratio \(=\frac{\text { Money earned by Seema }}{\text { Money saved by Seema }}\)

= \(\frac{150000}{50000}=\frac{15000+50000}{50000+50000}=\frac{3}{1}=3: 1\)

(2) ∴ Moeny spend by Seema = Earned money = Saved money

= (150000 – 50000) = ₹ 100000

∴ Required ratio \(=\frac{\text { Money saved by Seema }}{\text { Money spend by Seema }}\)

= \(\frac{50000}{100000}=\frac{50000 \div 50000}{100000 \div 50000}\)

= \(\frac{1}{2}\) = 1 : 2

Question 8. There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students.

Solution. Given, number of teachers = 102

and number of students = 3300

∴ Required ratio of the number of teachers to the number of students

= \(\frac{102}{3300}=\frac{102 \div 6}{3300 \div 6}\) [∴ HCF of 102 and 3300 is 6]

= \(\frac{17}{550}\) = 17 : 550

MP Board Class 6 Chapter 12 Maths

Question 9. In a college, out of 4320 students, 2300 are girls.

Solution. Given, number of girls = 2300

and total number of students = 4320

∴ Number of boys = Total number of students – Number of girls

= 4320 – 2300 = 2020

Question 10. Out of 1800 students in a school, 750 opted basketball, 800 opted cricket and remaining opted table tennis. If a student can opt only one game, find the ratio of

Solution. Given, total number of students = 1800

Number of students who opted basketball = 750

Number of students who opted cricket = 800

∴ Number of students who opted table tennis = Total number of students – (number of students who opted basket ball + number of students who opted cricket)

= 1800 – (150 + 800)

= 1800 – 1550 = 250

Question 11. Cost of a dozen pens is ₹ 180 and cost of 8 ball pens is ₹ 56. Find the ratio of the cost of a pen to the cost of a ball pen.

Solution. Given, cost of 12 pens = 180

∴ Cost of 1 pen \(=\frac{\text { Total cost of pens }}{\text { Number of pens }}\)

= \(\frac{180}{12}\) = ₹ 15

Also given, cost of 8 ball pens = ₹ 56 [∴ 1 dozen = 12 units]

∴ Cost of 1 ball pen \(=\frac{\text { Total cost of ball pens }}{\text { Number of ball pens }}=\frac{56}{8}=₹ 7\)

Hence, the required ratio \(=\frac{\text { Cost of } 1 \text { pen }}{\text { Cost of } 1 \text { ball pen }}\)

= \(\frac{15}{7}\) = 15 : 7

Question 12. Consider the statement: Ratio of breadth and length of a hall is 2:5. Complete the following table that shows some possible breadths and lengths of the hall.

Solution. Given, ratio of breadth and length of a hall = 2 : 5

Also given, breadth of the hall = 10

and length of the hall = 25

Then, the ratio of breadth and length = \(\frac{10}{25}=\frac{2}{5}=2: 5\)

Now, for finding first missing number, we have

25 x 2 = 50

i.e. when we multiply 25 by 2, we get 50.

So, to get first missing term, we multiply 10 by 2.

∴ 10 × 2 = 20

Hence, the second breadth of the hall = 20

and length of the hall = 50

For finding second missing number, we have

40 = 10 x 4

i.e. when we multiply 10 by 4, we get 40.

So, to get second missing term, we multiply 25 by 4.

∴ 25 x 4 = 100

Hence, third breadth of hall = 40 and length = 100

Thus, the complete table is

Word Problems on Ratio Class 6

Question 13. Divide 20 pens between Sheela and Sangeeta in the ratio of 3: 2.

Solution. Given, ratio is 3: 2, whose two parts are 3 and 2.

∴ Sum of two parts = 3 + 2 = 5

This means, if there are 5 pens, Sheela gets 3 pens and Sangeeta gets 2 pens.

We can say that Sheela gets 3 parts and Sangeeta gets 2 parts out of every 5 parts.

Now, total number of pens = 20

∴ Number of pens for Sheela = \(\frac{3}{5}\) x 20 = 12

and number of pens for Sangeeta = \(\frac{2}{5}\) x 20 = 8

Hence, out of 20 pens Sheela gets 12 pens and Sangeeta gets 8 pens.

Question 14. Mother wants to divide ₹ 36 between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya is 15 yr and age of Bhoomika is 12 yr find how much Shreya and Bhoomika will get.

Solution. Given, Shreya’s age = 15 yr

and Bhoomika’s age = 12 yr

∴ Ratio of their ages \(=\frac{\text { Shreya’s age }}{\text { Bhoomika’s age }}\)

= \(\frac{15}{12}=\frac{15+3}{12+3}=\frac{5}{4}=5: 4\)

Now, mother wants to divide 36 between her daughters in the ratio of their ages.

∴ Sum of the parts of ratios = 5 + 4 = 9

Amount which has to be divided = ₹ 36

Here, we can say that Shreya gets 5 parts and Bhoomika gets 4 parts out of every 9 parts.

∴ Shreya’s share = \(\frac{5}{9}\) x 36 = ₹ 20

and Bhoomika’s share = \(\frac{4}{9}\) x 36 = ₹ 16

Hence, Shreya gets ₹ 20 and Bhoomika gets ₹ 16.

Question 15. Present age of father is 42 yr and that of his son is 14 yr. Find the ratio of

(1) present age of father to the present age of son.

(2) age of the father to the age of son, when son was 12 yr old.

(3) age of father after 10 yr to the age of son after 10 yr.

(4) age of father to the age of son when father was 30 yr old.

Solution. Given, present age of father = 42 yr

and present age of son = 14 yr

(1) Required ratio \(=\frac{\text { Present age of father }}{\text { Present age of son }}\)

= \(\frac{42}{14}=\frac{42+14}{14 \div 14}=\frac{3}{1}=3: 1\)

(2) When son’s age was 12 yr i.e. 2 yr back (because son’s present age is 14 yr).

Then, father’s age = (42 – 2) = 40 yr

∴ Required ratio \(=\frac{2 \mathrm{yr} \text { back father’s age }}{2 \mathrm{yr} \text { back son’s age }}=\frac{40}{12}=\frac{40 \div 4}{12 \div 4}\)

[∴ HCF of 40 and 12 is 4]

= \(\frac{10}{3}\)

(3) After 10 yr, father and son’s age will be (42 + 10) yr and (14 + 10) yr respectively i.e. 52 yr and 24 yr.

∴ Required ratio \(=\frac{\text { After } 10 \mathrm{yr} \text { father’s age }}{\text { After } 10 \mathrm{yr} \text { son’s age }}\)

= \(\frac{52}{24}=\frac{52 \div 4}{24 \div 4}\)

[∴ HCF of 52 and 24 is 4]

= \(\frac{13}{6}\) = 13 : 6

(4) When father’s age was 30 yr i.e. 12 yr back (because father’s present age is 42 yr and (42 – 12) = 30 yr.

Then, son’s age (14 – 12) = 2 yr

∴ Required ratio \(=\frac{12 \mathrm{yr} \text { back father’s age }}{12 \mathrm{yr} \text { back son’s age }}\)

= \(\frac{30}{2}=\frac{30+2}{2+2}=\frac{15}{1}=15: 1\)

Question 16. 1 : 5 and 3 : 15

Solution. We have, 1 : 5 and 3 : 15

Here, \(3: 15=\frac{3}{15}=\frac{3 \div 3}{15+3}=\frac{1}{5}=1: 5\)

i.e. 1 : 5 and 3 : 15 are in proportion.

Thus, the proper form is 1 : 5 :: 3 : 15.

Question 17. 2 : 9 and 18 : 81

Solution. We have, 2 : 9 and 18 : 81

Here, \(18: 81=\frac{18}{81}=\frac{18 \div 9}{81 \div 9}\)

[∴ HCF of 18 and 81 is 9]

= \(\frac{2}{9}\) = 2 : 9

i.e. 2 : 9 and 18 : 81 are in proportion.

Thus, the proper form is 2 : 9 :: 18 : 81.

Question 18. 15 : 45 and 5 : 25

Solution. We have, 15 : 45 and 5 : 25

Here, \(15: 45=\frac{15}{45}=\frac{15 \div 15}{45 \div 15}=\frac{1}{3}=1: 3\)

and \(5: 25=\frac{5}{25}=\frac{5 \div 5}{25 \div 5}=\frac{1}{5}=1: 5\)

Here, 15 : 45 ≠ 5 : 25

Thus, 15 : 45 and 5 : 25 are not in proportion.

Word Problems on Ratio Class 6

Question 19. 4 : 12 and 9 : 27

Solution. We have, 4 : 12 and 9 : 27

Here, \(4: 12=\frac{4}{12}=\frac{4 \div 4}{12 \div 4}=\frac{1}{3}=1: 3\)

Now, \(9: 27=\frac{9}{27}=\frac{9 \div 9}{27 \div 9}=\frac{1}{3}=1: 3\)

Hence, 4 : 12 = 9 : 27 = 1 : 3 i.e. 4 : 12 and 9 : 27 are in proportion.

Thus, the proper form is 4 : 12 :: 9 : 27.

Question 20. ₹ 10 to ₹ 15 and 4 to 6

Solution. We have, ₹ 10 : ₹ 15 = 10 : 15 and 4 : 6

Now, \(10: 15=\frac{10}{15}=\frac{10 \div 5}{15 \div 5}=\frac{2}{3}=2: 3\)

and \(4: 6=\frac{4}{6}=\frac{4+2}{6+2}=\frac{2}{3}=2: 3\)

Here, 10 : 15 = 4 : 6 = 2 : 3 i.e. 10 : 15 and 4 : 6 are in proportion.

Thus, the proper form is 10 : 15 :: 4 : 6.

Chapter 12 Ratio And Proportion Exercise 12.2

Question 1. Determine, if the following are in proportion.

(1) 15, 45, 40, 120

(2) 33, 121, 9, 96

Solution. (1) We have, 15, 45, 40, 120

∴ Ratio of 15 to 45 = \(\frac{15}{45}=\frac{15 \div 15}{45 \div 15}=\frac{1}{3}=1: 3\)

[∴ HCF of 15 and 45 = 15]

and ratio of 40 to 120 = \(\frac{40}{120}=\frac{40 \div 40}{120 \div 40}=\frac{1}{3}=1: 3\)

[∴ HCF of 40 and 120 = 40]

Here, 15 : 45 = 40 : 120 = 1 : 3

Therefore, 15, 45, 40 and 120 are in proportion.

(2) We have 33, 121, 9, 96

∴ Ratio of 33 to 121 = \(\frac{33}{121}=\frac{33 \div 11}{121 \div 11}=\frac{3}{11}=3: 11\)

and ratio of 9 to 96 = \(\frac{9}{96}=\frac{9 \div 3}{96 \div 3}=\frac{3}{32}=3: 32\)

[∴ HCF of 9 and 96 = 3]

Here, 3 : 11 ≠ 3 : 32 i.e. 33 : 121 ≠ 9 : 96

Therefore, 33, 121, 9 and 96 are not in proportion.

Question 2. Write True (T) or False (F) against each of the following statements:

(1) 16 : 24 : 20 : 30

Solution. (1) We have, 16 : 24 :: 20 : 30

∴ Ratio of 16 to 24 = \(\frac{16}{24}=\frac{16+8}{24+8}=\frac{2}{3}=2: 3\)

and ratio of 20 to 30 = \(\frac{20}{30}=\frac{20+10}{30+10}=\frac{2}{3}=2: 3\)

Here, 16 : 24 = 20 : 30 = 2 : 3,

So, 16 : 24 :: 20 : 30

Hence, given statement is true.

Word Problems on Ratio Class 6

Question 3. Are the following statements true?

(1) 40 persons: 200 persons = ₹ 15 : ₹ 75

Solution. (1) 40 persons : 200 persons

= \(\frac{40}{200}=\frac{40 \div 10}{200 \div 10}=\frac{4}{20}=\frac{1}{5}=1: 5\)

and \(\text { ₹ } 15: ₹ 75=\frac{15}{75}=\frac{15 \div 15}{75 \div 15}=\frac{1}{5}=1: 5\)

Question 4. Determine, if the following ratios form a proportion. Also, write the middle term and extreme terms, where the ratios form a proportion.

(1) 25 cm : 1 m and ₹ 40 : ₹ 160

(2) 39 L : 65 L and 6 bottles : 10 bottles

(3) 2 kg : 80 kg and 25 g : 625 g

(4) 200 mL : 2.5 L and ₹ 4 : ₹ 50

Solution. (1) Here, 25 cm : 1 m = 25 cm : 1 x 100 cm

[∴ 1 m = 100 cm]

= \(25: 100=\frac{25}{100}=\frac{25 \div 25}{100 \div 25}=\frac{1}{4}=1: 4\)

and \(₹ 40: ₹ 160=40: 160=\frac{40}{160}=\frac{1}{4}=1: 4\)

Here, 1 : 4 = 1 : 4 i.e. 25 cm : 1 m = ₹ 40 : ₹ 160

So, the ratios of 25 cm : 1 m and ₹ 40 : ₹ 160 are in proportion.

i.e. 25 cm : 1m :: ₹ 40 : ₹ 160

Now, middle terms are 1 m and 40 and extreme terms are 25 cm and 160.

(2) Here, \(39 L : 65 L = 39: 65=\frac{39}{65}=\frac{39+13}{65+13}=\frac{3}{5}=3: 5\)

and 6 bottles: 10 bottles 6 : 10 = \(\frac{6}{10}\)

= \(\frac{6+2}{10+2}=\frac{3}{5}=3: 5\)

Here, 3 : 5 = 3 : 5 i.e. 39 L : 65 L

= 6 bottles : 10 bottles.

So, the ratio of 39 L: 65 L and 6 bottles : 10 bottles are in proportion

i.e. 39 L : 65 L :: 6 bottles : 10 bottles

Hence, middle terms of ratios are 65 L and 6 bottles and extreme terms of ratios are 39 L and 10 bottles

(3) Here, \(2 \mathrm{~kg}: 80 \mathrm{~kg}=2: 80=\frac{2}{80}=\frac{2 \div 2}{80 \div 2}=\frac{1}{40}=1: 40\)

and \(25 \mathrm{~g}: 625 \mathrm{~g}=25: 625=\frac{25}{625}=\frac{25 \div 25}{625 \div 25}=\frac{1}{25}=1: 25\)

Since, both ratios are not equal.

∴ 2 kg : 80 kg ≠ 25 g : 625 g

Hence, the given ratios are not in proportion.

(4) Here, \(200 \mathrm{~mL}: 2.5 \mathrm{~L}=200 \times \frac{1}{1000} \mathrm{~L}: 2.5 \mathrm{~L}\)

[∴ 1 mL = \(\frac{1}{1000}\) L]

= \(\frac{200}{1000} \mathrm{~L}: 2.5 \mathrm{~L}=0.200 \mathrm{~L}: 2.5 \mathrm{~L}\)

= \(0.200: 2.5=\frac{0.200}{2.5}=\frac{2}{25}=2: 25\)

and \(₹ 4: ₹ 50=4: 50=\frac{4}{50}=\frac{4 \div 2}{50 \div 2}=\frac{2}{25}=2: 25\)

Here, 2 : 25 = 2 : 25 i.e. 200 mL : 2.5 L = ₹ 4 : ₹ 50

So, the ratios of 200 mL : 2.5 L and ₹ 4 : ₹ 50 are in proportion.

i.e. 200 mL : 2.5 L :: ₹ 4 : ₹ 50

Hence, middle terms of ratios are 2.5 L and ₹ 4 and extreme terms of ratios are 200 mL and ₹ 50.

Question 5. Read the table and fill in the boxes.

Solution. From the above table,

Distance travelled by Kriti in 2 h = 6 km

∴ Distance travelled by Kriti in 1 h = \(\frac{6}{2}\) = 3 km

Now, distance travelled by Kriti in 4 h = 3 x 4 = 12 km

Also, distance travelled by Karan in 1 h = 4 km

∴ Distance travelled by Karan in 4 h = 4 x 4 = 16 km

On completing the boxes, we get the following table:

Chapter 12 Ratio And Proportion Exercise 12.3

Question 1. If the cost of 7 m of cloth is ₹ 1470, find the cost of 5 m of cloth.

Solution. Given, cost of 7 m of cloth = 1470

∴ Cost of 1 m of cloth = \(\frac{1470}{7}=₹ 210\)

∴ Cost of 5 m of cloth = 210 x 5 = ₹ 1050

Hence, the cost of 5 m of cloth is ₹ 1050.

Word Problems on Ratio Class 6

Question 2. Ekta earns ₹ 3000 in 10 days. How much will she earn in 30 days?

Solution. Here, the number of days is known and money earns is unknown.

Given, Ekta earns in 10 days = ₹ 3000

∴ Ekta earns in 1 day = \(\frac{3000}{10}=₹ 300\)

∴ Ekta earns in 30 days = 300 x 30 = 9000

Hence, Ekta earns 9000 in 30 days.

Question 3. If it has rained 276 mm in the last 3 days, how many centimetre of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.

Solution. Here, the number of days is known and rain fall is unknown.

Given, rainfall in 3 days = 276 mm

∴ Rainfall in 1 day. = \(\frac{276}{3}\) = 92 mm

∴ Rainfall in one full week i.e. 7 days = 92 x 7 = 644 mm

In centimetre, rainfall in one full week

= \(644 \times \frac{1}{10} \mathrm{~cm}=64.4 \mathrm{~cm}\) [∴ 1 mm = \(\frac{1}{10}\) cm]

Hence, 64.4 cm rain will fall in 7 days or in one full week.

Question 4. Cost of 5 kg of wheat is ₹ 91.50.

(1) What will be the cost of 8 kg of wheat?

(2) What quantity of wheat can be purchased in ₹ 183?

Solution. (1) Here, the quantity of wheat is known and cost is unknown.

Given, cost of 5 kg of wheat = ₹ 91.50

∴ Cost of 1 kg of wheat = \(\frac{91.50}{5}=₹ 18.3\)

∴ Cost of 8 kg of wheat = 18.30 x 8 = ₹ 146.40

Hence, the cost of 8 kg of wheat is ₹ 146.40.

(2) Here, the cost of wheat is known and quantity of wheat is unknown.

Given, in ₹ 91.50 quantity of wheat that can be purchased = 5 kg

∴ In ₹ 1, quantity of wheat that can be purchased

= \(\frac{5}{91.50}=\frac{5 \times 10}{915}=\frac{50}{915} \mathrm{~kg}\)

[multiplying numerator and denominator both by 10]

∴ In ₹ 183, quantity of wheat that can be purchased

= \(\frac{50}{915} \times 183=\frac{50}{5}=10 \mathrm{~kg}\)

Hence, 10 kg wheat can be purchased in ₹ 183.

MP Board Class 6 Maths Solutions

Question 5. The temperature dropped 15 degree celsius in the last 30 days. If the rate of temperature drop remains the same, how many degrees will the temperature drop in the next ten days?

Solution. Given, in last 30 days, temperature drop = 15 degree

∴ In 1 day, temperature drop = \(\frac{15}{30}=\frac{15+15}{30 \div 15}=\frac{1}{2} \text { degree }\)

∴ In next 10 days, temperature drop

= \(\frac{1}{2} \times 10 \text { degree }=5 \text { degree }\)

Hence, temperature dropped 5 degree in the next 10 days.

Question 6. Shaina pays ₹ 15000 as rent for 3 months. How much does she has to pay for a whole year, if the rent per month remains same?

Solution. Given, rent paid for 3 months = ₹ 15000

∴ Rent paid for 1 month = \(\frac{15000}{3}=₹ 5000\)

∴ Rent paid for a whole year i.e. 12 months

= 5000 × 12 = ₹ 60000

Hence, she has to pay ₹ 60000 for a whole year.

Question 7. Cost of 4 dozens bananas is ₹ 180. How many bananas can be purchased for ₹ 90?

Solution. We know that, I dozen = 12 unit

Given, in ₹ 180, number of bananas that can be purchased = 4 dozen

= 4 x 12 = 48

[∴ 1 dozen = 12 unit]

∴ In ₹ 1, number of bananas that can be purchased

∴ In ₹ 90, number of bananas that can be purchased

Hence, 24 bananas can be purchased for ₹ 90.

MP Board Class 6 Maths Solutions

Question 8. The weight of 72 books is 9 kg. What is the weight of 40 such books?

Solution. Given, weight of 72 books = 9 kg

∴ Weight of 1 book = \(\frac{9}{72}\)

∴ Weight of 40 books = \(\frac{9}{72} \times 40=\frac{360}{72} \mathrm{~kg}=\frac{360 \div 72}{72 \div 72}=5 \mathrm{~kg}\)

Hence, the weight of 40 books is 5 kg.

Question 9. A truck requires 108 L of diesel for covering a distance of 594 km. How much diesel will be required by the truck to cover a distance of 1650 km?

Solution. Given, diesel required for 594 km = 108 L

∴ Diesel required for 1 km = \(\frac{108}{594}=\frac{108 \div 54}{594 \div 54}=\frac{2}{11} L\)

∴ Diesel required for 1650 km = \(\frac{2}{11} \times 1650=2 \times 150=300 \mathrm{~L}\)

Hence, 300 L diesel required by the truck to cover 1650 km.

Question 10. Raju purchases 10 pens for ₹ 150 and Manish buys 7 pens for ₹ 84. Can you say who got the pens cheaper?

Solution. For Raju, cost of 10 pens=150

∴ Cost of 1 pen = \(\frac{150}{10}\) = ₹ 15

For Manish, cost of 7 pens = ₹ 84

∴ Cost of 1 pen = \(\frac{84}{7}\) ₹ 12

Here, ₹ 12 < ₹ 15

Hence, Manish got the pens cheaper.

Question 11. Anish made 42 runs in 6 overs and Anup made 63 runs in 7 overs. Who made more runs per over?

Solution. Runs made by Anish in 6 overs = 42

∴ Runs made by Anish in 1 over = \(\frac{42}{6}\) = 7

Runs made by Anup in 7 overs = 63

∴ Runs made by Anup in 1 over = \(\frac{63}{7}\) = 9

∴ 9 > 7

Hence, Anup made more runs per over.

Chapter 12 Ratio And Proportion Multiple Choice Questions

Question 1. The ratio of 6 books to 30 books is

1. 5 : 1
2. 2 : 3
3. 1 : 5
4. 2 : 5

Answer. 3. 1 : 5

Question 2. The simplest form of the ratio 384 : 480 is

1. 2 : 5
2. 4 : 5
3. 5 : 4
4. 3 : 5

Answer. 2. 4 : 5

Question 3. In a box, the ratio of red marbles to blue marbles is 7:4. Which of the following could be the total number of marbles in the box?

1. 18
2. 19
3. 21
4. 22

Answer. 4. 22

Question 4. The ratio of the number of sides of a triangle to the number of edges of a cube is

1. 4 : 1
2. 1 : 4
3. 1 : 3
4. 2 : 3

Answer. 2. 1 : 4

MP Board Class 6 Maths Solutions

Question 5. Margarette works in a factory and earns ₹ 955 per month. She saves 185 per month from her earnings. Then, the ratio of her income to her expenditure is Competency Based Question

1. 154 : 37
2. 191 : 37
3. 191 : 154
4. 37 : 191

Answer. 3. 191 : 154

Question 6. Avinash works as a lecturer and earns ₹ 12000 per month. His wife who is a doctor earns ₹ 15000 per month. Then, the ratio of Avinash’s income to their total income is

1. 4 : 9
2. 9 : 4
3. 4 : 5
4. 5 : 4

Answer. 1. 4 : 9

Question 7. If a bus travels 160 km in 4 h and a train travels 320 km in 5 h at uniform speeds, then the ratio of the distances travelled by them in one hour is

1. 1 : 2
2. 4 : 5
3. 5 : 8
4. 8 : 5

Answer. 3. 5 : 8

Question 8. A picture is 40 cm wide and 1.6 m long. The ratio of its width to its perimeter in lowest form is

1. 1 : 5
2. 1 : 10
3. 2 : 5
4. 1 : 8

Answer. 2. 1 : 10

Question 9. Which of the following is the equivalent ratio of 7 : 11?

1. 14 : 22
2. 14 : 121
3. 21 : 121
4. 49 : 66

Answer. 1. 14 : 22

Question 10. The ratio of number of circles and number of squares inside the following rectangle is

1. 12:11
2. 10:9
3. 11:10
4. 13:11

Answer. 3. 11 : 10

MP Board Class 6 Maths Solutions

Question 11. Mathematics textbook for Class VI has 320 pages. The chapter ‘Symmetry’ runs from page 261 to page 272. The ratio of the number of pages of this chapter to the total number of pages of the book is

1. 11:320
2. 3:40
3. 3:80
4. 272: 320

Answer. 3. 3 : 80

Question 12. If 66: 72 : x: 96, then x is equal to

1. 108
2. 78
3. 88
4. 48

Answer. 3. 88

Question 13. If 7 : 30 :: x : 15, then the value of x is

1. \(\frac{7}{2}\)
2. \(\frac{2}{7}\)
3. 6
4. 7

Answer. 1. \(\frac{7}{2}\)

Question 14. Which of the following are in proportion?

1. 1, 3, 11, 22
2. 2, 5, 40, 80
3. 3, 4, 15, 18
4. 2, 3, 20, 30

Answer. 4. 2, 3, 30, 20

Question 15. In a school library, the ratio of Mathematics books to Science books is same as the ratio of Science books to Hindi books. If there are 450 books of Science and 300 books of Hindi, then the number of books of Mathematics is Competency Based Question (c) 300 (d) 450

1. 720
2. 675
3. 300
4. 450

Answer. 2. 675

Chapter 12 Ratio And Proportion Assertion Reason

Question 1. Assertion (A) The monthly salary of Hari-Kishan is ₹ 80000. The monthly salary of Manish is ₹ 40000.

Reason (R) Two quantities can be compared only if they are in the same unit.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 2. Assertion (A) 1 : 2 is not equivalent to 10 : 5.

Reason (R) We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

MP Board Class 6 Maths Solutions

Question 3. Assertion (A) 25 km : 60 km :: ₹ 15 : ₹ 17.

Reason (R) If two ratios are equal, we say that they are in proportion and use the symbol ‘::’ or ‘=’ to equate the two ratios.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (d) A is false but R is true.

Question 4. Assertion (A) 15 : 40 :: 10 : 30.

Reason (R) Proportion says that two ratios (or fractions) are equal.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (d) A is false but R is true.

Chapter 12 Ratio And Proportion Fill in the Blanks

Question 1. A ratio expressed in lowest form has no common factor other than ….. in its terms.

Answer. 1

Question 2. To find the ratio of two quantities, they must be expressed in ….. unit.

Answer. Same

Question 3. The cost of 4 pens is ₹ 40. The cost of 11 pens is …. .

Answer. 110

Question 4. Maya can walk 6 km in 2 h. In 3 h, she can walk …… .

Answer. 9 km

Question 5. Sleeping time of a python in a 24 h clock is represented by the unshaded portion in figure.

The ratio of sleeping time to the awaking time is …… .

Answer. 1 : 3

Chapter 12 Ratio And Proportion True/False

Question 1. 4 : 7 = 20 : 35

Answer. True

Question 2. 15 m : 40 m = 40 cm : 80 cm

Answer. False

Question 3. The ratio of 20 kg to 200 kg is 1 : 10.

Answer. True

MP Board Class 6 Maths Solutions

Question 4. The ratio 8 : 40 is in its lowest form.

Answer. False

Question 5. If 10 : 30 :: 40 : x, then the value of x is 120.

Answer. True

Chapter 12 Ratio And Proportion Case Based Questions

Question 1. Sam organised a party. He decorated his house and arranged food for guests. He spent ₹ 1600 on decoration and ₹ 8000 on food.

(1) What is the ratio of the money that Sam spent on decoration to the money spent on food?

(a) 1 : 4

(b) 1 : 5

(c) 1 : 6

(d) 5 : 1

(2) Same used paper ribbons to decorate the walls. He made a pattern using groups of four ribbons. Each group has one blue ribbon and the remaining are yellow. What is the ratio of blue ribbons to the total number of ribbons in each pattern?

(3) To decorate one wall, Sam used 18 blue ribbons. How many yellow ribbons were used on that wall?

(a) 3

(b) 6

(c) 36

(d) 54

(4) Sam purchased 40 blue ribbons.

He orders the ribbons shown below.

How many rupees will Sam pay for the 40 ribbons?

Solution. (1) (b) Sam spent the money on decoration = ₹ 1600 and the money he spent on food = 8000

∴ Ratio of money spent on decoration to

money spent on food = \(\frac{1600}{8000}=\frac{1600 \div 1600}{8000 \div 1600}\)

[HCF of 1600 and 8000 = 1600]

= \(\frac{1}{5}\) = 1 : 5

Thus, the ratio of the money spent on decoration to money spent on food is 1:5.

(2) Sam made pattern using four ribbons.

Number of blue ribbons = 1

Number of yellow ribbons = 3

Total number of ribbons = 1 + 3 = 4

∴ Ratio of blue ribbons to the total number of ribbons

= 1 : 4

(3) (d) To decorate one wall Sam used 18 blue ribbons. From part (2), we have the ratio of Blue ribbon to yellow ribbon is 1:3.

If one blue ribbon is used, then 3 yellow ribbons will also used.

∴ We have, the number of blue ribbons = 18

∴ The number of yellow ribbons = 18 x 3 = 54

Thus, 54 yellow ribbons were used on the wall.

(4) Sam purchased 40 blue ribbons and 1 pack has 5 rolls with price of ₹ 25.

∴ Price of 5 rolls = ₹ 25

∴ Price of 1 roll of ribbon = \frac{25}{5} = ₹ 5

∴ Price of 40 rolls of ribbon = 5 x 40 = 200

Thus, Sam will pay 200 for 40 ribbons.

MP Board Class 6 Maths Solutions

Question 2. Sam ordered 21 sausages. Of the 15 guests that came to the party, 6 guests had two sausages each, three guests had one sausage each and the remaining guests did not have any sausages.

(1) What is the ratio of the number of sausages left to the number of sausages had by the guests?

(a) 2 : 5

(b) 2 : 7

(c) 5 : 2

(d) 5 : 7

(2) One pack of 3 sausages cost ₹ 120. What is the cost of 21 sausages?

(a) ₹ 40

(b) ₹ 630

(c) ₹ 840

(d) ₹ 140

Solution. (1) (a) Total number of sausages = 21

Out of 15 guests, 6 guests had two sausages each i.e. 6 guests had the number of sausages = 6 x 2 = 12 sausage

and the number of sausages had by 3 guests = 3 x 1 = 3 sausages

Total number of sausages had by guests

= 12 + 3 = 15 sausages

Number of sausages left = 21 – 15 = 6 sausages

Now, ratio of the number of sausages left to the number of sausages had by guests

= \(\frac{6}{15}=\frac{6 \div 3}{15 \div 3}=\frac{2}{5}=2: 5\)

Thus, the required ratio is 2:5.

(2) (c) Cost of 3 sausages = ₹ 120

Cost of 1 sausage = \(₹ \frac{120}{3}=₹ 40\)

∴ Cost of 21 sausages = 40 × 21 = 840

Thus, cost of 21 sausages is ₹ 840.

Chapter 12 Ratio And Proportion Very Short Answers Type Questions

Question 1. Write the following ratios in the simplest form.

(1) 600 g to 1 kg

(2) 2 cm to 4 m

Solution. (1) Ratio of 600 g to 1 kg = \(\frac{600}{1000}\) [∴ 1 kg = 1000 g]

= \(\frac{3}{5}\) = 3 : 5

(2) 2 cm to 4 m = \(\frac{2}{400}\) [∴ 1m = 100 cm]

Question 2. Give two equivalent ratios of 3 : 8.

Solution. \(3: 8=\frac{3}{8}=\frac{3 \times 2}{8 \times 2}=\frac{6}{16}, 3: 8=\frac{3}{8}=\frac{3 \times 3}{8 \times 3}=\frac{9}{24}\)

Hence, two equivalent ratios of 3 : 8 are 6 : 16 and 9 : 24.

Question 3. Find (1) the ratio of 70 cm to 1 m.

(2) the ratio of 50 paise to ₹ 2.

Solution. (1) We know that 1 m = 100 cm

∴ Required ratio = \(70: 100=\frac{70}{100}=7: 10\)

(2) We know that ₹ 1 = 100 paise

∴ Required ratio = \(\frac{50}{200}=\frac{1}{4}=1: 4\)

Question 4. If the cost of 10 bananas is ₹ 20. What will be the cost of 7 bananas?

Solution. Cost of 10 bananas = ₹ 20

Cost of 1 banana = \(\frac{20}{10}\) = ₹ 2

∴ Cost of 7 bananas = 7 x 2 = ₹ 14

Question 5. Determine whether the given ratios are equal.

30 : 45 and 60 : 100

Solution. We have, 30 : 45 = \(\frac{30}{45}\) = \(\frac{2}{3}\) = 2 : 3

and 60 : 100 = \(\frac{60}{100}\) = \(\frac{3}{5}\) = 3 : 5

So, the ratios 30 : 45 and 60 : 100 are not equal.

Question 6. The cost of 3 dozen pens is ₹ 72. What will be the cost of 7 bananas?

Solution. Cost of 3 dozen pens = ₹ 72

Cost of 1 dozen pens = \(\frac{72}{3}\) = ₹ 24

∴ Cost of 2 dozen pens 24 x 2 = ₹ 48

Question 7. Are the ratios 10 g : 40 g and 25 kg : 100 kg in proportion?

Solution. We have, 10 g : 40 g = \(\frac{10}{40}\) = 1 : 4

and 25 kg : 100 kg = \(\frac{25}{100}\) = 1 : 4

So, they are in proportion.

MP Board Class 6 Maths Solutions

Question 8. Are 10, 15, 20 and 30 in proportion?

Solution. Ratio of 10 to 15 = \(\frac{10}{15}\) = 2 : 3

Ratio of 20 to 30 = \(\frac{20}{30}\) = 2 : 3

Since, 10:15 = 20:30

Hence, 10, 15, 20 and 30 are in proportion.

Question 9. If 15 : 10 :: x : 20, then find the value of x.

Solution. Given, 15 : 10 :: x : 20

⇒ \(\frac{15}{10}=\frac{x}{20}\)

⇒ 10x = 15 x 20

⇒ \(x=\frac{15 \times 20}{10}=30\)

Chapter 12 Ratio And Proportion Short Answer Type Questions

Question 1. Which pair of ratios are equal and why?

(1) \(\frac{2}{3}\), \(\frac{4}{6}\)

(2) \(\frac{8}{4}\), \(\frac{2}{1}\)

(3) \(\frac{4}{5}\), \(\frac{12}{20}\)

Solution. (1) \(\frac{2}{3}=2: 3 \text { and } \frac{4}{6}=2: 3\)

Hence, \(\frac{2}{3}\) and \(\frac{4}{6}\) are equal.

(2) \(\frac{8}{4}=2: 1 \text { and } \frac{2}{1}=2: 1\)

Hence, \(\frac{8}{4}\) and \(\frac{2}{1}\) are equal.

(3) \(\frac{4}{5}=4: 5 \text { and } \frac{12}{20}=\frac{3}{5}=3: 5\)

Hence, \(\frac{4}{5}\) and \(\frac{12}{20}\) are not equal.

Question 2. Reshma prepared 18 kg of burfi by mixing khoya with sugar in the ratio of 7 : 2. How much khoya did she use?

Solution. Quantity of burfi = 18 kg

Given, Khoya : Sugar = 7 : 2

Total = 7 + 2 = 9

Quantity of khoya = \(\frac{7}{9} \times 18=14 \mathrm{~kg}\)

So, Reshma used 14 kg khoya.

Question 3. A line segment 56 cm long is to be divided into two parts in the ratio 2 : 5. Find the length of each part.

Solution. Length of line segment = 56 cm

Ratio of two parts = 2 : 5

Sum of parts = 2 + 5 = 7

∴ Length of first part = \(\frac{2}{7} \times 56=16 \mathrm{~cm}\)

and length of second part = \(\frac{5}{7} \times 56=40 \mathrm{~cm}\)

MP Board Class 6 Maths Solutions

Question 4. Ram and Mohan ran in a race. Ram covered 210 m while during the same time Mohan covered only 180 m. What is the ratio of the distance covered by Mohan to that by Ram?

Solution. Distance covered by Ram = 210 m

Distance covered by Mohan = 180 m

∴ Required ratio = \(\frac{180}{210}=\frac{6}{7}=6: 7\)

Question 5. School starts at 7 : 00 am and gets over at 12 : 30 pm. If the break time is from 9 : 50 am to 10 : 10 am. What is the ratio of the break time to the total time the students spend at school?

Solution. School starts at 7:00 am and gets over at 12:30 pm.

Total time the student spend at shcool

= 5 h 30 min = (5 x 60 + 30) m = 330 min

Break time = 9:50 am to 10 : 10 am = 20 min

∴ Required ratio = \(\frac{20}{330}=2: 33\)

Question 6. There are two rectangles A and B. A has a length of 12 cm and breadth of 6 cm. B has a length of 11 cm and breadth of 9 cm. Find the ratio of their perimeter.

Solution. For Rectangle A,

Length 12 cm and breadth = 6 cm

Perimeter of Rectangle A = 2 x (length + breadth)

= 2 (12 + 6)

= 36 cm

For Rectangle B, Length = 11 cm and breadth = 9 cm

Perimeter of Rectangle B = 2 (11 + 9) = 40 cm

∴ Required ratio = \(\frac{36}{40}=\frac{9}{10}=9: 10\)

Question 7. Line segment AB = 10 cm is divided at C in the ratio 1 : 4, what are the lengths of \(\overline{A C} \text { and } \overline{B C} \text { ? }\)

Solution. Length of line segment AB = 10 cm

and AC : BC = 1 : 4

Sum of parts AC and BC = AC + BC = 1 + 4 = 5

∴ Length of \(\overline{A C}=\frac{1}{5} \times 10=2 \mathrm{~cm}\)

Length of \(\overline{B C}=\frac{4}{5} \times 10=8 \mathrm{~cm}\)

MP Board Class 6 Maths Solutions

Question 8. 17 bags of cement costs ₹ 1675.50. How many bags of cement can be bought for ₹ 1182?

Solution. In ₹ 1675.50, number of bags purchased = 17

In ₹ 1, number of bags purchased = \(\frac{17}{1675.50}\)

In ₹ 1182, number of bags purchased = \(\frac{17}{1675.50} \times 1182\)

= 12 (approx.)

Question 9. The sides of a triangle are in the ratio 2 : 3 : 5. If the total perimeter of the triangle is 70 cm, then find the length of the longest side.

Solution. Given, ratio of sides of triangle = 2 : 3 : 5

Total perimeter = 70

Total of the sides = 2 + 3 + 5 = 10

∴ Length of the longest side = \(70 \times \frac{5}{10}=35 \mathrm{~cm}\)

Chapter 12 Ratio And Proportion Long Answer Type Questions

Question 1. Samira sells newspapers at Janpath crossing daily. On a particular day, she had 312 newspapers out of which 216 are in English and remaining in Hindi. Find the ratio of

(1) the number of English newspapers to the number of Hindi newspapers.

(2) the number of Hindi newspapers to the total number of newspapers.

Solution. Total number of newspapers = 312

Number of english newspapers = 216

Hindi newspapers = Total number of newspapers – Number of English newspapers

= 312 – 216 = 96

(1) Ratio of the number of English newspapers to the

number of Hindi newspapers = 216 : 96 = \(\frac{216}{96}=\frac{9}{4}=9: 4\)

(2) Ratio of the number of Hindi newspapers to the

total number of newspapers = \(\frac{96}{312}=\frac{4}{13}=4: 13\)

MP Board Class 6 Maths Solutions

Question 2. In a club having 100 members, 20 play carrom, 24 play table tennis, 16 play badminton and the remaining do not play any game (no member plays more than one game). Find the ratio of

(1) the number of members who play carrom to the numbers of those, who play table tennis.

(2) the number of members who play badminton to the number of those, who play carrom.

(3) the number of members who play table tennis to the number of those, who play badminton.

(4) the number of members who play badminton to the number of those, who do not play any game.

Solution. Total number of members = 100

Number of members, who play carrom = 20

Number of members, who play table tennis = 24

Number of members, who play badminton = 16

Number of members, who do not play any game

= 100 – (20 + 24 + 16) = 100 – 60 = 40

(1) Ratio of members who play carrom to the members who play table tennis

= \(20: 24=\frac{20}{24}=5: 6\)

(2) Ratio of members who play badminton to the members who play of carrom

= \(16: 20=\frac{16}{20} \approx \frac{4}{5}=4: 5\)

(3) Ratio of members who play table tennis to the member who play, badminton

= \(24: 16=\frac{24}{16}=\frac{3}{2}=3: 2\)

(4) Ratio of members who play badminton to the number of members, who do not play any game

= \(16: 40=\frac{16}{40}=\frac{2}{5}=2: 5\)

Question 3. Length and breadth of the floor of a room are 5 m and 3 m, respectively. Forty tiles, each with area \(\frac{1}{16}\) m2 are used to cover the floor partially. Find the ratio of the tiled and the non-tiled portion of the floor.

Solution. Given, length of floor of a room = 5 m

and breadth of floor of a room = 3 m

Area of floor = 5 x 3 = 15 m2

Area of one tile = \(\frac{1}{16}\) m2

Area of forty tiles = \(40 \times \frac{1}{16}=\frac{5}{2} \mathrm{~m}^2\)

Tiled portion of the floor = \(\frac{5}{2}\) m2

Now, non-tiled portion of the floor = \(\left(15-\frac{5}{2}\right) \mathrm{m}^2\)

= \(\left(\frac{30-5}{2}\right)=\frac{25}{2} \mathrm{~m}^2\)

So, ratio of tiled to the non-tiled portion of the floor

= \(\frac{5}{2}: \frac{25}{2}=\frac{\frac{5}{2}}{\frac{25}{2}}=\frac{5}{25}=\frac{1}{5}=1: 5\)

Hence, the required ratio is 1 : 5.

Question 4. In a year, Ravi earns ₹ 360000 and paid ₹ 24000 as income tax. Find the ratio of his

(1) income to income tax.

(2) income tax to income after paying income tax.

Solution. Given, Ravi earns in a year = ₹ 360000

and Ravi paid income tax in a year = ₹ 24000

(1) Ratio of income to the income tax paid

= 360000 : 24000

= 360 : 24 [dividing by 1000 in both ratios]

= 15 : 1 [dividing by 24 in both ratios]

Hence, the ratio of income to income tax is 15 : 1.

(2) After paying income tax, remaining income

= Total income – Income tax

= 360000 – 24000

= ₹ 336000

∴ Ratio of income tax to income after paying income tax

= 24000 : 336000

= 24 : 336 [dividing by 1000 in both ratios]

= 1 : 14 [dividing by 24 in both ratios]

Hence, the ratio of income tax to income after paying income tax is 1 : 14.

Question 5. Ramesh earns ₹ 28000 per month. His wife Rama earns ₹ 36000 per month. Find the ratio of

(1) Ramesh’s earnings to their total earnings.

(2) Rama’s earnings to their total earnings.

Solution. Given, Ramesh earns per month = ₹ 28000

and Rama earns per month = ₹ 36000

∴ Total earnings = Ramesh’s earning per month + Rama’s earning per month

= ₹ (28000 + 36000) = ₹ 64000

(1) Ratio of Ramesh’s earnings to their total earnings

= Ramesh’s earnings : Total earnings

= 28000 : 64000

= 28 : 64 [dividing by 1000 in both ratios]

= 7 : 16 [dividing by 4 in both ratios]

Hence, the ratio of Ramesh’s earnings to their total earnings is 7: 16.

(2) Rama’s earnings to their total earnings

= Rama’s earnings : Total earnings

= 36000: 64000

= 36 : 64 [dividing by 1000 in both ratios]

= 9 : 16 [dividing by 4 in both ratios]

Hence, the ratio of Rama’s earnings to income their total earnings is 9 : 16.

MP Board Class 6 Maths Solutions

Question 6. A recipe calls for 1 cup of milk for every \(2 \frac{1}{2}\) cups of flour to make a cake that would feed 6 persons. How many cups of both flour and milk will be needed to make a similar cake for 8 people?

Solution. Given, milk needed for making cake = 1 cup

and flour needed for making cake = \(2 \frac{1}{2} \text { cups }=\frac{5}{2} \text { cups }\)

Then, the total amount needed Milk + Flour

= \(\left(1+\frac{5}{2}\right) \text { cups }=\frac{7}{2} \text { cups }\)

So, \(\frac{7}{2}\) cups of milk and flour needed to make cake for 6 persons.

Let the needed amount of cups of milk and flour to make cake for 8 persons = x

[where, x is a multiple of cups]

By ratio and proportion law, \(\frac{2}{6}\) = \(\frac{x}{8}\)

⇒ \(\frac{7}{2} \times 8=6 \times x\)

⇒ x = \(\frac{28}{6}\)

⇒ x = \(\frac{14}{3}\) [dividing by 2]

Hence, the cups needed for 8 persons is \(\frac{14}{3}\).

Question 7. A scooter travels 120 km in 3 h and a car travels 120 km in 2 h. Find the ratio of their speeds. [Hint \(\text { Speed }=\frac{\text { Distance travelled }}{\text { Time taken }}\)]

Solution. Given, distance travelled by a scooter = 120 km

Time taken by a scooter = 3h

∴ \(\text { Speed of scooter }=\frac{\text { Distance travelled }}{\text { Time taken }}=\frac{120 \mathrm{~km}}{3 \mathrm{~h}}\)

= 40 km/h

and distance travelled by car = 120 km

and time taken by a car = 2h

∴ \(\text { Speed of the car }=\frac{\text { Distance travelled }}{\text { Time taken }}\)

= \(\frac{120 \mathrm{~km}}{2 \mathrm{~h}}\)

= 60 km/h

= Speed of the scooter : Speed of the car

= 40:60 = 2:3 [dividing by 20 in both ratios]

Hence, the ratio of their speeds is 2: 3.

Chapter 11 Algebra Matchstick Patterns

Matchsticks are used to make pattern of letters and other shapes.

Using matchsticks, we can write a general rule regarding the number of matchsticks required for a given shape. We introduce a variable which takes on values 1, 2, 3,…, denoted by letter n.

e.g. Let us consider the shape of a right angle.

(1) Number of right angle = 1 Number of matchsticks = 2

(2) Number of right angles = 2 Number of matchsticks = 4

(3) Number of right angles = 3 Number of matchsticks = 6 …… and so on.

Writing the above facts in a table, we have

From the table, we can say that the number of matchsticks required is twice the number of right angled formed.

i.e. Number of matchsticks required = 2 x Number of right angles formed

Read and Learn More MP Board Class 6 Maths Solutions

Hence, we can write as

Number of matchsticks required = 2n,

where n is the number of right angles formed.

Variable

A variable is a number which does not have a fixed value. It can take various values.

To show a variable, we may use any letter as n, m, l, p, x, y, z etc.

In the above example of the shape of right angle.

Number of matchsticks required = 2n

where n is called variable which is the number of right angles formed.

More Matchstick Patterns

We can make many letters of the alphabet and other shapes from matchsticks.

e.g. (1) Patterns of U (L), triangle (A), etc.

Hence, the number of matchsticks required = 3n

(2) Pattern of letter E

To make one E, five matchsticks are used

Hence, the number of matchsticks required = 5n

MP Board Class 6 Maths Solutions 

Example 1. Find the rule which gives the numbers of matchsticks required to make the following matchstick pattern. Use a variable to write the rule.

(1) A pattern of letter W

(2) A pattern of letter O

Solution. (1) One W can be formed by 4 matchsticks. Two W can be formed by 8 matchsticks.

So, let variable n denote the number of W’s.

Now, the number of matchsticks required to make pattern of W are given below.

For n = 1, the number of matchsticks required = 4 x 1 = 4

For n = 2, the number of matchsticks required = 4 x 2 = 8

For n=3, the number of matchsticks required = 4 x 3 = 12

For n = n, the number of matchsticks required = 4 x n = 4n

Hence, the required rule for a pattern of letter W is 4n.

(2). One O can be formed by 4 matchsticks and two O can be formed by 8 matchsticks.

Thus, we get the following pattern of letter O.

So, let variable n denote the number of O’s.

Now, the number of matchsticks required to make pattern of O are given below.

For n = 1, the number of matchsticks required = 4 × 1 = 4

For n = 2, the number of matchsticks required = 4 × 2 = 8

For n = 3, the number of matchsticks required = 4 x 3 = 12

For n = n, the number of matchsticks required = 4 × n = 4n

Hence, the required rule for a pattern of letter O is 4n.

Example 2. Look at the following matchstick pattern of hexagons in the given figures below. The hexagons are not separate. Two neighbouring hexagons have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of hexagons.

Solution. In figure,

(1) Number of hexagon = 1

and number of matchsticks = 6 = 5 x 1 + 1

(2) Number of hexagons = 2

= 5 x Number of hexagon + 1

and number of matchsticks = 11 = 5 x 2 + 1

(3) Number of hexagons = 3

= 5 x Number of hexagon + 1

and number of matchsticks = 16 = 5 × 3 + 1

= 5x Number of hexagon + 1

Thus, if number of hexagons = x

Then, the number of matchsticks

= 5 x Number of hexagons + 1

= 5x + 1

Hence, the required rule that gives the number of matchsticks is 5x + 1, where x is the number of hexagons.

Examples of Variables

Example 3. The teacher distributes 10 pencils per student. Can you tell how many pencils are needed, considering the number of students? (use x for the number of students).

Solution. Let the number of students be x.

Given, number of pencils distributed per student = 10

Now, number of pencils when

x = 1 is 10 or 10 x 1 = 10 x x

⇒ x = 2 is 20 or 10 x 2 = 10 x x

⇒ x = 3 is 30 or 10 x 3 = 10 x x

∴ Number of pencils for x students are 10x.

MP Board Class 6 Maths Solutions 

Example 4. School children are standing in a ground. There are 10 children in a row. What is the rule which gives the number of children, given the number of rows? (use n for the number of rows.)

Solution. Let the number of rows be n

Given, the number of children in each row = 10

∴ Total number of children = 10n

Here. = 1 child

Hence, the rule to find the number of children in row is 10n.

Example 5. If there are 40 apples in a box, how will you write the total number of apples in terms of the number of boxes? (use a for the number of boxes).

Solution. Given, a is the number of boxes and the number of apples in a box = 40

When there is one box

i.e. a = 1, then the number of apples = 40 x 1 = 40 When there are two boxes

i.e. a = 2, then the number of apples = 40 x 2 = 80 When there are three boxes

i.e. a = 3, then the number of apples = 40 x 3 = 120 When there are a boxes

i.e. a = a, then the number of apples = 40 × a = 40a

Hence, the total number of apples in terms of number of boxes can be written as 40a.

Example 6. In her birthday, Radha distributes 5 toffees per student. Can you tell how many toffees are needed, given the number of students? (use letter y for the number of students).

Solution. Let the number of students be y.

Given, the number of toffees distributed to each student = 5

When there is one student i.e. y = 1,

then the number of toffees = 5 x 1 = 5

When there are two students i.e. y = 2,

then the number of toffees = 5 x 2 = 10

When there are three students i.e. y = 3,

then the number of toffees = 5 x 3 = 15

When there are y students i.e. y = y, then the number of toffees = 5 x y = 5y

Hence, 5 y toffees are needed for y students.

Example 7. A drone files 2 km In one minute. Can you express the distance covered by drone in terms of its flying time in minutes? (use z for flying time in minutes).

Solution. Let flying time of drone be z min.

Then, distance covered by drone in one minute = 2 km

∴ Distance covered by drone in 2 min = z x 2 = 2zkm

Hence, the distance covered by the drone in its flying time i.e. in z min is 2z km.

Example 8. Lakhan is Bharat’s younger brother. Lakhan is 5 yr younger than Bharat. Can you write Lakhan’s age in terms of Bharat’s age? Take Bharat’s age to be myr.

Solution. Let Bharat’s age be m yr.

Given, the Lakhan is 5 yr younger than Bharat.

So, age of Lakhan = (Age of Bharat) – 5 yr

⇒ Age of Lakhan (m-5) yr

Thus, we can write Lakhan’s age in terms of Bharat’s age.

MP Board Class 6 Maths Solutions 

Example 9. Hema’s mother made some cookies. She gives some cookies to guests and family members, still 7 cookies remain. If the number of cookies her mother gave away is t, how many cookies did she make?

Solution. Given, the number of cookies was given away by her mother = t

and the number of cookies left over = 7

∴ Total number of cookies made by Hema’s mother

= Number of cookies gave away + Number of cookies left

= t + 7

Hence, the total number of cookies made by her mother is t + 7.

Example 10. Mangoes are to be transferred from larger boxes to smaller boxes. When a large box is emptied, the mangoes from it fill three smaller boxes and still 5 mangoes remain outside.

If the number of mangoes in a small box are taken to be m, what is the number of mangoes in the larger box?

Solution. Given, the number of mangoes in a small box = m

Since, one larger box is emptied to fill three smaller boxes.

So, the number of mangoes in three smaller boxes

= 3 x Number of mangoes in one small box = 3x m = 3m

Also, 5 mangoes remain outside when larger box is emptied to fill three smaller boxes.

So, the number of mangoes in the larger box

= Number of mangoes in three smaller boxes + Mangoes left over

= 3m + 5

Hence, the number of mangoes in the larger box is 3m +5.

Chapter 11 Algebra Exercise 11.1

Question 1. Find the rule which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.

(1) A pattern of letter T as T

(2) A pattern of letter Z as Z

Solution. (1) One T can be formed by 2 matchsticks and 2T can be formed by 4 matchsticks. Thus, we get the following patterns of letter T.

So, let variablen denotes the number of T’s.

Now, the number of matchsticks required to make pattern of T are given below:

For n = 1,

Number of matchsticks required = 2 × 1 = 2

For n=2,

Number of matchsticks required = 2 x 2 = 4

For n = 3,

Number of matchsticks required = 2 × 3 = 6

For n=n,

Number of matchsticks required = 2 x n = 2n

Hence, the required rule for a pattern of letter T is 2n.

(2) One Z can be formed by 3 matchsticks and 2Z can be formed by 6 matchsticks. Thus, we get the following patterns of letter Z.

So, let variable n denotes the number of Z’s.

Now, the number of matchsticks required to make pattern of Z are given below:

For n = 1,

Number of matchsticks required = 3 x 1 = 3

For n = 2,

Number of matchsticks required = 3 x 2 = 6

For n = 3,

Number of matchsticks required = 3 × 3 = 9

For n = n,

Number of matchsticks required = 3 x n = 3n

Hence, the required rule for a pattern of letter Z is 3n.

MP Board Class 6 Maths Solutions 

Question 2. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows?

(use n for the number of rows.)

Solution. Let the number of rows = n

Given, the number of cadets in each row = 5

∴ Total number of cadets = 5n

Here, ⚫ = 1 cadet

Hence, rule to find the number of cadets in n rows is 5n.

Question 3. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (use b for the number of boxes).

Solution. Given, b is the number of boxes and the number of mangoes in a box = 50

When there is one box i.e. b = 1,

then the number of mangoes = 50 x 1 = 50.

When there are two boxes i.e. b = 2,

then the number of mangoes = 50 x 2 = 100

When there are three boxes i.e. b = 3,

then the number of mangoes = 50 x 3 = 150

When there are b boxes i.e. b = b,

then the number of mangoes = 50 x b = 50b

Hence, the total number of mangoes in terms of number of boxes can be written as 50b.

Class 6 Maths Chapter 11 Solutions

Question 4. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (use S for the number of students).

Solution. Let the number of students be S.

Given, the number of pencils distributed to each student = 5

When there is one student i.e. S = 1,

then the number of pencils = 5 x 1 = 5

When there are two students i.e. S = 2,

then the number of pencils = 5 x 2 = 10

When there are three students i.e. S = 3,

then the number of pencils = 5 x 3 = 15

When there are S students i.e. S = S,

then the number of pencils = 5 x S = 5S.

Hence, 5$ pencils are needed for S students.

Question 5. A bird flies 1 km in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes? (use t for flying time in minutes).

Solution. Let flying time of bird be t min.

Then, bird flies in one min = 1 km

∴ Bird flies in t min = t x 1 = t km

Hence, the distance covered by the bird in its flying time i.e. int min is t km.

Class 6 Maths Chapter 11 Solutions

Question 6. Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots with chalk powder). She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there, if there are 8 rows? If there are 10 rows?

Solution. Given, the number of rows = r

and the number of dots in one row i.e. r = 1 is 9 x 1 = 9

∴ The number of dots in 2 rows i.e. r 2 is 9 x 2 = 18

The number of dots in 3 rows i.e. r = 3 is 9 x 3 = 27

∴ Total number of dots in r rows = 9 x r = 9r

Now, if there are 8 rows i.e. r = 8, then the number of dots

= 9 x 8 = 72 dots

and for r = 10,

The number of dots = 9 x 10 = 90 dots

Question 7. Leela is Radha’s younger sister. Leela is 4 yr younger than Radha. Can you write Leela’s age in terms of Radha’s age? Take Radha’s age to be x years.

Solution. Let Radha’s age be xyr.

Given, the Leela is 4 yr younger than Radha.

So, age of Leela = (Age of Radha) – 4 yr

⇒ Age of Leela = (x-4) yr

Thus, we can write Leela’s age in terms of Radha’s age.

Question 8. Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is I, how many laddus did she make?

Solution. Given, the number of laddus was given away by mother = l

and the number of laddus left over = 5

∴ Total number of laddus made by mother = Number of laddus gave away + Number of laddus left over

= 1 + 5

Hence, the number of laddus made by mother is l + 5.

Class 6 Maths Chapter 11 Solutions

Question 9. Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?

Solution. Given, the number of oranges in a small box = x

Since, one large box is emptied to fill two smaller boxes.

So, the number of oranges in two smaller boxes

= 2 x Number of oranges in one small box = 2 x x = 2x

Also, 10 oranges remain outside when large box is emptied to fill two smaller boxes.

So, the number of oranges in the larger box = Number of oranges in two smaller boxes + Oranges left over

= 2x + 10

Hence, the number of oranges in the large box is 2x + 10.

Question 10. Look at the following matchstick pattern of squares. The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares.

[Hint If you remove the vertical stick at the end, you will get a pattern of C’s.]

Solution.

(a) Number of square = 1

and number of matchsticks = 4 = 3 x 1 + 1 = 3 x Number of square + 1

(b) Number of squares = 2

and number of matchsticks = 7 = 3 x 2 + 1 = 3 x Number of squares + 1

(c) Number of squares = 3

and number of matchsticks = 10 = 3 x 3 + 1 = 3 x Number of squares + 1

(d) Number of squares = 4

and number of matchsticks = 13 = 3 x 4 + 1

= 3 x Number of squares + 1

Thus, if number of squares = x

Then, the number of matchsticks

= 3x Number of squares + 1

= 3x + 1

Hence, the required rule that gives the number of matchsticks is 3x+1, where x is the number of squares.

Chapter 11 Algebra Multiple Choice Questions

Question 1. Six trees are planted in a row. Then, the number of trees planted in n such rows are

1. 6n
2. 6n/5
3. 3n
4. n

Answer. 1. 6n

Question 2. Which of the following represents 6 x X.

1. 6x
2. \(\frac{x}{6}\)
3. 6+x
4. 6-x

Answer. 1. 6x

Question 3. If each matchbox contain 50 matchsticks, then the number of matchsticks required to fill n such boxes is

1. 50+ n
2. 50n
3. 50+ n
4. 50-n

Answer. 2. 50 n

Question 4. A box of fruits contain 60 oranges, the number of oranges required for y such boxes

1. 60+y
2. 60y+5
3. 60 y
4. 60 y-m

Answer. 3. 60 y

Class 6 Maths Chapter 11 Solutions

Question 5. If there are 25 pictures in an album, then the rule which gives total number of pictures in X albums is Competency Based Question

1. 25
2. X
3. 25X/2
4. 25x

Answer. 4. 25 x

Question 6. A train is moving at a speed of x km/h. Then, the rule which gives the distance covered by train in 7h is

1. 7x
2. 7
3. x
4. 7x-h

Answer. 1. 7x

Question 7. Variable means that it

1. has a fixed value
2. can take different values
3. can take only 2 values
4. can take only 3 values

Answer. 1. can take different values

Question 8. Garima puts a handful of seeds into an empty bird feeder. A bird comes and eats 7 of them. Which of the following expression can represent this situation algebraically? Competency Based Question

1. p+7
2. 7p
3. p-7
4. p+7

Answer. 3. p – 7

Question 9. Garima put some more seeds in the feeder. Which of the following expressions can represent this situation algebraically?

1. 2p
2. p + 7
3. p + q
4. p + q – 7

Answer. 4. p + q – 7

Question 10. If x takes the value of 7, then the value of x +13 Is

1. 20
2. 12
3. 21
4. 10

Answer. 1. 20

Question 11. If there are 40 coins in a box and x coins taken out from the box, then the remaining coins in the box can be represented in terms of number of coins taken out by the statement. Competency Based Question

1. 40 is subtracted x times
2. x is subtracted 40 times
3. x is subtracted from 40
4. 40 is subtracted from x

Answer. 3. x is subtracted from 40

Question 12. In algebra, letters may stand for

1. unknown quantities
2. know quantities
3. fixed numbers
4. None of these

Answer. 1. unknown quantities

Class 6 Maths Chapter 11 Solutions

Question 13. Look at the following matchstick pattern of octagons in the given figures below. The octagons are not separate. Two neighbouring octagons have a common matchstick. Then, the rule that gives the number of matchsticks in terms of the number of octagons is 

1. 6n+1
2. 7n+1
3. 8n
4. 8n+1

Answer. 2. 7n + 1

Question 14. The difference between Sanjana’s and her mother’s age is 27 yr. Then, the age of Sanjana’s mother is

1. (27-x)
2. (x+27) yr
3. (x-27) yr
4. 27x yr

Answer. 2. (x+27) yr

Question 15. An auto rickshaw charges 20 for the first kilometer, then 7 for each such subsequent kilometres. The total charge (in) for r kilometres is

1. 20+7r
2. 20 + (r-1)7
3. 20 + (r+1)7
4. 27r

Answer. 2. 20 + (r-1)7

Chapter 11 Algebra Assertion-Reason

Question 1. Assertion (A) The rule which gives the number of matchsticks required to make the matchstick pattern L, is 2n.

Reason (R) For n = 1, the number of matchsticks required = 2 x 1 = 2.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 2. Assertion (A) The rule which gives the number of matchsticks required to make the matchstick pattern C, is 3n.

Reason (R) For n = 2, the number of matchsticks required = 3 x 2 = 6

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 3. Assertion (A) n can take different values such as 1, 2, 3, 4, …. .

Reason (R) n is the example of a variable. Its value is not fixed. It can take different values.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Chapter 11 Algebra Fill in the Blanks

Question 1. The variable can take ….. values.

Answer. Different

Question 2. The number of days in w weeks is …. .

Answer. 7w

Question 3. If the present age of Ramandeep is n years, then her age after 7 yr will be ….. .

Answer. n+7

Question 4. The value of ….. is not fixed.

Answer. Variable

Question 5. In 2, 3, 5, l, 10, m and 13, the numbers of variables are …. .

Answer. Two

Class 6 Maths Chapter 11 Solutions

Chapter 11 Algebra True/False

Question 1. The number of matchsticks required to form the letter V is 3.

Answer. False

Question 2. t minutes are equal to 60 t seconds.

Answer. True

Question 3. The difference between the ages of two sisters Lila and Yamini is a variable.

Answer. False

Question 4. Variables can be denoted by any letter as a, b, c, l, m, n, …., x, y, z.

Answer. True

Question 5. 1 kg of potatoes are bought for ₹ 60. Cost of n kg of potatoes is 60 n.

Answer. True

Chapter 11 Algebra Match the Columns

Question 1. Match the Column A with Column B

Answer. (a) → (2), (b) → (3), (c) → (4), (d) → (1)

Chapter 11 Algebra Case Based Questions

Question 1. Sarah buy books from a dealer for her bookstall. She buys 20 comic books, 15 story books and 10 colouring books. A comic book cost ₹ a. A story book costs ₹ 5 more than a comic book and a colouring book costs ₹ 10 more than a story book.

On the basis of the given information, answer the following questions.

(1) Which of the following expression shows the total cost of the comic books?

(a) 20

(b) 20a

(c) 20 + a

(d) 20 – a

(2) Sarah gets a profit of ₹ 2 on the sale of each comic book. Which of the following expression shows the amount Sarah earns by selling 10 comic books?

(a) a + 2

(b) 20a – 20

(c) 10a + 20

(d) 20 + a + 2

Class 6 Maths Chapter 11 Solutions

(3) A colouring book costs ₹ 50. What is the cost of the comic book?

(a) 35

(b) 40

(c) 45

(d) 50

(4) Write an expression to show the total cost of 15 storybooks.

Solution. (1) (b) Since, Sarah bought 20 comic books and cost of 1 comic book is a.

∴ Total cost of comic books = Cost of 1 comic book × Total number of comic books

= a x 20 = 20a

(2) (c) Cost of 1 comic book = a

Cost of 1 comic book with profit of ₹ 2 = a + 2

Number of books she sold = 10

Therefore, the amount Sarah earns by selling 10 comic books = 10 (a + 2) = 10a + 20

(3) (a) Cost of a comic book is ₹ a.

Then, according to the question,

Cost of a story book = Cost of a comic book + ₹ 5

= a + 5

Cost of a colouring book Cost of a story book + ₹ 10 = (a + 5) + 10 = a + 15

Also, it is given that a colouring book costs ₹ 50.

Therefore, equation is a + 15 = 50 ⇒ a = 50 – 15 ⇒ a = 35

Hence, the cost of a comic book is 35.

(4) Cost of 1 story book = a + 5

and total number of story book = 15

Therefore, the total cost of 15 story books = Total number of story books × Cost of one story book

= 15(a + 5) = 15a + 75

Question 2. Sudhir observed the pattern shown below on a cloth. The pattern consists of 4 patches.

The pattern is repeated n number of times in a 4 m long cloth.

(1) Which of the following expressions shows the number of octagon patches on the cloth?

(a) n

(b) 4n

(c) n + 4

(d) n – 4

(2) The cloth is cut into two equal halves. Sudhir observed both cloth parts have an equal number of repeating blocks but the last line is not complete. Which of the following expression shows the number of complete repeating blocks?

(a) n – 1

(b) 2n – 1

(c) \(\frac{n}{2}\)

(d) \(\frac{n}{2}\) – 1

(3) Write an expression which shows the total number of patches on the cloth?

Solution. (1) (a) Since, the pattern is repeated number of times there are n number of octagon patches on the cloth.

(2) (d) Number of repetition of pattern = n

The cloth cut into two equal halves.

∴ Number of repetition of pattern = \(\frac{n}{2}\)

and given last line is not complete.

∴ Number of complete repeating block = \(\frac{n}{2}\) – 1

(3) Total number of patches on cloth = Number of repetition of pattern x Number of patches in each repetition

Since, 4 patches in each pattern and pattern repeated n number of time

∴ Total number of patches on the cloth = 4n

Class 6 Maths Chapter 11 Solutions

Chapter 11 Algebra Very Short Answer Type Questions

Question 1. The cost of one pen is ₹ 15. Find the cost of y pens.

Solution. Cost of one pen = ₹ 15

Cost of y pen = 15 x y = 15y

Question 2. Find the number of matchsticks required to make the pattern of a square.

Solution. The number of matchsticks required to make the pattern of a square is 4.

Question 3. The valye of x pencisl, if cost of 1 pencil is ₹ 10.

Solution. Cost of one pencil = 10.

Cost of x pencil = 10 x x = 10x

Question 4. How many matchsticks will be required to make the pattern of a triangle?

Solution. The number of matchsticks required to make the pattern of a triangle is 3.

Chapter 11 Algebra Short Answer Type Questions

Question 1. The teacher distributes 2 pencils per student. Can you tell how many penciles are needed, given the number of students? (use x for the number of students).

Solution. Teacher distributes pencils per student = 2

Number of students = x

∴ Need of pencils = 2 x x = 2x

Question 2. A dolphin swins 1 km in one minute. Can you express the distance covered by dolphin in terms of its swimming time in minutes? (use t for swimming time in minutes)

Solution. Let the swimming time of dolphin bet min.

Then, dolphin swims in one min = 1 km

∴ Dolphin swims in t min = t x 1 = t km

Hence, the distance covered by dolphin in swimming time i.e. in t min is t km.

Algebra Class 6 Maths Solutions

Question 3. In a village, there are 8 water tanks to collect rain water. On a particular day, x litres of rain water is collected per tank. If 100 L of water was already there in one of the tanks, what is the total amount of water in the tanks on that day?

Solution. Rain water collected on particular day per tank = x L

Number of tanks to collect water = 8

Total water in all tanks = 8x L

Water in one of the tanks = 100 L

∴ Total amount of water = Total water in all tanks + Water in one of the tanks

= (8x + 100) L

Chapter 11 Algebra Long Answer Type Questions

Question 1. Find the rule which gives the number of matchsticks required to make the following matchstick patterns.

A pattern of letter y as Y

Solution. One Y can be formed by 3 matchsticks and 2Y can be formed by 6 matchsticks.

Thus, we get the following patterns of letter Y.

Here, the number of Y’s are increasing.

So, let the variable n denote the number of Y’s.

Now, the number of matchsticks required to make pattern of Y are given below:

For n = 1,

the number of matchsticks required = 3 x 1 = 3 For n = 2,

the number of matchsticks required = 3 x 2 = 6 For n = 3,

the number of matchsticks required = 3 x 3 = 9 For n = n,

the number of matchsticks required = 3 x n = 3n

Hence, the required rule for a pattern of letter Y is 31.

Question 2. Army personnel are standing in an open ground. There are 6 personnel in a row. What is the rule which gives the number of army personnel, given the number of rows? (use n for the number of rows.)

Solution. Let the number of rows = n

Given, the number of army personnel in each row = 6

∴ Total number of army personnel = 6n

Hence, the rule to find the number of army personnel in n rows is бn.

Question 3. If there are 40 oranges in a box, how will you write the total number of oranges in term of the number of boxes? (use b for the number of boxes).

Solution. Given, the number of oranges in box = 40

Let the number of boxes = b

Total number of oranges in term of number of boxes can be written as 40b.

Algebra Class 6 Maths Solutions

Question 4. Sakshi is drawing a dot Rongolu (a beautiful pattern of lines joining dots with chalk powder). She has 6 dots in a row. Find,

(1) how many dots will her Rangoli have for r rows?

(2) how many dots are there, if there are 10 rows?

Solution. Given, the number of rows = r

(1) The number of dots in one row

i.e. r = l is 6 x 1 = 6

The number of dots in two rows

i.e. r = 2 is 6 x 2 = 12

∴ Total number of dots in r rows = 6 x r = 6r

(2) If number of rows = 10

∴ The number of dots = 10 x 6 = 60 dots

Question 5. Richa is Madan’s younger sister. Richa is 5 yr younger than Madan. Can you write Richa’s age in terms of Madan’s age? Take Madan’s age to be x yr.

Solution. Let Madan’s age be x yr.

Given, Richa is 5 yr younger than Madan.

So, age of Richa = (Age of Madan) – 5 yr

and age of Richa = (x – 5) yr

Question 6. Mother bought some candy. She gives some candies to guests and family members; still 10 candies to guests and family members; still 10 candies are remain. If the number of candies mother gave away is m, how many candies did she bought?

Solution. Given, the number of candies given to guest and family members = m

and the number of candies left over = 10

∴ Total number of candies she bought = Number of candies gave to guest and family members + Number of candies left over

= m + 10

Hence, the number of candies bought by mother is m + 10.

Question 7. Mangoes are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the mangoes from it fill three smaller boxes and still 20 mangoes remain outside.

If the number of mangoes in a small box are taken to be x, what is the number of mangoes in the larger box?

Solution. Given, the number of mangoes in a small box = x

Since, one large box is emptied to fill three smaller boxes.

So, the number of mangoes in three smaller boxes = 3 x Number of mangoes in one box = 3 x x = 3x

Also, 20 mangoes remain outside when large box is emptied to fill three smaller boxes.

Number of mangoes in the larger box = Number of mangoes in three smaller boxes + Mangoes left over

= 3x + 20

Algebra Class 6 Maths Solutions

Question 8. Sunitha is half the age of her mother Geeta. Find their ages

(1) after 4 yr?

(2) before 3 yr?

Solution. Let Sunita’s present age be x.

Given, Sunita is half the age of her mother Geeta.

∴ Geeta’s present age = 2x

(1) Sunita’s age after 4 yr = (x+4) yr

Geeta’s age after 4 yr = (2x+4) yr

(2) Sunita’s age before 3 yr = (x-3) yr

Geeta’s age before 3 yr = (2x-3) yr

Question 9. Look at the following matchstick pattern of pentagons in the figures given below. The pentagons are not separate. Two neighbouring pentagons have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of pentagons.

Solution. From figure,

(1) Number of pentagons = 1

and number of matchsticks = 5 = 4 x 1 + 1

= 4 x Number of pentagons + 1

(2) Number of pentagons = 2

and number of matchsticks = 9 = 4 x 2 + 1

= 4 x Number of pentagons + 1

(3) Number of pentagons = 3

and number of matchsticks = 13 = 4 x 3 + 1

= 4 x Number of pentagons + 1

Thus, if number of pentagons = x

Then, the number of matchsticks

= 4 x Number of pentagons + 1

= 4x + 1

Hence, the required rule that gives the number of matchsticks is 4x+1, where x is the number of pentagons.

Chapter 10 Mensuration Perimeter

The distance covered along the boundary forming a closed figure when you go round the figure once is called the perimeter. Thus, we can calculate the perimeter of a plane figure by calculating the sum of measurements of all its sides. Unit of perimeter is same as that of length.

In Diagram (1), perimeter of △ABC = AB + BC + CA

In Diagram (2), perimeter of pentagon ABCDE =AB + BC + CD + DE + EA

Example 1. Find the perimeter of the given figures.

Solution. (1) Perimeter of the figure ABCDEF

Sum of the measurements of all sides

= AB + BC + CD + DE + EF + FA

= 100 + 120 + 90 + 45 + 60 + 80 = 495 m

Hence, the perimeter of the given figure is 495 m.

Read and Learn More MP Board Class 6 Maths Solutions

(2) Perimeter of the figure ABCDEFG

= Sum of the measurements of all sides

= AB + BC + CD + DE + EF + FG + GA

= 3 + 1 + 3.5 + 3.5 + 1 + 3 + 2 = 17 cm

Hence, the perimeter of the given figure is 17 cm.

(3) Perimeter of the figure ABCDEFG

= Sum of the measurements of all sides.

= AB + BC + CD + DE + EF + FG + GA

= 4 + 3 + 6 + 3 + 1 + 3 + 3 = 23 cm

Hence, the perimeter of the given figure is 23 cm.

(4) Perimeter of the given figure

= Sum of the measurements of all sides

= AB + BC + CD + DE + EF + FA

= 5 + 5 + 5 + 5 + 5 + 5 = 30 cm

Hence, the perimeter of the given figure is 30 cm.

Perimeter of a Rectangle

The perimeter of a rectangle is the total distance covered by its boundaries or the sides.

In other words, the sum of the measurements of all four sides of a rectangle is called the perimeter of a rectangle.

Perimeter of a rectangle ABCD

= Sum of length of its sides

= AB + BC + CD + DA = AB + BC + AB + BC

[∴ opposite sides are equal, CD = AB and DA = BC]

= 2(AB + BC) = 2(1 + b)

where, l = Length of the rectangle

and b = Breadth of the rectangle

Hence, the perimeter of a rectangle is 2 (1+b).

Note it While calculating the perimeter of a rectangle, we must express the length and breadth in the same unit.

MP Board Class 6 Maths Solutions

Example 2. Rohan wants to put a lace border all around a rectangular table cover 5 m long and 3 m wide. Find the length of the lace required by Rohan.

Solution. Given, length of the rectangular table cover = 5 m

and breadth of the rectangular table cover = 3 m

∴ Perimeter of the rectangular table cover = 2 × (length + breadth)

= 2 x (5 + 3) = 2 x 8 = 16m

Hence, the length of the lace required is 16 m.

Example 3. Find the perimeter of a rectangle whose length and breadth are 250 cm and 2 m, respectively.

Solution. Given, length of the rectangle = 250 cm

and breadth of the rectangle = 2 m = 2×100 cm = 200 cm

∴ Perimeter of the rectangle = 2 x (length + breadth)

= 2 × (250 + 200)

= 2 x 450 = 900 cm

Hence, the perimeter of the given rectangle is 900 cm.

Example 4. If the perimeter of a rectangle Is 200 cm and the length is 75 cm, then find Its breadth.

Solution. Given, perimeter of the rectangle = 200 cm

and length of the rectangle = 75 cm

∴ Perimeter of the rectangle = 2 x (length + breadth)

200 = 2(75 + breadth)

= \(\frac{1}{2} \times 200-75\)

= 100 – 75

= 25 cm

Hence, the breadth of the rectangle is 25 cm.

MP Board Class 6 Maths Solutions

Example 5. An athlete takes 10 rounds of a rectangular field which is 30 m long and 20 m wide. Find the total distance covered by him.

Solution. Given, length of rectangular field (l) = 30 m

and breadth of rectangular field (b) = 20 m

Total distance covered by the athlete in one round

= Perimeter of field (rectangle)

= 2(1 + b)

= 2 (30 + 20)

= 100 m

Since, the distance covered in one round = 100 m

So, the distance covered in 10 rounds = 10 x 100 = 1000 m

Example 6. A man has rectangular piece of land of length and breadth 340 m and 260 m, respectively. If each side is to be fenced with 4 rounds of wires, then what will be the length of wire needed?

Solution. Given, length of rectangular piece of land = 340 m

and breadth of rectangular piece of land = 260 m

Now, perimeter of the field = 2x (length + breadth)

= 2 x (340 + 260)

= 2 × 600

= 1200 m

∴ Each side is to be fenced with 4 rounds of wire.

∴ Total length of the wire required = 4 × 1200 = 4800 m

Example 7. Find the cost of fencing a rectangular park of length 275 m and breadth 125 m at the rate of ₹ 15 per metre.

Solution. Given, length of the rectangular park = 275 m

and breadth of the rectangular park = 125 m

Perimeter of the rectangular park = 2 × (length + breadth)

= 2 x (275 + 125)

= 2 x 400 = 800 m

∴ Cost of fencing of 1 m of park = ₹ 15

∴ Total cost of fencing the park = 15 x 800 = ₹ 12000

Perimeter of Regular Shapes

In regular shapes, all sides are of equal length and all angles are of equal measure.

If a regular polygon has n sides, then

Perimeter = n x Length of a side

where, n = Number of sides

Note it

(1) Perimeter of a regular pentagon = 5 x Length of one side = 5a

(2) Perimeter of a regular hexagon = 6 x Length of one side = 6a

Example 8. Find the perimeter of a regular hexagon with each side measuring 4 cm.

Solution. The given regular hexagon has 6 sides, each with the length of 4 cm.

∴ Perimeter of the regular hexagon = 6 x 4 = 24 cm

MP Board Class 6 Maths Solutions

Example 9. The perimeter of a regular hexagon is 30 cm. How long is its one side?

Solution. Given, perimeter of a regular hexagon = 30 cm

∴ Perimeter of regular hexagon = 6 x Length of a side

⇒ 30 = 6 x Length of a side

∴ Length of a side = \(\frac{30}{6}\) = 5 cm

Hence, the length of each side of a regular hexagon is 5 cm.

Perimeter of a Square

Perimeter of a square ABCD = AB + BC + CD + DA

= AB + AB + AB +AB

= 4AB [∴ AB = BC = CD = AD]

Hence, the perimeter of a square

= 4 x Length of a side of the square

Example 10. Find the distance travelled by Soniya, if she takes three rounds of a square park of side 60 m.

Solution. Given, length of side of square park = 60 cm

Perimeter of a square park = 4 x Length of a side

= 4 × 60 = 240 m

Distance covered in one round = 240 m

Distance covered in three rounds = 3 x 240 = 720 m

MP Board Class 6 Maths Solutions

Example 11. Mohan runs 5 times around a rectangular park with length 140 m and breadth 90 m while Sohan runs 6 times around a square park of side 80 m. Who covers more distance and by how much?

Solution. Distance covered by Mohan in one round

= Perimeter of the rectangular park

= 2x (length + breadth)

= 2 x (140 + 90) = 2 x 230 = 460 m

∴ Distance covered by Mohan is 5 rounds

= 5 × 460 = 2300 m

Distance covered by Sohan in one round

= Perimeter of the square park

= 4 x Length of a side = 4 x 80 = 320 m

∴ Distance covered by Sohan in 6 rounds = 6 x 320 = 1920 m

Difference in the distance covered = 2300-1920 = 380 m

Hence, Mohan covers more distance by 380 m.

Perimeter of an Equilateral Triangle

Perimeter of an equilateral △ABC

= AB + BC + CA = 3AB [∴ AB = BC = CA]

Hence, the perimeter of an equilateral triangle

= 3 x Length of a side of the triangle.

Example 12. If one side of an equilateral triangle is 8 cm, then find its perimeter.

Solution. Perimeter of an equilateral triangle = 3 x Length of a side

[∴in equilateral triangle, all sides are equal, so length of each side will be 8 cm]

= 3 x 8 = 24 cm

Hence, the perimeter of rectangle is 24 cm.

Class 6 Maths Chapter 10 Solutions

Example 13. How many equilateral triangles of side 4 cm long can be formed with a strip of wire of length 84 cm?

Solution. Given, side of the equilateral triangle = 4 cm

∴ Perimeter of the equilateral triangle

= 3 x Length of a side of the triangle

= 3 x 4 = 12cm

Now, number of equilateral triangles, formed

Hence, the required number of equilateral triangles is 7.

Chapter 10 Mensuration Area of Closed Figures

The amount of surface enclosed by a closed figure is called its area.

To calculate the area of a figure using a square paper, the following conventions are adopted.

(1) Ignore portions of the area that are less than half a square.

(2) If more than half of a square is in a region, just count it as one square.

(3) If exactly half the square is counted, take its area as \(\frac{1}{2}\) sq unit.

Note it The area of one full square is taken as 1 sq unit. If it is a centimetre square sheet, then area of one full square will be 1 cm².

Example 1. Find the area of the figure shown below. (consider area of each square = 1 cm²)

Solution. Area of a square = 1 cm²

Area of figure = Number of (x) squares + Number of (✔) squares + \(\frac{1}{2}\) Number of (0) squares

= \(65+8+\frac{1}{2} \times 12\)

= 65 + 8 + 6 = 79 cm²

[since, x and squares are covered fully by the figure and 0 square are covered half]

Hence, the area of square is 79 cm².

Class 6 Maths Chapter 10 Solutions

Example 2. Draw any circle on a graph sheet. Count the squares and use them to estimate the area of the circular region.

Solution. First, make a circle of any suitable radius, on the graph paper. Then, count full, half and more than half or less than half squares coming under the circle.

In the figure, fully filled squares = 32

Half filled squares = 0

More than half filled squares = 20

∴ Total area = \(32 \times 1+0 \times \frac{1}{2}+20 \times 1\)

= 32 + 0 + 20 = 52 sq units

Example 3. By counting squares, estimate the area of the given figure.

Solution. Let area of one square = 1 cm²

In the figure,

Fully filled squares = 21

Half filled squares = 0

More than half filled squares = 20

∴ Total area = 21 \times 1+0 \times \frac{1}{2}+20 \times 1

= 21 + 0 + 20 = 41 cm²

Chapter 10 Mensuration Area of a Rectangle and Square

Area of a Rectangle

Let length of the rectangle bel and breadth be b.

∴ Area of a rectangle (A) = Length x Breath = l x b

Using this formula, l = \(\frac{A}{b}\)

or b = \(\frac{A}{l}\)

Note it The length and breadth of a rectangle must be in the same units.

Class 6 Maths Chapter 10 Solutions

Example 1. Find the area of a rectangle whose length and breadth are 12 cm and 4 cm, respectively.

Solution. Given, length of the rectangle (1) = 12 cm

and breadth of the rectangle (b) = 4 cm

∴ Area of rectangle = 1 x b = 12 x 4 = 48 cm²

Hence, the area of rectangle is 48 cm².

Example 2. The area of a rectangular piece of cardboard is 48 cm² and its breadth is 6 cm. What is the length of the cardboard?

Solution. Given, area = 48 cm² and breadth (b) = 6 cm

We know that Area = Length x Breadth

∴ \(\text { Length }=\frac{\text { Area }}{\text { Breadth }}=\frac{48}{6}=8 \mathrm{~cm}\)

Hence, the length of cardboard is 8 cm.

Example 3. Find the area in square metre of a piece of land 6 m 75 cm wide and 8 m long.

Solution. Length of the piece of land = 8 m

Breadth of the piece of land = 6 m 75 cm

= 6 + 0.75 = 6.75 m [∴ 1 m = 100 cm]

∴ Area of the piece of land = Length x Breadth

= 8 x 6.75 = 54 m²

Example 4. What is the cost of painting a wall of 500 cm long and 300 cm wide at the rate of 13 per hundred sq m?

Solution. Given, length of a wall = 500 cm

and breadth of a wall = 300 cm

∴ Area of the wall = Length x Breadth

= 500 x 300 = 150000 cm²

∴ Cost of painting per 100 m² = ₹ 13

∴ Cost of 1 m2 = \(₹ \frac{13}{100}\)

Now, cost of 150000 m² = \(150000 \times \frac{13}{100}=₹ 19500\)

Hence, the required cost is ₹ 19500.

Mensuration Class 6 Solutions

Example 5. Meena wants to cover the floor of a rectangular hall 9 m wide and 7 m long by square tiles. If each square tile is of side 1.5 m, then find the number of tiles required to cover the floor of the room.

Solution. Given, length of the rectangular hall = 7m

and breadth of the rectangular hall = 9 m

Area of the floor of the rectangular hall = Length x Breadth = 7 x 9 = 63 m²

Area of one square tile = Side x Side = 1.5 x 1.5 = 2.25 m²

Now, the number of required tiles \(=\frac{\text { Area of the floor }}{\text { Area of one tile }}\)

= \(\frac{63}{2.25}\) = 28 tiles

Hence, 28 tiles are required to cover the floor of the room.

Area of a Square

A four-sided polygon whose all sides are equal in length is called square.

Area of a square = Side x Side = Side²

Example 6. Find the area of a square whose side is 6 cm.

Solution. Given, side = 6 cm

∴ Area of a square Side x Side = 6 x 6 = 36cm²

Hence, the area of square is 36 cm².

Example 7. The perimeter of a square field is 60 m. Find its area.

Solution. Given, perimeter of a square field = 60 m

We know that perimeter of a square = 4 x Side

∴ Side of a square \(=\frac{\text { Perimeter }}{4}=\frac{60}{4}=15 \mathrm{~m}\)

Now, area of the square field = Side x Side

= 15 x 15 = 225 m²

Hence, the required area is 225 m².

Mensuration Class 6 Solutions

Example 8. What will happen to the area of a square, if its sides are doubled?

Solution. Let the side of a square = a cm

∴ Area of the square = a x a = a² cm² …(1)

Now, when the sides of the square doubled.

Then, the side of the square = 2a cm

∴ Area of the square = 2a x 2a = 4a² cm² …(2)

On comparing Eqs. (1) and (2), we can see, if the sides of a square are doubled, then its area becomes 4 times.

Question 1. Measure and write the length of the four sides of the top of your study table.

AB = ___cm

BC = ___cm

CD =___cm

DA = ___cm

Now, the sum of the lengths of the four sides

= AB + BC + CD + DA

= ___cm + ___cm + ___cm + ___cm = ___cm

What is the perimeter?

Solution. Let ABCD be the top of study table.

Here, AB and CD are equal and DA and BC are equal.

On measuring, we get

AB = CD = 60 cm

and DA = BC = 30 cm

Now, the sum of the lengths of the four sides

= AB + BC + CD + DA

= 60 + 30 + 60 + 30

= 60 + 30 + 60 + 30 = 180 cm

∴ Perimeter of the table

= Sum of the lengths of the four sides

= 180 cm

Hence, the perimeter of the study table is 180 cm.

Mensuration Class 6 Solutions

Question 2. Measure and write the lengths of the four sides of a page of your notebook. The sum of the lengths of the four sides.

= AB + BC + CD + DA

= ___cm + ___cm + ___cm + ___cm = ___cm

What is the perimeter of the page?

Solution. Let ABCD be the page of a notebook.

On measuring, AB = CD = 15 cm and BC = DA = 20 cm

Then, the sum of the lengths of four sides

= AB + BC + CD + DA

= 15 + 20 + 15 + 20

= 15 + 20 + 15 + 20 = 70 cm

Hence, the sum of four sides is 70 cm.

Now, perimeter of the page = Sum of the lengths of four sides = 70 cm

Question 3. Meera went to a park 150 m long and 80 m wide. She took one complete round on its boundary. What is the distance covered by her?

Solution. Let ABCD be a park whose lengths are BC,AD and widths are AB, CD respectively.

Here, AB = CD = 80 m

and BC = DA = 150 m

Now, sum of the lengths of four sides

= AB + BC + CD + DA

= 80 + 150 + 80 + 150 = 460 m

∴ Perimeter of the park

= Sum of the lengths of four sides of the park

= 460 m

Hence, the distance covered by Meera is 460 m.

Mensuration Class 6 Solutions

Question 4. Find the perimeter of the following figures.

Perimeter AB + BC + CD + DA

Solution. (1) From the given figure, we have

AB= 40 cm, BC = 10 cm,

CD = 40 cm and DA = 10 cm

Now, the sum of the lengths of the four sides

= AB + BC + CD + DA

= 40 + 10 + 40 + 10 = 100 cm

∴ Perimeter of the given figure

= Sum of the lengths of four sides

= 100 cm

Hence, the perimeter of the given figure is 100 cm.

(2) From the given figure, we have

AB = BC = CD = DA = 5 cm

i.e. each side of the given figure is 5 cm.

Now, the sum of the lengths of the four sides

= AB + BC + CD + DA

= 5 + 5 + 5 + 5 = 20 cm

∴ Perimeter of the given figure

= Sum of the lengths of four sides

= 20 cm

Hence, the perimeter of the given figure is 20 cm.

Mensuration Class 6 Solutions

Question 5. Find various objects from your surrounding which have regular shapes and find their perimeters.

Solution. Let’s take a blackboard which has a regular square shape with side 40 cm each.

Then, the perimeter of square

= 4 x Length side of a square

= 4 × 40

= 160 cm

Let’s take another example of dog’s house which has a pentagon shape with each side 15 m.

Then, the perimeter of dog’s house

= Perimeter of regular pentagon

= 5 x Length of side of pentagon

= 5 x 15 = 75 m

Chapter 10 Mensuration Exercise 10.1

Question 1. Find the perimeter of each of the following figures.

Solution. (1) Let the given figure be ABCD.

Here, AB = 5 cm, BC = 1 cm, CD = 2 cm and DA = 4 cm

Diagram

∴ Perimeter of the given figure

= Sum of the lengths of all sides

= AB + BC + CD + DA

= 5 + 1 + 2 + 4 = 12 cm

Hence, the perimeter of the given figure is 12 cm.

Question 2. A table-top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?

TIPS Firstly, change all the units in same unit and then find perimeter using 2 (length + breadth).

Solution. Given, length of table-top = 2 m 25 cm

= \(2 \mathrm{~m}+25 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(2 m+\frac{25}{100} m\)

= (2 + 0.25) m = 2.25 m

Breadth of table-top = 1 m 50 cm = 1 m + 50 cm

= \(1 m+50 \times \frac{1}{100} m\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(1 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=(1+0.50) \mathrm{m}=1.50 \mathrm{~m}\)

∴ Perimeter of table top = 2x (length + breadth)

= 2 x (2.25 + 1.50)

= 2 x 3.75 = 7.50 m

Hence, the perimeter of the table-top is 7.50 m.

MP Board Class 6 Chapter 10 Maths

Question 3. What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm, respectively?

Solution. Given, length of the wooden strip=32 cm

and breadth of the wooden strip = 21 cm

Now, wooden strip required

= Perimeter of the photograph

=2 x (Length + Breadth)

= 2 x (32 + 21) = 2 x 53 = 106 cm

Hence, the required length of wooden strip is 106 cm.

Question 4. Find the perimeter of each of the following shapes.

(1) A triangle of sides 3 cm, 4 cm and 5 cm.

Solution. (1) Here, AB = 3 cm, BC = 4 cm and CA = 5 cm

∴ Perimeter of a triangle

= Sum of the lengths of all sides

= AB + BC + CA

= 3 + 4 + 5 = 12 cm

Hence, the perimeter of a triangle is 12 cm.

Question 5. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.

Solution. Given, first side of triangle = 10 cm

Second side of triangle = 14 cm

and third side of triangle = 15 cm

∴ Perimeter of a triangle

= Sum of all sides of triangle

= 10 + 14 + 15 = 39 cm

Hence, the perimeter of a triangle is 39 cm.

Question 6. Find the side of the square whose perimeter is 20 m.

Solution. Given, the perimeter of a square = 20 m

∴ Perimeter of a square = 4 x Length of a side

We know that a square has 4 sides of equal length.

So, we can divide given perimeter by 4, to get the side of a square.

∴ One side of the square \(=\frac{\text { Perimeter of a square }}{4}\)

Hence, the side of a square is 5 m.

MP Board Class 6 Chapter 10 Maths

Question 7. A piece of string is 30 cm long. What will be the length of each side, if the string is used to form

(1) a square?

(2) an equilateral triangle?

(3) a regular hexagon?

Solution. (1) Here, length of string will be the perimeter of square.

∴ Perimeter of square = 30 cm

We know that a square has 4 equal sides.

∴ Perimeter of a square = 4 x Length of a side

Now, length of one side \(=\frac{\text { Perimeter of a square }}{4}\)

= \(\frac{30}{4}\) = 7.5 cm

Hence, the length of each side of a square is 7.5 cm.

(2) Here, length of string will be the perimeter of an equilateral triangle.

∴ Perimeter of equilateral triangle = 30 cm

We know that an equilateral triangle has 3 equal sides.

∴ Perimeter of an equilateral triangle = 3 x Length of a side

∴ Length of a side \(=\frac{\text { Perimeter of an equilateral triangle }}{3}\)

= \(\frac{30}{3}\) = 10 cm

Hence, the length of each side of an equilateral triangle is 10 cm.

(3) Here, length of string will be the perimeter of regular hexagon.

∴ Perimeter of regular hexagon = 30 cm

We know that a regular hexagon has 6 equal sides

Perimeter of a regular hexagon = 6 x Length of a side

∴ Length of a side \(=\frac{\text { Perimeter of a regular hexagon }}{6}\)

= \(\frac{30}{6}\) = 5 cm

Hence, the length of each side of a regular hexagon is 5 cm

Question 8. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle Is 36 cm. What is its third side?

Solution. Let △ABC be the given triangle and its sides AB = 12 cm and BC = 14 cm.

Also, perimeter of triangle = 36 cm We know that,

Perimeter of a triangle = Sum of all its sides

⇒ AB + BC + CA = 36 cm

⇒ 12 + 14 + CA = 36 cm

⇒ 26 + CA = 36 cm

∴ CA = 36 – 26 = 10 cm

Hence, the third side of the triangle is 10 cm.

MP Board Class 6 Chapter 10 Maths

Question 9. Find the cost of fencing a square park of side 250 m at the rate of ₹ 20 per metre.

Solution. Given, side of square park = 250 m

Then, the perimeter of square park

= 4 x Length of side of park

= 4 x 250 = 1000 m

Cost of fencing = ₹ 20 per metre

∴ Cost of fencing = 1000 x 20

= ₹ 20000

Hence, the cost of fencing a square park is ₹ 20000.

Question 10. What is the perimeter of each of the following figures? What do you infer from the answers?

Solution. (1) Given, the figure is a square whose each side is 25 cm.

∴ Perimeter of square = 4 x Length of a side

= 4 × 25 = 100 cm

(2) Given, the figure is a rectangle whose length = 40 cm and breadth = 10 cm

∴ Perimeter of rectangle = 2 x (length + breadth)

= 2 x (40 + 10)

= 2 x 50 = 100 cm

(3) Given, the figure is a rectangle whose length = 30 cm and breadth 20 cm

∴ Perimeter of rectangle = 2 x (length + breadth)

= 2 x (30 + 20) = 2 x 50 = 100 cm

(4) Given, the figure is an isosceles triangle whose sides are 30 cm, 30 cm and 40 cm, respectively.

∴ Perimeter of triangle = Sum of all sides of a triangle

= 30 + 30 + 40 = 100 cm

Here, we observe that the perimeter of each figure is 100 cm i.e. they have equal perimeters.

MP Board Class 6 Chapter 10 Maths

Question 11. Avneet buys 9 square paving slabs, each with a side ofm. He lays them in the form of a square.

(1) What is the perimeter of his arrangement in the figure(i)?

(2) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement in the figure (ii)?

(3) Which has greater perimeter?

(4) Avneet wonders, if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.)

Solution. (1) Avneet lays 9 squares in the form of a square as shown in the figure, then side of the square

∴ Perimeter of Avneet’s arrangement

= 4 x Length of a side = 4 x \(\frac{3}{2}\) m = 6 m

Hence, the perimeter of Avneet’s arrangement is 6 m.

(2) Shari lays 9 squares in the form of a cross as shown in figure, then

Perimeter of Shari’s arrangement = Sum of all sides

= AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA

= \(\left[\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)+\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)\right.\)

= \(\frac{1}{2}+1+1+\frac{1}{2}+1+1+\frac{1}{2}+1+1+\frac{1}{2}+1+1\)

= \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+8=1+1+8=10 \mathrm{~m}\)

Hence, the perimeter of Shari’s arrangement is 10 m.

(3) From above, it is clear that Shari’s arrangement i.e. a cross has greater perimeter.

(4) Yes, there is a way shown along side in which we get a greater perimeter.

Here, we have arrange the 9 squares in the form of a rectangle

Now, length of rectangle

= \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{9}{2} m\)

and breadth of rectangle = 1/2 m

∴ Perimeter of this rectangle

= 2 x (length + breadth)

= \(2 \times\left(\frac{9}{2}+\frac{1}{2}\right)=2 \times\left(\frac{9+1}{2}\right)\)

= \(2 \times \frac{10}{2}=10 \mathrm{~m}\)

It is clear that it has the perimeter equal to cross. So, we can say that cross has greater perimeter in comparison to square.

Question 12. Draw any circle on a graph sheet. Count the squares and use them to estimate the area of the circular region.

Solution. First, make a circle of any suitable radius, on the graph paper. Then, count full, half and more than half or less than half squares coming under the circle.

In the figure,

Fully filled squares = 16

Half filled squares = 8

More than half filled squares = 8

∴ Total area = \(16 \times 1+8 \times \frac{1}{2}+8 \times 1\)

= 16 + 4 + 8 = 28 sq units

Chapter 10 Mensuration Exercise 10.2

Question 1. Find the areas of the following figures by counting square

Solution. (1) Given, figure is covered by 9 full squares.

∴ Area = 9 x 1 = 9 sq units

(2) Given, figure is covered by 5 full squares.

∴ Area = 5 x 1 = 5 sq units

(3) Given, figure is covered by 2 full squares and 4 half squares.

∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)

(4) Given, figure is covered by 8 full squares.

∴ Area = 8 x 1 = 8 sq units

(5) Given, figure is covered by 10 full squares.

∴ Area = 10 x 1 = 10 sq units

(6) Given, figure is covered by 2 full squares and 4 half squares.

∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)

(7) Given, figure is covered by 4 full squares and 4 half squares.

∴ Area = \(4 \times 1+4 \times \frac{1}{2}=4+2=6 \text { sq units }\)

(8) Given, figure is covered by 5 full squares.

∴ Area = 5 x 1 = 5 sq units

(9) Given, figure is covered by 9 full squares.

∴ Area = 9 x 1 = 9 sq units

(10) Given, figure is covered by 2 full squares and 4 half squares.

∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)

(11) Given, figure is covered by 4 full squares and 2 half squares.

∴ Area = \(4 \times 1+2 \times \frac{1}{2}=4+1=5 \text { sq units }\)

(12) Given, figure is covered by 3 full squares, O half squares, 7 more than half squares and 1 less than half square.

∴ Area = 3 x 1 + 7 x 1 + 1 x 0

= 3 + 7 + 0 = 10 sq units

(13) Given, figure is covered by 7 full squares, 4 half squares, 5 more than half squares and 8 less than half squares.

∴ Area = \(7 \times 1+4 \times \frac{1}{2}+5 \times 1+8 \times 0\)

= 7 + 2 + 5 + 0 = 14 sq units

(14) Given, figure is covered by 9 full squares, 2 half squares, 8 more than half squares and 4 less than half squares.

∴ Area = \(9 \times 1+2 \times \frac{1}{2}+8 \times 1+4 \times 0\)

= 9 + 1 + 8 + 0 = 18 sq units

Chapter 10 Mensuration Exercise 10.3

Question 1. Find the areas of the rectangles whose sides are

(1) 3 cm and 4 cm

(2) 12 m and 21 m

Solution. (1) Here, length of the rectangle = 4 cm

and breadth of the rectangle = 3cm

∴ Area of rectangle = Length x Breadth = 4 x 3 = 12 cm²

Hence, the area of the rectangle is 12 cm².

(2) Here, length of the rectangle = 21 m

and breadth of the rectangle = 12 m

∴ Area of the rectangle = Length x Breadth

= 21 x 12 = 252 m²

Hence, the area of the rectangle is 252 m².

MP Board Class 6 Chapter 10 Maths

Question 2. The length and breadth of three rectangles are as given below.

(1) 9 m and 6 m

(2) 17 m and 3 m

(3) 4 m and 14 m

Which one has the largest area and which one has the smallest?

Solution. (1) Here, length of the rectangle = 9 m

and breadth of the rectangle = 6 m

∴ Area of the rectangle = Length x Breadth = 54 m²

Hence, the area of the rectangle is 54 m².

(2) Here, length of the rectangle = 17 m

and breadth of the rectangle = 3 m

∴ Area of the rectangle = Length x Breadth

= 17 x 3 = 51 m²

Hence, the area of the rectangle is 51 m².

(3) Here, length of the rectangle = 14 m

and breadth of the rectangle = 4 m

∴ Area of the rectangle = Length x Breadth

= 14 x 4 = 56 m²

Hence, the area of the rectangle is 56 m².

Now, we have 56 > 54 > 51

Hence, the rectangle having sides 4 m and 14 m has the largest area and the rectangle having sides 17 m and 3 m has the smallest area.

Question 3. The area of a rectangular garden 50 m long is 300 m². Find the width of the garden.

Solution. Given, area of the rectangular garden = 300 m²

and length of the rectangular garden = 50 m

We know that

Area of the rectangular garden = Length x Breadth

⇒ 300 m² = 50 x Breadth

∴ Breadth = \(\frac{300}{50}\) = 6 m

Hence, the breadth or width of the garden is 6 m.

Question 4. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of 8 per hundred sq m?

Solution. Given, length of a rectangular plot = 500 m

and breadth of a rectangular plot = 200 m

∴ Area of the rectangular plot = Length x Breadth

= 500 x 200 = 100000 m²

∴ Cost of tiling per husband square metres = ₹ 8

∴ Cost of 1 m² = \(₹ \frac{8}{100}\)

Now, cost of 100000 m² = \(100000 \times \frac{8}{100}=₹ 8000\)

Hence, the cost of tiling rectangular plot is ₹ 8000.

Calculating Perimeter for Class 6

Question 5. A table-top measures 2 m by 1m 50 cm. What is its area in square metres?

Solution. Given, length of the table-top = 2 m

and breadth of the table-top

= 1 m 50 cm = 1 m + 50 cm

= \(1 \mathrm{~m}+50 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(1 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=1 \mathrm{~m}+0.50 \mathrm{~m}=150 \mathrm{~m}\)

∴ Area of the table-top = Length x Breadth = 2 x 1.50 = 3

Hence, the area of the table-top is 3 m².

Question 6. A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?

Solution. Given, length of the room = 4 m

and breadth of the room = 3m 50 cm = 3 m + 50 cm

= \(3 \mathrm{~m}+50 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(3 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=3 \mathrm{~m}+0.50 \mathrm{~m}=3.50 \mathrm{~m}\)

∴ Carpet needed to cover the floor of room

= Area of the floor

= Length x Breadth = 4 m x 3.50 m = 14 m²

Hence, the carpet needed to cover the floor of the room is 14 m².

Question 7. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.

Solution. Given, length of the floor = 5 m

and breadth of the floor = 4 m

Then, area of the floor

= Length x Breadth

= 5 x 4 = 20 m²

Side of the square carpet = 3 m

∴ Area of the carpet = Side x Side = 3 x 3 = 9m²

Now, area of the floor that is not carpeted

= Area of the floor-Area of the carpet

= 20 – 9 = 11 m²

Hence, 11 m² area of the floor is not carpeted.

Calculating Perimeter for Class 6

Question 8. Five square flower beds each of sides 1 m are dug on a plece of land 5 m long and 4 m wide. What Is the area of the remaining part of the land?

Solution. Given, length of the piece of the land = 5 m

and breadth of the piece of the land = 4 m

Area of the piece of the land = Length x Breadth

= 5 x 4 = 20 m²

Given, side of one square flower bed = 1 m

∴ Area of one square flower bed = Side x Side

= 1 x 1 = 1m²

Then, area of 5 such flower beds

= 5 x Area of one square flower bed

= 5 x 1 = 5m²

Now, area of the remaining part of the land

= Area of the piece of the land – Area of 5 square flower beds

= 20 – 5 = 15 m²

Hence, the area of the remaining part of the land is 15 m².

Question 9. By splitting the following figures into rectangles, find their areas (the measures are given in centimetres).

Solution. (1) Let the given figure be divided into rectangles A, B, C and Dand their length and breadth be written on the figure.

For Rectangle A,.

Length = 4 cm and breadth = 2 cm

Now, area of the Rectangle A = Length x Breadth

= 4 x 2 = 8 cm²

For Rectangle B,

Length = 3 cm and breadth = 3 cm

Area of the Rectangle B = Length x Breadth

= 3 x 3 = 9cm²

For Rectangle C,

Length = 2 cm and breadth = 1 cm

Area of the Rectangle C = Length x Breadth

= 2 x 1 = 2cm²

For Rectangle D, length = 3 cm and breadth = 3 cm

∴ Area of the Rectangle D = Length x Breadth

= 3 x 3 = 9cm²

Now, total area of the given figure

= Area of the Rectangle A + Area of the Rectangle B + Area of the Rectangle C + Area of the Rectangle D

= 8 + 9 + 2 + 9 = 28 cm²

Hence, the required area is 28 cm²

(2) Let the given figure is divided into rectangles A, B and C and their length and breadth are written on the figure.

For Rectangle A,

Length = 2 cm and breadth = 1 cm

∴ Area of the Rectangle A = Length x Breadth

= 2 x 1 = 2 cm²

For Rectangle B,

Length = 5 cm and breadth = 1 cm

∴ Area of the Rectangle B = Length x Breadth = 5 x 1 = 5cm²

For Rectangle C,

Length = 2 cm and breadth = 1 cm

∴ Area of the Rectangle C = Length x Breadth

= 2 x 1 = 2cm²

Now, total area of the given figure

= Area of the Rectangle A + Area of the Rectangle B + Area of the Rectangle C

= 2 + 5 + 2 = 9 cm²

Hence, the area of the given figure is 9 cm².

Question 10. On a centimetre squared paper, make as many rectangles as you can, such that the area of the rectangle is 16 cm² (consider only natural number lengths).

(1) Which rectangle has the greatest perimeter?

(2) Which rectangle has the least perimeter?

If you take a rectangle of area 24 cm², what will be your answers? Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter? With the least perimeter? Give example and reason.

Solution. We know that

∴ Area of the rectangle = Length x Breadth

Here, the area of the rectangle is 16 cm².

So, for getting the area 16 cm², there are three cases.

Case 1 When length of the rectangle = 16 cm

and breadth of the rectangle = 1 cm

∴ Area of the rectangle = Length x Breadth

= 16 x 1 = 16cm²

and perimeter of the rectangle

= 2 x (Length + Breadth)

= 2 x (16 + 1) = 2 x 17 = 34 cm

Case 2 When length of the rectangle = 4 cm

and breadth of the rectangle = 4 cm

∴ Area of the rectangle = Length x Breadth

= 4 x 4 = 16cm²

and perimeter of the rectangle

= 2 x (Length + Breadth)

= 2 x (4 + 4) = 2 x 8 = 16 cm

Case 3 When length of the rectangle = 8 cm

and breadth of the rectangle = 2 cm

∴ Area of the rectangle = Length x Breadth

= 8 x 2 = 16 cm²

and perimeter of the rectangle

= 2x (length + breadth)

= 2 x (8 + 2)= 2 x 10 = 20 cm

(1) The rectangle which is made in Case I has the greatest perimeter.

(2) The rectangle which is made in Case II has the least perimeter.

Now, given that the area of the rectangle is 24 cm².

Again, for getting the area 24 cm2, there are four cases

Case 1 When length of the rectangle = 24 cm

and breadth of the rectangle = 1 cm

∴ Area of the rectangle = Length x Breadth

= 24 x 1 = 24 cm²

and perimeter of the rectangle

= 2 x (length + breadth)

= 2 x (24 + 1) = 2 x 25 = 50 cm

Case 2 When length of the rectangle = 12 cm

and breadth of the rectangle = 2 cm

∴ Area of the rectangle

= Length x Breadth = 12 x 2 = 24cm²

and perimeter of the rectangle

= 2 x (length + breadth)

= 2 x (12 + 2) = 2 × 14 = 28 cm

Case 3 When length of the rectangle = 6 cm

and breadth of the rectangle = 4 cm

∴ Area of the rectangle

= Length x Breadth = 6 x 4 = 24 cm²

and perimeter of the rectangle

= 2 x (length + breadth)

= 2 x (6 + 4) = 2 x 10 = 20 cm

Case 4 When length of the rectangle = 8 cm

and breadth of the rectangle = 3 cm

∴ Area of the rectangle

= Length x Breadth = 8 x 3 = 24 cm²

and perimeter of the rectangle

= 2 x (length + breadth)

= 2 x (8 + 3) = 2 x 11 = 22 cm

(1) The rectangle which is made in Case I has the greatest perimeter.

(2) The rectangle which is made in Case III has the least perimeter.

Yes, it is possible to predict the shape of the rectangle with greatest perimeter and with least perimeter.

e.g. A rectangle having area 16 cm² and greatest perimeter 34 cm is of the shape 16 cm x 1 cm

(i.e. length = 16 cm and breadth = 1 cm), also a rectangle having area 24 cm² and least perimeter 20 cm is of the shape 6 cm x 4 cm

(i.e. length = 6 cm and breadth = 4 cm).

The rectangle with the greatest length has the maximum perimeter and the rectangle with the smallest length has the least perimeter.

Chapter 10 Mensuration Multiple Choice Questions

Question 1. Following figures are formed by joining six unit squares. Which figure has the smallest perimeter?

1. 2
2. 3
3. 4
4. 1

Answer. 4. 1

Question 2. A square shaped park ABCD of side 100 m has two equal rectangular flower beds each of size 10 m x 5 m. Length of the boundary of the remaining park is

1. 360 m
2. 400 m
3. 340 m
4. 460 m

Answer. 3. 340 m

Question 3. The perimeter of a rectangle whose sides are 1 m 30 cm and 70 cm, is

1. 20 m
2. 4 m
3. 0.2 m
4. 2 m 30 cm

Answer. 2. 4 m

Calculating Perimeter for Class 6

Question 4. Cost of fencing a rectangular park of length 200 m and width 150 m at the rate of ₹ 25 per metre is

1. ₹ 17500
2. ₹ 1750
3. ₹ 1705
4. ₹ 10750

Answer. 1. ₹ 17500

Question 5. Length and breadth of a rectangular sheet of paper are 20 cm and 10 cm, respectively. A rectangular piece is cut from the sheet as shown in figure. Which of the following statements are correct for the remaining sheet?

1. Perimeter remains same but area changes
2. Area remains same but perimeter changes
3. Both area and perimeter are changing
4. Both area and perimeter remain the same

Answer. (c) Both area and perimeter are changing

Question 6. The top of a table is 1 m 20 cm wide and 1 m 50 cm long. The perimeter of this top is

1. 5.30 m
2. 5.40 m
3. 5.50 m
4. 5.60 m

Answer. 2. 5.40 m

Question 7. The ratio of the sides of rectangle is 5:4 and its perimeter is 72 cm. Then, the length of the rectangle is

1. 40 cm
2. 20 cm
3. 30 cm
4. 60 cm

Answer. 2. 20 cm

Question 8. The cost of fencing a rectangular field 24 m long and 18 m wide at ₹ 2.25 per meter is

1. ₹ 243
2. ₹ 234
3. ₹ 189
4. ₹ 198

Answer. 3. ₹ 189

Question 9. The side of a square is 10 cm. How many times will the new perimeter become, if the side of the square is doubled?

1. 2 times
2. 4 times
3. 6 times
4. 8 times

Answer. 2. 4 times

Question 10. The perimeter of a square whose each side is 1 m 30 cm 10 mm, is

1. 5.4 m
2. 5.14 m
3. 5.24 m
4. 5.04 m

Answer. 3. 5.24 m

Examples of Perimeter Problems

Question 11. The side of a square is 6 cm. If its side is doubled, then its new perimeter is

1. 48 cm
2. 36 cm
3. 60 cm
4. 24 cm

Answer. 1. 48 cm

Question 12. The perimeter of a triangle whose sides are 1.2 cm, 3.4 cm and 1.7 cm, is

1. 6.3 cm
2. 6.2 cm
3. 6.5 cm
4. 6.4 cm

Answer. 1. 6.3 cm

Question 13. The perimeter of an equilateral triangle of side 5 cm each is

1. \(\frac{\sqrt{3}}{4} \times 15 \mathrm{~cm}\)
2. \(\frac{\sqrt{3}}{4} \times 10 \mathrm{~cm}\)
3. 10 cm
4. 15 cm

Answer. 4. 15 cm

Question 14. The area of rectangle is 630 sq cm and breadth is 15 cm. What is its lenght.

1. 40 cm
2. 60 cm
3. 42 cm
4. 35 cm

Answer. 3. 42 cm

Question 15. Samuel wanted to dig some vertical poles along the boundary of his plot at a distance of 10 m each. If the length of the plot is 30 m and the breadth is 15 m. How many poles are required?

1. 450
2. 45
3. 9
4. 10

Answer. 3. 9

Chapter 10 Mensuration Assertion Reason

Question 1. Assertion (A) Manoj went to a park 20 m long and 10 m wide. He took one complete round of it. The distance covered by him is 60 m.

Reason (R) The amount of surface enclosed by a closed figure is called its area.

(a) Both A and R are true and R is the correct explanation of A

(b) Both A and R are true but R is not the correct explanation of A

(c) A is true but R is false

(d) A is false but R is true

Answer. (b) Both A and R are true but R is not the correct explanation of A

Question 2. Assertion (A) The perimeter of a square of side 1 m is 2 m.

Reason (R) Perimeter is the distance covered along the boundary forming a closed figure when you go around the figure once.

(a) Both A and R are true and R is the correct explanation of A

(b) Both A and R are true but R is not the correct explanation of A

(c) A is true but R is false

(d) A is false but R is true

Answer. (d) A is false but R is true

Examples of Perimeter Problems

Question 3. Assertion (A) The length of wire required to fence the pentagon-shaped park of side 24 cm is 120 cm.

Reason (R) Perimeter of a regular polygon with n sides = n x length of each side

(a) Both A and R are true and R is the correct explanation of A

(b) Both A and R are true but R is not the correct explanation of A

(c) A is true but R is false

(d) A is false but R is true

Answer. (a) Both A and R are true and R is the correct explanation of A

Question 4. Assertion (A) A page is 25 cm long and 20 cm wide. The area of this page is 90 cm.

Reason (R) The amount of surface enclosed by a closed figure is called its area.

(a) Both A and R are true and R is the correct explanation of A

(b) Both A and R are true but R is not the correct explanation of A

(c) A is true but R is false

(d) A is false but R is true

Answer. (d) A is false but R is true

Chapter 10 Mensuration Fill in the Blanks

Question 1. Perimeter of the shaded portion in figure is

AB + … + … + … + … + … + … + HA.

Answer. BM + MD + DE + EN + NG + GH

Question 2. Diagonal of a square is side x …..

Answer. √2

Question 3. Standard unit of area is …..

Answer. Square metre (i.e. m²)

Question 4. The amount of region enclosed by a plane closed figure is called its …..

Answer. Area

Question 5. The area of a play ground is 1190 m2. If its length is 35 m, the width is …..

Answer. 34 m

Chapter 10 Mensuration True/False

Question 1. 1 hectare = 100 x 100 m2.

Answer. True

Question 2. Perimeter of rectangle is (l + b).

Answer. False

Question 3. A farmer who wants to fence his field, must find the perimeter of the field.

Answer. True

Question 4. If length of a rectangle is halved and breadth is doubled, then the area of the rectangle obtained remains same.

Answer. True

Question 5. Area of a square is doubled, if the side of the square is doubled.

Answer. False

Chapter 10 Mensuration Match the Columns

Question 1. Mathc the Column I with Column II.

Solution. (a) → (3), (b) → (4), (c) → (2), (d) → (1)

Chapter 10 Mensuration Case Based Questions

Question 1. The figure below shows the football field for a school tournament.

(1) What is the perimeter (in m) of WURQ?

(a) 60 m

(b) 240 m

(c) 960 m

(d) 3344 m

(2) The area enclosed by QRUW is equal to the area enclosed by WUST:

Is the statement true? Give reason.

(3) What is the area (in m²) of the penalty area?

(a) 488 m²

(b) 272 m²

(c) 480 m²

(d) 720 m²

(4) Is the perimeter of the penalty area of the football field double the perimeter of the goal area? Give.

(5) Does the school football field meet the FIFA standards? Give reason.

(6) Find the perimeter of the shape WURMNOPQW.

(a) 280 m

(b) 320 m

(c) 240 m

(d) 420 m

Solution. (1) (b) Given, length of the football field = 88 m

breadth of the football field = 76 m

∴ \(W Q=\frac{1}{2} \times T Q=\frac{1}{2} \times 88=44 \mathrm{~m}\)

Now, perimeter of WURQ = 2x (length + breadth)

= 2 x (44 + 76)

= 2 × 120 = 240 m

Hence, perimeter of WURQ is 240 m.

(2) We have, TW = WQ = 44 m

and QR = WU = 76 m

Now, area enclosed by QRUW = Length x Breadth

= WQ x QR = 44 m x 76 m = 3344 m² ….(1)

Now, area enclosed by WUST = Length x Breadth

= TW x WU = 44 ….(2)

∴ From (1) and (2);

Area enclosed by QRUW = Area enclosed by WUST = 3344 m²

Hence, area enclosed by QRUW is equal to the area enclosed by WUST.

(3) (c) Given, length of the football field = 88 m

and breadth of the football field = 76 m

∴ Side of the small square in the field = \(\frac{88}{22}=4 \mathrm{~m}\)

∴ Area of small square in the field = 4 x 4 = 16 m²

Now, there are 30 small squares lie in the region of penalty area.

∴ Area of the penalty area = 30 x Area of small square

= 30 x 16 m² = 480 m²

Hence, the area of penalty area is 480 m².

(4) We have, side of small square = 4 m

∴ HG = 20 m, GF = 36 m, FE = 20 m, ED = 8 m, DC = 12 m, CB = 20 m, BA = 12 m and AH = 8 m

∴ Perimeter of penalty area

= HG + GF + FE + ED + DC + CB + BA + AH

= 20 + 36 + 20 + 8 + 12 + 20 + 12 + 8

= 136 m …(1)

Now, AB = 12 m, BC = 20 m, CD = 12 m and DA = 20 m

∴ Perimeter of goal area = AB + BC + CD + DA = 12 + 20 + 12 + 20 = 64 m

Hence, perimeter of the penalty area of the football field is not double the perimeter of the goal area.

(5) Yes, the school football field meet the FIFA standards because the areas of WUST and WURQ are the same which is 3344 m.

(a) because the length and the width of TQRS are 88 m and 76 m respectively, which lie with in the standard range which 120 m to 90 m for length and 90 m to 45 m for width.

(b) because the perimeter of TQRS is 328 m which lies with in the standard range which is 420 m to 270 m.

(c) because the area of TQRS is 6688 sq m which lies with in the standard range which 10800 sq m to 4050 sq m.

(6) (a) We have, side of small square=4 m

So, WU = 76 m, UR = 44 m, RM = 20 m, MN = 20 m, No = 36 m, OP = 20 m, PQ = 20 m and QW = 44 m

Now, perimeter of the shape WURMNOPQW

= WU + UR + RM + MN + NO + OP + PQ + QW

= 76 + 44 + 20 + 20 + 36 + 20 + 20 + 44 = 280 m

Hence, perimeter of the shape WURMNOPQW is 280 m

Examples of Perimeter Problems

Question 2. International Federation of Association Football (FIFA) is responsible for the organization and promotion of association football’s major international tournaments.

FIFA issues guidelines for the dimensions of football fields. The figure below shows the maximum and minimum lenghts and widths of a football field.

(1) What is the maximum area (in m²) of the football field?

(a) 30 m²

(b) 420 m²

(c) 1080 m²

(d) 10800 m²

(2) What can be the minimum perimeter (in m) of the football field?

(a) 90 m

(b) 135 m

(c) 270 m

(d) 4050 m

Solution. (1) (d) Given, maximum length of the football field

and maximum width of the football field = 90 m

∴ Maximum area of the football field

= Length x Breadth

= 120 m x 90 m = 10800 m²

Hence, the maximum area of the football field is 10800 m².

(2) (c) Given, minimum length of the football field = 90 m

and minimum width of the football field = 45 m

∴ Minimum perimeter of the football field

= 2x (length x breadth)

= 2 x (90 + 45) = 2 x 135 = 270 m

Hence, minimum perimeter of the football field is 270 m

Examples of Perimeter Problems

Question 3. The figure below shows a square wooden frame enclosing a square picture.

(1) What is the area (in cm²) of the frame?

(a) 81 cm²

(b) 144 cm²

(c) 181 cm²

(d) 225 cm²

(2) What is the perimeter (in cm) of the picture?

(a) 12 cm

(b) 48 cm

(c) 60 cm

(d) 144 cm

Solution. (1) (d) Given, side of square frame = 15 cm

Now, area of square frame = Side x Side

= 15 x 15 = 225 cm²

Hence, area of the frame is 225 cm².

(2) (b) Given, side of the square picture = 12 cm

Now, perimeter of square picture = 4 x Side

= 4 x 12 = 48 cm

Hence, perimeter of the picture is 48 cm.

Chapter 10 Mensuration Very Short Answer Type Questions

Question 1. Length of a rectangle is three times its breadth. Perimeter of the rectangle is 40 cm. Find its length and width.

Solution. Let width of rectangle (b) = x cm

Then, length of rectangle (1) = 3x cm

∴ Perimeter = 2 (1 + b)

⇒ 40 = 2(3x + x) = 8x = 40

⇒ 8x = 40

⇒ \(x=\frac{40}{8}=5 \mathrm{~cm}\)

Hence, the length is 15 cm and width is 5 cm.

Question 2. The perimeter of a regular pentagon is 1240 cm. How long is its each side?

Solution. Given, perimeter = 1240 cm

Perimeter of a regular pentagon = 5 x Length of each side

Length of each side = \(\frac{1240}{5}\) = 248 cm

Hence, its each side is 248 cm.

MP Board Class 6 Maths Solutions

Question 3. Find the side of an equilateral triangle, if its perimeter is 30 cm.

Solution. Given that perimeter of an equilateral triangle = 30 cm

∴ Perimeter of an equilateral triangle

= 3 x Side of a triangle

⇒ 30 = 3 x Side of a triangle

⇒ Side = \(\frac{30}{3}\) = 10 cm

Hence, the side of an equilateral triangle is 10 cm.

Question 4. Find the perimeter of a triangle, whose three sides are 5 cm, 6 cm and 7 cm, respectively.

Solution. Perimeter of a triangle = Sum of its all sides

= a + b + c

= (5 + 6 + 7) cm = 18 cm

Question 5. Find the perimeter of an equilateral triangle, whose each side is 5 cm.

Solution. Perimeter of an equilateral triangle = 3 × Side of length

= 3 x 5 cm = 15 cm [given]

Question 6. Perimeter of an isosceles triangle is 50 cm. If one of the two equal sides is 18 cm, find the third side.

Solution. Perimeter = 50 cm

Perimeter of an isosceles triangle = Sum of its all sides

⇒ Perimeter = a + b + c

⇒ 50 = 18 + 18 + Third side

⇒ 50 – 36 = Third side

⇒ Third side = 14 cm

MP Board Class 6 Maths Solutions

Question 7. Find the area of a rectangle whose length and width are 10 cm and 6 cm, respectively.

Solution. Given that length (1) = 10 cm

and width (b) = 6 cm

Area of a rectangle = 1 x b = 10 x 6 = 60 cm²

Question 8. If the area of a square is 36 cm², then find its perimeter.

Solution. Given, area of a square = 36 cm²

Area = Side x Side

⇒ 36 = Side x Side

⇒ Side x Side = 6 x 6

⇒ Side = 6 cm

∴ Perimeter of a square = 4 × Side = 4 × 6 = 24 cm

Chapter 10 Mensuration Short Answer Type Questions

Question 1. The length of a rectangular field is twice its breadth. Jamal jogged around it four times and covered a distance of 6 km. What is the length of the field?

Solution. Let breadth of rectangular field = x m

Then, length of rectangular field = 2x m

Distance covered in one round = Perimeter

Distance covered in four rounds = 4 x Perimeter

⇒ 4 × 2 (1 + b) = 6 x 1000 [ perimeter = 2 (1 + b)]

⇒ 8(l + b) = 6000

8(2x + x) = 6000

∴ Length of the field = 500 m

Question 2. A room is 9.5 m long and 7.4 m wide. A person wants that the floor of the room to be fitted with tiles of size 20 cm by 10 cm. Find the number of tiles needed.

Solution. Area of room 7.4 x 9.5 m² = 7.4 x 9.5 x 10000 cm²

Area of one tile = 20 x 10 = 200 cm²

Number of tiles \(=\frac{\text { Area of room }}{\text { Area of a tile }}=\frac{74 \times 95 \times 100}{200}\)

= \(\frac{74 \times 95}{2}=95 \times 37=3515\)

Question 3. Two plots of land having the same perimeter. One is a square with side 70 cm while other is rectangle of length 100 cm. Which plot has the greater area and by how much?

Solution. Area of square Side x Side = 70 x 70 sq cm

= 4900 cm2

Given, length of rectangle = 100 cm

Perimeter of rectangle = Perimeter of square

⇒ 2 (100 + b) = 4 × 70

⇒ 100 + b = 140 ⇒ b = 40 cm

Now, area of rectangle = 1 x b = 40 x 100 = 4000 cm²

Hence, the area of square is more than the area of rectangle by 900 cm².

MP Board Class 6 Maths Solutions

Question 4. Three squares are joined together as shown in figure. Their sides are 4 cm, 10 cm and 3 cm. Find the perimeter of the figure.

Solution. Given, sides of three squares are 4 cm, 10 cm and 3 cm, respectively.

Total perimeter of given squares

= Sum of all outer sides of the figure

= 4 + 4 + 4 + 6 + 10 + 7 + 3 + 3 + 3 + 10 = 54 cm

Question 5. Tahir measured the distance around a squared field as 200 rods (lathi). Later he found that the length of this rod was 140 cm. Find the side of this field in metres.

Solution. Distance around a square field = 200 rods

Length of this rod = 140 cm

Total distance around a squared field = 200 x 140 = 28000 cm

So, perimeter of this squared field = 28000 cm = 280 m

Sides of this field = \(\frac{280}{4}\) = 70 m

Question 6. The perimeter of rectangle and square are equal. If length of the rectangle is 8 m and breadth is 6 m. Find the area of square.

Solution. Given, length of rectangle (1) = 8 m

and breadth of rectangle (b) = 6 m

Perimeter of rectangle = Perimeter of square

2 (1 + b) = 4x Side of a square

⇒ 2(8 + 6) = 4 × Side of a square

Side of a square = \frac{2(8+6)}{4}=7 \mathrm{~m}

∴ Area of square = 7 x 7 = 49 m²

Question 7. The floor of a room is square in shape. If the side of the floor is 5 m. Find the area of the floor.

Solution. Given, side of the floor = 5 m

Area of the floor = Side x Side = 5 x 5 = 25m²

Hence, the area of the floor is 25 m².

MP Board Class 6 Maths Solutions

Question 8. From the following figure, find its

(1) Perimeter

(2) Area of square

Given, ABC is an equilateral triangle of side 3 cm each and BCED is a square.

Solution. (1) Perimeter = AB + AC + BC + BD + DE + CE

= 3 + 3 + 3 + 3 + 3 + 3 = 18 cm

(2) Area of square BCED = Side2 = 32 = 9 cm²

Chapter 10 Mensuration Long Answer Type Questions

Question 1. Length of a rectangular field is 250 m and width is 150 m. Anuradha runs around this field 3 times. How far did she run? How many times she should run around the field to cover a distance of 4 km?

Solution. Given, length of rectangular field (1) is 250 m and width is 150 m.

Perimeter of this field = 2(1 + b) = 2(250 + 150) m

= 2 x 400 m = 800 m

Distance covered in one round = Perimeter = 800 m

Distance covered in three rounds = 3 x 800 = 2400 m

Now, number of rounds to cover 4 km i.e. 4000 m.

= \(\frac{4000}{800}\) [∴ 1 km = 1000 m]

Hence, she should run 5 times around the field to cover the distance of 4 km.

Question 2. The lawn in front of Molly’s house is 12 m x 8 m, where as the lawn in front of Dolly’s house is 15 m x 5 m. A bamboo fencing is built around both the lawns. How much fencing is required for both?

Solution. Given, size of lawn in front of Molly’s house = 12 × 8

Perimeter = 2 (12 + 8) = 40 …(1)

Now, size of lawn in front of Dolly’s house = 15 x 5

Perimeter = 2(15 + 5) = 40 …(2)

From Eqs. (1) and (2), we get

40 + 40 = 80 m

Hence, the total length of bamboo fencing is 80 m.

Question 3. A room 9.68 m long and 6.2 m wide. Its floor is to be covered with glazed tiles of 22 cm by 10 cm each. If rate of tiles is ₹ 25 per tile. Find the total cost of tiles.

Solution. Given, length of floor of the room (l) = 9.68 m

and width of floor of the room (b) = 6.2 m

Area of the room = 9.68 x 6.2 m² …(1)

Also, given that length of each tile = 22 cm

and width of each tile = 10 cm

Now, area of each tile = 22 x 10 cm²   …(2)

Number of tiles required to cover the floor of the room

= \(\frac{9.68 \times 6.2 \times 100 \times 100}{22 \times 10}\) [∴ 1m = 100 cm]

= \(\frac{968 \times 62 \times 10}{22 \times 10}=\frac{968 \times 62}{22}=2728\)

∴ Total cost = ₹ 2728 x 25 = ₹ 68200

MP Board Class 6 Maths Solutions

Question 4. There is a rectangular lawn 10 m long and 4 m wide in front of Meena’s house. It is fenced along the two smaller sides and one longer side leaving a gap of 1 m for the entrance. Find the length of fencing.

Solution. Given, width of the lawn, AB = EF = 4 m and length of the lawn, BE = 10 m

Also, given length of gap, CD = 1 m

Total length of fencing = AB + (BC + DE) + EF

= AB + (BE-CD) + EF

= 4 + (10-1) + 4)

= 4 + 9 + 4 = 17 m

Hence, the length of fencing of the lawn is 17 m.

Question 5. Four regular hexagons are drawn, so as to form the design as shown in figure. If the perimeter of the design is 28 cm. Then, find the length of each side of the hexagon.

Solution. Given, four regular hexagons, as shown in the figure:

Perimeter of the design = 28 cm

∴ Perimeter of the given design = Sum of all outer sides of the four hexagon.

Here, this figure has 14 outer equal sides.

∴ Perimeter of the design = 14 x Length of one side of hexagon

⇒ 28 = 14 x Length of one side of hexagon

Length of one side of hexagon = \(\frac{28}{14}\) = 2 cm

Hence, the length of each side of the hexagon is 2 cm.

Question 6. In the given figure, all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid-points fo the sides. What is the perimeter of the figure?

Solution. Given, △ABC is an equilateral triangle.

Here, AB = 8 units

∴ AB = BC = CA = 8 units

Now, △ADE is an equilateral triangle.

Here, E is the mid-point of AB.

∴ \(A E=B E=\frac{A B}{2}=\frac{8}{2}=4 \text { units }\)

Now, in △ADE, AD = DE = EA = 4 units

Similarly, equilateral triangles are △BOT and △UPC, having each sides equal

i.e. BO = OT = BT = UC = PC = PU = 4 units

It is also clear that OC = PA = 4 units

Also, △DIF is an equilateral triangle.

Here, F is the mid-point of DE.

∴ \(D F=F E=\frac{D E}{2}=\frac{4}{2}=2 \text { units }\)

In ADIF, DI = IF = DF = 2 units

Similarly, in △TKN and △RQU,

TK = KN = TN = RQ = UQ = UR = 2 units

It is also clear that NO = RP = 2 units

Also, △HIG is an equilateral triangle.

Here, G is the mid-point of IF.

∴ \(I G=G F=\frac{I F}{2}=\frac{2}{2}=1 \text { unit }\)

Now, in △HIG, HG = HI = GI = 1 unit

Similarly, in △MLK and △XQS,

ML = MK = LK = SQ = XS = QX = 1 unit

It is also clear that LN = XR = 1 unit

Now, perimeter of the given figure

= Sum of all outer sides of the given figure

= AD + DI + IH + HG + GF + FE + EB + BT + TK + KM + LM + LN + NO + OC + CU + UQ + QS + XS + XR + PR + PA

= [4 + 2 + 1 + 1 + 1 + 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4]

= 45 units

Hence, the perimeter of the given figure is 45 units.

MP Board Class 6 Maths Solutions

Question 7. If length of a rectangle is halved and breadth is doubled, then the area of the rectangle obtained remains same. Is it true?

Solution. True, let the length and breadth of a rectangle bel and b respectively.

We know that

Area of the initial rectangle = Length x Breadth

= 1 x b sq units

If length of a rectangle is halved and breadth is doubled.

i.e. New length = \(\frac{1}{2}\) units

and new breadth = 2b units

Then, the area of new rectangle

= New length x New breadth = \(\frac{1}{2}\) x 2b

= lb sq units

Question 8. In the given figure, each square is of unit length.

(1) What is the perimeter of the rectangle ABCD?

(2) What is the area of the rectangle ABCD?

(3) Divide this rectangle into ten parts of equal area by shading squares. (Two parts of equal area are shown here)

(4) Find the perimeter of each part which you have divided. Are they all equal?

Solution. Given, each side of square is of unit length. Figure contains length of 10 squares and width of 6 squares. Now, the length of rectangle, AD = BC

= Sum of length of a side of 10 squares

= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

= 10 x 1 = 10 units

and breadth of rectangle, AB = DC = Width of 6 squares = 6 x 1 = 6 units

(1) The perimeter of the rectangle ABCD

= AB + BC + CD + DA

= 6 + 10 + 6 + 10

= 32 units

(2) The area of the rectangle ABCD = Length x Breadth

= AD X AB

= 10 × 6

= 60 sq units

(3) The total area of rectangle = 60 units

Now, we have to divide the rectangle into 10 equal parts i.e. \(\frac{60}{10}\) = 6 squares units

i.e. we have to take a group of 6-6 square blocks, which is shown in the figure.

(4) Now, we find the perimeter of Part 1.

We know that perimeter of a figure is the total length of its boundary.

∴ Perimeter of Part 1

= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

= 12 units

Similarly, we can find the perimeters of remaining 9 parts, all the parts have same perimeter i.e. 12 units.

Yes, all the parts have same perimeter.

Chapter 9 Data Handling Data

A collection of numbers (values) gathered to give some information is called data.

Recording Data

Recording data is information in numbers collected for a specific purpose. The collection of data is also called recording of data. In order to record the data, we need to make a table and record it.

e.g. If you collects the marks obtained by 6 students in a batch to analyse their performance in unit test. We find that Raghav scored 11 out of 20, Maria scored 18 out of 20, Punit scored 15 out of 20, Zoya scored 8 out of 20, Salman scored 2 out of 20 and Manoj scored 12 out of 20.

From this data, we conclude that highest marks obtained by Maria and lowest marks obtained by Salman.

Organisation of Data

The data that is collected for the first time is called raw data or upgrouped data. When the data is arranged in any data it becomes grouped data. When the data is very large, it is difficult to arrange them in a grouped form. In this case, small bars are used to represent data; such method is called tally method.

Read and Learn More MP Board Class 6 Maths Solutions

To get the required information, all observations should be recorded. We depict each observation with the help of tally marks.

Tally marks are used to organise the observations. Record every observation by a vertical mark, but every fifth observation should be recorded by a mark across the four earlier marks. The fifth observation tally mark looks like this

Example 1. In a class test, the following marks were obtained in the unit test of algebra by 35 students. Arrange these marks in a table using tally marks.

(1) Find how many students obtained marks equal to or less than 5.

(2) How many students obtained marks above 6?

Solution. The table with tally marks is shown below

(1) Here, we have to find out the students, who obtained marks equal to or less than 5. So, we have to add the number of students who obtained marks equal to 5 or less than 5 i.e. marks 3, 4 and 5.

∴ Number of students = 4 + 9 + 8 = 21

Hence, 21 students obtained marks equal to or less than 5.

(2) Here, we have to find out the students who obtained marks above 6.

So, we have to add the number of students who obtained marks above 6 i.e. marks 7 and 8.

∴ Number of students = 4 + 3 = 7

Hence, 7 students obtained marks above 6.

MP Board Class 6 Maths Solutions

Example 2. In a shop, different size of shoes sold in a week as shown below 7, 9, 10, 8, 7, 9, 7, 9, 6, 3, 5, 5, 7, 10, 7, 8, 7, 9, 6, 7, 6, 7, 10, 5, 4, 3, 5, 7, 8, 7, 9, 7.

Arrange the above data in ascending order and construct a table using tally marks.

Also, answer the following questions.

(1) Which shoes size had the maximum sale?

(2) Which shoes size had the minimum sale?

(3) Find the number of shoes sold of size 7 or greater than 7.

Solution. Ascending order of the given data is 3, 3, 4, 5, 5, 5, 5, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10

The table with tally marks is given below

(1) Here, the shoes size had the maximum sale = 7

(2) Here, the shoes size had the minimum sale = 4 (iii) Here, we have to find out the number of shoes sold of size 7 or greater than 7.

So, we have to add number of shoes sold of size 7 or greater than 7 i.e., size 7, 8, 9 and 10.

∴ Required number of shoes = 11 + 3 + 5 + 3 = 22

Hence, 22 shoes sold of size of 7 or greater than 7.

Chapter 9 Data Handling Pictograph

Pictograph is the way of representing data using pictures of objects. Each picture (image) stands for a certain number of objects. It helps us to answer the questions on the data at a glance.

Interpretation of a Pictograph

Interpretation of a pictograph means finding some conclusions from it. In interpretation of a pictograph, the first step is to know what it represents or what information is given by it.

It is also important to know the number of units represented by one picture symbol.

Example 3. Following pictograph represents some surnames of people listed in the telephone directory of a city.

Observe the pictograph and answer the following questions:

(1) How many people have surname Roy?

(2) Which surname appears the maximum number of times in the telephone directory ?

(3) Which surname appears the least number of times in the telephone directory ?

(4) Which two surnames appear an equal number of times?

Solution. (1) The number of people having surname Roy are 400. Because in the given pictograph, the picture symbol represents 100 people.

(2) Surname Patel appears maximum number of times. Because in the given pictograph, the picture symbol represents 100 people. According to this, surname Patel appears 500 times.

(3) The surname Saikia appears the least number of times. Because in the given pictograph, the picture symbol represents 100 people. According to this, surname Saikia appears 200 times.

(4) The surname Rao and Roy appears an equal number of times.

Example 4. The colours of car preferred by people living in a society are shown by the following pictograph.

Look at this and answer the following questions.

(1) Find the number of people preferring white colour.

(2) How many people liked green colour?

(3) Find the sum of number of people who prefers black and red colour.

Solution. (1) White colour is preferred by 300 people.

(2) For 5 complete picture, we get 5 x 100 = 500 people and for 1 incomplete picture, we may roughly take it as 50 people.

Hence, the number of people prefers green colour is nearly 550.

(3) We have to find the sum of number of people who prefers black and red colour. So, we have to add the number of peoples who preferred black and red colour.

Now, the number of people who prefers black colour = 4 × 100 = 400

and the number of people who prefers red colour = 2 × 100 = 200

∴ Sum of number of people prefers black and red colour = 400 + 200 = 600

Hence, 600 people prefers the black and red colour.

MP Board Class 6 Maths Solutions

Example 5. A survey was carried out in a certain school to find out different modes of transport used by students to travel to school each day, 30 students of Class VI were interviewed and the data obtained was displayed in the form of pictographs given below.

Look at this and answer the following questions.

(1) Which is the most popular mode of travel?

(2) Find the number of students who used walking as mode of travel.

(3) Which mode of travel is least used by the student?

Solution. (1) Maximum number of students use the school bus. Therefore, this is the most popular mode of travel.

(2) The number of students who use walking as mode of travel is 8.

(3) Cycle is used only by three students. Therefore, this mode of travel is least used by the students.

Chapter 9 Data Handling Exercise 9.1

Question 1. In a Mathematics test, the following marks were obtained by 40 students. Arrange these marks in a table using tally marks.

(1) How many students obtained marks equal to or more than 7?

(2) How many students obtained marks below 4?

Solution. The table with tally marks is shown below

(1) Here, we have to find out the students, who obtained marks equal to 7 or more than 7.

So, we have to add the number of students who obtained marks equal to 7 or more than 7 i.e. marks 7, 8 and 9.

∴ Number of required students = 5 + 4 + 3 = 12

Hence, 12 students obtained marks equal to 7 or more than 7.

(2) Here, we have to find out the students who obtained marks below 4.

So, we have to add the number of students who obtained marks below 4 i.e., 1, 2 and 3.

∴ Number of required students = 3 + 3 + 2 = 8

Hence, 8 students obtained marks below 4.

MP Board Class 6 Maths Solutions

Question 2. Following is the choice of sweets for 30 students of Class VI.

Ladoo, Barfi, Ladoo, Jalebi, Ladoo, Rasgulla, Jalebi, Ladoo, Barfi, Rasgulla, Ladoo, Jalebi, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo, Rasgulla, Ladoo, Ladoo, Barfi, Rasgulla, Rasgulla, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi and Ladoo.

(1) Arrange the names of sweets in a table using tally marks.

(2) Which sweet is preferred by most of the students?

Solution. (1) The table with tally marks is shown below

(2) By examine the above table, we see that Ladoo is preferred by most of the students. i.e. 11 students.

Question 3. Catherine threw a dice 40 times and noted the number appearing each time as shown below

Make a table and enter the data using tally marks. Find the number that appeared

(1) the minimum number of times.

(2) the maximum number of times.

(3) Find those numbers that appear an equal number of times.

Solution. The table with tally marks is shown below.

(1) From the above table, number 4 appeared 4 times while throwing a dice.

Thus, number 4 appeared the minimum number of times i.e. 4 times.

(2) While throwing a dice, number 5 appeared 11 times which is highest.

Thus, the maximum number of times the number 5 appeared.

(3) Number 1 and number 6 both appeared 6 times while throwing a dice.

Hence, number 1 and number 6 appeared an equal number of times.

Question 4. Following pictograph shows the number of tractors in five villages.

Observe the pictograph and answer the following questions.

(1) Which village has the minimum number of tractors?

(2) Which village has the maximum number of tractors?

(3) How many more tractors village C has as compared to village B?

(4) What is the total number of tractors in all the five villages?

Solution. (1) Observing the pictograph, it is clear that village D has the minimum number of tractors i.e. only 3 tractors.

(2) Observing the pictograph, it is clear that village Chas the maximum number of tractors i.e. 8 tractors.

(3) Observing the pictograph, it is clear that village C has 8 tractors and village B has 5 tractors.

So, village C has 8 – 5 = 3 more tractors as compared to village B.

(4) Total number of tractors in all the five villages

= Sum of all tractors in villages A, B, C, D and E

= 6 + 5 + 8 + 3 + 6 = 28

Hence, there are 28 tractors in all the five villages.

MP Board Class 6 Maths Solutions

Question 5. The number of girl students in each class of a co-educational middle school is depicted by the pictograph.

Observe this pictograph and answer the following questions.

(1) Which class has the minimum number of girl students?

(2) Is the number of girls in Class VI less than the number of girls in Class V?

(3) How many girls are there in Class VII?

Solution. In the given pictograph, 1 picture = 4 girls, half picture = 2 girls

(1) Observing the pictograph, it is clear that the minimum number of girl students are in Class VIII i.e. 4 + 2 = 6

(2) Observing the pictograph, it is clear that

Number of girls in Class VI = 4 x 4 = 16

and number of girls in Class V = 2 x 4 + 1 × 2 = 8 + 2 = 10

∴ 10 < 16

So, it is clear that number of girls in Class VI is not less than the number of girls in Class V.

(3) Observing the pictograph, number of girls in Class VII = 3 x 4 = 12

Class 6 Maths Chapter 9 Solutions

Question 6. The sale of electric bulbs on different days of a week is shown below

Observe the pictograph and answer the following questions.

(1) How many bulbs were sold on Friday?

(2) on which day, were the maximum number of bulbs sold?

(3) on which of the days, same number of bulbs were sold?

(4) On which of the days, minimum number of bulbs were sold?

(5) If one big carton can hold 9 bulbs. How many cartons were needed in the given week?

Solution. In the given pictograph, 1 picture = 2 bulbs

Now, number of bulbs sold on Monday = 6 pictures = 6 x 2 = 12 bulbs

Number of bulbs sold on Tuesday = 8 x 2 = 16 bulbs

Number of bulbs sold on Wednesday = 4 x 2 = 8 bulbs

Number of bulbs sold on Thursday = 5 x 2 = 10 bulbs

Number of bulbs sold on Friday = 7 x 2 = 14 bulbs

Number of bulbs sold on Saturday = 4 x 2 = 8 bulbs

Number of bulbs sold on Sunday = 9 x 2 = 18 bulbs

(1) Number of bulbs sold on Friday = 7 x 2 = 14 bulbs

(2) Maximum number of bulbs were sold on Sunday i.e. 18 bulbs.

(3) The same number of bulbs were sold on Wednesday and Saturday i.e. 8 bulbs.

(4) The minimum number of bulbs were sold on Wednesday and Saturday i.e. 8 bulbs.

(5) Total number of bulbs sold in a week

= 12 + 16 + 8 + 10 + 14 + 8 + 18 = 86

Now, number of cartons which can hold 9 bulbs = 1

∴ Number of cartons which can hold 1 bulb = \(\frac{1}{9}\)

= \(\frac{1 \times 86}{9}\)

= \(\frac{86}{9} = 9 \frac{5}{9} = 10\)

[as number of cartons should be an integer]

Hence, 10 cartons were needed in the given week.

Chapter 9 Data Handling Multiple Choice Questions

Question 1. The marks (out of 10) obtained by 28 students in a Mathematics test are listed as given below.

8, 1, 2, 6, 5, 5, 5, 0, 1, 9, 7, 8, 0, 5, 8, 3, 0, 8, 10, 10, 3, 4, 8, 7, 8, 9, 2, 0

The number of students who obtained marks more than or equal to 5 is

1. 13
2. 15
3. 16
4. 17

Answer. 4. 17

Question 2. In question 1 (above), the number of students who scored marks less than 4 is

1. 15
2. 13
3. 12
4. 10

Answer. 4 10

Class 6 Maths Chapter 9 Solutions

Question 3. The choices of the fruits of 42 students in a class are as follows.

A, O, B, M, A, G, B, G, A, G, B, M, A, G, M, A, B, G, M, B, A, O, M, O, G, B, O, M, G, A, A, B, M, O, M, G, B, A, M, O, M, Observe

Where A, B, G, M and O stand for the fruits Apple, Banana, Grapes, Mango and Orange, respectively. Which two fruits are liked by an equal number of students?

1. A and M
2. M and B
3. B and O
4. B and G

Answer. 4. B and G

Question 4. According to data of question 4, which fruit is liked by most of the students?

1. O
2. G
3. M
4. A
5. Answer. 3. M

Question 5. Following table shows the number of bikes manufactured in a factory during the year 1998 to 2002.

In which year were the maximum number of bikes manufactured?

1. 2002
2. 2001
3. 2000
4. 1999

Answer. 1. 2002

Question 6. Using the data of question (8). Find the difference between number of bikes manufactured in the years 1999 and 2000.

1. 300
2. 305
3. 310
4. 410

Answer. 3. 310

Question 7. A pictograph represents data in the form of

1. vertical bar
2. horizontal bar
3. pictures
4. None of these

Answer. 3. pictures

Class 6 Maths Chapter 9 Solutions

Chapter 9 Data Handling Assertion-Reason

Question 1. Assertion (A) The students get a marks in Maths test out of 20 are 10, 15, 19, 17, 05, 8, 12.

So, the maximum marks in the test obtained by the students is 19.

Reason (R) The tally marks represents 10.

(a) Both A and R are True And R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (b) Both A and R are true but R is not the correct explanation of A.

Question 2. Assertion (A) The sale of balls on different days of a week is shown below.

The balls sold on Thursday are 15.

Reason (R) A pictograph represents data through symbols or pictures.

(a) Both A and R are True And R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Chapter 9 Data Handling Fill in the Blanks

Question 1. A ….. is a collection of numbers gathered to give some meaningful information.

Answer. data

Question 2. The data can be arranged in a tabular form using …. marks.

Answer. tally

Question 3. The tally marks represents |||| represents …… .

Answer. 4

Question 4. Representation of data in form of pictures is called ….. .

Answer. pictograph

Question 5. In a pictograph, if a symbol * represents 20 flowers in a basket, then *** stands for ….. flowers.

Answer. 60

Class 6 Maths Chapter 9 Solutions

Chapter 9 Data Handling True/False

Question 1. An observation occurring five times in a data is recorded as |||||, using tally marks.

Answer. False

Question 2. Tally marks |||| represents 4.

Answer. True

Question 3. Pictograph is pictorial representations of the numerical data.

Answer. True

Question 4. In a pictograph, if a symbol represents 50 books in a library shelf, then the symbol represents 25 books.

Answer. True

Question 5. In a pictograph, if a symbol represents 100 books in a library shelf, then the symbol represents 50 books.

Answer. False

Chapter 9 Data Handling Match The Columns

Question 1. Match the items of Column 1 with their respective value in Column 2.

Answer. (a) → (4), (b) → (3), (c) → (2), (d) → (1).

Chapter 9 Data Handling Case Based Questions

Question 1. Shobit works for a shoe store. He records the shoe sizes and the number of pairs sold every day. On Tuesday, he sold 60 pairs. His record for the day is shown below.

(1) How many pairs of size 8 were sold on Tuesday?

(a) 3

(b) 10

(c) 11

(d) 13

(2) Which shoe size sold the most?

(a) 6

(b) 7

(c) 8

(d) 9

Class 6 Maths Chapter 9 Solutions

(3) Shobit realised that he had not fully recorded the sale for Tuesday. How many sold pairs had he not recorded?

(4) The unrecorded data was of shoe size 7. Shobit corrected his record accordingly. Which of the following statements will be true now?

(a) Shoe size 8 sold the least now

(b) Shoe size 7 sold the most now

(c) Shoe size 5 is the new mode of the data

(d) Number of shoe pairs of size 3 can be calculated

(5) The price of one shoe pair of size 5 is ₹ 800. How much money had Shobit collected by selling all the shoe pairs of size 5?

Solution. (1) (d) On Tuesday, Shobit sold 13 pairs of shoes.

(2) (a) Shoe size 6 sold the most.

(3) Shobit recorded the sale of 55 pairs for Tuesday, but he sold 60 pairs. Thus, he had not recorded 5 pairs of shoes.

(4) (b) The correct statements after Shobit corrected his record is that shoe size 7 sold the most now i.e., 16 pairs.

(5) Shobit sold 7 pairs of shoes of size 5 on Tuesday. And the price of one shoe pair of size 5 is 800.

Thus, the money collected by selling all the shoe pairs of size 5 = 7 x 800 = ₹ 5600

Question 2. The marks obtained by 10 students in Science test are given below.

53, 36, 95, 3, 62, 42, 25, 78, 75, 62

Answer the following questions that are related to the given data.

(1) The maximum marks obtained by any student is

(a) 60

(b) 95

(c) 78

(d) 25

(2) The minimum marks obtained by any student is

(a) 42

(b) 36

(c) 25

(d) 73

(3) How many students got the same marks?

(a) 3

(b) 4

(c) 2

(d) None of above

(4) How many students got 78 or more marks?

(a) 2

(b) 3

(c) 1

(d) 4

(5) How many students got marks below 62?

(a) 3

(b) 4

(c) 5

(d) 2

Solution. (1) → (b), (2) → (c), (3) → (c), (4) → (a), (5) → (b)

Chapter 9 Data Handling Very Short Answer Type Questions

Question 1. The following are the weight in kg of 20 students of a class 25, 15, 17, 15, 23, 10, 9, 15, 16, 17, 15, 16, 23, 25, 16, 15, 23, 9, 10, 16

Prepare a table using tally marks for the given data.

Also, answer the following questions.

(1) Find the number of students whose weights are equal to 17 or more than 17.

(2) How many students whose weights are below 16.

Solution.

(1) 7

(2) 8

Question 2. Following is the choice of sports for 20 students of Class 6. Cricket, Football, Cricket, Tennis, Cricket, Badminton, Football, Cricket, Football, Tennis, Cricket, Badminton, Basketball, Football, Golf, Football, Hockey, Football, Hockey, Football

(1) Arrange the names of sports in a table using tally marks.

(2) Which sports is preferred by most of the students?

Solution.

(2) 7 students preferred football which is highest. Thus, football is preferred by most of the students.

Question 3. Maria threw a dice 30 times and noted the number appearing each time as shown below.

Prepare a table using tally marks and answer the following questions.

(1) Find the number that appeared the minimum number of times.

(2) Find the number that appeared the maximum number of times.

(3) How many times the number 2 and 3 appeared?

Solution.

(1) 4

(2) 5

(3) 4 times

Class 6 Maths Chapter 9 Solutions

Question 4. The pictograph shows the number of persons using various brands of perfumes.

(1) How many persons use R brand?

(2) Which brand is used by maximum number of persons?

Solution. (1) 24 persons (2) R brand

Chapter 9 Data Handling Short Answer Type Questions

Question 1. The following pictograph shows the number of private buses in six cities.

(1) In which city the number of private buses are least?

(2) In which city the number of private buses are highest?

(3) How many more buses in Delhi as compared to Agra?

(4) Find the total number of buses in all the six cities.

Solution. (1) Noida

(2) Jaipur

(3) 20

(4) 270

Question 2. In a electrical shop, the sale of fans on different days of a week is shown by below pictograph.

By observing the given pictograph answer the following questions.

(1) Find the number of fans sold on Tuesday.

(2) On which of the days, the number of fans were sold is same?

(3) On which day, the number of fans were sold is maximum?

(4) On which day, the number of fans were sold is minimum?

(5) Find the total number of fans were sold in all the days of this week.

Solution. (1) 20

(2) Monday and Friday

(3) Saturday

(4) Wednesday

Class 6 Maths Chapter 9 Solutions

Question 3. Following is the pictograph of the number of cycles manufacture by a factory on six different working days of a week.

By observing the given pictograph and answer the following questions.

(1) On which day were the least number of cycles manufactured?

(2) On which day were the maximum number of cycles manufactured?

(3) Find the approximate number of cycles manufactured in all the six working days of the given week.

(4) On which of the days, the number of cycles manufactured is same?

Solution. (1) Wednesday

(2) Thursday

(3) 275

(4) Monday and Saturday

Question 4. The blood groups of 25 students are recorded as follows

A, B, O, A, AB, O, A, O, B, A, O, B, A, AB, AB, A, A, B, B, O, B, AB, O, A, B. Arrange the information in a table using tally marks.

Solution. The information in a table using tally marks is as follows:

Question 5. Rakesh is playing with a dice. He threw the dice 40 times and noted the outcomes as follows.

1, 2, 1, 5, 3, 5, 5, 3, 2, 2, 1, 6, 6, 6, 4, 6, 3, 5, 2, 3, 3, 5, 4, 1, 5, 5, 2, 4, 5, 5, 2, 4, 5, 5, 2, 4, 1, 6, 6, 1, 5, 6, 1, 5.

Prepare a table using tally marks.

Solution. We draw the following table using tally marks from given information.

MP Board Class 6 Chapter 9 Maths

Question 6. Thirty students were interviewed to find out what they want to be in future. Their responses are listed as below

doctor, engineer, doctor, pilot, officer, doctor, engineer, doctor, pilot, officer, pilot, engineer, officer, pilot, doctor, engineer, pilot, officer, doctor, officer, doctor, pilot, engineer, doctor, pilot, officer, doctor, pilot, doctor, engineer.

Arrange the data in a table using tally marks.

Solution. We draw the following table using tally marks for given information.

Chapter 9 Data Handling Long Answer Type Questions

Question 1. The following pictograph depicts the information about the areas in sq km (to nearest hundred) of some districts of Chattisgarh State.

(1) What is the area of Koria district?

(2) Which two districts have the same area?

(3) How many districts have area more than 5000 km?

Solution. (1) Area of Koria district = 6000 sq km

(2) Raigarh and Jashpur have the same area.

(3) Four districts have area more than 5000 sq km.

Question 2. Fill in the blanks in the following table, which represents shirt size of 40 students of a school.

Solution. (1) shows four vertical lines and one intersecting line.

∴ It counts to be four plus one (i.e. 5).

(2) We know that

8 = 5 + 3

Here, 5 is represented by and 3 is represented by |||.

∴ 8 is represented by |||.

(3) || means 5 + 2 i.e. 7.

(4) We know that

10 = 5 + 5

Here, 5 is represented by .

∴ 10 is represented by

(5) We know that 7 = 5 + 2

Here, 5 is represented by and 2 is represented by ||.

∴ 7 is represented by ||.

Thus, the complete table is shown below

MP Board Class 6 Chapter 9 Maths

Question 3. The number of scouts in a school is depicted by the following pictograph.

Observe the pictograph and answer the following questions.

(1) Which class has the minimum number of scouts?

(2) Which class has the maximum number of scouts?

(3) How many scouts are there in class 6?

(4) Which class has exactly four times the scouts as that of Class 10?

(5) What is the total number of scouts in the classes 6 to 10?

Solution. (1) Class 10 has minimum number of scouts i.e. 10.

(2) Class 8 has maximum number of scouts i.e. 60.

(3) Number of scouts in Class 6 = 40

(4) Number of scouts in Class 10 = 10

Hence, Class 6 has exactly four times the scouts as that of Class 10.

(5) Total number of scouts in classes 6 to 10

= 40 + 20 + 60 + 30 + 10 = 160

Chapter 6 Integers and Number Line

Natural Numbers Natural numbers are counting numbers i.e. 1, 2, 3,…

Whole Numbers If we include 0 (zero) with natural numbers, then they are called as whole numbers. Negative Numbers The numbers which are less than 0 are called negative numbers. To differentiate these negative numbers from whole numbers, we use a (-) minus sign attached to the number. This indicates that numbers with negative sign are less than zero.

e.g. 1 is less than zero is written as 1, 2 is less than zero is written as -2 etc.

Sign with Numbers

In our day-to-day life, we see some situations in which some numbers carry a negative sign and some carry positive sign. These situations are represented by appropriate signs i.e. ‘+’ sign and ‘-‘ sign.

e.g. Profit is represented by ‘+’ sign and loss is represented by ‘-‘ sign.

Example 1. Write the opposite of each of the following:

(1) Profit of 50.

(2) Deposit of 1000.

(3) 50 km towards South.

Solution. The opposite of each, is

(1) loss of ₹ 50.

(2) withdraw of ₹ 1000.

(3) 50 km towards North.

Read and Learn More MP Board Class 6 Maths Solutions

Example 2. Write the following numbers with appropriate signs:

(1) 200 m below sea level.

(2) 20°C below 0°C temperature.

(3) 25°C above 0°C temperature.

(4) A deposit of 50.

(5) Any four numbers less than 0.

Solution. (1) 200 m below sea level means – 200 m.

(2) 20°C below 0°C temperature means -20°C.

(3) 25°C above 0°C temperature means + 25°C.

(4) A deposit of 50 means + ₹ 50.

(5) Every negative integer is less than zero and every positive integer is greater than zero.

∴ Numbers less than zero are -1, -2, -3 and -4.

Integers

If we put the whole numbers and the negative numbers together, the new collection of numbers will look like …-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, .., and this collection of numbers is known as integers.

Here, 1, 2, 3,… are said to be positive integers and -1, -2, -3, … are said to be negative integers.

Note It Zero is an integer which is neither positive nor negative. One more than given number gives its successor and one less than that of given number gives its predecessor.

Representation of Integers on a Number Line

To represent integers on a number line, draw a line and mark the points at equal distance on it, as shown in the figure given below. Mark a point as zero on it. Points to the right of zero are positive integers marked as +1, +2, +3 etc or simply 1, 2, 3 etc. Points to the left of zero are negative integers marked as -1, -2, -3, etc.

MP Board Class 6 Maths Solutions

Example 3. Represent the following numbers on the number line

(1)-2

(2) +6

(3) – 5

(4) -1

(5) +5

Solution. Draw a line and mark some points at equal distance on it. Mark a point as zero on it. Points to the right of zero are positive integers and are marked as +1, +2, +3 or simply by 1, 2, 3 etc. Points to the left of zero are negative integers and are marked by-1, -2, -3, etc.

(1) Representation of -2 To mark-2 on the number line, we move 2 points to the left of zero as shown in figure. A

In the above figure, point A represents – 2.

(2) Representation of 6 To mark +6 on the number line, we move 6 points to the right of zero as shown in the figure.

In the above figure, point B represents + 6.

(3) Representation of -5 To mark-5 on the number line, we move 5 points to the left of zero as shown in figure.

In the above figure, point C represents-5.

(4) Representation of -1 To mark-1 on the number line, we move 1 point to the left of zero as shown in figure.

In the above figure, point E represents – 1.

(5) Representation of + 5 To mark + 5 on the number line, we move 5 points to the right of zero as shown in figure.

In the above figure, point F represents + 5.

Example 4. The given figure is a horizontal line representing integers. Observe it and locate the following points.

(1) If point D is +7, then which point is – 7

(2) Find that the point G is a negative or a positive integer.

(3) Write the integers of points F and C.

(4) Which point marked on this number line has the greatest value?

(5) Arrange all the points in increasing order of value.

Solution.

(1) From the figure, it is clear that + 7 is on point D, then for getting-7, we should move left of zero.

After moving 7 steps left of zero, we reach at the point H.

So, point H represents-7.

(2) The point G is left of zero. So, G is a negative integer.

(3) The integers for point F is -3 and for point C is 5.

(4) The point D has the greatest value i.e. 7.

(5) We know that on a number line, the number increases as we move to right. So, increasing order of value of all points is given here.

H, G, FE, O, A, B, C, D

MP Board Class 6 Maths Solutions

Example 5. Given below are the temperatures in some cities.

(1) Write the temperature of these cities in the form of integers.

(2) Which is the coolest city out of these cities?

(3) Give the names of cities, where temperature is above 5°C.

(4) Plot the temperature of cities on the number line.

Solution. (1) The temperature of Shimla is -10°C.

The temperature of Leh is -15 °C.

The temperature of Delhi is + 25 °C.

The temperature of Nagpur is + 30°C.

(2) After checking the temperature of all places, we can say that the Leh (-15°C) is the coolest place.

(3) Delhi (25°C) and Nagpur (30°C) are the cities, where temperature is above 5 °C.

(4)

Example 6. In the given following pairs which number is to the right of the other on the number line?

(1) 3,8

(2) -4, -9

(3) 0, -4

(4) -13, 8

Solution.

(1)

Here, 3 and 8 both are on the right of zero but 8 is farther from zero in comparison of 3. So, number 8 is right of number 3.

(2)

Here, -4 and -9 both are on the left of zero, but – 4 is nearer to zero in comparison of-9. So, -4 is right of

(3)

Here, 0 is right of -4.

(4) Here, -13 is left of zero and 8 is right of zero. So, 8 is right of -13.

Ordering of Integers

On the number line, the number increases as we move to the right and decreases as we move to the left.

Therefore, -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 and so on.

Note it The greater the positive integer, the lesser is its opposite.

e.g. 7 > 4 but -7 < -4.

MP Board Class 6 Maths Solutions

Example 7. Compare the following pairs of numbers using > or <.

(1) 0 – -6

(2)-1 – -12

(3) 5 – -5

(4) 11 – 17

Solution.

(1) We know that -6 is to the left of 0 (zero) on number line. So,0 > -6

(2) We know that-1 is to the right of-12 on the number line. So -1 > -12

(3) We know that 5 is to right of-5. So, 5 > -5

(4) We Know that 17 is to right of 11. So, 11 < 17

Example 8. Write five negative integers

(1) greater than 30.

(2) less than -15.

Solution.

(1) When we move on the number line to the right, then the value of integer increases.

So, from the above figure, we get the five negative integers greater than 30 are 29,-28,-27,-26 and – 25.

(2) When we move on the number line to the left, then the value of integer decreases.

So, from the above figure, we get the five negative integers less than -15 and -16,-17, -18,-19 and – 20.

Example 9. Write all the integers between

(1) 0 and -9

(2) -15 and -5

and write them in the decreasing order.

Solution. (1) Integers 0 and -9 are shown on the number line as below.

From the above number line, it is clear that integers between 0 and -9 are-1,-2,-3,-4,-5, -6, -7 and – 8.

Now, decreasing order of these integers is

-1 > -2 > -3 > -4 > -5 > -6 > -7 > -8

(2) Integers-15 and -5 are shown on the number line as below.

From the above number line, it is clear that integers between 15 and -5 are -14,-13,-12,-11,-10,-9, -8,-7,-6

Now, decreasing order of these integers is

-6 > -7 > -8 > -9 > -10 > -11 > -12 > -13 > -14

Example 10. For the following statements, write true (T) or false (F). If the statement is false, correct the statement.

(1)-6 is to the right of -12 on a number line.

(2)-70 is to the right of 30 on a number line.

(3) Smallest positive integer is 1.

(4)-24 is greater than -23.

Solution. (1) True, because on the number line going to the right, value of integer increases. Here, – 6 is greater than -12. So,-6 is to the right of-12 on the number line.

(2) False, because on the number line going to the left. value of integer decreases. Here, – 70 is less than 30. So,-70 is to the left of- 30 on the number line.

(3) True, because on the number line 1 is situated on the left of all positive integers. So, it is the smallest positive integer.

(4) False, because – 23 is on the right of – 24 on the number line. So, 23 is greater than – 24.

MP Board Class 6 Maths Solutions

Example 11. Draw a number line and answer the following:

(1) Which number will we reach, if we move 5 numbers to the left of -1?

(2) Which number will we reach, if we move 4 numbers to the right 2?

(3) If we are at 6 on the number line, in which direction should we move to reach -11?

(4) If we are at 9 on the number line, in which direction should we move to reach – 3?

Solution. (1)

On the number line, starting from -1 and moving 5 points towards left (each step being equal to 1 unit), we will reach at -6.

(2)

On the number line, starting from 2 and moving 4 points towards right (each step being equal to 1 unit), we will reach at 6.

(3) Here,-6-11. So, -11 is on the left of -6.

Hence, if we are at -6 on the number line, then move to the left from 6 to reach at -11.

(4) Here, -3>9. So, – 3 is on the right of -9.

Hence, if we are at -9 on the number line, then move to the right from-9 to reach at – 3.

Example 12. Write the following numbers (integers) in increasing and decreasing order with using sign < and >’.

(1) 0,5, 10, 6, -3, 9

(2) 8, 6, 136, 32, -80, 120, 1

(3) 9, 8, 4, -3, -2, 1, 10

(4) 99, 98, 97, 97, 4, 1, 90

Solution. (1) Given numbers are 0, -5, 10,6,-3,9.

Increasing order is -5 < -3 < 0 < 6 < 9 < 10.

Decreasing order is 10 > 9 > 6 > 0 > -3 > -5.

(2) Given numbers are 8, 6,-136, 32, -80, 120, 1.

Increasing order is -136 < -80 < 1 < 6 < 8 < 32 < 120

Decreasing order is 120 > 32 > 8 > 6 > 1 > -80 > -136.

(3) Given numbers are 9, 8, 4, 3, 2, 1, 10.

Increasing order is -3 < -2 < 1 < 4 < 8 < 9 < 10.

Decreasing order is 10 > 9 > 8 > 4 > 1 > -2 > -3

(4) Given numbers are – 99, 98, -97, 97, 4, 1, 90.

Increasing order is -99 < -97 < 1 < 4 < 90 < 97 < 98.

Decreasing order is 98 > 97 > 90 > 4 > 1 > -97 > -99.

Chapter 6 Integers Addition of Integers

To add two positive integers, we simply add them and to add two negative integers, we firstly add them and then put negative sign before the sum.
e.g. (+3) + (+2) = +5

and (-2) + (-3) = -(2+3) = -5

When we have one positive and one negative integer, then we must subtract but answer will take the sign of the integer which has greater value to it.

e.g. (-3) + (+2) = -3 + 2 = -1

Note it The sum of two positive integers is always a positive integer and the sum of two negative integers is always a negative integer.

MP Board Class 6 Maths Solutions

Example 1. Write the answer of the following

(1) (+11) + (+6)

(2) (+17) + (+37)

(3) (-23) + (-7)

(4) (-9) + (-16)

Solution. (1) (+11) + (+6) = +(11 + 6) = 17

(2) (+17) + (+37) = +(17 + 37) = 54

(3) (-23) + (-7) = -(23 + 7) = -30

(4) (-9) + (-16) = -(9 + 16) = -25

Example 2. Find the answer of the following.

(1) (-8) + (+9)

(2) (-11) + (+16)

(3) (+11) + (-17)

(4) (+23) + (-6)

Solution. (1) (-8) + (+9) = (-8) + (+8) + (+1) [∵ 8 + 1 = 9]

= 0 + (+1) [∵ (-8) + (+8) = 0]

= +1

(2) (-11) + (+16) = (-11) + (+11) + (+5) [∵ 11 + 5 = 16]

= 0 + (+5) [∵ (-11) + (+11) = 0]

= +5

(3) (+11) + (-17) = (+11) + (-11-6) [-17 = -11-6]

= (+11) + (-11) + (-6)

= 0 + (-6) [∵ (+11) + (-11) = 0]

= -6

(4) (+23) + (-6) = (+17) + (+6) + (-6) [∵ 23 = 17 + 6]

= (+17) + 0

= +17

Example 3. Find the sum of

(1) 257 and -107

(2) -18 and 18

(3) -214, 65 and 104

(4) -40, -180 and 250

Solution. (1) We have, 257 + (-107)

= (+150) + (+107) + (-107) [∵ 257 = 150 + 107]

= (+150) + 0 = 150 [∵ (+107) + (-107) = 0]

(2) We have, -18 + (+18) = 0

(3) We have, -214 + 65 + 104

= -214 + 169

= (-169) + (-45) + 169

[∵ 214 = 169 + 45 = -214 = (-169) + (-45)]

= (-169) + 169 + (-45)

= 0 + (-45) = -45 [∵ (-169) + 169 = 0]

(4) We have, (-40) + (-180) + 250

= -(40+180) + 250 = (-220) + 250 [∵ 250 = 220 + 30]

= (-220) + (+220) + (+0) [∵ (-220) + (220) = 0]

= 0 + 30 = 30

MP Board Class 6 Maths Solutions

Example 4. Find the sum of

(1) (-8) + (-11) + (6) + (17)

(2) (36) + (-4) + (-70) + (-8)

(3) (-26) + (14) + (-1) + (16)

(4) (-14) + (-16) + (7) + (18)

Solution. (1) We have, (-8) + (-11) + (6) + (17)