- Chapter 1 Knowing Our Numbers
- Chapter 2 Whole Numbers
- Chapter 3 Playing With Numbers
- Chapter 4 Basic Geometrical Ideas
- Chapter 5 Understanding Elementary Shapes

Fraction
A fraction is a number representing part of a whole. The whole may be a single object or a group of objects. It is defined as
\(\text { Fraction }=\frac{\text { Numerator }}{\text { Denominator }}=\frac{a}{b}\)Here, the denominator can never be zero.
e.g. (1) \(\frac{1}{5}\) is a fraction and it is read as one-fifth, which means that 1 part out of 5 equal parts in which the whole is divided. Also, here 1 is called, the numerator and 5 is called, the denominator.
(2) If we take a pizza and divide it equally among 4 persons, then each person will have \(\frac{1}{4}\) or written in word, one quarter of the pizza.
Read and Learn More MP Board Class 6 Maths Solutions

Example 1. What fraction of a day is 15 h?
Solution. We know that, one day = 24 h
∴ The required fraction = \(\frac{15 \mathrm{~h}}{24 \mathrm{~h}}=\frac{15}{24}\)
MP Board Class 6 Maths Solutions
Example 2. Write the fraction representing the shaded portion.
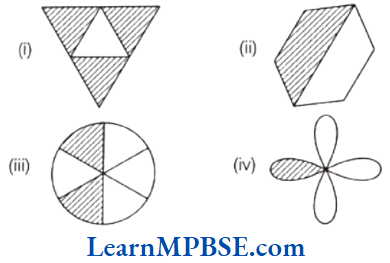
Solution. (1) Total number of equal parts = 4 and shaded parts = 3
∴ Fraction representing the shaded portion
\(=\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{3}{4}\)(2) Total number of equal parts = 2 and shaded part = 1
∴ Fraction representing the shaded portion
\(=\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{1}{2}\)(3) Total number of equal parts = 6 and shaded parts = 2
∴ Fraction representing the shaded portion
\(=\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{2}{6}\)(4) Total number of equal parts = 4 and shaded part = 1
∴ Fraction representing the shaded portion
\(=\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{1}{4}\)Example 3. Shade the part according to the given fraction.
Solution. The figures are shaded as per given fraction shown below
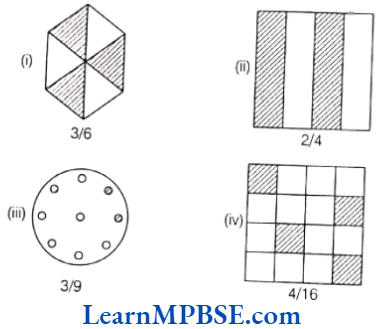
Example 4. Identify the error, if any.
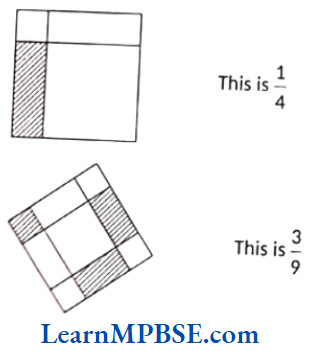
Solution. (1) In this given figure, four parts are not equal.
So, fraction is not equal to \(\frac{1}{4}\)
(2) In this given figure, all the nine parts are not equal.
Fraction is not equal to \(\frac{3}{9}\).
Example 5. What fraction of these boxes have a cross (x) In them?

Solution. Total number of boxes = 8,
Number of boxes having cross sign (x) = 3
∴ Required fraction
\(=\frac{\text { Number of boxes having cross sign ( } \mathbf{x})}{\text { Total number of boxes }}=\frac{3}{8}\)MP Board Class 6 Maths Solutions
Example 6. Write the natural numbers from 113 to 125. What fraction of them are prime numbers?
Solution. Natural numbers from 113 to 125
= 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125.
Total natural numbers = 13
Prime number from 113 to 125 = 113
Total prime numbers = 1
∴ Required fraction \(=\frac{\text { Total prime numbers }}{\text { Total natural numbers }}=\frac{1}{13}\)
Example 7. Three girls Manisha, Sakshi and Shubhangini shared lunch at school. Manisha has brought two burgers, one is veg burger and one is non-veg. The other two girls forget to bring their lunch.
Manisha agreed to share her burgers so that each person will have an equal share of each burgers.
(1) How can Manisha divided her burgers so that each person has an equal share?
(2) What part of a burger will every girl receive?
Solution. Total number of burgers = 2,
Total number of girls = 3
(1) Here, Manisha has to divide 2 burgers into three person. So, she will divided each burger into three equal parts and give one part of each burger to each of them.
Thus, each person will get \(\frac{2}{3}\) burgers.
(2) One burger is to be divided among three girls.
Total number of parts = 6
Each gets 2 parts out of 6.
Then, the fraction = \(\frac{2}{6}\)
∴ Each girl will get = part of a burger.
Fraction on the Number Line
Every fraction has a point associated with it on the number line. For this, we will need to divide the gap of 0 to 1 into as many equal parts as in the denominator of that fraction.
Suppose, we want to denote the fraction \(\frac{5}{7}\) on the number line. Now, take a line OP of unit length.
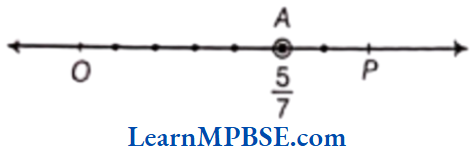
Divide line OP into seven equal parts and take 5 parts out of it to reach the point A. Then, the point A represents the number \(\frac{5}{7}\).
MP Board Class 6 Maths Solutions
Example 1. Show \(\frac{4}{5}\) on a number line.
Solution. We know that \(\frac{4}{5}\) is greater than zero but less than 1. So, it will lie between 0 and 1.
Now, we have to show \(\frac{4}{5}\) on a number line.
So, we have to divide the length between 0 and 1 into 5 equal parts and take 4 parts out of it to reach point A.
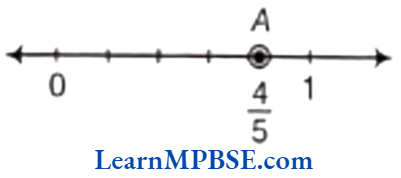
Then, the point A represents the number
Example 2. Write the fraction denoted by point A

Solution. Point A is marked at fifth place out of 10.
Therefore, fraction is \(\frac{5}{10}\).
MP Board Class 6 Maths Solutions
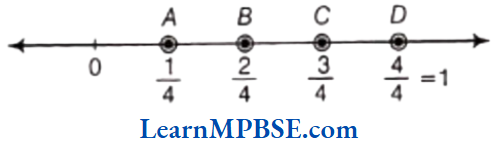
Example 3. Show \(\frac{2}{9}, \frac{5}{9}, \frac{0}{9} \text { and } \frac{9}{9}\) on a number line.
Solution. We know that, all given fractions are greater than or equal to zero but less than or equal to 1.
So, we have to divide the gap between 0 and 1 into nine equal parts, then each part shows \(\frac{1}{9}\) and 2 part shows \(\frac{2}{9}\), 5 part shows \(\frac{5}{9}\), 9 part shows \(\frac{9}{9}\)
Also, 0 shows \(\frac{0}{9}\).
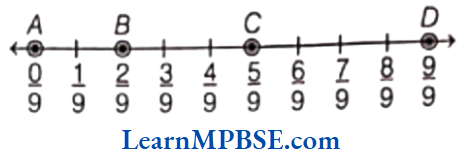
Hence, points A, B, C and D respectively represents the fraction \(\frac{0}{9}, \frac{2}{9}, \frac{5}{9} \text { and } \frac{9}{9} \text {. }\)
Example 4. Write five fraction between 0 and 1 that you can show and depict them on the number line.
Solution. As, we know that, we can show many fractions which are greater than 0 and less than 1
i.e. between 0 and 1.
Five fractions are \(\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6} \text { and } \frac{5}{6}\)
These fraction are shown on a number line as given below.
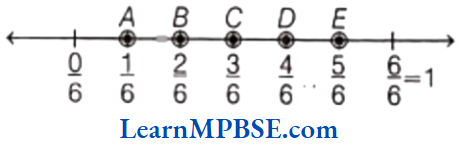
Hence, points A, B, C, D and E represent \(\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}\) and \(\frac{5}{6}\) respectively.
Note It Between two whole numbers, there lie infinite fractions.
Types of Fraction
Proper Fraction
A fraction whose numerator is always less than the denominator is called a proper fraction.
i.e. Numerator < Denominator.
e.g. \(\frac{9}{10}\), \(\frac{5}{8}\) are proper fractions. It is always less than 1. So, if 10’8 we represent a proper fraction on a number line, it will always lie to the left of 1.
MP Board Class 6 Maths Solutions
Example 5. Choose the proper fraction from the following numbers.
\(6 \frac{1}{2}, \frac{8}{3}, \frac{2}{9}, 7 \frac{2}{3}\)
Solution. A fraction is proper fraction, if numerator is less than denominator.
Therefore, \(\frac{2}{9}\) is a proper fraction.
Example 6. Give a proper fraction:
(1) Whose numerator is 4 and denominator is 7.
(2) Whose denominator is 8 and numerator is 1.
(3) Whose numerator and denominator add upto 8. How many fractions of this kind can you make?
(4) Whose denominator is 3 more than numerator. (Give any five. How many more can you make?)
Solution. (1) Numerator = 4 and denominator = 7
∴ Required fraction = \(\frac{4}{7}\)
(2) Numerator = 1 and denominator = 8
∴ Required fraction = \(\frac{1}{8}\)
(3) Possible pairs of numerator and denominator which
add upto 8 are (0, 8), (1, 7), (2, 6), (3, 5).
Now, proper fractions = \(\frac{0}{8}, \frac{1}{7}, \frac{2}{6}, \frac{3}{5}\)
There are four fraction.
So, we can make four such fractions.
(4) There can be infinite number of fractions whose denominator is 3 more than the numerator.
Some of them \(\frac{0}{3}, \frac{1}{4}, \frac{2}{5}, \frac{3}{6}, \frac{4}{7} \ldots \ldots\) so on.
Improper Fraction
A fraction whose numerator is always greater than the denominator is called an improper fraction.
i.e. Numerator > denominator.
e.g. \(\frac{3}{2}\), \(\frac{18}{5}\) are improper fractions.
It is always greater than 1. So, if we represent an improper fraction on a number line, it will always lie to the right of 1.
MP Board Class 6 Maths Solutions
Example 7. Write five improper fractions with denominator 8.
Solution. Five improper fractions with denominator 8 are \(\frac{9}{8}, \frac{10}{8}, \frac{11}{8}, \frac{12}{8}, \frac{13}{8}\)
Mixed Fraction
A fraction which is a combination of a whole number and a proper fraction (or part) is called a mixed fraction.
e.g. \(1 \frac{1}{4}\) is a mixed fraction. Here, I is a whole number and \(\frac{1}{4}\) is a proper fraction.
Example 8. Combine the following as a mixed fraction.
(1) 2 and one-third
(2) 5 and \(\frac{3}{5}\)
Solution. (1) We have, 2 and one-third.
Here, whole part = 2
and proper fraction part = One-third = \(\frac{1}{3}\)
∴ Mixed fraction = \(2 \frac{1}{3}\)
(2) We have, 5 and \(\frac{3}{5}\)
Here, whole part = 5 and proper fraction = \(\frac{3}{5}\)
∴ Mixed fraction = \(5 \frac{3}{5}\)
Conversion of an Improper Fraction into a Mixed Fraction
To express an improper fraction as a mixed fraction, firstly we divide the numerator by denominator to obtain the quotient and the remainder. Then,
Mixed fraction = \(\text { Quotient } \frac{\text { Remainder }}{\text { Divisor }}\)
e.g. Consider an improper fraction = \(\frac{17}{4}\)
Now, dividing numerator by denominator
i.e. 17 by 4, we get quotient = 4 and remainder = 1
Hence, mixed fraction = \(4 \frac{1}{4}\)
MP Board Class 6 Maths Solutions
Example 9. Express the following as mixed fractions.
(1) \(\frac{19}{3}\)
(2) \(\frac{14}{4}\)
(3) \(\frac{17}{7}\)
(4) \(\frac{33}{9}\)
Solution. (1) We have, \(\frac{19}{3}\)
On dividing 19 by 3, we get quotient = 6 and remainder = 1.
Hence, mixed fraction = \(6 \frac{1}{3}\)
(2) We have, \(\frac{14}{4}\)
On dividing 14 by 4, we get quotient = 3 and remainder = 2
Hence, mixed fraction = \(3 \frac{2}{4}\)
(3) We have, \(\frac{17}{7}\)
On dividing 17 by 7, we get quotient = 2 and remainder = 3
Hence, mixed fraction = \(2 \frac{3}{7}\)
(4) We have \(\frac{33}{9}\)
On dividing 33 by 9, we get quotient = 3 and remainder = 6
Hence, mixed fraction = \(3 \frac{6}{9}\)
Conversion of a Mixed Fraction into an Improper Fraction
Multiply the whole number with denominator of the fraction and then add the numerator of the fraction. This gives the numerator of the required improper fraction. Its denominator is the same as the denominator of the fractional part of mixed fraction.
Improper fraction \(=\frac{\text { Whole part } \times \text { Denominator }+ \text { Numerator }}{\text { Denominator }}\)
MP Board Class 6 Maths Solutions
Example 10. Express the following fractions as improper fractions.
(1) \(3 \frac{2}{5}\)
(2) \(2 \frac{3}{7}\)
(3) \(7 \frac{1}{4}\)
(4) \(3 \frac{1}{6}\)
(5) \(7 \frac{3}{8}\)
(6) \(11 \frac{3}{2}\)
Solution.
(1) We have, \(3 \frac{2}{5}=3+\frac{2}{5}=\frac{3 \times 5+2}{5}=\frac{17}{5}\)
(2) We have, \(2 \frac{3}{7}=2+\frac{3}{7}=\frac{2 \times 7+3}{7}=\frac{17}{7}\)
(3) We have, \(7 \frac{1}{4}=7+\frac{1}{4}=\frac{7 \times 4+1}{4}=\frac{29}{4}\)
(4) We have, \(3 \frac{1}{6}=3+\frac{1}{6}=\frac{3 \times 6+1}{6}=\frac{19}{6}\)
(5) We have, \(7 \frac{3}{8}=7+\frac{3}{8}=\frac{7 \times 8+3}{8}=\frac{59}{8}\)
(6) We have, \(11 \frac{3}{2}=11+\frac{3}{2}=\frac{22+3}{2}=\frac{25}{2}\)
Equivalent Fraction
Fractions having the same values are called equivalent fractions. To find an equivalent fraction of a given number, we multiply or divide the numerator and the denominator of the given fraction by the same non-zero number.
Example 1. Find five equivalent fractions of each of the following
(1) \(\frac{2}{3}\)
(2) \(\frac{1}{5}\)
Solution.
(1) Given, fraction is \(\frac{2}{3}\).
∴ \(\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{2 \times 3}{3 \times 3}=\frac{2 \times 4}{3 \times 4}=\frac{2 \times 5}{3 \times 5}=\frac{2 \times 6}{3 \times 6}\)
⇒ \(\frac{4}{6}=\frac{6}{9}=\frac{8}{12}=\frac{10}{15}=\frac{12}{18}\)
Hence, the five fractions equivalent to \(\frac{2}{3}\) are \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15} \text { and } \frac{12}{18}\).
(2) Given, fraction is \(\frac{1}{5}\).
\(\frac{1}{5}=\frac{1 \times 2}{5 \times 2}=\frac{1 \times 3}{5 \times 3}=\frac{1 \times 4}{5 \times 4}=\frac{1 \times 5}{5 \times 5}=\frac{1 \times 6}{5 \times 6}\)⇒ \(\frac{2}{10}=\frac{3}{15}=\frac{4}{20}=\frac{5}{25}=\frac{6}{30}\)
Hence, the five fractions equivalent to \(\frac{1}{5}\) are \(\frac{2}{10}, \frac{3}{15}, \frac{4}{20}, \frac{5}{25} \text { and } \frac{6}{30} .\)
Example 2. Give example of four equivalent fractions.
Solution. Four equivalent fractions are \(\frac{1}{3}, \frac{2}{6}, \frac{3}{9}, \frac{4}{12},\) etc.
To Test Whether Two Given Fractions are Equivalent or not
We can check whether two fractions are equivalent or not by finding their cross product i.e. we multiply the numerator of first fraction with the denominator of second fraction and the denominator of first fraction with the numerator of sechond fraction. If the two products are equal, then the given fractions are equivalent, otherwise not.
Let \(\frac{a}{b}\) and \(\frac{c}{d}\) be two given fractions. Their cross multiplication shown as
(1) If ad = bc, then \(\frac{a}{b}\) and \(\frac{c}{d}\) are equivalent.
(2) If ad < bc, then \(\frac{a}{b}\) < \(\frac{c}{d}\)
(3) If ad > bc, then \(\frac{a}{b}\) > \(\frac{c}{d}\)
Class 6 Maths Chapter 7 Solutions
Example 3. Check whether the fractions \(\frac{5}{8}\) and \(\frac{15}{24}\) are equivalent or not.
Solution. Let \(\frac{a}{b}\) = \(\frac{5}{8}\), \(\frac{c}{d}\) = \(\frac{15}{24}\).
By Cross multiplication \(\frac{a}{b} \times \frac{c}{d}\)
We have \(\frac{5}{8} \times \frac{15}{24}\),
Here, ad = bc i.e. 5 x 24 = 15 x 8 = 120
So, \(\frac{5}{8}\) and \(\frac{15}{24}\) are equivalent.
Example 4. Identify the fractions in each. Are these fractions equivalent?

Solution. (1) Here, the total parts is 4, out of which 2 parts are shaded. So, required fraction = \(\frac{2}{4}\)
(2) Here, total parts are 6, out of which 3 parts are shaded. So, required fraction = \(\frac{3}{6}\)
Now, take \(\frac{2}{4}\) and \(\frac{3}{6}\). Here, 2 x 6 = 12 and 3 × 4 = 12
∴ 12 = 12,
∴ \(\frac{2}{4}\) and \(\frac{3}{6}\) are equivalent.
Example 5. Write a fraction equivalent to \(\frac{3}{5}\) with numerator 12.
Solution. Let D stands for denominator.
Given, numerator of an equivalent fraction = 12
\(\frac{12}{D}\) = \(\frac{3}{5}\) ⇒ D x 3 = 12 x 5 ⇒ D = \(\frac{12 \times 5}{3}=20\)
Hence, required equivalent fraction of \(\frac{3}{5}\) is \(\frac{12}{20}\).
Example 6. Write a fraction equivalent to with denominator 35.
Solution. Let N stands for numerator.
Given, denominator of an equivalent fraction = 35
\(\frac{N}{35}\) = \(\frac{5}{7}\) ⇒ N x 7 = 35 x 5 ⇒ N = \(\frac{35 \times 5}{7}\) = 25
Hence, required equivalent fraction of \(\frac{5}{7}\) is \(\frac{25}{35}\).
Simplest Form of a Fraction
A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1. i.e their HCF =1.
To find the equivalent fraction in the simplest form, firstly we find the HCF of the numerator and denominator and then divide both of them by their HCF.
Class 6 Maths Chapter 7 Solutions
Example 7. Write the simplest form of
(1) \(\frac{28}{42}\)
(2) \(\frac{36}{49}\)
Solution. (1) We have, \(\frac{28}{42}\)
Now, factors of 28 = 2, 2, 7 and factors of 42 = 2, 3, 7 Common factors = 2 and 7
∴ HCF of 28 and 42 = 2 x 7 = 14
Then, \(\frac{28}{42}=\frac{28 \div 14}{42 \div 14}=\frac{2}{3}\)
Hence, fraction \(\frac{2}{3}\) is the simplest form of given fraction.
(2) Here, factors of 36 = 6, 6 and factors of 49 = 7, 7
∴ 36 and 49 have no common factor except 1.
Hence, fraction \(\frac{36}{49}\) is in simplest form.
Like and Unlike Fractions
Fractions having same denominator are called like fractions.
e.g. \(\frac{1}{7}, \frac{2}{7}, \frac{3}{7}\) etc.
While fractions having the different denominator are called unlike fractions.
e.g. \(\frac{2}{3}, \frac{1}{5}, \frac{2}{15}, \frac{7}{9}\) etc.
Conversion of Unlike Fraction into Like Fraction
Unlike fractions are converted into like fractions by converting each of them into their equivalent fractions having denominator equal to the LCM of all the denominators of all unlike fractions.
Example 1. Convert the fractions \(\frac{1}{2}\), \(\frac{2}{3}\) and \(\frac{5}{6}\) into like fractions.
Solution. The given fractions are \(\frac{1}{2}\), \(\frac{2}{3}\) and \(\frac{5}{6}\).
LCM of denominators 2, 3 and 6 = 6
We convert each of the fraction into an equivalent fraction with 6 as the denominator.
\(\frac{1}{2}=\frac{1 \times 3}{2 \times 3}=\frac{3}{6}\) \(\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6}\)and \(\frac{5}{6}=\frac{5 \times 1}{6 \times 1}=\frac{5}{6}\)
The required like fractions are \(\frac{3}{6}\), \(\frac{4}{6}\) and \(\frac{5}{6}\).
Comparing Fractions
There are two methods of comparison of fractions which are given below
Comparison of Like Fractions
If two fractions have same denominator, then the fraction with the greater numerator is greater.
e.g. Between \(\frac{11}{20}\) and \(\frac{13}{20}\), the fraction \(\frac{13}{20}\) is grater.
Class 6 Maths Chapter 7 Solutions
Example 2. Which is the larger fraction?
(1) \(\frac{6}{10}\) or \(\frac{7}{10}\)
(2) \(\frac{12}{24}\) or \(\frac{13}{24}\)
Solution. We have, \(\frac{6}{10}\) or \(\frac{7}{10}\)
Here, denominators of both fractions are same and 7 > 6.
So, \(\frac{7}{10}\) > \(\frac{6}{10}\)
(2) We have, \(\frac{12}{24}\) or \(\frac{13}{24}\)
Here, denominator of both fractions are same and 13 > 12.
So, \(\frac{13}{24}\) > \(\frac{12}{24}\)
Example 3. Parul reads 20 pages of a novel containing 100 pages. Sachin reads \(\frac{2}{5}\) of the same book. Who read less?
Solution. Fraction of book read by Parul = \(\frac{20}{100}\) = \(\frac{1}{5}\)
Fraction of novel read by Sachin = \(\frac{2}{5}\)
Here, denominator of both fractions are same and 2 > 1.
∴ \(\frac{1}{5}\) < \(\frac{2}{5}\)
Hence, Parul reads less pages of the novel.
Example 4. Write the following in ascending and descending order.
(1) \(\frac{2}{9}, \frac{7}{9}, \frac{5}{9}\)
(2) \(\frac{1}{3}, \frac{11}{3}, \frac{4}{3}, \frac{7}{3}, \frac{5}{3}\)
Solution. (1) We have, \(\frac{2}{9}, \frac{7}{9}, \frac{5}{9}\)
Here, denominator of all fractions are same.
∴ Ascending order of numerator = 2 < 5 < 7
and descending order of numerator = 7 > 5 > 2
∴ Ascending order of fraction = \(\frac{2}{9}<\frac{5}{9}<\frac{7}{9}\)
and descending order of fraction = \(\frac{7}{9}>\frac{5}{9}>\frac{2}{9}\)
(2) Since, denominator of all fractions are same.
∴ Ascending order of fraction = \(\frac{1}{3}<\frac{4}{3}<\frac{5}{3}<\frac{7}{3}<\frac{11}{3}\)
and descending order of fraction = \(\frac{11}{3}>\frac{7}{3}>\frac{5}{3}>\frac{4}{3}>\frac{1}{3}\)
Class 6 Maths Chapter 7 Solutions
Example 5. Write shaded portion as fraction. Arrange them in ascending and descending order using correct sign,>’ between the fractions.
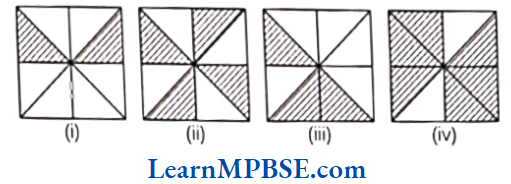
Solution. Here, total number of equal parts in all figures = 8
Shaded portion of figure (1) represents fraction = \(\frac{2}{8}\)
Shaded portion of figure (2) represents fraction = \(\frac{4}{8}\)
Shaded portion of figure (3) represents fraction = \(\frac{3}{8}\)
Shaded portion of figure (4) represents fraction = \(\frac{6}{8}\)
∴ Denominator of all fractions are same. So, we arrange them in ascending order and descending order according to their numerators.
∴ Ascending order of fractions \(\frac{2}{8}<\frac{3}{8}<\frac{4}{8}<\frac{6}{8}\)
[∴ fraction with small numerator will be smaller]
and descending order of fractions = \(\frac{6}{8}>\frac{4}{8}>\frac{3}{8}>\frac{2}{8}\)
[∴ fraction having greatest numerator will be greatest].
Comparison of Unlike Fractions
There are two types of comparison of unlike fractions.
Comparison of Unlike Fractions with Same Numerators
Among two fractions having same numerator, the one with the smaller denominator is the greater of the two.
e.g. \(\frac{7}{11}>\frac{7}{13} \text { and } \frac{11}{23}>\frac{11}{25}\)
MP Board Class 6 Chapter 7 Maths
Example 6. Arrange the following in ascending and descending order.
\(\frac{2}{13}, \frac{2}{11}, \frac{2}{17}, \frac{2}{5}, \frac{2}{7}, \frac{2}{9}, \frac{2}{55}\)
Solution. Here, numerator of all fractions are same.
Descending order of denominators
= 55 > 17 > 13 > 11 > 9 > 7 > 5.
∴ Ascending order of fraction
= \(\frac{2}{55}<\frac{2}{17}<\frac{2}{13}<\frac{2}{11}<\frac{2}{9}<\frac{2}{7}<\frac{2}{5}\)
∴ [\(\frac{2}{55}\) has larger denominator, so it is smallest fraction].
and descending order of fractions.
= \(\frac{2}{5}>\frac{2}{7}>\frac{2}{9}>\frac{2}{11}>\frac{2}{13}>\frac{2}{17}>\frac{2}{55}\)
Example 7. Kanchan and Kiran are two friends. Kanchan get one-fifth of a bottle of apple juice and Kiran get one-fourth of a bottle of apple juice. Who gets more?
Solution. Here, we will compare one-fifth i.e. \(\frac{1}{5}\) and one-fourth i.e. \(\frac{1}{4}\).
Since \(\frac{1}{5}\) and \(\frac{1}{4}\) have same numerator, so the fraction with smaller denominator is greater.
Thus, \(\frac{1}{4}\) > \(\frac{1}{5}\)
Thus, Kiran gets more apple juice.
Comparison of Unlike Fractions with Different Numerators
If numerator and denominator both are different of given two fractions, then for comparing, we use the method of equivalent fractions i.e. we change the denominator of a fraction without changing its value.
MP Board Class 6 Chapter 7 Maths
Example 8. Compare \(\frac{5}{6}\) and \(\frac{13}{15}\).
Solution. The given fractions are unlike, we should first get their equivalent fractions with a denominator, which is common multiple of 6 and 15 i.e 30.
Now, \(\frac{5 \times 5}{6 \times 5}=\frac{25}{30} \text { and } \frac{13 \times 2}{15 \times 2}=\frac{26}{30}\)
Since, \(\frac{26}{30}>\frac{25}{30}, \text { so } \frac{13}{15}>\frac{5}{6}\)
Example 9. Arrange the following in ascending and descending order.
\(\frac{2}{3}, \frac{1}{9}, \frac{5}{12} \text { and } \frac{7}{36}\)
Solution. We have, \(\frac{2}{3}, \frac{1}{9}, \frac{5}{12}, \frac{7}{36}\)
LCM of 3, 9, 12 and 36 = 3 x 3 x 4 = 36
So, we convert each of the given fraction into an equivalent fraction with denominator 36.
Clearly, \(\frac{24}{36}>\frac{15}{36}>\frac{7}{36}>\frac{4}{36}\)
Hence, \(\frac{2}{3}>\frac{5}{12}>\frac{7}{36}>\frac{1}{9}\)
∴ Ascending order is \(\frac{1}{9}<\frac{7}{36}<\frac{5}{12}<\frac{2}{3}\) and descending order is \(\frac{2}{3}>\frac{5}{12}>\frac{7}{36}>\frac{1}{9}\)
Example 10. Find answer to the following. Write and indicate how you solved them.
(1) is \(\frac{5}{4}\) equal to \(\frac{9}{5}\) ?
(2) is \(\frac{20}{16}\) equal to \(\frac{5}{4}\) ?
Solution. (1) LCM of 4 and 5 = 20
Now, \(\frac{5}{4}=\frac{5 \times 5}{4 \times 5}=\frac{25}{20}\)
and \(\frac{9}{5}=\frac{9 \times 4}{5 \times 4}=\frac{36}{20}\)
Thus, both fractions are like fractions but \(\frac{25}{20} \neq \frac{36}{20}\)
∴ \(\frac{5}{4}\) ≠ \(\frac{9}{5}\)
(2) LCM of 16 and 4 = 16
Now, \(\frac{20}{16}=\frac{20 \times 1}{16 \times 1}=\frac{20}{16}\)
and \(\frac{5}{4}=\frac{5 \times 4}{4 \times 4}=\frac{20}{16}\)
Thus, both fraction are like fractions and \(\frac{20}{16}\) = \(\frac{20}{16}\)
∴ \(\frac{20}{16}\) = \(\frac{5}{4}\)
MP Board Class 6 Chapter 7 Maths
Example 11. Ravish takes \(2 \frac{1}{5}\) min to walk across the school ground. Rahul takes \(1 \frac{3}{4}\) min to do the same. Who takes less time and by what fraction?
Solution. Time taken by Ravish to walk across the school ground = \(2 \frac{1}{5}\) min = \(\frac{11}{5}\) min
Time taken by Rahul to walk across the school ground = \(1 \frac{3}{4}\) min = \(\frac{7}{4}\) min
The LCM of 5 and 4 = 20
∴ \(\frac{11}{5}=\frac{11 \times 4}{5 \times 4}=\frac{44}{20} \text { and } \frac{7}{4}=\frac{7 \times 5}{4 \times 5}=\frac{35}{20}\)
Now, \(\frac{35}{20}\) < \(\frac{44}{20}\)
∴ \(\frac{7}{4}\) < \(\frac{11}{5}\)
⇒ Rahul takes less time.
The difference between the time taken by Ravish and Rahul to walk across the school ground = \(\frac{11}{5}\) – \(\frac{7}{4}\)
= \(\frac{44-35}{20}=\frac{9}{20} \min\)
Thus, Rahul takes \(\frac{9}{20}\) min less than Ravish.
Example 12. Asha and Deepa have bookshelves of the same size partly filled with books. Asha’s shelf is \(\frac{5}{7}\) th full and Deepa’s shelf is \(\frac{3}{5}\) th full. Whose bookshelf is more full? By what fraction?
Solution. Here, we have to compare two unlike fractions.
Asha’s shelf = \(\frac{5}{7}\)th
Deepa’s shelf = \(\frac{3}{5}\)th
∴ LCM of 7 and 5 = 35
∴ \(\frac{5}{7}=\frac{5 \times 5}{7 \times 5}=\frac{25}{35} \text { and } \frac{3}{5}=\frac{3 \times 7}{5 \times 7}=\frac{21}{35}\)
∴ 25 > 21
∴ \(\frac{5}{7}\) > \(\frac{3}{5}\)
Hene, Asha’s bookshelf is filled more than Deepa’s bookshelf.
∴ Difference = \(\frac{5}{7}-\frac{3}{5}=\frac{25}{35}-\frac{21}{35}=\frac{4}{35}\)
Therefore, Asha’s bookshelf is more full by \(\frac{4}{35}\) th than Deepa’s bookshelf.
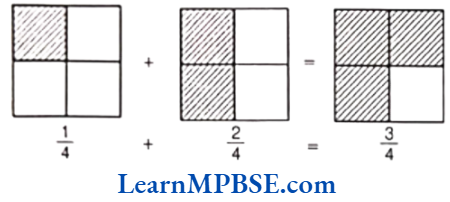
Addition of Like Fractions
To add like fractions, we add their numerators keeping denominator unchanged and then write it in simplest form.
Suppose, we have two like fractions \(\frac{a}{b}\) and \(\frac{c}{b}\) , then sum = \(\frac{a+c}{b}\)
∴ Sum of like fractions \(=\frac{\text { Sum of their numerators }}{\text { Common denominator }}\)
e.g. By pictorial representation
MP Board Class 6 Chapter 7 Maths
Example 1. Add
(1) \(\frac{1}{8}+\frac{1}{8}\)
(2) \(\frac{2}{5}+\frac{3}{5}\)
Solution. (1) Let \(\frac{a}{b}\) = \(\frac{1}{8}\) and \(\frac{c}{b}\) = \(\frac{1}{8}\), then sum = \(\frac{a+c}{b}=\frac{1+1}{8}=\frac{2}{8}=\frac{1}{4}\)
Hence, the sum of \(\frac{1}{8}\) and \(\frac{1}{8}\) is \(\frac{1}{4}\).
(2) Let \(\frac{a}{b}\) = \(\frac{2}{5}\) and \(\frac{c}{b}\) = \(\frac{3}{5}\), then sum = \(\frac{a+c}{b}=\frac{2+3}{5}=\frac{5}{5}=1\)
Hence, the sum of \(\frac{2}{5}\) and \(\frac{3}{5}\) is 1.
Example 2. Add the shaded part of the fraction for the given figure.
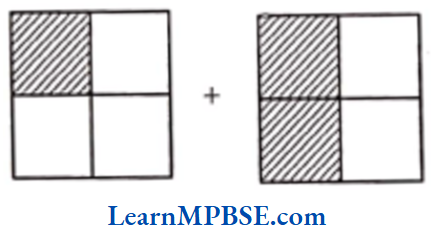
Solution. We have,
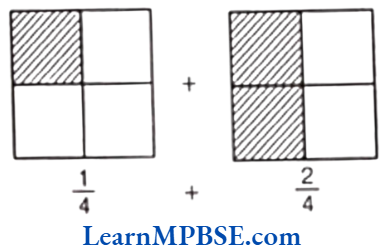
Then, pictorial representation of \(\frac{3}{4}\) is

MP Board Class 6 Chapter 7 Maths
Example 3. Add these with the help of a diagram.
(1) \(\frac{2}{6}+\frac{3}{6}\)
(2) \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\)
Solution. (1) Here, draw two rectangles and divide them into 6 equal parts separately. In first rectangle, 2 parts out of 6 parts are shaded and in second rectangle, 3 parts out of 6 parts are shaded. On adding them, we get
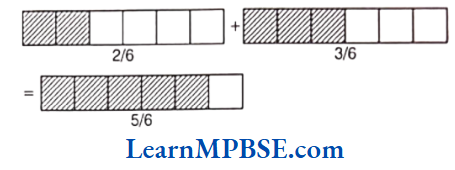
i.e. \(\frac{2}{6}+\frac{3}{6}=\frac{2+3}{6}=\frac{5}{6}\)
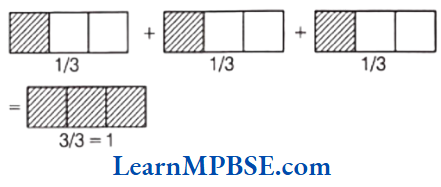
i.e. \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=\frac{1+1+1}{3}=\frac{3}{3}=1\)
Example 4. On her birthday Niharika divided a cake into 6 equal parts. She distributed 2 parts in her family and 3 parts in neighbourhood. How much cake did she distributed together?
Solution. Here, Niharika divided the cake into 6 equal parts, so each part will represent \(\frac{1}{6}\). She gave two parts in her family, i.e. \(\frac{2}{6}\) and she gave three parts in the neighbourhood, i.e. \(\frac{3}{6}\).
Part of cake she distributed = \(\frac{3}{6}+\frac{2}{6}\)
∴ Here, denominator of both fractions are same. So, we add numerator to find their sum.
i.e. \(\frac{3+2}{6}=\frac{5}{6}\)
Hence, she distributed \(\frac{5}{6}\) of the cake into her family and neighbourhood.
Subtraction of Like Fractions
To subtract like fractions, we subtract the smaller numerator from the greater numerator, keeping denominator unchanged and then write it in simplest form.
Suppose, we have two like fractions \(\frac{a}{b}\) and \(\frac{c}{b}\) (a > c), then
Difference = \(\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}\)
∴ Difference of like fractions \(=\frac{\text { Difference of their numerators }}{\text { Common denominator }}\)
MP Board Class 6 Chapter 7 Maths
Example 5. Find the difference of \(\frac{7}{9}\) and \(\frac{2}{9}\)
Solution. Let \(\frac{a}{b}\) = \(\frac{7}{9}\) and \(\frac{c}{b}\) = \(\frac{2}{9}\)
Here, a > c i.e. 7 > 2
So, Difference \(\frac{\text { Difference of their numerators }}{\text { Common denominator }}=\frac{7-2}{9}=\frac{5}{9}\)
Example 6. Mohit was reading a book. He read one-third of book on Sunday. He read another one-third on Wednesday and the remaining on Friday. What fraction of the book did he read on Friday?
Solution. Book read by Mohit on Sunday = \(\frac{1}{3}\)
Book read by Mohit on Wednesday = \(\frac{1}{3}\)
∴ Book read by him on Friday = \(1-\frac{1}{3}-\frac{1}{3}=\frac{3}{3}-\frac{1}{3}-\frac{1}{3}\)
[∴ 1 and \(\frac{3}{3}\) are equivalent fractions]
= \(\frac{3-1-1}{3}=\frac{1}{3}\)
Hence, he read one-third of the book on Friday.
Example 7. Add the difference of \(\frac{7}{10}\) and \(\frac{2}{10}\) to \(\frac{8}{20}\)
Solution. Difference of \(\frac{7}{10}\) and \(\frac{2}{10}\) is equal to \(\frac{7}{10}\) – \(\frac{2}{10}\).
[Since, both are like fractions and 7 is greater than 2, so subtract \(\frac{2}{10}\) from \(\frac{7}{10}\)]
Now, \(\frac{7}{10}-\frac{2}{10}=\frac{7-2}{10}=\frac{5}{10} \text { or } \frac{1}{2}\)
Now, adding \(\frac{5}{10} \text { to } \frac{8}{20} \text { i.e. } \frac{5}{10}+\frac{8}{20}\)
Here, LCM of 10 and 20 are 20.
∴ \(\frac{5 \times 2}{10 \times 2}+\frac{8}{20}=\frac{10}{20}+\frac{8}{20}=\frac{18}{20}=\frac{9}{10}\)
MP Board Class 6 Chapter 7 Maths
Addition of Unlike Fractions
To add unlike fractions, we first convert them into equivalent fractions with the same denominator (which is LCM of denominators) and then add them as like fractions.
Example 1. Add the following
(1) \(\frac{2}{6}\) and \(\frac{3}{4}\)
(2) \(\frac{3}{7}\) and \(\frac{5}{8}\)
Solution. (1) We have, \(\frac{2}{6}+\frac{3}{4}\)
LCM of 6 and 4 = 12
∴ \(\frac{2}{6}+\frac{3}{4}=\frac{2 \times 2}{6 \times 2}+\frac{3 \times 3}{4 \times 3}=\frac{4}{12}+\frac{9}{12}=\frac{13}{12}\)
Hence, \(\frac{2}{6}+\frac{3}{4}=\frac{13}{12}\)
(2) We have,\( \frac{3}{7}+\frac{5}{8}\)
LCM of 7 and 8 = 56
∴ \(\frac{3}{7}+\frac{5}{8}=\frac{3 \times 8}{7 \times 8}+\frac{5 \times 7}{8 \times 7}=\frac{24}{56}+\frac{35}{56}=\frac{59}{56}\)
Hence, \(\frac{3}{7}+\frac{5}{8}=\frac{59}{56}\)
Example 2. Karishma bought \(\frac{3}{5}\) m of cloth for her college dress and her mother bought \(\frac{2}{7}\) m of cloth. What is the total length of the cloth they bought?
Solution. Given, cloth bought by Karishma = \(\frac{3}{5}\) m
and cloth bought by her mother = \(\frac{2}{7}\) m
∴ Total length of cloth bought by them = \(\left(\frac{3}{5}+\frac{2}{7}\right) \mathrm{m}\)
Now, LCM of 5 and 7 = 35
∴ \(\frac{3}{5}+\frac{2}{7}=\frac{3 \times 7}{5 \times 7}+\frac{2 \times 5}{7 \times 5}\)
= \(\frac{21}{35}+\frac{10}{35}=\frac{31}{35}\)
Hence, total length of cloth bought by them = \(\frac{31}{35}\)m.
Subtraction of Unlike Fractions
To subtract unlike fractions, we first convert them into equivalent fractions with the same denominator (which is LCM of denominators) and then subtract them as like fractions.
Example 3. Subtract the following
(1) \(\frac{2}{3}\) from \(\frac{4}{5}\)
(2) \(\frac{3}{7}\) from \(\frac{5}{9}\)
Solution. (1) We have, \(\frac{4}{5}-\frac{2}{3}\)
LCM of 5 and 3 = 15
∴ \(\frac{4}{5}-\frac{2}{3}=\frac{4 \times 3}{5 \times 3}-\frac{2 \times 5}{3 \times 5}=\frac{12}{15}-\frac{10}{15}=\frac{12-10}{15}=\frac{2}{15}\)
(2) We have, \(\frac{5}{9}-\frac{3}{7}\)
LCM of 9 and 7 = 63
∴ \(\frac{5}{9}-\frac{3}{7}=\frac{5 \times 7}{9 \times 7}-\frac{3 \times 9}{7 \times 9}=\frac{35}{63}-\frac{27}{63}=\frac{8}{63}\)
MP Board Class 6 Chapter 7 Maths
Example 4. A thread \(\frac{5}{9}\) m long cut into two pieces. One piece was \(\frac{1}{3}\) m long. How long is the other piece?
Solution. Given, total length of a piece of thread = \(\frac{5}{9}\) m
Length of one piece of thread = \(\frac{1}{3}\) m
∴ Length of another piece = \(\left(\frac{5}{9}-\frac{1}{3}\right) \mathrm{m}\)
LCM of 9 and 3 = 9
∴ \(\frac{5}{9}-\frac{1}{3}=\frac{5 \times 1}{9 \times 1}-\frac{1 \times 3}{3 \times 3}\)
= \(\frac{5}{9}-\frac{3}{9}=\frac{2}{9}\)
Hence, the length of another piece of thread is \(\frac{2}{9}\) m.
Example 5. Two kid Vehan and Vijay have the glass of same size partly filled with milk. Vehan glass is \(\frac{5}{6}\)th full and Vijay’s glass is \(\frac{2}{5}\)th full. Whose glass is more full? By what fraction?
Solution. The portion of Vehan’s glass filled by milk = \(\frac{5}{6}\) part
and the portion of Vijay’s glass filled by milk = \(\frac{2}{5}\) part.
Now, LCM of 6 and 5 = 30
Equivalent fractions of \(\frac{5}{6}\) are
\(\frac{5 \times 2}{6 \times 2}, \frac{5 \times 3}{6 \times 3}, \frac{5 \times 4}{6 \times 4}, \frac{5 \times 5}{6 \times 5}, \ldots \ldots \ldots \text { i.e. } \frac{10}{12}, \frac{15}{18}, \frac{20}{24}, \frac{25}{30}, \ldots\)and equivalent fraction of \(\frac{2}{5}\) are
\(\frac{2 \times 2}{5 \times 2}, \frac{2 \times 3}{5 \times 3}, \frac{2 \times 4}{5 \times 4}, \frac{2 \times 5}{5 \times 5}, \frac{2 \times 6}{5 \times 6} \text {, i.e. } \frac{4}{10}, \frac{6}{15}, \frac{8}{20}, \frac{10}{25}, \frac{12}{30}, \ldots\)Here, equivalent fractions \(\frac{12}{30}\) and \(\frac{25}{30}\) have same denominator.
∴ 25 > 12
∴ \(\frac{25}{30}>\frac{12}{30} \text { i.e. } \frac{5}{6}>\frac{2}{5}\)
Now, \(\frac{5}{6}-\frac{2}{5}=\frac{25}{30}-\frac{12}{30}\)
\(\frac{25-12}{30}=\frac{13}{30}\)Hence, Vehan’s glass is more full by fraction \(\frac{13}{30}\).
Example 6. Complete the addition and subtraction box.
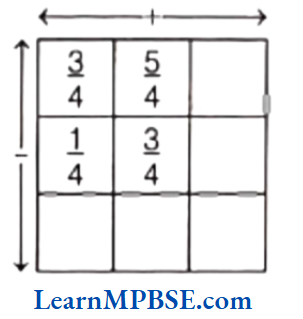
Solution. Here, \(\frac{3}{4}+\frac{5}{4}=\frac{3+5}{4}=\frac{8}{4}=2 \text { and } \frac{1}{4}+\frac{3}{4}=\frac{1+3}{4}=\frac{4}{4}=1\)
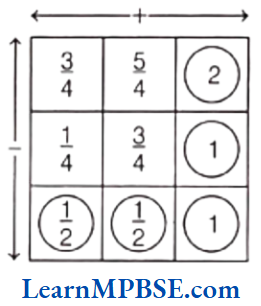
Now, \(\frac{3}{4}-\frac{1}{4}=\frac{3-1}{4}=\frac{2}{4}=\frac{1}{2}\)
and \(\frac{5}{4}-\frac{3}{4}=\frac{5-3}{4}=\frac{2}{4}=\frac{1}{2}\)
Also, we have 2 – 1 = 1
and \(\frac{1}{2}+\frac{1}{2}=\frac{1+1}{2}=\frac{2}{2}=1\)
Hence, the required complete box is shown above.
Addition and Subtraction of Mixed Fractions
Firstly, we convert both mixed fractions into improper fractions and then add them by converting into equivalent fractins with the same denominator.
To subtract mixed fractions, we subtract smaller whole part from greater whole part and then subtract corresponding fractional parts.
Mixed fractions cab be written either as a whole part plus a proper fraction or entirely as an improper fraction. One way to add (or subtract) mixed fractions is to do the operation separately for the whole parts and other way is to write the mixed fractions as improper fractions and then directly add (or subtract) them.
MP Board Class 6 Chapter 7 Maths
Example 7. Add \(2 \frac{2}{5}\) and \(3 \frac{5}{6}\).
Solution. We have, \(2 \frac{2}{5}\) and \(3 \frac{5}{6}\)
To add mixed fractions, first convert both mixed fractions into improper fractions.
Now, \(2 \frac{2}{5}=\frac{12}{5} \text { and } 3 \frac{5}{6}=\frac{23}{6}\)
⇒ \(2 \frac{2}{5}+3 \frac{5}{6}=\frac{12}{5}+\frac{23}{6}\)
Now, converting them into equivalent fractions with the same denominator.
We have, \(\frac{12}{5}=\frac{12 \times 6}{5 \times 6}=\frac{72}{30} \text { and } \frac{23}{6}=\frac{23 \times 5}{6 \times 5}=\frac{115}{30}\) [LCM of 5 and 6 is 30]
∴ \(2 \frac{2}{5}+3 \frac{5}{6}=\frac{72}{30}+\frac{115}{30}=\frac{187}{30}=6 \frac{7}{30}\)
Example 8. Subtract \(3 \frac{5}{9}\) from \(5 \frac{1}{6}\).
Solution. We have, \(3 \frac{5}{9}\) and \(5 \frac{1}{6}\)
To subtract mixed fractions, first convert both mixed fractions into improper fractions.
∴ \(5 \frac{1}{6}-3 \frac{5}{9}=\frac{31}{6}-\frac{32}{9}\)
= \(\frac{31 \times 3}{6 \times 3}-\frac{32 \times 2}{9 \times 2}=\frac{93}{18}-\frac{64}{18}\)
= \(\frac{93-64}{18}=\frac{29}{18}\) [∴ LCM of 6 and 9 is 18]
⇒ \(5 \frac{1}{6}-3 \frac{5}{9}=1 \frac{11}{18}\)
Example 9. Simplify \(3 \frac{1}{3}+6 \frac{2}{3}-2 \frac{2}{3}\)
Solution. \(\left(3+\frac{1}{3}\right)+\left(6+\frac{2}{3}\right)-\left(2+\frac{2}{3}\right)\)
= \(\frac{(3 \times 3)+1}{3}+\frac{(6 \times 3)+2}{3}-\frac{(3 \times 2)+2}{3}\)
= \(\frac{10}{3}+\frac{20}{3}-\frac{8}{3}=\frac{10+20-8}{3}=\frac{30-8}{3}=\frac{22}{3}\)
Example 10. What should be added to \(7 \frac{4}{15}\) to get \(8 \frac{2}{5}\)
Solution. Let x be added to the \(7 \frac{4}{15}\),
i.e. \(7 \frac{4}{15}+x=8 \frac{2}{5}\)
⇒ \(\frac{109}{15}+x=\frac{42}{5}\)
⇒ \(x=\frac{42}{5}-\frac{109}{15}=\frac{126-109}{15}\)
[∴ LCM of 5 and 15 = 15]
∴ \(x=\frac{17}{15}=1 \frac{2}{15}\)
Example 11. Rahul was given \(1 \frac{1}{5}\) piece of bread and Garima was given \(1 \frac{1}{4}\) piece of bread. Find the total amount of bread was given to both of them.
Solution. Bread given to Rahul = \(1 \frac{1}{5}\) piece
Bread given to Garima = \(1 \frac{1}{4}\) piece.
Total bread given to both of them = \(1 \frac{1}{5}+1 \frac{1}{4}\)
= \(\frac{5 \times 1+1}{5}+\frac{4 \times 1+1}{4}=\frac{6}{5}+\frac{5}{4}\)
LCM of 5 and 4 = 20
∴ \(\frac{6}{5}+\frac{5}{4}=\frac{6 \times 4}{5 \times 4}+\frac{5 \times 5}{4 \times 5}=\frac{24}{20}+\frac{25}{20}=\frac{24+25}{20}=\frac{49}{20}\)
Hence, total bread given to both of them = \(\frac{49}{20}\)
MP Board Class 6 Chapter 7 Maths
Example 12. Add the difference of \(1 \frac{3}{4}\) and \(\frac{4}{5}\) to the sum of \(\frac{3}{5}\) and \(\frac{2}{7}\).
Solution. We have, \(1 \frac{3}{4}-\frac{4}{5} \text { and } \frac{3}{5}+\frac{2}{7}\)
Now, \(\frac{7}{4}-\frac{4}{5}=\frac{35-16}{20}=\frac{19}{20} \text { and } \frac{3}{5}+\frac{2}{7}=\frac{21+10}{35}=\frac{31}{35}\)
Now, according to the question, \frac{19}{30}+\frac{31}{35}
∴ LCM of 20 and 35 = 140
∴ \(\frac{19 \times 7}{20 \times 7}+\frac{31 \times 4}{35 \times 4}=\frac{133}{140}+\frac{124}{140}=\frac{133+124}{140}=\frac{257}{140}=1 \frac{117}{140}\)
Example 13. Savita bought \(\frac{2}{5}\) m of ribbon and Kavita bought \(\frac{3}{4}\) m of the ribbon. What was the total length of the ribbon they bought?
Solution. The ribbon bought by Savita = \(\frac{2}{5}\) m
The ribbon bought by Kavita = \(\frac{3}{4}\) m
∴ Total ribbon bought by them = \(\frac{3}{4}+\frac{2}{5}\)
LCM of 4 and 5 = 20
∴ \(\frac{3}{4}+\frac{2}{5}=\frac{3 \times 5}{4 \times 5}+\frac{2 \times 4}{5 \times 4}=\frac{15}{20}+\frac{8}{20}=\frac{23}{20} \mathrm{~m}\)
Hence, total ribbon bought by both = \(\frac{23}{20}\) m
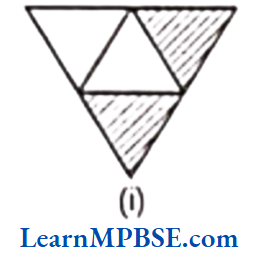
Question 1. Write the fraction representing the shaded portion.
Solution.
Total number of equal parts = 4;
Shaded parts = 2
∴ Fraction representing the shaded portion \(=\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{2}{4}=\frac{1}{2}\)
Types of Fractions Class 6
Question 2. Colour the part according to the given fraction.
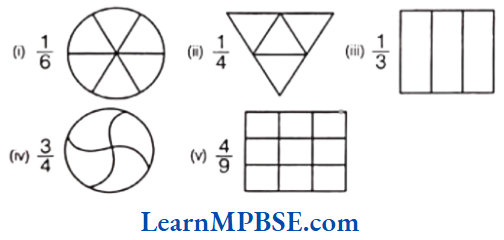
Solution. (1) Here, fraction 1/6 shows that out of 6 equal parts, 1 part is shaded. So, the required figure is shown alongside.

(2) Here, fraction 1/4 shows that out of 4 equal parts, 1 part is shaded. So, the required figure is shown alongside.
(3) Here, fraction 1/3 shows that out of 3 equal parts, 1 part is shaded. So, the required figure is shown alongside.

(4) Here, fraction 3/4 shows that out of 4 equal parts, 3 parts are shaded. So, the required figure is shown along side.

(5) Here, fraction \frac{4}{9} shows that out of 9 equal parts, 4 parts are shaded. So, the required figure is shown along side.
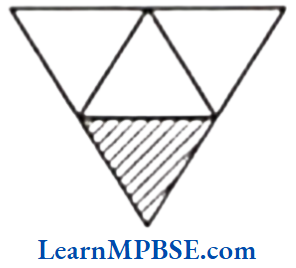
Question 3. Identify the error if any.
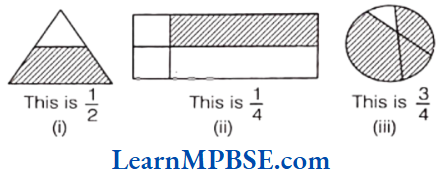
Solution. (1) In the given figure, shaded portion is not equal to unshaded portion. So, fraction is not equal to 1/2.
(2) In the given figure, four parts are not equal.
∴ Fraction is not equal to 1/4.
(3) In the given figure, four parts are not equal.
∴ Fraction is not equal to 3/4.
Types of Fractions Class 6
Question 4. What fraction of a day is 8 hours?
Solution. We know that total hours in a day = 24 h
∴ Required fraction \(=\frac{8 \mathrm{~h}}{24 \mathrm{~h}}=\frac{8}{24}=\frac{1}{3}\)
Question 5. What fraction of an hour is 40 minutes?
Solution. We know that total minutes in an hour = 60 min
∴ Required fraction \(=\frac{40 \mathrm{~min}}{60 \mathrm{~min}}=\frac{40}{60}=\frac{2}{3}\)
Question 6. Arya, Abhimanyu and Vivek shared lunch. Arya has brought two sandwiches, one made of vegetable and one of jam. The other two boys forgot to bring their lunch. Arya agreed to share his sandwiches, so that each person will have an equal share of each sandwich.
(1) How can Arya divide his sandwiches, so that each person has an equal share?
(2) What part of a sandwich will each boy receive?
Solution. Total number of sandwiches = 2
Total number of boys = 3
(1) Here, Arya has to divide 2 sandwiches into 3 persons. So, he will divide each sandwich into three equal parts and give one part of each sandwich to each of them.
Thus, each person gets 2/3 sandwiches.
(2) One sandwich is to be divided among three boys.
∴ Each boy will get = 1/3 part of a sandwich.
Types of Fractions Class 6
Question 7. Kanchan dyes dresses. She had to dye 30 dresses. She has so far finished 20 dresses. What fraction of dresses has she finished?
Solution. Total number of dresses to be dyed = 30
Number of dresses finished = 20
∴ Required fraction of finished dresses \(=\frac{\text { Number of dress finished }}{\text { Total number of dresses }}=\frac{20}{30}=\frac{2}{3}\)
Question 8. Write the natural numbers from 2 to 12. What fraction of them are prime numbers?
Solution. Natural numbers from 2 to 12=2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
Total natural numbers = 11
Prime numbers from 2 to 12 = 2, 3, 5, 7, 11
Total prime numbers = 5
∴ Required fraction \(=\frac{\text { Total prime numbers }}{\text { Total natural numbers }}=\frac{5}{11}\)
Question 9. What fraction of these circles have X in them?

Solution. Total number of circles = 8; Number of circles having X = 4
∴ Required fraction \(=\frac{\text { Number of circles having } X}{\text { Total number of circles }}\)
= \(\frac{4}{8}\) = \(\frac{1}{2}\)
Types of Fractions Class 6
Question 10. Kristin received a CD player for her birthday. She bought 3 CDs and received 5 others as gifts. What fraction of her total CDs did she buy and what fraction did she receive as gifts?
Solution. Number of CDs bought by Kristin = 3
Number of CDs recived as gifts = 5
∴ Total number of CDs = 3 + 5 = 8
Hence, the fraction of CDs bought by Kristin
\(=\frac{\text { Number of CDs bought by Kristin }}{\text { Total number of CDs }}=\frac{3}{8}\)and fraction of CDs, she received as gifts
\(=\frac{\text { Number of CDs recieved as gift }}{\text { Total number of CDs }}=\frac{5}{8}\)Question 11. Show 3/5 on a number line.
Solution. We know that 3/5 is greater than zero but less than 1. So, it will lie between 0 and 1.
Since, we have to show 3/5, so we have to divide the gap between 0 and 1 into five equal parts. Then, each part shows 1/5 and 3 parts will show 3/5.
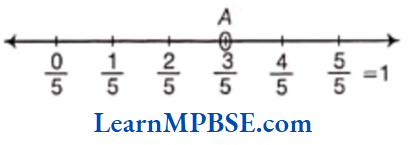
[also, \(\frac{0}{5}\) = 0]
Hence, point A represents 3/5.
Question 12. Show \(\frac{1}{10}\), \(\frac{0}{10}\), \(\frac{5}{10}\) and \(\frac{10}{10}\) on a number line.
Solution. We know that all given fractions are greater than or equal to zero but less than or equal to 1.
So, we have to divide the gap between 0 and 1 into ten equal parts, then each part shows \(\frac{1}{10}\) and 5 parts show \(\frac{5}{10}\), 10 parts show \(\frac{10}{10}\). Also, 0 shows \(\frac{0}{10}\)
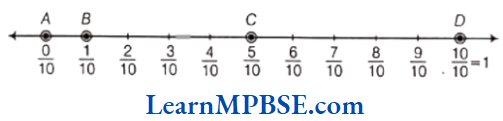
[also, \(\frac{0}{10}\) = 0]
Hence, points A, B, C and D represent the fractions \(\frac{0}{10}, \frac{1}{10}, \frac{5}{10} \text { and } \frac{10}{10}\) and respectively.
Types of Fractions Class 6
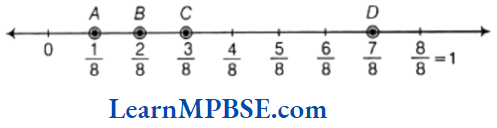
Question 13. Can you show any other fraction between 0 and 1? Write five more fractions that you can show and depict them on the number line.
Solution. Yes, we can show many other fractions which are greater than 0 and less than 1 i.e. between 0 and 1.
Five other fractions are \(\frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{4}{8} \text { and } \frac{5}{8}\)
These fractions are shown on a number line as given below
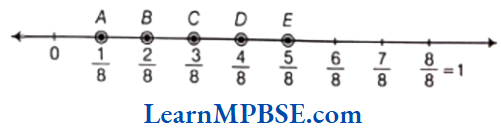
Here, points A, B, C, D and E represent \(\frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{4}{8} \text { and } \frac{5}{8}\) respectively.
Question 14. How many fractions lle between 0 and 1? Think, discuss and write your answer?
Solution. There are infinite number of points between 0 and 1 on the number line. So, there are infinite number of fractions lie between 0 and 1.
Question 15. Give a proper fraction,
(1) whose numerator is 5 and denominator is 7.
(2) whose denominator is 9 and numerator is 5.
(3) whose numerator and denominator add upto 10. How many fractions of this kind can you make?
(4) whose denominator is 4 more than the numerator.
Give any five. How many more can you make?
Solution. (1) Numerator = 5 and denominator = 7
∴ Required fraction = \(\frac{5}{7}\)
(2) Numerator = 5 and denominator = 9
∴ Required fraction = \(\frac{5}{9}\)
(3) Possible pairs of numerator and denominator which add upto 10 are (0,10), (1, 9), (2, 8), (3, 7) and (4, 6).
Now, proper fractions = \(\frac{0}{10}, \frac{1}{9}, \frac{2}{8}, \frac{3}{7} \text { and } \frac{4}{6}\)
There are five fractions. So, we can make five such fractions.
(4) There can be infinite number of fractions whose denominator is 4 more than the numerator. Some of them are \(\frac{0}{4}, \frac{1}{5}, \frac{2}{6}, \frac{3}{7} \text { and } \frac{4}{8}\)
Types of Fractions Class 6
Question 1. Draw number lines and locate the points on them.
(1) \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{3}{4}\), \(\frac{4}{4}\)
(2) \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\), \(\frac{7}{8}\)
(3) \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{8}{5}\), \(\frac{4}{5}\)
Solution. Here, fractions are \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{3}{4}\), \(\frac{4}{4}\). Also, \(\frac{1}{2}=\frac{1 \times 2}{2 \times 2}=\frac{2}{4}\)
Now, draw a number line, mark two points 0 and 1 on it. Divide the gap between 0 and 1 into four equal parts because denominator is 4, then each part will show \(\frac{1}{4}\). Also, 2 parts show \(\frac{2}{4}\), 3 parts show \(\frac{3}{4}\) and 4 parts show \(\frac{4}{4}\).
Hence, A, B, C and D represent \(\frac{1}{4}\), \(\frac{2}{4}\), \(\frac{3}{4}\) and \(\frac{4}{4}\) respectively.
Here, fractions are \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\) and \(\frac{7}{8}\).
Now, draw a number line, mark two points 0 and 1 on it. Divide the gap between 0 and 1 into eight equal parts because denominator is 8, then each part will show \(\frac{1}{8}\). Also, 2 parts show \(\frac{2}{8}\), 3 parts show \(\frac{3}{8}\) and 7 parts show \(\frac{7}{8}\).
Hence, A, B, C and D represent \(\frac{1}{8}\), \(\frac{2}{8}\), \(\frac{3}{8}\) and \(\frac{7}{8}\) respectively.
(3) Here, fractions are \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\) and \(\frac{8}{5}\).
Now, draw a number line, mark two points 0 and 1 on it. Divide the gap between 0 and 1 into five equal parts because denominator is 5, then each part will show \(\frac{1}{5}\).
Also, 2 parts show \(\frac{2}{5}\), 3 parts show \(\frac{3}{5}\), 4 parts show \(\frac{4}{5}\) and \(\frac{8}{5}\) lies between 2 and 2.
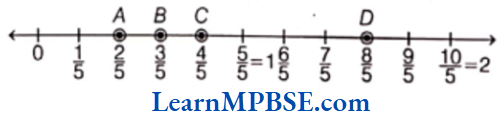
Hence, A, B, C and D represent \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\) and \(\frac{8}{5}\) respectively.
Question 2. Express the following as mixed fractions.
(1) \(\frac{20}{3}\)
(2) \(\frac{11}{5}\)
Solution. (1) We have, \(\frac{20}{3}\)
On dividing 20 by 3, we get quotient = 6, remainder = 2
∴ \(\frac{20}{3}\) = \(6 \frac{2}{3}\) i.e. 6 whole and \(\frac{2}{3}\) more
(2) We have, \(\frac{11}{5}\)
On dividing 11 by 5, we get quotient = 2, remainder = 1
∴ \(\frac{11}{5}\) = \(2 \frac{1}{5}\) i.e. 2 whole and \(\frac{1}{5}\) more
Types of Fractions Class 6
Question 3. Express the following as improper fractions.
(1) \(7 \frac{3}{4}\)
(2) \(5 \frac{6}{7}\)
(3) \(2 \frac{5}{6}\)
(4) \(10 \frac{3}{5}\)
(5) \(9 \frac{3}{7}\)
(6) \(8 \frac{4}{9}\)
Solution. (1) \(7 \frac{3}{4}=7+\frac{3}{4}=\frac{7 \times 4+3}{4}=\frac{31}{4}\)
(2) \(5 \frac{6}{7}=5+\frac{6}{7}=\frac{5 \times 7+6}{7}=\frac{41}{7}\)
(3) \(2 \frac{5}{6}=2+\frac{5}{6}=\frac{2 \times 6+5}{6}=\frac{17}{6}\)
(4) \(10 \frac{3}{5}=10+\frac{3}{5}=\frac{10 \times 5+3}{5}=\frac{53}{5}\)
(5) \(9 \frac{3}{7}=9+\frac{3}{7}=\frac{9 \times 7+3}{7}=\frac{66}{7}\)
(6) \(8 \frac{4}{9}=8+\frac{4}{9}=\frac{8 \times 9+4}{9}=\frac{76}{9}\)
Question 4. Are \(\frac{1}{3}\) and \(\frac{2}{7}\); \(\frac{2}{5}\) and \(\frac{2}{7}\); \(\frac{2}{9}\) and \(\frac{6}{27}\) equivalent? Give reason.
Solution. (1) \(\frac{1}{3}\) and \(\frac{2}{7}\)
Here, 1 x 7 = 7 and 3 x 2 = 6
∴ 7 ≠ 6, So \(\frac{1}{3}\) and \(\frac{2}{7}\) are not equivalent fractions.
(2) \(\frac{2}{5}\) and \(\frac{2}{7}\)
Here, 2 x 7 = 14 and 5 x 2 = 10
∴ 14 ≠ 10, so \(\frac{2}{5}\) and \(\frac{2}{7}\) are not equivalent fractions.
(3) \(\frac{2}{9}\) and \(\frac{6}{27}\)
Here, 2 x 27 = 54 and 9 x 6 = 54
∴ 54 = 54, so \(\frac{2}{9}\) and \(\frac{6}{27}\) are equivalent fractions.
Question 5. Give examples of four equivalent fractions.
Solution. Four equivalent fractions are \(\frac{1}{2}, \frac{2}{4}, \frac{3}{6}, \frac{4}{8},\) etc.
Comparing Fractions Class 6
Question 6. Find five equivalent fractions of each of the following.
(1) \(\frac{2}{3}\)
(2) \(\frac{1}{5}\)
Solution. (1) Five equivalent fractions of \(\frac{2}{3}\) are as follows.
\(\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6} ; \frac{2}{3}=\frac{2 \times 3}{3 \times 3}=\frac{6}{9} ; \frac{2}{3}=\frac{2 \times 4}{3 \times 4}=\frac{8}{12}\) \(\frac{2}{3}=\frac{2 \times 5}{3 \times 5}=\frac{10}{15} ; \frac{2}{3}=\frac{2 \times 6}{3 \times 6}=\frac{12}{18}\)Thus, five equivalent fractions of \(\frac{2}{3}\) are \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}\) and \(\frac{12}{18}\).
(2) Five equivalent fractions of \(\frac{1}{5}\) are as follows.
\(\frac{1}{5}=\frac{1 \times 2}{5 \times 2}=\frac{2}{10} ; \frac{1}{5}=\frac{1 \times 3}{5 \times 3}=\frac{3}{15} ;\) \(\frac{1}{5}=\frac{1 \times 4}{5 \times 4}=\frac{4}{20} ; \frac{1}{5}=\frac{1 \times 5}{5 \times 5}=\frac{5}{25},\) \(\frac{1}{5}=\frac{1 \times 6}{5 \times 6}=\frac{6}{30}\)Thus, five equivalent fractions of \(\frac{1}{5}\) are \(\frac{2}{10}, \frac{3}{15}, \frac{4}{20}, \frac{5}{25}\) and \(\frac{6}{30}\).
Question 7. Write the simplest form of:
(1) \(\frac{15}{75}\)
(2) \(\frac{16}{72}\)
Solution. (1) We have, \(\frac{15}{75}\)
Now, factors of 15 = 3 x 5
and factors of 75 = 3 x 5 x 5
Common factors = 3 and 5
∴ HCF of 15 and 75 = 3 x 5 = 15
Then, \(\frac{15}{75}=\frac{15+15}{75+15}=\frac{1}{5}\)
Hence, fraction \(\frac{1}{5}\) is the simplest form of given fraction.
(2) We have, \(\frac{16}{72}\)
Now, factors of 16 = 2 x 2 x 2 x 2
and factors of 72 = 2 x 2 x 2 x 3 x 3
Common factors = 2, 2 and 2
∴ HCF of 16 and 72 = 2 x 2 x 2 = 8
Then, \(\frac{16}{72}=\frac{16 \div 8}{72 \div 8}=\frac{2}{9}\)
Hence, fraction \(\frac{2}{9}\) is the simplest form of given fraction.
Comparing Fractions Class 6
Question 8. Is \(\frac{49}{64}\) in its simplest form?
Solution. Here, factors of 49 = 7 x 7 and factors of 64 = 8 x 8
∴ 49 and 64 have no common factor except 1.
Hence, fraction \(\frac{49}{64}\) is in simplest form.
Question 1. Write the fractions. Are all these fractions equivalent?
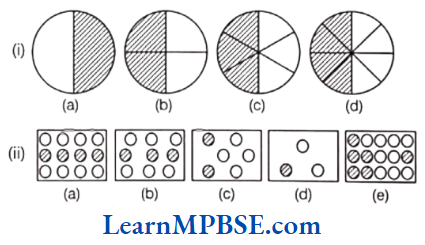
Solution. (1) (a) Total number of equal parts = 2
Number of shaded parts = 1
∴ Fraction of shaded portion \(=\frac{\text { Number of shaded parts }}{\text { Total number of equal paarts }}=\frac{1}{2}\)
(b) Total number of equal parts = 4;
Number of shaded parts = 2
∴ Fraction of shaded portion = \(\frac{2}{4}\)
(c) Total number of equal parts = 6;
Number of shaded parts = 3
∴ Fraction of shaded portion = \(\frac{3}{6}\)
(d) Total number of equal parts = 8;
Number of shaded parts = 4
∴ Fraction of shaded portion = \(\frac{4}{8}\)
Now, \(\frac{2}{4}=\frac{2+2}{4 \div 2}=\frac{1}{2}\) [∴ HCF of 2 and 4 is 2]
\(\frac{3}{6}=\frac{3 \div 3}{6+3}=\frac{1}{2}\) [∴ HCF of 3 and 6 is 3]
\(\frac{4}{8}=\frac{4 \div 4}{8 \div 4}=\frac{1}{2}\) [∴ HCF of 4 and 8 is 4]
Since, all fractions in simplest form are same.
∴ \(\frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\frac{4}{8}\) i.e. the fractions are equivalent.
(2) (a) Total number of equal parts = 12;
Number of shaded parts = 4
∴ Fraction of shaded portion = \(\frac{4}{12}\)
(b) Total number of equal parts = 9;
Number of shaded parts = 3
∴ Fraction of shaded portion = \(\frac{3}{9}\)
(c) Total number of equal parts = 6;
Number of shaded parts = 2
∴ Fraction of shaded portion = \(\frac{1}{3}\)
(d) Total number of equal parts = 3;
Number of shaded parts = 1
∴ Fraction of shaded portion = \(\frac{1}{3}\)
(e) Total number of equal parts = 15;
Number of shaded parts = 6
∴ Fraction of shaded portion = \(\frac{6}{15}\)
Now, \(\frac{4}{12}=\frac{4 \div 4}{12 \div 4}=\frac{1}{3}\) [∴ HCF of 4 and 12 is 4]
\(\frac{3}{9}=\frac{3+3}{9+3}=\frac{1}{3}\) [∴ HCF of 3 and 9 is 3]
\(\frac{2}{6}=\frac{2+2}{6+2}=\frac{1}{3}\) [∴ HCF of 2 and 6 is 2]
\(\frac{6}{15}=\frac{6+3}{15+3}=\frac{2}{5}\) [∴ HCF of 6 and 15 is 3]
Here, except \(\frac{6}{15}\) all the fractions in simplest form are same.
Question 2. Find the equivalent fraction of \(\frac{3}{5}\) having
(1) denominator 20
(2) numerator 9
Solution. Let N stands for the numerator and D stands for the denominator.
(1) Given, denominator of an equivalent fraction = 20
∴ \(\frac{N}{20}\) = \(\frac{3}{5}\) ⇒ N x 5 = 20 x 3
So, N x 5 = 4 x 5 x 3 [∴ 20 = 4 x 5]
⇒ N x 5 = 12 x 5
On comparing, we get N = 12
∴ Required equivalent fraction of \(\frac{3}{5}=\frac{N}{D}=\frac{12}{20}\)
(2) Given, numerator of an equivalent fraction = 9
∴ \(\frac{9}{D}\) = \(\frac{3}{5}\) ⇒ D x 3 = 9 x 5
So, D x 3 = 3 x 3 x 5 [∴ 9 = 3 x 3]
⇒ D x 3 = 15 x 3
On comparing, we get D = 15
∴ Required equivalent fraction of \(\frac{3}{5}=\frac{N}{D}=\frac{9}{15}\)
Comparing Fractions Class 6
Question 3. Check whether the given fractions are equivalent.
(1) \(\frac{5}{9}\), \(\frac{30}{54}\)
(2) \(\frac{3}{10}\), \(\frac{12}{50}\)
(3) \(\frac{7}{13}\), \(\frac{5}{11}\)
Solution.
(1) We have, \(\frac{5}{9}\) and \(\frac{30}{54}\)
Now, 5 x 54 = 270; 9 x 30 = 270 [by cross-product]
∴ 270 = 270
∴ \(\frac{5}{9}\) and \(\frac{30}{54}\) are equivalent fractions.
(2) We have, \(\frac{3}{10}\) and \(\frac{12}{50}\)
Now, 3 x 50 = 150; 10 x 12 = 120 [by cross-product]
But 150 ≠ 120
∴ \(\frac{3}{10}\) and \(\frac{12}{50}\) are not equivalent fractions.
(3) We have, \(\frac{7}{13}\) and \(\frac{5}{11}\)
Now, 7 x 11 = 77; 13 x 5 = 65 [by cross-product]
But 77 ≠ 65
∴ \(\frac{7}{13}\) and \(\frac{5}{11}\) are not equivalent fractions.
Question 4. Reduce the following fractions to simplest form.
(1) \(\frac{48}{60}\)
(2) \(\frac{150}{60}\)
Solution. (1) We have, \(\frac{48}{60}\)
Now, factors of 48 = 2, 2, 2, 2, 3
and factors of 60 = 2, 2, 3, 5
Common factors = 2, 2 and 3
HCF of 48 and 60 = 2 x 2 x 3 = 12
∴ \(\frac{48}{60}=\frac{48+12}{60+12}=\frac{4}{5}\)
Hence, the simplest form of the fraction \(\frac{48}{60}\) is \(\frac{4}{5}\).
(2) We have, \(\frac{150}{60}\)
Now, factors of 150 = 2, 3, 5, 5
and factors of 60 = 2, 2, 3, 5
Common factors = 2, 3 and 5
HCF of 150 and 60 = 2 x 3 x 5 = 30
∴ \(\frac{150}{60}=\frac{150+30}{60+30}=\frac{5}{2}\)
Hence, the simplest form of the fraction \(\frac{150}{60}\) is \(\frac{5}{2}\).
Comparing Fractions Class 6
Question 5. Ramesh had 20 pencils, Sheelu had 50 pencils and Jamaal had 80 pencils. After 4 months, Ramesh used up 10 pencils, Sheelu used up 25 pencils and Jamaal used up 40 pencils. What fraction did each used up? Check if each has used up an equal fraction of her/his pencils?
Solution. Here, the fraction of pencils used by Ramesh = \(\frac{10}{20}\)
Fraction of pencils used by Sheelu = \(\frac{25}{50}\)
Fraction of pencils used by Jamaal = \(\frac{40}{80}\)
Now, \(\frac{10}{20}=\frac{10 \div 10}{20 \div 10}=\frac{1}{2}\) [∴ HCF of 10 and 20 is 10]
\(\frac{25}{50}=\frac{25 \div 25}{50 \div 25}=\frac{1}{2}\) [∴ HCF of 25 and 50 is 25]
and \(\frac{40}{80}=\frac{40 \div 40}{80 \div 40}=\frac{1}{2}\) [∴ HCF of 40 and 80 is 40]
Thus, \(\frac{10}{20}=\frac{25}{50}=\frac{40}{80}=\frac{1}{2}\)
Question 6. You get one-fifth of a bottle of juice and your sister gets one-third of the same size of a bottle of juice. Who gets more?
Solution. Here, we will compare one-fifth i.e. \(\frac{1}{5}\) and one-third i.e. \(\frac{1}{3}\).
Since \(\frac{1}{5}\) and \(\frac{1}{3}\) have same numerator, so the fraction with smaller denominator is greater.
Thus, \(\frac{1}{3}\) > \(\frac{1}{5}\)
Thus, your sister gets more juice.
Question 7. Write these is ascending and also in descending order.
(1) \(\frac{1}{8}, \frac{5}{8}, \frac{3}{8}\)
Solution. (1) We have, \(\frac{1}{8}, \frac{5}{8}, \frac{3}{8}\)
Here, denominators of all fractions are same.
∴ Ascending order of numerators = 1 < 3 < 5
and descending order of numerators = 5 > 3 > 1
∴ Ascending order of fractions = \(\frac{1}{8}<\frac{3}{8}<\frac{5}{8}\)
and descending order of fractions = \(\frac{5}{8}>\frac{3}{8}>\frac{1}{8}\)
Question 8. Arrange the following in ascending and descending order.
(1) \(\frac{1}{12}, \frac{1}{23}, \frac{1}{5}, \frac{1}{7}, \frac{1}{50}, \frac{1}{9}, \frac{1}{17}\)
(2) \(\frac{3}{7}, \frac{3}{11}, \frac{3}{5}, \frac{3}{2}, \frac{3}{13}, \frac{3}{4}, \frac{3}{17}\)
(3) Write 3 more similar examples and arrange them in ascending and descending order.
Solution. (1) Here, numerators of all fractions are same.
Descending order of denominators = 50 > 23 > 17 > 12 > 9 > 7 > 5
∴ Ascending order of fractions = \(\frac{1}{50}<\frac{1}{23}<\frac{1}{17}<\frac{1}{12}<\frac{1}{9}<\frac{1}{7}<\frac{1}{5}\)
[∴ \(\frac{1}{50}\) has larger denominator, so it is smallest fraction]
and descending order of fractions = \(\frac{1}{5}>\frac{1}{7}>\frac{1}{9}>\frac{1}{12}>\frac{1}{17}>\frac{1}{23}>\frac{1}{50}\)
(2) Here, numerators of all fractions are same.
Descending order of denominators = 17 > 13 > 11 > 7 > 5 > 4 > 2
∴ Ascending order of fractions = \(\frac{3}{17}<\frac{3}{13}<\frac{3}{11}<\frac{3}{7}<\frac{3}{5}<\frac{3}{4}<\frac{3}{2}\)
and descending order of fractions = \(\frac{3}{2}>\frac{3}{4}>\frac{3}{5}>\frac{3}{7}>\frac{3}{11}>\frac{3}{13}>\frac{3}{17}\)
(3) Three more similar examples can be taken as
(a) \(\frac{2}{11}, \frac{2}{21}, \frac{2}{9}, \frac{2}{7}, \frac{2}{8}, \frac{2}{15}\)
Here, descending order of denominators = 21 > 15 > 11 > 9 > 8 > 7
∴ Ascending order of fractions = \(\frac{2}{21}<\frac{2}{15}<\frac{2}{11}<\frac{2}{9}<\frac{2}{8}<\frac{2}{7}\)
and descending order of fractions = \(\frac{2}{7}>\frac{2}{8}>\frac{2}{9}>\frac{2}{11}>\frac{2}{15}>\frac{2}{21}\)
(b) \(\frac{4}{5}, \frac{4}{6}, \frac{4}{13}, \frac{4}{2}, \frac{4}{9}, \frac{4}{11}\)
Here, descending order of denominators = 13 > 11 > 9 > 6 > 5 > 2
∴ Ascending order of fractions = \(\frac{4}{13}<\frac{4}{11}<\frac{4}{9}<\frac{4}{6}<\frac{4}{5}<\frac{4}{2}\)
and descending order of fractions = \(\frac{4}{2}>\frac{4}{5}>\frac{4}{6}>\frac{4}{9}>\frac{4}{11}>\frac{4}{13}\)
(c) \(\frac{7}{11}, \frac{7}{13}, \frac{7}{5}, \frac{7}{2}, \frac{7}{3}, \frac{7}{4}\)
Here, descending order of denominators = 13 > 11 > 5 > 4 > 3 > 2
∴ Ascending order of fractions = \(\frac{7}{13}<\frac{7}{11}<\frac{7}{5}<\frac{7}{4}<\frac{7}{3}<\frac{7}{2}\)
and descending order of fractions = \(\frac{7}{2}>\frac{7}{3}>\frac{7}{4}>\frac{7}{5}>\frac{7}{11}>\frac{7}{13}\)
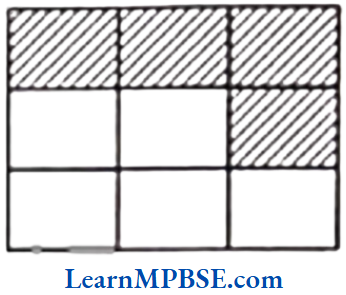
Question 1. Write shaded portion as fraction. Arrange them in ascending and descending order using correct sign ‘<‘, ‘=’, ‘>’ between the fractions.
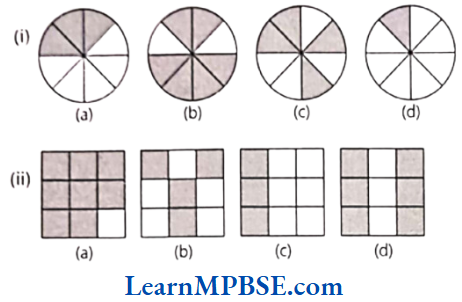
Solution. (1) Here, the total number of equal parts in all figures = 8
Shaded portion of figure (a) represents fraction = \(\frac{3}{8}\)
Shaded portion of figure (b) represents fraction = \(\frac{6}{8}\)
Shaded portion of figure (c) represents fraction = \(\frac{4}{8}\)
Shaded portion of figure (d) represents fraction = \(\frac{1}{8}\)
∴ Denominators of all fractions are same. So, we arrange them in ascending and descending order according to their numerators.
∴ Ascending order of fractions = \(\frac{1}{8}<\frac{3}{8}<\frac{4}{8}<\frac{6}{8}\)
[∴ fraction having small numerator will be smaller]
and descending order of fractions = \(\frac{6}{8}>\frac{4}{8}>\frac{3}{8}>\frac{1}{8}\)
[∴ fraction having greatest numerator will be greatest]
(2) Here, the total number of equal parts in all figures = 9
Shaded portion of figure (a) represents fraction = \(\frac{8}{9}\)
Shaded portion of figure (b) represents fraction = \(\frac{4}{9}\)
Shaded portion of figure (c) represents fraction = \(\frac{3}{9}\)
Shaded portion of figure (d) represents fraction = \(\frac{6}{9}\)
∴ Denominators of all fractions are same. So, we arrange them in ascending and descending order according to their numerators.
∴ Ascending order of fractions = \(\frac{3}{9}<\frac{4}{9}<\frac{6}{9}<\frac{8}{9}\)
and descending order of fractions = \(\frac{8}{9}>\frac{6}{9}>\frac{4}{9}>\frac{3}{9}\)
Comparing Fractions Class 6
Question 2. The following fractions represent just three different numbers. Separate them into three groups of equivalent fractions, by changing each one to its simplest form.
(1) \(\frac{2}{12}\)
(2) \(\frac{3}{15}\)
(3) \(\frac{8}{50}\)
(4) \(\frac{16}{100}\)
(5) \(\frac{10}{60}\)
(6) \(\frac{15}{75}\)
(7) \(\frac{12}{60}\)
(8) \(\frac{16}{96}\)
(9) \(\frac{12}{75}\)
(10) \(\frac{12}{72}\)
(11) \(\frac{3}{18}\)
(12) \(\frac{4}{25}\)
Solution. First, we have to convert all the fractions in its simplest form.
(1) We have, \(\frac{2}{12}\) ⇒ \(\frac{2 \div 2}{12 \div 2}=\frac{1}{6}\) [∴ HCF of 2 and 12 = 2]
(2) We have, \(\frac{3}{15}\) ⇒ \(\frac{3 \div 3}{15 \div 3}=\frac{1}{5}\) [∴ HCF of 3 and 15 = 3]
(3) We have, \(\frac{8}{50}\) ⇒ \(\frac{8 \div 2}{50 \div 2}=\frac{4}{25}\) [∴ HCF of 8 and 50 = 2]
(4) We have, \(\frac{16}{100}\) ⇒ \(\frac{16 \div 4}{100 \div 4}=\frac{4}{25}\) [∴ HCF of 16 and 100 = 4]
(5) We have, \(\frac{10}{60}\) ⇒ \(\frac{10+10}{60+10}=\frac{1}{6}\) [∴ HCF of a0 and 60 = 10]
(6) We have, \(\frac{15}{75}\) ⇒ \(\frac{15+15}{75+15}=\frac{1}{5}\) [∴ HCF of 15 and 75 = 15]
(7) We have, \(\frac{12}{60}\) ⇒ \(\frac{12+12}{60+12}=\frac{1}{5}\) [∴ HCF of 12 and 60 = 12]
(8) We have, \(\frac{16}{96}\) ⇒ \(\frac{16+16}{96+16}=\frac{1}{6}\) [∴ HCF of 16 and 96 = 16]
(9) We have, \(\frac{12}{75}\) ⇒ \(\frac{12 \div 3}{75+3}=\frac{4}{25}\) [∴ HCF of 12 and 75 = 3]
(10) We have, \(\frac{3}{18}\) ⇒ \(\frac{3 \div 3}{18 \div 3}=\frac{1}{6}\) [∴ HCF of 12 and 72 = 12]
(11) We have, \(\frac{3}{18}\) ⇒ \(\frac{3 \div 3}{18 \div 3}=\frac{1}{6}\) [∴ HCF of 3 and 18 = 3]
(12) We have, \(\frac{4}{25}\) ⇒ \(\frac{4 \div 1}{25 \div 1}=\frac{4}{25}\) [∴ HCF of 4 and 25 = 1]
Now, on grouping into three groups of equivalent fractions with the help of simplest form of fractions, we get
(a) \(\frac{2}{12}=\frac{10}{60}=\frac{16}{96}=\frac{12}{72}=\frac{3}{18}\)
[simplest form of each fraction = \(\frac{1}{6}\)]
(b) \(\frac{3}{15}=\frac{15}{75}=\frac{12}{60}\)
[simplest form of each fraction = \(\frac{1}{5}\)]
(c) \(\frac{8}{50}=\frac{16}{100}=\frac{12}{75}=\frac{4}{25}\)
[simplest form of each fraction = \(\frac{4}{25}\)]
Question 3. Find answers to the following. Write and indicate how you solved them.
(1) Is \(\frac{5}{9}\) equal to \(\frac{4}{5}\)?
(2) Is \(\frac{9}{16}\) equal to \(\frac{5}{9}\)?
Solution. LCM of 9 and 5 = 45
Now, \(\frac{5}{9}=\frac{5 \times 5}{9 \times 5}=\frac{25}{45} \text { and } \frac{4}{5}=\frac{4 \times 9}{5 \times 9}=\frac{36}{45}\)
Thus, both fractions are like fractions but \(\frac{25}{45} \neq \frac{36}{45}\)
∴ \(\frac{5}{9} \neq \frac{4}{5}\)
(2) LCM of 16 and 9 = 144
Now, \(\frac{9}{16}=\frac{9 \times 9}{16 \times 9}=\frac{81}{144} \text { and } \frac{5}{9}=\frac{5 \times 16}{9 \times 16}=\frac{80}{144}\)
Thus, both fractions are like fractions but \(\frac{81}{144} \neq \frac{80}{144}\)
∴ \(\frac{9}{16} \neq \frac{5}{9}\)
Comparing Fractions Class 6
Question 4. Ila reads 25 pages of a book containing 100 pages. Lalita reads \(\frac{2}{5}\) of the same book. Who read less?
Solution. Fraction of book read b Ila = \(\frac{25}{100}\)
= \(\frac{25+25}{100+25}=\frac{1}{4}\)
[∴ HCF of 25 and 100 = 25]
Fraction of book read by Lalita = \(\frac{2}{5}\)
For comparing \(\frac{1}{4}\) and \(\frac{2}{5}\)
We have, 1 x 5 = 5 and 4 x 2 = 8 [by cross-product]
∴ 5 < 8
∴ \(\frac{1}{4}\) < \(\frac{2}{5}\)
Hence, Ila reads less pages of a book.
Question 5. Rafiq exercised for \(\frac{3}{6}\) of an hour, while Rohit exercised for \(\frac{3}{4}\) of an hour. Who exercised for a longer time?
Solution. Rafiq exercised for \(\frac{3}{6}\) h. Rohit exercised for \(\frac{3}{4}\) h.
Now, we have to compare \(\frac{3}{6}\) and \(\frac{3}{4}\).
Here, numerator of both fractions are same.
We know that if two fractions have same numerator, then the fraction having less denominator will be greater.
∴ \(\frac{3}{4}>\frac{3}{6}\)
Hence, Rohit exercised for a longer time.
Comparing Fractions Class 6
Question 6. In a class A of 25 students, 20 passed with 60% or more marks; in another class B of 30 students, 24 passed with 60% or more marks. In which class, was a greater fraction of students getting with 60% or more marks?
Solution. Fraction of students who got 60% or more marks in class A
= \(\frac{20}{25}=\frac{20 \div 5}{25+5}=\frac{4}{5}\)
[∴ HCF of 20 and 25 = 5]
Fraction of students who got 60% or more marks in class B
= \(\frac{24}{30}=\frac{24+6}{30 \div 6}=\frac{4}{5}\)
[∴ HCF of 24 and 30 = 6]
∴ \(\frac{20}{25}=\frac{24}{30}=\frac{4}{5}\)
So, it is clear that an equal number of students got 60% or more marks in both the classes.
Question 7. My mother divided an apple into 4 equal parts. She gave me two parts and to my brother one part. How much apple did she give to both of us together?
Solution. Here, mother divided an apple into 4 equal parts, so each part will represents \(\frac{1}{4}\). She gave me two parts i.e. \(\frac{2}{4}\) apple and she gave to my brother one part i.e. \(\frac{1}{4}\) part.
Part of apple she gave to both of us = \(\frac{2}{4}+\frac{1}{4}\)
∴ Here, denominators of both fractions are same, so we add numerator to find their sum.
i.e. \(\frac{2+1}{4}=\frac{3}{4}\)

Hence, she gave \(\frac{3}{4}\) apple to both of us
Question 8. Mother asked Neelu and her brother to pick stones from the wheat. Neelu picked one-fourth of the total stones in it and her brother also picked up one-fourth of the stones. What fraction of the stones did both pick up together?
Solution. Neelu and her brother picked up \(\frac{1}{4}\) th of stones each from the wheat.
∴ Total stones picked up by both of them
= \(\frac{1}{4}+\frac{1}{4}=\frac{1+1}{4}=\frac{2}{4}=\frac{1}{2}\)
Hence, both together picked up \(\frac{1}{2}\) fraction of the stones.
Question 9. Sohan was putting covers on his notebooks. He put one-fourth of the covers on Monday. He put another one-fourth on Tuesday and the remaining on Wednesday. What fraction of the covers did he put on Wednesday?
Solution. Covers putting by Sohan on Monday = \(\frac{1}{4}\)
Covers putting by him on Tuesday = \(\frac{1}{4}\)
∴ Covers putting by him on Wednesday
= \(1-\frac{1}{4}-\frac{1}{4}=\frac{4}{4}-\frac{1}{4}-\frac{1}{4}\)
[∴ 1 and \(\frac{4}{4}\) are equivalent fractions]
= \(\frac{4-1-1}{4}=\frac{2}{4}=\frac{1}{2}\)
Hence, he put one-half of the covers on Wednesday.
Comparing Fractions Class 6
Question 10. Add with the help of a diagram.
(1) \(\frac{1}{8}+\frac{1}{8}\)
(2) \(\frac{2}{5}+\frac{3}{5}\)
Solution.
(1) Here, draw two rectangles and divide them into 8 equal parts out of which 1 part is shaded. On adding them, we get 2 parts shaded out of 8 equal parts. Thus,
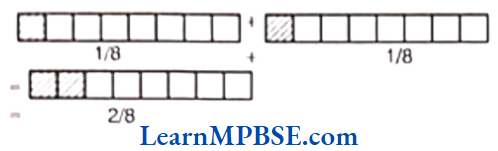
i.e. \(\frac{1}{8}+\frac{1}{8}=\frac{1+1}{8}=\frac{2}{8}=\frac{1}{4}\)
(2) Here, draw two rectangles and divide them into 5 equal parts separately. In first rectangle, 2 parts out of 5 parts are shaded and in second rectangle, 3 parts out of 5 parts are shaded. On adding them, we get all 5 parts shaded. Thus,
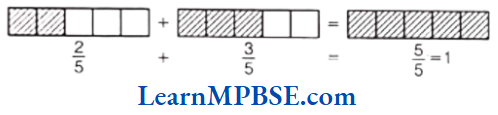
i.e. \(\frac{2}{5}+\frac{3}{5}=\frac{2+3}{5}=\frac{5}{5}=1\)
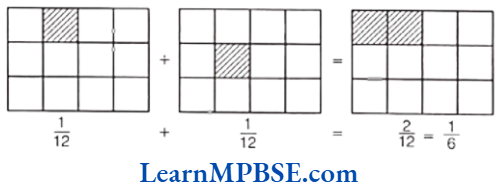
Question 11. Add \(\frac{1}{12}+\frac{1}{12}\). How will we show this pictorially? Using paper folding?
Solution. We have, \(\frac{1}{12}+\frac{1}{12}=\frac{1+1}{12}=\frac{2}{12}=\frac{1}{6}\)
Pictorially, it can be shown as
By folding paper, it can be shown in the following way Take a square piece of paper say ABCD.
Fold it by overlapping its edge AB and CD to get a figure.
Again, refold it by taking EF over C(A) D(B) to get a figure.

Now, reopen it, then we get the following figure
Now, fold it vertically at two places to obtain three equal vertical portion as shown in figure.
Shaded \(\frac{1}{12}\) portion twice,
We see that \(\frac{1}{12}+\frac{1}{12}=\frac{1+1}{12}=\frac{2}{12}=\frac{1}{6}\)
Question 12. Make 5 more examples of problems given in 1 and 2 above. Solve them with your friends.
Solution.
(1) \(\frac{1}{4}+\frac{1}{4}=\frac{1+1}{4}=\frac{2}{4}=\frac{1}{2}\)
[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]
(2) \(\frac{3}{6}+\frac{7}{6}+\frac{1}{6}=\frac{3+7+1}{6}=\frac{11}{6}\)
[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]
(3) \(\frac{5}{9}+\frac{8}{9}=\frac{5+8}{9}=\frac{13}{9}\)
[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]
(4) \(\frac{1}{10}+\frac{9}{10}=\frac{1+9}{10}=\frac{10}{10}=1\)
[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]
(5) \(\frac{11}{12}+\frac{4}{12}+\frac{5}{12}+\frac{6}{12}=\frac{11+4+5+6}{12}=\frac{26}{12}=\frac{13}{6}\)
[Since, denominator of both fractions are same. Thus, to add these we only add the numerators of both fractions and denominators remain same]
Comparing Fractions Class 6
Question 13. Find the difference between \(\frac{7}{8}\) and \(\frac{3}{8}\).
Solution. Given, \(\frac{7}{8}\) and \(\frac{3}{8}\)
∴ Difference = \(\frac{7}{8}-\frac{3}{8}=\frac{7-3}{8}=\frac{4}{8}=\frac{1}{2}\)
Question 14. Mother made a gud patti in a round shape. She divided it into 5 parts. Seema ate one piece from it. If I eat another piece, then how much would be left?
Solution. Total number of equal parts of gud patti = 5
Gud patti eaten by Seema = \(\frac{1}{5}\); Gud patti eaten by me = \(\frac{1}{5}\)
Fraction of gud patti eaten by Seema and me
= \(\frac{1}{5}+\frac{1}{5}=\frac{1+1}{5}=\frac{2}{5}\)
∴ Fraction of gud patti left out = \(\frac{1}{1}-\frac{2}{5}=\frac{5-2}{5}=\frac{3}{5}\)
Hence, \(\frac{3}{5}\)th of the gud patti would be left.
Question 15. My elder sister divided the watermelon into 16 parts. I ate 7 out of them. My friend ate 4. How much did we eat between us? How much more of the watermelon did I eat than my friend? What portion of the watermelon remained?
Solution. Here, a watermelon is divided into 16 parts.
∴ Each part = \(\frac{1}{16}\)
I ate 7 parts out of 16 parts i.e. \(\frac{7}{16}\) part
My friend ate 4 parts out of 16 parts i.e. \(\frac{4}{16}\) part
Now, the part which we eat together
= \(\frac{7}{16}+\frac{4}{16}=\frac{7+4}{16}=\frac{11}{16} \text { part }\)
Now, difference between our parts = \(\frac{7}{16}-\frac{4}{16}=\frac{7-4}{16}=\frac{3}{16}\)
So, I ate \(\frac{3}{16}\) part of watermelon more than my friend.
Now, remaining part of the watermelon = \(1-\frac{11}{16}=\frac{16}{16}-\frac{11}{16}\)
[∴ \(\frac{16}{16}\) and 1 are equivalent fractions]
= \(\frac{16-11}{16}=\frac{5}{16}\)
Question 1. Write these fractions appropriately as additions or subtractions:
Solution. (1) In first figure, fraction for shaded portion = \(\frac{1}{5}\)
In second figure, fraction for shaded portion = \(\frac{2}{5}\)
and in third figure, fraction for shaded portion = \(\frac{3}{5}\)
Here, third figure represents more shaded portion than first and second figures.
So, \(\frac{1}{5}+\frac{2}{5}=\frac{1+2}{5}=\frac{3}{5}\)
∴ The given figure will be as follows

(2) In first figure, fraction for shaded portion = 1 or \(\frac{5}{5}\)
In second figure, fraction for shaded portion = \(\frac{3}{5}\)
and in third figure, fraction for shaded portion = \(\frac{2}{5}\)
Here, third figure represents less shaded portion than first and second figure.
So, \(1-\frac{3}{5}=\frac{5-3}{5}=\frac{2}{5}\)
∴ The given figure represented as follows

Question 2. Solve
1. \(\frac{1}{18}+\frac{1}{18}\)
2. \(\frac{8}{15}+\frac{3}{15}\)
3. \(\frac{7}{7}-\frac{5}{7}\)
4. \(\frac{1}{22}+\frac{21}{22}\)
5. \(\frac{12}{15}-\frac{7}{15}\)
6. \(\frac{5}{8}+\frac{3}{8}\)
7. \(1-\frac{2}{3}\)
8. \(\frac{1}{4}+\frac{0}{4}\)
9. \(3-\frac{12}{5}\)
Solution. (1) We have, \(\frac{1}{18}+\frac{1}{18}=\frac{1+1}{18}=\frac{2}{18}=\frac{1}{9}\) [simplest form]
(2) We have, \(\frac{8}{15}+\frac{3}{15}=\frac{8+3}{15}=\frac{11}{15}\) [simplest form]
(3) We have, \(\frac{7}{7}-\frac{5}{7}=\frac{7-5}{7}=\frac{2}{7}\) [simplest form]
(4) We have, \(\frac{1}{22}+\frac{21}{22}=\frac{1+21}{22}=\frac{22}{22}=1\) [simplest form]
(5) We have, \(\frac{12}{15}-\frac{7}{15}=\frac{12-7}{15}=\frac{5}{15}=\frac{1}{3}\) [simplest form]
(6) We have, \(\frac{5}{8}+\frac{3}{8}=\frac{5+3}{8}=\frac{8}{8}=1\) [simplest form]
(7) We have, \(1-\frac{2}{3}=\frac{3}{3}-\frac{2}{3}=\frac{3-2}{3}=\frac{1}{3}\)
[∴ 1 and \(\frac{3}{3}\) are (simplest form) equivalent fractions]
(8) We have, \(\frac{1}{4}+\frac{0}{4}=\frac{1+0}{4}=\frac{1}{4}\) [simplest form]
(9) We have, \(3-\frac{12}{5}=\frac{3}{1}-\frac{12}{5}=\frac{3 \times 5}{1 \times 5}-\frac{12}{5}\)
[converting \(\frac{3}{1}\) into like fraction by multiplying numerator and denominator by 5]
= \(\frac{15}{5}-\frac{12}{5}=\frac{15-12}{5}=\frac{3}{5}\) [simplest form]
Question 3. Shubham painted \(\frac{2}{3}\) of the wall space in his room. His sister Madhavi helped and painted \(\frac{1}{3}\) of the wall space. How much did they paint together?
Solution. Portion of the wall painted by Shubham = \(\frac{2}{3}\)
Portion of the wall painted by Madhavi = \(\frac{1}{3}\)
Portion of the wall painted by both = \(\frac{2}{3}+\frac{1}{3}=\frac{2+1}{3}=\frac{3}{3}=1\)
Hence, they painted complete wall together.
Comparing Fractions Class 6
Question 4. Javed was given \(\frac{5}{7}\) of a basket of oranges. What fraction of oranges was left in the basket?
Solution. Let full basket = 1 = \(\frac{7}{7}\)
Part of oranges given to Javed = \(\frac{5}{7}\)
∴ Part of oranges left in the basket = \(\frac{7}{7}-\frac{5}{7}=\frac{7-5}{7}=\frac{2}{7}\)
Hence, \(\frac{2}{7}\) part of oranges was left in the basket.
Question 5. Add \(\frac{2}{5}\) and \(\frac{3}{7}\)
Solution. We have, \(\frac{2}{5}+\frac{3}{7}\)
LCM of 5 and 7 = 35
∴ \(\frac{2}{5}+\frac{3}{7}=\frac{2 \times 7}{5 \times 7}+\frac{3 \times 5}{7 \times 5}=\frac{14}{35}+\frac{15}{35}=\frac{14+15}{35}=\frac{29}{35}\)
Hence, \(\frac{2}{5}+\frac{3}{7}=\frac{29}{35}\)
Question 6. Subtract \(\frac{2}{5}\) from \(\frac{5}{7}\).
Solution. We have, \(\frac{5}{7}-\frac{2}{5}\)
LCM of 5 and 7 = 35
∴ \(\frac{5}{7}-\frac{2}{5}=\frac{5 \times 5}{7 \times 5}-\frac{2 \times 7}{5 \times 7}=\frac{25}{35}-\frac{14}{35}=\frac{25-14}{35}=\frac{11}{35}\)
Hence, \(\frac{5}{7}-\frac{2}{5}=\frac{11}{35}\)
Question 1. Solve
1. \(\frac{2}{3}\) + \(\frac{1}{7}\)
2. \(\frac{3}{10}\) + \(\frac{7}{15}\)
3. \(1 \frac{1}{3}+3 \frac{2}{3}\)
4. \(\frac{16}{5}-\frac{7}{5}\)
5. \(\frac{4}{3}-\frac{1}{2}\)
Solution. (1) We have, \(\frac{2}{3}\) + \(\frac{1}{7}\) (LCM of 3 and 7 = 21)
∴ \(\frac{2}{3}+\frac{1}{7}=\frac{2 \times 7}{3 \times 7}+\frac{1 \times 3}{7 \times 3}=\frac{14}{21}+\frac{3}{21}=\frac{14+3}{21}=\frac{17}{21}\)
Hence, \(\frac{2}{3}+\frac{1}{7}=\frac{17}{21}\)
(2) We have, \(\frac{3}{10}\) + \(\frac{7}{15}\) (LCM of 10 and 15 = 30)
∴ \(\frac{3}{10}+\frac{7}{15}=\frac{3 \times 3}{10 \times 3}+\frac{7 \times 2}{15 \times 2}=\frac{9}{30}+\frac{14}{30}=\frac{9+14}{30}=\frac{23}{30}\)
Hence, \(\frac{3}{10}+\frac{7}{15}=\frac{23}{30}\)
(3) We have, \(1 \frac{1}{3}+3 \frac{2}{3}\)
= \(1+\frac{1}{3}+3+\frac{2}{3}\)
= \((1+3)+\left(\frac{1}{3}+\frac{2}{3}\right)=4+\frac{1}{3}+\frac{2}{3}\)
Now, \(\frac{1}{3}+\frac{2}{3}=\frac{1+2}{3}=\frac{3}{3}=1\)
∴ \(4+\frac{1}{3}+\frac{2}{3}=4+1=5\)
Hence, \(1 \frac{1}{3}+3 \frac{2}{3}=5\)
(4) We have, \(\frac{16}{5}-\frac{7}{5}\)
∴ \(\frac{16}{5}-\frac{7}{5}=\frac{16-7}{5}=\frac{9}{5}\)
Hence, \(\frac{16}{5}-\frac{7}{5}=\frac{9}{5}\)
(5) We have, \(\frac{4}{3}-\frac{1}{2}\)
LCM of 3 and 2 = 6
∴ \(\frac{4}{3}-\frac{1}{2}=\frac{4 \times 2}{3 \times 2}-\frac{1 \times 3}{2 \times 3}=\frac{8}{6}-\frac{3}{6}=\frac{8-3}{6}=\frac{5}{6}\)
Hence, \(\frac{4}{3}-\frac{1}{2}=\frac{5}{6}\)
Comparing Fractions Class 6
Question 2. Sarita bought \(\frac{2}{5}\) metre of ribbon and Lalita bought \(\frac{3}{4}\) metre of ribbon. What is the total length of the ribbon they bought?
Solution. Given, ribbon bought by Sarita = \(\frac{2}{5}\) m
and ribbon bought by Lalita = \(\frac{3}{4}\) m
∴ Total length of the ribbon bought buy them = \(\frac{2}{5}\) + \(\frac{3}{4}\)
Now, LCM of 5 and 4 = 20
∴ \(\frac{2}{5}+\frac{3}{4}=\frac{2 \times 4}{5 \times 4}+\frac{3 \times 5}{4 \times 5}=\frac{8}{20}+\frac{15}{20}=\frac{8+15}{20}=\frac{23}{20}\)
Hence, the total length of ribbon bought by them is \(\frac{23}{20}\) m.
Question 3. Naina was given \(1 \frac{1}{2}\) piece of cake and Najma was given \(1 \frac{1}{3}\) piece of cake. Find the total amount of cake was given to both of them.
Solution. Cake given to Naina = \(1 \frac{1}{2}\) piece
Cake given to Najma = \(1 \frac{1}{3}\) piece
Total cake given to both of them
\(=1 \frac{1}{2}+1 \frac{1}{3}=\frac{1 \times 2+1}{2}+\frac{1 \times 3+1}{3}=\frac{3}{2}+\frac{4}{3}\)LCM of 2 and 3 = 6
∴ \(\frac{3}{2}+\frac{4}{3}=\frac{3 \times 3}{2 \times 3}+\frac{4 \times 2}{3 \times 2}=\frac{9}{6}+\frac{8}{6}=\frac{9+8}{6}=\frac{17}{6}\)
Hence, the total cake given to both of them = \(\frac{17}{6}\) piece
Question 4. Complete the addition subtraction box.
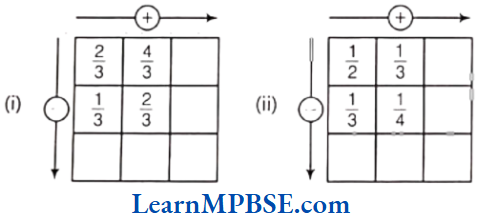
Solution. (1) Here, \(\frac{2}{3}+\frac{4}{3}=\frac{2+4}{3}=\frac{6}{3}=2 \text { and } \frac{1}{3}+\frac{2}{3}=\frac{1+2}{3}=\frac{3}{3}=1\)
Now, \(\frac{2}{3}-\frac{1}{3}=\frac{2-1}{3}=\frac{1}{3} \text { and } \frac{4}{3}-\frac{2}{3}=\frac{4-2}{3}=\frac{2}{3}\)
Also, we have 2 – 1 = 1 and \(\frac{1}{3}+\frac{2}{3}=\frac{1+2}{3}=\frac{3}{3}=1\)
Hence, the required complete box is
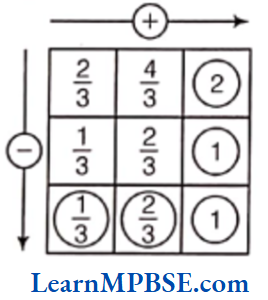
(2) Here, \(\frac{1}{2}+\frac{1}{3}=\frac{1 \times 3}{2 \times 3}+\frac{1 \times 2}{3 \times 2}=\frac{3}{6}+\frac{2}{6}=\frac{3+2}{6}=\frac{5}{6}\)
[∴ LCM of 2 and 3 = 6]
and \(\frac{1}{3}+\frac{1}{4}=\frac{1 \times 4}{3 \times 4}+\frac{1 \times 3}{4 \times 3}=\frac{4}{12}+\frac{3}{12}\)
= \(\frac{4+3}{12}=\frac{7}{12}\) [∴ LCM of 3 and 4 = 12]
Now, \(\frac{1}{2}-\frac{1}{3}=\frac{1 \times 3}{2 \times 3}-\frac{1 \times 2}{3 \times 2}\)
= \(\frac{3}{6}-\frac{2}{6}=\frac{3-2}{6}=\frac{1}{6}\)
[∴ LCM of 2 and 3 = 6]
and \(\frac{1}{3}-\frac{1}{4}=\frac{1 \times 4}{3 \times 4}-\frac{1 \times 3}{4 \times 3}\)
= \(\frac{4}{12}-\frac{3}{12}=\frac{4-3}{12}=\frac{1}{12}\)
[∴ LCM of 3 and 4 = 12]
Also, we have \(\frac{5}{6}-\frac{7}{12}=\frac{5 \times 2}{6 \times 2}-\frac{7 \times 1}{12 \times 1}\)
[∴ LCM of 6 and 12 = 12]
= \(\frac{10}{12}-\frac{7}{12}=\frac{10-7}{12}=\frac{3}{12}=\frac{1}{4}\)
[dividing numerator and denominator by 3]
and \(\frac{1}{6}+\frac{1}{12}=\frac{1 \times 2}{6 \times 2}+\frac{1 \times 1}{12 \times 1}\)
= \(\frac{2}{12}+\frac{1}{12}=\frac{2+1}{12}=\frac{3}{12}=\frac{1}{4}\)
[∴ LCM of 6 and 12 = 12]
[dividing numerator and denominator by 3]
Hence, the required complete box is
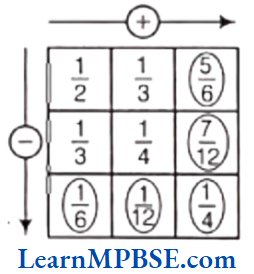
Question 5. A piece of wire \(\frac{7}{8}\) meter long broke into two pieces. One piece was \(\frac{1}{4}\) metre long. How long is the other piece?
Solution. Given, total length of a piece of wire = \(\frac{7}{8}\) m
Length of one piece of wire = \(\frac{1}{4}\) m
∴ Length of another piece = \(\left(\frac{7}{8}-\frac{1}{4}\right) \mathrm{m}\)
LCM of 8 and 4 = 8
∴ \(\frac{7}{8}-\frac{1}{4}=\frac{7 \times 1}{8 \times 1}-\frac{1 \times 2}{4 \times 2}\)
= \(\frac{7}{8}-\frac{2}{8}=\frac{7-2}{8}=\frac{5}{8}\)
Hence, the length of another piece of wire is \(\frac{5}{8}\) m.
Comparing Fractions Class 6
Question 6. Nandini’s house is \(\frac{9}{10}\) km from her school. She walked some distance and then took a bus for \(\frac{1}{2}\)km to reach the school. How far did she walk?
Solution. Given, distance of school from Nandini’s house = \(\frac{9}{10}\) km
Distance covered by Nandini by bus = \(\frac{1}{2}\) km
∴ Distance covered by Nandini by walking = \(\frac{9}{10}\) – \(\frac{1}{2}\)
LCM of 10 and 2 = 10
\(\frac{9}{10}-\frac{1}{2}=\frac{9 \times 1}{10 \times 1}-\frac{1 \times 5}{2 \times 5}=\frac{9}{10}-\frac{5}{10}\)= \(\frac{9-5}{10}=\frac{4}{10}=\frac{2}{5} \mathrm{~km}\)
Hence, she walked \(\frac{2}{5}\) km.
Question 7. Asha and Samuel have bookshelves of the same size partly filled with books. Asha’s shelf is \(\frac{5}{6}\)th full and Samuel’s shelf is \(\frac{2}{5}\)th full. Whose bookshelf is more full ? By what fraction?
Solution. The protion of Asha’s shelf filled by books = \(\frac{5}{6}\) part
and the portion of Samuel’s shelf filled by books = \(\frac{2}{5}\) part
Now, LCM of 6 and 5 = 30
Equivalent fractions of \(\frac{5}{6}\) are \(\frac{5 \times 2}{6 \times 2}, \frac{5 \times 3}{6 \times 3}, \frac{5 \times 4}{6 \times 4}, \frac{5 \times 5}{6 \times 5}, \ldots\)
i.e. \(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}, \frac{25}{30}, \ldots\)
and equivalent fractions of \(\frac{2}{5}\) are
\(\frac{2 \times 2}{5 \times 2}, \frac{2 \times 3}{5 \times 3}, \frac{2 \times 4}{5 \times 4}, \frac{2 \times 5}{5 \times 5}, \frac{2 \times 6}{5 \times 6}, \ldots\)i.e. \(\frac{4}{10}, \frac{6}{15}, \frac{8}{20}, \frac{10}{25}, \frac{12}{30}, \ldots\)
Here, equivalent fractions \(\frac{12}{30}\) and \(\frac{25}{30}\) have same denominator.
∴ 25 > 12
∴ \(\frac{25}{30}>\frac{12}{30} \text { i.e. } \frac{5}{6}>\frac{2}{5}\)
Now, \(\frac{5}{6}-\frac{2}{5}=\frac{25}{30}-\frac{12}{30}=\frac{25-12}{30}=\frac{13}{30}\)
Hence, Asha’s book shelf is more full by fraction \(\frac{13}{30}\).
Question 8. Jaidev takes \(2 \frac{1}{5}\) minutes to walk across the school ground. Rahul takes \(\frac{7}{4}\) minutes to do the same. Who takes less time and by what fraction?
Solution. Time taken by Jaidev to walk across the school ground = \(2 \frac{1}{5} \min =\frac{11}{5} \min\)
and time taken by Rahul to walk across the school ground = \(\frac{7}{4}\) min
Now, equivalent fractions of \(\frac{11}{5}\) are
\(\frac{11 \times 2}{5 \times 2}, \frac{11 \times 3}{5 \times 3}, \frac{11 \times 4}{5 \times 4}, \frac{11 \times 5}{5 \times 5}, \ldots \text { i.e. } \frac{22}{10}, \frac{33}{15}, \frac{44}{20}, \frac{55}{25}, \ldots\)and equivalent fractions of \(\frac{7}{4} are \frac{7 \times 2}{4 \times 2}, \frac{7 \times 3}{4 \times 3}, \frac{7 \times 4}{4 \times 4}, \frac{7 \times 5}{4 \times 5},\)
i.e. \(\frac{14}{8}, \frac{21}{12}, \frac{28}{16}, \frac{35}{20}, \ldots\)
Here, equivalent fractions \(\frac{44}{20}\) and \(\frac{35}{20}\) have same denominators.
∴ 44 > 35
∴ \(\frac{44}{20}>\frac{35}{20} \text { i.e. } \frac{11}{5}>\frac{7}{4}\)
Now, \(\frac{11}{5}-\frac{7}{4}=\frac{44}{20}-\frac{35}{20}=\frac{44-35}{20}=\frac{9}{20}\)
Hence, Rahul takes less time by \(\frac{9}{20}\) min.
Question 1. The two consecutive integers between which the fraction \(\frac{5}{7}\) lies are
Answer. 2. 0 and 1
Question 2. How is the fractional number of “3 out of 7 of the fruits are apples” written ?
Answer. 1. \(\frac{3}{7}\)
Comparing Fractions Class 6
Question 3. \(\frac{21}{19}\) can be expressed in form
Answer. 3. \(1 \frac{1}{19}\)
Question 4. Raju scored 9 m arks in maths test. If the maximum marks of the test is 25, how is Raju’s score represented as a fraction?
Answer. 3. \(\frac{9}{25}\)
Question 5. The fraction which is not equal to \(\frac{4}{5}\) is
Answer. 4. \(\frac{9}{15}\)
Question 6. If \(\frac{3}{4}\) is equivalent to \(\frac{x}{24}\), then the value of x is
Answer. 4. 18
Question 7. Which option given an equivalent fraction of \(\frac{13}{25}\) ?
Answer. 3. \(\frac{156}{300}\)
Question 8. When \(\frac{1}{4}\) is written with denominator as 12, its numerator is
Answer. 1. 3
Comparing Fractions Class 6
Question 9. When \(\frac{1}{7}\) is written with denominator as 56, its numerator is
Answer. 2. 8
Question 10. Which of the following is not in the lowest form?
Answer. 2. \(\frac{15}{20}\)
Question 11. Which of the following fraction is smallest?
Answer. 3. \(\frac{9}{23}\)
Question 12. If \(\frac{5}{8}\) = \(\frac{20}{p}\), then value of p is
Answer. 3. 32
Question 13. If \(\frac{7}{9}\) = \(\frac{28}{p}\), then value of p is
Answer. 3. 36
Question 14. What are the fractions with the same denominator called?
Answer. 3. Like fractions
Question 15. The ascending order of the fractions \(\frac{14}{17}, \frac{10}{12}, \frac{6}{7}\) and \(\frac{18}{22}\) is
Answer. 2. \(\frac{18}{22}, \frac{14}{17}, \frac{10}{12}, \frac{6}{7}\)
Question 16. Sum of \(\frac{4}{17}\) and \(\frac{15}{17}\) is
Answer. 2. \(1 \frac{2}{17}\)
Question 17. On subtracting \(\frac{6}{13}\) from \(\frac{11}{13}\), the result is
Answer. 1. \(\frac{5}{13}\)
Comparing Fractions Class 6
Question 18. What should be added to \(\frac{11}{17}\) to make it \(\frac{15}{17}\) ?
Answer. 3. \(\frac{4}{17}\)
Question 19. Choose the correct option for the sum of shaded parts of the given boxes.

Answer. 2. \(\frac{2}{5}+\frac{1}{5}=\frac{3}{5}\)
Question 1. Assertion (A) \(\frac{2}{7}\) is obtained when we divide a whole into seven equal parts and take two part.
Reason (R) A fraction is a number representing part of a whole.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 2. Assertion (A) The simplest form of \(\frac{12}{20}\) is \(\frac{3}{5}\)
Reason (R) A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 3. Assertion (A) \(\frac{4}{5}\) > \(\frac{6}{5}\)
Reason (R) For two fract ions with the same denominator, the fraction with greater numerator is greater.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (d) A is false but R is true.
Question 1. A number representing a part of a ….. is called a fraction.
Answer. Whole
Question 2. 1 whole = …. tenths.
Answer. 10
Question 3. A fraction with numerator greater than the denominator is called an ….. fraction.
Answer. Improper
Question 4. \(\frac{21}{13}\) is an ….. fraction.
Answer. Improper
Question 5. \(13 \frac{5}{18}\) is a …… fraction.
Answer. Mixed
Comparing Fractions Class 6
Question 1. If a whole of an object is divided into a number of equal parts, then each parts, then each part represents a fraction.
Answer. True
Question 2. The fraction represented by the shaded portion in the following figure is \(\frac{3}{8}\).

Answer. True
Question 3. The fraction represented by the unshaded portion in the following figure is \(\frac{5}{9}\).

Answer. False
Question 4. Ali divided one fruit cake equally among six persons. The part of the cake he gave to each person is \(\frac{1}{6}\).
Answer. True
Question 5. Sum of \(\frac{5}{12}\) and \(\frac{7}{12}\) is \(1 \frac{7}{12}\)
Answer. False
Question 1.
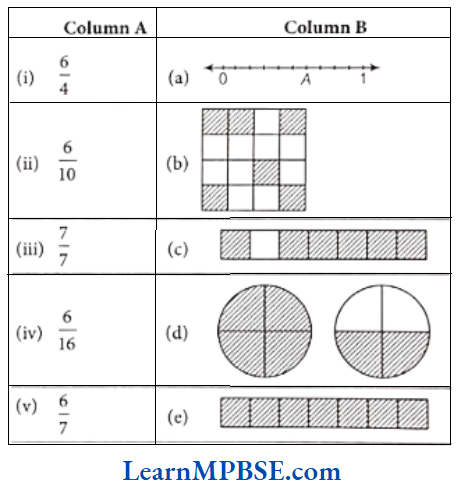
Solution. (i) → (d), (ii) → (a), (iii) → (e), (iv) → (b), (v) → (c)
Question 2.
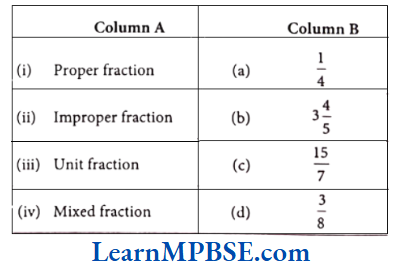
Solution. (i) → (d), (ii) → (c), (iii) → (a), (iv) → (b)
Question 3.
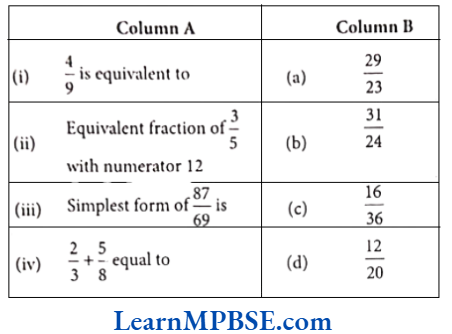
Solution. (i) → (c), (ii) → (d), (iii) → (a), (iv) → (b)
Question 1. Cross country is a running even in which runners completed a pre-decided distance.
It includes different activities in which runners cover different environments. A cross country running event of 11 km is as follows.
(1) What fraction of the total distance is the mud run?
(a) \(\frac{11}{1}\)
(b) \(\frac{1}{10}\)
(c) \(\frac{1}{11}\)
(d) 1
(2) What fraction of the total distance is the distance covered on paved and unpaved roads?
(a) \(\frac{3}{2}\)
(b) \(\frac{5}{5}\)
(c) \(\frac{5}{6}\)
(d) \(\frac{5}{11}\)
Solution. (1) (c) Total distance runner covers = 11km
Distance in mud run = 1 km
∴ Fraction of total distance in mud run \(=\frac{\text { Distance in mud run }}{\text { Total distance runner covers }}=\frac{1}{11}\)
(2) (d) Distance in paved road = 3 km.
Distance in unpaved road = 2 km.
∴ Total distance in both = \(\frac{3+2}{11}=\frac{5}{11}\)
Question 2. Katherine completed the cross country in 1 hr. She completed the run on the paved and unpaved roads in one-fourth of an hour while Juliana covered it in half an hour.
(1) In how many minutes did Katherine cover the distance on the paved and unpaved roads?
(a) 10 min
(b) 15 min
(c) 20 min
(d) 30 min
(2) How much more time (in hrs) was taken by Juliana than Katherine?
Solution. (1) (b) Katherine completed the cross country = 1hr
∴ Katherine covered the run on the paved and unpaved roads in one-fourth of an hour, which is equal to
\(\frac{1}{4} \times 1 \mathrm{~h}=\frac{1}{4} \times 60 \mathrm{~min}=15 \mathrm{~min}\)Thus, Katherine coveres the distance on paved and unpaved roads in 15 min.
(2) Katherine completed the run on the paved and unpaved road = \(\frac{1}{4}\) of 1 h = \(\frac{1}{4}\) x 60 min = 15 min
While Juliana covered the run on the paved and unpaved road = \(\frac{1}{2}\) of 1 h = \(\frac{1}{2}\) x 60 min = 30 min
Thus, Juliana time – Katherine time
= (30 – 15) = 15 min
Thus, Juliana takes 15 min or \(\frac{1}{4}\) of an hour more than Katherine.
Question 3. Parul and two of her friends share a pizza equally among themselves.
(1) Parul says, ‘Here are three equal halves of the pizza.’ Is parul’s statement correct? Give reasons.
(2) Which fraction represents one part of the whole pizza?
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) 3
Later, three more friends join Parul. Parul divides the pizza again to have 6 parts.
(3) Does every one get an equal portion? Give reasons.
(4) Suggest a way to divide the pizza into six equal parts.
Solution. (1) No, Parul’s statement is not correct. Pizza is divided into three equal parts, which is not half of the pizza.
(2) (b) Pizza divided into 3 parts.
Therefore, one part of pizza = \(\frac{1}{3}\).
(3) Three more friends joined Parul means now remaining pizza is divided again.
So, everyone does not get an equal portion of pizza.
(4) Usually pizzas are circular. Therefore, total angle = 360°
To divide 360 into 6 parts divide 360 by 6
i.e. \(\frac{360^{\circ}}{6}=60^{\circ}\)
Now, measure 60° and cut the pizza into 6 equal parts.
Question 1. 3 mm is what fraction of a metre?
Solution. We know that 1 m = 1000 mm
3 mm = \(\frac{3}{1000}\) made
So, 3 mm is \(\frac{3}{1000}\) of a metre.
Question 2. Write \(\frac{2}{3}\) of 60 kg.
Solution. We have, \(\frac{2}{3}\) of 60 kg = \(\frac{2 \times 60}{3}=2 \times 20=40 \mathrm{~kg}\)
Question 3. What fraction of the week is 3 days?
Solution. We know that 1 week = 7 days 3
∴ 3 days = \(\frac{3}{7}\) week
So, 3 days are of a week.
Question 4. 30 seconds is what fraction of a minute?
Solution. We know that 1 min = 60 s
i.e. 60 s = 1 min
\(30 \mathrm{~s}=\frac{30}{60} \mathrm{~min}=\frac{1}{2} \mathrm{~min}\)So, 30 sec are \(\frac{1}{2}\) of a minute.
Question 5. Name the fraction which are always less than 1.
Solution. We know that proper fractions are always less than 1.
Question 1. Write the natural numbers from 205 to 219. What fraction of them are odd numbers?
Solution. Natural numbers from 205 to 219 are 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219.
Total natural numbers = 15
Odd numbers = 8
∴ Required fraction = \(\frac{\text { Odd numbers }}{\text { Natural numbers }}=\frac{8}{15}\)
Question 2. What fraction of a kg is 650 gm?
Solution. We know that 1 kg = 1000 g
∴ \(650 \mathrm{gm}=\frac{650}{1000} \mathrm{~kg}=\frac{65}{100}\)
= \(\frac{65 \div 5}{100 \div 5}\) [∴ HCF of 65 and 100 is 5]
= \(\frac{13}{20}\)
So, 650 gm is \(\frac{13}{20}\) of a kg.
Question 3. Find the fraction that represents the number of natural numbers to total numbers of natural numbers to total numbers in the collection 0, 1, 2, 3, 4, 5. What fraction will it be for whole numbers?
Solution. Given collection is 0, 1, 2, 3, 4, 5.
Natural numbers = 1, 2, 3, 4, 5
∴ The fraction of natural numbers to the collection = \(\frac{5}{6}\)
Now, whole numbers = 0, 1, 2, 3, 4, 5
The fraction of whole numbers to the collection = \(\frac{6}{6}\) i.e. \(\frac{1}{1}\)
Question 4. Express the following as improper fraction.
(1) \(5 \frac{1}{4}\)
(2) \(7 \frac{2}{3}\)
Solution. (1) We have, \(5 \frac{1}{4}\)
Now, \(5 \frac{1}{4}=5+\frac{1}{4}=\frac{5 \times 4+1}{4}=\frac{21}{4}\)
(2) We have, \(7 \frac{2}{3}=7+\frac{2}{3}=\frac{7 \times 3+2}{3}=\frac{23}{3}\)
Question 5. Express the following as mixed fractions.
(1) \(\frac{15}{4}\)
(2) \(\frac{25}{6}\)
Solution. (1) We have, improper fraction = \(\frac{15}{4}\)
∴ \(\frac{15}{4}=3 \frac{3}{4}\)
(2) We have, improper fraction = \(\frac{25}{6}\)
∴ \(\frac{25}{6}=4 \frac{1}{6}\)
Question 6. Check whether the given fractions are equivalent.
(1) \(\frac{5}{7}\), \(\frac{9}{12}\)
(2) \(\frac{7}{5}\), \(\frac{21}{15}\)
Solution.
(1) We have, \(\frac{5}{7}\), \(\frac{9}{12}\) = \(\frac{5}{7}\) = \(\frac{9}{12}\)
⇒ 5 x 12 = 9 x 7
60 ≠ 63
So, \(\frac{5}{7}\), \(\frac{9}{12}\) are not equivalent fractions.
(2) We have, \(\frac{7}{5}\), \(\frac{21}{15}\) = \(\frac{7}{5}\) = \(\frac{21}{15}\)
⇒ 7 x 15 = 105, 21 x 5 = 105
So, \(\frac{7}{5}\), \(\frac{21}{15}\) are equivalent fractions.
Question 7. Write \(\frac{156}{60}\) in its lowest form.
Solution. We have, \(\frac{156}{60}\)
Now, we find the HCF of 156 and 60.
∴ HCF of 156 and 60 is 12.
So, \(\frac{156}{60}=\frac{156 \div 12}{60 \div 12}=\frac{13}{5}\)
Question 8. Compare \(4 \frac{2}{3} \text { and } 5 \frac{3}{7}\).
Solution. We have, \(4 \frac{2}{3} \text { and } 5 \frac{3}{7}\)
Now, \(4 \frac{2}{3}=\frac{4 \times 3+2}{3}=\frac{14}{3} \text { and } 5 \frac{3}{7}=\frac{5 \times 7+3}{7}=\frac{38}{7}\)
Now, let us compare \(\frac{14}{3}\) and \(\frac{38}{7}\) by cross-multiplication.
We have, \(\frac{14}{3}\) = \(\frac{38}{7}\)
14 x 7 = 98 and 38 x 3 = 114
∴ 114 > 98
∴ \(\frac{38}{7}\) > \(\frac{14}{3}\)
So, \(5 \frac{3}{7}>4 \frac{2}{3}\)
Question 9. Find the value of the following:
(1) \(\frac{6}{17}+\frac{3}{17}+\frac{11}{17}\)
(2) \(\frac{1}{2}+\frac{3}{4}+1 \frac{1}{3}\)
Solution.
(1) We have, \(\frac{6}{17}+\frac{3}{17}+\frac{11}{17}=\frac{6+3+11}{17}=\frac{20}{17}=1 \frac{3}{17}\)
(2) We have, \(\frac{1}{2}+\frac{3}{4}+1 \frac{1}{3}=\frac{1}{2}+\frac{3}{4}+\frac{4}{3}=\frac{6+9+16}{12}\)
[∴ LCM of 2, 4 and 3 is 12]
= \(\frac{31}{12}=2 \frac{7}{12}\)
Question 10. Neelam’s father needs \(1 \frac{3}{4}\) m of cloth for the skirt of Neelam’s new dress and \(\frac{1}{2}\) m for the scarf. How much cloth must he buy in all?
Solution. Cloth required for skirt = \(1 \frac{3}{4}\) m
Cloth required for scarf = \(\frac{1}{2}\) m
∴ Total cloth = \(\left(1 \frac{3}{4}+\frac{1}{2}\right) \mathrm{m}=\frac{7}{4}+\frac{1}{2}\)
\(\frac{7+2}{4}=\frac{9}{4}=2 \frac{1}{4} \mathrm{~m}\) [∴ LCM of 2 and 4 is 4]
So, he must buy \(2 \frac{1}{4}\) m cloth.
Question 11. Sunil purchased \(12 \frac{1}{2}\) L of juice on Monday and \(14 \frac{3}{4}\) L of lace for her new dress. How much lace is left with her?
Solution. Sunil purchased juice on Monday = \(12 \frac{1}{2}\) L
Juice purchased on Tuesday = \(14 \frac{3}{4}\) L
∴ Total juice purchased = \(12 \frac{1}{2}+14 \frac{3}{4}=\frac{25}{2}+\frac{59}{4}\)
= \(\frac{50+59}{4}=\frac{109}{4}=27 \frac{1}{4} \mathrm{~L}\)
So, he purchased \(27 \frac{1}{4}\) L of juice in two days.
Question 12. Simplify the following:
(1) \(6-\frac{3}{4}\)
(2) \(\frac{7}{12}-\frac{4}{15}\)
Solution. (1) We have, \(6-\frac{3}{4}=\frac{6}{1}-\frac{3}{4}=\frac{24-3}{4}=\frac{21}{4}=5 \frac{1}{4}\)
(2) We have, \(\frac{7}{12}-\frac{4}{15}=\frac{35-16}{60}=\frac{19}{60}\)
Question 13. A cup is \(\frac{1}{3}\) full of milk. What part of the cup is still to be filled by milk to make it full?
Solution. Given, cup is \(\frac{1}{3}\) full of milk.
∴ Required milk = \(1-\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}\)
Hence, \(\frac{2}{3}\) part of the cup is required to make it full.
Question 14. May bought \(3 \frac{1}{2} \mathrm{~m}\) of lace. She used \(1 \frac{3}{4} \mathrm{~m}\) of lace
Solution. Mary bought lace = \(3 \frac{1}{2} \mathrm{~m}\)
Lace used for new dress = \(1 \frac{3}{4} \mathrm{~m}\)
∴ Lace left with her = \(3 \frac{1}{2}-1 \frac{3}{4}=\frac{7}{2}-\frac{7}{4}=\frac{14-7}{4}=\frac{7}{4}=1 \frac{3}{4} m\)
So, \(1 \frac{3}{4} \mathrm{~m}\) lace is left with her.
Question 15. Nazima gave \(2 \frac{3}{4}\) L out of the \(5 \frac{1}{2} \mathrm{~L}\) of juice she purchased to her friends. How many litres of juice is left with her?
Solution. Quantity of juice Nazima has = \(5 \frac{1}{2} \mathrm{~L}\)
She gave \(2 \frac{3}{4}\) L out of this to her friends.
Now, juice left with her = \(5 \frac{1}{2}-2 \frac{3}{4}=\frac{11}{2}-\frac{11}{4}\)
= \(\frac{22-11}{4}=\frac{11}{4}=2 \frac{3}{4} \mathrm{~L}\)
So, \(2 \frac{3}{4} \mathrm{~L}\) of juice is left with her.
Question 1. It was estimated that because of people switching to Metro trains, about 33000 tonne of CNG, 3300 tonne of diesel and 21000 tonne of petrol was saved by the end of year 2007.
Find the fraction of
(1) the quantity of diesel saved to the quantity of petrol saved.
(2) the quantity of diesel saved to the quantity of CNG saved.
Solution. Given, quantity of CNG saved = 33000 tonne
Quantity of diesel saved = 3300 tonne
Quantity of petrol saved = 21000 tonne
(1) The fraction of the quantity of diesel saved to the quantity of petrol saved=
= \(\frac{3300}{21000}=\frac{33}{210}=\frac{33 \div 3}{210 \div 3}\)
[∴ HCF of 33 and 210 is 3]
= \(\frac{11}{70}\)
(2) The fraction of the quantity of diesel to the quantity of CNG saved
= \(\frac{3300}{33000}=\frac{33}{330}=\frac{33+33}{330+33}=\frac{1}{10}\)
Question 2. Poorvi cut a cake into 8 equal pieces. If she wanted to divide each of them into 3 equal pieces, what fraction of the whole cake would each small pieces be?
Solution. Number of pieces in which the cake cut = 8
Number of pieces each cut piece divided into = 3
∴ Total number of pieces = 8 x 3 = 24
Hence, each piece is represented by the fraction \(\frac{1}{24}\)
Question 3. The energy content of different foods are as follows:
Which food provides the least energy and which provides the maximum? Also, express the least energy as a fraction of the maximum energy.
Solution. In the given table, we see that the minimum value is 3.0J and maximum value is 5.3 J.
∴ Least energy provide by food = 3.0J i.e. Milk
Food which provide the maximum energy = 5.3J i.e. Rice Least energy 30 30
∴ Required fraction \(=\frac{\text { Least energy }}{\text { Maximum energy }}=\frac{3.0}{5.3}=\frac{30}{53}\)
Question 4. A rectangle is divided into certain number of equal parts. If 16 of the parts so formed represent the fraction \(\frac{1}{4}\), find the number of parts in which the rectangle has been divided.
Solution. Let a rectangle be divided into x equal parts.
Now, 16 of the parts represent \(\frac{1}{4}\)
∴ \(\frac{16}{x}=\frac{1}{4}\) ⇒ x = 16 x 4 ⇒ x = 64 parts
Hence, rectangle is divided into 64 equal parts.
Question 5. From school X out of 750 students, 250 were selected for an essay writing and from another school Y out of 1200 students, 300 were selected. From which school, more students were selected?
Solution. Total students in school X = 750
Selected students = 250
∴ Fraction of selected students to the total students
= \(\frac{250}{750}=\frac{1}{3}\) …(1)
Now, total students in school Y = 1200
Selected students = 300
∴ Fraction of selected students to the total students
= \(\frac{300}{1200}=\frac{1}{4}\) …(2)
From Eqs. (1) and (2), \(\frac{1}{3}\) > \(\frac{1}{4}\) [∴ 4 > 3]
Hence, from the school X more students were selected.
Question 6. The fish caught bu Neetu was of weight \(3 \frac{3}{4}\) kg and the fish caught by Narendra was of weight \(2 \frac{1}{2}\) kg. How much more was Neetu’s fish weight than that of Narendra?
Solution. Given, weight of fish caught by Neetu = \(3 \frac{3}{4} \mathrm{~kg}=\frac{15}{4} \mathrm{~kg}\)
and weight of the fish caught by Narendra = \(2 \frac{1}{2}=\frac{5}{2} \mathrm{~kg}\)
∴ Difference between their weights
= \(\frac{15}{4}-\frac{5}{2}=\frac{15}{4}-\frac{5 \times 2}{2 \times 2}\)
= \(\frac{15}{4}-\frac{10}{4}=\frac{15-10}{4}=\frac{5}{4} \mathrm{~kg}\)
Hence, Neetu’s fish weight is kg more than the Narendra’s fish weight.
Question 7. On an average, \(\frac{1}{10}\) of the food eaten is turned into organism’s own body and is available for the next level of consumer in a food chain. What fraction of the food eaten is not available for the next level?
Solution. Quantity of food eaten which turned into organism’s own body = \(\frac{1}{10}\) of the total food
Now, the quantity of food eaten which is not available
for the next level = \(1-\frac{1}{10}=\frac{10-1}{10}=\frac{9}{10}\)
Hence, the required fraction = \(\frac{9}{10}\)
Question 8. Mr. Rajan got a job at the age of 24 yr and he got retired from the job at the age of 60 yr. What fraction of his age till retirement was he in the job?
Solution. Given, Rajan’s age on the joining = 24 yr and retirement age = 60 yr
The number of years, he did the job
= Retirement age – Joining age
= 60 – 24 = 36 yr
∴ The fraction of his age till retirement, when he was in the job
\(=\frac{\text { Total years he did the job }}{\text { Retirement age }}=\frac{36}{60}\)= \(\frac{36 \div 12}{60 \div 12}=\frac{3}{5}\)
Hence, the required fraction is \(\frac{3}{5}\).
Question 9. Roma gave a wooden board of length \(150 \frac{1}{4}\)cm to a carpenter for making a shelf. The carpendter sawed off a piece of \(40 \frac{1}{5}\) cm from it. What is the length of the remaining piece?
Solution. Given, length of a wooden board = \(150 \frac{1}{4} \mathrm{~cm}=\frac{601}{4} \mathrm{~cm}\)
Carpenter sawed off a piece of wooden board = \(40 \frac{1}{5} \mathrm{~cm}=\frac{201}{5} \mathrm{~cm}\)
∴ Length of the remaining piece = \(\frac{601}{4}-\frac{201}{5}\)
∴ LCM of 4 and 5 = 20
∴ \(\frac{601}{4}-\frac{201}{5}=\frac{601 \times 5}{4 \times 5}-\frac{201 \times 4}{5 \times 4}\)
= \(\frac{3005}{20}-\frac{804}{20}\)
= \(\frac{3005-804}{20}=\frac{2201}{20} \mathrm{~cm}\)
Hence, the length of remaining piece is \(\frac{2201}{20}\) or \(110 \frac{1}{20}\) cm
The comparison of two numbers or quantities by the method of division is known as the ratio of the numbers and it is denoted by symbol “:”
e.g. Let two numbers be a and b, where b 0, then the ratio of a and b is a:b.
The first term a is called the antecedent and the second term b is called the consequent.
Suppose, we have 5 pens and 9 toys. The ratio of number of pens to number of toys is 5:9 or 5 is to 9.
Ratio in Simplest Form
The ratio a : b is said to be in the simplest form or lowest form if the HCF of a and b is 1. A ratio in the simplest form is also called the ratio in the lowest term.
e.g. The ratio 11:18 is in the simplest form. Since, the HCF of 11 and 18 is 1. To convert a given ratio a: b to its simplest form, we divide each term by the HCF of a and b.
Example 1. Find the ratio of the following
(1) 21 to 84
(2) 30 min to 60 min
(3) 80 cm to 1.2 m
Solution. (1) Here, HCF of 21 and 84 = 21
∴ Ratio = \(\frac{21+21}{84+21}=\frac{1}{4}=1: 4\)
(2) Since, given quantities are in same unit.
∴ HCF of 30 and 60 = 30
∴ Ratio = \(\frac{30 \div 30}{50 \div 30}=\frac{1}{2}=1: 2\)
(3) Since, given quantities are not in the same unit.
Firstly, we have to convert them into same unit.
Read and Learn More MP Board Class 6 Maths Solutions
We know that 1 m = 100 cm
⇒ 1.2 m = 1.2 x 100 cm
= 120 cm
∴ Ratio of 80 cm to 1.2 m i.e. 80 cm to 120 cm = \(\frac{80}{120}\)
∴ HCF of 80 and 120 = 40
∴ Ratio = \(\frac{80 \div 40}{120 \div 40}=\frac{2}{3}\)
Hence, the required ratio is 2 : 3.
Note it Two quantities can be compared if they are expressed in the same unit and ratio has no unit.
Equivalent Ratio
We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.
e.g. 2:3 and 4:6 are equivalent ratios.
MP Board Class 6 Maths Solutions
Example 2. Give two equivalent ratios of 3 : 5.
Solution. Given, ratio = 3 : 5
Firstly, multiply the numerator and denominator with the same number.
\(\frac{3}{5}=\frac{3 \times 2}{5 \times 2}=\frac{6}{10} \text { and } \frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\)Hence, two equivalent ratios of 3:5 are 6: 10 and 9: 15.
Note it A ratio does not change, if its numerator and denominator are multiplied or divided by the same non-zero number.
Example 3. Consider the statement : Ratio of the breadth to the length of a room is 1 : 2. Complete the following table that shows some possible breadths and lengths of the room.

Solution. Given, the ratio of the breadth to the length of a room = 1 : 1
Also given, breadth of room = 12 m
and length of room = 24 m
Then, the ratio of breadth and length = \(\frac{12}{24}\)
= \(\frac{1}{2}\) = 1 : 2
Now, for missing, we have 24 x 2 = 48
i.e. when we multiply 24 by 2, we get 48.
So to get first missing term, we multiply 12 by 2
∴ 12 x 2 = 24
Thus, the complete table is

Example 4. In a year, there are 55 holidays. What is the ratio of the number of holidays to the number of days in one year?
Solution. Given, number of holidays in one year = 55
We know that number of days in one year = 365
∴ Ratio of the number of holidays to the number of days in one year
\(=\frac{\text { Number of holidays }}{\text { Number of days }}=\frac{55}{365}\)\(= \frac{55 \div 5}{365 \div 5}=\frac{11}{73}\) [∴ HCF of 55 and 365 = 5]
Hence, the required ratio is 11 : 73.
MP Board Class 6 Maths Solutions
Example 5. Dhoni takes 1 h to reach playground from his house and Sehwag takes 20 min to reach playground from his house. Find the ratio of the time taken by Dhoni to the time taken by Sehwag.
Solution. Here, time taken by Dhoni is in hours and time taken by Sehwag is in minutes.
So, we have to convert time taken by both into the same unit.
∴ Time taken by Dhoni = 1 h = 1 x 60 min = 60 min [∴ 1h = 60 min]
and time taken by Sehwag = 20 min
∴ Ratio of the time taken by Dhoni to the time taken by Sehwag
\(=\frac{\text { Time taken by Dhoni }}{\text { Time taken by Sehwag }}=\frac{60}{20}\)= \(\frac{60+20}{20+20}=\frac{3}{1}=3: 1\) [∴ HCF of 60 and 20 = 20]
Hence, the required ratio is 3 : 1.
Example 6. Out of 40 students in a class, 10 like cricket, 20 like football and remaining like tennis. Find the ratio of
(1) the number of students liking cricket to the number of student liking tennis.
(2) the number of students liking football to the total number of student.
Solution. Given, the total number of students in a class = 40
Number of students who like cricket = 10
Number of students who like football = 20
Then, the number of students who like tennis = Total number of students -(Number of students who like football + Number of students who like cricket)
= 40 – (10 + 20) = 10
(1) Ratio of the number of students liking cricket to the number of student liking tennis
\(=\frac{\text { Number of students who like cricket }}{\text { Number of students who like tennis }}=\frac{10}{10}=1: 1\)(2) Ratio of the number of students liking football to the total number of students
\(=\frac{\text { Number of students who like football }}{\text { Total number of students }}\)\(=\frac{20}{40}=\frac{20 \div 20}{40 \div 20}=\frac{1}{2}\) [HCF of 20 and 40 = 20]
= 1 : 2
Example 7. See the figure and find the ratio of
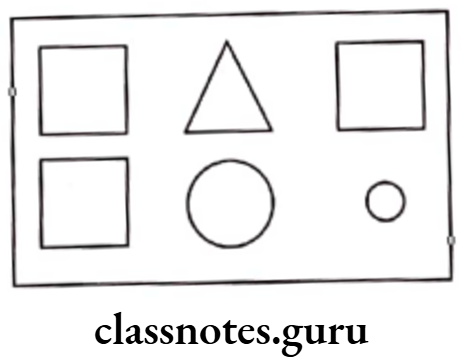
(1) the number of squares to the number of circles Inside the rectangle.
(2) the number of circles to the all shapes inside rectangle.
Solution. In the given figure, number of triangles = 1,
number of squares = 3 and number of circles = 2
∴ Total number of shapes = 1 + 3 + 2 = 6
(1) Required ratio of the number of squares to the number of circles
\(=\frac{\text { Number of squares }}{\text { Number of circles }}=\frac{3}{2}=3: 2\)(2) Required ratio of the number of circles to the all shapes
\(=\frac{\text { Number of circles }}{\text { Total number of shapes }}=\frac{2}{6}=\frac{2+2}{6+2}\) [HCF of 2 and 6 = 6]
= \(\frac{1}{3}\) = 1 : 3
MP Board Class 6 Maths Solutions
Example 8. Distance travelled by Rakesh and Vishal in an hour are 8 km and 12 km, respectively. Find the ratio of the speed of Rakesh to the speed of Vishal.
Solution. We know that
\(\text { Speed }=\frac{\text { Distance }}{\text { Time }}\)Given, distance travelled by Rakesh in one hour = 8 km Distance 8
∴ Speed of Rakesh \(=\frac{\text { Distance }}{\text { Time }}=\frac{8}{1}=8 \mathrm{~km} / \mathrm{h}\)
and distance travelled by Vishal in one hour = 12 km
∴ Speed of Vishal = \(\frac{12}{1}\) km/h
∴ Ratio of the speed of Rakesh to the speed of Vishal
\(=\frac{\text { Speed of Rakesh }}{\text { Speed of Vishal }}=\frac{8}{12}=\frac{8 \div 4}{12 \div 4}=\frac{2}{3}=2: 3\) [∴ HCF of 8 and 12 = 4]
Example 9. Cost of 8 pens is 160 and cost of 6 pencils is 60. Find the ratio of the cost of a pen to the cost of a pencil.
Solution. Given, cost of 8 pens = ₹ 160
∴ Cost of 1 pen \(=\frac{\text { Total cost of pens }}{\text { Numbers of pens }}=\frac{160}{8}=₹ 20\)
Also given, cost of 6 pencils = ₹ 60
∴ Cost of 1 pencil \(=\frac{\text { Total cost of pencils }}{\text { Number of pencils }}=\frac{60}{6}=₹ 10\)
Hence, the required ratio \(=\frac{\text { Cost of } 1 \text { pen }}{\text { Cost of } 1 \text { pencil }}=\frac{20}{10}=\frac{2}{1}=2: 1\)
Example 10. Father wants to divide ₹ 42 between his sons Ritesh and Raj in the ratio of their ages. If the age of Ritesh is 16 yr and the age of Raj is 12 yr. Find how much Ritesh and Raj will get.
Solution. Given, Ritesh’s age=16 yr and Raj’s age = 12 yr
∴ Ratio of their ages \(=\frac{\text { Ritesh’s age }}{\text { Raj’s age }}=\frac{16}{12}=\frac{16 \div 4}{12 \div 4}=\frac{4}{3}=4: 3\)
[∴ HCF of 16 and 12 = 4]
Now, father wants to divide ₹ 42 between his sons in the ratio of their ages i.e.4 : 3.
∴ Sum of the parts of the ratio = 4 + 3 = 7
Amount which has to be divided = ₹ 42
Here, we can say that Ritesh gets 4 parts and Raj gets 3 parts out of every 7 parts.
∴ Ritesh’s share = \(\frac{4}{7}\) x 42 = ₹ 24
and Raj’s share = \(\frac{3}{7}\) x 42 = ₹ 18
Hence, Ritesh gets ₹ 24 and Raj gets ₹ 18.
Class 6 Maths Chapter 12 Solutions
Example 11. Present age of father is 36 yr and that of his son is 6 yr. Find the ratio of the
(1) present age of father to the present age of son.
(2) age of father to the age of son, when son was 4 yr old.
(3) age of father after 10 yr to the age of son after 10 yr.
Solution. Given, present age of father = 36 yr
and present age of son = 6 yr
(1) Required ratio \(=\frac{\text { Present age of father }}{\text { Present age of son }}\)
= \(\frac{36}{6}=\frac{36+6}{6 \div 6}\) [HCF of 36 and 6 = 6]
= \(\frac{6}{1}\) = 6 : 1
(2) When son’s age was 4 yr i.e. 2 yr back (because son’s present age is 6 yr), then father’s age
= 36 – 2 = 34 yr
∴ Required ratio \(=\frac{2 \mathrm{yr} \text { back father’s age }}{2 \mathrm{yr} \text { back son’s age }}\)
\(=\frac{34}{4}=\frac{34+2}{4+2}=\frac{17}{2}=17: 2\)[∴ HCF of 34 and 4 = 2]
(3) After 10 yr, father’s and son’s age will be (36 + 10) yr and (6 + 10) yr, respectively, i.e. 46 yr and 16 yr.
∴ Required ratio \(=\frac{\text { Father’s age after } 10 \mathrm{yr}}{\text { Son’s age after } 10 \mathrm{yr}}\)
= \(\frac{46}{16}=\frac{46 \div 2}{16+2}=\frac{23}{8}=23: 8\)
[∴ HCF of 46 and 16 = 2]
If the ratio of the first and second quantities is equal to the ratio of the third and fourth quantities, then the quantities are said to be in proportion and it is denoted by symbol ‘::’ or ‘=’.
Four numbers a, b, c and d are said to be in proportion, if a:bc:d and it is written as a:b::c:d, where a, b, c and d are respectively, known as first, second, third and fourth terms of the proportion.
First and fourth terms are called extreme terms or extremes, whereas second and third terms are called the middle terms or means.
Example 1. Are the ratios in proportion?
(1) 45 : 60 and 36 : 48
(2) 150 : 100 and 135 : 90
Solution. (1) ∴ Ratio of 45 to 60 = \(\frac{45}{60}=\frac{3}{4}=3: 4\)
and ratio of 36 to 48 = \(\frac{36}{48}=\frac{3}{4}=3: 4\)
∴ The ratio of 45 to 60 is equal to 36 to 48
So, 45 : 60 :: 36 : 48
Hence, 45 : 60 and 36 : 48 are in proportion.
(2) ∴ Ratio of 150 to 100 = \(\frac{150}{100}\) = 3 : 2
and ratio of 135 to 90 = \(\frac{135}{90}\) = 3 : 2
∴ The ratio of 150 to 100 is equal to 135 to 90.
So, 150 : 100 :: 135 : 90
Hence, 150, 100, 135 and 90 are in proportion.
Class 6 Maths Chapter 12 Solutions
Example 2. If 36 : 81 :: x : 63, then find the value of x.
Solution. Given, 36 : 81 :: x : 63
⇒ \(\frac{36}{81}=\frac{x}{63}\)
⇒ \(\frac{4}{9}=\frac{x}{63}\)
⇒ 9x = 4 x 63
⇒ \(x=\frac{4 \times 63}{9}\)
⇒ x = 4 x 7
Hence, the value of x is 28.
Example 3. Check whether the given ratios are equal i.e. they are in proportion. If yes, then write them in proper form.
(1) 1 : 4 and 5 : 20
(2) 2 : 7 and 8 : 28
(3) 3 : 11 and 4 : 21
(4) ₹ 4 to ₹ 7 and 16 to 28
Solution. (1) We have, 1 : 4 and 5 : 20
Here, \(5: 20=\frac{5}{20}=\frac{5+5}{20+5}=\frac{1}{4}=1: 4\)
[∴ HCF of 5 and 20 = 5]
i.e. 1:4 and 5:20 are in proportion.
Thus, the proper form is 1 : 4 :: 5 : 20.
(2) We have, 2 : 7 and 8 : 28
Here, \(8: 28=\frac{8}{28}=\frac{8 \div 4}{28+4}=\frac{2}{7}=2: 7\)
[∴ HCF of 8 and 28 = 47]
Therefore, 2 : 7 and 8 : 28 are in proportion.
Thus, the proper form is 2 : 7 :: 8 : 28.
(3) We have, 3 : 11 and 4 : 21
Here, \(3: 11=\frac{3}{11} \text { and } 4: 21=\frac{4}{21}\)
Here, 3 : 11 ≠ 4 : 21
Thus, 3:11 and 4:21 are not in proportion.
(4) We have, ₹ 4 : ₹ 7 = 4 : 7 and 16 : 28
Now, \(4: 7=\frac{4}{7} \text { and } 16: 28=\frac{16}{28}=\frac{16 \div 4}{28 \div 4}=\frac{4}{7}\)
[∴ HCF of 16 and 28 = 4]
Hence, 4 : 7 and 16 : 28 are in proportion.
Thus, the proper form is 4 : 7 :: 16 : 28.
Example 4. Determine whether the following are in proportion.
(1) 3, 9, 7,21
(2) 3, 55, 77, 17
Solution. (1) We have, 3, 9, 7, 21
∴ Ratio of 3 to 9 = \(\frac{3}{9}=\frac{3 \div 3}{9+3}\)
[∴ HCF of 3 and 9 = 3]
= \(\frac{1}{3}\) = 1 : 3
and ratio of 7 to 21 = \(\frac{7}{21}=\frac{7 \div 7}{21 \div 7}=\frac{1}{3}=1: 3\)
[∴ HCF of 7 and 21=7]
Therefore, 3, 9,7 and 21 are in proportion.
(2) We have, 3, 55, 77, 17
∴ Ratio of 3 to 55 = \(\frac{3}{55}\) and ratio of 77 to 17 = \(\frac{77}{17}\)
Here, 3 : 55 ≠ 77 : 17
Therefore, 3, 55, 77 and 17 are not in proportion.
Class 6 Maths Chapter 12 Solutions
Example 5. Write true (T) and false (F) against each of the following statements:
(1) 0.9 : 0.36 :: 12 : 48
(2) 20 m : 30 m :: 16 s : 24 s
Solution. (1) We have, 0.9 : 0.36 :: 12 : 48
Ratio of 0.9 to 0.36 = \(\frac{0.9}{0.36}=\frac{90}{36}=\frac{90 \div 18}{36+18}=\frac{5}{2}=5: 2\)
[∴ HCF of 90 and 36 = 18]
and ratio of 12 to 48 = \(\frac{12}{48}=\frac{12+12}{48+12}=\frac{1}{4}\)
[∴ HCF of 12 and 48 = 12]
Here, 0.9 : 0.36 ≠ 12 : 48
Hence, the given statement is false.
(2) We have, 20 : 30 :: 16 : 24
Ratio of 20 to 30 = \(\frac{20}{30}=\frac{20+10}{30+10}\)
[∴ HCF of 20 and 30 = 10]
\frac{2}{3} = 2 : 3
and ratio of 16 to 24 = \(\frac{16}{24}=\frac{16 \div 8}{24 \div 8}=\frac{2}{3}=2: 3\)
[∴ HCF of 16 and 24 = 8
Here, 20 : 30 = 16 : 24 = 2 : 3
Hence, the given statement is true.
Example 6. Are the following ratios form a proportion? Also, write the middle terms and extreme terms, where the ratios form a proportion.
(1) 50 cm : 1 m and 80 : 160
(2) 24 L : 60 L and 6 bottles : 15 bottles
Solution. (1) We have, 50 cm : 1 m
= 50 cm : 1 x 100 cm [∴ 1m = 100 cm]
= 50 cm : 100 cm
= \(\frac{50}{100}=\frac{50 \div 50}{100 \div 50}=\frac{1}{2}=1: 2\)
[∴ HCF of 50 and 100 = 50]
and ₹ 80 : ₹ 160 = 80 : 160 = \(\frac{80}{160}=\frac{80 \div 80}{160 \div 80}=\frac{1}{2}=1: 2\)
[∴ HCF of 80 and 160 = 80]
Here, 1 : 2 = 1 : 2
i.e. 50 cm : 1 m = ₹ 80 : ₹ 160
So, the ratios of 50 cm: 1m and 80: 160 are in proportion.
Hence, middle terms are 1 m and 80 and extreme terms are 50 cm and 160.
(2) We have, 24 L : 60 L and 6 bottles : 15 bottles
Now, 24 L to 60 L = \(\frac{24 \mathrm{~L}}{60 \mathrm{~L}}=\frac{24}{60}=\frac{24 \div 12}{60 \div 12}\)
[∴ HCF of 24 and 60 = 12]
= \(\frac{2}{5}\) = 2 : 5
and 6 bottles : 15 bottles = 6 : 15 = \(\frac{6}{15}=\frac{6 \div 3}{15 \div 3}\)
[∴ HCF of 6 and 25 = 3]
= \(\frac{2}{5}\) = 2 : 5
Here, 2:5 = 2:5
i.e. 24 L : 60 L and 6 bottles : 15 bottles are in proportion.
i.e. 24 L : 60 L :: 6 bottles : 15 bottles
Hence, middle terms of ratios are 60 L and 6 bottles and extreme terms of ratios are 24 L and 15 bottles.
A method in which first we find the value of one unit and then the value of required number of units is called unitary method.
e.g. If the cost of any number of article is given, then the cost of 1 article can be obtained by dividing the cost of given number of articles with the number of articles.
i.e. Cost of 1 article \(=\frac{\text { Cost of the given number of articles }}{\text { Number of articles }}\)
Now, with the help of 1 article, we find the any number of articles. Thus, in this method, the price of 1 article help us, in finding the price of any number of articles.
In unitary method, we follow the following trivial rules of variation:
(1) To get more, we multiply.
(2) To get less, we divide.
Example 1. If the cost of 15 mangoes is ₹90. Find the cost of 17 mangoes.
Solution. Given, the cost of 15 mangoes = ₹ 90
The cost of 1 mango = \(\frac{90}{15}\)
Now, the cost of 17 mangoes = 17 x 6 = ₹ 102
Hence, the cost of 17 mangoes is ₹ 102.
Class 6 Maths Chapter 12 Solutions
Example 2. The yield of wheat from 8 hectares of land is 360 quintals. Find the number of hectares of land required for a yield of 540 quintals.
Solution. Required area of land to yield 360 quintals wheat = 8 hectares
Required area of land to yield 1 quintal wheat = \(\frac{8}{360}\) hectares
Required area of land to yield 540 quintals wheat = \(540 \times \frac{8}{360}=\frac{3 \times 8}{2}=12 \text { hectares }\)
Example 3. If the cost of 5 m of ribbon is 500, then find the cost of 2m of ribbon.
Solution. Given, the cost of 5m of ribbon = ₹ 500
∴ Cost of 1 m of ribbon = \(\frac{500}{5}\) = ₹ 100
∴ Cost of 2m of ribbon = 100 × 2 = ₹ 200
Hence, the cost of 2m of ribbon is ₹ 200.
Example 4. Abhimanyu earns ₹ 2500 in 10 days. How much will he earn in 30 days?
Solution. Here, the number of days is known and money earn is unknown.
Given, Abhimanyu earns in 10 days = ₹ 2500
∴ Abhimanyu earns in 1 day = \(\frac{2500}{10}\) = ₹ 250
∴ Abhimanyu earns in 30 days = 250 x 30 = 7500
Hence, Abhimanyu earns ₹7500 in 30 days.
Example 5. During a rainy season, it has rained 369 mm in last 3 days, how many centimetres of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.
Solution. Here, the number of days is known and rainfall is unknown.
Given, rainfall in 3 days = 369 mm
∴ Rainfall in 1 day = \(\frac{369}{3}\) = 123 mm
∴ Rainfall in one full week i.e. 7 days = 123 × 7 mm = 861 mm
In centimetre, rainfall in one full week
= \(861 \times \frac{1}{10} \mathrm{~cm}=861 \mathrm{~cm}\) [∴ 1 mm = \(\frac{1}{10}\) cm]
Hence, 86.1 cm rain will fall in 7 days or one full week.
Example 6. The cost of 8 kg of sugar is ₹ 48.80.
(1) What will be the cost of 10 kg of sugar?
(2) What quantity of sugar can be purchased in ₹ 81?
Solution. (1) Here, the quantity of sugar is known and cost is unknown.
Given, the cost of 8 kg of sugar = ₹ 48.80
∴ Cost of 1 kg of sugar = \(\frac{48.80}{8}=₹ 6.10\)
∴ Cost of 10 kg of sugar = 6.10 x 10 = ₹ 61.0
Hence, the cost of 10 kg of sugar is ₹ 61.
(2) Here, the cost of sugar is known and quantity of sugar is unknown.
Given, in ₹ 48.80 quantity of sugar that can be purchased = 8 kg
∴ In ₹ 1, quantity of sugar that can be purchased = \(\frac{8}{48.80}=\frac{8 \times 10}{488}=\frac{80}{488} \mathrm{~kg}\)
∴ In ₹ 81, quantity of sugar that can be purchased = \(\frac{80}{188} \times 81=13.28 \mathrm{~kg}\)
Hence, 13.28 kg sugar can be purchased in ₹ 81.
Example 7. Venus pays ₹ 7000 as rent for 2 months. How much does she has to pay for a whole year, if the rent per month remains the same?
Solution. Given, rent paid for 2 months = ₹ 7000
∴ Rent paid for 1 month = \(\frac{7000}{2}=₹ 3500\)
∴ Rent paid for a whole year i.e. 12 months = 3500 × 12 = ₹ 42000
Hence, she has to pay ₹ 42000 for a whole year.
MP Board Class 6 Chapter 12 Maths
Example 8. The cost of 2 dozen bananas is ₹ 80. How many bananas can be purchased for ₹ 20?
Solution. We know that I dozen = 12 units
Given, in 80 the number of bananas that can be purchased = 2 dozen = 2 x 12 = 24
∴ In ₹ 1, the number of bananas that can be purchased
\(=\frac{24}{80}=\frac{24 \div 8}{80 \div 8}=\frac{3}{10}\) [∴ HCF of 24 and 80 = 8]
∴ In ₹ 20, the number of bananas that can be purchased
\(=\frac{3}{10} \times 20=\frac{60}{10}=6\)Example 9. A vehicle requires 120 L of petrol for covering a distance of 720 km. How much petrol will be required by the vehicle to cover a distance of 1850 km?
Solution. Given, petrol required for 720 km = 120 L
∴ Petrol required for 1 km = \(\frac{120}{720}=\frac{120+120}{720+120}=\frac{1}{6} L\)
∴ Petrol required for 1850 km = \(\frac{1}{6} \times 1850=308.33 \mathrm{~L}\)
Hence, 308.33 L petrol will be required by the vehicle to cover 1850 km.
Example 10. Arjun purchases 20 pens for ₹ 260 and Aryan purchases 8 pens for ₹ 96. Can you say who got the pens cheaper?
Solution. For Arjun, the cost of 20 pens = ₹ 260
∴ Cost of 1 pen = \(\frac{260}{20}=₹ 13\)
For Aryan, cost of 8 pens = ₹ 96
∴ Cost of 1 pen = \(\frac{96}{8}=₹ 12\)
Here, ₹ 12 < ₹ 13
Hence, Aryan got the pens cheaper.
Question 1. In a class, there are 20 boys and 40 girls. What is the ratio of the number of boys to the number of girls?
Solution. Here, number of boys = 20 and number of girls = 40
∴ Ratio of the number of boys to the number of girls
\(=\frac{\text { Number of boys }}{\text { Number of girls }}=\frac{20}{40}=\frac{2}{4}=\frac{1}{2}=1: 2\)Hence, the required ratio is 1 : 2.
Question 2. Ravi walks 6 km in an hour while Roshan walks 4 km in an hour. What is the ratio of the distance covered by Ravi to the distance covered by Roshan?
Solution. Given, Ravi walks 6 km in an hour
i.e. distance covered by Ravi in one hour = 6 km
and Roshan walks 4 km in an hour
i.e. distance covered by Roshan in one hour = 4 km
∴ Ratio of the distance covered by Ravi to the distance covered by Roshan
\(=\frac{\text { Distance covered by Ravi in one hour }}{\text { Distance covered by Roshan in one hour }}=\frac{6}{4}=\frac{3}{2}=3: 2\)Hence, the required ratio is 3 : 2.
MP Board Class 6 Chapter 12 Maths
Question 3. Saurabh takes 15 min to reach school from his house and Sachin takes one hour to reach school from his house. Find the ratio of the time taken by Saurabh to the time taken by Sachin.
Solution. Here, time taken by Saurabh is in minutes and time taken by Sachin is in hours. So, we have to convert time taken by both into the same unit.
∴ Time taken by Sachin = 1 h = 1 x 60 min = 60 min
[∴ 1 h = 60 min]
and time taken by Saurabh = 15 min
∴ Ratio of the time taken by Saurabh to the time taken by Sachin
\(=\frac{\text { Time taken by Saurabh }}{\text { Time taken by Sachin }}=\frac{15}{60}=\frac{15 \div 15}{60 \div 15}\)[∴ HCF of 15 and 60 = 15]
= \(\frac{1}{4}\) = 1 : 4
Hence, the required ratio is 1:4.
Question 4. Cost of a toffee is 50 paise and cost of a chocolate is ₹ 10. Find the ratio of the cost of a toffee to the cost of a chocolate.
Solution. Here, cost of a toffee and a chocolate are not in the same unit. So, we have to convert both into the same unit.
∴ Cost of a toffee = 50 paise
and cost of a chocolate = ₹ 10 = 10 x 100 paise
= 1000 paise [∴ ₹ 1 = 100 paise]
∴ Ratio of the cost of a toffee to the cost of a chocolate
\(=\frac{\text { Cost of a toffee }}{\text { Cost of a chocolate }}=\frac{50}{1000}=\frac{50 \div 50}{1000 \div 50}\)[∴ HCF of 50 and 1000 = 50]
= \(\frac{1}{20}\) = 1 : 20
Hence, the required ratio is 1 : 20.
Question 5. In a school, there were 73 holidays in one year. What is the ratio of the number of holidays to the number of days in one year?
Solution. Given, number of holidays in one year = 73
We know that number of days in one year = 365
∴ Ratio of the number of holidays to the number of days in one year
\(=\frac{\text { Number of holidays }}{\text { Total number of days }}=\frac{73}{365}=\frac{73 \div 73}{365 \div 73}\)[∴ HCF of 73 and 365 = 73]
= \(\frac{1}{5}\) = 1 : 5
Hence, the required ratio is 1 : 5.
Question 1. There are 20 girls and 15 boys in a class.
(1) What is the ratio of number of girls to the number of boys?
(2) What is the ratio of number of girls to the total number of students in the class?
Solution. Given, number of girls = 20 and number of boys = 15
∴ Total number of students in the class = 20 + 15 = 35
(1) Ratio of the number of girls to the number of boys
\(=\frac{\text { Number of girls }}{\text { Number of boys }}=\frac{20}{15}=\frac{20+5}{15+5}=\frac{4}{3}=4: 3\)(2) Ratio of the number of girls to the total number of students in the class
\(=\frac{\text { Number of girls }}{\text { Total number of students }}=\frac{20}{35}\)= \(\frac{20+5}{35 \div 5}=\frac{4}{7}=4: 7\)
Question 2. Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of
(1) number of students liking football to the number of students liking tennis.
(2) number of students liking cricket to total number of students.
Solution. Given, the total number of students in a class = 30
Number of students who like football = 6
Number of students who like cricket = 12
Then, the number of students who like tennis
= Total number of students – (Number of students who like football + Number of students who like cricket)
= 30 – (6 + 12) = 30 – 18 = 12
(1) Ratio of the number of students liking football to the number of students liking tennis
\(=\frac{\text { Number of students who like football }}{\text { Number of students who like tennis }}\)= \(\frac{6}{12}=\frac{6 \div 6}{12 \div 6}=\frac{1}{2}=1: 2\)
(2) Ratio of the number of students liking cricket to the total number of students
\(=\frac{\text { Number of students who like cricket }}{\text { Total number of students }}\) \(=\frac{12}{30}=\frac{12 \div 6}{30 \div 6}=\frac{2}{5}\)MP Board Class 6 Chapter 12 Maths
Question 3. See the figure and find the ratio of
(1) number of triangles to the number of circles inside the rectangle.
(2) number of squares to all the figures inside the rectangle.
(3) number of circles to all the figures inside the rectangle.
Solution. In the given figure,
Number of triangles = 3; Number of squares = 2; Number of circles = 2
∴ Total number of shapes = 3 + 2 + 2 = 7
(1) Required ratio of the number of triangles to the number of circles
\(=\frac{\text { Number of triangles }}{\text { Number of circles }}=\frac{3}{2}=3: 2\)(2) Required ratio of the number of squares to all the shapes
\(=\frac{\text { Number of squares }}{\text { Total number of shapes }}=\frac{2}{7}=2: 7\)(3) Required ratio of the number of circles to all the shapes
\(=\frac{\text { Number of circles }}{\text { Total number of shapes }}=\frac{2}{7}=2: 7\)Question 4. Distances travelled by Hamid and Akhtar in an hour are 9 km and 12 km, respectively. Find the ratio of speed of Hamid to the speed of Akhtar.
Solution. Given, distance travelled by Hamid in one hour = 9 km
∴ Speed of Hamid = \(\frac{\text { Distance }}{\text { Time }}=\frac{9}{1}=9 \mathrm{~km} / \mathrm{h}\)
and distance travelled by Akhtar in one hour = 12 km
∴ Speed of Akhtar = \(\frac{12}{1}\) = 12 km/h
∴ Ratio of the speed of Hamid to the speed of Akhtar \(=\frac{\text { Speed of Hamid }}{\text { Speed of Akhtar }}=\frac{9}{12}=\frac{9 \div 3}{12 \div 3}=\frac{3}{4}=3: 4\)
MP Board Class 6 Chapter 12 Maths
Question 5. Find the ratio of the following.
(1) 81 to 108
Solution.
(1) Required ratio = \(\frac{81}{108}=\frac{81+27}{108+27}=\frac{3}{4}=3: 4\)
Question 6. Find the ratio of the following.
(1) 30 min to 1.5 h
(2) 40 cm to 1.5 m
(3) 55 paise to 1
(4) 500 mL to 2 L
Solution. (1) Here, we have to convert 1.5 h into min.
We know that 1 h = 60 min
∴ 1.5 h = 1.5 x 60 min = 90 min
∴ Required ratio = \(\frac{30}{90}=\frac{30 \div 30}{90 \div 30}=\frac{1}{3}=1: 3\)
(2) Here, we have to convert 1.5 m into cm.
We know that 1 m = 100 cm
∴ 1.5 m = 1.5 x 100 cm = 150 cm
∴ Required ratio = \(\frac{40}{150}=\frac{40 \div 10}{150+10}=\frac{4}{15}=4: 15\)
(3) Here, we have to convert ₹ 1 into paise.
We know that ₹ 1 = 100 paise
∴ Required ratio = \(\frac{55}{100}=\frac{55 \div 5}{100 \div 5}=\frac{11}{20}=11: 20\)
(4) Here, we have to convert L into mL.
We know that 1 L = 1000 mL
∴ 2 L = 2 x 1000 mL = 2000 mL
∴ Required ratio = \(\frac{500}{2000}=\frac{5}{20}=\frac{1}{4}=1: 4\)
Question 7. In a year, Seema earns ₹ 150000 and saves ₹ 50000. Find the ratio of
(1) money that Seema earns to the money she saves.
(2) money that she saves to the money she spends.
Solution. Given, money earned by Seema = ₹ 150000
and money saved by Seema = ₹ 50000
(1) Required ratio \(=\frac{\text { Money earned by Seema }}{\text { Money saved by Seema }}\)
= \(\frac{150000}{50000}=\frac{15000+50000}{50000+50000}=\frac{3}{1}=3: 1\)
(2) ∴ Moeny spend by Seema = Earned money = Saved money
= (150000 – 50000) = ₹ 100000
∴ Required ratio \(=\frac{\text { Money saved by Seema }}{\text { Money spend by Seema }}\)
= \(\frac{50000}{100000}=\frac{50000 \div 50000}{100000 \div 50000}\)
= \(\frac{1}{2}\) = 1 : 2
Question 8. There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students.
Solution. Given, number of teachers = 102
and number of students = 3300
∴ Required ratio of the number of teachers to the number of students
\(=\frac{\text { Number of teachers }}{\text { Number of students }}\)= \(\frac{102}{3300}=\frac{102 \div 6}{3300 \div 6}\) [∴ HCF of 102 and 3300 is 6]
= \(\frac{17}{550}\) = 17 : 550
MP Board Class 6 Chapter 12 Maths
Question 9. In a college, out of 4320 students, 2300 are girls.
Solution. Given, number of girls = 2300
and total number of students = 4320
∴ Number of boys = Total number of students – Number of girls
= 4320 – 2300 = 2020
Question 10. Out of 1800 students in a school, 750 opted basketball, 800 opted cricket and remaining opted table tennis. If a student can opt only one game, find the ratio of
Solution. Given, total number of students = 1800
Number of students who opted basketball = 750
Number of students who opted cricket = 800
∴ Number of students who opted table tennis = Total number of students – (number of students who opted basket ball + number of students who opted cricket)
= 1800 – (150 + 800)
= 1800 – 1550 = 250
Question 11. Cost of a dozen pens is ₹ 180 and cost of 8 ball pens is ₹ 56. Find the ratio of the cost of a pen to the cost of a ball pen.
Solution. Given, cost of 12 pens = 180
∴ Cost of 1 pen \(=\frac{\text { Total cost of pens }}{\text { Number of pens }}\)
= \(\frac{180}{12}\) = ₹ 15
Also given, cost of 8 ball pens = ₹ 56 [∴ 1 dozen = 12 units]
∴ Cost of 1 ball pen \(=\frac{\text { Total cost of ball pens }}{\text { Number of ball pens }}=\frac{56}{8}=₹ 7\)
Hence, the required ratio \(=\frac{\text { Cost of } 1 \text { pen }}{\text { Cost of } 1 \text { ball pen }}\)
= \(\frac{15}{7}\) = 15 : 7
Question 12. Consider the statement: Ratio of breadth and length of a hall is 2:5. Complete the following table that shows some possible breadths and lengths of the hall.

Solution. Given, ratio of breadth and length of a hall = 2 : 5
Also given, breadth of the hall = 10
and length of the hall = 25
Then, the ratio of breadth and length = \(\frac{10}{25}=\frac{2}{5}=2: 5\)
Now, for finding first missing number, we have
25 x 2 = 50
i.e. when we multiply 25 by 2, we get 50.
So, to get first missing term, we multiply 10 by 2.
∴ 10 × 2 = 20
Hence, the second breadth of the hall = 20
and length of the hall = 50
For finding second missing number, we have
40 = 10 x 4
i.e. when we multiply 10 by 4, we get 40.
So, to get second missing term, we multiply 25 by 4.
∴ 25 x 4 = 100
Hence, third breadth of hall = 40 and length = 100
Thus, the complete table is

Word Problems on Ratio Class 6
Question 13. Divide 20 pens between Sheela and Sangeeta in the ratio of 3: 2.
Solution. Given, ratio is 3: 2, whose two parts are 3 and 2.
∴ Sum of two parts = 3 + 2 = 5
This means, if there are 5 pens, Sheela gets 3 pens and Sangeeta gets 2 pens.
We can say that Sheela gets 3 parts and Sangeeta gets 2 parts out of every 5 parts.
Now, total number of pens = 20
∴ Number of pens for Sheela = \(\frac{3}{5}\) x 20 = 12
and number of pens for Sangeeta = \(\frac{2}{5}\) x 20 = 8
Hence, out of 20 pens Sheela gets 12 pens and Sangeeta gets 8 pens.
Question 14. Mother wants to divide ₹ 36 between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya is 15 yr and age of Bhoomika is 12 yr find how much Shreya and Bhoomika will get.
Solution. Given, Shreya’s age = 15 yr
and Bhoomika’s age = 12 yr
∴ Ratio of their ages \(=\frac{\text { Shreya’s age }}{\text { Bhoomika’s age }}\)
= \(\frac{15}{12}=\frac{15+3}{12+3}=\frac{5}{4}=5: 4\)
Now, mother wants to divide 36 between her daughters in the ratio of their ages.
∴ Sum of the parts of ratios = 5 + 4 = 9
Amount which has to be divided = ₹ 36
Here, we can say that Shreya gets 5 parts and Bhoomika gets 4 parts out of every 9 parts.
∴ Shreya’s share = \(\frac{5}{9}\) x 36 = ₹ 20
and Bhoomika’s share = \(\frac{4}{9}\) x 36 = ₹ 16
Hence, Shreya gets ₹ 20 and Bhoomika gets ₹ 16.
Question 15. Present age of father is 42 yr and that of his son is 14 yr. Find the ratio of
(1) present age of father to the present age of son.
(2) age of the father to the age of son, when son was 12 yr old.
(3) age of father after 10 yr to the age of son after 10 yr.
(4) age of father to the age of son when father was 30 yr old.
Solution. Given, present age of father = 42 yr
and present age of son = 14 yr
(1) Required ratio \(=\frac{\text { Present age of father }}{\text { Present age of son }}\)
= \(\frac{42}{14}=\frac{42+14}{14 \div 14}=\frac{3}{1}=3: 1\)
(2) When son’s age was 12 yr i.e. 2 yr back (because son’s present age is 14 yr).
Then, father’s age = (42 – 2) = 40 yr
∴ Required ratio \(=\frac{2 \mathrm{yr} \text { back father’s age }}{2 \mathrm{yr} \text { back son’s age }}=\frac{40}{12}=\frac{40 \div 4}{12 \div 4}\)
[∴ HCF of 40 and 12 is 4]
= \(\frac{10}{3}\)
(3) After 10 yr, father and son’s age will be (42 + 10) yr and (14 + 10) yr respectively i.e. 52 yr and 24 yr.
∴ Required ratio \(=\frac{\text { After } 10 \mathrm{yr} \text { father’s age }}{\text { After } 10 \mathrm{yr} \text { son’s age }}\)
= \(\frac{52}{24}=\frac{52 \div 4}{24 \div 4}\)
[∴ HCF of 52 and 24 is 4]
= \(\frac{13}{6}\) = 13 : 6
(4) When father’s age was 30 yr i.e. 12 yr back (because father’s present age is 42 yr and (42 – 12) = 30 yr.
Then, son’s age (14 – 12) = 2 yr
∴ Required ratio \(=\frac{12 \mathrm{yr} \text { back father’s age }}{12 \mathrm{yr} \text { back son’s age }}\)
= \(\frac{30}{2}=\frac{30+2}{2+2}=\frac{15}{1}=15: 1\)
Question 16. 1 : 5 and 3 : 15
Solution. We have, 1 : 5 and 3 : 15
Here, \(3: 15=\frac{3}{15}=\frac{3 \div 3}{15+3}=\frac{1}{5}=1: 5\)
i.e. 1 : 5 and 3 : 15 are in proportion.
Thus, the proper form is 1 : 5 :: 3 : 15.
Question 17. 2 : 9 and 18 : 81
Solution. We have, 2 : 9 and 18 : 81
Here, \(18: 81=\frac{18}{81}=\frac{18 \div 9}{81 \div 9}\)
[∴ HCF of 18 and 81 is 9]
= \(\frac{2}{9}\) = 2 : 9
i.e. 2 : 9 and 18 : 81 are in proportion.
Thus, the proper form is 2 : 9 :: 18 : 81.
Question 18. 15 : 45 and 5 : 25
Solution. We have, 15 : 45 and 5 : 25
Here, \(15: 45=\frac{15}{45}=\frac{15 \div 15}{45 \div 15}=\frac{1}{3}=1: 3\)
and \(5: 25=\frac{5}{25}=\frac{5 \div 5}{25 \div 5}=\frac{1}{5}=1: 5\)
Here, 15 : 45 ≠ 5 : 25
Thus, 15 : 45 and 5 : 25 are not in proportion.
Word Problems on Ratio Class 6
Question 19. 4 : 12 and 9 : 27
Solution. We have, 4 : 12 and 9 : 27
Here, \(4: 12=\frac{4}{12}=\frac{4 \div 4}{12 \div 4}=\frac{1}{3}=1: 3\)
Now, \(9: 27=\frac{9}{27}=\frac{9 \div 9}{27 \div 9}=\frac{1}{3}=1: 3\)
Hence, 4 : 12 = 9 : 27 = 1 : 3 i.e. 4 : 12 and 9 : 27 are in proportion.
Thus, the proper form is 4 : 12 :: 9 : 27.
Question 20. ₹ 10 to ₹ 15 and 4 to 6
Solution. We have, ₹ 10 : ₹ 15 = 10 : 15 and 4 : 6
Now, \(10: 15=\frac{10}{15}=\frac{10 \div 5}{15 \div 5}=\frac{2}{3}=2: 3\)
and \(4: 6=\frac{4}{6}=\frac{4+2}{6+2}=\frac{2}{3}=2: 3\)
Here, 10 : 15 = 4 : 6 = 2 : 3 i.e. 10 : 15 and 4 : 6 are in proportion.
Thus, the proper form is 10 : 15 :: 4 : 6.
Question 1. Determine, if the following are in proportion.
(1) 15, 45, 40, 120
(2) 33, 121, 9, 96
Solution. (1) We have, 15, 45, 40, 120
∴ Ratio of 15 to 45 = \(\frac{15}{45}=\frac{15 \div 15}{45 \div 15}=\frac{1}{3}=1: 3\)
[∴ HCF of 15 and 45 = 15]
and ratio of 40 to 120 = \(\frac{40}{120}=\frac{40 \div 40}{120 \div 40}=\frac{1}{3}=1: 3\)
[∴ HCF of 40 and 120 = 40]
Here, 15 : 45 = 40 : 120 = 1 : 3
Therefore, 15, 45, 40 and 120 are in proportion.
(2) We have 33, 121, 9, 96
∴ Ratio of 33 to 121 = \(\frac{33}{121}=\frac{33 \div 11}{121 \div 11}=\frac{3}{11}=3: 11\)
and ratio of 9 to 96 = \(\frac{9}{96}=\frac{9 \div 3}{96 \div 3}=\frac{3}{32}=3: 32\)
[∴ HCF of 9 and 96 = 3]
Here, 3 : 11 ≠ 3 : 32 i.e. 33 : 121 ≠ 9 : 96
Therefore, 33, 121, 9 and 96 are not in proportion.
Question 2. Write True (T) or False (F) against each of the following statements:
(1) 16 : 24 : 20 : 30
Solution. (1) We have, 16 : 24 :: 20 : 30
∴ Ratio of 16 to 24 = \(\frac{16}{24}=\frac{16+8}{24+8}=\frac{2}{3}=2: 3\)
and ratio of 20 to 30 = \(\frac{20}{30}=\frac{20+10}{30+10}=\frac{2}{3}=2: 3\)
Here, 16 : 24 = 20 : 30 = 2 : 3,
So, 16 : 24 :: 20 : 30
Hence, given statement is true.
Word Problems on Ratio Class 6
Question 3. Are the following statements true?
(1) 40 persons: 200 persons = ₹ 15 : ₹ 75
Solution. (1) 40 persons : 200 persons
= \(\frac{40}{200}=\frac{40 \div 10}{200 \div 10}=\frac{4}{20}=\frac{1}{5}=1: 5\)
and \(\text { ₹ } 15: ₹ 75=\frac{15}{75}=\frac{15 \div 15}{75 \div 15}=\frac{1}{5}=1: 5\)
Question 4. Determine, if the following ratios form a proportion. Also, write the middle term and extreme terms, where the ratios form a proportion.
(1) 25 cm : 1 m and ₹ 40 : ₹ 160
(2) 39 L : 65 L and 6 bottles : 10 bottles
(3) 2 kg : 80 kg and 25 g : 625 g
(4) 200 mL : 2.5 L and ₹ 4 : ₹ 50
Solution. (1) Here, 25 cm : 1 m = 25 cm : 1 x 100 cm
[∴ 1 m = 100 cm]
= \(25: 100=\frac{25}{100}=\frac{25 \div 25}{100 \div 25}=\frac{1}{4}=1: 4\)
and \(₹ 40: ₹ 160=40: 160=\frac{40}{160}=\frac{1}{4}=1: 4\)
Here, 1 : 4 = 1 : 4 i.e. 25 cm : 1 m = ₹ 40 : ₹ 160
So, the ratios of 25 cm : 1 m and ₹ 40 : ₹ 160 are in proportion.
i.e. 25 cm : 1m :: ₹ 40 : ₹ 160
Now, middle terms are 1 m and 40 and extreme terms are 25 cm and 160.
(2) Here, \(39 L : 65 L = 39: 65=\frac{39}{65}=\frac{39+13}{65+13}=\frac{3}{5}=3: 5\)
and 6 bottles: 10 bottles 6 : 10 = \(\frac{6}{10}\)
= \(\frac{6+2}{10+2}=\frac{3}{5}=3: 5\)
Here, 3 : 5 = 3 : 5 i.e. 39 L : 65 L
= 6 bottles : 10 bottles.
So, the ratio of 39 L: 65 L and 6 bottles : 10 bottles are in proportion
i.e. 39 L : 65 L :: 6 bottles : 10 bottles
Hence, middle terms of ratios are 65 L and 6 bottles and extreme terms of ratios are 39 L and 10 bottles
(3) Here, \(2 \mathrm{~kg}: 80 \mathrm{~kg}=2: 80=\frac{2}{80}=\frac{2 \div 2}{80 \div 2}=\frac{1}{40}=1: 40\)
and \(25 \mathrm{~g}: 625 \mathrm{~g}=25: 625=\frac{25}{625}=\frac{25 \div 25}{625 \div 25}=\frac{1}{25}=1: 25\)
Since, both ratios are not equal.
∴ 2 kg : 80 kg ≠ 25 g : 625 g
Hence, the given ratios are not in proportion.
(4) Here, \(200 \mathrm{~mL}: 2.5 \mathrm{~L}=200 \times \frac{1}{1000} \mathrm{~L}: 2.5 \mathrm{~L}\)
[∴ 1 mL = \(\frac{1}{1000}\) L]
= \(\frac{200}{1000} \mathrm{~L}: 2.5 \mathrm{~L}=0.200 \mathrm{~L}: 2.5 \mathrm{~L}\)
= \(0.200: 2.5=\frac{0.200}{2.5}=\frac{2}{25}=2: 25\)
and \(₹ 4: ₹ 50=4: 50=\frac{4}{50}=\frac{4 \div 2}{50 \div 2}=\frac{2}{25}=2: 25\)
Here, 2 : 25 = 2 : 25 i.e. 200 mL : 2.5 L = ₹ 4 : ₹ 50
So, the ratios of 200 mL : 2.5 L and ₹ 4 : ₹ 50 are in proportion.
i.e. 200 mL : 2.5 L :: ₹ 4 : ₹ 50
Hence, middle terms of ratios are 2.5 L and ₹ 4 and extreme terms of ratios are 200 mL and ₹ 50.
Question 5. Read the table and fill in the boxes.

Solution. From the above table,
Distance travelled by Kriti in 2 h = 6 km
∴ Distance travelled by Kriti in 1 h = \(\frac{6}{2}\) = 3 km
Now, distance travelled by Kriti in 4 h = 3 x 4 = 12 km
Also, distance travelled by Karan in 1 h = 4 km
∴ Distance travelled by Karan in 4 h = 4 x 4 = 16 km
On completing the boxes, we get the following table:
Question 1. If the cost of 7 m of cloth is ₹ 1470, find the cost of 5 m of cloth.
Solution. Given, cost of 7 m of cloth = 1470
∴ Cost of 1 m of cloth = \(\frac{1470}{7}=₹ 210\)
∴ Cost of 5 m of cloth = 210 x 5 = ₹ 1050
Hence, the cost of 5 m of cloth is ₹ 1050.
Word Problems on Ratio Class 6
Question 2. Ekta earns ₹ 3000 in 10 days. How much will she earn in 30 days?
Solution. Here, the number of days is known and money earns is unknown.
Given, Ekta earns in 10 days = ₹ 3000
∴ Ekta earns in 1 day = \(\frac{3000}{10}=₹ 300\)
∴ Ekta earns in 30 days = 300 x 30 = 9000
Hence, Ekta earns 9000 in 30 days.
Question 3. If it has rained 276 mm in the last 3 days, how many centimetre of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.
Solution. Here, the number of days is known and rain fall is unknown.
Given, rainfall in 3 days = 276 mm
∴ Rainfall in 1 day. = \(\frac{276}{3}\) = 92 mm
∴ Rainfall in one full week i.e. 7 days = 92 x 7 = 644 mm
In centimetre, rainfall in one full week
= \(644 \times \frac{1}{10} \mathrm{~cm}=64.4 \mathrm{~cm}\) [∴ 1 mm = \(\frac{1}{10}\) cm]
Hence, 64.4 cm rain will fall in 7 days or in one full week.
Question 4. Cost of 5 kg of wheat is ₹ 91.50.
(1) What will be the cost of 8 kg of wheat?
(2) What quantity of wheat can be purchased in ₹ 183?
Solution. (1) Here, the quantity of wheat is known and cost is unknown.
Given, cost of 5 kg of wheat = ₹ 91.50
∴ Cost of 1 kg of wheat = \(\frac{91.50}{5}=₹ 18.3\)
∴ Cost of 8 kg of wheat = 18.30 x 8 = ₹ 146.40
Hence, the cost of 8 kg of wheat is ₹ 146.40.
(2) Here, the cost of wheat is known and quantity of wheat is unknown.
Given, in ₹ 91.50 quantity of wheat that can be purchased = 5 kg
∴ In ₹ 1, quantity of wheat that can be purchased
= \(\frac{5}{91.50}=\frac{5 \times 10}{915}=\frac{50}{915} \mathrm{~kg}\)
[multiplying numerator and denominator both by 10]
∴ In ₹ 183, quantity of wheat that can be purchased
= \(\frac{50}{915} \times 183=\frac{50}{5}=10 \mathrm{~kg}\)
Hence, 10 kg wheat can be purchased in ₹ 183.
MP Board Class 6 Maths Solutions
Question 5. The temperature dropped 15 degree celsius in the last 30 days. If the rate of temperature drop remains the same, how many degrees will the temperature drop in the next ten days?
Solution. Given, in last 30 days, temperature drop = 15 degree
∴ In 1 day, temperature drop = \(\frac{15}{30}=\frac{15+15}{30 \div 15}=\frac{1}{2} \text { degree }\)
∴ In next 10 days, temperature drop
= \(\frac{1}{2} \times 10 \text { degree }=5 \text { degree }\)
Hence, temperature dropped 5 degree in the next 10 days.
Question 6. Shaina pays ₹ 15000 as rent for 3 months. How much does she has to pay for a whole year, if the rent per month remains same?
Solution. Given, rent paid for 3 months = ₹ 15000
∴ Rent paid for 1 month = \(\frac{15000}{3}=₹ 5000\)
∴ Rent paid for a whole year i.e. 12 months
= 5000 × 12 = ₹ 60000
Hence, she has to pay ₹ 60000 for a whole year.
Question 7. Cost of 4 dozens bananas is ₹ 180. How many bananas can be purchased for ₹ 90?
Solution. We know that, I dozen = 12 unit
Given, in ₹ 180, number of bananas that can be purchased = 4 dozen
= 4 x 12 = 48
[∴ 1 dozen = 12 unit]
∴ In ₹ 1, number of bananas that can be purchased
\(=\frac{48}{180}=\frac{48 \div 12}{180+12}=\frac{4}{15}\)∴ In ₹ 90, number of bananas that can be purchased
\(=\frac{4}{15} \times 90=4 \times 6=24\)Hence, 24 bananas can be purchased for ₹ 90.
MP Board Class 6 Maths Solutions
Question 8. The weight of 72 books is 9 kg. What is the weight of 40 such books?
Solution. Given, weight of 72 books = 9 kg
∴ Weight of 1 book = \(\frac{9}{72}\)
∴ Weight of 40 books = \(\frac{9}{72} \times 40=\frac{360}{72} \mathrm{~kg}=\frac{360 \div 72}{72 \div 72}=5 \mathrm{~kg}\)
Hence, the weight of 40 books is 5 kg.
Question 9. A truck requires 108 L of diesel for covering a distance of 594 km. How much diesel will be required by the truck to cover a distance of 1650 km?
Solution. Given, diesel required for 594 km = 108 L
∴ Diesel required for 1 km = \(\frac{108}{594}=\frac{108 \div 54}{594 \div 54}=\frac{2}{11} L\)
∴ Diesel required for 1650 km = \(\frac{2}{11} \times 1650=2 \times 150=300 \mathrm{~L}\)
Hence, 300 L diesel required by the truck to cover 1650 km.
Question 10. Raju purchases 10 pens for ₹ 150 and Manish buys 7 pens for ₹ 84. Can you say who got the pens cheaper?
Solution. For Raju, cost of 10 pens=150
∴ Cost of 1 pen = \(\frac{150}{10}\) = ₹ 15
For Manish, cost of 7 pens = ₹ 84
∴ Cost of 1 pen = \(\frac{84}{7}\) ₹ 12
Here, ₹ 12 < ₹ 15
Hence, Manish got the pens cheaper.
Question 11. Anish made 42 runs in 6 overs and Anup made 63 runs in 7 overs. Who made more runs per over?
Solution. Runs made by Anish in 6 overs = 42
∴ Runs made by Anish in 1 over = \(\frac{42}{6}\) = 7
Runs made by Anup in 7 overs = 63
∴ Runs made by Anup in 1 over = \(\frac{63}{7}\) = 9
∴ 9 > 7
Chapter 12 Ratio And Proportion Multiple Choice Questions
Question 1. The ratio of 6 books to 30 books is
Answer. 3. 1 : 5
Question 2. The simplest form of the ratio 384 : 480 is
Answer. 2. 4 : 5
Question 3. In a box, the ratio of red marbles to blue marbles is 7:4. Which of the following could be the total number of marbles in the box?
Answer. 4. 22
Question 4. The ratio of the number of sides of a triangle to the number of edges of a cube is
Answer. 2. 1 : 4
MP Board Class 6 Maths Solutions
Question 5. Margarette works in a factory and earns ₹ 955 per month. She saves 185 per month from her earnings. Then, the ratio of her income to her expenditure is Competency Based Question
Answer. 3. 191 : 154
Question 6. Avinash works as a lecturer and earns ₹ 12000 per month. His wife who is a doctor earns ₹ 15000 per month. Then, the ratio of Avinash’s income to their total income is
Answer. 1. 4 : 9
Question 7. If a bus travels 160 km in 4 h and a train travels 320 km in 5 h at uniform speeds, then the ratio of the distances travelled by them in one hour is
Answer. 3. 5 : 8
Question 8. A picture is 40 cm wide and 1.6 m long. The ratio of its width to its perimeter in lowest form is
Answer. 2. 1 : 10
Question 9. Which of the following is the equivalent ratio of 7 : 11?
Answer. 1. 14 : 22
Question 10. The ratio of number of circles and number of squares inside the following rectangle is

Answer. 3. 11 : 10
MP Board Class 6 Maths Solutions
Question 11. Mathematics textbook for Class VI has 320 pages. The chapter ‘Symmetry’ runs from page 261 to page 272. The ratio of the number of pages of this chapter to the total number of pages of the book is
Answer. 3. 3 : 80
Question 12. If 66: 72 : x: 96, then x is equal to
Answer. 3. 88
Question 13. If 7 : 30 :: x : 15, then the value of x is
Answer. 1. \(\frac{7}{2}\)
Question 14. Which of the following are in proportion?
Answer. 4. 2, 3, 30, 20
Question 15. In a school library, the ratio of Mathematics books to Science books is same as the ratio of Science books to Hindi books. If there are 450 books of Science and 300 books of Hindi, then the number of books of Mathematics is Competency Based Question (c) 300 (d) 450
Answer. 2. 675
Question 1. Assertion (A) The monthly salary of Hari-Kishan is ₹ 80000. The monthly salary of Manish is ₹ 40000.
Reason (R) Two quantities can be compared only if they are in the same unit.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 2. Assertion (A) 1 : 2 is not equivalent to 10 : 5.
Reason (R) We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
MP Board Class 6 Maths Solutions
Question 3. Assertion (A) 25 km : 60 km :: ₹ 15 : ₹ 17.
Reason (R) If two ratios are equal, we say that they are in proportion and use the symbol ‘::’ or ‘=’ to equate the two ratios.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (d) A is false but R is true.
Question 4. Assertion (A) 15 : 40 :: 10 : 30.
Reason (R) Proportion says that two ratios (or fractions) are equal.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (d) A is false but R is true.
Question 1. A ratio expressed in lowest form has no common factor other than ….. in its terms.
Answer. 1
Question 2. To find the ratio of two quantities, they must be expressed in ….. unit.
Answer. Same
Question 3. The cost of 4 pens is ₹ 40. The cost of 11 pens is …. .
Answer. 110
Question 4. Maya can walk 6 km in 2 h. In 3 h, she can walk …… .
Answer. 9 km
Question 5. Sleeping time of a python in a 24 h clock is represented by the unshaded portion in figure.
The ratio of sleeping time to the awaking time is …… .
Answer. 1 : 3
Question 1. 4 : 7 = 20 : 35
Answer. True
Question 2. 15 m : 40 m = 40 cm : 80 cm
Answer. False
Question 3. The ratio of 20 kg to 200 kg is 1 : 10.
Answer. True
MP Board Class 6 Maths Solutions
Question 4. The ratio 8 : 40 is in its lowest form.
Answer. False
Question 5. If 10 : 30 :: 40 : x, then the value of x is 120.
Answer. True
Question 1. Sam organised a party. He decorated his house and arranged food for guests. He spent ₹ 1600 on decoration and ₹ 8000 on food.
(1) What is the ratio of the money that Sam spent on decoration to the money spent on food?
(a) 1 : 4
(b) 1 : 5
(c) 1 : 6
(d) 5 : 1
(2) Same used paper ribbons to decorate the walls. He made a pattern using groups of four ribbons. Each group has one blue ribbon and the remaining are yellow. What is the ratio of blue ribbons to the total number of ribbons in each pattern?
(3) To decorate one wall, Sam used 18 blue ribbons. How many yellow ribbons were used on that wall?
(a) 3
(b) 6
(c) 36
(d) 54
(4) Sam purchased 40 blue ribbons.

He orders the ribbons shown below.
How many rupees will Sam pay for the 40 ribbons?
Solution. (1) (b) Sam spent the money on decoration = ₹ 1600 and the money he spent on food = 8000
∴ Ratio of money spent on decoration to
money spent on food = \(\frac{1600}{8000}=\frac{1600 \div 1600}{8000 \div 1600}\)
[HCF of 1600 and 8000 = 1600]
= \(\frac{1}{5}\) = 1 : 5
Thus, the ratio of the money spent on decoration to money spent on food is 1:5.
(2) Sam made pattern using four ribbons.
Number of blue ribbons = 1
Number of yellow ribbons = 3
Total number of ribbons = 1 + 3 = 4
∴ Ratio of blue ribbons to the total number of ribbons
\(=\frac{\text { Number of blue ribbons }}{\text { Number of total ribbons }}=\frac{1}{4}\)= 1 : 4
(3) (d) To decorate one wall Sam used 18 blue ribbons. From part (2), we have the ratio of Blue ribbon to yellow ribbon is 1:3.
If one blue ribbon is used, then 3 yellow ribbons will also used.
∴ We have, the number of blue ribbons = 18
∴ The number of yellow ribbons = 18 x 3 = 54
Thus, 54 yellow ribbons were used on the wall.
(4) Sam purchased 40 blue ribbons and 1 pack has 5 rolls with price of ₹ 25.
∴ Price of 5 rolls = ₹ 25
∴ Price of 1 roll of ribbon = \frac{25}{5} = ₹ 5
∴ Price of 40 rolls of ribbon = 5 x 40 = 200
Thus, Sam will pay 200 for 40 ribbons.
MP Board Class 6 Maths Solutions
Question 2. Sam ordered 21 sausages. Of the 15 guests that came to the party, 6 guests had two sausages each, three guests had one sausage each and the remaining guests did not have any sausages.
(1) What is the ratio of the number of sausages left to the number of sausages had by the guests?
(a) 2 : 5
(b) 2 : 7
(c) 5 : 2
(d) 5 : 7
(2) One pack of 3 sausages cost ₹ 120. What is the cost of 21 sausages?
(a) ₹ 40
(b) ₹ 630
(c) ₹ 840
(d) ₹ 140
Solution. (1) (a) Total number of sausages = 21
Out of 15 guests, 6 guests had two sausages each i.e. 6 guests had the number of sausages = 6 x 2 = 12 sausage
and the number of sausages had by 3 guests = 3 x 1 = 3 sausages
Total number of sausages had by guests
= 12 + 3 = 15 sausages
Number of sausages left = 21 – 15 = 6 sausages
Now, ratio of the number of sausages left to the number of sausages had by guests
\(=\frac{\text { Number of sausages left }}{\text { Number of sausages had by guests }}\)= \(\frac{6}{15}=\frac{6 \div 3}{15 \div 3}=\frac{2}{5}=2: 5\)
Thus, the required ratio is 2:5.
(2) (c) Cost of 3 sausages = ₹ 120
Cost of 1 sausage = \(₹ \frac{120}{3}=₹ 40\)
∴ Cost of 21 sausages = 40 × 21 = 840
Thus, cost of 21 sausages is ₹ 840.
Question 1. Write the following ratios in the simplest form.
(1) 600 g to 1 kg
(2) 2 cm to 4 m
Solution. (1) Ratio of 600 g to 1 kg = \(\frac{600}{1000}\) [∴ 1 kg = 1000 g]
= \(\frac{3}{5}\) = 3 : 5
(2) 2 cm to 4 m = \(\frac{2}{400}\) [∴ 1m = 100 cm]
Question 2. Give two equivalent ratios of 3 : 8.
Solution. \(3: 8=\frac{3}{8}=\frac{3 \times 2}{8 \times 2}=\frac{6}{16}, 3: 8=\frac{3}{8}=\frac{3 \times 3}{8 \times 3}=\frac{9}{24}\)
Hence, two equivalent ratios of 3 : 8 are 6 : 16 and 9 : 24.
Question 3. Find (1) the ratio of 70 cm to 1 m.
(2) the ratio of 50 paise to ₹ 2.
Solution. (1) We know that 1 m = 100 cm
∴ Required ratio = \(70: 100=\frac{70}{100}=7: 10\)
(2) We know that ₹ 1 = 100 paise
∴ Required ratio = \(\frac{50}{200}=\frac{1}{4}=1: 4\)
Question 4. If the cost of 10 bananas is ₹ 20. What will be the cost of 7 bananas?
Solution. Cost of 10 bananas = ₹ 20
Cost of 1 banana = \(\frac{20}{10}\) = ₹ 2
∴ Cost of 7 bananas = 7 x 2 = ₹ 14
Question 5. Determine whether the given ratios are equal.
30 : 45 and 60 : 100
Solution. We have, 30 : 45 = \(\frac{30}{45}\) = \(\frac{2}{3}\) = 2 : 3
and 60 : 100 = \(\frac{60}{100}\) = \(\frac{3}{5}\) = 3 : 5
So, the ratios 30 : 45 and 60 : 100 are not equal.
Question 6. The cost of 3 dozen pens is ₹ 72. What will be the cost of 7 bananas?
Solution. Cost of 3 dozen pens = ₹ 72
Cost of 1 dozen pens = \(\frac{72}{3}\) = ₹ 24
∴ Cost of 2 dozen pens 24 x 2 = ₹ 48
Question 7. Are the ratios 10 g : 40 g and 25 kg : 100 kg in proportion?
Solution. We have, 10 g : 40 g = \(\frac{10}{40}\) = 1 : 4
and 25 kg : 100 kg = \(\frac{25}{100}\) = 1 : 4
So, they are in proportion.
MP Board Class 6 Maths Solutions
Question 8. Are 10, 15, 20 and 30 in proportion?
Solution. Ratio of 10 to 15 = \(\frac{10}{15}\) = 2 : 3
Ratio of 20 to 30 = \(\frac{20}{30}\) = 2 : 3
Since, 10:15 = 20:30
Hence, 10, 15, 20 and 30 are in proportion.
Question 9. If 15 : 10 :: x : 20, then find the value of x.
Solution. Given, 15 : 10 :: x : 20
⇒ \(\frac{15}{10}=\frac{x}{20}\)
⇒ 10x = 15 x 20
⇒ \(x=\frac{15 \times 20}{10}=30\)
Question 1. Which pair of ratios are equal and why?
(1) \(\frac{2}{3}\), \(\frac{4}{6}\)
(2) \(\frac{8}{4}\), \(\frac{2}{1}\)
(3) \(\frac{4}{5}\), \(\frac{12}{20}\)
Solution. (1) \(\frac{2}{3}=2: 3 \text { and } \frac{4}{6}=2: 3\)
Hence, \(\frac{2}{3}\) and \(\frac{4}{6}\) are equal.
(2) \(\frac{8}{4}=2: 1 \text { and } \frac{2}{1}=2: 1\)
Hence, \(\frac{8}{4}\) and \(\frac{2}{1}\) are equal.
(3) \(\frac{4}{5}=4: 5 \text { and } \frac{12}{20}=\frac{3}{5}=3: 5\)
Hence, \(\frac{4}{5}\) and \(\frac{12}{20}\) are not equal.
Question 2. Reshma prepared 18 kg of burfi by mixing khoya with sugar in the ratio of 7 : 2. How much khoya did she use?
Solution. Quantity of burfi = 18 kg
Given, Khoya : Sugar = 7 : 2
Total = 7 + 2 = 9
Quantity of khoya = \(\frac{7}{9} \times 18=14 \mathrm{~kg}\)
So, Reshma used 14 kg khoya.
Question 3. A line segment 56 cm long is to be divided into two parts in the ratio 2 : 5. Find the length of each part.
Solution. Length of line segment = 56 cm
Ratio of two parts = 2 : 5
Sum of parts = 2 + 5 = 7
∴ Length of first part = \(\frac{2}{7} \times 56=16 \mathrm{~cm}\)
and length of second part = \(\frac{5}{7} \times 56=40 \mathrm{~cm}\)
MP Board Class 6 Maths Solutions
Question 4. Ram and Mohan ran in a race. Ram covered 210 m while during the same time Mohan covered only 180 m. What is the ratio of the distance covered by Mohan to that by Ram?
Solution. Distance covered by Ram = 210 m
Distance covered by Mohan = 180 m
∴ Required ratio = \(\frac{180}{210}=\frac{6}{7}=6: 7\)
Question 5. School starts at 7 : 00 am and gets over at 12 : 30 pm. If the break time is from 9 : 50 am to 10 : 10 am. What is the ratio of the break time to the total time the students spend at school?
Solution. School starts at 7:00 am and gets over at 12:30 pm.
Total time the student spend at shcool
= 5 h 30 min = (5 x 60 + 30) m = 330 min
Break time = 9:50 am to 10 : 10 am = 20 min
∴ Required ratio = \(\frac{20}{330}=2: 33\)
Question 6. There are two rectangles A and B. A has a length of 12 cm and breadth of 6 cm. B has a length of 11 cm and breadth of 9 cm. Find the ratio of their perimeter.
Solution. For Rectangle A,
Length 12 cm and breadth = 6 cm
Perimeter of Rectangle A = 2 x (length + breadth)
= 2 (12 + 6)
= 36 cm
For Rectangle B, Length = 11 cm and breadth = 9 cm
Perimeter of Rectangle B = 2 (11 + 9) = 40 cm
∴ Required ratio = \(\frac{36}{40}=\frac{9}{10}=9: 10\)
Question 7. Line segment AB = 10 cm is divided at C in the ratio 1 : 4, what are the lengths of \(\overline{A C} \text { and } \overline{B C} \text { ? }\)

Solution. Length of line segment AB = 10 cm
and AC : BC = 1 : 4
Sum of parts AC and BC = AC + BC = 1 + 4 = 5
∴ Length of \(\overline{A C}=\frac{1}{5} \times 10=2 \mathrm{~cm}\)
Length of \(\overline{B C}=\frac{4}{5} \times 10=8 \mathrm{~cm}\)
MP Board Class 6 Maths Solutions
Question 8. 17 bags of cement costs ₹ 1675.50. How many bags of cement can be bought for ₹ 1182?
Solution. In ₹ 1675.50, number of bags purchased = 17
In ₹ 1, number of bags purchased = \(\frac{17}{1675.50}\)
In ₹ 1182, number of bags purchased = \(\frac{17}{1675.50} \times 1182\)
= 12 (approx.)
Question 9. The sides of a triangle are in the ratio 2 : 3 : 5. If the total perimeter of the triangle is 70 cm, then find the length of the longest side.
Solution. Given, ratio of sides of triangle = 2 : 3 : 5
Total perimeter = 70
Total of the sides = 2 + 3 + 5 = 10
∴ Length of the longest side = \(70 \times \frac{5}{10}=35 \mathrm{~cm}\)
Question 1. Samira sells newspapers at Janpath crossing daily. On a particular day, she had 312 newspapers out of which 216 are in English and remaining in Hindi. Find the ratio of
(1) the number of English newspapers to the number of Hindi newspapers.
(2) the number of Hindi newspapers to the total number of newspapers.
Solution. Total number of newspapers = 312
Number of english newspapers = 216
Hindi newspapers = Total number of newspapers – Number of English newspapers
= 312 – 216 = 96
(1) Ratio of the number of English newspapers to the
number of Hindi newspapers = 216 : 96 = \(\frac{216}{96}=\frac{9}{4}=9: 4\)
(2) Ratio of the number of Hindi newspapers to the
total number of newspapers = \(\frac{96}{312}=\frac{4}{13}=4: 13\)
MP Board Class 6 Maths Solutions
Question 2. In a club having 100 members, 20 play carrom, 24 play table tennis, 16 play badminton and the remaining do not play any game (no member plays more than one game). Find the ratio of
(1) the number of members who play carrom to the numbers of those, who play table tennis.
(2) the number of members who play badminton to the number of those, who play carrom.
(3) the number of members who play table tennis to the number of those, who play badminton.
(4) the number of members who play badminton to the number of those, who do not play any game.
Solution. Total number of members = 100
Number of members, who play carrom = 20
Number of members, who play table tennis = 24
Number of members, who play badminton = 16
Number of members, who do not play any game
= 100 – (20 + 24 + 16) = 100 – 60 = 40
(1) Ratio of members who play carrom to the members who play table tennis
= \(20: 24=\frac{20}{24}=5: 6\)
(2) Ratio of members who play badminton to the members who play of carrom
= \(16: 20=\frac{16}{20} \approx \frac{4}{5}=4: 5\)
(3) Ratio of members who play table tennis to the member who play, badminton
= \(24: 16=\frac{24}{16}=\frac{3}{2}=3: 2\)
(4) Ratio of members who play badminton to the number of members, who do not play any game
= \(16: 40=\frac{16}{40}=\frac{2}{5}=2: 5\)
Question 3. Length and breadth of the floor of a room are 5 m and 3 m, respectively. Forty tiles, each with area \(\frac{1}{16}\) m2 are used to cover the floor partially. Find the ratio of the tiled and the non-tiled portion of the floor.
Solution. Given, length of floor of a room = 5 m
and breadth of floor of a room = 3 m
Area of floor = 5 x 3 = 15 m2
Area of one tile = \(\frac{1}{16}\) m2
Area of forty tiles = \(40 \times \frac{1}{16}=\frac{5}{2} \mathrm{~m}^2\)
Tiled portion of the floor = \(\frac{5}{2}\) m2
Now, non-tiled portion of the floor = \(\left(15-\frac{5}{2}\right) \mathrm{m}^2\)
= \(\left(\frac{30-5}{2}\right)=\frac{25}{2} \mathrm{~m}^2\)
So, ratio of tiled to the non-tiled portion of the floor
= \(\frac{5}{2}: \frac{25}{2}=\frac{\frac{5}{2}}{\frac{25}{2}}=\frac{5}{25}=\frac{1}{5}=1: 5\)
Hence, the required ratio is 1 : 5.
Question 4. In a year, Ravi earns ₹ 360000 and paid ₹ 24000 as income tax. Find the ratio of his
(1) income to income tax.
(2) income tax to income after paying income tax.
Solution. Given, Ravi earns in a year = ₹ 360000
and Ravi paid income tax in a year = ₹ 24000
(1) Ratio of income to the income tax paid
= 360000 : 24000
= 360 : 24 [dividing by 1000 in both ratios]
= 15 : 1 [dividing by 24 in both ratios]
Hence, the ratio of income to income tax is 15 : 1.
(2) After paying income tax, remaining income
= Total income – Income tax
= 360000 – 24000
= ₹ 336000
∴ Ratio of income tax to income after paying income tax
= 24000 : 336000
= 24 : 336 [dividing by 1000 in both ratios]
= 1 : 14 [dividing by 24 in both ratios]
Hence, the ratio of income tax to income after paying income tax is 1 : 14.
Question 5. Ramesh earns ₹ 28000 per month. His wife Rama earns ₹ 36000 per month. Find the ratio of
(1) Ramesh’s earnings to their total earnings.
(2) Rama’s earnings to their total earnings.
Solution. Given, Ramesh earns per month = ₹ 28000
and Rama earns per month = ₹ 36000
∴ Total earnings = Ramesh’s earning per month + Rama’s earning per month
= ₹ (28000 + 36000) = ₹ 64000
(1) Ratio of Ramesh’s earnings to their total earnings
= Ramesh’s earnings : Total earnings
= 28000 : 64000
= 28 : 64 [dividing by 1000 in both ratios]
= 7 : 16 [dividing by 4 in both ratios]
Hence, the ratio of Ramesh’s earnings to their total earnings is 7: 16.
(2) Rama’s earnings to their total earnings
= Rama’s earnings : Total earnings
= 36000: 64000
= 36 : 64 [dividing by 1000 in both ratios]
= 9 : 16 [dividing by 4 in both ratios]
Hence, the ratio of Rama’s earnings to income their total earnings is 9 : 16.
MP Board Class 6 Maths Solutions
Question 6. A recipe calls for 1 cup of milk for every \(2 \frac{1}{2}\) cups of flour to make a cake that would feed 6 persons. How many cups of both flour and milk will be needed to make a similar cake for 8 people?
Solution. Given, milk needed for making cake = 1 cup
and flour needed for making cake = \(2 \frac{1}{2} \text { cups }=\frac{5}{2} \text { cups }\)
Then, the total amount needed Milk + Flour
= \(\left(1+\frac{5}{2}\right) \text { cups }=\frac{7}{2} \text { cups }\)
So, \(\frac{7}{2}\) cups of milk and flour needed to make cake for 6 persons.
Let the needed amount of cups of milk and flour to make cake for 8 persons = x
[where, x is a multiple of cups]
By ratio and proportion law, \(\frac{2}{6}\) = \(\frac{x}{8}\)
⇒ \(\frac{7}{2} \times 8=6 \times x\)
⇒ x = \(\frac{28}{6}\)
⇒ x = \(\frac{14}{3}\) [dividing by 2]
Hence, the cups needed for 8 persons is \(\frac{14}{3}\).
Question 7. A scooter travels 120 km in 3 h and a car travels 120 km in 2 h. Find the ratio of their speeds. [Hint \(\text { Speed }=\frac{\text { Distance travelled }}{\text { Time taken }}\)]
Solution. Given, distance travelled by a scooter = 120 km
Time taken by a scooter = 3h
∴ \(\text { Speed of scooter }=\frac{\text { Distance travelled }}{\text { Time taken }}=\frac{120 \mathrm{~km}}{3 \mathrm{~h}}\)
= 40 km/h
and distance travelled by car = 120 km
and time taken by a car = 2h
∴ \(\text { Speed of the car }=\frac{\text { Distance travelled }}{\text { Time taken }}\)
= \(\frac{120 \mathrm{~km}}{2 \mathrm{~h}}\)
= 60 km/h
= Speed of the scooter : Speed of the car
= 40:60 = 2:3 [dividing by 20 in both ratios]
Hence, the ratio of their speeds is 2: 3.
Matchsticks are used to make pattern of letters and other shapes.
Using matchsticks, we can write a general rule regarding the number of matchsticks required for a given shape. We introduce a variable which takes on values 1, 2, 3,…, denoted by letter n.
e.g. Let us consider the shape of a right angle.
(1) Number of right angle = 1 Number of matchsticks = 2
(2) Number of right angles = 2 Number of matchsticks = 4
(3) Number of right angles = 3 Number of matchsticks = 6 …… and so on.
Writing the above facts in a table, we have

From the table, we can say that the number of matchsticks required is twice the number of right angled formed.
i.e. Number of matchsticks required = 2 x Number of right angles formed
Read and Learn More MP Board Class 6 Maths Solutions
Hence, we can write as
Number of matchsticks required = 2n,
where n is the number of right angles formed.
Variable
A variable is a number which does not have a fixed value. It can take various values.
To show a variable, we may use any letter as n, m, l, p, x, y, z etc.
In the above example of the shape of right angle.
Number of matchsticks required = 2n
where n is called variable which is the number of right angles formed.
More Matchstick Patterns
We can make many letters of the alphabet and other shapes from matchsticks.
e.g. (1) Patterns of U (L), triangle (A), etc.
Hence, the number of matchsticks required = 3n
(2) Pattern of letter E
To make one E, five matchsticks are used
Hence, the number of matchsticks required = 5n
MP Board Class 6 Maths Solutions
Example 1. Find the rule which gives the numbers of matchsticks required to make the following matchstick pattern. Use a variable to write the rule.
(1) A pattern of letter W
(2) A pattern of letter O
Solution. (1) One W can be formed by 4 matchsticks. Two W can be formed by 8 matchsticks.
So, let variable n denote the number of W’s.
Now, the number of matchsticks required to make pattern of W are given below.
For n = 1, the number of matchsticks required = 4 x 1 = 4
For n = 2, the number of matchsticks required = 4 x 2 = 8
For n=3, the number of matchsticks required = 4 x 3 = 12
For n = n, the number of matchsticks required = 4 x n = 4n
Hence, the required rule for a pattern of letter W is 4n.
(2). One O can be formed by 4 matchsticks and two O can be formed by 8 matchsticks.
Thus, we get the following pattern of letter O.
So, let variable n denote the number of O’s.
Now, the number of matchsticks required to make pattern of O are given below.
For n = 1, the number of matchsticks required = 4 × 1 = 4
For n = 2, the number of matchsticks required = 4 × 2 = 8
For n = 3, the number of matchsticks required = 4 x 3 = 12
For n = n, the number of matchsticks required = 4 × n = 4n
Hence, the required rule for a pattern of letter O is 4n.
Example 2. Look at the following matchstick pattern of hexagons in the given figures below. The hexagons are not separate. Two neighbouring hexagons have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of hexagons.
Solution. In figure,
(1) Number of hexagon = 1
and number of matchsticks = 6 = 5 x 1 + 1
(2) Number of hexagons = 2
= 5 x Number of hexagon + 1
and number of matchsticks = 11 = 5 x 2 + 1
(3) Number of hexagons = 3
= 5 x Number of hexagon + 1
and number of matchsticks = 16 = 5 × 3 + 1
= 5x Number of hexagon + 1
Thus, if number of hexagons = x
Then, the number of matchsticks
= 5 x Number of hexagons + 1
= 5x + 1
Hence, the required rule that gives the number of matchsticks is 5x + 1, where x is the number of hexagons.
Examples of Variables
Example 3. The teacher distributes 10 pencils per student. Can you tell how many pencils are needed, considering the number of students? (use x for the number of students).
Solution. Let the number of students be x.
Given, number of pencils distributed per student = 10
Now, number of pencils when
x = 1 is 10 or 10 x 1 = 10 x x
⇒ x = 2 is 20 or 10 x 2 = 10 x x
⇒ x = 3 is 30 or 10 x 3 = 10 x x
∴ Number of pencils for x students are 10x.
MP Board Class 6 Maths Solutions
Example 4. School children are standing in a ground. There are 10 children in a row. What is the rule which gives the number of children, given the number of rows? (use n for the number of rows.)
Solution. Let the number of rows be n
Given, the number of children in each row = 10

∴ Total number of children = 10n
Here. = 1 child
Hence, the rule to find the number of children in row is 10n.
Example 5. If there are 40 apples in a box, how will you write the total number of apples in terms of the number of boxes? (use a for the number of boxes).
Solution. Given, a is the number of boxes and the number of apples in a box = 40
When there is one box
i.e. a = 1, then the number of apples = 40 x 1 = 40 When there are two boxes
i.e. a = 2, then the number of apples = 40 x 2 = 80 When there are three boxes
i.e. a = 3, then the number of apples = 40 x 3 = 120 When there are a boxes
i.e. a = a, then the number of apples = 40 × a = 40a
Hence, the total number of apples in terms of number of boxes can be written as 40a.
Example 6. In her birthday, Radha distributes 5 toffees per student. Can you tell how many toffees are needed, given the number of students? (use letter y for the number of students).
Solution. Let the number of students be y.
Given, the number of toffees distributed to each student = 5
When there is one student i.e. y = 1,
then the number of toffees = 5 x 1 = 5
When there are two students i.e. y = 2,
then the number of toffees = 5 x 2 = 10
When there are three students i.e. y = 3,
then the number of toffees = 5 x 3 = 15
When there are y students i.e. y = y, then the number of toffees = 5 x y = 5y
Hence, 5 y toffees are needed for y students.
Example 7. A drone files 2 km In one minute. Can you express the distance covered by drone in terms of its flying time in minutes? (use z for flying time in minutes).
Solution. Let flying time of drone be z min.
Then, distance covered by drone in one minute = 2 km
∴ Distance covered by drone in 2 min = z x 2 = 2zkm
Hence, the distance covered by the drone in its flying time i.e. in z min is 2z km.
Example 8. Lakhan is Bharat’s younger brother. Lakhan is 5 yr younger than Bharat. Can you write Lakhan’s age in terms of Bharat’s age? Take Bharat’s age to be myr.
Solution. Let Bharat’s age be m yr.
Given, the Lakhan is 5 yr younger than Bharat.
So, age of Lakhan = (Age of Bharat) – 5 yr
⇒ Age of Lakhan (m-5) yr
Thus, we can write Lakhan’s age in terms of Bharat’s age.
MP Board Class 6 Maths Solutions
Example 9. Hema’s mother made some cookies. She gives some cookies to guests and family members, still 7 cookies remain. If the number of cookies her mother gave away is t, how many cookies did she make?
Solution. Given, the number of cookies was given away by her mother = t
and the number of cookies left over = 7
∴ Total number of cookies made by Hema’s mother
= Number of cookies gave away + Number of cookies left
= t + 7
Hence, the total number of cookies made by her mother is t + 7.
Example 10. Mangoes are to be transferred from larger boxes to smaller boxes. When a large box is emptied, the mangoes from it fill three smaller boxes and still 5 mangoes remain outside.
If the number of mangoes in a small box are taken to be m, what is the number of mangoes in the larger box?
Solution. Given, the number of mangoes in a small box = m
Since, one larger box is emptied to fill three smaller boxes.
So, the number of mangoes in three smaller boxes
= 3 x Number of mangoes in one small box = 3x m = 3m
Also, 5 mangoes remain outside when larger box is emptied to fill three smaller boxes.
So, the number of mangoes in the larger box
= Number of mangoes in three smaller boxes + Mangoes left over
= 3m + 5
Hence, the number of mangoes in the larger box is 3m +5.
Question 1. Find the rule which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.
(1) A pattern of letter T as T
(2) A pattern of letter Z as Z
Solution. (1) One T can be formed by 2 matchsticks and 2T can be formed by 4 matchsticks. Thus, we get the following patterns of letter T.

So, let variablen denotes the number of T’s.
Now, the number of matchsticks required to make pattern of T are given below:
For n = 1,
Number of matchsticks required = 2 × 1 = 2
For n=2,
Number of matchsticks required = 2 x 2 = 4
For n = 3,
Number of matchsticks required = 2 × 3 = 6
For n=n,
Number of matchsticks required = 2 x n = 2n
Hence, the required rule for a pattern of letter T is 2n.
(2) One Z can be formed by 3 matchsticks and 2Z can be formed by 6 matchsticks. Thus, we get the following patterns of letter Z.
So, let variable n denotes the number of Z’s.
Now, the number of matchsticks required to make pattern of Z are given below:
For n = 1,
Number of matchsticks required = 3 x 1 = 3
For n = 2,
Number of matchsticks required = 3 x 2 = 6
For n = 3,
Number of matchsticks required = 3 × 3 = 9
For n = n,
Number of matchsticks required = 3 x n = 3n
Hence, the required rule for a pattern of letter Z is 3n.
MP Board Class 6 Maths Solutions
Question 2. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows?
(use n for the number of rows.)
Solution. Let the number of rows = n
Given, the number of cadets in each row = 5
∴ Total number of cadets = 5n
Here, ⚫ = 1 cadet
Hence, rule to find the number of cadets in n rows is 5n.
Question 3. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (use b for the number of boxes).
Solution. Given, b is the number of boxes and the number of mangoes in a box = 50
When there is one box i.e. b = 1,
then the number of mangoes = 50 x 1 = 50.
When there are two boxes i.e. b = 2,
then the number of mangoes = 50 x 2 = 100
When there are three boxes i.e. b = 3,
then the number of mangoes = 50 x 3 = 150
When there are b boxes i.e. b = b,
then the number of mangoes = 50 x b = 50b
Hence, the total number of mangoes in terms of number of boxes can be written as 50b.
Class 6 Maths Chapter 11 Solutions
Question 4. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (use S for the number of students).
Solution. Let the number of students be S.
Given, the number of pencils distributed to each student = 5
When there is one student i.e. S = 1,
then the number of pencils = 5 x 1 = 5
When there are two students i.e. S = 2,
then the number of pencils = 5 x 2 = 10
When there are three students i.e. S = 3,
then the number of pencils = 5 x 3 = 15
When there are S students i.e. S = S,
then the number of pencils = 5 x S = 5S.
Hence, 5$ pencils are needed for S students.
Question 5. A bird flies 1 km in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes? (use t for flying time in minutes).
Solution. Let flying time of bird be t min.
Then, bird flies in one min = 1 km
∴ Bird flies in t min = t x 1 = t km
Hence, the distance covered by the bird in its flying time i.e. int min is t km.
Class 6 Maths Chapter 11 Solutions
Question 6. Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots with chalk powder). She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there, if there are 8 rows? If there are 10 rows?
Solution. Given, the number of rows = r
and the number of dots in one row i.e. r = 1 is 9 x 1 = 9
∴ The number of dots in 2 rows i.e. r 2 is 9 x 2 = 18
The number of dots in 3 rows i.e. r = 3 is 9 x 3 = 27
∴ Total number of dots in r rows = 9 x r = 9r
Now, if there are 8 rows i.e. r = 8, then the number of dots
= 9 x 8 = 72 dots
and for r = 10,
The number of dots = 9 x 10 = 90 dots
Question 7. Leela is Radha’s younger sister. Leela is 4 yr younger than Radha. Can you write Leela’s age in terms of Radha’s age? Take Radha’s age to be x years.
Solution. Let Radha’s age be xyr.
Given, the Leela is 4 yr younger than Radha.
So, age of Leela = (Age of Radha) – 4 yr
⇒ Age of Leela = (x-4) yr
Thus, we can write Leela’s age in terms of Radha’s age.
Question 8. Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is I, how many laddus did she make?
Solution. Given, the number of laddus was given away by mother = l
and the number of laddus left over = 5
∴ Total number of laddus made by mother = Number of laddus gave away + Number of laddus left over
= 1 + 5
Hence, the number of laddus made by mother is l + 5.
Class 6 Maths Chapter 11 Solutions
Question 9. Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?
Solution. Given, the number of oranges in a small box = x
Since, one large box is emptied to fill two smaller boxes.
So, the number of oranges in two smaller boxes
= 2 x Number of oranges in one small box = 2 x x = 2x
Also, 10 oranges remain outside when large box is emptied to fill two smaller boxes.
So, the number of oranges in the larger box = Number of oranges in two smaller boxes + Oranges left over
= 2x + 10
Hence, the number of oranges in the large box is 2x + 10.
Question 10. Look at the following matchstick pattern of squares. The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares.
[Hint If you remove the vertical stick at the end, you will get a pattern of C’s.]
Solution.
(a) Number of square = 1
and number of matchsticks = 4 = 3 x 1 + 1 = 3 x Number of square + 1
(b) Number of squares = 2
and number of matchsticks = 7 = 3 x 2 + 1 = 3 x Number of squares + 1
(c) Number of squares = 3
and number of matchsticks = 10 = 3 x 3 + 1 = 3 x Number of squares + 1
(d) Number of squares = 4
and number of matchsticks = 13 = 3 x 4 + 1
= 3 x Number of squares + 1
Thus, if number of squares = x
Then, the number of matchsticks
= 3x Number of squares + 1
= 3x + 1
Hence, the required rule that gives the number of matchsticks is 3x+1, where x is the number of squares.
Question 1. Six trees are planted in a row. Then, the number of trees planted in n such rows are
Answer. 1. 6n
Question 2. Which of the following represents 6 x X.
Answer. 1. 6x
Question 3. If each matchbox contain 50 matchsticks, then the number of matchsticks required to fill n such boxes is
Answer. 2. 50 n
Question 4. A box of fruits contain 60 oranges, the number of oranges required for y such boxes
Answer. 3. 60 y
Class 6 Maths Chapter 11 Solutions
Question 5. If there are 25 pictures in an album, then the rule which gives total number of pictures in X albums is Competency Based Question
Answer. 4. 25 x
Question 6. A train is moving at a speed of x km/h. Then, the rule which gives the distance covered by train in 7h is
Answer. 1. 7x
Question 7. Variable means that it
Answer. 1. can take different values
Question 8. Garima puts a handful of seeds into an empty bird feeder. A bird comes and eats 7 of them. Which of the following expression can represent this situation algebraically? Competency Based Question
Answer. 3. p – 7
Question 9. Garima put some more seeds in the feeder. Which of the following expressions can represent this situation algebraically?
Answer. 4. p + q – 7
Question 10. If x takes the value of 7, then the value of x +13 Is
Answer. 1. 20
Question 11. If there are 40 coins in a box and x coins taken out from the box, then the remaining coins in the box can be represented in terms of number of coins taken out by the statement. Competency Based Question
Answer. 3. x is subtracted from 40
Question 12. In algebra, letters may stand for
Answer. 1. unknown quantities
Class 6 Maths Chapter 11 Solutions
Question 13. Look at the following matchstick pattern of octagons in the given figures below. The octagons are not separate. Two neighbouring octagons have a common matchstick. Then, the rule that gives the number of matchsticks in terms of the number of octagons is
Answer. 2. 7n + 1
Question 14. The difference between Sanjana’s and her mother’s age is 27 yr. Then, the age of Sanjana’s mother is
Answer. 2. (x+27) yr
Question 15. An auto rickshaw charges 20 for the first kilometer, then 7 for each such subsequent kilometres. The total charge (in) for r kilometres is
Answer. 2. 20 + (r-1)7
Question 1. Assertion (A) The rule which gives the number of matchsticks required to make the matchstick pattern L, is 2n.
Reason (R) For n = 1, the number of matchsticks required = 2 x 1 = 2.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 2. Assertion (A) The rule which gives the number of matchsticks required to make the matchstick pattern C, is 3n.
Reason (R) For n = 2, the number of matchsticks required = 3 x 2 = 6
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 3. Assertion (A) n can take different values such as 1, 2, 3, 4, …. .
Reason (R) n is the example of a variable. Its value is not fixed. It can take different values.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 1. The variable can take ….. values.
Answer. Different
Question 2. The number of days in w weeks is …. .
Answer. 7w
Question 3. If the present age of Ramandeep is n years, then her age after 7 yr will be ….. .
Answer. n+7
Question 4. The value of ….. is not fixed.
Answer. Variable
Question 5. In 2, 3, 5, l, 10, m and 13, the numbers of variables are …. .
Answer. Two
Class 6 Maths Chapter 11 Solutions
Question 1. The number of matchsticks required to form the letter V is 3.
Answer. False
Question 2. t minutes are equal to 60 t seconds.
Answer. True
Question 3. The difference between the ages of two sisters Lila and Yamini is a variable.
Answer. False
Question 4. Variables can be denoted by any letter as a, b, c, l, m, n, …., x, y, z.
Answer. True
Question 5. 1 kg of potatoes are bought for ₹ 60. Cost of n kg of potatoes is 60 n.
Answer. True
Question 1. Match the Column A with Column B

Answer. (a) → (2), (b) → (3), (c) → (4), (d) → (1)
Question 1. Sarah buy books from a dealer for her bookstall. She buys 20 comic books, 15 story books and 10 colouring books. A comic book cost ₹ a. A story book costs ₹ 5 more than a comic book and a colouring book costs ₹ 10 more than a story book.
On the basis of the given information, answer the following questions.
(1) Which of the following expression shows the total cost of the comic books?
(a) 20
(b) 20a
(c) 20 + a
(d) 20 – a
(2) Sarah gets a profit of ₹ 2 on the sale of each comic book. Which of the following expression shows the amount Sarah earns by selling 10 comic books?
(a) a + 2
(b) 20a – 20
(c) 10a + 20
(d) 20 + a + 2
Class 6 Maths Chapter 11 Solutions
(3) A colouring book costs ₹ 50. What is the cost of the comic book?
(a) 35
(b) 40
(c) 45
(d) 50
(4) Write an expression to show the total cost of 15 storybooks.
Solution. (1) (b) Since, Sarah bought 20 comic books and cost of 1 comic book is a.
∴ Total cost of comic books = Cost of 1 comic book × Total number of comic books
= a x 20 = 20a
(2) (c) Cost of 1 comic book = a
Cost of 1 comic book with profit of ₹ 2 = a + 2
Number of books she sold = 10
Therefore, the amount Sarah earns by selling 10 comic books = 10 (a + 2) = 10a + 20
(3) (a) Cost of a comic book is ₹ a.
Then, according to the question,
Cost of a story book = Cost of a comic book + ₹ 5
= a + 5
Cost of a colouring book Cost of a story book + ₹ 10 = (a + 5) + 10 = a + 15
Also, it is given that a colouring book costs ₹ 50.
Therefore, equation is a + 15 = 50 ⇒ a = 50 – 15 ⇒ a = 35
Hence, the cost of a comic book is 35.
(4) Cost of 1 story book = a + 5
and total number of story book = 15
Therefore, the total cost of 15 story books = Total number of story books × Cost of one story book
= 15(a + 5) = 15a + 75
Question 2. Sudhir observed the pattern shown below on a cloth. The pattern consists of 4 patches.
The pattern is repeated n number of times in a 4 m long cloth.
(1) Which of the following expressions shows the number of octagon patches on the cloth?
(a) n
(b) 4n
(c) n + 4
(d) n – 4
(2) The cloth is cut into two equal halves. Sudhir observed both cloth parts have an equal number of repeating blocks but the last line is not complete. Which of the following expression shows the number of complete repeating blocks?
(a) n – 1
(b) 2n – 1
(c) \(\frac{n}{2}\)
(d) \(\frac{n}{2}\) – 1
(3) Write an expression which shows the total number of patches on the cloth?
Solution. (1) (a) Since, the pattern is repeated number of times there are n number of octagon patches on the cloth.
(2) (d) Number of repetition of pattern = n
The cloth cut into two equal halves.
∴ Number of repetition of pattern = \(\frac{n}{2}\)
and given last line is not complete.
∴ Number of complete repeating block = \(\frac{n}{2}\) – 1
(3) Total number of patches on cloth = Number of repetition of pattern x Number of patches in each repetition
Since, 4 patches in each pattern and pattern repeated n number of time
∴ Total number of patches on the cloth = 4n
Class 6 Maths Chapter 11 Solutions
Question 1. The cost of one pen is ₹ 15. Find the cost of y pens.
Solution. Cost of one pen = ₹ 15
Cost of y pen = 15 x y = 15y
Question 2. Find the number of matchsticks required to make the pattern of a square.
Solution. The number of matchsticks required to make the pattern of a square is 4.

Question 3. The valye of x pencisl, if cost of 1 pencil is ₹ 10.
Solution. Cost of one pencil = 10.
Cost of x pencil = 10 x x = 10x
Question 4. How many matchsticks will be required to make the pattern of a triangle?
Solution. The number of matchsticks required to make the pattern of a triangle is 3.

Question 1. The teacher distributes 2 pencils per student. Can you tell how many penciles are needed, given the number of students? (use x for the number of students).
Solution. Teacher distributes pencils per student = 2
Number of students = x
∴ Need of pencils = 2 x x = 2x
Question 2. A dolphin swins 1 km in one minute. Can you express the distance covered by dolphin in terms of its swimming time in minutes? (use t for swimming time in minutes)
Solution. Let the swimming time of dolphin bet min.
Then, dolphin swims in one min = 1 km
∴ Dolphin swims in t min = t x 1 = t km
Hence, the distance covered by dolphin in swimming time i.e. in t min is t km.
Algebra Class 6 Maths Solutions
Question 3. In a village, there are 8 water tanks to collect rain water. On a particular day, x litres of rain water is collected per tank. If 100 L of water was already there in one of the tanks, what is the total amount of water in the tanks on that day?
Solution. Rain water collected on particular day per tank = x L
Number of tanks to collect water = 8
Total water in all tanks = 8x L
Water in one of the tanks = 100 L
∴ Total amount of water = Total water in all tanks + Water in one of the tanks
= (8x + 100) L
Question 1. Find the rule which gives the number of matchsticks required to make the following matchstick patterns.
A pattern of letter y as Y
Solution. One Y can be formed by 3 matchsticks and 2Y can be formed by 6 matchsticks.
Thus, we get the following patterns of letter Y.

Here, the number of Y’s are increasing.
So, let the variable n denote the number of Y’s.
Now, the number of matchsticks required to make pattern of Y are given below:
For n = 1,
the number of matchsticks required = 3 x 1 = 3 For n = 2,
the number of matchsticks required = 3 x 2 = 6 For n = 3,
the number of matchsticks required = 3 x 3 = 9 For n = n,
the number of matchsticks required = 3 x n = 3n
Hence, the required rule for a pattern of letter Y is 31.
Question 2. Army personnel are standing in an open ground. There are 6 personnel in a row. What is the rule which gives the number of army personnel, given the number of rows? (use n for the number of rows.)
Solution. Let the number of rows = n
Given, the number of army personnel in each row = 6
∴ Total number of army personnel = 6n
Hence, the rule to find the number of army personnel in n rows is бn.
Question 3. If there are 40 oranges in a box, how will you write the total number of oranges in term of the number of boxes? (use b for the number of boxes).
Solution. Given, the number of oranges in box = 40
Let the number of boxes = b
Total number of oranges in term of number of boxes can be written as 40b.
Algebra Class 6 Maths Solutions
Question 4. Sakshi is drawing a dot Rongolu (a beautiful pattern of lines joining dots with chalk powder). She has 6 dots in a row. Find,
(1) how many dots will her Rangoli have for r rows?
(2) how many dots are there, if there are 10 rows?
Solution. Given, the number of rows = r
(1) The number of dots in one row
i.e. r = l is 6 x 1 = 6
The number of dots in two rows
i.e. r = 2 is 6 x 2 = 12
∴ Total number of dots in r rows = 6 x r = 6r
(2) If number of rows = 10
∴ The number of dots = 10 x 6 = 60 dots
Question 5. Richa is Madan’s younger sister. Richa is 5 yr younger than Madan. Can you write Richa’s age in terms of Madan’s age? Take Madan’s age to be x yr.
Solution. Let Madan’s age be x yr.
Given, Richa is 5 yr younger than Madan.
So, age of Richa = (Age of Madan) – 5 yr
and age of Richa = (x – 5) yr
Question 6. Mother bought some candy. She gives some candies to guests and family members; still 10 candies to guests and family members; still 10 candies are remain. If the number of candies mother gave away is m, how many candies did she bought?
Solution. Given, the number of candies given to guest and family members = m
and the number of candies left over = 10
∴ Total number of candies she bought = Number of candies gave to guest and family members + Number of candies left over
= m + 10
Hence, the number of candies bought by mother is m + 10.
Question 7. Mangoes are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the mangoes from it fill three smaller boxes and still 20 mangoes remain outside.
If the number of mangoes in a small box are taken to be x, what is the number of mangoes in the larger box?
Solution. Given, the number of mangoes in a small box = x
Since, one large box is emptied to fill three smaller boxes.
So, the number of mangoes in three smaller boxes = 3 x Number of mangoes in one box = 3 x x = 3x
Also, 20 mangoes remain outside when large box is emptied to fill three smaller boxes.
Number of mangoes in the larger box = Number of mangoes in three smaller boxes + Mangoes left over
= 3x + 20
Algebra Class 6 Maths Solutions
Question 8. Sunitha is half the age of her mother Geeta. Find their ages
(1) after 4 yr?
(2) before 3 yr?
Solution. Let Sunita’s present age be x.
Given, Sunita is half the age of her mother Geeta.
∴ Geeta’s present age = 2x
(1) Sunita’s age after 4 yr = (x+4) yr
Geeta’s age after 4 yr = (2x+4) yr
(2) Sunita’s age before 3 yr = (x-3) yr
Geeta’s age before 3 yr = (2x-3) yr
Question 9. Look at the following matchstick pattern of pentagons in the figures given below. The pentagons are not separate. Two neighbouring pentagons have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of pentagons.
Solution. From figure,
(1) Number of pentagons = 1
and number of matchsticks = 5 = 4 x 1 + 1
= 4 x Number of pentagons + 1
(2) Number of pentagons = 2
and number of matchsticks = 9 = 4 x 2 + 1
= 4 x Number of pentagons + 1
(3) Number of pentagons = 3
and number of matchsticks = 13 = 4 x 3 + 1
= 4 x Number of pentagons + 1
Thus, if number of pentagons = x
Then, the number of matchsticks
= 4 x Number of pentagons + 1
= 4x + 1
Hence, the required rule that gives the number of matchsticks is 4x+1, where x is the number of pentagons.
The distance covered along the boundary forming a closed figure when you go round the figure once is called the perimeter. Thus, we can calculate the perimeter of a plane figure by calculating the sum of measurements of all its sides. Unit of perimeter is same as that of length.
In Diagram (1), perimeter of △ABC = AB + BC + CA
In Diagram (2), perimeter of pentagon ABCDE =AB + BC + CD + DE + EA
Example 1. Find the perimeter of the given figures.
Solution. (1) Perimeter of the figure ABCDEF
Sum of the measurements of all sides
= AB + BC + CD + DE + EF + FA
= 100 + 120 + 90 + 45 + 60 + 80 = 495 m
Hence, the perimeter of the given figure is 495 m.
Read and Learn More MP Board Class 6 Maths Solutions
(2) Perimeter of the figure ABCDEFG
= Sum of the measurements of all sides
= AB + BC + CD + DE + EF + FG + GA
= 3 + 1 + 3.5 + 3.5 + 1 + 3 + 2 = 17 cm
Hence, the perimeter of the given figure is 17 cm.
(3) Perimeter of the figure ABCDEFG
= Sum of the measurements of all sides.
= AB + BC + CD + DE + EF + FG + GA
= 4 + 3 + 6 + 3 + 1 + 3 + 3 = 23 cm
Hence, the perimeter of the given figure is 23 cm.
(4) Perimeter of the given figure
= Sum of the measurements of all sides
= AB + BC + CD + DE + EF + FA
= 5 + 5 + 5 + 5 + 5 + 5 = 30 cm
Hence, the perimeter of the given figure is 30 cm.
Perimeter of a Rectangle
The perimeter of a rectangle is the total distance covered by its boundaries or the sides.
In other words, the sum of the measurements of all four sides of a rectangle is called the perimeter of a rectangle.
Perimeter of a rectangle ABCD
= Sum of length of its sides
= AB + BC + CD + DA = AB + BC + AB + BC
[∴ opposite sides are equal, CD = AB and DA = BC]
= 2(AB + BC) = 2(1 + b)
where, l = Length of the rectangle
and b = Breadth of the rectangle
Hence, the perimeter of a rectangle is 2 (1+b).
Note it While calculating the perimeter of a rectangle, we must express the length and breadth in the same unit.
MP Board Class 6 Maths Solutions
Example 2. Rohan wants to put a lace border all around a rectangular table cover 5 m long and 3 m wide. Find the length of the lace required by Rohan.
Solution. Given, length of the rectangular table cover = 5 m
and breadth of the rectangular table cover = 3 m
∴ Perimeter of the rectangular table cover = 2 × (length + breadth)
= 2 x (5 + 3) = 2 x 8 = 16m
Hence, the length of the lace required is 16 m.
Example 3. Find the perimeter of a rectangle whose length and breadth are 250 cm and 2 m, respectively.
Solution. Given, length of the rectangle = 250 cm
and breadth of the rectangle = 2 m = 2×100 cm = 200 cm
∴ Perimeter of the rectangle = 2 x (length + breadth)
= 2 × (250 + 200)
= 2 x 450 = 900 cm
Hence, the perimeter of the given rectangle is 900 cm.
Example 4. If the perimeter of a rectangle Is 200 cm and the length is 75 cm, then find Its breadth.
Solution. Given, perimeter of the rectangle = 200 cm
and length of the rectangle = 75 cm
∴ Perimeter of the rectangle = 2 x (length + breadth)
200 = 2(75 + breadth)
= \(\frac{1}{2} \times 200-75\)
= 100 – 75
= 25 cm
Hence, the breadth of the rectangle is 25 cm.
MP Board Class 6 Maths Solutions
Example 5. An athlete takes 10 rounds of a rectangular field which is 30 m long and 20 m wide. Find the total distance covered by him.
Solution. Given, length of rectangular field (l) = 30 m
and breadth of rectangular field (b) = 20 m
Total distance covered by the athlete in one round
= Perimeter of field (rectangle)
= 2(1 + b)
= 2 (30 + 20)
= 100 m
Since, the distance covered in one round = 100 m
So, the distance covered in 10 rounds = 10 x 100 = 1000 m
Example 6. A man has rectangular piece of land of length and breadth 340 m and 260 m, respectively. If each side is to be fenced with 4 rounds of wires, then what will be the length of wire needed?
Solution. Given, length of rectangular piece of land = 340 m
and breadth of rectangular piece of land = 260 m
Now, perimeter of the field = 2x (length + breadth)
= 2 x (340 + 260)
= 2 × 600
= 1200 m
∴ Each side is to be fenced with 4 rounds of wire.
∴ Total length of the wire required = 4 × 1200 = 4800 m
Example 7. Find the cost of fencing a rectangular park of length 275 m and breadth 125 m at the rate of ₹ 15 per metre.
Solution. Given, length of the rectangular park = 275 m
and breadth of the rectangular park = 125 m
Perimeter of the rectangular park = 2 × (length + breadth)
= 2 x (275 + 125)
= 2 x 400 = 800 m
∴ Cost of fencing of 1 m of park = ₹ 15
∴ Total cost of fencing the park = 15 x 800 = ₹ 12000
Perimeter of Regular Shapes
In regular shapes, all sides are of equal length and all angles are of equal measure.
If a regular polygon has n sides, then
Perimeter = n x Length of a side
where, n = Number of sides
Note it
(1) Perimeter of a regular pentagon = 5 x Length of one side = 5a
(2) Perimeter of a regular hexagon = 6 x Length of one side = 6a
Example 8. Find the perimeter of a regular hexagon with each side measuring 4 cm.
Solution. The given regular hexagon has 6 sides, each with the length of 4 cm.
∴ Perimeter of the regular hexagon = 6 x 4 = 24 cm
MP Board Class 6 Maths Solutions
Example 9. The perimeter of a regular hexagon is 30 cm. How long is its one side?
Solution. Given, perimeter of a regular hexagon = 30 cm
∴ Perimeter of regular hexagon = 6 x Length of a side
⇒ 30 = 6 x Length of a side
∴ Length of a side = \(\frac{30}{6}\) = 5 cm
Hence, the length of each side of a regular hexagon is 5 cm.
Perimeter of a Square
Perimeter of a square ABCD = AB + BC + CD + DA
= AB + AB + AB +AB
= 4AB [∴ AB = BC = CD = AD]
Hence, the perimeter of a square
= 4 x Length of a side of the square
Example 10. Find the distance travelled by Soniya, if she takes three rounds of a square park of side 60 m.
Solution. Given, length of side of square park = 60 cm
Perimeter of a square park = 4 x Length of a side
= 4 × 60 = 240 m
Distance covered in one round = 240 m
Distance covered in three rounds = 3 x 240 = 720 m
MP Board Class 6 Maths Solutions
Example 11. Mohan runs 5 times around a rectangular park with length 140 m and breadth 90 m while Sohan runs 6 times around a square park of side 80 m. Who covers more distance and by how much?
Solution. Distance covered by Mohan in one round
= Perimeter of the rectangular park
= 2x (length + breadth)
= 2 x (140 + 90) = 2 x 230 = 460 m
∴ Distance covered by Mohan is 5 rounds
= 5 × 460 = 2300 m
Distance covered by Sohan in one round
= Perimeter of the square park
= 4 x Length of a side = 4 x 80 = 320 m
∴ Distance covered by Sohan in 6 rounds = 6 x 320 = 1920 m
Difference in the distance covered = 2300-1920 = 380 m
Hence, Mohan covers more distance by 380 m.
Perimeter of an Equilateral Triangle
Perimeter of an equilateral △ABC
= AB + BC + CA = 3AB [∴ AB = BC = CA]
Hence, the perimeter of an equilateral triangle
= 3 x Length of a side of the triangle.
Example 12. If one side of an equilateral triangle is 8 cm, then find its perimeter.
Solution. Perimeter of an equilateral triangle = 3 x Length of a side
[∴in equilateral triangle, all sides are equal, so length of each side will be 8 cm]
= 3 x 8 = 24 cm
Hence, the perimeter of rectangle is 24 cm.
Class 6 Maths Chapter 10 Solutions
Example 13. How many equilateral triangles of side 4 cm long can be formed with a strip of wire of length 84 cm?
Solution. Given, side of the equilateral triangle = 4 cm
∴ Perimeter of the equilateral triangle
= 3 x Length of a side of the triangle
= 3 x 4 = 12cm
Now, number of equilateral triangles, formed
\(=\frac{\text { Total length of wire }}{\text { Perimeter of triangle }}=\frac{84}{12}=7\)Hence, the required number of equilateral triangles is 7.
The amount of surface enclosed by a closed figure is called its area.
To calculate the area of a figure using a square paper, the following conventions are adopted.
(1) Ignore portions of the area that are less than half a square.
(2) If more than half of a square is in a region, just count it as one square.
(3) If exactly half the square is counted, take its area as \(\frac{1}{2}\) sq unit.
Note it The area of one full square is taken as 1 sq unit. If it is a centimetre square sheet, then area of one full square will be 1 cm2.
Example 1. Find the area of the figure shown below. (consider area of each square = 1 cm2)
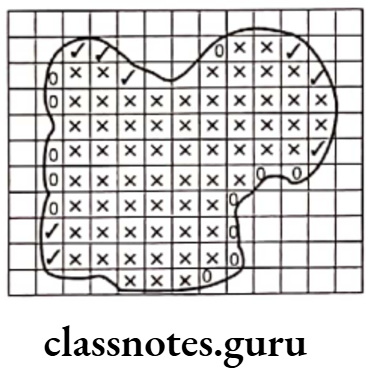
Solution. Area of a square = 1 cm2
Area of figure = Number of (x) squares + Number of (✔) squares + \(\frac{1}{2}\) Number of (0) squares
= \(65+8+\frac{1}{2} \times 12\)
= 65 + 8 + 6 = 79 cm2
[since, x and squares are covered fully by the figure and 0 square are covered half]
Hence, the area of square is 79 cm2.
Class 6 Maths Chapter 10 Solutions
Example 2. Draw any circle on a graph sheet. Count the squares and use them to estimate the area of the circular region.
Solution. First, make a circle of any suitable radius, on the graph paper. Then, count full, half and more than half or less than half squares coming under the circle.
In the figure, fully filled squares = 32
Half filled squares = 0
More than half filled squares = 20
∴ Total area = \(32 \times 1+0 \times \frac{1}{2}+20 \times 1\)
= 32 + 0 + 20 = 52 sq units
Example 3. By counting squares, estimate the area of the given figure.
Solution. Let area of one square = 1 cm2
In the figure,
Fully filled squares = 21
Half filled squares = 0
More than half filled squares = 20
∴ Total area = 21 \times 1+0 \times \frac{1}{2}+20 \times 1
= 21 + 0 + 20 = 41 cm2
Area of a Rectangle
Let length of the rectangle bel and breadth be b.
∴ Area of a rectangle (A) = Length x Breath = l x b
Using this formula, l = \(\frac{A}{b}\)
or b = \(\frac{A}{l}\)
Note it The length and breadth of a rectangle must be in the same units.
Class 6 Maths Chapter 10 Solutions
Example 1. Find the area of a rectangle whose length and breadth are 12 cm and 4 cm, respectively.
Solution. Given, length of the rectangle (1) = 12 cm
and breadth of the rectangle (b) = 4 cm
∴ Area of rectangle = 1 x b = 12 x 4 = 48 cm2
Hence, the area of rectangle is 48 cm2.
Example 2. The area of a rectangular piece of cardboard is 48 cm2 and its breadth is 6 cm. What is the length of the cardboard?
Solution. Given, area = 48 cm2 and breadth (b) = 6 cm
We know that Area = Length x Breadth
∴ \(\text { Length }=\frac{\text { Area }}{\text { Breadth }}=\frac{48}{6}=8 \mathrm{~cm}\)
Hence, the length of cardboard is 8 cm.
Example 3. Find the area in square metre of a piece of land 6 m 75 cm wide and 8 m long.
Solution. Length of the piece of land = 8 m
Breadth of the piece of land = 6 m 75 cm
= 6 + 0.75 = 6.75 m [∴ 1 m = 100 cm]
∴ Area of the piece of land = Length x Breadth
= 8 x 6.75 = 54 m2
Example 4. What is the cost of painting a wall of 500 cm long and 300 cm wide at the rate of 13 per hundred sq m?
Solution. Given, length of a wall = 500 cm
and breadth of a wall = 300 cm
∴ Area of the wall = Length x Breadth
= 500 x 300 = 150000 cm2
∴ Cost of painting per 100 m2 = ₹ 13
∴ Cost of 1 m2 = \(₹ \frac{13}{100}\)
Now, cost of 150000 m2 = \(150000 \times \frac{13}{100}=₹ 19500\)
Hence, the required cost is ₹ 19500.
Mensuration Class 6 Solutions
Example 5. Meena wants to cover the floor of a rectangular hall 9 m wide and 7 m long by square tiles. If each square tile is of side 1.5 m, then find the number of tiles required to cover the floor of the room.
Solution. Given, length of the rectangular hall = 7m
and breadth of the rectangular hall = 9 m
Area of the floor of the rectangular hall = Length x Breadth = 7 x 9 = 63 m2
Area of one square tile = Side x Side = 1.5 x 1.5 = 2.25 m2
Now, the number of required tiles \(=\frac{\text { Area of the floor }}{\text { Area of one tile }}\)
= \(\frac{63}{2.25}\) = 28 tiles
Hence, 28 tiles are required to cover the floor of the room.
Area of a Square
A four-sided polygon whose all sides are equal in length is called square.
Area of a square = Side x Side = Side2
Example 6. Find the area of a square whose side is 6 cm.
Solution. Given, side = 6 cm
∴ Area of a square Side x Side = 6 x 6 = 36cm2
Hence, the area of square is 36 cm2.
Example 7. The perimeter of a square field is 60 m. Find its area.
Solution. Given, perimeter of a square field = 60 m
We know that perimeter of a square = 4 x Side
∴ Side of a square \(=\frac{\text { Perimeter }}{4}=\frac{60}{4}=15 \mathrm{~m}\)
Now, area of the square field = Side x Side
= 15 x 15 = 225 m2
Hence, the required area is 225 m2.
Mensuration Class 6 Solutions
Example 8. What will happen to the area of a square, if its sides are doubled?
Solution. Let the side of a square = a cm
∴ Area of the square = a x a = a2 cm2 …(1)
Now, when the sides of the square doubled.
Then, the side of the square = 2a cm
∴ Area of the square = 2a x 2a = 4a2 cm2 …(2)
On comparing Eqs. (1) and (2), we can see, if the sides of a square are doubled, then its area becomes 4 times.
Question 1. Measure and write the length of the four sides of the top of your study table.
AB = ___cm
BC = ___cm
CD =___cm
DA = ___cm
Now, the sum of the lengths of the four sides
= AB + BC + CD + DA
= ___cm + ___cm + ___cm + ___cm = ___cm
What is the perimeter?
Solution. Let ABCD be the top of study table.
Here, AB and CD are equal and DA and BC are equal.
On measuring, we get
AB = CD = 60 cm
and DA = BC = 30 cm
Now, the sum of the lengths of the four sides
= AB + BC + CD + DA
= 60 + 30 + 60 + 30
= 60 + 30 + 60 + 30 = 180 cm
∴ Perimeter of the table
= Sum of the lengths of the four sides
= 180 cm
Hence, the perimeter of the study table is 180 cm.
Mensuration Class 6 Solutions
Question 2. Measure and write the lengths of the four sides of a page of your notebook. The sum of the lengths of the four sides.
= AB + BC + CD + DA
= ___cm + ___cm + ___cm + ___cm = ___cm
What is the perimeter of the page?
Solution. Let ABCD be the page of a notebook.
On measuring, AB = CD = 15 cm and BC = DA = 20 cm
Then, the sum of the lengths of four sides
= AB + BC + CD + DA
= 15 + 20 + 15 + 20
= 15 + 20 + 15 + 20 = 70 cm
Hence, the sum of four sides is 70 cm.
Now, perimeter of the page = Sum of the lengths of four sides = 70 cm
Question 3. Meera went to a park 150 m long and 80 m wide. She took one complete round on its boundary. What is the distance covered by her?
Solution. Let ABCD be a park whose lengths are BC,AD and widths are AB, CD respectively.
Here, AB = CD = 80 m
and BC = DA = 150 m
Now, sum of the lengths of four sides
= AB + BC + CD + DA
= 80 + 150 + 80 + 150 = 460 m
∴ Perimeter of the park
= Sum of the lengths of four sides of the park
= 460 m
Hence, the distance covered by Meera is 460 m.
Mensuration Class 6 Solutions
Question 4. Find the perimeter of the following figures.
Perimeter AB + BC + CD + DA
Solution. (1) From the given figure, we have
AB= 40 cm, BC = 10 cm,
CD = 40 cm and DA = 10 cm
Now, the sum of the lengths of the four sides
= AB + BC + CD + DA
= 40 + 10 + 40 + 10 = 100 cm
∴ Perimeter of the given figure
= Sum of the lengths of four sides
= 100 cm
Hence, the perimeter of the given figure is 100 cm.
(2) From the given figure, we have
AB = BC = CD = DA = 5 cm
i.e. each side of the given figure is 5 cm.
Now, the sum of the lengths of the four sides
= AB + BC + CD + DA
= 5 + 5 + 5 + 5 = 20 cm
∴ Perimeter of the given figure
= Sum of the lengths of four sides
= 20 cm
Hence, the perimeter of the given figure is 20 cm.
Mensuration Class 6 Solutions
Question 5. Find various objects from your surrounding which have regular shapes and find their perimeters.
Solution. Let’s take a blackboard which has a regular square shape with side 40 cm each.
Then, the perimeter of square
= 4 x Length side of a square
= 4 × 40
= 160 cm
Let’s take another example of dog’s house which has a pentagon shape with each side 15 m.
Then, the perimeter of dog’s house
= Perimeter of regular pentagon
= 5 x Length of side of pentagon
= 5 x 15 = 75 m
Question 1. Find the perimeter of each of the following figures.
Solution. (1) Let the given figure be ABCD.
Here, AB = 5 cm, BC = 1 cm, CD = 2 cm and DA = 4 cm
Diagram
∴ Perimeter of the given figure
= Sum of the lengths of all sides
= AB + BC + CD + DA
= 5 + 1 + 2 + 4 = 12 cm
Hence, the perimeter of the given figure is 12 cm.
Question 2. A table-top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?
TIPS Firstly, change all the units in same unit and then find perimeter using 2 (length + breadth).
Solution. Given, length of table-top = 2 m 25 cm
= \(2 \mathrm{~m}+25 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]
= \(2 m+\frac{25}{100} m\)
= (2 + 0.25) m = 2.25 m
Breadth of table-top = 1 m 50 cm = 1 m + 50 cm
= \(1 m+50 \times \frac{1}{100} m\) [∴ 1 cm = \(\frac{1}{100}\) m]
= \(1 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=(1+0.50) \mathrm{m}=1.50 \mathrm{~m}\)
∴ Perimeter of table top = 2x (length + breadth)
= 2 x (2.25 + 1.50)
= 2 x 3.75 = 7.50 m
Hence, the perimeter of the table-top is 7.50 m.
MP Board Class 6 Chapter 10 Maths
Question 3. What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm, respectively?
Solution. Given, length of the wooden strip=32 cm
and breadth of the wooden strip = 21 cm
Now, wooden strip required
= Perimeter of the photograph
=2 x (Length + Breadth)
= 2 x (32 + 21) = 2 x 53 = 106 cm
Hence, the required length of wooden strip is 106 cm.
Question 4. Find the perimeter of each of the following shapes.
(1) A triangle of sides 3 cm, 4 cm and 5 cm.
Solution. (1) Here, AB = 3 cm, BC = 4 cm and CA = 5 cm
∴ Perimeter of a triangle
= Sum of the lengths of all sides
= AB + BC + CA
= 3 + 4 + 5 = 12 cm
Hence, the perimeter of a triangle is 12 cm.
Question 5. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
Solution. Given, first side of triangle = 10 cm
Second side of triangle = 14 cm
and third side of triangle = 15 cm
∴ Perimeter of a triangle
= Sum of all sides of triangle
= 10 + 14 + 15 = 39 cm
Hence, the perimeter of a triangle is 39 cm.
Question 6. Find the side of the square whose perimeter is 20 m.
Solution. Given, the perimeter of a square = 20 m
∴ Perimeter of a square = 4 x Length of a side
We know that a square has 4 sides of equal length.
So, we can divide given perimeter by 4, to get the side of a square.
∴ One side of the square \(=\frac{\text { Perimeter of a square }}{4}\)
Hence, the side of a square is 5 m.
MP Board Class 6 Chapter 10 Maths
Question 7. A piece of string is 30 cm long. What will be the length of each side, if the string is used to form
(1) a square?
(2) an equilateral triangle?
(3) a regular hexagon?
Solution. (1) Here, length of string will be the perimeter of square.
∴ Perimeter of square = 30 cm
We know that a square has 4 equal sides.
∴ Perimeter of a square = 4 x Length of a side
Now, length of one side \(=\frac{\text { Perimeter of a square }}{4}\)
= \(\frac{30}{4}\) = 7.5 cm
Hence, the length of each side of a square is 7.5 cm.
(2) Here, length of string will be the perimeter of an equilateral triangle.
∴ Perimeter of equilateral triangle = 30 cm
We know that an equilateral triangle has 3 equal sides.
∴ Perimeter of an equilateral triangle = 3 x Length of a side
∴ Length of a side \(=\frac{\text { Perimeter of an equilateral triangle }}{3}\)
= \(\frac{30}{3}\) = 10 cm
Hence, the length of each side of an equilateral triangle is 10 cm.
(3) Here, length of string will be the perimeter of regular hexagon.
∴ Perimeter of regular hexagon = 30 cm
We know that a regular hexagon has 6 equal sides
Perimeter of a regular hexagon = 6 x Length of a side
∴ Length of a side \(=\frac{\text { Perimeter of a regular hexagon }}{6}\)
= \(\frac{30}{6}\) = 5 cm
Hence, the length of each side of a regular hexagon is 5 cm
Question 8. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle Is 36 cm. What is its third side?
Solution. Let △ABC be the given triangle and its sides AB = 12 cm and BC = 14 cm.
Also, perimeter of triangle = 36 cm We know that,
Perimeter of a triangle = Sum of all its sides
⇒ AB + BC + CA = 36 cm
⇒ 12 + 14 + CA = 36 cm
⇒ 26 + CA = 36 cm
∴ CA = 36 – 26 = 10 cm
Hence, the third side of the triangle is 10 cm.
MP Board Class 6 Chapter 10 Maths
Question 9. Find the cost of fencing a square park of side 250 m at the rate of ₹ 20 per metre.
Solution. Given, side of square park = 250 m
Then, the perimeter of square park
= 4 x Length of side of park
= 4 x 250 = 1000 m
Cost of fencing = ₹ 20 per metre
∴ Cost of fencing = 1000 x 20
= ₹ 20000
Hence, the cost of fencing a square park is ₹ 20000.
Question 10. What is the perimeter of each of the following figures? What do you infer from the answers?
Solution. (1) Given, the figure is a square whose each side is 25 cm.
∴ Perimeter of square = 4 x Length of a side
= 4 × 25 = 100 cm
(2) Given, the figure is a rectangle whose length = 40 cm and breadth = 10 cm
∴ Perimeter of rectangle = 2 x (length + breadth)
= 2 x (40 + 10)
= 2 x 50 = 100 cm
(3) Given, the figure is a rectangle whose length = 30 cm and breadth 20 cm
∴ Perimeter of rectangle = 2 x (length + breadth)
= 2 x (30 + 20) = 2 x 50 = 100 cm
(4) Given, the figure is an isosceles triangle whose sides are 30 cm, 30 cm and 40 cm, respectively.
∴ Perimeter of triangle = Sum of all sides of a triangle
= 30 + 30 + 40 = 100 cm
Here, we observe that the perimeter of each figure is 100 cm i.e. they have equal perimeters.
MP Board Class 6 Chapter 10 Maths
Question 11. Avneet buys 9 square paving slabs, each with a side ofm. He lays them in the form of a square.
(1) What is the perimeter of his arrangement in the figure(i)?
(2) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement in the figure (ii)?
(3) Which has greater perimeter?
(4) Avneet wonders, if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.)
Solution. (1) Avneet lays 9 squares in the form of a square as shown in the figure, then side of the square
\(=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{1+1+1}{2}=\frac{3}{2} m\)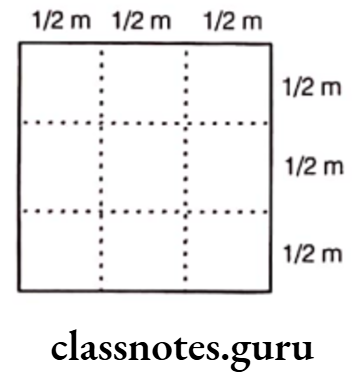
∴ Perimeter of Avneet’s arrangement
= 4 x Length of a side = 4 x \(\frac{3}{2}\) m = 6 m
Hence, the perimeter of Avneet’s arrangement is 6 m.
(2) Shari lays 9 squares in the form of a cross as shown in figure, then
Perimeter of Shari’s arrangement = Sum of all sides
= AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA
= \(\left[\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)+\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)\right.\)
\(\left.+\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)+\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)\right]\)= \(\frac{1}{2}+1+1+\frac{1}{2}+1+1+\frac{1}{2}+1+1+\frac{1}{2}+1+1\)
= \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+8=1+1+8=10 \mathrm{~m}\)
Hence, the perimeter of Shari’s arrangement is 10 m.
(3) From above, it is clear that Shari’s arrangement i.e. a cross has greater perimeter.
(4) Yes, there is a way shown along side in which we get a greater perimeter.
Here, we have arrange the 9 squares in the form of a rectangle
Now, length of rectangle
= \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{9}{2} m\)
and breadth of rectangle = 1/2 m
∴ Perimeter of this rectangle
= 2 x (length + breadth)
= \(2 \times\left(\frac{9}{2}+\frac{1}{2}\right)=2 \times\left(\frac{9+1}{2}\right)\)
= \(2 \times \frac{10}{2}=10 \mathrm{~m}\)
It is clear that it has the perimeter equal to cross. So, we can say that cross has greater perimeter in comparison to square.
Question 12. Draw any circle on a graph sheet. Count the squares and use them to estimate the area of the circular region.
Solution. First, make a circle of any suitable radius, on the graph paper. Then, count full, half and more than half or less than half squares coming under the circle.
In the figure,
Fully filled squares = 16
Half filled squares = 8
More than half filled squares = 8
∴ Total area = \(16 \times 1+8 \times \frac{1}{2}+8 \times 1\)
= 16 + 4 + 8 = 28 sq units
Question 1. Find the areas of the following figures by counting square
Solution. (1) Given, figure is covered by 9 full squares.
∴ Area = 9 x 1 = 9 sq units
(2) Given, figure is covered by 5 full squares.
∴ Area = 5 x 1 = 5 sq units
(3) Given, figure is covered by 2 full squares and 4 half squares.
∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)
(4) Given, figure is covered by 8 full squares.
∴ Area = 8 x 1 = 8 sq units
(5) Given, figure is covered by 10 full squares.
∴ Area = 10 x 1 = 10 sq units
(6) Given, figure is covered by 2 full squares and 4 half squares.
∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)
(7) Given, figure is covered by 4 full squares and 4 half squares.
∴ Area = \(4 \times 1+4 \times \frac{1}{2}=4+2=6 \text { sq units }\)
(8) Given, figure is covered by 5 full squares.
∴ Area = 5 x 1 = 5 sq units
(9) Given, figure is covered by 9 full squares.
∴ Area = 9 x 1 = 9 sq units
(10) Given, figure is covered by 2 full squares and 4 half squares.
∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)
(11) Given, figure is covered by 4 full squares and 2 half squares.
∴ Area = \(4 \times 1+2 \times \frac{1}{2}=4+1=5 \text { sq units }\)
(12) Given, figure is covered by 3 full squares, O half squares, 7 more than half squares and 1 less than half square.
∴ Area = 3 x 1 + 7 x 1 + 1 x 0
= 3 + 7 + 0 = 10 sq units
(13) Given, figure is covered by 7 full squares, 4 half squares, 5 more than half squares and 8 less than half squares.
∴ Area = \(7 \times 1+4 \times \frac{1}{2}+5 \times 1+8 \times 0\)
= 7 + 2 + 5 + 0 = 14 sq units
(14) Given, figure is covered by 9 full squares, 2 half squares, 8 more than half squares and 4 less than half squares.
∴ Area = \(9 \times 1+2 \times \frac{1}{2}+8 \times 1+4 \times 0\)
= 9 + 1 + 8 + 0 = 18 sq units
Question 1. Find the areas of the rectangles whose sides are
(1) 3 cm and 4 cm
(2) 12 m and 21 m
Solution. (1) Here, length of the rectangle = 4 cm
and breadth of the rectangle = 3cm
∴ Area of rectangle = Length x Breadth = 4 x 3 = 12 cm2
Hence, the area of the rectangle is 12 cm2.
(2) Here, length of the rectangle = 21 m
and breadth of the rectangle = 12 m
∴ Area of the rectangle = Length x Breadth
= 21 x 12 = 252 m2
Hence, the area of the rectangle is 252 m2.
MP Board Class 6 Chapter 10 Maths
Question 2. The length and breadth of three rectangles are as given below.
(1) 9 m and 6 m
(2) 17 m and 3 m
(3) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Solution. (1) Here, length of the rectangle = 9 m
and breadth of the rectangle = 6 m
∴ Area of the rectangle = Length x Breadth = 54 m2
Hence, the area of the rectangle is 54 m2.
(2) Here, length of the rectangle = 17 m
and breadth of the rectangle = 3 m
∴ Area of the rectangle = Length x Breadth
= 17 x 3 = 51 m2
Hence, the area of the rectangle is 51 m2.
(3) Here, length of the rectangle = 14 m
and breadth of the rectangle = 4 m
∴ Area of the rectangle = Length x Breadth
= 14 x 4 = 56 m2
Hence, the area of the rectangle is 56 m2.
Now, we have 56 > 54 > 51
Hence, the rectangle having sides 4 m and 14 m has the largest area and the rectangle having sides 17 m and 3 m has the smallest area.
Question 3. The area of a rectangular garden 50 m long is 300 m2. Find the width of the garden.
Solution. Given, area of the rectangular garden = 300 m2
and length of the rectangular garden = 50 m
We know that
Area of the rectangular garden = Length x Breadth
⇒ 300 m2 = 50 x Breadth
∴ Breadth = \(\frac{300}{50}\) = 6 m
Hence, the breadth or width of the garden is 6 m.
Question 4. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of 8 per hundred sq m?
Solution. Given, length of a rectangular plot = 500 m
and breadth of a rectangular plot = 200 m
∴ Area of the rectangular plot = Length x Breadth
= 500 x 200 = 100000 m2
∴ Cost of tiling per husband square metres = ₹ 8
∴ Cost of 1 m2 = \(₹ \frac{8}{100}\)
Now, cost of 100000 m2 = \(100000 \times \frac{8}{100}=₹ 8000\)
Hence, the cost of tiling rectangular plot is ₹ 8000.
Calculating Perimeter for Class 6
Question 5. A table-top measures 2 m by 1m 50 cm. What is its area in square metres?
Solution. Given, length of the table-top = 2 m
and breadth of the table-top
= 1 m 50 cm = 1 m + 50 cm
= \(1 \mathrm{~m}+50 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]
= \(1 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=1 \mathrm{~m}+0.50 \mathrm{~m}=150 \mathrm{~m}\)
∴ Area of the table-top = Length x Breadth = 2 x 1.50 = 3
Hence, the area of the table-top is 3 m2.
Question 6. A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Solution. Given, length of the room = 4 m
and breadth of the room = 3m 50 cm = 3 m + 50 cm
= \(3 \mathrm{~m}+50 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]
= \(3 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=3 \mathrm{~m}+0.50 \mathrm{~m}=3.50 \mathrm{~m}\)
∴ Carpet needed to cover the floor of room
= Area of the floor
= Length x Breadth = 4 m x 3.50 m = 14 m2
Hence, the carpet needed to cover the floor of the room is 14 m2.
Question 7. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution. Given, length of the floor = 5 m
and breadth of the floor = 4 m
Then, area of the floor
= Length x Breadth
= 5 x 4 = 20 m2
Side of the square carpet = 3 m
∴ Area of the carpet = Side x Side = 3 x 3 = 9m2
Now, area of the floor that is not carpeted
= Area of the floor-Area of the carpet
= 20 – 9 = 11 m2
Hence, 11 m2 area of the floor is not carpeted.
Calculating Perimeter for Class 6
Question 8. Five square flower beds each of sides 1 m are dug on a plece of land 5 m long and 4 m wide. What Is the area of the remaining part of the land?
Solution. Given, length of the piece of the land = 5 m
and breadth of the piece of the land = 4 m
Area of the piece of the land = Length x Breadth
= 5 x 4 = 20 m2
Given, side of one square flower bed = 1 m
∴ Area of one square flower bed = Side x Side
= 1 x 1 = 1m2
Then, area of 5 such flower beds
= 5 x Area of one square flower bed
= 5 x 1 = 5m2
Now, area of the remaining part of the land
= Area of the piece of the land – Area of 5 square flower beds
= 20 – 5 = 15 m2
Hence, the area of the remaining part of the land is 15 m2.
Question 9. By splitting the following figures into rectangles, find their areas (the measures are given in centimetres).
Solution. (1) Let the given figure be divided into rectangles A, B, C and Dand their length and breadth be written on the figure.
For Rectangle A,.
Length = 4 cm and breadth = 2 cm
Now, area of the Rectangle A = Length x Breadth
= 4 x 2 = 8 cm2
For Rectangle B,
Length = 3 cm and breadth = 3 cm
Area of the Rectangle B = Length x Breadth
= 3 x 3 = 9cm2
For Rectangle C,
Length = 2 cm and breadth = 1 cm
Area of the Rectangle C = Length x Breadth
= 2 x 1 = 2cm2
For Rectangle D, length = 3 cm and breadth = 3 cm
∴ Area of the Rectangle D = Length x Breadth
= 3 x 3 = 9cm2
Now, total area of the given figure
= Area of the Rectangle A + Area of the Rectangle B + Area of the Rectangle C + Area of the Rectangle D
= 8 + 9 + 2 + 9 = 28 cm2
Hence, the required area is 28 cm2
(2) Let the given figure is divided into rectangles A, B and C and their length and breadth are written on the figure.
For Rectangle A,
Length = 2 cm and breadth = 1 cm
∴ Area of the Rectangle A = Length x Breadth
= 2 x 1 = 2 cm2
For Rectangle B,
Length = 5 cm and breadth = 1 cm
∴ Area of the Rectangle B = Length x Breadth = 5 x 1 = 5cm2
For Rectangle C,
Length = 2 cm and breadth = 1 cm
∴ Area of the Rectangle C = Length x Breadth
= 2 x 1 = 2cm2
Now, total area of the given figure
= Area of the Rectangle A + Area of the Rectangle B + Area of the Rectangle C
= 2 + 5 + 2 = 9 cm2
Hence, the area of the given figure is 9 cm2.
Question 10. On a centimetre squared paper, make as many rectangles as you can, such that the area of the rectangle is 16 cm2 (consider only natural number lengths).
(1) Which rectangle has the greatest perimeter?
(2) Which rectangle has the least perimeter?
If you take a rectangle of area 24 cm2, what will be your answers? Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter? With the least perimeter? Give example and reason.
Solution. We know that
∴ Area of the rectangle = Length x Breadth
Here, the area of the rectangle is 16 cm2.
So, for getting the area 16 cm2, there are three cases.
Case 1 When length of the rectangle = 16 cm
and breadth of the rectangle = 1 cm
∴ Area of the rectangle = Length x Breadth
= 16 x 1 = 16cm2
and perimeter of the rectangle
= 2 x (Length + Breadth)
= 2 x (16 + 1) = 2 x 17 = 34 cm
Case 2 When length of the rectangle = 4 cm
and breadth of the rectangle = 4 cm
∴ Area of the rectangle = Length x Breadth
= 4 x 4 = 16cm2
and perimeter of the rectangle
= 2 x (Length + Breadth)
= 2 x (4 + 4) = 2 x 8 = 16 cm
Case 3 When length of the rectangle = 8 cm
and breadth of the rectangle = 2 cm
∴ Area of the rectangle = Length x Breadth
= 8 x 2 = 16 cm2
and perimeter of the rectangle
= 2x (length + breadth)
= 2 x (8 + 2)= 2 x 10 = 20 cm
(1) The rectangle which is made in Case I has the greatest perimeter.
(2) The rectangle which is made in Case II has the least perimeter.
Now, given that the area of the rectangle is 24 cm2.
Again, for getting the area 24 cm2, there are four cases
Case 1 When length of the rectangle = 24 cm
and breadth of the rectangle = 1 cm
∴ Area of the rectangle = Length x Breadth
= 24 x 1 = 24 cm2
and perimeter of the rectangle
= 2 x (length + breadth)
= 2 x (24 + 1) = 2 x 25 = 50 cm
Case 2 When length of the rectangle = 12 cm
and breadth of the rectangle = 2 cm
∴ Area of the rectangle
= Length x Breadth = 12 x 2 = 24cm2
and perimeter of the rectangle
= 2 x (length + breadth)
= 2 x (12 + 2) = 2 × 14 = 28 cm
Case 3 When length of the rectangle = 6 cm
and breadth of the rectangle = 4 cm
∴ Area of the rectangle
= Length x Breadth = 6 x 4 = 24 cm2
and perimeter of the rectangle
= 2 x (length + breadth)
= 2 x (6 + 4) = 2 x 10 = 20 cm
Case 4 When length of the rectangle = 8 cm
and breadth of the rectangle = 3 cm
∴ Area of the rectangle
= Length x Breadth = 8 x 3 = 24 cm2
and perimeter of the rectangle
= 2 x (length + breadth)
= 2 x (8 + 3) = 2 x 11 = 22 cm
(1) The rectangle which is made in Case I has the greatest perimeter.
(2) The rectangle which is made in Case III has the least perimeter.
Yes, it is possible to predict the shape of the rectangle with greatest perimeter and with least perimeter.
e.g. A rectangle having area 16 cm2 and greatest perimeter 34 cm is of the shape 16 cm x 1 cm
(i.e. length = 16 cm and breadth = 1 cm), also a rectangle having area 24 cm2 and least perimeter 20 cm is of the shape 6 cm x 4 cm
(i.e. length = 6 cm and breadth = 4 cm).
The rectangle with the greatest length has the maximum perimeter and the rectangle with the smallest length has the least perimeter.
Question 1. Following figures are formed by joining six unit squares. Which figure has the smallest perimeter?
Answer. 4. 1
Question 2. A square shaped park ABCD of side 100 m has two equal rectangular flower beds each of size 10 m x 5 m. Length of the boundary of the remaining park is
Answer. 3. 340 m
Question 3. The perimeter of a rectangle whose sides are 1 m 30 cm and 70 cm, is
Answer. 2. 4 m
Calculating Perimeter for Class 6
Question 4. Cost of fencing a rectangular park of length 200 m and width 150 m at the rate of ₹ 25 per metre is
Answer. 1. ₹ 17500
Question 5. Length and breadth of a rectangular sheet of paper are 20 cm and 10 cm, respectively. A rectangular piece is cut from the sheet as shown in figure. Which of the following statements are correct for the remaining sheet?
Answer. (c) Both area and perimeter are changing
Question 6. The top of a table is 1 m 20 cm wide and 1 m 50 cm long. The perimeter of this top is
Answer. 2. 5.40 m
Question 7. The ratio of the sides of rectangle is 5:4 and its perimeter is 72 cm. Then, the length of the rectangle is
Answer. 2. 20 cm
Question 8. The cost of fencing a rectangular field 24 m long and 18 m wide at ₹ 2.25 per meter is
Answer. 3. ₹ 189
Question 9. The side of a square is 10 cm. How many times will the new perimeter become, if the side of the square is doubled?
Answer. 2. 4 times
Question 10. The perimeter of a square whose each side is 1 m 30 cm 10 mm, is
Answer. 3. 5.24 m
Examples of Perimeter Problems
Question 11. The side of a square is 6 cm. If its side is doubled, then its new perimeter is
Answer. 1. 48 cm
Question 12. The perimeter of a triangle whose sides are 1.2 cm, 3.4 cm and 1.7 cm, is
Answer. 1. 6.3 cm
Question 13. The perimeter of an equilateral triangle of side 5 cm each is
Answer. 4. 15 cm
Question 14. The area of rectangle is 630 sq cm and breadth is 15 cm. What is its lenght.
Answer. 3. 42 cm
Question 15. Samuel wanted to dig some vertical poles along the boundary of his plot at a distance of 10 m each. If the length of the plot is 30 m and the breadth is 15 m. How many poles are required?
Answer. 3. 9
Question 1. Assertion (A) Manoj went to a park 20 m long and 10 m wide. He took one complete round of it. The distance covered by him is 60 m.
Reason (R) The amount of surface enclosed by a closed figure is called its area.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true
Answer. (b) Both A and R are true but R is not the correct explanation of A
Question 2. Assertion (A) The perimeter of a square of side 1 m is 2 m.
Reason (R) Perimeter is the distance covered along the boundary forming a closed figure when you go around the figure once.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true
Answer. (d) A is false but R is true
Examples of Perimeter Problems
Question 3. Assertion (A) The length of wire required to fence the pentagon-shaped park of side 24 cm is 120 cm.
Reason (R) Perimeter of a regular polygon with n sides = n x length of each side
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true
Answer. (a) Both A and R are true and R is the correct explanation of A
Question 4. Assertion (A) A page is 25 cm long and 20 cm wide. The area of this page is 90 cm.
Reason (R) The amount of surface enclosed by a closed figure is called its area.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true
Answer. (d) A is false but R is true
Question 1. Perimeter of the shaded portion in figure is
AB + … + … + … + … + … + … + HA.
Answer. BM + MD + DE + EN + NG + GH
Question 2. Diagonal of a square is side x …..
Answer. √2
Question 3. Standard unit of area is …..
Answer. Square metre (i.e. m2)
Question 4. The amount of region enclosed by a plane closed figure is called its …..
Answer. Area
Question 5. The area of a play ground is 1190 m2. If its length is 35 m, the width is …..
Answer. 34 m
Question 1. 1 hectare = 100 x 100 m2.
Answer. True
Question 2. Perimeter of rectangle is (l + b).
Answer. False
Question 3. A farmer who wants to fence his field, must find the perimeter of the field.
Answer. True
Question 4. If length of a rectangle is halved and breadth is doubled, then the area of the rectangle obtained remains same.
Answer. True
Question 5. Area of a square is doubled, if the side of the square is doubled.
Answer. False
Question 1. Mathc the Column I with Column II.
Solution. (a) → (3), (b) → (4), (c) → (2), (d) → (1)
Question 1. The figure below shows the football field for a school tournament.
(1) What is the perimeter (in m) of WURQ?
(a) 60 m
(b) 240 m
(c) 960 m
(d) 3344 m
(2) The area enclosed by QRUW is equal to the area enclosed by WUST:
Is the statement true? Give reason.
(3) What is the area (in m2) of the penalty area?
(a) 488 m2
(b) 272 m2
(c) 480 m2
(d) 720 m2
(4) Is the perimeter of the penalty area of the football field double the perimeter of the goal area? Give.
(5) Does the school football field meet the FIFA standards? Give reason.
(6) Find the perimeter of the shape WURMNOPQW.
(a) 280 m
(b) 320 m
(c) 240 m
(d) 420 m
Solution. (1) (b) Given, length of the football field = 88 m
breadth of the football field = 76 m
∴ \(W Q=\frac{1}{2} \times T Q=\frac{1}{2} \times 88=44 \mathrm{~m}\)
Now, perimeter of WURQ = 2x (length + breadth)
= 2 x (44 + 76)
= 2 × 120 = 240 m
Hence, perimeter of WURQ is 240 m.
(2) We have, TW = WQ = 44 m
and QR = WU = 76 m
Now, area enclosed by QRUW = Length x Breadth
= WQ x QR = 44 m x 76 m = 3344 m2 ….(1)
Now, area enclosed by WUST = Length x Breadth
= TW x WU = 44 ….(2)
∴ From (1) and (2);
Area enclosed by QRUW = Area enclosed by WUST = 3344 m2
Hence, area enclosed by QRUW is equal to the area enclosed by WUST.
(3) (c) Given, length of the football field = 88 m
and breadth of the football field = 76 m
∴ Side of the small square in the field = \(\frac{88}{22}=4 \mathrm{~m}\)
∴ Area of small square in the field = 4 x 4 = 16 m2
Now, there are 30 small squares lie in the region of penalty area.
∴ Area of the penalty area = 30 x Area of small square
= 30 x 16 m2 = 480 m2
Hence, the area of penalty area is 480 m2.
(4) We have, side of small square = 4 m
∴ HG = 20 m, GF = 36 m, FE = 20 m, ED = 8 m, DC = 12 m, CB = 20 m, BA = 12 m and AH = 8 m
∴ Perimeter of penalty area
= HG + GF + FE + ED + DC + CB + BA + AH
= 20 + 36 + 20 + 8 + 12 + 20 + 12 + 8
= 136 m …(1)
Now, AB = 12 m, BC = 20 m, CD = 12 m and DA = 20 m
∴ Perimeter of goal area = AB + BC + CD + DA = 12 + 20 + 12 + 20 = 64 m
Hence, perimeter of the penalty area of the football field is not double the perimeter of the goal area.
(5) Yes, the school football field meet the FIFA standards because the areas of WUST and WURQ are the same which is 3344 m.
(a) because the length and the width of TQRS are 88 m and 76 m respectively, which lie with in the standard range which 120 m to 90 m for length and 90 m to 45 m for width.
(b) because the perimeter of TQRS is 328 m which lies with in the standard range which is 420 m to 270 m.
(c) because the area of TQRS is 6688 sq m which lies with in the standard range which 10800 sq m to 4050 sq m.
(6) (a) We have, side of small square=4 m
So, WU = 76 m, UR = 44 m, RM = 20 m, MN = 20 m, No = 36 m, OP = 20 m, PQ = 20 m and QW = 44 m
Now, perimeter of the shape WURMNOPQW
= WU + UR + RM + MN + NO + OP + PQ + QW
= 76 + 44 + 20 + 20 + 36 + 20 + 20 + 44 = 280 m
Hence, perimeter of the shape WURMNOPQW is 280 m
Examples of Perimeter Problems
Question 2. International Federation of Association Football (FIFA) is responsible for the organization and promotion of association football’s major international tournaments.
FIFA issues guidelines for the dimensions of football fields. The figure below shows the maximum and minimum lenghts and widths of a football field.
(1) What is the maximum area (in m2) of the football field?
(a) 30 m2
(b) 420 m2
(c) 1080 m2
(d) 10800 m2
(2) What can be the minimum perimeter (in m) of the football field?
(a) 90 m
(b) 135 m
(c) 270 m
(d) 4050 m
Solution. (1) (d) Given, maximum length of the football field
and maximum width of the football field = 90 m
∴ Maximum area of the football field
= Length x Breadth
= 120 m x 90 m = 10800 m2
Hence, the maximum area of the football field is 10800 m2.
(2) (c) Given, minimum length of the football field = 90 m
and minimum width of the football field = 45 m
∴ Minimum perimeter of the football field
= 2x (length x breadth)
= 2 x (90 + 45) = 2 x 135 = 270 m
Hence, minimum perimeter of the football field is 270 m
Examples of Perimeter Problems
Question 3. The figure below shows a square wooden frame enclosing a square picture.
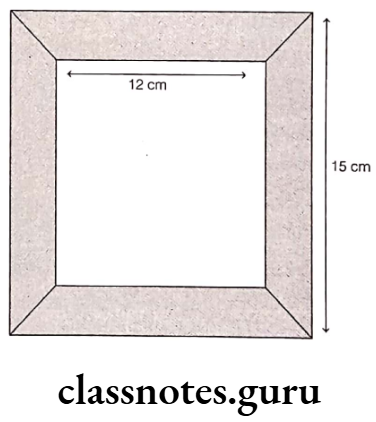
(1) What is the area (in cm2) of the frame?
(a) 81 cm2
(b) 144 cm2
(c) 181 cm2
(d) 225 cm2
(2) What is the perimeter (in cm) of the picture?
(a) 12 cm
(b) 48 cm
(c) 60 cm
(d) 144 cm
Solution. (1) (d) Given, side of square frame = 15 cm
Now, area of square frame = Side x Side
= 15 x 15 = 225 cm2
Hence, area of the frame is 225 cm2.
(2) (b) Given, side of the square picture = 12 cm
Now, perimeter of square picture = 4 x Side
= 4 x 12 = 48 cm
Hence, perimeter of the picture is 48 cm.
Question 1. Length of a rectangle is three times its breadth. Perimeter of the rectangle is 40 cm. Find its length and width.
Solution. Let width of rectangle (b) = x cm
Then, length of rectangle (1) = 3x cm
∴ Perimeter = 2 (1 + b)
⇒ 40 = 2(3x + x) = 8x = 40
⇒ 8x = 40
⇒ \(x=\frac{40}{8}=5 \mathrm{~cm}\)
Hence, the length is 15 cm and width is 5 cm.
Question 2. The perimeter of a regular pentagon is 1240 cm. How long is its each side?
Solution. Given, perimeter = 1240 cm
Perimeter of a regular pentagon = 5 x Length of each side
Length of each side = \(\frac{1240}{5}\) = 248 cm
Hence, its each side is 248 cm.
MP Board Class 6 Maths Solutions
Question 3. Find the side of an equilateral triangle, if its perimeter is 30 cm.
Solution. Given that perimeter of an equilateral triangle = 30 cm
∴ Perimeter of an equilateral triangle
= 3 x Side of a triangle
⇒ 30 = 3 x Side of a triangle
⇒ Side = \(\frac{30}{3}\) = 10 cm
Hence, the side of an equilateral triangle is 10 cm.
Question 4. Find the perimeter of a triangle, whose three sides are 5 cm, 6 cm and 7 cm, respectively.
Solution. Perimeter of a triangle = Sum of its all sides
= a + b + c
= (5 + 6 + 7) cm = 18 cm
Question 5. Find the perimeter of an equilateral triangle, whose each side is 5 cm.
Solution. Perimeter of an equilateral triangle = 3 × Side of length
= 3 x 5 cm = 15 cm [given]
Question 6. Perimeter of an isosceles triangle is 50 cm. If one of the two equal sides is 18 cm, find the third side.
Solution. Perimeter = 50 cm
Perimeter of an isosceles triangle = Sum of its all sides
⇒ Perimeter = a + b + c
⇒ 50 = 18 + 18 + Third side
⇒ 50 – 36 = Third side
⇒ Third side = 14 cm
MP Board Class 6 Maths Solutions
Question 7. Find the area of a rectangle whose length and width are 10 cm and 6 cm, respectively.
Solution. Given that length (1) = 10 cm
and width (b) = 6 cm
Area of a rectangle = 1 x b = 10 x 6 = 60 cm2
Question 8. If the area of a square is 36 cm2, then find its perimeter.
Solution. Given, area of a square = 36 cm2
Area = Side x Side
⇒ 36 = Side x Side
⇒ Side x Side = 6 x 6
⇒ Side = 6 cm
∴ Perimeter of a square = 4 × Side = 4 × 6 = 24 cm
Question 1. The length of a rectangular field is twice its breadth. Jamal jogged around it four times and covered a distance of 6 km. What is the length of the field?
Solution. Let breadth of rectangular field = x m
Then, length of rectangular field = 2x m
Distance covered in one round = Perimeter
Distance covered in four rounds = 4 x Perimeter
⇒ 4 × 2 (1 + b) = 6 x 1000 [ perimeter = 2 (1 + b)]
⇒ 8(l + b) = 6000
8(2x + x) = 6000
\(x=\frac{6000}{24}=250 \mathrm{~m}\)∴ Length of the field = 500 m
Question 2. A room is 9.5 m long and 7.4 m wide. A person wants that the floor of the room to be fitted with tiles of size 20 cm by 10 cm. Find the number of tiles needed.
Solution. Area of room 7.4 x 9.5 m2 = 7.4 x 9.5 x 10000 cm2
Area of one tile = 20 x 10 = 200 cm2
Number of tiles \(=\frac{\text { Area of room }}{\text { Area of a tile }}=\frac{74 \times 95 \times 100}{200}\)
= \(\frac{74 \times 95}{2}=95 \times 37=3515\)
Question 3. Two plots of land having the same perimeter. One is a square with side 70 cm while other is rectangle of length 100 cm. Which plot has the greater area and by how much?
Solution. Area of square Side x Side = 70 x 70 sq cm
= 4900 cm2
Given, length of rectangle = 100 cm
Perimeter of rectangle = Perimeter of square
⇒ 2 (100 + b) = 4 × 70
⇒ 100 + b = 140 ⇒ b = 40 cm
Now, area of rectangle = 1 x b = 40 x 100 = 4000 cm2
Hence, the area of square is more than the area of rectangle by 900 cm2.
MP Board Class 6 Maths Solutions
Question 4. Three squares are joined together as shown in figure. Their sides are 4 cm, 10 cm and 3 cm. Find the perimeter of the figure.
Solution. Given, sides of three squares are 4 cm, 10 cm and 3 cm, respectively.
Total perimeter of given squares
= Sum of all outer sides of the figure
= 4 + 4 + 4 + 6 + 10 + 7 + 3 + 3 + 3 + 10 = 54 cm
Question 5. Tahir measured the distance around a squared field as 200 rods (lathi). Later he found that the length of this rod was 140 cm. Find the side of this field in metres.
Solution. Distance around a square field = 200 rods
Length of this rod = 140 cm
Total distance around a squared field = 200 x 140 = 28000 cm
So, perimeter of this squared field = 28000 cm = 280 m
Sides of this field = \(\frac{280}{4}\) = 70 m
Question 6. The perimeter of rectangle and square are equal. If length of the rectangle is 8 m and breadth is 6 m. Find the area of square.
Solution. Given, length of rectangle (1) = 8 m
and breadth of rectangle (b) = 6 m
Perimeter of rectangle = Perimeter of square
2 (1 + b) = 4x Side of a square
⇒ 2(8 + 6) = 4 × Side of a square
Side of a square = \frac{2(8+6)}{4}=7 \mathrm{~m}
∴ Area of square = 7 x 7 = 49 m2
Question 7. The floor of a room is square in shape. If the side of the floor is 5 m. Find the area of the floor.
Solution. Given, side of the floor = 5 m
Area of the floor = Side x Side = 5 x 5 = 25m2
Hence, the area of the floor is 25 m2.
MP Board Class 6 Maths Solutions
Question 8. From the following figure, find its
(1) Perimeter
(2) Area of square
Given, ABC is an equilateral triangle of side 3 cm each and BCED is a square.
Solution. (1) Perimeter = AB + AC + BC + BD + DE + CE
= 3 + 3 + 3 + 3 + 3 + 3 = 18 cm
(2) Area of square BCED = Side2 = 32 = 9 cm2
Question 1. Length of a rectangular field is 250 m and width is 150 m. Anuradha runs around this field 3 times. How far did she run? How many times she should run around the field to cover a distance of 4 km?
Solution. Given, length of rectangular field (1) is 250 m and width is 150 m.
Perimeter of this field = 2(1 + b) = 2(250 + 150) m
= 2 x 400 m = 800 m
Distance covered in one round = Perimeter = 800 m
Distance covered in three rounds = 3 x 800 = 2400 m
Now, number of rounds to cover 4 km i.e. 4000 m.
= \(\frac{4000}{800}\) [∴ 1 km = 1000 m]
Hence, she should run 5 times around the field to cover the distance of 4 km.
Question 2. The lawn in front of Molly’s house is 12 m x 8 m, where as the lawn in front of Dolly’s house is 15 m x 5 m. A bamboo fencing is built around both the lawns. How much fencing is required for both?
Solution. Given, size of lawn in front of Molly’s house = 12 × 8
Perimeter = 2 (12 + 8) = 40 …(1)
Now, size of lawn in front of Dolly’s house = 15 x 5
Perimeter = 2(15 + 5) = 40 …(2)
From Eqs. (1) and (2), we get
40 + 40 = 80 m
Hence, the total length of bamboo fencing is 80 m.
Question 3. A room 9.68 m long and 6.2 m wide. Its floor is to be covered with glazed tiles of 22 cm by 10 cm each. If rate of tiles is ₹ 25 per tile. Find the total cost of tiles.
Solution. Given, length of floor of the room (l) = 9.68 m
and width of floor of the room (b) = 6.2 m
Area of the room = 9.68 x 6.2 m2 …(1)
Also, given that length of each tile = 22 cm
and width of each tile = 10 cm
Now, area of each tile = 22 x 10 cm2 …(2)
Number of tiles required to cover the floor of the room
= \(\frac{9.68 \times 6.2 \times 100 \times 100}{22 \times 10}\) [∴ 1m = 100 cm]
= \(\frac{968 \times 62 \times 10}{22 \times 10}=\frac{968 \times 62}{22}=2728\)
∴ Total cost = ₹ 2728 x 25 = ₹ 68200
MP Board Class 6 Maths Solutions
Question 4. There is a rectangular lawn 10 m long and 4 m wide in front of Meena’s house. It is fenced along the two smaller sides and one longer side leaving a gap of 1 m for the entrance. Find the length of fencing.
Solution. Given, width of the lawn, AB = EF = 4 m and length of the lawn, BE = 10 m
Also, given length of gap, CD = 1 m
Total length of fencing = AB + (BC + DE) + EF
= AB + (BE-CD) + EF
= 4 + (10-1) + 4)
= 4 + 9 + 4 = 17 m
Hence, the length of fencing of the lawn is 17 m.
Question 5. Four regular hexagons are drawn, so as to form the design as shown in figure. If the perimeter of the design is 28 cm. Then, find the length of each side of the hexagon.

Solution. Given, four regular hexagons, as shown in the figure:
Perimeter of the design = 28 cm
∴ Perimeter of the given design = Sum of all outer sides of the four hexagon.
Here, this figure has 14 outer equal sides.
∴ Perimeter of the design = 14 x Length of one side of hexagon
⇒ 28 = 14 x Length of one side of hexagon
Length of one side of hexagon = \(\frac{28}{14}\) = 2 cm
Hence, the length of each side of the hexagon is 2 cm.
Question 6. In the given figure, all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid-points fo the sides. What is the perimeter of the figure?
Solution. Given, △ABC is an equilateral triangle.
Here, AB = 8 units
∴ AB = BC = CA = 8 units
Now, △ADE is an equilateral triangle.
Here, E is the mid-point of AB.
∴ \(A E=B E=\frac{A B}{2}=\frac{8}{2}=4 \text { units }\)
Now, in △ADE, AD = DE = EA = 4 units
Similarly, equilateral triangles are △BOT and △UPC, having each sides equal
i.e. BO = OT = BT = UC = PC = PU = 4 units
It is also clear that OC = PA = 4 units
Also, △DIF is an equilateral triangle.
Here, F is the mid-point of DE.
∴ \(D F=F E=\frac{D E}{2}=\frac{4}{2}=2 \text { units }\)
In ADIF, DI = IF = DF = 2 units
Similarly, in △TKN and △RQU,
TK = KN = TN = RQ = UQ = UR = 2 units
It is also clear that NO = RP = 2 units
Also, △HIG is an equilateral triangle.
Here, G is the mid-point of IF.
∴ \(I G=G F=\frac{I F}{2}=\frac{2}{2}=1 \text { unit }\)
Now, in △HIG, HG = HI = GI = 1 unit
Similarly, in △MLK and △XQS,
ML = MK = LK = SQ = XS = QX = 1 unit
It is also clear that LN = XR = 1 unit
Now, perimeter of the given figure
= Sum of all outer sides of the given figure
= AD + DI + IH + HG + GF + FE + EB + BT + TK + KM + LM + LN + NO + OC + CU + UQ + QS + XS + XR + PR + PA
= [4 + 2 + 1 + 1 + 1 + 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4]
= 45 units
Hence, the perimeter of the given figure is 45 units.
MP Board Class 6 Maths Solutions
Question 7. If length of a rectangle is halved and breadth is doubled, then the area of the rectangle obtained remains same. Is it true?
Solution. True, let the length and breadth of a rectangle bel and b respectively.
We know that
Area of the initial rectangle = Length x Breadth
= 1 x b sq units
If length of a rectangle is halved and breadth is doubled.
i.e. New length = \(\frac{1}{2}\) units
and new breadth = 2b units
Then, the area of new rectangle
= New length x New breadth = \(\frac{1}{2}\) x 2b
= lb sq units
Question 8. In the given figure, each square is of unit length.
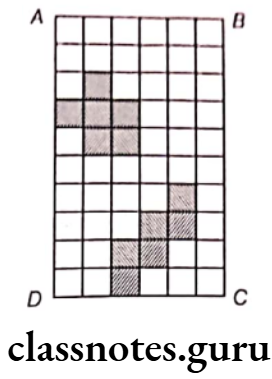
(1) What is the perimeter of the rectangle ABCD?
(2) What is the area of the rectangle ABCD?
(3) Divide this rectangle into ten parts of equal area by shading squares. (Two parts of equal area are shown here)
(4) Find the perimeter of each part which you have divided. Are they all equal?
Solution. Given, each side of square is of unit length. Figure contains length of 10 squares and width of 6 squares. Now, the length of rectangle, AD = BC
= Sum of length of a side of 10 squares
= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
= 10 x 1 = 10 units
and breadth of rectangle, AB = DC = Width of 6 squares = 6 x 1 = 6 units
(1) The perimeter of the rectangle ABCD
= AB + BC + CD + DA
= 6 + 10 + 6 + 10
= 32 units
(2) The area of the rectangle ABCD = Length x Breadth
= AD X AB
= 10 × 6
= 60 sq units
(3) The total area of rectangle = 60 units
Now, we have to divide the rectangle into 10 equal parts i.e. \(\frac{60}{10}\) = 6 squares units
i.e. we have to take a group of 6-6 square blocks, which is shown in the figure.
(4) Now, we find the perimeter of Part 1.
We know that perimeter of a figure is the total length of its boundary.
∴ Perimeter of Part 1
= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
= 12 units
Similarly, we can find the perimeters of remaining 9 parts, all the parts have same perimeter i.e. 12 units.
Yes, all the parts have same perimeter.
A collection of numbers (values) gathered to give some information is called data.
Recording Data
Recording data is information in numbers collected for a specific purpose. The collection of data is also called recording of data. In order to record the data, we need to make a table and record it.
e.g. If you collects the marks obtained by 6 students in a batch to analyse their performance in unit test. We find that Raghav scored 11 out of 20, Maria scored 18 out of 20, Punit scored 15 out of 20, Zoya scored 8 out of 20, Salman scored 2 out of 20 and Manoj scored 12 out of 20.
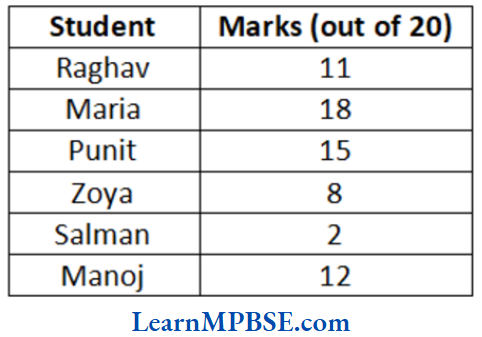
From this data, we conclude that highest marks obtained by Maria and lowest marks obtained by Salman.
Organisation of Data
The data that is collected for the first time is called raw data or upgrouped data. When the data is arranged in any data it becomes grouped data. When the data is very large, it is difficult to arrange them in a grouped form. In this case, small bars are used to represent data; such method is called tally method.
Read and Learn More MP Board Class 6 Maths Solutions
To get the required information, all observations should be recorded. We depict each observation with the help of tally marks.
Tally marks are used to organise the observations. Record every observation by a vertical mark, but every fifth observation should be recorded by a mark across the four earlier marks. The fifth observation tally mark looks like this ![]()
Example 1. In a class test, the following marks were obtained in the unit test of algebra by 35 students. Arrange these marks in a table using tally marks.
(1) Find how many students obtained marks equal to or less than 5.
(2) How many students obtained marks above 6?
Solution. The table with tally marks is shown below
(1) Here, we have to find out the students, who obtained marks equal to or less than 5. So, we have to add the number of students who obtained marks equal to 5 or less than 5 i.e. marks 3, 4 and 5.
∴ Number of students = 4 + 9 + 8 = 21
Hence, 21 students obtained marks equal to or less than 5.
(2) Here, we have to find out the students who obtained marks above 6.
So, we have to add the number of students who obtained marks above 6 i.e. marks 7 and 8.
∴ Number of students = 4 + 3 = 7
Hence, 7 students obtained marks above 6.
MP Board Class 6 Maths Solutions
Example 2. In a shop, different size of shoes sold in a week as shown below 7, 9, 10, 8, 7, 9, 7, 9, 6, 3, 5, 5, 7, 10, 7, 8, 7, 9, 6, 7, 6, 7, 10, 5, 4, 3, 5, 7, 8, 7, 9, 7.
Arrange the above data in ascending order and construct a table using tally marks.
Also, answer the following questions.
(1) Which shoes size had the maximum sale?
(2) Which shoes size had the minimum sale?
(3) Find the number of shoes sold of size 7 or greater than 7.
Solution. Ascending order of the given data is 3, 3, 4, 5, 5, 5, 5, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10
The table with tally marks is given below
(1) Here, the shoes size had the maximum sale = 7
(2) Here, the shoes size had the minimum sale = 4 (iii) Here, we have to find out the number of shoes sold of size 7 or greater than 7.
So, we have to add number of shoes sold of size 7 or greater than 7 i.e., size 7, 8, 9 and 10.
∴ Required number of shoes = 11 + 3 + 5 + 3 = 22
Hence, 22 shoes sold of size of 7 or greater than 7.
Pictograph is the way of representing data using pictures of objects. Each picture (image) stands for a certain number of objects. It helps us to answer the questions on the data at a glance.
Interpretation of a Pictograph
Interpretation of a pictograph means finding some conclusions from it. In interpretation of a pictograph, the first step is to know what it represents or what information is given by it.
It is also important to know the number of units represented by one picture symbol.
Example 3. Following pictograph represents some surnames of people listed in the telephone directory of a city.

Observe the pictograph and answer the following questions:
(1) How many people have surname Roy?
(2) Which surname appears the maximum number of times in the telephone directory ?
(3) Which surname appears the least number of times in the telephone directory ?
(4) Which two surnames appear an equal number of times?
Solution. (1) The number of people having surname Roy are 400. Because in the given pictograph, the picture symbol represents 100 people.
(2) Surname Patel appears maximum number of times. Because in the given pictograph, the picture symbol represents 100 people. According to this, surname Patel appears 500 times.
(3) The surname Saikia appears the least number of times. Because in the given pictograph, the picture symbol represents 100 people. According to this, surname Saikia appears 200 times.
(4) The surname Rao and Roy appears an equal number of times.
Example 4. The colours of car preferred by people living in a society are shown by the following pictograph.

Look at this and answer the following questions.
(1) Find the number of people preferring white colour.
(2) How many people liked green colour?
(3) Find the sum of number of people who prefers black and red colour.
Solution. (1) White colour is preferred by 300 people.
(2) For 5 complete picture, we get 5 x 100 = 500 people and for 1 incomplete picture, we may roughly take it as 50 people.
Hence, the number of people prefers green colour is nearly 550.
(3) We have to find the sum of number of people who prefers black and red colour. So, we have to add the number of peoples who preferred black and red colour.
Now, the number of people who prefers black colour = 4 × 100 = 400
and the number of people who prefers red colour = 2 × 100 = 200
∴ Sum of number of people prefers black and red colour = 400 + 200 = 600
Hence, 600 people prefers the black and red colour.
MP Board Class 6 Maths Solutions
Example 5. A survey was carried out in a certain school to find out different modes of transport used by students to travel to school each day, 30 students of Class VI were interviewed and the data obtained was displayed in the form of pictographs given below.

Look at this and answer the following questions.
(1) Which is the most popular mode of travel?
(2) Find the number of students who used walking as mode of travel.
(3) Which mode of travel is least used by the student?
Solution. (1) Maximum number of students use the school bus. Therefore, this is the most popular mode of travel.
(2) The number of students who use walking as mode of travel is 8.
(3) Cycle is used only by three students. Therefore, this mode of travel is least used by the students.
Question 1. In a Mathematics test, the following marks were obtained by 40 students. Arrange these marks in a table using tally marks.
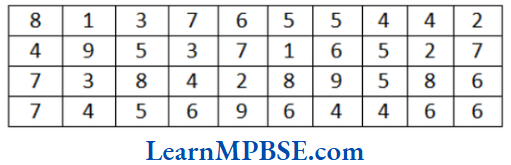
(1) How many students obtained marks equal to or more than 7?
(2) How many students obtained marks below 4?
Solution. The table with tally marks is shown below
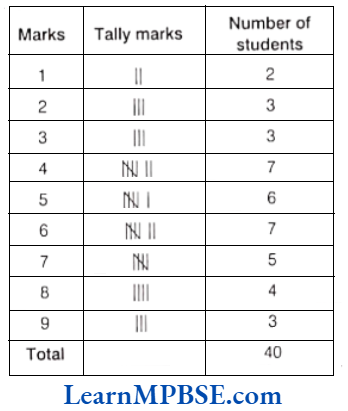
(1) Here, we have to find out the students, who obtained marks equal to 7 or more than 7.
So, we have to add the number of students who obtained marks equal to 7 or more than 7 i.e. marks 7, 8 and 9.
∴ Number of required students = 5 + 4 + 3 = 12
Hence, 12 students obtained marks equal to 7 or more than 7.
(2) Here, we have to find out the students who obtained marks below 4.
So, we have to add the number of students who obtained marks below 4 i.e., 1, 2 and 3.
∴ Number of required students = 3 + 3 + 2 = 8
Hence, 8 students obtained marks below 4.
MP Board Class 6 Maths Solutions
Question 2. Following is the choice of sweets for 30 students of Class VI.
Ladoo, Barfi, Ladoo, Jalebi, Ladoo, Rasgulla, Jalebi, Ladoo, Barfi, Rasgulla, Ladoo, Jalebi, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo, Rasgulla, Ladoo, Ladoo, Barfi, Rasgulla, Rasgulla, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi and Ladoo.
(1) Arrange the names of sweets in a table using tally marks.
(2) Which sweet is preferred by most of the students?
Solution. (1) The table with tally marks is shown below
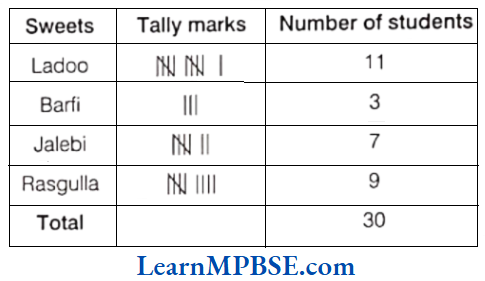
(2) By examine the above table, we see that Ladoo is preferred by most of the students. i.e. 11 students.
Question 3. Catherine threw a dice 40 times and noted the number appearing each time as shown below

Make a table and enter the data using tally marks. Find the number that appeared
(1) the minimum number of times.
(2) the maximum number of times.
(3) Find those numbers that appear an equal number of times.
Solution. The table with tally marks is shown below.
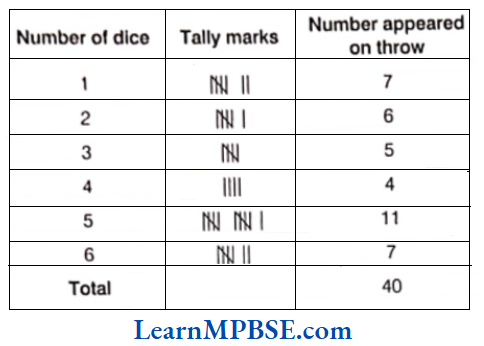
(1) From the above table, number 4 appeared 4 times while throwing a dice.
Thus, number 4 appeared the minimum number of times i.e. 4 times.
(2) While throwing a dice, number 5 appeared 11 times which is highest.
Thus, the maximum number of times the number 5 appeared.
(3) Number 1 and number 6 both appeared 6 times while throwing a dice.
Hence, number 1 and number 6 appeared an equal number of times.
Question 4. Following pictograph shows the number of tractors in five villages.

Observe the pictograph and answer the following questions.
(1) Which village has the minimum number of tractors?
(2) Which village has the maximum number of tractors?
(3) How many more tractors village C has as compared to village B?
(4) What is the total number of tractors in all the five villages?
Solution. (1) Observing the pictograph, it is clear that village D has the minimum number of tractors i.e. only 3 tractors.
(2) Observing the pictograph, it is clear that village Chas the maximum number of tractors i.e. 8 tractors.
(3) Observing the pictograph, it is clear that village C has 8 tractors and village B has 5 tractors.
So, village C has 8 – 5 = 3 more tractors as compared to village B.
(4) Total number of tractors in all the five villages
= Sum of all tractors in villages A, B, C, D and E
= 6 + 5 + 8 + 3 + 6 = 28
Hence, there are 28 tractors in all the five villages.
MP Board Class 6 Maths Solutions
Question 5. The number of girl students in each class of a co-educational middle school is depicted by the pictograph.

Observe this pictograph and answer the following questions.
(1) Which class has the minimum number of girl students?
(2) Is the number of girls in Class VI less than the number of girls in Class V?
(3) How many girls are there in Class VII?
Solution. In the given pictograph, 1 picture = 4 girls, half picture = 2 girls
(1) Observing the pictograph, it is clear that the minimum number of girl students are in Class VIII i.e. 4 + 2 = 6
(2) Observing the pictograph, it is clear that
Number of girls in Class VI = 4 x 4 = 16
and number of girls in Class V = 2 x 4 + 1 × 2 = 8 + 2 = 10
∴ 10 < 16
So, it is clear that number of girls in Class VI is not less than the number of girls in Class V.
(3) Observing the pictograph, number of girls in Class VII = 3 x 4 = 12
Class 6 Maths Chapter 9 Solutions
Question 6. The sale of electric bulbs on different days of a week is shown below

Observe the pictograph and answer the following questions.
(1) How many bulbs were sold on Friday?
(2) on which day, were the maximum number of bulbs sold?
(3) on which of the days, same number of bulbs were sold?
(4) On which of the days, minimum number of bulbs were sold?
(5) If one big carton can hold 9 bulbs. How many cartons were needed in the given week?
Solution. In the given pictograph, 1 picture = 2 bulbs
Now, number of bulbs sold on Monday = 6 pictures = 6 x 2 = 12 bulbs
Number of bulbs sold on Tuesday = 8 x 2 = 16 bulbs
Number of bulbs sold on Wednesday = 4 x 2 = 8 bulbs
Number of bulbs sold on Thursday = 5 x 2 = 10 bulbs
Number of bulbs sold on Friday = 7 x 2 = 14 bulbs
Number of bulbs sold on Saturday = 4 x 2 = 8 bulbs
Number of bulbs sold on Sunday = 9 x 2 = 18 bulbs
(1) Number of bulbs sold on Friday = 7 x 2 = 14 bulbs
(2) Maximum number of bulbs were sold on Sunday i.e. 18 bulbs.
(3) The same number of bulbs were sold on Wednesday and Saturday i.e. 8 bulbs.
(4) The minimum number of bulbs were sold on Wednesday and Saturday i.e. 8 bulbs.
(5) Total number of bulbs sold in a week
= 12 + 16 + 8 + 10 + 14 + 8 + 18 = 86
Now, number of cartons which can hold 9 bulbs = 1
∴ Number of cartons which can hold 1 bulb = \(\frac{1}{9}\)
= \(\frac{1 \times 86}{9}\)
= \(\frac{86}{9} = 9 \frac{5}{9} = 10\)
[as number of cartons should be an integer]
Hence, 10 cartons were needed in the given week.
Question 1. The marks (out of 10) obtained by 28 students in a Mathematics test are listed as given below.
8, 1, 2, 6, 5, 5, 5, 0, 1, 9, 7, 8, 0, 5, 8, 3, 0, 8, 10, 10, 3, 4, 8, 7, 8, 9, 2, 0
The number of students who obtained marks more than or equal to 5 is
Answer. 4. 17
Question 2. In question 1 (above), the number of students who scored marks less than 4 is
Answer. 4 10
Class 6 Maths Chapter 9 Solutions
Question 3. The choices of the fruits of 42 students in a class are as follows.
A, O, B, M, A, G, B, G, A, G, B, M, A, G, M, A, B, G, M, B, A, O, M, O, G, B, O, M, G, A, A, B, M, O, M, G, B, A, M, O, M, Observe
Where A, B, G, M and O stand for the fruits Apple, Banana, Grapes, Mango and Orange, respectively. Which two fruits are liked by an equal number of students?
Answer. 4. B and G
Question 4. According to data of question 4, which fruit is liked by most of the students?
Question 5. Following table shows the number of bikes manufactured in a factory during the year 1998 to 2002.
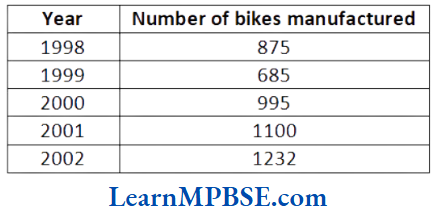
In which year were the maximum number of bikes manufactured?
Answer. 1. 2002
Question 6. Using the data of question (8). Find the difference between number of bikes manufactured in the years 1999 and 2000.
Answer. 3. 310
Question 7. A pictograph represents data in the form of
Answer. 3. pictures
Class 6 Maths Chapter 9 Solutions
Question 1. Assertion (A) The students get a marks in Maths test out of 20 are 10, 15, 19, 17, 05, 8, 12.
So, the maximum marks in the test obtained by the students is 19.
Reason (R) The tally marks represents 10.
(a) Both A and R are True And R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (b) Both A and R are true but R is not the correct explanation of A.
Question 2. Assertion (A) The sale of balls on different days of a week is shown below.
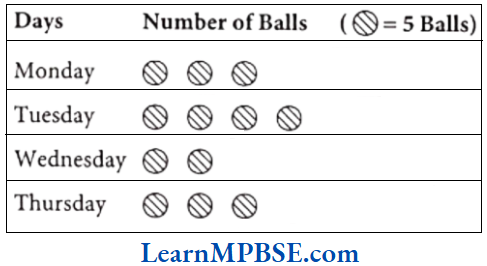
The balls sold on Thursday are 15.
Reason (R) A pictograph represents data through symbols or pictures.
(a) Both A and R are True And R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 1. A ….. is a collection of numbers gathered to give some meaningful information.
Answer. data
Question 2. The data can be arranged in a tabular form using …. marks.
Answer. tally
Question 3. The tally marks represents |||| represents …… .
Answer. 4
Question 4. Representation of data in form of pictures is called ….. .
Answer. pictograph
Question 5. In a pictograph, if a symbol * represents 20 flowers in a basket, then *** stands for ….. flowers.
Answer. 60
Class 6 Maths Chapter 9 Solutions
Question 1. An observation occurring five times in a data is recorded as |||||, using tally marks.
Answer. False
Question 2. Tally marks |||| represents 4.
Answer. True
Question 3. Pictograph is pictorial representations of the numerical data.
Answer. True
Question 4. In a pictograph, if a symbol represents 50 books in a library shelf, then the symbol represents 25 books.
Answer. True
Question 5. In a pictograph, if a symbol represents 100 books in a library shelf, then the symbol represents 50 books.
Answer. False
Question 1. Match the items of Column 1 with their respective value in Column 2.
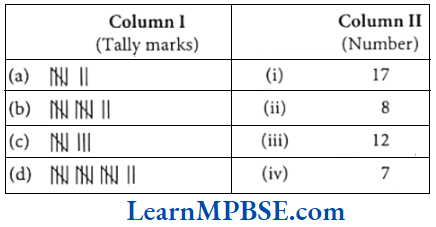
Answer. (a) → (4), (b) → (3), (c) → (2), (d) → (1).
Question 1. Shobit works for a shoe store. He records the shoe sizes and the number of pairs sold every day. On Tuesday, he sold 60 pairs. His record for the day is shown below.
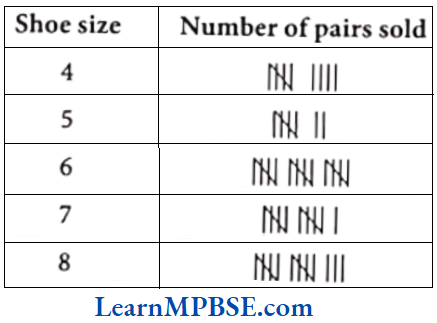
(1) How many pairs of size 8 were sold on Tuesday?
(a) 3
(b) 10
(c) 11
(d) 13
(2) Which shoe size sold the most?
(a) 6
(b) 7
(c) 8
(d) 9
Class 6 Maths Chapter 9 Solutions
(3) Shobit realised that he had not fully recorded the sale for Tuesday. How many sold pairs had he not recorded?
(4) The unrecorded data was of shoe size 7. Shobit corrected his record accordingly. Which of the following statements will be true now?
(a) Shoe size 8 sold the least now
(b) Shoe size 7 sold the most now
(c) Shoe size 5 is the new mode of the data
(d) Number of shoe pairs of size 3 can be calculated
(5) The price of one shoe pair of size 5 is ₹ 800. How much money had Shobit collected by selling all the shoe pairs of size 5?
Solution. (1) (d) On Tuesday, Shobit sold 13 pairs of shoes.
(2) (a) Shoe size 6 sold the most.
(3) Shobit recorded the sale of 55 pairs for Tuesday, but he sold 60 pairs. Thus, he had not recorded 5 pairs of shoes.
(4) (b) The correct statements after Shobit corrected his record is that shoe size 7 sold the most now i.e., 16 pairs.
(5) Shobit sold 7 pairs of shoes of size 5 on Tuesday. And the price of one shoe pair of size 5 is 800.
Thus, the money collected by selling all the shoe pairs of size 5 = 7 x 800 = ₹ 5600
Question 2. The marks obtained by 10 students in Science test are given below.
53, 36, 95, 3, 62, 42, 25, 78, 75, 62
Answer the following questions that are related to the given data.
(1) The maximum marks obtained by any student is
(a) 60
(b) 95
(c) 78
(d) 25
(2) The minimum marks obtained by any student is
(a) 42
(b) 36
(c) 25
(d) 73
(3) How many students got the same marks?
(a) 3
(b) 4
(c) 2
(d) None of above
(4) How many students got 78 or more marks?
(a) 2
(b) 3
(c) 1
(d) 4
(5) How many students got marks below 62?
(a) 3
(b) 4
(c) 5
(d) 2
Solution. (1) → (b), (2) → (c), (3) → (c), (4) → (a), (5) → (b)
Question 1. The following are the weight in kg of 20 students of a class 25, 15, 17, 15, 23, 10, 9, 15, 16, 17, 15, 16, 23, 25, 16, 15, 23, 9, 10, 16
Prepare a table using tally marks for the given data.
Also, answer the following questions.
(1) Find the number of students whose weights are equal to 17 or more than 17.
(2) How many students whose weights are below 16.
Solution.
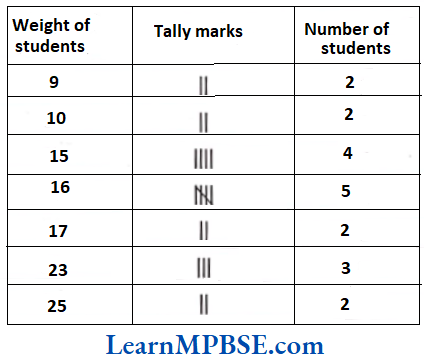
(1) 7
(2) 8
Question 2. Following is the choice of sports for 20 students of Class 6. Cricket, Football, Cricket, Tennis, Cricket, Badminton, Football, Cricket, Football, Tennis, Cricket, Badminton, Basketball, Football, Golf, Football, Hockey, Football, Hockey, Football
(1) Arrange the names of sports in a table using tally marks.
(2) Which sports is preferred by most of the students?
Solution.
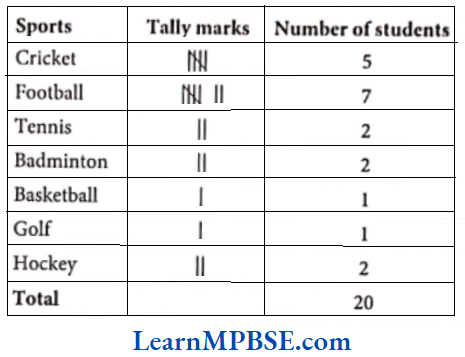
(2) 7 students preferred football which is highest. Thus, football is preferred by most of the students.
Question 3. Maria threw a dice 30 times and noted the number appearing each time as shown below.
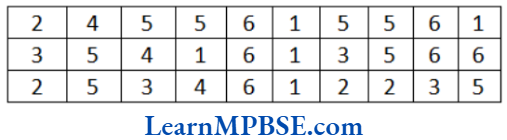
Prepare a table using tally marks and answer the following questions.
(1) Find the number that appeared the minimum number of times.
(2) Find the number that appeared the maximum number of times.
(3) How many times the number 2 and 3 appeared?
Solution.
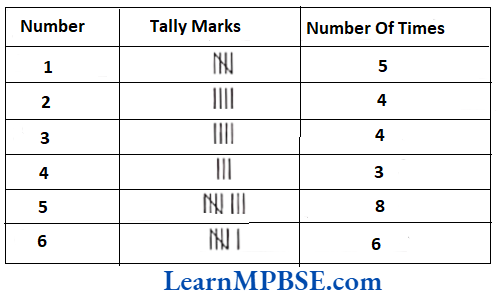
(1) 4
(2) 5
(3) 4 times
Class 6 Maths Chapter 9 Solutions
Question 4. The pictograph shows the number of persons using various brands of perfumes.

(1) How many persons use R brand?
(2) Which brand is used by maximum number of persons?
Solution. (1) 24 persons (2) R brand
Question 1. The following pictograph shows the number of private buses in six cities.

(1) In which city the number of private buses are least?
(2) In which city the number of private buses are highest?
(3) How many more buses in Delhi as compared to Agra?
(4) Find the total number of buses in all the six cities.
Solution. (1) Noida
(2) Jaipur
(3) 20
(4) 270
Question 2. In a electrical shop, the sale of fans on different days of a week is shown by below pictograph.

By observing the given pictograph answer the following questions.
(1) Find the number of fans sold on Tuesday.
(2) On which of the days, the number of fans were sold is same?
(3) On which day, the number of fans were sold is maximum?
(4) On which day, the number of fans were sold is minimum?
(5) Find the total number of fans were sold in all the days of this week.
Solution. (1) 20
(2) Monday and Friday
(3) Saturday
(4) Wednesday
Class 6 Maths Chapter 9 Solutions
Question 3. Following is the pictograph of the number of cycles manufacture by a factory on six different working days of a week.

By observing the given pictograph and answer the following questions.
(1) On which day were the least number of cycles manufactured?
(2) On which day were the maximum number of cycles manufactured?
(3) Find the approximate number of cycles manufactured in all the six working days of the given week.
(4) On which of the days, the number of cycles manufactured is same?
Solution. (1) Wednesday
(2) Thursday
(3) 275
(4) Monday and Saturday
Question 4. The blood groups of 25 students are recorded as follows
A, B, O, A, AB, O, A, O, B, A, O, B, A, AB, AB, A, A, B, B, O, B, AB, O, A, B. Arrange the information in a table using tally marks.
Solution. The information in a table using tally marks is as follows:
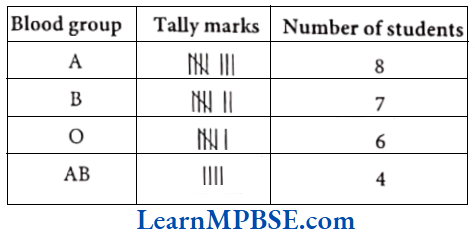
Question 5. Rakesh is playing with a dice. He threw the dice 40 times and noted the outcomes as follows.
1, 2, 1, 5, 3, 5, 5, 3, 2, 2, 1, 6, 6, 6, 4, 6, 3, 5, 2, 3, 3, 5, 4, 1, 5, 5, 2, 4, 5, 5, 2, 4, 5, 5, 2, 4, 1, 6, 6, 1, 5, 6, 1, 5.
Prepare a table using tally marks.
Solution. We draw the following table using tally marks from given information.
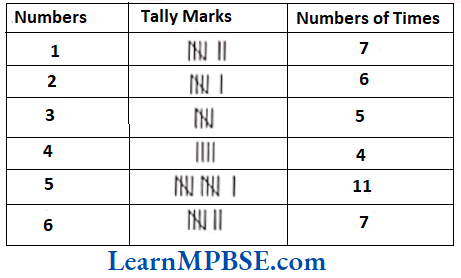
MP Board Class 6 Chapter 9 Maths
Question 6. Thirty students were interviewed to find out what they want to be in future. Their responses are listed as below
doctor, engineer, doctor, pilot, officer, doctor, engineer, doctor, pilot, officer, pilot, engineer, officer, pilot, doctor, engineer, pilot, officer, doctor, officer, doctor, pilot, engineer, doctor, pilot, officer, doctor, pilot, doctor, engineer.
Arrange the data in a table using tally marks.
Solution. We draw the following table using tally marks for given information.
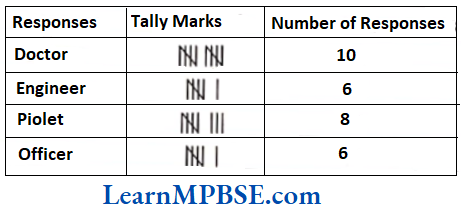
Question 1. The following pictograph depicts the information about the areas in sq km (to nearest hundred) of some districts of Chattisgarh State.
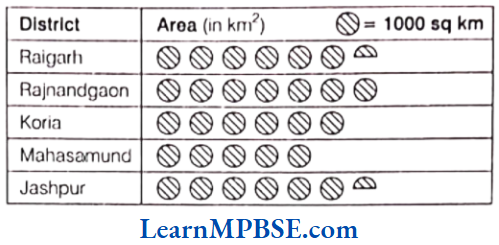
(1) What is the area of Koria district?
(2) Which two districts have the same area?
(3) How many districts have area more than 5000 km?
Solution. (1) Area of Koria district = 6000 sq km
(2) Raigarh and Jashpur have the same area.
(3) Four districts have area more than 5000 sq km.
Question 2. Fill in the blanks in the following table, which represents shirt size of 40 students of a school.
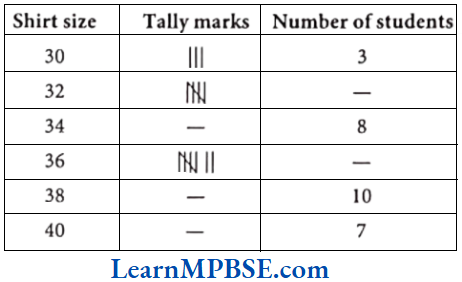
Solution. (1) ![]() shows four vertical lines and one intersecting line.
shows four vertical lines and one intersecting line.
∴ It counts to be four plus one (i.e. 5).
(2) We know that
8 = 5 + 3
Here, 5 is represented by ![]() and 3 is represented by |||.
and 3 is represented by |||.
∴ 8 is represented by ![]() |||.
|||.
(3) ![]() || means 5 + 2 i.e. 7.
|| means 5 + 2 i.e. 7.
(4) We know that
10 = 5 + 5
Here, 5 is represented by ![]() .
.
∴ 10 is represented by ![]()
![]()
(5) We know that 7 = 5 + 2
Here, 5 is represented by ![]() and 2 is represented by ||.
and 2 is represented by ||.
∴ 7 is represented by ![]() ||.
||.
Thus, the complete table is shown below
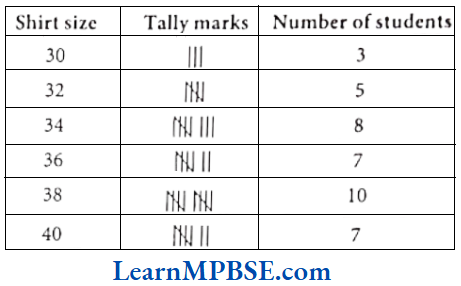
MP Board Class 6 Chapter 9 Maths
Question 3. The number of scouts in a school is depicted by the following pictograph.

Observe the pictograph and answer the following questions.
(1) Which class has the minimum number of scouts?
(2) Which class has the maximum number of scouts?
(3) How many scouts are there in class 6?
(4) Which class has exactly four times the scouts as that of Class 10?
(5) What is the total number of scouts in the classes 6 to 10?
Solution. (1) Class 10 has minimum number of scouts i.e. 10.
(2) Class 8 has maximum number of scouts i.e. 60.
(3) Number of scouts in Class 6 = 40
(4) Number of scouts in Class 10 = 10
Hence, Class 6 has exactly four times the scouts as that of Class 10.
(5) Total number of scouts in classes 6 to 10
= 40 + 20 + 60 + 30 + 10 = 160
Natural Numbers Natural numbers are counting numbers i.e. 1, 2, 3,…
Whole Numbers If we include 0 (zero) with natural numbers, then they are called as whole numbers. Negative Numbers The numbers which are less than 0 are called negative numbers. To differentiate these negative numbers from whole numbers, we use a (-) minus sign attached to the number. This indicates that numbers with negative sign are less than zero.
e.g. 1 is less than zero is written as 1, 2 is less than zero is written as -2 etc.
Sign with Numbers
In our day-to-day life, we see some situations in which some numbers carry a negative sign and some carry positive sign. These situations are represented by appropriate signs i.e. ‘+’ sign and ‘-‘ sign.
e.g. Profit is represented by ‘+’ sign and loss is represented by ‘-‘ sign.
Example 1. Write the opposite of each of the following:
(1) Profit of 50.
(2) Deposit of 1000.
(3) 50 km towards South.
Solution. The opposite of each, is
(1) loss of ₹ 50.
(2) withdraw of ₹ 1000.
(3) 50 km towards North.
Read and Learn More MP Board Class 6 Maths Solutions
Example 2. Write the following numbers with appropriate signs:
(1) 200 m below sea level.
(2) 20°C below 0°C temperature.
(3) 25°C above 0°C temperature.
(4) A deposit of 50.
(5) Any four numbers less than 0.
Solution. (1) 200 m below sea level means – 200 m.
(2) 20°C below 0°C temperature means -20°C.
(3) 25°C above 0°C temperature means + 25°C.
(4) A deposit of 50 means + ₹ 50.
(5) Every negative integer is less than zero and every positive integer is greater than zero.
∴ Numbers less than zero are -1, -2, -3 and -4.
Integers
If we put the whole numbers and the negative numbers together, the new collection of numbers will look like …-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, .., and this collection of numbers is known as integers.
Here, 1, 2, 3,… are said to be positive integers and -1, -2, -3, … are said to be negative integers.
Note It Zero is an integer which is neither positive nor negative. One more than given number gives its successor and one less than that of given number gives its predecessor.
Representation of Integers on a Number Line
To represent integers on a number line, draw a line and mark the points at equal distance on it, as shown in the figure given below. Mark a point as zero on it. Points to the right of zero are positive integers marked as +1, +2, +3 etc or simply 1, 2, 3 etc. Points to the left of zero are negative integers marked as -1, -2, -3, etc.
MP Board Class 6 Maths Solutions
Example 3. Represent the following numbers on the number line
(1)-2
(2) +6
(3) – 5
(4) -1
(5) +5
Solution. Draw a line and mark some points at equal distance on it. Mark a point as zero on it. Points to the right of zero are positive integers and are marked as +1, +2, +3 or simply by 1, 2, 3 etc. Points to the left of zero are negative integers and are marked by-1, -2, -3, etc.
(1) Representation of -2 To mark-2 on the number line, we move 2 points to the left of zero as shown in figure. A
In the above figure, point A represents – 2.
(2) Representation of 6 To mark +6 on the number line, we move 6 points to the right of zero as shown in the figure.
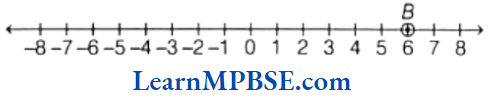
In the above figure, point B represents + 6.
(3) Representation of -5 To mark-5 on the number line, we move 5 points to the left of zero as shown in figure.
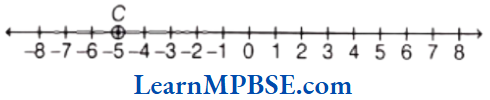
In the above figure, point C represents-5.
(4) Representation of -1 To mark-1 on the number line, we move 1 point to the left of zero as shown in figure.
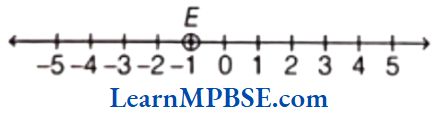
In the above figure, point E represents – 1.
(5) Representation of + 5 To mark + 5 on the number line, we move 5 points to the right of zero as shown in figure.
In the above figure, point F represents + 5.
Example 4. The given figure is a horizontal line representing integers. Observe it and locate the following points.

(1) If point D is +7, then which point is – 7
(2) Find that the point G is a negative or a positive integer.
(3) Write the integers of points F and C.
(4) Which point marked on this number line has the greatest value?
(5) Arrange all the points in increasing order of value.
Solution.
(1) From the figure, it is clear that + 7 is on point D, then for getting-7, we should move left of zero.
After moving 7 steps left of zero, we reach at the point H.
So, point H represents-7.
(2) The point G is left of zero. So, G is a negative integer.
(3) The integers for point F is -3 and for point C is 5.
(4) The point D has the greatest value i.e. 7.
(5) We know that on a number line, the number increases as we move to right. So, increasing order of value of all points is given here.
H, G, FE, O, A, B, C, D
MP Board Class 6 Maths Solutions
Example 5. Given below are the temperatures in some cities.

(1) Write the temperature of these cities in the form of integers.
(2) Which is the coolest city out of these cities?
(3) Give the names of cities, where temperature is above 5°C.
(4) Plot the temperature of cities on the number line.
Solution. (1) The temperature of Shimla is -10°C.
The temperature of Leh is -15 °C.
The temperature of Delhi is + 25 °C.
The temperature of Nagpur is + 30°C.
(2) After checking the temperature of all places, we can say that the Leh (-15°C) is the coolest place.
(3) Delhi (25°C) and Nagpur (30°C) are the cities, where temperature is above 5 °C.
(4)

Example 6. In the given following pairs which number is to the right of the other on the number line?
(1) 3,8
(2) -4, -9
(3) 0, -4
(4) -13, 8
Solution.
(1)

Here, 3 and 8 both are on the right of zero but 8 is farther from zero in comparison of 3. So, number 8 is right of number 3.
(2)
Here, -4 and -9 both are on the left of zero, but – 4 is nearer to zero in comparison of-9. So, -4 is right of
(3)
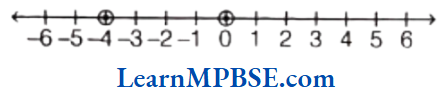
Here, 0 is right of -4.
(4) Here, -13 is left of zero and 8 is right of zero. So, 8 is right of -13.
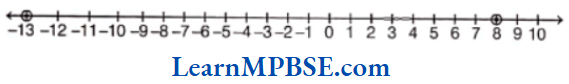
Ordering of Integers
On the number line, the number increases as we move to the right and decreases as we move to the left.
Therefore, -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 and so on.
Note it The greater the positive integer, the lesser is its opposite.
e.g. 7 > 4 but -7 < -4.
MP Board Class 6 Maths Solutions
Example 7. Compare the following pairs of numbers using > or <.
(1) 0 – -6
(2)-1 – -12
(3) 5 – -5
(4) 11 – 17
Solution.
(1) We know that -6 is to the left of 0 (zero) on number line. So,0 > -6
(2) We know that-1 is to the right of-12 on the number line. So -1 > -12
(3) We know that 5 is to right of-5. So, 5 > -5
(4) We Know that 17 is to right of 11. So, 11 < 17
Example 8. Write five negative integers
(1) greater than 30.
(2) less than -15.
Solution.
(1) When we move on the number line to the right, then the value of integer increases.
So, from the above figure, we get the five negative integers greater than 30 are 29,-28,-27,-26 and – 25.
(2) When we move on the number line to the left, then the value of integer decreases.
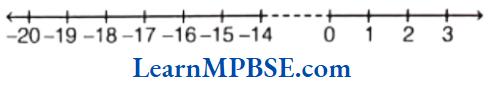
So, from the above figure, we get the five negative integers less than -15 and -16,-17, -18,-19 and – 20.
Example 9. Write all the integers between
(1) 0 and -9
(2) -15 and -5
and write them in the decreasing order.
Solution. (1) Integers 0 and -9 are shown on the number line as below.
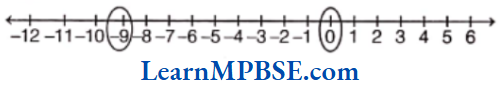
From the above number line, it is clear that integers between 0 and -9 are-1,-2,-3,-4,-5, -6, -7 and – 8.
Now, decreasing order of these integers is
-1 > -2 > -3 > -4 > -5 > -6 > -7 > -8
(2) Integers-15 and -5 are shown on the number line as below.
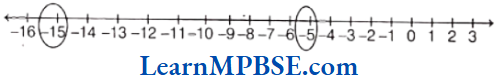
From the above number line, it is clear that integers between 15 and -5 are -14,-13,-12,-11,-10,-9, -8,-7,-6
Now, decreasing order of these integers is
-6 > -7 > -8 > -9 > -10 > -11 > -12 > -13 > -14
Example 10. For the following statements, write true (T) or false (F). If the statement is false, correct the statement.
(1)-6 is to the right of -12 on a number line.
(2)-70 is to the right of 30 on a number line.
(3) Smallest positive integer is 1.
(4)-24 is greater than -23.
Solution. (1) True, because on the number line going to the right, value of integer increases. Here, – 6 is greater than -12. So,-6 is to the right of-12 on the number line.
(2) False, because on the number line going to the left. value of integer decreases. Here, – 70 is less than 30. So,-70 is to the left of- 30 on the number line.
(3) True, because on the number line 1 is situated on the left of all positive integers. So, it is the smallest positive integer.
(4) False, because – 23 is on the right of – 24 on the number line. So, 23 is greater than – 24.
MP Board Class 6 Maths Solutions
Example 11. Draw a number line and answer the following:
(1) Which number will we reach, if we move 5 numbers to the left of -1?
(2) Which number will we reach, if we move 4 numbers to the right 2?
(3) If we are at 6 on the number line, in which direction should we move to reach -11?
(4) If we are at 9 on the number line, in which direction should we move to reach – 3?
Solution. (1)

On the number line, starting from -1 and moving 5 points towards left (each step being equal to 1 unit), we will reach at -6.
(2)
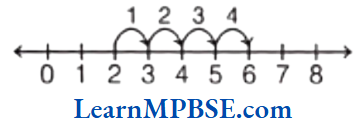
On the number line, starting from 2 and moving 4 points towards right (each step being equal to 1 unit), we will reach at 6.
(3) Here,-6-11. So, -11 is on the left of -6.
Hence, if we are at -6 on the number line, then move to the left from 6 to reach at -11.
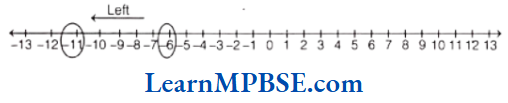
(4) Here, -3>9. So, – 3 is on the right of -9.
Hence, if we are at -9 on the number line, then move to the right from-9 to reach at – 3.
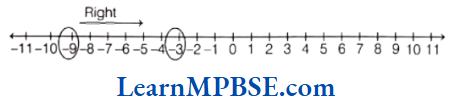
Example 12. Write the following numbers (integers) in increasing and decreasing order with using sign < and >’.
(1) 0,5, 10, 6, -3, 9
(2) 8, 6, 136, 32, -80, 120, 1
(3) 9, 8, 4, -3, -2, 1, 10
(4) 99, 98, 97, 97, 4, 1, 90
Solution. (1) Given numbers are 0, -5, 10,6,-3,9.
Increasing order is -5 < -3 < 0 < 6 < 9 < 10.
Decreasing order is 10 > 9 > 6 > 0 > -3 > -5.
(2) Given numbers are 8, 6,-136, 32, -80, 120, 1.
Increasing order is -136 < -80 < 1 < 6 < 8 < 32 < 120
Decreasing order is 120 > 32 > 8 > 6 > 1 > -80 > -136.
(3) Given numbers are 9, 8, 4, 3, 2, 1, 10.
Increasing order is -3 < -2 < 1 < 4 < 8 < 9 < 10.
Decreasing order is 10 > 9 > 8 > 4 > 1 > -2 > -3
(4) Given numbers are – 99, 98, -97, 97, 4, 1, 90.
Increasing order is -99 < -97 < 1 < 4 < 90 < 97 < 98.
Decreasing order is 98 > 97 > 90 > 4 > 1 > -97 > -99.
To add two positive integers, we simply add them and to add two negative integers, we firstly add them and then put negative sign before the sum.
e.g. (+3) + (+2) = +5
and (-2) + (-3) = -(2+3) = -5
When we have one positive and one negative integer, then we must subtract but answer will take the sign of the integer which has greater value to it.
e.g. (-3) + (+2) = -3 + 2 = -1
Note it The sum of two positive integers is always a positive integer and the sum of two negative integers is always a negative integer.
MP Board Class 6 Maths Solutions
Example 1. Write the answer of the following
(1) (+11) + (+6)
(2) (+17) + (+37)
(3) (-23) + (-7)
(4) (-9) + (-16)
Solution. (1) (+11) + (+6) = +(11 + 6) = 17
(2) (+17) + (+37) = +(17 + 37) = 54
(3) (-23) + (-7) = -(23 + 7) = -30
(4) (-9) + (-16) = -(9 + 16) = -25
Example 2. Find the answer of the following.
(1) (-8) + (+9)
(2) (-11) + (+16)
(3) (+11) + (-17)
(4) (+23) + (-6)
Solution. (1) (-8) + (+9) = (-8) + (+8) + (+1) [∵ 8 + 1 = 9]
= 0 + (+1) [∵ (-8) + (+8) = 0]
= +1
(2) (-11) + (+16) = (-11) + (+11) + (+5) [∵ 11 + 5 = 16]
= 0 + (+5) [∵ (-11) + (+11) = 0]
= +5
(3) (+11) + (-17) = (+11) + (-11-6) [-17 = -11-6]
= (+11) + (-11) + (-6)
= 0 + (-6) [∵ (+11) + (-11) = 0]
= -6
(4) (+23) + (-6) = (+17) + (+6) + (-6) [∵ 23 = 17 + 6]
= (+17) + 0
= +17
Example 3. Find the sum of
(1) 257 and -107
(2) -18 and 18
(3) -214, 65 and 104
(4) -40, -180 and 250
Solution. (1) We have, 257 + (-107)
= (+150) + (+107) + (-107) [∵ 257 = 150 + 107]
= (+150) + 0 = 150 [∵ (+107) + (-107) = 0]
(2) We have, -18 + (+18) = 0
(3) We have, -214 + 65 + 104
= -214 + 169
= (-169) + (-45) + 169
[∵ 214 = 169 + 45 = -214 = (-169) + (-45)]
= (-169) + 169 + (-45)
= 0 + (-45) = -45 [∵ (-169) + 169 = 0]
(4) We have, (-40) + (-180) + 250
= -(40+180) + 250 = (-220) + 250 [∵ 250 = 220 + 30]
= (-220) + (+220) + (+0) [∵ (-220) + (220) = 0]
= 0 + 30 = 30
MP Board Class 6 Maths Solutions
Example 4. Find the sum of
(1) (-8) + (-11) + (6) + (17)
(2) (36) + (-4) + (-70) + (-8)
(3) (-26) + (14) + (-1) + (16)
(4) (-14) + (-16) + (7) + (18)
Solution. (1) We have, (-8) + (-11) + (6) + (17)
= -(8+11) + 6 + 17 [∵ 23 = 19 + 4]
= (-19) + 23
= (-19) + (+19) + (+4) [∵ (-19) + (19) = 0]
= 0 + (+4) = 4
(2) We have, (36) + (-4) + (-70) + (-8)
= (36) – (4+70+8) = (36) – (82)
[∵ 82 = 36 + 46 ⇒ -82 = (-36) + (-46)]
= (36) + (-36) + (-46) [∵ (36) + (-36) = 0]
= 0 + (-46) = -46
(3) We have, (-26) + (14) + (-1) + (16)
= -(26+1) + (14) + (16) = (-27) + (30)
= (-27) + (+27) + (3) [∵ 30 = 27 + 3]
= 0 + 3 = 3 [∵ (-27) + (+27) = 0]
(4) We have, (-14) + (-16) + (7) + (18)
= -(14+16) + (7) + (18)
= (-30) + 25
= (-25) + (-5) + 25 [∵ 30 = 25 + 5 ⇒ -30 = (-25) + (-5)]
= (-25) + (+25) + (-5)
= 0 + (-5) [∵ (-25) + (+25) = 0]
= -5
Addition of Integers with the help of Number line
Firstly, draw the number line and represent first integer on it. Then, to add a positive integer number in first integer, we move right to the first integer and to add a negative integer, we move left to the first integer.
e.g. To add 6 and 2, we start from 6 and go to 2 steps to the right of 6 and reach at 8.
So, 6 + 2 = 8
Class 6 Maths Chapter 5 Solutions
Example 5. Find the solution of the following using number line.
(1) (-2) + 6
(2) (-6) + 2
(3) (-2) + (-9)
(4) (-3) + 7 + (-5)
Solution. (1) First, mark at -2 on the number line. Now, move 6 steps to the right of it. We reach at the point +4.
∴ -2 + 6 = +4
(2) First, mark at -6 on the number line. Now, move 2 steps to the right of it. We reach at point-4.

Hence, -6 + 2 = -4
(3) First, mark at -2 on the number line. Now, move 9 steps to the left of it. We reach at point-11.
∴ (-2) + (-9) = -11
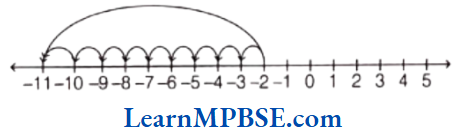
(4) First, mark at-3 on the number line. Now, first move 7 steps to the right of it and then move 5 steps to the left of +4. We reach at the point -1.
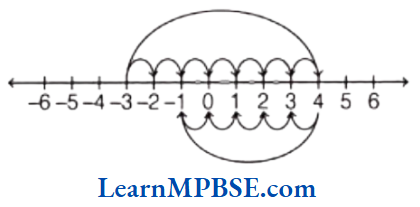
∴ -3 + (+7) + (-5) = -1
Example 6. Using the number line, write the integer which is
(1) 2 more than -1
(2) 5 less than 2.
Solution. (1) First, mark at -1 on the number line and move 2 steps to the right, we reach at point 1.
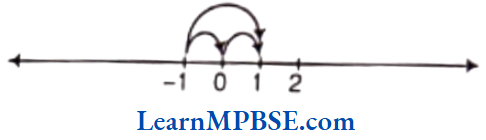
(2) First, mark at 2, on the number line and move 5 steps to the left, we reach at point -3.

Note it To find a number more than the given number, we move to the right of that given number and to find a number less than the given number, we move to the left of that number.
Example 7. A boy walked 6 km towards East, then he comes 9 km towards West. Find his position from the beginning point.
Solution. Let O be the beginning point of boy. East direction can be taken as positive and West as negative.
Then, walking 6 km towards East can be taken as + 6 km.
Walking 9 km towards West can be taken as – 9 km.
The final position = +6-9=-3km
Here, the negative sign shows that he is in West direction with respect to his beginning point.
∴ The boy’s final position is 3 km to the West with respect to his beginning point.
To subtract an integer from another integer, we add the additive inverse of the integer that is being subtracted from the other integer.
e.g. (-10) – (-4) = (-10) + Additive inverse of -4
= -10 + 4 = -6
i.e. subtraction of an integer is the same as the addition of its additive inverse.
Additive Inverse
Numbers such as 4 and -4, 2 and -2 when added to each other give the sum zero. They are called additive inverse of each other.
If two numbers when added to each other give the sum zero, then they are called additive inverse of each other. e.g. 3+(-3)=0. So, 3 is additive inverse of -3 and -3 is additive inverse of 3.
Class 6 Maths Chapter 5 Solutions
Example 1. Find the value of the following:
(1)-20 – (-5)
(2) 39 – 16
Solution. (1) -20 – (-5) = -20 + Additive inverse of -5
We have one negative and one positive value. So, we will subtract and take sign of greater value.
= -20 + 5 = -15
(2) 39 – 16 = 39 + Additive inverse of 16
We have one negative and one positive value. So, we will subtract and take sign of greater value.
= 39 + (-16) = 23
Example 2. Find
(1) (-9) + (-7) – (-80)
(2) (-14) + 31 – 9 – 1
Solution. (1) We have, (-9) + (-7) – (-80)
= -(9+7) + Additive inverse of-80 = -16 + 80 = 64
(2) We have, (-14) + 31 – 9 – 1 = (-14) + 31 – 10
= (-14) + 31 + Additive inverse of 10
= (-14) + 31 + (-10)
= -14 – 10 + 31 = 24 + 31 = 7
Example 3. Subtract the following
(1)-8 from 13
(2) – 12 from – 7
Solution. (1) 13 – (-8) = 13+ Additive inverse of – 8
= 13 + 8 = 21
(2) -7 – (-12) = -7+ Additive inverse of -12
= -7 + 12 = 5
Example 4. Subtract -15 from the sum of 15 and 25.
Solution. The sum of 15 and 25 = 15 + 25 = 40
Now, subtract -15 from 40
40 – (-15) = 40 + Additive inverse of -15
= 40 + 15 = 55
Example 5. The sum of two integers is -33. If one of them is 8. Find the other.
Solution. Other integer = Sum of two integers – The given integer
= -33 – (-8) = 33+ Additive inverse of -8
= -33 + 8 = 25
Example 6. Fill in the blanks with >, < or = Sign.
(1) (-5) + (-7)…… (-5) – (-7)
(2) (-31) – (-15)……(-41) + (-16)
(3) 30 – (-10)…….45 + (-2)
(4) (-44) – (-21) ……..(-10) – (-35)
Solution. (1) We have. (-5) + (-7)……..(-5) – (-7)
LHS = (-5) + (-7) = -12
RHS = (-5) – (-7) = (-5) + Additive inverse of -7
= -5 + 7 = 2
Since, -12 is a negative integer and 2 is a positive integer.
∴ 12 < 2
(2) We have, (-31) – (-15) ………. (-41) + (-16)
LHS = -31 – (-15) = -31 + Additive inverse -15
= 31 + 15 = -16
RHS = (-41) + (-16) = -57
Here, both are negative integers but-57 is the left of -16
∴ -16 > -57
(3) We have, 30 – (-10) …….. 45 + (-2)
LHS = 30 – (-10) = 30 + Additive inverse of -10
= 30 + 10 = 40
RHS = 45 + (-2) = 43
Here, both are positive integers but 43 is right to the 40.
∴ 40 < 43
(4) We have, (-44) – (-21) ……. (-10) – (-35)
LHS = (44) – (-21) = -44 + Additive inverse of – 21
= -44 + 21 = -23
RHS = (-10) – (-35) = -10 + Additive inverse of -35
= -10 + 35 = 25
Since, 23 is a negative integers and 25 is a positive integer.
∴ -23 < 25
Example 7. Fill in the blanks.
(1) (-6)+ …. = 0
(2) 16 + …. = 0
(3) 14 + (-14) = …..
(4) -4 + … = -14
Solution. (1) We have, (-6) + … = 0
⇒ (-6) + 6 = 0 [∴ additive inverse of-6 is 6]
(2) We have, 16+…=0
⇒ 16 + (-16) = 0 [∴ additive inverse of-16 is 16]
(3) We have, 14 + (-14) = ….
⇒ 14 + (-14) = 0 [∴ 14 and 14 are additive inverse of each other]
(4) We have, (-4) + … = -14
Here, the sum of two integers is not zero, so here we cannot write additive inverse of -4.
⇒ -4+ …. = -14
⇒ -4 +… (4+10)
⇒ -4 + …. (-4) + (-10)
So, on comparing both sides, we get -10 to fill the blank space.
∴ (-4) + (-10) = -14
Subtraction of Integers With the Help of Number Line
Firstly, draw the number line and represent first integer on it. Then, to subtract a positive integer from first integer, we move left to the first integer and to subtract a negative integer, we move right to the first integer.
e.g. To subtract 3 from 5, we move 3 steps to the left of 5 and reach at 2.

So, 5 – 3 = 2
and to subtract-4 from 3, we move 4 steps to the right of 3 and reach at 7.
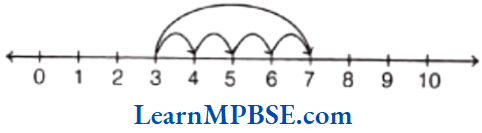
So, 3 – (-4) = 7
Class 6 Maths Chapter 5 Solutions
Example 8. Find the value of the following using the number line
(1) 6 – 2
(2) 2 – 3
(3) 6 – (-3)
(4) -4 – (-2)
Solution. (1) We have, 6 – 2 = 4

(2) We have, 2 – 3 = -1

(3) We have, 6 – (-3) = 6 + Additive inverse of -3
= 6 + 3 = 9

(4) We have, -4 – (-2) = -4 + Additive inverse of -2.
= -4 + 2 = -2

Question 1. Suppose David and Mohan have started walking from zero position in opposite directions. Let the steps to the right of zero be represented by ‘+’ sign and to the left of zero be represented by sign. If Mohan moves 5 steps to the right of zero, it can be represented as +5 and if David moves 5 steps to the left of zero, it can be represented as -5. Now, represent the following positions with + sign or – sign.
(1) 8 steps to the left of zero.
(2) 7 steps to the right of zero.
(3) 11 steps to the right of zero.
(4) 6 steps to the left of zero.
Solution. We know that on the number line, all numbers to the right of 0 are positive integers and all numbers to the left of 0 are negative integers.
Thus, the representation of numbers on the number line is as follows
(1) 8 steps to the left of zero is represented by -8.
(2) 7 steps to the right of zero is represented by +7.
(3) 11 steps to the right of zero is represented by +11.
(4) 6 steps to the left of zero is represented by -6.
Question 2. Write the succeeding number of the following.
Solution. We know that one more than given number gives a successor. So, the succeeding numbers of given numbers are given as below:
Class 6 Maths Chapter 5 Solutions
Question 3. Write the preceding number of the following.
Solution. We know that one less than a given number gives a predecessor. So, the preceding numbers of the given numbers are given as below:
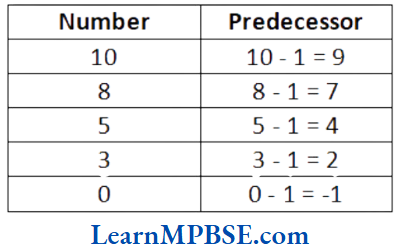
Question 4. Write the following numbers with appropriate signs:
(1) 100 m below sea level.
(2) 25°C above 0°C temperature.
(3) 15°C below 0°C temperature.
(4) Any five numbers less than 0.
Solution.
(1) We can write 100 m below sea level as -100 m, because below sea level represents – sign and above sea level represents ‘+’ sign.
(2) We can write 25°C above 0°C temperature as +25°C, because temperature above 0°C is denoted by ‘+’ sign and temperature below 0°C is denoted by ‘-‘ sign.
(3) We can write 15°C below 0°C temperature as -15°C, because temperature above 0°C is denoted by ‘+’ sign and temperature below 0°C is denoted by ”sign.
(4) Every negative integer is less than zero and every positive integer is greater than zero.
∴ Numbers less than 0 are -1, -2, -3, -4, -5 …
Question 5. Mark -3, 7, -4, -8, -1 and +3 on the number line.
Solution. Draw a line and mark some points at equal distance on it as shown in the figure given below. Mark a point on it as zero. Points to the right of zero are positive integers and marked by +1, +2, +3 etc. or simply by 1, 2, 3 etc and points to the left of zero are negative integers and marked by-1,-2,-3 etc.
Now, -3 is a negative integer (since, -3 has negative sign). So, move 3 points to the left of zero and represent it by point C.
7 is a positive integer (since, + 7 has positive sign). So, move 7 points to the right of zero and represent it by point F.
To mark – 4 on this line, move 4 points to the left of zero and represent it by point B.
To mark – 8 on this line, move 8 points to the left of zero and represent it by point A.
To mark – 1 on this line, move 1 point to the left of zero and represent it by point D.
To mark 3 on this line, move 3 points to the right of zero and represent it by point E.
Thus, we get the following representation of these integers on the number line

Question 6. Compare the following pairs of numbers using > or <.
(1) 0 … -8
(2) -1 … -15
(3) 5 … -5
(4) 11 … 15
(5) 0 … 6
(6) -20 … 2
From the above exercise, Rohini arrived at the following conclusions:
(a) Every positive integer is larger than every negative integer.
(b) Zero is less than every positive integer.
(c) Zero is larger than every negative integer.
(d) Zero is neither a negative integer nor a positive integer.
(e) Farther a number from zero on the right, larger is its value.
(f) Farther a number from zero on the left, smaller is its value.
Do you agree with her? Give examples.
Solution. (1) We have,
0 … -8
Since, 0 is to the right of -8.
∴ 0 > -8
(2) We have,
-1 … -15
Since, 1 is to the right of -15.
∴ -1 > -15
(3) We have,
5 … -5
Since, 5 is to the right of -5.
∴ 5 > -5
(4) We have,
11 … 15
Since, 11 is to the left of 15.
∴ 11 < 15
(5) We have,
0 … 6
Since, 0 is to the left of 6.
∴ 0 < 6
(6) We have,
-20 … 2
Since, 20 is to the left of 2.
∴ -20 < 2
Yes, I agree with Rohini. Some examples are as follow
(a) Every positive integer is larger than every negative integer. e.g. 5 > -2.
(b) Zero is less than every positive integer. e.g. 0 < 3.
(c) Zero is larger than every negative integer.
e.g. 0 > -4.
(d) Zero is neither a negative integer nor a positive integer, because 0 has neither + sign nor ‘-‘ sign.
(e) Farther a number from zero, on the right side, larger is its value, because on number line, every integer on the right from zero is greater than zero. e.g. 5 > 0.
(f) Farther a number from zero, on the left side, smaller is its value because on number line, every integer on the left from zero is smaller than zero. e.g. -8 < 0.
Question 1. Write opposites of the following:
(1) Increase in weight
(2) 30 km North
(3) 80 m East
(4) Loss of 700
(5) 100 m above sea level
Solution.
(1) Opposite of increase in weight is decrease in weight.
(2) Opposite of 30 km North is 30 km South.
(3) Opposite of 80 m East is 80 m West.
(4) Opposite of loss of 700 is profit of 700.
(5) Opposite of 100 m above sea level is 100 m below sea level.
Question 2. Represent the following numbers as Integers with appropriate signs.
(1) An aeroplane is flying at a height of two thousand metre above the ground.
(2) A submarine is moving at a depth, eight hundred metre below the sea level.
(3) A deposit of rupees two hundred.
(4) Withdrawal of rupees seven hundred.
Solution.
(1) An aeroplane is flying at a height of two thousand metre above the ground can be written as +2000 m because height above the ground is taken as positive.
(2) A submarine is moving at a depth of eight hundred metre below the sea level can be written as -800 m, because depth below the sea level is taken as negative.
(3) A deposit of rupees two hundred can be written as + 200, because deposit is represented with + sign.
(4) Withdrawal of rupees seven hundred can be written as-700, because withdrawal is represented with- sign.
Class 6 Maths Chapter 5 Solutions
Question 3. Represent the following numbers on a number line :
(1) +5
(2) -10
Solution. Draw a line and mark some points at equal distance on it. Mark a point as zero on it. Points to the right of zero are positive integers and are marked by +1, +2, +3 or simply by 1, 2, 3 etc. Points to the left of zero are negative integers and are marked by-1,-2,-3 etc.
(1) Representation of +5 To mark +5 on the number line, we move 5 points to the right of zero as shown in the figure.
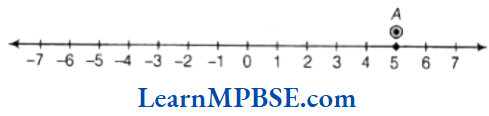
In the above figure, Point A represents +5.
(2) Representation of -10 To mark-10 on the number line, we move 10 points to the left of zero as shown in the figure.

In the above figure, Point B represents -10.
Question 4. Adjacent figure is a vertical number line, representing integers. Observe it and locate the following points.
(1) If Point D is +8, then which point is -8?
(2) Is Point G, a negative integer or a positive integer?
(3) Write integers for points B and E
(4) Which point marked on this number line has the least value?
(5) Arrange all the points in decreasing order of value?
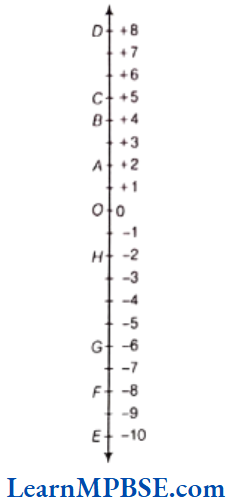
Solution. (1) Now, from the figure, it is clear that +8 is on Point D, then for getting -8, we should move below to 0.
After moving 8 steps below 0, we reach at point F. So, Point Frepresents – 8.
(2) We know that points lie above zero are positive F-8 integers and lie below zero are negative integers.
Here, we see that point G lies below zero.
So, G is a negative integer.
(3) On the given number line, point B lies above zero and point E lies below zero.
So, it is clear that point B is a positive integer and point E is a negative integer. Now, counting from 0, the distance of B is +4 units, because it is on right of zero and counting from 0, the distance of Eis-10 units because it is on left of zero.
∴ Integer B = +4 and integer E = -10
(4) Here, we see that the distance of point E is far from 0 and below from 0 and we know that on vertical number line below from 0 the value of integers are negative. Hence, the Point E has least value.
(5) We know that on a number line the number decreases as we move to left. Here, vertical number line is given to us, so the number decreases as we move to down. So, decreasing order of values of all points is given here.
Question 5. Following is the list of temperatures of five places in India on a particular day of the year.
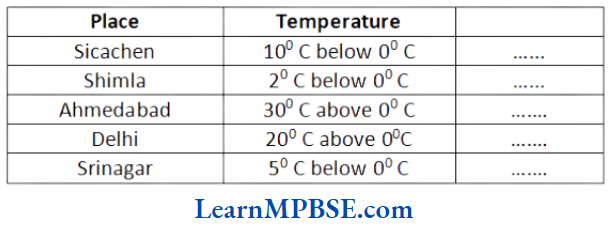
(1) Write the temperatures of these places in the form of integers in the blank column.
(2) Following is the number line representing the temperature in degree celsius.
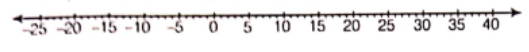
Plot the name of the city against its temperature.
(3) Which is the coolest place?
(4) Write the names of the places, where temperature are above 10°C.
Solution.
(1)
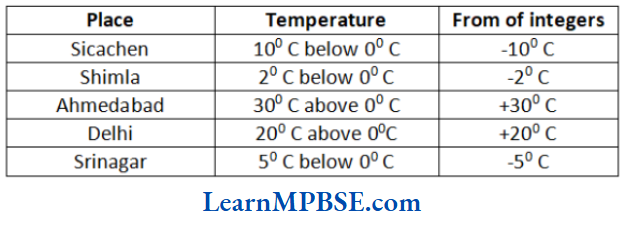
(2) The name of city against its temperature on the number line is given below
(3) After checking the temperature of all places, we can say that the Siachin (-10°) is the coolest place.
(4) Delhi (+20°C) and Ahmedabad (+30°C) are the places, where temperature is above 10°C.
Class 6 Maths Chapter 5 Solutions
Question 6. In each of the following pairs which number is to the right of the other on the number line?
(1) 2, 9
(2)-3, -8
Solution
(1)
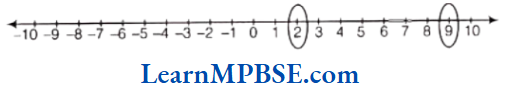
Here, 2 and 9 both are on the right of zero but 9 is farther from zero in comparison of 2. So, number 9 is right of number 2.
(2)
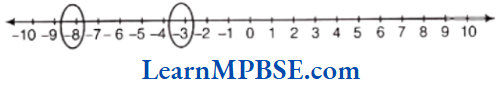
Here, -3 and -8 both are on the left of zero but-3 is near to the zero in comparison of -8. So, -3 is to the right of -8.
Question 7. Write all the integers between the given pairs (write them in the increasing order).
(1) 0 and -7
(2)-4 and 4
Solution. (1) Integers 0 and -7 are on the number line are shown as below:
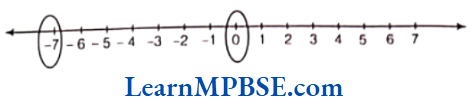
From the above figure, it is clear that integers between 0 and -7 are-1, -2, -3, -4, -5 and -6.
Now, increasing order of these integers is -6 < -5 < -4 < -3 < -2 < -1 because we are moving to the right from -7 to 0.
(2) Integers-4 and 4 on number line are shown as below

From the above figure, it is clear that integers between -4 and 4 are -3, -2, -1, 0, 1, 2 and 3.
Now, increasing order of these integers is -3 < -2 < -1 < 0 < 1 < 2 < 3 because we are moving to the right from -4 to 4.
Question 8. Write four negative integers greater than -20.
Solution. When we move on the number line to the right, then the value of integer increases.
So, from the above figure, we get four negative integers greater than -20 are -19,-18, -17 and -16.
Class 6 Maths Chapter 5 Solutions
Question 9. For the following statements, write True (T) or False (F). If the statement is false, correct the statement.
(1) -8 is to the right of -10 on a number line.
(2) -100 is to the right of -50 on a number line.
(3) Smallest negative integer is -1.
(4) -26 is greater than -25.
Solution.
(1) True, because on the number line going to the right, value of integer is increases. Here, -8 is greater to -10, so-8 is to the right of-10 on number line.
(2) False, because on the number line going to the left, value of integer is decreases. Here, -100 is less than -50. So, -100 is to the left of -50 on number line.
(3) False, because on the number line -1 is situated on the right of all negative integers. So, it is the greatest negative integer.
(4) False, because on the number line -25 is on the right of-26. So.-25 is greater than -26.
Question 10. Draw a number line and answer the following
(1) Which number will we reach, if we move 4 numbers to the right of -2?
(2) Which number will we reach, if we move 5 numbers to the left of 1?
(3) If we are at -8 on the number line, in which direction should we move to reach -13?
(4) If we are at -6 on the number line, in which direction should we move to reach -1?
Solution. (1)
On the number line, starting from -2 and moving 4 points towards right (each step being equal to 1 unit), we will reach at 2.
(2)

On the number line, starting from 1 and moving 5 points towards left (each step being equal to 1 unit), we will reach at-4.
(3) Here, -8 – 13. So, -13 is on the left of -8. Hence, if we are at -8 on the number line, then move to the left from-8 to reach at -13.

(4)

Here, -1 – 6. So, -1 is on the right of -6. Hence, if we are at -6 on the number line, then move to the right from -6 to reach at -1.
Question 11. Find the answers of the following additions:
(1) (-11) + (-12)
(2) (+10) + (+4)
(3) (-32) + (-25)
(4) (+23) + (+40)
Solution. (1) (-11) + (-12) = (11+12) = -23
(2) (+10) + (+4) = +(10 +4) = +14
(3) (-32) + (-25) = (32+25) = -57
(4) (+23) + (+40) + (23+40) = +63
Question 12. Find the solution of the following:
(1) (-7) + (+8)
(2) (-9) + (+13)
(3) (+7) + (-10)
(4) (+12) + (-7)
Solution.
(1) (-7) + (+8) = (-7) + (+7) + (+1) [∴ 7 + 1 = 8]
= 0 + (+1) = +1 [∴ (-7) + (+7) = 0]
(2) (-9) + (+13) = (-9) + (+9) + (+4) [∴ 9 + 4 = 13]
= 0 + (+4) = +4 [∴ (-9) + (+9) = 0]
(3) (+7) + (-10) = (+7) + (-7) + (-3) [∴ -10 = – 7 – 3]
= 0 + (-3) = -3 [∴ (+7) + (-7) = 0]
(4) (+12) + (-7) = (+5) + (+7) + (-7) [∴ 12 = 5 + 7]
= (+5) + 0 = +5 [∴ (+7) + (-7) = 0]
Class 6 Maths Chapter 5 Solutions
Question 13. Find the solution of the following additions using a number line:
(1) (-2) + 6
(2) (-6) + 2
Make two such questions and solve them using the number line.
Solution. (1)
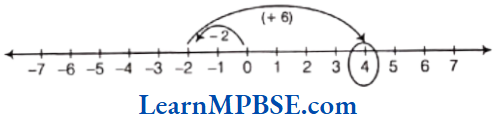
Firstly, draw a number line. Here, -2 is a negative integer and 6 is a positive integer. Then, we first move 2 steps to the left of 0 reaching at -2, then we move 6 steps to the right of-2 and reach at 4.
Thus, (-2) + 6 + 4.
(2)
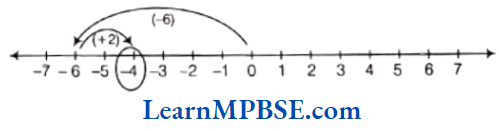
Firstly, draw a number line. Here, -6 is a negative integer and 2 is a positive integer. Then, we first move 6 steps to the left of 0 reaching at -6, then we move 2 steps to the right of-6 and reach at-4.
Thus, (-6) + 2 = -4.
Two such questions are as follow
(a) (-3) + 5
(b) 5 + (-1)
(a) We have, (-3) + 5
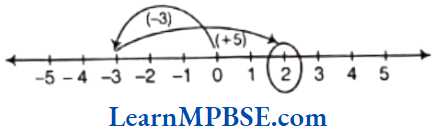
Here, we first move 3 steps to the left of 0 reaching at-3, then we move 5 steps to the right of-3 and reach at 2. Thus, (-3)+5=+2.
(b) We have, 5 + (-1)

Here, we first move 5 steps to the right of zero (0) reaching at 5, then we move 1 step to the left of 5 and reach at 4.
Thus, 5 + (-1) = 4.
Question 1. Using the number line write the Integer which is
(1) 3 more than 5
(2) 5 more than -5
(3) 6 less than 2
(4) 3 less than -2
Solution. (1) To get the integer 3 more than 5, we start from 5 and move 3 steps to the right of 5 and reach at 8, as shown in the figure given below

Hence, 3 more than 5 is 8.
(2) To get the integer 5 more than -5, we start from -5 and move 5 steps to the right of -5 and reach at 0, as shown in the figure given below
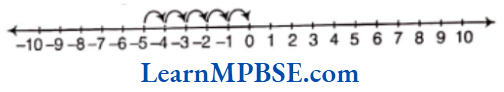
Hence, 5 more than -5 is 0.
(3) To get the integer 6 less than 2, we start from 2 and move 6 steps to the left of 2 and reach at-4, as shown in the figure given below

Hence, 6 less than 2 is -4.
(4) To get the integer 3 less than -2, we start from -2 and moves 3 steps to the left of-2 and reach at-5, as shown in the figure given below
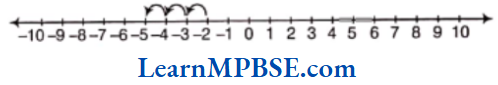
Hence, 3 less than -2 is -5.
Question 2. Use number line and add the following integers :
(1)9 + (-6)
(2) 5 + (-11)
Solution. (1) We have, 9 + (-6)
Firstly, draw a number line, then we move 9 steps to the right of 0 and reach at 9. Now, we move 6 steps to the left of 9 [-6 is a negative integer] and reach at 3, as shown in the above figure. Hence, 9 + (-6) = 3
(2) We have, 5 + (-11)

Firstly, draw the number line, then we move 5 steps to the right of 0 and reach at 5. Now, we move 11 steps to the left of 5 [-11 is a negative integer] and reach at -6, as shown in the above figure. Hence, 5 + (-11) = -6.
Class 6 Maths Chapter 5 Solutions
Question 3. Find the sum:
(1) (-7) + (-9) + 4 + 16
(2) (37) + (-2) + (-65) + (-8)
Solution.
(1) We have, (-7) + (-9) + 4 + 16 = -(7 + 9) + 4 + 16
= -16 + 20 = -16 + (+16) + (+4) [∴ 20 = 16 + 4]
= 0 + (+4) = (+4) [∴ (-16) + (+16) = 0]
(2) We have, (37) + (-2) + (-65) + (-8)
= 37 – (2 + 65 + 8) = 37 – 75 = 37 – 37 – 38 [∴ 75 = 37 + 38 ⇒ -75 = -37 – 38]
= 0 – 38 = -38 [∴ -37 + 37 = 0]
Question 1. Find
(1) 35 – (20)
(2) 72 – (90)
(3) (-15) – (-18)
(4) (-20) – (13)
Solution.
(1) We have, 35 – (20) = 35 + Additive inverse of 20
= 35 + (-20)
= 15 + 20 + (-20) [∴35 = 20 + 15]
= 15 + 0 = 15 [∴ 20 + (-20) = 0]
(2) We have, 72 – 90 = 72 + Additive inverse of 90
= 72 + (-90) = 72 + (-72) + (-18)
[∴ 90 = 72 + 18 ⇒ -90 = -72 + (-18)]
= 0 + (-18) = -18 [∴ 72 + (-72) = 0]
(3) We have, (-15) – (-18) = -15 + Additive inverse of -18
= -15 + 18
= (-15) + (15) + (3) [18 = 15 + 3]
= 0 + 3 = 3 [∴ (-15) + (15) = 0]
(4) We have, (-20) – (13) = (-20) + Additive inverse of 13
= (-20) + (-13) = (20+13)
= -33
MP Board Class 6 Chapter 5 Maths
Question 2. Fill in the blanks with >, < or = Sign.
(1) (-3) + (-6) ______ (-3) – (-6)
(2) (-21) – (-10) ______ (-31) + (-11)
(3) 45 – (-11) ______ 57 + (-4)
Solution. (1) We have, (-3) + (-6) ______ (-3) – (-6)
LHS = (-3) + (-6) = -9
RHS = (-3) – (-6) = (-3) + Additive inverse of (-6)
= -3 + 6 = 3
Since, -9 is a negative integer and 3 is a positive integer.
∴ -9 < 3
(2) We have, (-21) – (-10) ______ (-31) + (-11)
LHS = (-21) – (-10) = -21 + Additive inverse of -10
= -21 + 10 = -11
RHS = (-31) + (-11) = -42
Here, both are negative integers but -42 is to the left of -11.
∴ -11 > -42
(3) We have, 45 – (-11) ______ 57 + (-4)
LHS = 45 – (-11) = 45 + 11 [∴ additive inverse of -11 is 11]
= 56
Here, both are positive integers but 56 is to the right of 53.
∴ 56 > 53
Question 3. Fill in the blanks.
(1) (-8) + ______ = 0
(2) 13 + ______ = 0
(3) 12 + (-12) = ______
(4) (-4) + ______ = -12
(5) ______ – 15 = -10
Solution. (1) We have, (-8) + ______ = 0
(-8) + 8 = 0 [∴ additive inverse of -8 is 8]
(2) We have, 13 + ______ = 0
13 + (-13) = 0 [∴ additive inverse of -13 is 13]
(3) We have, 12 + (-12) = 12 + (-12) = 0
[∴ 12 and -12 are additive inverse of each other]
(4) We have, (-4) + ______ = -12
Here, the sum of two integers is not zero, so here we cannot write additive inverse of -4.
-4 + ______ = -12
⇒ -4 + ______ = -(4+8)
⇒ -4 + ______ = (-4) + (-8)
So, on comparing both sides, we get -8 to fill the blank space.
Thus, (-4) + (-8) = -12
(5) We have, ______ – 15 = -10
⇒ ______ – (10+5) = -10
⇒ ______ -10 – 5 = -10
To get RHS = -10, we need to add additive inverse of -5 i.e. 5 in RHS.
so, + 5 – 10 – 5 = -10
Hence, +5 – 15 = -10
MP Board Class 6 Chapter 5 Maths
Question 4. Find
(1) (-7) – 8 (-25)
(2) (-13) + 32 – 8 – 1
(3) (-7) + (-8) + (-90)
(4) 50 – (-40) – (-2)
Solution. (-7) – 8 – (-25) = (-7) + (-8) + 25
[∴ additive inverse of -25 is 25]
= -15 + 25
= -15 + 15 + 10 [∴ 25 = 15 + 10]
= 0 + 10 = 10 [∴ -15 + 15 = 0]
(2) (-13) + 32 – 8 – 1 = (-13) + 32 – 9
= -13 + 32 + Additive inverse of 9
= (-13) + 32 + (-9) = -13 – 9 + 32
= -22 + 32 [∴ 32 = 22 + 10]
= -22 + 22 + 10 = 0 + 10 = 10 [∴ -22 + 22 = 0]
(3) (-7) + (-8) + (-90) = -15 + (-90) = -105
(4) 50 – (-40) – (-2)
= 50 + Additive inverse of (-40) + Additive of (-2)
= 50 + 40 + 2 = 92
Question 1. The predecessor of the integer -1 is
Answer. 3. -2
Question 2. The successor of the predecessor of -20 is
Answer. 1. -20
Question 3. An integer with positive sign (+) is always greater than
Answer. 4. 0
MP Board Class 6 Chapter 5 Maths
Question 4. The statement ‘When an integer is added to itself, the sum is greater than the integer’ is
Answer. 4. true for non-negative integers
Question 5. Every integer less than 0 has the sign
Answer. 4. None of these
Question 6. The integer 5 units to the right of 0 on the number line is
Answer. 1. +5
Question 7. Number of integers lying between -2 and 2 is
Answer. 1. 3
Question 8. Number of whole numbers lying between -7 and 6 is
Answer. 4. 6
Question 9. The least integer lying between -10 and -16 is
Answer. 3. -15
Question 10. Amulya and Amar visited two places A and B, respectively in Kashmir and recorded the minimum temperatures on a particular day as -4°C at A and -1°C at B. Which of the following statement is true?
A is cooler than B.
B is cooler than A.
There is a difference of 2°C in the temperature.
The temperature at A is 4°C higher than that at B.
Answer. 1. A is cooler than B.
Question 11. When a negative integer is subtracted from another negative integer, the sign of the result
Answer. 4. depends on the numerical value of the integers.
Question 12. Which of the following shows the maximum rise in temperature?
Answer. 2. -4°C to 8°C
Question 13. The additive inverse of a negative integer
Answer. 2. is always positive
Question 14. On the number line, the integer 47 is located
Answer. 3. to the right of 41
Question 15. In which of the following pair of integers, the first integer is not on the left of the other integer on the number line?
Answer. 1. (-3, -4)
Question 1. Assertion (A) The preceding number of the number 1 is -1.
Reason (R) Preceding number is the number which comes before a number.
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (d) (A) is false but (R) is true.
Question 2. Assertion (A) Sum of two positive number is always negative.
Reason (R) The addition is taking two or more numbers and adding them.
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (d) (A) is false but (R) is true.
Question 1. On the number line, -15 is to the ….. of zero.
Answer. Left
Question 2. The number of integers lying between -5 and 5 is …..
Answer. 9
Question 3. ….. – 3040 = -7910
Answer. -4870
Question 4. The additive inverse of -1 is ……
Answer. 1
Question 5. The additive inverse of 0 is ……
Answer. 0
Question 1. Every positive integer is greater than every negative integer.
Answer. True
Question 2. The sum of any two negative integers is always smaller than both the integers.
Answer. True
Question 3. The sum of any two negative integers is always greater than both the integers
Answer. False
MP Board Class 6 Chapter 5 Maths
Question 4. The sum of any two positive integers is greater than both the integers.
Answer. True
Question 5. The difference between an integer and its additive inverse is always even.
Answer. True
Question 1. Match the Column A with Column B.

Solution. (1) → (b), (2) → (e), (3) → (d), (4) → (a), (5) → (b)
Question 1. The leavel of the surface of oceans or seas is called the sea level. Land and hills are raised and are at some height from the sea level.
City A is 10 m below sea level, city B is 28 m below sea level and city C is 14 m above sea level.
(1) Which of the three cities is at the highest elevation from the sea level?
(2) Aditi uses the following rules to represent the elevation of different locations.
The sea level is considered to be zero elevation.
Below sea level is shown using the ‘-‘ sign.
Above sea level is shown using the ‘+’ sign.
e.g. the elevation of City A is shown as -10. what would be the elevation of city B?
(3) The elevation of city D is 1 m above the elevation of city B. What is the elevation of city D?
(4) A submarine at the depth of 45 m rises to 20 m below sea level. What is the depth of the submarine after rising?
(5) A diver at the depth of 60 m spotted a seaweed 23 m below him. What is the depth of the seaweed from the sea level?
(6) 8 – 8 = 0
Which of the following is true for the numbers shown above?
(a) -8 is a multiplicative inverse of 8.
(b) -8 is a multiplicative identity of 8.
(c) -8 is the additive identity of 8.
(d) -8 is the additive inverse of 8.
Solution. (1) Let’s consider the sea level be 0.
City A is 10 m below sea level is -10.
City B is 28 m below sea level is – 28.
City C is 14 m above sea level is +14.
Hence, City C is at the highest elevation from the sea level.
(2)-28 is the elevation for City B.
(3) City B is 28 m below sea level is – 28.
Add 1 m to the elevation of city B i.e.-28
– 28 m +1 m = -27m
Hence, – 27 m is the elevation for City D.
(4) Given, a submarine at the depth of 45 m rises to 20 m below sea level.
Depth of a submarine at 45 m is + 45.
20 m below sea level is – 20.
Add the depth rises below sea level
+45 m + (-20 m) = +25 m
Hence, the depth of the submarine after rising is 25 m.
(5) Given, a diver at the depth of 60 m spotted a seaweed 23 m below him.
∴ 60 + 23 = 83
Hence, 83 m is the depth of the seaweed from the sea level.
(6) (d) Given, 8 – 8 = 0
⇒ 8 + (-8) = 0
Hence, -8 is the additive inverse of 8.
MP Board Class 6 Chapter 5 Maths
Question 2. The figure shows the position of the satellite above earth.
PR is the line joining the satellite and the centre of earth. P is the position of the satellite, Q is a point on the surface of earth and R is the centre of earth.

The distance between P and Q is 1300 km and the distance between the centre of earth and the satellite is 7671 km.
(1) What is the distance between the points Q and R?
(a) 1300 km
(b) 6371 km
(c) 7671 km
(d) 8971 km
(2) Shobhit marks Q as zero and the direction from Q to P is positive. What is the distance of R with reference to P?
Solution. (1) (b) Distance between Q and R
= Distance between P and R – Distance between P and Q
⇒ QR = PR – PQ
⇒ QR = 7671 – 1300 = 6371 km
(2) Shobhit marks Q as zero and the direction from Q to P is positive.
Thus, distance from Q to P is +1300 km.
The distance from P to R is 7671 km.
Q is zero and below Q are negative values.
Hence,-7671 km is the distance of R with reference to P.
Question 3. The picture below shows the control panel of a lift in a mall.

MP Board Class 6 Chapter 5 Maths
O is the ground floor. The two-wheeler parking area -1 is at basement level 1 and the car parking area -2 is at basement level 2.
(1) Ahmed enters the lift at floor 3 and exits at the two-wheeler parking area. How many floors did the lift go down?
(2) Meera entered the lift at the car parking floor. She pressed ‘6’ on the control panel of the lift. How many floors up does she want to go?
Solution. (1) Ahmed enters the lift at floor 3 and exists at the two-wheeler parking area.
Ahmed travels in lift from
3 → 2,2 → 1,1 → 0,0 → 1
Hence, 4 floors lift go down.
(2) Meera entered the lift at the car parking floor. She pressed 6 on the control panel of the lift car parking floor is -2.
Meera starts from -2.
-2 → -1,-1 → -0, 0 → -1, 1 → 2, 2 → -3, 3 → -4, 4 → -5,5 → -6
Hence, 8 floors lift goes up.
Question 1. Write the following numbers with appropriate sign
(1) 100 m below sea level.
(2) 15° C below 0°C temperature.
Solution. (1) 100 m below sea level means -100 m.
(2) 15°C below 0°C temperature means- 15°C.
Question 2. Write the integer which is 2 less than its additive inverse.
Solution. 1 because 1 – 2 = -1.
Question 3. Write additive inverse of -121.
Solution. Additive inverse of -121 is + 121.
Question 4. Find the value of 10+(-5).
Solution. Here, 10 + (-5) = 10 – 5 = 5
Question 5. Write two distinct integers whose sum is equal to one of the integers.
Solution. Any two integers with one of them as 0 i.e. 4 and 0.
Question 1. Represent the following using integers with proper sign
(1) 35 km above sea level
(2) A loss of ₹ 400
Solution. Given, statements can be represented using integer
(1) +35 (2)-400
Question 2. How many integers are there between -8 and -2?
Solution. The integers -7,-6, -5,-4 and -3 lie between -8 and -2. So, there are 5 integers between -8 and -2.
MP Board Class 6 Chapter 5 Maths
Question 3. Find the sum of the pairs of integers.
(1) -6, -5
(2) +4, -3
Solution. (1)-6, -5 both have negative signs.
So, -6 + (-5) = -(6+5) = -11
(2) +4 and -3 have opposite sign.
So, 4 + (-3) = 4 – 3 = 1
Question 4. Find the sum of -3 and -4 using the number line.
Solution. To add -3 and -4. Mark-3 on the number line. Move 4 steps to left of-3, we reach at -7.

∴ -3 + (-4) = -7
Question 5. Write two integers whose sum is less than both the integers.
Solution. For the required integers, we can take any two negative integers.
So, the required integers can be -5, and -7.
Question 6. Write four pairs of integers which are at the same distance from 2 on the number line?
Solution. We draw a number line.
Now, four pairs are (0, 4), (-1,5), (- 3,7) and (1, 3).
MP Board Class 6 Chapter 5 Maths
Question 7. Write the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 in this order and insert ‘+’ or ‘-‘ between them to get the result.
(1) 7
(2) -5
Solution. (1) To get the sum =7
0 – 1 + 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9
= 2 + 3 + 5 + 7 + 9 – (1 + 4 + 6 + 8) = 26 – 19 = 7
(2) To get the sum = -5
0 – 1 – 2 + 3 + 4 – 5 + 6 + 7 – 8 – 9
= 3 + 4 + 6 + 7 – (1 + 2 + 5 + 8 + 9)
= 20 – 25 = -5
Question 8. The sum of two integers is 35. If one of the integer is -12, find the other integer.
Solution. Given, sum is 35. The other integer is obtained by subtracting-12 from 35. So, the required integer
= 35 – (-12) = 35 + 12 = 47.
Question 9. Subtract
(1) 5 from -6
(2) -3 from -6
Solution. (1) The additive inverse of 5 is -5.
So, -6 – 5 – 6 + (-5) = -(6+5) = -11
(2) The additive inverse of -3 is +3.
So, -6 – (-3) = -6 + 3 = -3
MP Board Class 6 Chapter 5 Maths
Question 10. Subtract using the number line.
(1) 3 form -2
(2) -5 from -3
Solution. (1) Move 3 steps from -2 on the left, we reach at -5.
So, -2 – 3 = -5
(2) Move 5 steps from -3 on the right, we reach at 2.

So, -3 – (-5) = -3 + 5 = 2.
Question 1. Complete each of the following
(1) 30 + (-50) + (-20)
(2) 40 + (-10) + (-15)
(3) 45 – (-5) + 10
(4) 60 – 10 + 5 – (-5)
(5) 16 + (-13) + (-10)
(6) 0 + 5 – (-6) + (-7)
Solution. According to the rules of addition and subtraction of integers.
(1) 30 + (-50) + (-20) = 30 – (50+20) = 30 – 70 = -40
(2) 40 + (-10) + (-15) = 40 – (10+15) = 40 – 25 = 15
(3) 45 – (-5) + 10 = 45 + 5 + 10 = 60
(4) 60 – 10 + 5 – (-5) = 60 + 5 + 5 – 10 = 70 – 10 = 60
(5) 16 + (-13) + (-10) = 16 – (13+10) = 16 – 23 = -7
(6) 0 + 5 – (-6) + (-7) = 0 + 5 + 6 – 7 ⇒ 11 – 7 = 4
MP Board Class 6 Chapter 5 Maths
Question 2. If we denote the height of a place above sea level by a positive integer and depth below the sea level by a negative integer, write the following using integers with the appropriate signs:
(1) 200 m above sea level
(2) 100 m below sea level
(3) 10 m above sea level
(4) Sea level
Solution. (1) 200 m above sea level = +200 m
(2) 100 m below sea level = -100 m
(3) 10 m above sea level = +10 m
(4) Sea level = 0
Question 3. Write six distinct integers whose sum is 7.
Solution. Let the six integers be 1, 2, -2, 3, -3 and 6.
Now, sum of the above integers
= 1 + 2 + (-2) + 3 + (-3) + 6
We can arrange the numbers, so that the positive integers and the negative integers are grouped together.
We have, 1 + 2 + 3 + 6 + (-2) + (-3) = 12 – 2 – 3
= 12 – 5 = 7
Hence, the required integers are 1, 2, -2, 3, -3 and 6.
MP Board Class 6 Chapter 5 Maths
Question 4. Write the integer which is 4 more than its additive inverse.
Solution. Firstly, draw a number line.
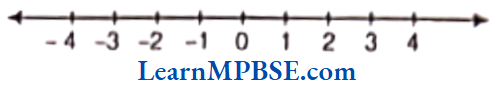
Let +1 be an integer and its additive inverse is -1. From the number line, we see that +1 is 2 more than its additive inverse. So, we reject this integer.
Again, let +2 be an integer, its additive inverse is -2.
From the number line, we see that +2 is 4 more than its additive inverse.
Hence, the required integer is 2.
Question 5. Temperature of a place at 12:00 noon was +5°C. Temperature increased by 3°C in first hour and decreased by 1°C in the second hour. What was the temperature at 2:00 pm?
Solution. Given, initial temperature at 12:00 noon was +5°C.
Since, the temperature increased by 3°C in first hour.
∴ Temperature at 1:00 pm = 5°C + 3°C = 8°C
Also, the temperature decreased by 1°C in the second hour.
∴ Temperature at 2:00 pm = 8°C – 1°C = 7°C
Hence, the temperature at 2:00 pm is 7°C.
Line Segment
A line segment is a fixed portion of a line. This make it possible to measure a line segment. The distance between the end points of a line segment is called its length. We use the length to compare line segments.
To compare any two line segments, a relationship between their lengths is established.
1. Comparison by Observation
We can compare the line segments by just looking at them.
e.g.
Here, \(\overline{A B}>\overline{P Q}\)
Note it You cannot always be sure about your usual judgement.
2. Comparison by Tracing
In this method, we can compare the line segment using tracing paper. This method depends upon the accuracy in tracing the line segment. If you want to compare the length of a line segment with another line segment, you have to trace another line segment.
e.g.
![]()
To compare \(\overline{A B}\) and \(\overline{C D}\), trace CD and place the traced segment on \(\overline{A B}\). As a result, we get
\(\overline{A B}>\overline{C D}\)3. Comparison using Ruler and Divider Ruler and Divider
A graduated ruler and the divider are useful to compare lengths of line segments. One side of the ruler is divided into 15 parts.
Each of these 15 parts is of length 1 cm.. Each centimetre is divided into 10 subparts. Each subpart of the division of 1 cm is 10 mm.
MP Board Class 6 Maths Solutions
Read and Learn More MP Board Class 6 Maths Solutions
1 cm = 10 mm
Note it
1 mm = 0.1 cm, 2 mm = 0.2 cm
3.6 cm = 3 cm and 6 mm.
Use of Ruler to Measure Length
For comparison, place the 0 mark of the ruler at A. Read the mark against B. This gives the length of AB.
Suppose, the length of AB is 6 cm, we may write Length AB = 6 cm or more simply as \(\overline{A B}\) = 6 cm.
There are chances of errors even in this procedure.
Positioning Error
To get correct measure, the eye should be correctly positioned, just vertically above the mark. Otherwise, errors can happen due to angular viewing.
We can avoid this problem using divider.
Let us use the divider to measure length.
MP Board Class 6 Maths Solutions
Use of Divider to Measure Length
Open the divider. Place the end point of one of its arms at A and the end point of the second arm at B. Taking care that opening of the divider is not disturbed, lift the divider and place it on the ruler. Ensure that one end point is at the zero mark of the ruler. Now, read the mark against the other end point.
Angle
An angle is a figure formed by two rays with the same initial point. It is measured in degrees (°). The common initial point is also known as the vertex of the angle.
Revolution
Turning by a full rotation or a complete 360° angle in the same direction is called a revolution.

e.g. When hour or minute hand of a
clock moves from 12 to 12, it makes one revolution.
We can see such revolutions on clock-faces.
When the hand of a clock moves from one position to another, it turns through an angle.

When the hand of a clock starts at 12 and reaches 3, it has reached quarter past and has made \(\frac{1}{4}\) of a revolution or 1 right angle which is equal to 90°.

When the hand of a clock starts at 12 and reaches 6 1 (half past), the hand has made \(\frac{1}{2}\) of a revolution or 1 straight angle or 2 right angles which equals to 180°.

When the hand of a clock starts at 12 and reaches 9 (quarter to), the hand has made three quarter or \(\frac{3}{4}\) of a revolution or 3 right angles which equals to 270°.
When the hand of a clock starts at 12 and reaches 12 again, it has moved exactly one round of the clock i.e. it has made one complete revolution and the angle for one revolution and the angle for one revolution is called complete angle or 2 straight angles or 4 right angles which equals t 360°.

MP Board Class 6 Maths Solutions
Example 1. What fraction of a clockwise revolution does the hour hand of a clock turn through when it goes from
(1) 8 to 11
(2) 2 to 5
Solution. Moving of hour hand from 8 to 11 on clock is given in the figure.
Hence, from 8 to 11, hour hand turns through \(\frac{1}{4}\) of a revolution, clockwise.

(2) Moving of hour hand from 2 to 5 on clock is given in the figure. Hence, from 2 to 5, hour hand turns through \(\frac{1}{4}\) of a revolution, clockwise.

Example 2. Where will the hand of a clock stop, if it
(1) starts at 1 and makes \(\frac{1}{2}\) of a revolution, clockwise?
(2) starts at 4 and makes \(\frac{3}{4}\) of a revolution, clockwise?
(3) starts at 8 and makes \(\frac{1}{4}\) of a revolution, clockwise?
Solution. (1) If the hand of a clock starts at 1 and makes of a \(\frac{1}{2}\) revolution clockwise, it stops at 7.
(2) If the hand of a clock starts at 4 and makes \(\frac{3}{4}\) of a revolution, clockwise, it stops at 1.
(3) If hand of a clock starts at 8 and makes \(\frac{1}{4}\) of a revolution, clockwise, it stops at 11.
Class 6 Maths Chapter 5 Solutions
Example 3. Draw a rough diagram of the clock for each of the following
(1) One-fourth revolution
(2) Half revolution
(3) Three-fourth revolution
Solution.
Example 4. How many right angles will hour hand of clock make in half revolution?
Solution. We know that 1 revolution = 4 right angles
Now, dividing by 2 on both sides, we get
\(\frac{1}{2}\) revolution = \(\frac{4}{2}\)right angles
∴ \(\frac{1}{2}\) revolution = 2 right angles
Example 5. Which direction will you face, if you start facing
(1) West and makes \(\frac{1}{2}\) of a revolution, clockwise?
(2) East and make \(\frac{3}{4}\) of revolution, anti-clockwise?
Solution. (1) If we start facing West and \(\frac{1}{2}\) make of a revolution clockwise i.e. two right angles, we will face East.
(2) If we start facing East and make \(\frac{3}{4}\) of revolution anti-clockwise i.e. three right angles, we will face south.
Example 6. Write the number of right angles turned through, by the hour hand of clock when it goes from
(1) 4 to 7
(2) 10 to 4
Solution.
(1) Here, the hour hand moves from 4 to 7. It starts from 4 and covers 5, 6 and 7. So, hour hand turned by one right angle.
(2) Here, the hour hand moves from 10 to 4. It starts from 10 and covers 11, 12, 1, 2, 3 and 4. So, hour hand turned by two right angles.
Class 6 Maths Chapter 5 Solutions
Example 7. How many right angles do you make, if you start facing
(1) East and turn clockwise to South?
(2) North and turn anti-clockwise to South?
(3) South and turn to South?
Solution.
(1) If we start turning clockwise from East to South, we make one right angle.
(2) If we start turning anti-clockwise from North to South we make two right angles.
(3) If we start turning clockwise or anti-clockwise from South to South, we make four right angles.
Example 8. Where will the hour hand of a clock stop, if it starts
(1) from 7 and turns through 1 right angle?
(2) from 9 and turns through 2 right angles?
(3) from 11 and turns through 3 right angles?
Solution.
(1) It is clear from the figure that the hour hand starts from 7 and turns through 1 right angle. Hence, it will reach at 10.

(2) It is clear from the figure that the hour hand starts from 9 and turns through 2 right angles. Hence, it will be at 3.

(3) It is clear from the figure that the hour hand starts from 11 and turns through 3 right angles. Hence, it will be at 8.

Example 9. If the hands of clock make one right angle. Then, show it by two different figure.
Solution. Two different figure are

Class 6 Maths Chapter 5 Solutions
Example 10. If a clock hand makes three complete revolution, then how many right angles will be formed?
Solution. We know that there are four right angles in a complete revolution. Therefore, if a clock hand makes three revolution, then the number of right angles
= 3 x 4
= 12 right angles
Example 11. Find the number of straight angles turned by the hour hand of a clock when it goes from 3 to 9.
Solution. When hour hand goes from 3 to 9, it makes one straight angle.

Example 12. Where will the hour hand of a clock stop if it starts
(1) from 6 and turns through 2 straight angles.
(2) from 9 and turns through 1 straight angle.
Solution. (1) It is clear from the figure that the hour hand starts from 6 and turns through 2 straight angles. Hence, it will be reach at 6 because 2 straight angles is equal to 4 right angles.

(2) It is clear from the figure that the hour hand starts from 9 and turns through 1 straight angle. Hence, it will reach at 3 because 1 straight angle is equal to 2 right angles.

Acute Angle
An angle smaller than a right angle is called an acute angle or less than \(\frac{1}{4}\) of a revolution.
e.g. When hour hand moves from 12 to 2, it makes an acute angle.

Class 6 Maths Chapter 5 Solutions
Example 1. How does the angle made by the hour hand of the clock look like when it moves from 6 to 8. Is the angle moved more than 1 right angle?
Solution. It looks like an acute angle.
We know that hour hand of a clock makes a right angle when it covers \(\frac{1}{4}\) of the revolution.

(∵ it covers 7, 8 and 9). Here, hour hand moves from 6 to 8 (covers only two numbers 7 and 8). So, that angle moved by hour hand is less than 1 right angle.
Obtuse Angle
An angle larger than a right angle but less than straight angle is called an obtuse angle.

e.g. When hour hand moves from 12 to 4, it makes an obtuse angle.
Example 2. The hour hand of a clock moves from 3 to 7. Is the revolution of the hour hand more than 1 right angle?
Solution. Yes, it is clear from the figure that hour hand makes one right angle from 3 to 6. So, revolution of the hour hand is more than 1 right angle. It looks like an obtuse angle.

Class 6 Maths Chapter 5 Solutions
Example 3. If a boy facing East and makes \(\frac{1}{4}\) revolution clockwise. Further makes \(\frac{1}{6}\)revolution clockwise. Then, name the angle that he turned totally?
Solution. When boy makes \(\frac{1}{4}\) revolution clockwise.
He makes a right angle. Then, he further makes revolution \(\frac{1}{6}\) which is greater than right angle and smaller than straight angle. Therefore, the angle he made is obtuse angle.
Reflex Angle
An angle larger than the straight angle but less than complete angle is called reflex angle.
e.g. When hour hand moves from 12 to 7, it makes a reflex angle.
Understanding Elementary Shapes Class 6
Example 4. The hour hand of a clock moves from 3 to 10. Is the revolution of the hour hand more than 2 right angle?
Solution. Yes, it is clear from the figure that hour hand makes 2 right angles from 3 to 9. So, the revolution of the hour hand is more than 2 right angle. It look like a reflex angle.
One complete revolution is divided into 360 equal parts. Each part is of one degree (i.e.1°) and we can write one complete revolution as 360° to say ‘three hundred sixty degrees.
Thus, in a clock, 12 divisions = 360°.
To find the measure of an angle, we use an instrument named as protractor.
The Protractor
You can find a protractor in your ‘instrument box’. The curved edge of protractor is divided into 180 equal parts. Each part is equal to one degree.

The markings start from 0° on the right side and ends with 180° on the left side and vice-versa.
Steps of Measuring an Angle
Suppose you want to measure an ZABC, follow the steps given below.
Step 1. Place the protractor, so that the mid-point (M in the figure) of its straight edge lies on the vertex B of the ∠ABC
Step 2. Adjust the protractor, so that ray BC is along the straight-edge of the protractor.
Step 3. There are two ‘scales’ on the protractor, read that scale which has the 0° mark coinciding with the straight-edge (i.e. with ray BC).
Step 4. The mark shown by ray BA on the curved edge gives the degree measure of the angle.
We write m ∠ABC = 40° or simply ∠ABC = 40°.
Understanding Elementary Shapes Class 6
Example 1. Measure the angles given below using the protractor and write down the measure.
Solution. On measuring the given angles using protractor, we find that
(1) The measure of the given angle is 20°.
(2) The measure of the given angle is 110°.
(3) The measure of the given angle is 45°.
(4) The measure of the given angle is 90°.
(5) The measure of the given angle is 135°.
Example 2. Compare the given angles by their measurement.
Solution. The measurement of ∠P = 30°
The measurement of ∠Q = 90°,
Hence, ∠Q > ∠P
Example 3. Write down the measure of
(1) some acute angles
(2) some obtuse angles
(give atleast two examples of each)
Solution. We know that the measure of an acute angle is always less than 90°. So, 89°,77°,75°, 60°, 40° all are acute angles.
Also, we know that the measure of an obtuse angle is always greater than 90°. So, 95°, 122°, 111° all are obtuse angles.
Example 4. Which angle has a larger measure?
First estimate and then measure ∠A and ∠B
Solution. Observing the given angles, we find that ∠A > ∠B
Measure of ∠A = 120°, Measure of ∠B = 100°
Understanding Elementary Shapes Class 6
Example 5. From these two angles which has larger measure? Estimate and then confirm by measuring them.

Solution. On observing, we find that ∠B > ∠A.
On measuring, we find that ∠A = 30° and ∠B = 60° Thus, ∠B > ∠A
Example 6. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor)
Solution. On estimating with eyes, the measure of angle shown in figure are as follows
(1) 30°
(2) 130°
(3) 80°
Now, on measuring with the protractor, measure of angle shown in figure are as follows:
(1) 35°
(2) 135°
(3) 75°
MP Board Class 6 Chapter 5 Maths
Example 7. Find the angle measure between the hands of the clock in each figure.
Solution.
(1) Number of divisions between 12 to 3 = 3
We know that 12 divisions = 360°
\(1 \text { division }=\frac{360^{\circ}}{12}\)∴ \(3 \text { divisions }=\frac{360^{\circ}}{12} \times 3=90^{\circ}\)
Hence, the angle between the hands of clock is 90°.
(2) Number of divisions between 9 to 3=6
We know that 12 divisions = 360°
\(1 \text { division }=\frac{360^{\circ}}{12}\)∴ \(6 \text { divisions }=\frac{360^{\circ}}{12} \times 6=180^{\circ}\)
Hence, the angle between the hands of clock 180°.
If two lines intersect each other and the angle between them is a right angle, then these lines are said to be perpendicular lines.
e.g. In the following figure, line AB is perpendicular to line CD i.e. AB ⊥ CD
and point O is the point of intersection of line segments AB and CD.
Example 1. Which of the following are models for perpendicular lines?
(1) The opposite edge of a ruler.
(2) The letter Z
(3) Railway lines
(4) The letter L
Solution. (1) No, the opposite edges of a ruler does not make a model of perpendicular lines.
(2) No, the letter Z does not make a model of perpendicular lines.
(3) No, railway lines does not make a model of perpendicular lines.
(4) Yes, the letter L does make a model of perpendicular lines.
MP Board Class 6 Chapter 5 Maths
Example 2. Consider a line AB is perpendicular to the line XY. If AB and XY intersect at the point Q, then find the measure of ∠AOY.
Solution. Given, AB is perpendicular to XY and AB and XY both intersect each other at the point O.
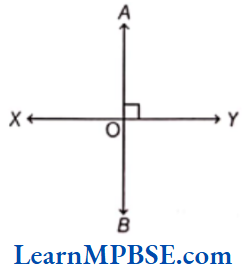
So, it is clear from the adjoining figure that ∠AOY = 90°
Example 3. Find the angle Indicated below and write name of lines which are perpendicular to each other.
Solution. (1) ∠POQ = 90° and PO ⊥ QR
(2) ∠BOD = 90° and BO ⊥ OD
Perpendicular Bisector
The perpendicular bisector of a line segment is perpendicular to the line segment that divide it into two equal parts.
e.g. In the given figure, CD is perpendicular bisector to line segment AB.
MP Board Class 6 Chapter 5 Maths
Example 4. Study the following diagram. The line / and line mare perpendicular to each others.
(1) Is RS = ST?
(2) Does AS bisect PV?
(3) Identify any two lines segments for which AS is the perpendicular bisector.
(4) Are these true?
(a) PR > TU
(b) QR = UV
(c) PQ < TW
Solution.
(1) From the given figure,
RS = 1 unit
ST = 1 unit
∴ RS = ST = 1 unit
(2) PS = 3 units
SV = 3 units
∴ PS = SV = 3 units
Now, PS = SV
So, S is the mid-point of PV.
Thus, AS bisects PV.
(3) In the given figure, we can see that AS is the perpendicular to the given line segment.
Since, RS = ST [each = 1 unit]
So, AS is the perpendicular bisector of RT.
Again, QS = SU [each 2 unit]
So, AS is the perpendicular bisector of QU.
(4) (a) Here, PR = PQ + QR
= 1 + 1 = 2 units[PQ = QR = 1 unit]
and TU = 1 unit
∴ PR > TU is true.
(b) Here, QR = 1 unit and UV = 1 unit.
∴ QR = UV = 1 unit
∴ QR = UV is true.
(c) Here, PQ = 1 unit and TW = 3 unit
∴ PQ < TW is true.
Example 5. List out English alphabets which are examples of perpendicular. Write, if any.
Solution. Letter F, L and T are examples of perpendicular lines segments.
Example 6. Observe the following figure, if the line segments PQ and RS are perpendicular bisector of each other and PQ = 6 cm and RS = 8 cm, then find PO and OR?
Solution. Since, PQ and RS are perpendicular bisector to each other, therefore they divide each other equally.
Now, PQ = 6 cm
∴ PO + OQ = 6 cm
PO = 3cm
and RS = 8 cm
∴ RO = \(\frac{8}{2}\) = 4 cm
Hence, PO = 3 cm
and RO = 4 cm
A polygon with least number of sides is called a triangle or we can say a plane figure bounded by three lines is called triangle.
Classification Based on Length of the Sides
A triangle is classified according to the measurement of its sides as given below
1. Scalene Triangle
A triangle having all three unequal sides is called a scalene triangle. e.g. ΔABC is a scalene triangle where, AB ≠ BC ≠ CA
2. Isosceles Triangle
A triangle having two equal sides is called an isosceles triangle.
e.g. ΔABC is an isosceles triangle where, AB = AC
3. Equilateral Triangle
A triangle having three equal sides is called an equilateral triangle.
e.g. ΔABC is an equilateral triangle. where, AB = BC = CA
MP Board Class 6 Chapter 5 Maths
Example 1. Name the triangle with lengths of sides
(1) 9 cm, 10 cm and 11 cm.
(2) 7 cm, 7 cm and 9 cm.
(3) ΔPQR such that PQ = QR = PR = 6 cm.
Solution. (1) Given, first side = 9 cm, second side = 10 cm, and third side = 11 cm
i.e. all the sides are of different length.
So, it is a scalene triangle.
(2) Given, first side = 7 cm, second side = 7 cm and third side = 9 cm
i.e. two sides are equal. So, it is an isosceles triangle.
(3) Given, PQ = QR = PR = 6 cm
i.e. all sides of triangle are equal.
So, it is an equilateral triangle.
Classification Based on Measurement of Angles
A triangle is further classified according to the measurement of its angles as given below
1. Acute Angled Triangle
If each angle of a triangle is less than 90°, then the triangle is called an acute angled triangle.
e.g. ΔPQR is an acute angled triangle where, ∠P, ∠Q and ∠R are acute angles i.e. less than 90°.
2. Right Angled Triangle
If any one angle of a triangle is a right angle, then the triangle is called a right angled triangle.
e.g. ΔPQR is a right angled triangle where, ∠Q = 90°.
3. Obtuse Angled Triangle
If any one angle of a triangle is greater than 90° but less than 180°, then the triangle is called an obtuse angled triangle.
e.g. ΔPQR is an obtuse angled triangle, where ∠Q > 90°.
MP Board Class 6 Chapter 5 Maths
Important Properties of Triangles
1. If three sides of a triangle are equal, then the three angles are also equal. Its vice-versa is also true.
2. If two sides of a triangle are equal, then it has two equal angles. Its vice-versa is also true.
3. If three sides of a triangle are unequal, then the three angles are also unequal.
Example 2. Classify the triangles given below.
(1) ΔPQR, m∠P = 40°, m∠Q = 75° and m∠R = 65°.
(2) ΔABC m∠B = 90°.
(3) ΔLMN, m∠M = 90° and LM = MN.
Solution. (1) Given, m∠P = 40°, m∠Q = 75° and m∠R = 65°
Since, all the angles are different and less than 90°. So, it is an acute angled triangle.
(2) Given, m∠B = 90°
i.e. measure of ∠B = 90°.
So, it is a right angled triangle.
(3) Given, m∠M = 90°
i.e. measure of ∠M = 90° and LM = MN
Here, one angle is right angle and two sides are equal.
So, it is an isosceles right angled triangle.
Example 3. In a ΔABC, ∠A = ∠B = ∠C = 60°, then what can you say about the length of sides of ΔABC? Also, write the name of the triangle.
Solution. It is the property of triangle that if all the angles of a triangle are equal, then the three sides of a triangle are also equal.
Thus, the given triangle is an equilateral triangle.
Example 4. In a ΔXYZ, XY = XZ and ZY = 65°. Then, find the value of ∠Z.
Solution. Since, the XY = XZ i.e. two sides of a triangle are equal, therefore it is an isosceles triangle.
So, ∠Y = ∠Z
∴ ∠Z = 65°
Example 5. Name each of the following triangles in two different ways. (You may judge the nature of the angle by observation)
Solution.
A quadrilateral is a polygon which has four sides, four angles and two diagonals.
Classification of Quadrilaterals
Quadrilaterals can be classified as given below
1. Rectangle

(1) PQ = SR,
PQ || SR
SP = RQ,SP || RQ
(2) ∠P = ∠Q = ∠R = ∠S = 90°
(3) SQ = PR
2. Square
(1) PQ || SR and SP || QR
and PQ = QR = RS = SP
(2) ∠P = ∠Q = ∠R = ∠S = 90°
(3) PR = SQ
3. Parallelogram
(1) PQ = SR, PQ || SR, SP = QR, SP || QR
(2) ∠P = ∠R, and ∠S = ∠Q
(3) PR ≠ SQ (some times PR=SQ) and OS = OQ, and OR = OP
4. Rhombus
(1) PQ || SR and PS || QR
PQ = QR = RS = SP
(2) ∠P = ∠R and ∠S = ∠Q
(3) PR ≠ SQ (sometimes it may be equal) and
OP = OR, OS = OQ
5. Trapezium
(1) SR || PQ
(2) SR ≠ PQ and SP ≠ RQ
A trapezium is said to be an isosceles trapezium, if its non-parallel sides are equal i.c. SP = RQ
Example 1. Write the number of pairs of opposite sides which are parallel?
Solution. In the adjoining figure, a parallelogram is given.
Here, PQ || SR and PS || QR
Therefore, the number of pairs of opposite sides which are parallel is 2.
MP Board Class 6 Chapter 5 Maths
Example 2. In the given figure PQRS is a quadrilateral, if PR ⊥ SQ, then name all the right angles.

Solution. The right angles in the given figure are ∠POQ, ∠QOR, ∠ROS, ∠SOP.
Example 3. In the adjoining figure, a rectangle is given. Write how many right angles are there.

Solution. According to the property of a rectangle, all the interior angles of a rectangle are right angle (i.e. 90°).
∴ There are four right angles in a rectangle.
Example 4. What is regular quadrilateral? Draw its figure.
Solution. We know that a square has all its sides and angles equal, so it is said to be a regular quadrilateral
where, PQ = QR = RS = SP
and ∠P = ∠Q = ∠R = ∠S = 90°
Example 5. State the condition under which a rectangle is considered a square.
Solution. A rectangle will be considered as a square, if all the sides of a rectangle are equal.
Example 6. Fill in the blanks
(1) The opposite sides of a rectangle are ……. in length.
(2) The diagonals of a square are ……. to one another.
(3) the opposite sides of a trapezium are ……
(4) Each angle of a rectangle is a ……
Solution. (1) equal
(2) perpendicular
(3) parallel
(4) right angle
Example 7. State the reason for the following, if it is true.
(1) A square is the special case of the rectangle.
(2) Parallelogram is a special case of the rectangle.
Solution. (1) Yes, its true. In square, opposite sides are equal and all angles are right angles, so a square is a special case of rectangle.
(2) No, it is not true.
MP Board Class 6 Chapter 5 Maths
Example 8. Write the name of the quadrilaterals in which diagonals are perpendicular to each other?
Solution. In square and rhombus, diagonals are perpendicular to each other.
Polygon is a closed shape made of line segments only.
Polygons are classified according to the number of their
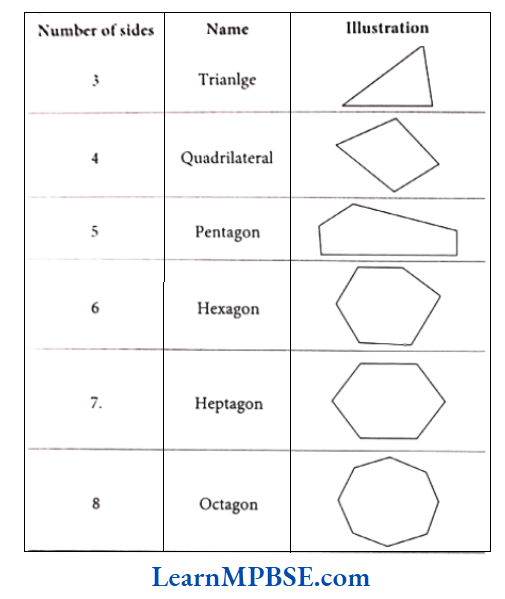
These shapes can be seen in everyday life. Windows, doors, walls, almirahs, blackboards, notebooks etc. are usually rectangular in shapes.
Note It
(1) If a polygon has all equal sides, then it is said to be a regular polygon.
(2) The angle determined by two sides meeting at a vertex is called an angle of the polygon.
Example 1. Examine whether the following are polygons. If any one among them is not, say why?
Solution. (1) It is an open figure. So, it is not a polygon.
(2) It is closed figure. So, it is a polygon with six sides i.e. hexagon.
(3) It is not made by line segments. So, it is not a polygon.
(4) It is made by two line segments and curved line. So, it is not a polygon.
Example 2. Name each polygon. Make one more example of each of these.

Solution. (1) This polygon has four sides, so it is quadrilateral. e.g.
(2) This polygon has three sides, so it is a triangle. e.g.
(3) This polygon has five sides, so it is pentagon. e.g.
Example 3. Can you draw an equilateral triangle inside a regular hexagon. Show.
Solution. Consider, a regular hexagon ABCDEF.
Joining its alternate vertices B, D and F, we get ABDF, which is a regular triangle, (since, all sides are equal).
Thus, the triangle, so formed is an equilateral triangle.
Example 4. Can you make any two rectangle inside a regular octagon. Show.
Solution. Consider, PQRSTUVW is a regular octagon.
Join vertices P and U, we get \(\overline{P U}\).
Join Q and T, we get \(\overline{Q T}\). Thus, we get a rectangle PQTU.
Again, by joining W, Rand V, S we can get another rectangle WRSV.
MP Board Class 6 Chapter 5 Maths
Example 5. A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw
(1) pentagon and its diagonals
(2) hexagon and its diagonals
Solution. (1) Here, PQRST is a pentagon.
By joining any two vertices, we get diagonals as \(\overline{T R}, \overline{T Q}, \overline{P R}, \overline{P S} \text { and } \overline{S Q} \text {. }\)
(2) Here, ABCDEF is a hexagon
By joining any two vertices, we get diagonals as \(\overline{A D}, \overline{A C}, \overline{A E}, \overline{B F}, \overline{B E}, \overline{F C}, \overline{E C}, \overline{B D}, \overline{F D} .\)
Example 6. What is the condition for a polygon to be considered as a regular polygon? Give any two examples of it.
Solution. When all sides of the polygon are equal in length, the polygon is considered as regular polygon.
e.g. (1) An equilateral triangle
(2) A square
Example 7. Write the number of sides and name of the following figure.
Solution. (1) It is a triangle. The number of sides is 3.
(2) It is a heptagon.
The number of sides is 7.
(3) It is a quadrilateral.
The number of sides is 4.
Example 8. Given a regular pentagon PQRST, where QR = 3 cm, then find the value of x.
Solution. Since, QR = 3cm
∴ x = PT = 3cm
because in a regular pentagon, all sides are equal.
Question 1. What is the disadvantage in comparing line segments by mere observation?
Solution.
The disadvantage in comparing line segments by mere observation is that sometimes the difference in lengths between Q two line segments may not accurate. So, we cannot always be sure about our usual judgement. e.g. In the given figure, the line segments \(\overline{P Q}\) and \(\overline{R S}\) seems to be equal but actually they are not equal.
Question 2. Why is it better to use a divider than a ruler, while measuring the length of a line segment?
Solution. When we measure the length of a line segment by ruler, there may be some errors due to its thickness and angular viewing. These errors can be removed by measuring a line segment with the help of a divider. Hence, the use of a divider is better than a ruler.
Question 3. Draw any line segment, say \(\overline{A B}\) Take any point Clying in between A and B Measure the lengths of AB, BC and AC. Is AB = AC + CB?
Solution. Let AB be the line segment of length 6 cm and point C lying between A and B.
On measuring the lengths of line segments AB, AC and CB using ruler, we find that AB = 6 cm, AC = 4 cm and CB = 2 cm
Now, AC + CB = 4 + 2 = 6 cm = AB
i.e. AC + CB = AB
So, we can say that C lies between A and B.
Note If A. B and C are any three points on a line such that AC + CB = AB, then point C will lie between points A and B. Its converse is also true.
Types of Shapes for Class 6
Question 4. If A, B amd C are three points on a line such that AB = 5 cm, BC = 3 cm and AC = 8 cm, which one of them lies between the other two?
Solution. Firstly, draw a line AV of 8 cm. Take a point B on AC such that AB = 5 cm.
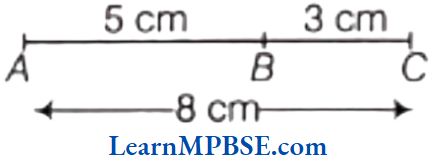
Now, length of BC = AC – AB = 8 – 5 = 3cm
Thus, AB + BC = AC
So, the point B lies between point A and C.
Question 5. Verify whether Dis the mid-point of \(\overline{A G}\).

Solution. From the given figure, it is clear that
AD = AB + BC + CD = 1 + 1 + 1 = 3 units
and DG = DE + EF + FG = 1 + 1 + 1 = 3 units Now,
AG = AD + DG = 3 + 3 = 6 units
and AD = DG 3 units
∴ D lies between A and G.
∴ D is the mid-point of AG.
Question 6. If Bis the mid-point of \(\overline{A C}\) and C is the mid-point of \(\overline{B D}\), where A, B, Cand Dlie on a straight line, say why AB = CD?
Solution. Given, B is the mid-point of \(\overline{A C}\).
∴ AB = BC …(1)
and C is the mid-point of \(\overline{B D}\).
∴ BC = CD …(2)
i.e.
Now, on adding Eqs. (1) and (2), we get
AB + BC = BC + CD
AB = CD
Hence proved
Question 7. Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Solution.
(1) Here, we draw a ΔABC
in which AB = 3 cm,
BC = 35 cm and AC = 39 cm
Now, by adding two sides of ΔABC
i.e. AB + BC = 3 + 3.5 = 6.5 cm Clearly,
AB + BC > AC
(2) Here, we draw a ΔABC in which AB = 3cm, BC = 4 cm and AC = 5 cm
Now, by adding two sides of ΔABC
i.e. AB + BC = 3 + 4 = 7cm
Clearly, AB + BC > AC
(3) Here, we draw a ΔABC in which
AB = BC = AC = 25 cm
Now, by adding two sides of ΔABC
i.e. AB + BC = 2.5 + 2.5 = 5cm
Clearly, AB + BC > AC
(4) Here, we draw a ΔABC in which
AB = 3cm, BC = 35 cm and AC = 4 cm
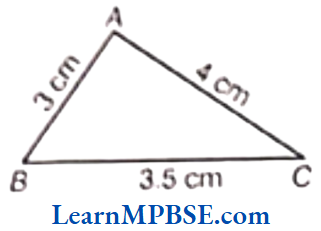
Now, by adding two sides of ΔABC
i.e. AB + BC = 3 + 3.5 = 6.5 cm
Clearly, AB + BC > AC
(5) Here, we draw a ΔABC in which
AB = 2 cm, BC = 4 cm and AC = 45 cm
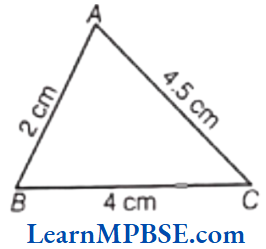
Now, by adding two sides of ΔABC
i.e. AB + BC = 2 + 4 = 6 cm
Clearly, AB + BC > AC
From all these triangles, we observe that in each case, the sum of the lengths of any two sides is greater tahn the third side. So, the sum of the lengths of any two sides can never be less than the third side.
Types of Shapes for Class 6
Question 8. What is the angle name for half a revolution?
Solution. We know that 1 revolution = 2 straight angles
Now, dividing by 2 both sides, we get
\(\frac{1}{4}\) revolution = \(\frac{2}{2}\) straight angle = 1 straight angle
Hence, the angle name for half a revolution is straight angle or two right angles.
Question 9. What is the angle name for one-fourth revolution?
Solution. We know that I revolution = 4 right angles
Now, dividing by 4 on both sides, we get
\(\frac{1}{4}\) revolution = \(\frac{4}{4}\) right angles
\(\frac{1}{4}\) revolution = 1 right angle
Hence, the angle name for one-fourth revolution is one right angle.
Question 10. Draw five other situations of one-fourth, half and three-fourth revolution on a clock.
Solution. (1) One-fourth revolution For one-fourth revolution, the clock hand moves in many individual routes. Some of these situations on a clock are as follows:

(2) Half revolution For half revolution, the clock hand moves in many individual routes. Some of these situations on a clock are as follows
(3) Three-fourth revolution For three-fourth revolution, the clock hand moves in many individual routes. Some of these situations on a clock are as follows:

Question 1. What part of a revolution have you turned through, if you stand facing
(1) East and turn clockwise to face North?
(2) South and turn clockwise to face East?
(3) West and turn clockwise to face East?
Solution.
(1) Here, the turn from East to South is one right angle from South to West is one right angle and from West to North is one right angle. So, the turn from East to North is three right angles.
Hence, 3/4 of a revolution is required to turn from East to North.
(2) Here, the turn from South to West is one right angle, from West to North is one right angle and from North to East is one right angle. So, W+ the turn from South to East is three right angles.
Hence, 3/4 of a revolution is required to turn from South to East.
(3) Here, the turn from West to North is one right angle, from North to East is one right angle. So, the turn from West to East is two right angles.
Hence, 1/2 of a revolution is required to turn from West to East.
Types of Shapes for Class 6
Question 2. The hour hand of a clock moves from 12 to 5. Is the revolution of the hour hand more than 1 right angle?

Solution. Yes, it is clear from the figure that hour hand makes one right angle from 12 to 3 and since 19 5 lies between 3 and 6. So, revolution of the hour hand is more than 1 right angle.

Question 2. What does the angle made by the hour hand of the clock look like when it moves from 5 to 7. Is the angle moved more than 1 right angle?

Solution. It looks like an acute angle. We know that hour hand of a clock makes a right angle to cover three digits as from 12 to 3, it makes a right angle
(∴ it covers three digits 1, 2 and 3). Here, hour hand moves from 5 to 7 (covers only two digits 6 and 7). So, the angle moved by hour hand is less than 1 right angle.
Question 3. Draw the following and check the angle with your RA (right angle) tester going
(1) from 12 to 2
(2) from 6 to 7
(3) from 4 to 8
(4) from 2 to 5
Solution.
(1) On checking the angle moved by an hour hand, while going from 12 to 2 by RA (right angle) tester, it is clear that it is less than 1 right angle.

(2) On checking the angle moved by an hour hand, while going from 6 to 7 by RA (right angle) tester, it is clear that it is less than 1 right angle.

(3) On checking the angle moved by an hour hand, while going from 4 to 8 by RA (right angle) tester, it is clear that it is more than 1 right angle.

(4) On checking the angle moved by an hour hand, while going from 2 to 5 by RA (right angle) tester, it is clear that it is equal to 1 right angle.

Question 1. Match the following

Solution. (1) Straight angle is half of a revolution.
(2) Right angle is one-fourth of a revolution.
(3) Acute angle is less than one-fourth of a revolution.
(4) Obtuse angle is between 1/4 and 1/2 of a revolution. (v) Reflex angle is more than half of a revolution.
So, (1) → (c), (2) → (d), (3) → (a), (4) → (e), (5) → (b)
Types of Shapes for Class 6
Question 2. Classify each one of the following angles as right, straight, acute, obtuse or reflex.
Solution.
(1) Given angle is smaller than a right angle, so it is an acute angle.
(2) Given angle is more than a right angle, so it is an obtuse angle.
(3) Given angle is a right angle.
(4) Given angle is more than a straight angle, so it is a reflex angle.
(5) Given angle is a straight angle.
(6) Both angles are smaller than a right angle, so both these are acute angles.
Question 1. What is the measure of
(1) a right angle?
(2) a straight angle?
Solution.
(1) The measure of a right angle = 90°
(2) The measure of a straight angle
= 2 × right angles = 2 x 90° = 180°
Question 2. Say true or false.
(1) The measure of an acute angle < 90°.
(2) The measure of an obtuse angle < 90°.
(3) The measure of a reflex angle > 180°.
(4) The measure of one complete revolution = 360°.
(5) If m∠A = 53° and m∠B = 35°, then m∠A > m∠B.
Solution.
(1) True, because the measure of an acute angle is always less than 90°.
(2) False, because the measure of an obtuse angle is always greater than 90°.
(3) True, because the measure of a reflex angle is always greater than 180° and less than 360°.
(4) True, because the measure of one complete revolution is equal to 360°.
(5) True, because the measure of ∠A is greater than ∠B.
Question 3. Write down the measures of
(1) some acute angles.
(2) some obtuse angles.
(give atleast two examples of each)
Solution. (1) We know that the measure of an acute angle is always less than 90″.
So, 45, 50, 55°, 60°, 65° all are acute angles.
(2) We know that the measure of an obtuse angle is always greater than 90° but less than 180°.
So, 120, 125, 135°, 140° all are obtuse angles.
Types of Shapes for Class 6
Question 4. Measure the angles given below using the protractor and write down the measure.
Solution. On measuring the given angles using protractor, we find that
(1) angle is 45°.
(2) angle is 125°.
(3) angle is 90°.
(4) angles are 60°, 125° and 90°, respectively.
Question 5. Which angle has a larger measure?

First estimate and then measure.
Measure of ∠A =
Measure of ∠B =
Solution. Observing the given angles, we find that ∠B > ∠A.
On measuring, we find that
Measure of ∠A = 40°
Measure of ∠B = 65°
∴ ∠B > ∠A
Question 6. From these two angles which has larger measure? Estimate and then confirm by measuring them.
Solution. On observing, we find that ∠B > ∠A.
On measuring, we find that
∠A = 45° and ∠B = 60°
Thus, ∠B > ∠A
Question 7. Fill in the blanks with acute, obtuse, right or straight angle.
(1) An angle whose measure is less than that of a right angle is.
(2) An angle whose measure is greater than that of a right angle is
(3) An angle whose measure is the sum of the measures of two right angles is
(4) When the sum of the measures of two angles is that of a right angle, then each one of them is
(5) When the sum of the measures of two angles is that of a straight angle and if one of them is acute, then the other should be.
Solution. (1) acute angle
(2) obtuse angle
(3) straight angle
(4) acute angle
(5) obtuse angle
Question 8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor)
Solution. On estimating with eyes, the measure of angle shown in figure are as follows
(1) 45°
(2) 125°
(3) 60°
(4) 135°
Now, on measuring with the protractor, measure of angle shown in figure are as follows
(1) 40°
(2) 130°
(3) 65°
(4) 135°
Types of Shapes for Class 6
Question 9. Investigate In the given figure, the angle measures 30°. Look at the same figure through a magnifying glass. Does the angle becomes larger? Does the size of the angle change?

Solution. No, looking through a magnifying glass does not make the angle larger.
Also, the size of angle does not change.
Question 1. Which of the following are models for perpendicular lines?
(1) The adjacent edges of a table top.
(2) The lines of a railway track.
(3) The line segments forming the letter ‘L’.
(4) The letter ‘V’.
Solution. (1) Yes, the adjacent edges of a table top make a model of perpendicular lines.
(2) No, the lines of a railway track does not make a model of perpendicular lines.
(3) Yes, the line segments forming the letter ‘L’ makes a model of perpendicular lines.
(4) No, the letter ‘V’ does not make a model of perpendicular lines.
Question 2. Let \(\overline{P Q}\) be the perpendicular to the line segment \(\overline{X Y}\). Let \(\overline{P Q}\) and \(\overline{X Y}\) Intersect at the point A. What is the measure of ∠PAY?
Solution. Given, \(\overline{P Q}\) is perpendicular to \(\overline{X Y}\) and \(\overline{P Q}\) and \(\overline{X Y}\) both intersect each other at the point A.
So, it is clear from the adjoining figure that ∠PAY=90°
Types of Shapes for Class 6
Question 3. There are two set-squares in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?
Solution. We have two set-squares in our box. In one of them, angles are of 30°, 60°, 90° and in the other, angles are of 45°, 45°, 90°.
Clearly, they have one angle measure in common, which is
Question 4. Study the following diagram. The line l is perpendicular to line m.
(1) CE = EG?
(2) Does PE bisect CG?
(3) Identify any two line segments for which PE is the perpendicular bisector.
(4) Are these true?
(a) AC > FG (b) CD = GH (c) BC < EH
Solution. (1) From given figure,
CE = CD + DE [CD = DE = 1 unit]
= 1 + 1 = 2 units
and EG = EF + FG [EF = FG = 1 unit]
= 1 + 1 = 2 units
∴ CE = EG 2 units
(2) Since, CE = EG
So, E is the mid-point of CG.
Thus, PE bisects CG.
(3) In the given figure, we can see that PE is perpendicular to the given line segment.
Since, DE = EF [each = 1 unit]
So, PE is the perpendicular bisector of DF.
Again, CE = EG [each = 2 units]
So, PE is the perpendicular bisector of CG.
(4) (a) Here, AC = AB + BC = 1 + 1= 2 units
[AB = BC = l unit]
and FG = 1 unit
∴ AC > FG is true.
(b) Here, CD = 1 unit and GH = 1 unit
∴ CD = GH is true.
(c) Here, BC = 1 unit
and EH = EF + FG + GH
= 1 + 1 + 1 = 3 units
∴ BC < EH is true.
Question 1. Match the following:
Solution. (1) → (e), (2) → (g), (3) → (a), (4) → (f), (5) → (d), (6) → (c), (7) → (b)
Question 2. Name each of the following triangles in two different ways. (you may judge the nature of the angle by observation)
Solution. By observing the given triangles in two different ways, name of each triangle is given below
(1) In the given triangle, two sides are equal, so it is an isosceles triangle and all the angles are acute angles. So, it is an acute angled triangle also.
(2) In the given triangle, all the sides are different, so it is a scalene triangle and one angle is right angle. So, it is a right angled triangle also.
(3) In the given triangle, two sides are equal, so it is an isosceles triangle and one angle is an obtuse angle. So, it is an obtuse angled triangle also.
(4) In the given triangle, two sides are equal, so it is an isosceles triangle and one angle is right angle. So, it is a right angled triangle also.
(5) In the given triangle, all the sides are equal, so it is an equilateral triangle and all the angles are acute. So, it is an acute angled triangle also.
(6) In the given triangle, all the sides are different, so it is a scalene triangle and one angle is an obtuse angle. So, it is an obtuse angled triangle also.
Types of Shapes for Class 6
Question 3. Try to construct triangles using matchsticks. Some are shown here.
Can you make a triangle with
(1) 3 matchsticks?
(2) 4 matchsticks?
(3) 5 matchsticks?
(4) 6 matchsticks?
(Remember you have to use all the available matchsticks in each case)
Name the type of triangle in each case.
If you cannot make a triangle, think of reason for it.
Solution. (1) With the help of 3 matchsticks, we can make an equilateral triangle. Since, all three matchsticks are of equal length.
(2) With the help of 4 matchsticks, we cannot make any triangle because in this case, sum of two sides is equal to the third side and we know that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
(3) With the help of 5 matchsticks, we can make an isosceles triangle. Since, we get two sides equal in this case.
(4) With the help of 6 matchsticks, we can make an equilateral triangle. Since, we get three sides equal in this case.
Question 1. Say true or false.
(1) Each angle of a rectangle is a right angle.
(2) The opposite sides of a rectangle are equal in length.
(3) The diagonals of a square are perpendicular to one another.
(4) All the sides of a rhombus are of equal length.
(5) All the sides of a parallelogram are of equal length.
(6) The opposite sides of a trapezium are parallel.
Solution. (1) True
(2) True
(3) True
(4) True
(5) False, because opposite sides of a parallelogram are of equal length and parallel.
(6) False, because a pair of opposite sides of trapezium are parallel and other pair of opposite sides are non-parallel.
Properties of Shapes Class 6
Question 2. Give reason for the following
(1) A square can be thought of as a special rectangle.
(2) A rectangle can be thought of as a special parallelogram.
(3) A square can be thought of as a special rhombus.
(4) Squares, rectangles, parallelograms are all quadrilaterals.
(5) Square is also a parallelogram.
Solution. (1) We know that in a rectangle, opposite sides are equal and each angle is a right angle. If all its sides are equal, then it becomes square.
So, a square can be thought of as a special rectangle.
(2) We know that in a parallelogram, opposite sides are parallel as well as equal and opposite angles are equal. If its opposite angles are right angles, then it becomes a rectangle. So, a rectangle can be thought of as a special parallelogram.
(3) We know that in a rhombus, all four sides are equal and opposite sides are parallel. If its all angles are right angles, then it becomes a square. So, a square can be thought of as a special rhombus.
(4) We know that a polygon, which has four sides is called a quadrilateral. Square, rectangle and parallelogram also have four sides. So, these all are quadrilaterals.
(5) We know that in a parallelogram, opposite sides are parallel as well as equal and opposite angles are equal. In a square, opposite sides are parallel as well as equal and opposite angles are equal to right angle. So, a square is also a parallelogram.
Question 3. A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Solution. Yes, a square is a regular quadrilateral because all sides and angles of a square are equal.
Question 1. Examine whether the following are polygons. If any one among them is not, say why?
Solution. (1) It is an open figure. So, it is not a polygon.
(2) It is closed figure. So, it is a polygon with six sides i.e. hexagon.
(3) It is not made by line segments. So, it is not a polygon.
(4) It is made by two line segments and a curved line. So, it is not a polygon.
Properties of Shapes Class 6
Question 2. Name each polygon.
Make two more examples of each of these.
Solution. (1) This polygon has four sides, so it is a quadrilateral. e.g.
(2) This polygon has three sides, so it is a triangle. e.g.
(3) This polygon has five sides, so it is a pentagon.
e.g.
(4) This polygon has eight sides, so it is an octagon.
e.g.
Question 3. Draw a rough sketch of a regular hexagon. Connecting any three of its vertices, draw a triangle. Identify the type of the triangle you have drawn.
Solution. Here, PQRSTU is a regular hexagon.
Joining its alternate vertices P, Rand T, we get ATPR, which is a regular triangle (since, all sides are equal).
Thus, the triangle so formed is an equilateral triangle.
Question 4. Draw a rough sketch of a regular octagon. (Use squared paper, If you wish).
Draw a rectangle by joining exactly four of the vertices of the octagon.
Solution. Here, ABCDEFGH is a regular octagon. Joining vertices G and D, we get \(\overline{G D}\). Again, joining H and C, we get H\(\overline{H C}\).
Thus, we get a rectangle HCDG.
Again, by joining A, F and B, E, we can get another rectangle ABEF.
Question 5. A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.
Solution. Rough sketch is shown below
Here, ABCDE is a pentagon.
By joining any two vertices, we get diagonals as \(\overline{A C}, \overline{A D}, \overline{B D}, \overline{B E} and \overline{C E}\).
Question 1. Measures of the two angles between hour and minutes hands of a clock at 9 O’ clock are
Answer. 2. 270°, 90°
Question 2. If a bicycle wheel has 48 spokes, then the angle between a pair of two consecutive spokes is
Answer. 2. \(\left(7 \frac{1}{2}\right)^{\circ}\)
Question 3. If figure, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of ∠BPY is
Answer. 2. 45°
Properties of Shapes Class 6
Question 4. Where will the hand of a clock stop if it starts at 5 and makes \(\frac{1}{4}\) revolution clockwise?
Answer. 2. 8
Question 5. If you are facing South and turn through a straight angle in which direction will you face now?
Answer. 2. North
Question 6. Where will the hour hand of a clock stop if it starts at 7 and makes \(\frac{3}{4}\) revolution clockwise?
Answer. 3. 4
Question 7. The angle measure of one-fourth revolution is
Answer. 3. 90°
Question 8. How is the measure of an angle expressed?
Answer. 3. Degrees
Question 9. If the sum of two angles is greater than 180°, then which of the following is not possible for the two angles?
Answer. 4. Two right angles
Question 10. 179° is an example of
Answer. 2. an obtuse angle
Question 11. In figure, AB = BC and AD = BD = DC. Then, the number of isosceles triangles in the figure is
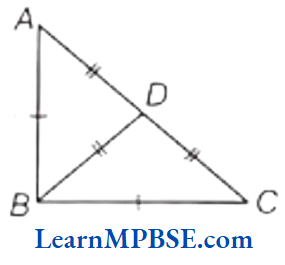
Answer. 3. 3
Question 12. The instrument to measure an angle is about
Answer. 2. protractor
Question 13. The polygon with the least number of sides is a
Answer. 1. triangle
Question 14. A rhombus with four right angles is known as
Answer. 2. square
Properties of Shapes Class 6
Question 15. A polygon has the prime number of sides. Its number of sides is equal to the sum of the two least consecutive primes. The number of diagonals of the polygon is
Answer. 2. 5
Question 1. Assertion (A) When we measure the length of a line segment by a ruler, there may be some errors due to angular viewing, these errors can be removed by making a line segment with the help of a divider.
Reason (R) The use of divider is better than a ruler.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (b) Both A and R are true but R is not the correct explanation of A.
Question 2. Assertion (A) When the hand of a clock moves from one position to another, it turns through an angle.
Reason (R) The angle for one revolution is a complete angle.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (b) Both A and R are true but R is not the correct explanation of A.
Question 1. The hour hand of a clock stops at ….., if it starts at 12 and makes \(\frac{1}{2}\) revolution clockwise.
Answer. 6
Question 2. The angle formed in half-revolution is ………..
Answer. 180°
Question 3. Angle formed between the hands of a clock, when the time is 3 o’clock ……….
Answer. 90°
Question 4. A pair of opposite sides of a rectangle are ………… and ………….
Answer. Equal, parallel
Question 5. The number of diagonals in a hexagon is.
Answer. Nine
Question 1. If the arms of an angle on the paper are increased, the angle increases.
Answer. False
Question 2. If the arms of an angle on the paper are decreased, the angle decreases.
Answer. False
Question 3. A horizontal line and a vertical line always intersect at right angle.
Answer. True
Question 4. Perpendicular bisector of the line segment is perpendicular to the line.
Answer. True
Question 5. A trapezium is a parallelogram.
Answer. False
Question 1. Match the Column 1 with Column 2 with their respective values.
Solution. (1) → (c), (2) → (b), (3) → (d), (4) → (a)
Question 1. A truss is a structural framework of wood or metal arranged in a pattern which is used to support roofs or bridges.
The structure of a truss made of iron rods is shown in the figure below.
The rods EF, DG, AH, IK and JL are perpendicular to the base BC. A number of triangles are formed by the rods. In ΔABC, side AB = AC. In ΔAGK, all sides are equal and H is the mid-point of GK.
(1) Which type of triangle is ABC?
(a) Scalene
(b) Isosceles
(c) Equilateral
(d) Right-angled triangle
(2) Is ΔDGF a right-angled triangle? Justify your answer.
(3) Is AH the perpendicular bisector of line segment GK? Justify your answer.
(4) The sides of ΔIJL are of length 3 m, 4 m and 5 m. Is ΔIJL an isosceles triangle? Why?
Solution. (1) (b) Since, it given that in ΔABC, AB = AC, which means two sides of this triangle are equal. Therefore, it is an isosceles triangle.
(2) Yes, ADGF is a right-angled triangle because DG is perpendicular to BC, therefore ∠DGF = 90°, making ΔDGF a right-angled triangle.
(3) Yes, AH is the perpendicular bisector of line segment GK.
Since, it is given that H is the mid-point of GK and AH is perpendicular on it.
Therefore, AH is a perpendicular bisector of GK.
(4) If ΔIJL length of sides are 3m, 4m and 5m.
Therefore, ΔIJL is not an isosceles triangle because all the sides of this are unequal or there is no pair of equal sides.
Properties of Shapes Class 6
Question 2. The figure below shows a combination of shapes.
In the figure, US is parallel to WP and UV is parallel to QP.
PQRS is a square. WRTU is a rectangle. PSW and WUV are triangles.
(1) Arun joins Sand Q. SQ is an extension of US Which type of quadrilateral is PQUV? Justify your answer.
(2) Which of the following quadrilaterals is regular?
(a) PQRS
(b) PSUV
(c) RWUT
(d) PQTV
(3) Looking at the figure, Raji claims that, ‘PWUSis rhombus’. Do we have sufficient information to accept her claim? Justify your answer.
Solution. (1) Arun joins S and Q. SQ is an extension of US. PQUV is a parallelogram as its opposite sides are parallel.
(2) PQRS is a regular quadrilateral as its all sides are equal.
(3) No, there is no information on sides lengths of PWUS and opposite angles of PWUS.
Question 1. Write the name of triangle whose each angle is acute.
Solution. It is an acute angled triangle.
Question 2. Write the name of triangle whose all three sides are unequal in length.
Solution. A triangle which has all unequal sides is scalene triangle. Here, ΔABC is a scalene triangle.
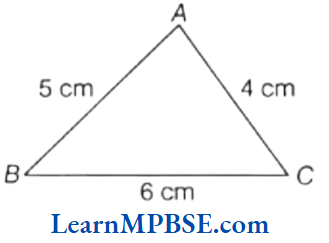
where, AB ≠ BC ≠ CA
Question 3. Write the name of polygon which has 5 sides.
Solution. A polygon which has 5 sides is pentagon.
Question 4. Find the number of sides in a quadrilateral. What can you say about the number of angles? Is it greater than the number of sides?
Solution. Number of sides in a quadrilateral is 4 and number of angles is also 4
No, the number of angles is same as the number of sides.
Question 5. If in a quadrilateral, one pair of opposite sides are parallel, then what is the name of such quadrilateral?
Solution. If one pair of opposite sides are parallel, then it is a trapezium. i.e. PS || QR
MP Board Class 6 Maths Solutions
Question 6. What is the difference between a square and a rhombus?
Solution. In a square, all angles are right angle whereas, in rhombus angles may right angle or not.
Question 7. The figure given below shows a tyre of a bicycle.
What type of angle does Spoke 1 make with Spoke 11?
Solution. Spoke 1 makes reflex angle and obtuse angle with Spoke 11.
Question 1. Will the lengths of line segment AB and line segment BC make the length of line segment AC in figure?
Solution. Here, \(\overline{A B}+\overline{B C}=\overline{A C}\)
Hence, the length of line segment \(\overline{A B}+\overline{B C}\) make the length of line segment \(\overline{A C}\).
Question 2. Will the measure of ∠ABC and ∠CBD make the measure of ∠ABD in figure?
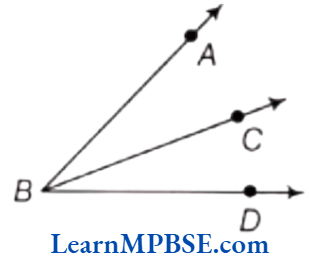
Solution. Here, ∠ABD = ∠ABC + ∠CBD
Hence, the measure of ∠ABC and ∠CBD makes the measure of ∠ABD.
Question 3. By simply looking at the pair of angles given below. State which of the angles in each pair is greater.
Solution. From the given figures, we can say that
(1) ∠AOB > ∠DEF
(2) ∠JKL > ∠GHI
(3) Reflex angle ∠MON > ∠QPR
(4) ∠0 > ∠SUT
Question 4. Which points in figure, appear to be mid-point of the line segments? When you locate a mid-point, name the two equal line segments formed by it.

Solution. In the figure,
(1) There is no mid-point in \(\overline{A B}\).
(2) O is the mid-point of \(\overline{A B} \text { and } \overline{O A}=\overline{O B}\)
(3) D is the mid-point of \(\overline{B C} \text { and } \overline{B D}=\overline{C D}\)
Question 5. Is it possible for the same
(1) line segment to have two different lengths?
(2) angle to have two different measures?
Solution. (1) No, a line segment cannot have two different lengths.
(2) No, an angle cannot have two different measurements.
Question 6. State the type of angle in the following.
Solution. In the given figures, we have
(1) ∠AOB is a right angle.
(2) ∠AOB is a straight angle.
(3) ∠AOB is an acute angle.
(4) ∠AOB is an obtuse angle.
(5) ∠AOB is an obtuse angle.
(6) ∠O is a complete angle.
MP Board Class 6 Maths Solutions
Question 7. Using a ruler onlu, draw an acute, obtuse and reflex angle.
Solution. (1) Acute ∠AOB
(2) Obtuse ∠POQ
(3) Reflex ∠ROS
Question 8. Convert the following angles (in degrees) into fraction of right angle.
(1) 10°
(2) 20°
(3) 135°
Solution. We know that 1 right angle = 90°
i.e. 1°= \(\frac{1}{90}\) right angle
(1) \(10^{\circ}=\frac{10^{\circ}}{90^{\circ}}=\left(\frac{1}{9}\right) \text { right angle }\)
(2) \(20^{\circ}=\frac{20^{\circ}}{90^{\circ}}=\left(\frac{2}{9}\right) \text { right angle }\)
(3) \(135^{\circ}=\frac{135^{\circ}}{90^{\circ}}=\left(\frac{3}{2}\right) \text { right angle }\)
Question 9. Convert the following into degree.
(1) \(\frac{2}{9}\) right angle
(2) \(\frac{3}{4}\) right angle
Solution. We know that right angle = 90°
(1) \(\frac{2}{9} \text { right angle }=\frac{2}{9} \times 90^{\circ}=20^{\circ}\)
(2) \(\frac{3}{4} \text { right angle } \frac{3}{4} \times 90^{\circ}=675^{\circ}\)
Question 10. In the given figure, PQ ⊥ AB and PO = OQ. Is PQ, the perpendicular bisector of line segment AB? Why or why not?
Solution. PQ is not the perpendicular bisector of line segment AB because AO ≠ BO.
[Note AB is the perpendicular bisector of line segment PQ].
Question 11. Draw any triangle of your choice, then draw all the three medians. Are they passing through one point?
Solution. According to the given information, APQR has medians \(\overline{P S}, \overline{Q T} \text { and } \overline{R N}\). Yes, these medians passing through one point ‘O’.
MP Board Class 6 Maths Solutions
Question 12. Which direction will you face, if you start facing East and make \(\frac{3}{4}\) of a revolution clockwise?
Solution. We face towards North.

Question 13. If each side of a triangle is 6 cm. Name the type of triangle.
Solution. Given that, each side of a triangle is 6 cm.
Hence, it is an equilateral triangle.
Question 14. Find the measure of ∠POQ if PR ⊥ QT.
Solution. Here, ∠POQ = 90°
Question 1. Construct two line segments AB and CD of lengths 2.5 cm and 3.2 cm. Construct another segment EF, whose length is the sum of these two line segments. Measure the new length.
Solution. Now, first of all, we draw AB = 2.5 cm and CD = 3.2 cm
Now, we have to draw a line segment

∴ \(\overline{E F}=\overline{A B}+\overline{C D}\) = 2.5 + 3.2 = 5.7 cm
Hence, new length is 5.7 cm.
Question 2. Name the type of triangle and also draw it rough sketch.
(1) ΔABC; ∠A = ∠B = ∠C = 60°
(2) ΔABC; ∠B = ∠C = 50°
(3) ΔABC; ∠A = 45°, ∠B = 45°, ∠C = 90°
(4) ΔABC; ∠A = 50°, ∠B = 60°, ∠C = 70°
Solution. (1) Given, ∠A = ∠B = ∠C = 60°
Hence, it is an equilateral triangle.
(2) Given, ∠B = ∠C = 50°
So, AB = AC
Hence, it is an isosceles triangle.
(3) Given, ∠A = 45°, ∠B = 45°, ∠C = 90°
So, AC = BC
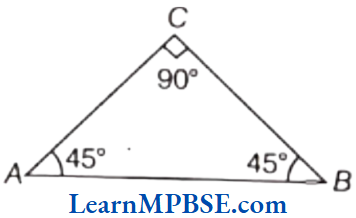
Hence, it is an isosceles right angled triangle.
(4) Given, ∠A = 50°, ∠B = 60°, ∠C = 70°
So, AB ≠ BC ≠ CA
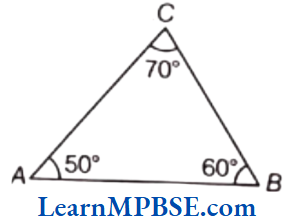
Hence, it is a scalene and acute angled triangle.
MP Board Class 6 Maths Solutions
Question 3. During Maths lab activity, each student was given four broom sticks of length 8 cm, 8 cm, 5 cm, 5 cm to make different types of quadrilaterals.
(1) How many types of quadrilateral can be formed using four broom sticks?
(2) Name the types of quadrilateral formed.
Solution. Given, four broom sticks of length 8 cm, 8 cm, 5 cm and 5 cm.
(1) Three types of quadrilaterals can be formed.
(2) Name of the quadrilaterals are rectangle, parallelogram and kite.
Question 4. Name the following angles of figure using three alphabets
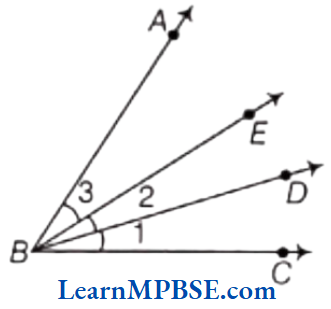
(1) ∠1
(2) ∠2
(3) ∠3
(4) ∠1 + ∠2
(5) ∠2 + ∠3
(6) ∠1 + ∠2 + ∠3
(7) ∠CBA – ∠1
Solution. Name of the angles are as follows:
(1) ∠1 = ∠CBD
(2) ∠2 = ∠DBE
(3) ∠3= ∠EBA
(4) ∠1 + ∠2 = ∠CBE
(5) ∠2 + ∠3 = ∠DBA
(6) ∠1 + ∠2 + ∠3 = ∠CBA
(7) Put the value of ∠CBA [∴ ∠CBA = ∠1 + ∠2 + ∠3]
Now, ∠CBA – ∠1 = ∠1 + ∠2 + ∠3 – ∠1
= ∠2 + ∠3 = ∠DBA [∴ ∠DBA ∠2+ ∠3]
Question 5. In which of the following figures
(1) perpendicular bisector is shown?
(2) bisector is shown?
(3) only bisector is shown?
(4) only perpendicular is shown?
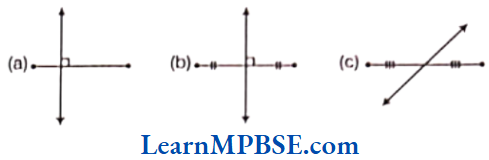
Solution. (1) Perpendicular bisector means, a line is perpendicular to the another line and divides it into two equal parts.
Here, in figure (b), perpendicular bisector is shown.
(2) Bisector means, a line divides the another line in two equal parts.
Here, in figures (b) and (c), bisectors are shown.
(3) Only bisector is shown in figure (c).
(4) Only perpendicular is shown in figure (a).
MP Board Class 6 Maths Solutions
Question 6. Using the given information, name the right angles in the following figures.
(1) AC ⊥ BD
(2) AE ⊥ CE
(3) AC ⊥ CD
(4) OP ⊥ ABC
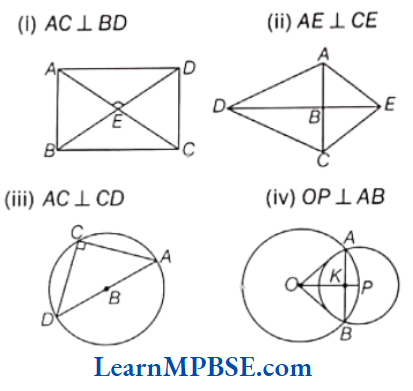
Solution. (1) Since, AC ⊥ BD, it means ∠E = 90°.
∴ ∠AEB, ∠BEC, ∠CED and ∠AED are right angles.
(2) Since, AE ⊥ CE, it means ∠E = 90°
∴ ∠AEC is a right angle.
(3) Since, AC ⊥ CD, it means ∠C = 90°
∴ ∠ACD is a right angle.
(4) Since, OP ⊥ AB, it means ∠K = 90°
∴ ∠AKO, ∠OKB, ∠BKP and ∠AKP are right angles.
MP Board Class 6 Maths Solutions
Question 7. What conclusion can be drawn in each part of figure?
(1) DB is the bisector of ∠ADC.
(2) BD bisects ∠ABC.
(3) DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB.
Solution. We know that bisector line divides an angle into two equal angles.
(1) Since, BD is the bisector of ∠ADC,
∴ ∠ADB = ∠BDC
(2) Since, BD bisects ∠ABC,
∴ ∠ABD = ∠CBD
(3) Since, DC is the bisector of ∠ADB and CA ⊥ DA and CB ⊥ DB
∴ ∠ADC = ∠BDC and ∠CAD = 90°, ∠CBD = 90°
Point
A point determines a location and has no length, breadth or height. It is denoted by a single capital letter like P, Q, R etc. We can mark unlimited points on a plane.
•P
•Q
•R
The above points will be read as point P, point Q and point R.
e.g.
Example 1. Tip of an ice-cream cone gives us an idea of a point. Identify such few situations in your daily life and write them.
Solution. Such few situations in our daily life are as follows:
(1) The corners of a room
(2) Finger tip
(3) The location of a place on map
(4) A satellite in the space
(5) Moon from longer distance
Read and Learn More MP Board Class 6 Maths Solutions
Line Segment
A line segment is the shortest distance between two points which has a definite length.
The line segment joining points A and B is denoted by \(\overline{A B}\) or \(\overline{B A}\). These points A and B are called the end points of the line segment \(\overline{A B}\).

e.g. The edge of a box, a tubelight, the edge of a postcard, etc.
MP Board Class 6 Maths Solutions
Example 2. Name any five line segments in the following figure:
Solution. The five line segments in the figure are
\(\overline{A B}\),\(\overline{B C}\),\(\overline{C D}\),\(\overline{D E}\) and \(\overline{F G}\)
Example 3. Name the line segments in the given figure. Is P, the end point of each line segment?
Solution. The line segment in the given figure are as follows: (1) \(\overline{P Q}\) (or \(\overline{Q P}\))
(2) \(\overline{P R}\) (or \(\overline{R P}\))
(iii) \(\overline{P S}\) (or \(\overline{S R}\))
Yes, from the figure, it is clear that point P is the end point of each line segment.
Line
A line is obtained when a line segment \(\overline{A B}\) is extended on both sides indefinitely and denoted by \(\overleftrightarrow{A B}\). Sometimes it is denoted by a single letter as 1, m.
In other words, two points are enough to fix a line.
i.e. Exactly one line can be drawn through the two given points.

A line has length only. It has neither width nor thickness. An endless line can be drawn on a paper by using two arrow heads one at each end of the portion of the line which indicates that it extends in both directions, indefinitely.

Example 4. Name the line given in all possible ways, choosing only two letters at a time from the three given letters.
Solution. Name of lines in all possible ways are as follows:
(1) By taking P, all possible ways are \(\overleftrightarrow{P Q}\) and \(\overleftrightarrow{P S}\).
(2) By taking Q, all possible ways are \(\overleftrightarrow{Q P}\) and \(\overleftrightarrow{Q S}\).
(3) By taking S, all possible ways are \(\overleftrightarrow{S Q}\) and \(\overleftrightarrow{S P}\).
Intersecting Lines
If two lines have one common point, then they are called intersecting lines. The point at which lines meet is called the point of intersection.
In the figure, lines, l1 and l2 are intersecting lines, which intersects at point O.
e.g. Two adjacent edges of a notebook, the english alphabet X, crossing roads etc.
MP Board Class 6 Maths Solutions
Example 5. Find
(1) two lines can intersect at how many points ?
(2) how many lines can intersect at one point?
Solution. (1) By the definition of intersecting lines, if two lines have one common point, then they are called intersecting lines. So, two lines can intersect at only one point.
Here, l and m have only one intersecting point i.e. O.
(2) There are infinite number of lines that can intersect at one point.
Here, lines l, m, nand p have one common point O, which is there intersecting point.
Note it The number of lines intersect at one point are infinite.
Parallel Lines
Two lines in a plane which are at equal distance from each other and never meet at any point or cross each other even if extended in any direction, are called parallel lines.

In the above figure, lines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) does not intersect each other and the common difference between them is always constant. Hence, \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are parallel to each other and are called parallel lines which can be denoted as \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{C D}\)
e.g. The opposite edges of ruler (or scale), the railway lines etc.
MP Board Class 6 Maths Solutions
Example 6. From the following figure, find the
(1) pairs of intersecting lines.
(2) parallel lines.
(3) point of Intersection.
Solution. (1) Pairs of intersecting lines, F and G, F and H, F and I, G and I, H and I, G and H, J and H, J and G, K and G, K and H.
(2) Parallel lines are J ∥ I, J ∥ K, I ∥ K
(3) Point of intersection are A, B, E, C and D.
Ray
A ray is a portion of a line which starts at a point (called as starting point or initial point) and going in one direction endlessly.
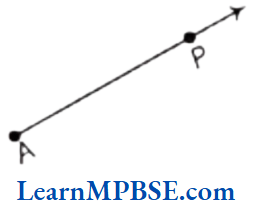
In the above figure, \(\overrightarrow{A P}\) is a ray whose starting point is A and P is a point on the path of the ray. Here, the arrow indicates that the ray \(\overrightarrow{A P}\) is endless in the direction from A to P.
e.g. Beam of light from a lighthouse, ray of light from a torch, Sun rays etc.
Example 7. Identify the rays from the following figure.
Solution. The rays are \(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D}, \overrightarrow{B C}, \overrightarrow{B D} \text { and } \overrightarrow{C D}\).
MP Board Class 6 Maths Solutions
Example 8. From the given figure answer the following.
(1) Identify the rays and name them.
(2) Is M, a starting point of each of these rays?
Solution. (1) In the given figure, there are four rays namely \(\overrightarrow{M N}\), \(\overrightarrow{M A}\), \(\overrightarrow{N A}\) and \(\overrightarrow{M B}\).
(2) No, M is not the starting point of each of these rays. M is starting point of \(\overrightarrow{M N}\), \(\overrightarrow{M A}\), \(\overrightarrow{M B}\) and for \(\overrightarrow{N A}\), M is not the starting point.
Example 9. In the given figure, name all the rays with initial points as P, Q and R, respectively.
(1) Is ray \(\overrightarrow{P Q}\) different from ray \(\overrightarrow{P R}\)
(2) Is ray \(\overrightarrow{R A}\) different from ray \(\overrightarrow{R B}\).
Solution. \(\overrightarrow{P A}, \overrightarrow{P Q}, \overrightarrow{P R}, \overrightarrow{P B}, \overrightarrow{Q A}, \overrightarrow{Q P}, \overrightarrow{Q R}, \overrightarrow{Q B}, \overrightarrow{R A}, \overrightarrow{R P}, \overrightarrow{R Q}, \overrightarrow{R B}\)
(1) No
(2) Yes
Example 10. By using following figure, write
(1) all the points.
(2) a line.
(3) two rays with initial point Q.
(4) two line segments.
Solution. From the given figure,
(1) all the given points are P, Q, O, R and S.
(2) a line is \(\overleftrightarrow{P R}\)
(3) two rays with initial point Q is \(\overrightarrow{Q P}\) and \(\overrightarrow{Q O}\).
(4) two line segments are \(\overline{O Q} \text { and } \overline{O S}\).
MP Board Class 6 Maths Solutions
Example 11. Use the following figure to name
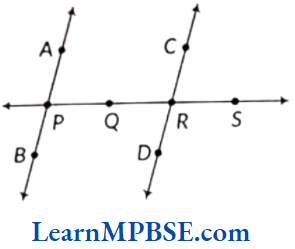
(1) Line containing point R.
(2) Line passing through point Q.
(3) Line on which C lies.
(4) Pair of intersecting lines.
Solution. (1) Here, two lines contain point R, one of them is \(\overleftrightarrow{P S}\).
(2) Here, line passing through point Q is \(\overleftrightarrow{P S}\).
(3) C lies on \(\overleftrightarrow{C D}\).
(4) Two pairs of intersecting lines are \(\overleftrightarrow{P S}\), \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P S}\), \(\overleftrightarrow{C D}\).
Example 12. Draw a rough figure and label suitably in each of the following cases.
(1) Point P, Q, R lies on \(\overline{A B}\).
(2) \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P Q}\) intersect at M.
(3) A line \(\overleftrightarrow{A B}\) which does not contain O.
(4) \(\overleftrightarrow{P Q}\) \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{P S}\) meet at P.
Solution. A rough figure in each of the cases is given below.
(1) Point P, Q, R lies on \(\overline{A B}\).
(2) \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P Q}\) intersect at M.
(3) A line \(\overleftrightarrow{A B}\) which does not contain O.

(4) \(\overleftrightarrow{P Q}\) \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{P S}\) meet at P.
Class 6 Maths Chapter 4 Solutions
Example 13. From the figure, name
(1) All pairs of parallel lines.
(2) All pairs of intersecting lines.
(3) Lines whose point of intersection is P.
(4) Lines whose point of intersection is C.
(5) Lines whose point of intersection is R.
Solution. (1) l ∥ m, l ∥ n, m ∥ n
(2) p and q, p and l, p and m, p and n,q and l, q and m,q and n
(3) l and p
(4) q and m
(5) p and n
Example 14. Consider the following figure of line \(\overleftrightarrow{X Y}\). Say whether following statements are true or false in context of the given figure.
(1) Point Y does not lie on \(\overleftrightarrow{A C}\).
(2) A and C are the end points of line segment \(\overleftrightarrow{A Y}\).
(3) X and Y lies on the extended portion of \(\overleftrightarrow{A C}\).
(4) Point B lies outside of \(\overleftrightarrow{X Y}\).
Solution.
(1) False, because Y lies on the extended portion of \(\overleftrightarrow{A C}\).
(2) False, because it is clear from the figure that point C is between A and Y.
(3) True, it is clear from the figure that point X and Y lie on the extended portion of \(\overleftrightarrow{A C}\).
(4) False, point B lies between \(\overleftrightarrow{X Y}\).
Curve
Any drawing on the paper done without lifting the pencil from the paper and without use of ruler is called a curve. In this sense, a line is also called a curve.
e.g.
There are mainly three types of curves which are given below:
(1) Simple curve If a curve does not cross itself, is called a simple curve.
e.g.
(2) Open curve If a curve does not cut itself, is called an open curve.
In other words, when the end point of a curve are not joined, is called an open curve.
e.g.

(3) Closed curve If a curve cuts itself, is called a closed curve.
In other words, when the end points of a curve are joined, then it is called a closed curve.
e.g.
Position in a Figure
In a closed curve, there are three positions, which are as follows:
In the figure below, A is in the interior, B is on the curve and C is in the exterior.

The interior of a curve together with its boundary is called its region.
Example 1. Classify the following curves as
(1) Open
(2) Closed

Solution. (1) (a) and (c) are open curves.
(2) (b) and (d) are closed curves.
Example 2. Look at the alphabets given below and answer the questions.
P X S B C D V F
Which of the above letters are made of
(1) straight lines only?
(2) curves only?
(3) both straight line and curves?
Solution. (1) Straight lines only : X V F
(2) Curves only : S C
(3) Both straight line and curves : P B D
Class 6 Maths Chapter 4 Solutions
Example 3. Consider the given figure and answer the following questions.
(1) Is it curve ?
(2) Is it closed?
Solution. Since, any drawn figure made without lifting the pencil from the paper is called a curve and if its ends points are joined, it is called a closed curve.
(1) Yes, it is a curve.
(2) Yes, it is closed curve.
Polygon
A simple closed curve made up of line segments is called a polygon.
e.g.

A polygon has finite number of sides.
In the given figure, ABCDE is a polygon.
(1) Sides The line segments, forming a polygon are called its sides. In polygon ABCDE, AB, BC, CD, DE and EA are its sides.
(2) Vertex The meeting point of a pair of sides is called its vertex. In polygon ABCDE, A, B, C, D and E are its vertices.
(3) Adjacent sides Any two sides with a common end point (vertex) are called the adjacent sides of the polygon.
In polygon ABCDE, one pair of adjacent sides is AB and BC (where, B is a common vertex).
(4) Adjacent vertices The end points of the same side of a polygon are called the adjacent vertices.
In polygon ABCDE, A and B, B and C, C and D, D and E, E and A are adjacent vertices.
(5) Diagonals A diagonal is a line segment joining any two non-consecutive vertices.
In polygon ABCDE, AC, AD, BD, BE and CE are diagonals.
Note It No two line segments with a common ends points are coincident.
Example 4. Identify the polygons from the following figures:
Solution. (1) The given figure is not closed. Hence, it is not a polygon.
(2) The given figure is closed. Hence, it is a polygon.
(3) The given figure is closed. Hence, it is a polygon.
(4) In the given figure, two sides are arc. Hence, it is not a polygon.
Class 6 Maths Chapter 4 Solutions
Example 5. Draw a polygon with four line segments and write its
(1) vertices
(2) sides
(3) diagonals
Solution. (1) Vertices of polygon PQRS are P, Q, R and S.
(2) Sides are PQ, QR, RS and SP.
(3) Diagonals are PR and QS.
Example 6. Illustrate, if possible, each one of the following with a rough diagram:
(1) A polygon with five sides.
(2) A polygon with two sides.
Solution. (1) The following figure is shows a polygon with five sides.

(2) It is not possible, because a polygon of two sides cannot be drawn. A minimum of three sides are required to form a polygon.
Example 7. In the given figure, write the
(1) number of sides.
(2) number of vertices.
Solution. (1) The following figure is drawn by joining the sides PQ, QR, RS, ST, TU and UP.
∴ Number of sides = 6
(2) Vertices in the given figure are P, Q, R, S, T and U.
∴ Number of vertices = 6
Class 6 Maths Chapter 4 Solutions
Example 8. From the following figure, P answer the following question.
(1) Is PQRTS a polygon ?
(2) Is M lies in the exterior of the polygon?
(3) Is N lies in the interior of the polygon?
Solution. (i) Yes, since PQRTS is a simple closed curve entirely made of line segments, therefore it is a polygon.
(2) No, M lies in the interior of the polygon.
(3) No, N lies in the exterior of the polygon.
Example 9. Name the points which are inside the figure, on the figure and outside the figure.
Solution. Points in the interior of figure: B, M and Q
Points on the figure: A, D, U and S;
Points on the exterior of the figure: C, E and R.
An angle is made up of two rays starting from a common starting/initial point. The two rays forming the angle are called the arms or sides of the angle and the common initial point is the vertex of the angle.
In the given figure, AOB is an angle and it is denoted by ∠AOB or ∠BOA or ∠O.
Here, OA and OB are arms or sides of angle and O is the vertex of the angle.
(1) In specifying the angle, the vertex is always written as the middle letter.
(2) An angle leads to three divisions of a region i.e. on the angle, the interior of the angle and the exterior of the angle.
In this diagram, point X is in the interior of the angle. Point P, point S and point R are on the angle and point Y is in the exterior of the angle.
Example 1. Write the name of angles in the given figure.
Solution. Here, angles are ∠AOB, ∠BOC and ∠AOC.
Class 6 Maths Chapter 4 Solutions
Example 2. Name the vertex and the arms of ∠PQR, given in the figure below.
Solution. Q is the vertex, PQ and QR are the arms of angle ∠PQR
Example 3. Name the angles in the given figure.
Solution. We know that an angle is made up of two rays starting from a common initial point. So, the angles in given figure are as follow:
(1) ∠A or ∠BAD
(2) ∠B or ∠ABC
(3) ∠C or ∠BCD
(4) ∠D or ∠CDA
Basic Geometrical Ideas Class 6
Example 4. Draw rough diagrams of two angles for the conditions which are possible.
(1) One point in common.
(2) Three points in common.
(3) Four points in common.
Solution. (1) In the diagram, ∠POQ and ∠ROS have point O in common.
(2) In the diagram, ∠POR and ∠ROS have points O, Q and R in common.
(3) In the diagram, ∠POR and ∠QOR have points O, R, S and T common.
Example 5. Draw rough diagrams of two angles such that they have one ray in common.
Solution. Here, ∠ABC and ∠DBA have ray \(\overrightarrow{B A}\) in common.
Example 6. Write the alternate name of the angle ∠SRQ in the given figure.
Solution. The alternate name for the angle ∠SRQ is ∠R
Basic Geometrical Ideas Class 6
Example 7. In the following figure, how many angles are there? Name them.
Solution. There are 6 angles i.e. ∠BOA, ∠COA, ∠DOA, ∠BOC, ∠BOD and ∠COD.
Example 8. How many angles does a polygon of six sides has?
Solution. Angles are formed when corners are formed. Following figure is the polygon with six sides.
Here, six corners are formed.
So, the polygon with six sides has 6 angles.
Note it The number of angles in a polygon is equal to the number of sides of the polygon.
Example 9. Name each of the following angles in different ways.
Solution. (1) ∠RQP or ∠PQR or ∠Q or ∠5
(2) ∠ZYX or ∠XYZ or ∠Y or ∠7
(3) ∠CBA or ∠ABC or ∠B or ∠9
MP Board Class 6 Chapter 4 Maths
Example 10. In figure, write another name for
(1) ∠1
(2) ∠2
(3) ∠3
(4) ∠4
(5) ∠5
Solution.
(1) ∠1 → ∠DAE or ∠EAD
(2) ∠2 → ∠QAC or ∠CAQ
(3) ∠3 → ∠ACD or ∠DCA
(4) ∠4 → ∠ADC or ∠CDA
(5) ∠5 → ∠ARE or ∠ERA
Example 11. In the given diagram, name the point(s).
(1) In the interior of ∠AOB
(2) In the exterior of ∠BOC
(3) On ∠AOB
Solution. (1) In the given figure, point E lies between the sides OA and OB. So, it is in the interior of ∠AOB.
(2) In the given figure, points E, A and G are in the exterior of ∠BOC.
(3) In the given figure, point A, O, D and B lies on the sides OB and OA of ∠AOB, so these points are on ∠AOB.
Question 1. With a sharp tip of the pencil, mark four points on a paper and name them by the letters A, C, P, H. Try to name these points in different ways. One such way could be this
Solution. We can give the name to these given points in different ways as follows:

Question 2. A star in the sky also gives us an idea of a point. Identify atleast five such situations in your daily life.
Solution. Five situations of a point in our daily life are as follow:
(1) Tip of an ice cream cone.
(2) An edge of a table.
(3) Corner of a room.
(4) Corner of a desk.
(5) Corner of a paper.
Question 3. Name the line segments in the figure. Is A, the end point of each line segment?
Solution. We know that the shortest distance between two points is called a line segment.
The line segment joining two points A and B is denoted by \(\overline{A B} \text { or } \overline{B A}\). The line segment in the given figure are as follows:
(1) \(\overline{A B}\) (or \(\overline{B A}\))
(2) \(\overline{A C}\) (or \(\overline{C A}\))
Yes, from the figure, it is clear that point A is the end point of each line segment.
MP Board Class 6 Chapter 4 Maths
Question 4. Take a sheet of paper. Make two folds (and crease them) to represent a pair of intersecting lines and discuss.
(1) Can two lines intersect in more than one point?
(2) Can more than two lines intersect in one point?
Solution. We know that if two lines have one common point, then they are called intersecting lines. By making two folds of a sheet of paper and crease them, we get the following figures.
(1) From figure, it is clear that line l and m intersect at one point O (say) only. So, two lines cannot intersect in more than one point.
(2) Now, we again fold the paper diagonally (i.e. fold the paper three times) and crease them. We get the following figure.
In the figure, four lines l, m, n and o are intersecting at one point O’ (say) only. So, it is clear from the above figure, that more than two lines intersect in one point.
Question 5. (i) Name the rays given in this picture.
(2) Is T a starting point of each of these rays?
Solution. We know that a ray is a part of a line which starts at one point and goes endlessly in a direction.
(1) In the given figure, there are four rays namely \(\overrightarrow{T A}\), \(\overrightarrow{T N}\), \(\overrightarrow{N B}\) and \(\overrightarrow{T B}\).
(2) No, T is not a starting point of each of these rays. T is a starting point of \(\overrightarrow{T A}\), \(\overrightarrow{T B}\) and \(\overrightarrow{T N}\) only but not of \(\overrightarrow{N B}\).
Question 1. Use the figure to name
(1) five points.
(2) a line.
(3) four rays.
(4) five line segments.
Solution. From the given figure,
(1) Five points are B, C, D, E, and O.
(2) A line is \(\overleftrightarrow{B D}\) (or \(\overleftrightarrow{D B}\)).
(3) Four rays are \(\overrightarrow{O B}\), \(\overrightarrow{O C}\), \(\overrightarrow{O E}\) and \(\overrightarrow{O D}\).
(4) Five line segments in the given figure are \(\overline{O B}\), \(\overline{O C}\), \(\overline{O E}\), \(\overline{O D}\) and \(\overline{D E}\)
Note Two points are enough to fix a line. Hence, we can say that two points determine a line.
Question 2. Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given letters.
Solution. We know that a line is a line segment which can extend indefinitely in both directions. Name of lines in all possible ways are as follow:
(1) By taking A, all possible ways are \(\overleftrightarrow{A B}\), \(\overleftrightarrow{A C}\) and \(\overleftrightarrow{A D}\).
(2) By taking B, all possible ways are \(\overleftrightarrow{B C}\), \(\overleftrightarrow{B D}\) and \(\overleftrightarrow{B A}\).
(3) By taking C, all possible ways are \(\overleftrightarrow{C D}\), \(\overleftrightarrow{C A}\) and \(\overleftrightarrow{C B}\).
(4) By taking D, all possible ways are \(\overleftrightarrow{D A}\), \(\overleftrightarrow{D B}\) and \(\overleftrightarrow{D C}\).
MP Board Class 6 Chapter 4 Maths
Question 3. Use the figure to name
(1) line containing point E
(2) line passing through A.
(3) line on which O lies.
(4) two pairs of intersecting lines.
Solution. (1) Here, two lines contain point E, one of them is \(\overleftrightarrow{A E}\).
(2) Here, one line is passing through A, i.e. \(\overleftrightarrow{A E}\).
(3) Line on which O lies, is \(\overleftrightarrow{C O}\) or \(\overleftrightarrow{O C}\).
(4) There are two pairs of intersecting lines i.e. \(\overleftrightarrow{C O}\), \(\overleftrightarrow{A E}\) and \(\overleftrightarrow{A E}\), \(\overleftrightarrow{E F}\).
Question 4. How many lines can pass through
(1) one given point?
(2) two given points?
Solution. (1) Infinite number of lines can pass through one given point.
Let there be a point O on a surface. Now, we can draw infinite lines through it.
(2) Exactly one and only one line can pass through two given points (say A and B)
i.e

Question 5. Draw a rough figure and label suitably in each of the following cases.
(1) Point P lies on \(\overline{A B}\).
(2) \(\overleftrightarrow{X Y}\) and \(\overleftrightarrow{P Q}\) intersect at M.
(3) Line l contains E and F but not D.
(4) \(\overleftrightarrow{O P}\) and \(\overleftrightarrow{O Q}\) meet at 0.
Solution. A rough figure in each of the cases is given below
(1) Point P lies on \(\overline{A B}\).
(2) \(\overleftrightarrow{X Y}\) and \(\overleftrightarrow{P Q}\) intersect at M.
(3) Line l contains E and F but not D.

(4) \(\overleftrightarrow{O P}\) and \(\overleftrightarrow{O Q}\) meet at O.
MP Board Class 6 Chapter 4 Maths
Question 6. Consider the following figure of line \(\overleftrightarrow{M N}\). Say whether following statements are true or false in context of the given figure.
(1) Q, M, O, N, Pare points on the line \(\overleftrightarrow{M N}\).
(2) M, O, N are points on a line segment \(\overline{M N}\).
(3) M and N are end points of line segment \(\overline{M N}\).
(4) O and N are end points of line segment \(\overline{O P}\).
(5) M is one of the end points of line segment \(\overline{Q O}\).
(6) M is point on ray \(\overrightarrow{O P}\).
(7) Ray \(\overrightarrow{O P}\) is different from ray \(\overrightarrow{Q P}\).
(8) Ray \(\overrightarrow{O P}\) is same as ray \(\overrightarrow{O M}\).
(9) Ray OM is not opposite to ray \(\overrightarrow{O P}\).
(10) O is not an initial point of \(\overrightarrow{O P}\).
(11) N is the initial point of \(\overrightarrow{N P}\) and \(\overrightarrow{N M}\).
Solution.
(1) True, because points M, O and N lie on the line \(\overleftrightarrow{M N}\) and points Q, Plie on the extended portion of \(\overleftrightarrow{M N}\) on both sides.
(2) True, because points M, O, N lie on the line segment \(\overline{M N}\).
(3) True, because M to N is the shortest route of line segment \(\overline{M N}\).
(4) False, because it is clear from figure that point Nis between O and P.
(5) False, because it is clear from figure that point Mis between Qand O.
(6) False, because M is outside from ray OP.
(7) True, because all the rays have their own existence.
(8) False, because rays \(\overrightarrow{O P}\) and \(\overrightarrow{O M}\) are in opposite directions.
(9) False, because it is clear from figure that rays OM and OP are opposite.
(10) False, because it is clear from figure that point O is the initial point of \(\overrightarrow{O P}\).
(11) True, because it is clear from figure that ray \(\overrightarrow{N P}\) and \(\overrightarrow{N M}\) start from point N.
Question 7. Try to form a polygon with
(1) Five matchsticks.
(2) Four matchsticks.
(3) Three matchsticks.
(4) Two matchsticks.
In which case was it not possible? Why?
Solution. We know that if a closed simple figure is made up entirely of line segments, then it is called a polygon.
(1) Polygon with five matchsticks
(2) Polygon with four matchsticks.
(3) Polygon with three matchsticks
(4) We know that a polygon is a closed plane figure, bounded by line segments. So, with the help of two matchsticks, it is not possible to make a closed plane figure. Hence, no polygon is formed by two matchsticks.
Question 1. Classify the following curves as (1) Open or (2) Closed.
TIPS A simple curve is one, that does not cross itself. Besides, when the ends of a curve are joined, it is called a closed curve. If its ends are not joined, it is called an open curve.
Solution. (1) (a) and (c) are open curves.
(2) (b), (d) and (e) are closed curves.
Question 2. Draw rough diagram to illustrate the following:
(1) Open curve
(2) Closed curve
Solution. (1) The curve given below is an open curve, since its ends are not joined

(2) The curve given below is a closed curve, since its ends are joined
Question 3. Draw any polygon and shade its interior.
TIPS We know that a simple closed figure made up entirely of line segments is called a polygon and in a closed curve, the interior is inside of the curve.
Solution. ABCD is a polygon, where interior is shaded as given below:
Question 4. Consider the given figure and answer the questions.

(1) Is it a curve?
(2) Is it closed?
TIPS Any drawing drawn without lifting the pencil from the paper is called a curve. A curve is said to be a closed curve, if its ends are joined.
Solution. (1) Yes, it is a curve.
(2) Yes, it is closed.
MP Board Class 6 Chapter 4 Maths
Question 5. Illustrate, if possible, each one of the following with a rough diagram:
(1) A closed curve that is not a polygon.
(2) An open curve made up entirely of line segments.
(3) A polygon with two sides.
Solution. (1) The following figure shows a closed curve, but not a polygon, because a polygon is made by line segments only.

(2) The following figure shows an open curve made up entirely of line segments.

(3) It is not possible, because a polygon of two sides cannot be drawn.
Question 1. Name the angles in the given figure.
Solution. We know that an angle is made up of two rays starting from a common initial point. So, the angles in given figure are as follow:
(1) ∠A or ∠DAB
(2) ∠B or ∠ABC
(3) ∠C or ∠DCB
(4) ∠D or ∠ADC
Question 2 In the given diagram, name the point(s).
(1) In the interior of ∠DOE
(2) In the exterior of ∠EOF.
(3) On ∠EOF.
Solution. (1) In given figure, point A lies between the sides OD and OE.
So, it is in the interior of ∠DOE.
(2) In given figure, points C, A and D are in the exterior of ∠EOF.
(3) In given figure, point E, B, O and Flie on the sides OE and OF of ∠EOF.
So, these points are on ZEOF
MP Board Class 6 Chapter 4 Maths
Question 3. Draw rough diagrams of two angles such that they have
(1) One point in common.
(2) Two points in common.
(3) Three points in common.
(4) Four points in common.
(5) One ray in common.
Solution. (1) The diagram is shown as below:

Here, ∠ROQ and ∠QOP have one point O in common.
(2) The diagram is shown as below:
Here, ∠MON and ∠ONR have two points O and N in common.
(3) The diagram is shown as below:
Here, ∠AOB and ∠BOC have three points B, E and D in common.
(4) The diagram is shown as below:

Here, ∠AOP and ∠AOQ have four points O, A, B and C in common.
(5) In the figure given below, ZSOT and ZPOT have one ray \(\overrightarrow{O T}\) in common.
Question 1. How many points are marked in the following figure?

Answer. 4. 4
Question 2. Number of line segments in figure is

Answer. 2. 10
Question 3. Which of the following has two end points?
Answer. 3. Line segment
Question 4. A line segment has two end points and a line has …. end points.
Answer. 3. 0
Question 5. Number of lines which can be drawn from one point
Answer. 3. Infinite
MP Board Class 6 Chapter 4 Maths
Question 6. If two lines intersect each other, then the common point between them is known as ……
Answer. 3. intersection point
Question 7. Which of these is an example for a pair of the parallel lines?
Answer. 2. Railway track
Question 8. A curve which does not cut itself called
Answer. 1. Open Curve
Question 9. The number of interior points of the following figure is
Answer. 2. 3
Question 10. The least number of line segment required to make a polygon is
Answer. 3. 3
Question 11. In the given figure, JLKM is polygon.
Which of the following is true for the polygon JLKM?
Answer. 3. Side JL is opposite to side MK.
Class 6 Geometry Concepts
Question 12. The number of diagonals of the following figure is
5
2
6
9
Answer. 3. 6
Question 13. Which of the following are the diagonals of the given polygon?
Answer. 1. AD and BE
Question 14. In the given figure, ∠XYZ cannot be written as
Answer. 2. ∠ZXY
Question 15. The number of angles in the given figure are
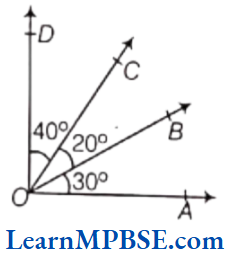
Answer. 4.
Question 1. Assertion (A) Sharper the tip, thinner will be the dot.
Reason (R) A point determines a location.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 2. Assertion (A) A line contains a countless number of points.
Reason (R) Line extends indefinitely in both directions.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 3. Assertion (A) A ray PQ can be written as PQ.
Reason (R) A ray has one end point and extends without limit in one direction only.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 1. Two lines intersect at ……….point.
Solution. One
Question 2. In the given figure, points lying in the interior of the polygon are……….., that in the exterior of the polygon are……….and that on the polygon itself are………….
Solution. O and S, T and N; P, Q, R, M
Class 6 Geometry Concepts
Question 3. The number of common points in the two angles marked in the given figure is …..
Solution. Two
Question 4. The common part between the two angles BAC and DAB in figure is ……
Solution. AB
Question 5. The number of common points in the two angles marked in the given figure is
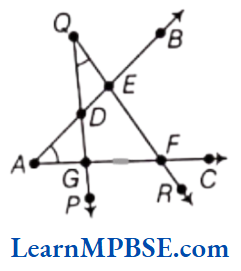
Solution. Four
Question 1. A curve is said to be closed, if its end are not joined.
Solution. False
Question 2. Two parallel lines meet each other at some point.
Solution. False
Question 3. Two non-parallel line segments will always intersect.
Solution. False
Question 4. An angle is made up of two rays starting from a common initial point.
Solution. True
Question 5. Two adjacent angles have exactly one common arm.
Solution. True
Question 1. Match the item of Column A in Column B with their respective value.
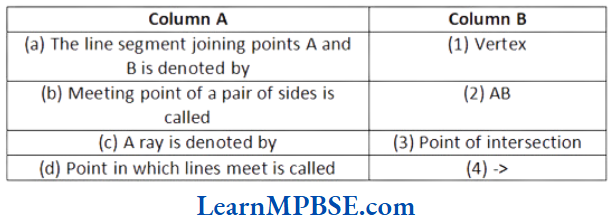
Solution. (a) → (2), (b) → (1), (c) → (4), (d) → (3)
Question 1. Joy learns the art of knitting from his grandmother.
On the basis of the given information, answer the following questions.
(1) Which of the following pictures can be an example of a line segment?

(2) Which of the following is an open curve?

(3) Why is the below figure not considered a polygon?

(4) How many lines can pass through a point?
Solution. (1) (b) Option (b) is the example of a line segment.
(2) (b) An open curve does not cut itself.
(3) Since, a polygon is entirely made up of line segments. Therefore, the following figure is not considered a polygon because it is formed by two line segment and an arc.
(4) By observing the following figure we can say that many lines or infinite number of lines can pass through a point.
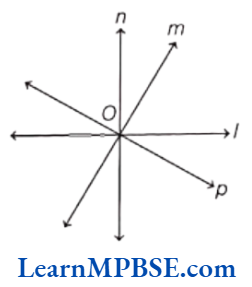
Question 2. Ankit marks five points by folding a rectangular paper sheet as shown below.
On the basis of the given information, answer the following questions.
(1) Choose the right word and fill in the blank. CE is an example of
(a) A ray
(b) An angle
(c) A point
(d) A line segment
(2) Which of the following is not true for both a ray and a line?
(a) They have end points.
(b) They have start points.
(c) They have no thickness.
(d) They can have infinite length.
(3) Fill in the blank with the correct word.
A line segment is a ….. of a line.
Solution. (1) (d) A line segment
(2) (a) A ray is a portion of a line, which starts at a point and goes endlessly in one direction, and a line obtained, when a line segment is extended on both sides indefinitely. Therefore, both does not have end points.
(3) A line segment is part or section of a line.
Question 1. Use the follwoing figure to name:
(1) all the points.
(2) two rays
Solution. (1) The points are O, A, B and C.
(2) Two rays are \(\overrightarrow{O A} \text { and } \overrightarrow{O C}\)
Question 2. Name all the line segments in given figure.

Solution. All the line segments are \(\overline{P Q}, \overline{P R}, \overline{P S}, \overline{Q R}, \overline{Q S} \text { and } \overline{R S} \text {. }\)
Class 6 Geometry Concepts
Question 3. Name the line segments shown in the figure given below.
Solution. The line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E} \text { and } \overline{A E}\)
Question 4. Consider the following figure and write the name of
(1) a ray which contains point A.
(2) a ray which contains point B.
Solution. (1) Ray, which contains point A is \(\overrightarrow{P A}\).
(2) Ray, which contains point B is \(\overrightarrow{Q B}\).
Question 5. Draw two curves that are open.
Solution. The open curves are
Question 6. Draw two curves that are closed.
Solution. The closed curves are
Question 7. Write all exterior and interior points of the given figure.
Solution. Here, interior points are H, I and exterior point is M.
Class 6 Geometry Concepts
Question 8. Name the vertices in given figure.
Solution. The vertices in the above figure are A, B, C and D.
Question 9. Write vertex of opposite side of AB and BC of the given figure.
Solution. Vertex of opposite side of AB is C and of BC is A.
Question 10. Write all vertices of the given figure.
Solution. In the given figure, vertices are A,B,C,D and E.
Question 11. The number of common points in the two angles marked in the given figure is ….
Solution. The common point in ∠BAC and ∠DAE is point A.
Question 1. How many lines can pass through
(1) one given point?
(2) two given points?
Solution. (1) Through one given point, infinite number of lines can be drawn.
(2) Through two given points, only one line can be drawn.
Question 2. Identify parallel line segments in each of the figure given below.
Solution. Parallel lines in the above figures are
(1) ST and QR.
(2) PQ and SR, SP and QR.
(3) PQ and SR, QR and SP.
(4) PQ and TS, QR and TN, SR and NP.
Class 6 Geometry Concepts
Question 3. Name the vertices and the line segments in the given figure.
Solution. The vertices of the figure are A, B, C,D, E and the line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{E A}, \overline{A C}, \overline{A D}\)
Question 4. What is common in the following figures (1) and (2)?
Is figure (1) is a triangle? If not, why?
Solution. In the given figures (1) and (2), both have three line segments. Figure (1) is not a triangle, because it is not a closed curve.
Question 5. Is PQRS a figure of polygon?
Solution. Yes, it is a polygon, because it is a simple closed curve made up of line segments only.
Question 6. In the given figure, list the points which
(1) are in the interior of ∠AOB.
(2) are in exterior of ∠AOB.
(3) lie on ∠AOB.
Solution. (1) The interior points of ∠AOB are S and Q.
(2) The exterior points of ∠AOB are P and R.
(3) The points, which lie on ∠AOB are A, O, B, T and N.
Polygons and Curves for Class 6
Question 7. In the given figure, name the points, which are
(1) in its exterior.
(2) in its interior.
(3) on the figure
Solution. (1) The points which lie in the exterior are F, G and H.
(2) Interior points are A, O and C.
(3) The points which lie on the figure are B, D and E.
Question 8. In the given figure, write
(1) name of the vertex of ∠3.
(2) name of the common arm of ∠1 and ∠2.
(3) name the vertex of ∠4.
Solution. (1) The vertex of ∠3 is B.
(2) Common arm of ∠1 and ∠2 is AC.
(3) The vertex of ∠4 is C.
Polygons and Curves for Class 6
Question 9. Write down six angles involved in the given figure.
Solution. Six angles involved in the above figure are ∠ABC, ∠BCA, ∠CAB, ∠AEC, ∠ABD and ∠DBC.
Question 10. In the following figure, name the angles using three letters.
(1) ∠1 (2) ∠2 (3) ∠3
Solution. Here, we can write the name of angles with the help of given figure:
(1) ∠1 = ∠AOB (2) ∠2 = ∠BOC (3) ∠3 = ∠COD
Question 1. Name the points and then the line segments in each of the following figures.
Solution. (1) The points are A, B, C and line segments are \(\overline{P Q}, \overline{R S}, \overline{P S}\).
(2) The points are A, B, C, D and line segments are \(\overline{A B}, \overline{B C}, \overline{C D} \text { and } \overline{A D}\).
(3) The points are A, B, C, D, E and line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{A E}\).
(4) The points are A, B, C, D, E, F and line segments are \(\overline{A B}, \overline{C D}, \overline{E F}\).
Polygons and Curves for Class 6
Question 2. In the given figure, write
(1) parallel lines.
(2) point of intersection of the line l and n.
(3) point of intersection of the line q and r.
(4) point of intersection of the line m and r.
(5) point of intersection of the line p and m.
Solution. (1) The lines / and m are parallel lines.
(2) Point of intersection of the lines / and n is A.
(3) Point of intersection of the lines q and r is B.
(4) Point of intersection of the lines m and r is D.
(5) Point of intersection of the lines p and m is D.
Question 3. Sohan wants to show gratitude toward his teacher by giving a card made by him. He has three pieces of paper pasted one above the other as shown in the figure. These pieces are arranged in a way that AB ∥ HC ∥ GD ∥ FE.
He wants to decorate the card by putting up a coloured paper on non-parallel sides of the card.
(1) Write the non-parallel sides of the card.
(2) which value is depicted by the Sohan?
Solution. (1) Non-parallel sides are AF and BE.
(2) Respect to teacher, happiness, beauty, and knowledge.
Polygons and Curves for Class 6
Question 4. Look at the following figure and answer the following questions.
(1) Name the four sides of figure made by joining PQRS.
(2) Name the four pairs of adjacent sides.
(3) Name two pairs of opposite sides.
(4) Name a pair of diagonal.
Solution. (1) Four sides of figure PQRS are \(\overline{P Q}, \overline{R S}, \overline{P S} \text { and } \overline{Q R}\).
(2) Four pairs of adjacent sides are PQ and QR, QR and RS, RS and SP, SP and PQ.
(3) Two pairs of opposite sides are QR and PS, PQ and SR.
(4) Pair of diagonal is PR and QS.
Circle Basics Class 6 Solutions
Question 5. Look at figure and mark a point
(1) A, which is in the interior of both ∠1 and ∠2.
(2) B, which is in the interior of only ∠1.
(3) C in the interior of ∠1.
Now, state whether points B and C lie in the interior of ∠2 also.
Solution.
Yes, it is clear from the figure, that the points B and C lie in the interior of ∠2 also.
A factor of a number is an exact divisor of that number i.e. the factor divides the number completely without leaving any remainder.
e.g. 1, 2, 3 and 6 are exact divisors of 6. So, 1, 2, 3 and 6 are factors of 6.
A number is a multiple of each of its factor.
e.g. When 123 x 4, then we can say that 12 is a multiple of 3 and 4.
Diagram
Let us discuss some points about factors and multiples.
(1) I is a factor of every number.
(2) Every number is a factor of itself.
(3) Every factor is less than or equal to the given number.
(4) Number of factors of a given number are finite.
e.g. The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 and 96 which are finite.
(5) Every multiple of a number is greater than or equal to that number.
e.g. Multiples of 3 are 3, 6, 9, 12, 15, …
(6) The number of multiples of a given number is infinite.
e.g. Multiples of 4 are 4, 8, 12, 16, 20,…
(7) Every number is a multiple of itself.
e.g. 7 = 7 x 1 and 11 = 11 x 1
Read and Learn More MP Board Class 6 Maths Solutions
MP Board Class 6 Maths Solutions
Example 1. Write all the possible factors of the following numbers.
(1) 16
(2) 30
(3) 27
(4) 19
Solution. (1) Here, 16 = 1 x 16,16 = 2 x 8,16 = 4 x 4
∴ Factors of 16 are 1, 2, 4, 8 and 16.
(2) Here, 30 = 1 x 30, 30 = 2 x 15, 30 = 3 x 10, 30 = 5 x 6
∴ Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.
(3) Here, 27 = 1 x 27, 27 = 3 × 9
∴ Factors of 27 are 1, 3, 9 and 27.
(4) Here, 19 = 1 × 19
∴ Factors of 19 are 1 and 19.
Note that 0 is not the factor of any number.
Example 2. Write the first four multiples of the following numbers
(1) 5
(2) 12
(3) 13
Solution. (1) Multiples of 5 are
5 x 1 = 5,5 x 2 = 10,5 x 3 = 15,5 x 4 = 20
Hence, the first four multiples of 5 are 5, 10, 15 and 20.
(2) Multiples of 12 are
12 x 1 = 12,12 x 2 = 24,12 x 3 = 36,12 x 4 = 48
Hence, the first four multiples of 12 are 12, 24, 36 and 48.
(3) Multiples of 13 are
13 x 1 = 13, 13 x 2 = 26, 13 x 3 = 39,13 x 4 = 52
Hence, the first four multiples of 13 are 13, 26, 39 and 52.
Note It We can also write the table of required number to get the multiples of that number.
Example 3. Write all the multiples of
(1) 7 upto 90.
(2) 16 less than 150.
Solution. (1) The multiples of 7 upto 90 are
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
7 × 10 = 70
7 x 11 = 77
7 x 12 = 84
Hence, all the multiples of 7 upto 90 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77 and 84..
(2) The multiples of 16 less than 150 are
16 x 1 = 16
16 x 2 = 32
16 x 3 = 48
16 x 4 = 64
16 x 5 = 80
16 X 6 = 96
16 x 7 = 112
16 x 8 = 128
16 x 9 = 144
Hence, all the multiples of 16 less than 150 are 16, 32, 48, 64, 80, 96, 112, 128 and 144.
MP Board Class 6 Maths Solutions
Example 4. Write
(1) the sixth multiple of 19.
(2) the seventh multiple of 23.
Solution. (1) Multiples of 19 are
19, 38, 57, 76, 95, 114, 133, ….
Hence, the sixth multiple of 19 is 114.
(2) Multiples of 23 are
23, 46, 69, 92, 115, 138, 161, 184, 207, 230,….
Hence, the seventh multiple of 23 is 161.
To understand prime and composite numbers, first of all, we have to study about even and odd numbers.
Even Numbers
The numbers which are multiples of 2 are called even numbers. e.g. 2, 4, 6, …, etc. are even numbers.
Odd Numbers
The numbers which are not completely divided by 2 are known as odd numbers. e.g. 1, 3, 5, 7,…, etc. are odd numbers.
Note It A positive integer equal to the sum of its factors. excluding the number itself is said to be a perfect number. The numbers 6, 28,496 and 8128 are perfect numbers.
Example 1. Write the odd and even numbers between the following numbers
(1) 11 and 23
(2) 101 and 115
Solution.
(1) The odd numbers between 11 and 23 are 13, 15, 17, 19 and 21 and the even numbers between 11 and 23 are 12, 14, 16, 18, 20 and 22.
(2) The odd numbers between 101 and 115 are 103, 105, 107, 109, 111 and 113 and the even numbers between 101 and 115 are 102, 104, 106, 108, 110, 112 and 114.
MP Board Class 6 Maths Solutions
Example 2. Show that sum of any two odd or any two even numbers is an even number.
Solution. Let the two odd numbers be 7 and 9.
Their sum = 7 + 9 = 16 (even number)
Hence, the sum of any two odd numbers is an even number.
Again, let the two even numbers be 10 and 12.
Their sum = 10 + 12 = 22 (even number)
Hence, the sum of any two odd or even numbers is an even number.
Note it The sum of any two odd numbers or any two even numbers is always an even number.
Example 3. Write the odd and even multiples of
(1) 9 less than 120
(2) 13 upto 140
Solution. (1) Multiples of 9 less than 120 are
9 x 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 x 5 = 45
9 × 6 = 54
9 x 7 = 63
9 × 8 = 72
9 x 9 = 81
9 × 10 = 90
9 x 11 = 99
9 × 12 = 108
9 × 13 = 117
∴ The odd multiples of 9 less than 120 are 9, 27, 45, 63, 81, 99, 117 and the even multiples of 9 less than 120 are 18, 36, 54, 72, 90, 108.
(2) Multiples of 13 upto 140 are
13 x 1 = 13
13 x 2 = 26
13 × 3 = 39
13 x 4 = 52
13 x 5 = 65
13 × 6 = 78
13 x 7 = 91
13 x 8 = 104
13 x 9 = 117
13 x 10 = 130
∴ The odd multiples of 13 upto 140 are 13, 39, 65, 91, 117 and the even multiples of 13 upto 140 are 26, 52, 78, 104, 130.
Prime Numbers
The numbers other than 1, whose only factors are 1 and the number itself are called prime numbers.
e.g. 2, 3, 5, 7, 11,…, etc. are prime numbers.
2 is the smallest prime number which is even and every prime number except 2 is odd.
Two prime numbers whose difference is 2 are called twin prime numbers.
Method of Finding Prime Numbers
Step 1 List all numbers from 1 to 100.
Step 2 Cross out 1 because it is not a prime number.
Step 3 Encircle 2, cross out all the multiples of 2, other than 2 itself i.e. 4, 6, 8 and so on.
Step 4 You will find that the next uncrossed number is 3. Encircle 3 and cross out all the multiples of 3, other than 3 itself.
Step 5 The next uncrossed number is 5. Encircle 5 and cross out all the multiples of 5, other than 5 itself.
Step 6 Continue this process till all the numbers in the list are either encircled or crossed out.
All the encircled numbers are prime numbers.
All the crossed out numbers, other than 1 are composite numbers.
This method is called the Sieve of Eratosthenes which is invented by Greek mathematician Eratosthenes.
Example 4. Check whether the following number are prime or not?
(1) 17
(2) 39
(3) 41
(4) 56
Solution.
(1) 17 = 1 x 17, 17 = 17 x 1
Since, 17 has only two factors i.e. 1 and 17.
Therefore, 17 is a prime number.
(2) 39 = 1 x 39, 39 = 3 x 13
Since, 39 has four factors i.e. 1, 3, 13 and 39.
Therefore, 39 is not a prime number.
(3) 41 = 1 x 41, 41 = 41 x 1
Since, 41 has only two factors i.e. 1 and 41. Therefore, 41 is a prime number.
(4) 56 = 1 x 56, 56 = 2 x 28, 56 = 4 x 14, 56 = 7 x 8
Since, 56 has eight factors i.e. 1, 2, 4, 7, 8, 14, 28 and 56.
Therefore, 56 is not a prime number.
Example 5. Give two pairs of prime numbers whose difference is 2.
Solution. Two pairs of prime numbers whose difference is 2 are
(1) 3 and 5 (i.e. 5 – 3 = 2) (2) 29 and 31 (i.e. 31 – 29 = 2)
MP Board Class 6 Maths Solutions
Example 6. Observe that 3 x4+1=13 is a prime number. Here, 1 has been added to a multiple of 3 to get a prime number. Give some more examples of this type.
Solution. Some more examples of this type are
3 x 2 + 1 = 7,
3 x 6 + 1 = 19,
3 × 10 + 1 = 31,
3 x 12 + 1 = 37,
3 × 14 + 1 = 43,
3 x 20 + 1 = 61
Here, all numbers 7, 19, 31, 37, 43 and 61 are prime numbers as 1 has been added to the multiples of 3 to get these prime numbers.
Example 7. Find the greatest prime number between 10 and 20.
Solution. Prime numbers between 10 and 20 are 11, 13, 17 and 19. Therefore, the greatest prime number between 10 and 20 is 19.
Example 8. Write four pairs of prime numbers less than 20, whose sum is divisible by 8.
Solution. Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.
Here, 3 + 5 = 8 (divisible by 8) 5 + 11 = 16 (divisible by 8) 11 + 13 = 24 (divisible by 8) 13 + 19 = 32 (divisible by 8)
Hence, four pairs of prime numbers whose sum is divisible by 8 are (3, 5), (5, 11), (11, 13) and (13, 19).
Example 9. The numbers 17 and 71 are prime numbers. Both these numbers have same digits 1 and 7. Find the such pairs of prime numbers upto 100.
Solution. All prime numbers upto 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
Out of these, pairs of prime numbers having same digits are (13, 31), (17,71), (37, 73) and (79,97). Hence, there are 4 pairs of such type.
MP Board Class 6 Maths Solutions
Example 10. Express the following as the sum of two odd prime numbers.
(1) 32
(2) 40
(3) 34
Solution.
(1) We have, 32 = 29 + 3
(2) We have, 40 = 37 +3
(3) We have, 34 = 31 + 3 or 29+5
Example 11. Express each of the following numbers as the sum of three odd primes.
(1) 41
(2) 25
(3) 27
(4) 71
Solution. (1) We have, 41 ⇒ 41 = 11 + 13 + 17,
where 11, 13 and 17 are odd prime numbers.
(2) We have, 25 ⇒ 25 = 5 + 7 + 13,
where 5, 7 and 13 are odd prime number.
(3) We have, 27 ⇒ 27 = 3 + 5 + 19,
where 3, 5 and 19 are odd prime numbers.
(4) We have, 71 ⇒ 71 = 13 + 17 + 41,
where 13, 17 and 41 are odd prime numbers.
Composite Numbers
The numbers having more than two factors are called composite numbers.
e.g. 4, 6, 8, 9, 10,…, etc. are composite numbers.
Note it 1 is neither a prime number nor a composite number because it has only one factor.
Class 6 Maths Chapter 3 Solutions
Example 12. Write all the prime and composite numbers less than 15.
Solution. Prime numbers less than 15 are 2, 3, 5, 7, 11 and 13.
Composite numbers less than 15 are
4, 6, 8, 9, 10, 12 and 14.
Example 13. Write five consecutive composite numbers less than 100, so that there is no prime number between them.
Solution. Five consecutive composite numbers of such type are 54, 55, 56, 57 and 58.
Example 14. State whether the following statements are true or false.
(1) The sum of three even numbers is even.
(2) The sum of two odd numbers and one even number is odd.
(3) All prime numbers are even.
(4) Sum of two prime numbers is always odd.
(5) The product of two even numbers is always odd.
Solution. (1) True, because the sum of three even numbers is always even.
e.g. 2 + 4 + 6 = 12 (even)
(2) False, because the sum of two odd numbers and one even number is always an even number.
e.g. 1 + 5 + 4 = 10 (even)
(3) False, because 2 is only an even prime number. So, all prime numbers are not even.
(4) False, because the sum of two prime numbers is either odd or even.
e.g. 3 + 5 = 8 (even) and 2 + 3 = 5 (odd)
(5) False, because the product of two even numbers is always even.
e.g. 4 × 6 = 24
Class 6 Maths Chapter 3 Solutions
Example 15. Fill in the blanks
(1) The numbers other than 1 whose only factors are 1 and the number itself are called ……..
(2) The smallest odd prime number is……..
(3) Two prime numbers whose difference is 2 are called…….
(4)……. is the smallest prime number which is even …….
Solution.
(1) The numbers other than 1 whose only factors are 1 and the number itself are called prime numbers.
(2) The smallest odd prime number is 3.
(3) Two prime numbers whose difference is 2 are called twin primes.
(4) 2 is the smallest prime number which is even.
To check the divisibility of any number by other, we normally perform actual divison and see whether remainder is zero or not.
To check without actual division, some divisibility test of different numbers are given below
Test of Divisibility by 2
A number is divisible by 2, if it has any of the digits 0, 2, 4, 6 or 8 at its ones place.
Example 1. Check whether the number 246 is divisible by 2 or not.
Solution. Here, in 246 the digit at the ones place is 6.
Hence, 246 is divisible by 2.
Test of Divisibility by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
Example 2. Check whether the number 32523 is divisible by 3 or not.
Solution. Given number is 32523.
Sum of the digits = 3 + 2 + 5 + 2 + 3 = 15, which is divisible by 3.
Hence, the number 32523 is divisible by 3.
Test of Divisibility by 4
A number with three or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4.
Class 6 Maths Chapter 3 Solutions
Example 3. Check whether the number 9524624 is divisible by 4 or not.
Solution. Given number is 9524624.
The number formed by last two digits is 24, which is divisible by 4.
Hence, 9524624 is divisible by 4.
Test of Divisibility by 5
A number is divisible by 5 if it has either 0 or 5 at its ones place.
e.g. Each of the number 60, 225, 625 is divisible by 5.
Test of Divisibility by 6
A number is divisible by 6 if the number is divisible by 2 and 3 both.
Example 4. Check whether the number 297144 is divisible by 6 or not.
Solution. Given number is 297144.
We know that a number is divisible by 6 if it is divisible by both 2 and 3.
The number 297144 has an even digit at its ones place. Therefore, it is divisible by 2.
Sum of all the digits in 297144
= 2 + 9 + 7 + 1 + 4 + 4 = 27, which is divisible by 3.
Therefore, the number 297144 is divisible by 6.
Test of Divisibility by 8
A number with 4 or more digits is divisible by 8 if the number formed by the last three digits is divisible by 8.
Example 5. Check whether the number 79152 is divisible by 8 or not.
Solution. Given number is 79152.
The number formed by last three digits is 152 which is divisible by 8.
Hence, 79152 is divisible by 8.
MP Board Class 6 Chapter 3 Maths
Example 6. Which of the following numbers is divisible by both 4 and 8?
(1) 9638
(2) 9640
Solution. (1) We have, 9638
(a) Divisibility by 4
Number formed by last two digits = 38 On dividing 38 by 4, we get
Remainder ≠ 0
∵ 38 is not divisible by 4, so 9638 is also not divisible by 4.
(b) Divisibility by 8
Number formed by last three digits = 638
On dividing 638 by 8, we get
Remainder ≠ 0
∵ 638 is not divisible by 8, so 9638 is also not divisible by 8.
So, 9638 is not divisible by both 4 and 8.
(ii) We have, 9640
(a) Divisibility by 4
Number formed by last two digits=40
On dividing 40 by 4, we get
Remainder = 0
∵ 40 is divisible by 4, so 9640 is also divisible by 4.
(b) Divisibility by 8
Number formed by last three digits=640
On dividing 640 by 8, we get
Remainder = 0
∵ 640 is divisible by 8, so 9640 is also divisible by 8.
Hence, 9640 is divisible by both 4 and 8.
Test of Divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
Example 7. Is 65403 divisible by 9?
Solution. Given number is 65403.
Sum of the digits of the given number = 6 + 5 + 4 + 0 + 3 = 18, which is divisible by 9.
Hence, 65403 is divisible by 9.
Test of Divisibility by 10
A number is divisible by 10 if it has 0 at its ones place.
Example 8. Check whether the number 49600 is divisible by 10 or not?
Solution. Given number is 49600.
Here, the number 49600 has 0 at its ones place.
Therefore, 49600 is divisible by 10.
Test of Divisibility by 11
A number is divisible by 11 if the difference between the sum of the digits at odd places (from the right to left) and the sum of the digits at even places (from the right to left) of the number is either 0 or divisible by 11, then the number is divisible by 11.
MP Board Class 6 Chapter 3 Maths
Example 9. Is 73854 divisible by 11?
Solution. The given number is 73854.
Sum of its digits at odd places = 4 + 8 + 7 = 19
Sum of its digits at even places = 5 + 3 = 8
Difference of these sums = 19 – 8 = 11, which is divisible by 11.
Hence, 73854 is divisible by 11.
Example 10. Using divisibility tests, determine which of the following numbers are divisible by 2, by 3, by 4, by 5, by 6, by 8, by 9, by 10 and by 11 (say yes or no)?
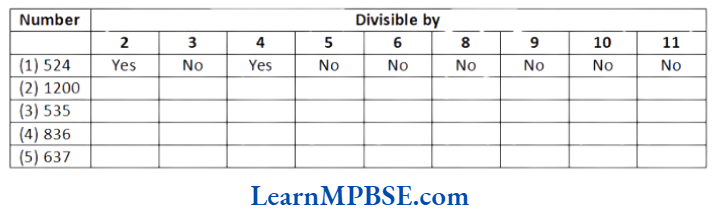
Solution. We know that a number is divisible by
2, if it has digits 0, 2, 4, 6 or 8 at its ones place.
3, if the sum of the digits is a multiple of 3 or it is divisible by 3.
4, if last two digits of the number is completely divisible by 4.
5, if a number has 0 or 5 at its ones place.
6, if it is divisible by 2 and 3 both.
8, if last three digits of the number is completely divisible by 8.
9, if the sum of the digits of the number is divisible by 9.
10, if a number has 0 at its ones place.
11, if the difference of sum of the digits at even place and sum of the digits at odd place is either 0 or multiple of 11. Hence,
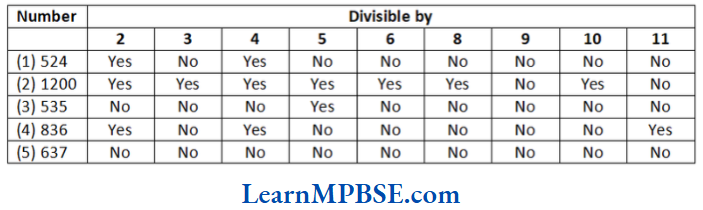
Example 11. In each of the following replace by the smallest and the greatest digit, so that the number formed is divisible by 3.
(1) 12525 * 2
(2) 251 * 3373
Solution. (1) We have, 12525 * 2
Sum of the given digits = 1 + 2 + 5 + 2 + 5 + 2 = 17
∵ Multiples of 3 greater than 17 are
18, 21, 24, 27, 30,…
∴ 18 – 17 = 1; 21 – 17 = 4; 24 – 17 = 7; 27 – 17 = 10
But 10 is not a single digit.
∴ Smallest digit = 1 and greatest digit = 7
(2) We have, 251 3373
Sum of the given digits=2+5+1+3+3+7+3=24
∵ 24 is a multiple of 3, so smallest digit = 0
Now, multiples of 3 greater than 24 are
27, 30, 33, 36,…
∴ 27 – 24 = 3; 30 – 24 = 6; 33 – 24 = 9; 36 – 24 = 12
But 12 is not a single digit.
∴ Smallest digit = 0 and greatest digit=9
Example 12. In each of the following replace by a digit so that the number formed is divisible by 11. (II) 866194
(1) 64 * 2456
(2) 86 * 6194
Solution. (1) Let the required unknown digit be x. Then, the number becomes
where, O = odd and E = even
Sum of digits at odd places from right = 6 + 4 + x + 6
= 16 + x
Sum of digits at even places from right = 5 + 2 + 4 = 11
∵ Number is divisible by 11.
∴ Difference of digits will be 0 or 11.
⇒ 16 + x – 11 = 0 or 11 ⇒ x + 5 = 0 or 11
On taking difference 0, x + 5 = 0 ⇒ x = -5 (not possible)
On taking difference 11, x + 5 = 11 ⇒ x = 11 – 5
⇒ x = 6
So, the required digit to write in place of * is 6.
(2) Let the required unknown digit be x.
Then, the number becomes
where, O = odd and E = even
Sum of digits at odd places from right
4 + 1 + x + 8 = 13 + x
Sum of digits at even places from right=9+6+6=21
∵ Number is divisible by 11.
∴ Difference of digits will be 0 or 11.
⇒ 13 + x – 21 = 0 or 11 ⇒ x – 8 = 0 or 11
On taking difference 0, x – 8 = 0 ⇒ x = 8
On taking difference 11, x – 8 = 11
⇒ x = 11 + 8 ⇒ x = 19
[but 19 is not a single digit number, so it is not possible]
So, required digit to write in place of * is 8.
In the first topic, we have studied about factors and multiples of numbers. Now, we will study about common factors and common multiples.
Common Factors
The factors which are common of each of the given numbers are called their common factors.
Example 1. Find the common factors of
(1) 8 and 20
(2) 35 and 50
(3) 6, 12 and 18
(4) 8, 16 and 24
Solution. (1) Factors 8 = 1,2,4,8
Factors of 20 = 1, 2, 4, 5, 10, 20
Hence, the common factors of 8 and 20 are 1, 2 and 4.
(2) Factors 35 = 1,5,7,35
Factors of 50 = 1, 2, 5, 10, 25, 50
Hence, the common factors of 35 and 50 are 1 and 5.
(3) Factors of 6 = 1, 2, 3, 6
Factors of 12= 1, 2, 3, 4, 6, 12
Factors of 181, 2, 3, 6, 9, 18
Hence, the common factors of 6, 12 and 18 are 1, 2, 3 and 6.
(4) Factors of 8 = 1, 2, 4, 8
Factors of 16 = 1, 2, 4, 8, 16
Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Hence, the common factors of 8, 16 and 24 are 1, 2, 4 and 8.
Example 2. A number is divisible by 14. By what other numbers will that number be divisible?
Solution. If any number is divisible by 14, then this number will also be divisible by the factors of 14 i.e. by 1, 2 and 7.
Example 3. A number is divisible by 2, 3 and 5. By which other number will that number be always divisible?
Solution. If a number is divisible by 2, 3 and 5, then it is always divisible by their products i.e. 2 × 3 × 5 = 30
Note it If a number is divisible by any two or more numbers, then it is always divisible by their products.
Common Multiples
The multiples which are common to each of the given numbers are called their common multiples.
MP Board Class 6 Chapter 3 Maths
Example 4. Find the first three common multiples of
(1) 2 and 3
(2) 12 and 18
Solution. (1) Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18,…
Multiple of 3 are 3, 6, 9, 12, 15, 18, …
Hence, the first three common multiples of 2 and 3 are 6, 12 and 18.
(2) Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108,…
Multiples of 18 are 18, 36, 54, 72, 90, 108, …
Hence, the first three common multiples of 12 and 18 are 36, 72 and 108.
Example 5. Write all the numbers less than 100 which are common multiples of 4 and 5.
Solution. Multiples of 4 less than 100 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96
Multiples of 5 less than 100 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95
Hence, the common multiples of 4 and 5 less than 100 are 20, 40, 60 and 80.
Co-prime Numbers
Two numbers which have only 1 as their common factor are called co-prime numbers.
Note it Any two prime numbers are always co-primes but two co-prime numbers need not to be prime numbers.
MP Board Class 6 Chapter 3 Maths
Example 6. Which of the following pairs are co-primes?
(1) 8, 25
(2) 4, 10
Solution. (1) Factors of 8 = 1, 2,4,8
Factors of 25 = 1, 5, 25
∴ 8 and 25 have only 1 as common factor.
∴ 8 and 25 are co-prime numbers.
(2) Factors of 4 = 1,2,4
Factors of 10 = 1, 2, 5,10
∴ 4 and 10 have 1, 2 as common factors.
∴ 4 and 10 are not co-prime numbers.
If a natural number is expressed as the product of prime numbers, then the factorisation of the number is called its prime factorisation.
Example 1. Find the prime factorisation of 630.
Solution. By division method,
∴ 630 = 2 × 3 × 3 x 5 x 7
which is the required prime factorisation.
Prime Factorisation by Factor Tree Method
Expressing a number with the help of factor tree. Let us factorise 36 in three different ways as given below:
Thus, 36 = 2 x 2 x 3 x 3; 36 = 3 x 2 x 2 x 3; 36 = 3 × 3 × 2 × 2
In all the above factorisations of 36, we ultimately arrive only one factorisation 2 x2 x3x3 and such a factorisation is called a prime factorisation.
Example 2. Find the prime factorisation of 90.
Solution. By factor tree method,
∴ 90 = 2 × 3 × 3 × 5 which is the required prime factorisation.
Hence, the missing numbers are 2, 3 and 3.
Class 6 Maths Prime And Composite Numbers
Example 3. Write down the missing numbers in the below factor trees of 72.
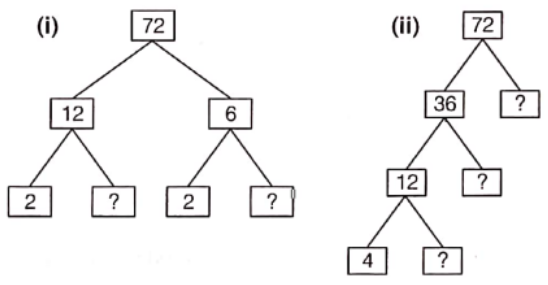
Solution. (1) ∴ 12 = 2 x 6 and 6 = 2 x 3
Hence, the missing numbers are 6 and 3.
(2) ∴ 72 = 36 × 2,
36 12 x 3 and 12=4×3
Example 4. Fill in the given space.
Prime factorisation of 3927 = 3 x 7 x … x 17
Solution. We have, 3927

∴ Prime factorisation of 3927 = 3 x 7 x 11 x 17
So, the required number to write in given space is 11.
Example 5. Write the smallest 4-digit number and all its prime factors.
Solution. Smallest 4-digit number = 1000

∴ Prime factors of 1000 = 2 x 2 x 2 x 5 x 5 x 5
Class 6 Maths Prime And Composite Numbers
Example 6. Write the greatest 5-digit number and all its prime factors.
Solution. Greatest 5-digit number = 99999

∴ Prime factors of 99999 = 3 x 3 x 41 x 271
Example 7. In which of the following expression, prime factorisation has been done?
(1) 36 = 2 × 3 × 6
(2) 54 = 2 x 3 x 3 x 3
(3) 56 = 2 x 4 x 7
(4) 76 = 2 x 2 x 19
Solution. (1) We have, 36 = 2 × 3 × 6
Here, 6 is not a prime number.
So, it is not the prime factorisation of 36.
(2) We have, 54 = 2 x 3 x 3 x 3
Here, 2 and 3 are prime numbers.
So, it is the prime factorisation of 54.
(3) We have, 56 = 2 x 4 x 7
Here, 4 is not a prime number.
So, it is not the prime factorisation of 56.
(4) We have, 76 = 2 x 2 x 19
Here, 2 and 19 are prime numbers.
So, it is a prime factorisation of 76.
Example 8. I am the smallest number, having four different odd prime factors. Can you find me?
Solution. Since, the number is smallest, so four different smallest odd prime factors are 3, 5, 7 and 11.
∴ Smallest number having four different odd prime factors
= 3 x 5 x 7 x 11 = 1155.
Example 9. Write all the prime factors of 105 and arrange them in ascending order. Is there Is any relation between the two consecutive prime factors?
Solution. Prime factorisation of 105
∴ 105 = 3 x 5 x 7
Ascending order of prime factors of 105 is 3, 5, 7.
Here, 5 – 3 = 2 and 7 – 5 = 2
So, the relation between two consecutive
prime factors of 105 is that the difference of two consecutive prime factors is 2.
The Highest Common Factor (HCF) of two or more numbers is the highest (or greatest) factor out of their common factors. It is also known as Greatest Common Divisor (GCD).
Example 1. Find the HCF of the following numbers.
(1) 24 and 48
(2) 18 and 60
(3) 15, 25 and 30
(4) 12, 16 and 28
Solution. (1) We have, 24 and 48.
Factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.
The common factors of 24 and 48 are 1, 2, 3, 4, 6, 8, 12 and 24.
∴ HCF of 24 and 48 = 24
(2) We have, 18 and 60.
Factors of 18 are 1, 2, 3, 6, 9 and 18.
Factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60.
The common factors of 18 and 60 are 1, 2, 3 and 6.
∴ HCF of 18 and 60=6
(3) We have, 15, 25 and 30.
Factors of 15 are 1, 3, 5 and 15.
Factors of 25 are 1, 5 and 25.
Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.
The common factors of 15, 25 and 30 are 1 and 5.
∴ HCF of 15, 25 and 30=5
(4) We have 12, 16 and 28.
Factors of 12 are 1, 2, 3, 4, 6 and 12.
Factors of 16 are 1, 2, 4, 8 and 16.
Factors of 28 are 1, 2, 4, 7, 14 and 28.
The common factors of 12, 16 and 28 are 1, 2 and 4.
∴ HCF of 12, 16 and 28 = 4
Class 6 Maths Prime And Composite Numbers
Example 2. What is the HCF of
(1) two prime numbers?
(2) two consecutive even numbers?
Solution. (1) Let two prime numbers be 7 and 17.
Factors of 7 are 1 and 7.
Factors of 17 are 1 and 17.
∴ HCF of 7 and 17 is 1.
∴ Hence, HCF of two prime numbers is 1.
(2) Let the two consecutive even numbers be 8 and 10.
Factors of 8 are 1, 2, 4 and 8.
Factors of 10 are 1, 2, 5 and 10
The common factors of 8 and 10 are 1 and 2.
∴ HCF of 8 and 10 is 2.
∴ Hence, HCF of two consecutive even numbers is 2.
HCF by Prime Factorisation Method
In this method, first we find the prime factorisation of each of the given numbers. HCF is the product of all the different common prime factors of the given numbers using each common prime factor the least number of times it appears in the prime factorisation of all of the given numbers.
Example 3. Find the HCF of
(1) 48 and 84
(2) 18 and 60
(3) 15, 25 and 30
(4) 12, 16 and 28
Solution. (1) Here, the given numbers are 48 and 84.
Now, prime factorisation of given numbers are
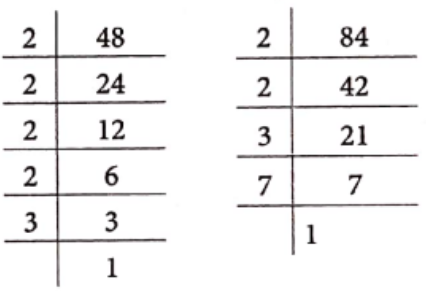
So, 48 = 2 x 2 x 2 x 2 x 3 and 84 = 2 × 2 × 3 × 7
Here, 2 occurs as a common prime factor atleast 2 times and 3 atleast 1 time in both given numbers. Hence, HCF of 48 and 84 = 2×2 x3=12
(2) Here, the given numbers are 18 and 60.
Now, prime factorisation of given numbers are
So, 18 = 2 x 3 x 3 and 60 = 2 x 2 x 3 x 5
Here, 2 and 3 each occurs as a common factor atleast once in both the given numbers.
Hence, HCF of 18 and 60=2×3=6
(3) Here, the given numbers are 15, 25 and 30.
Now, prime factorisation of given numbers are
So, 15 = 3 x 5, 25 = 5 x 5, and 30 = 2 x 3 x 5
Here, 5 occurs as a common factor atleast once in each of the given number.
Hence, HCF of 15, 25 and 30=5.
(4) Here, the given numbers are 12, 16 and 28.
Now, prime factorisation of given numbers are
So, 12 = 2 x 2 x 3
16 = 2 × 2 × 2 × 2
and 28 = 2 × 2 x 7
Here, 2 occurs as a common factor atleast 2 times in each of the given number.
Hence, HCF of 12, 16 and 28 = 2 x 2 = 4
Class 6 Maths Prime And Composite Numbers
Example 4. In the factorisation of two co-prime numbers 6 and 25, we found that there is no common prime factor In the prime factorisation of 6 and 25, so HCF of 6 and 25 is 0. Check whether the answer is correct or not and if not correct, then find the correct HCF?
Solution. Prime factorisation of 6 = 2 x 3
Prime factorisation of 25 = 5 x 5
No, the answer is not correct.
Because 0 (zero) cannot be the factor of any number.
If there is no common factor, then it means 1 is the common factor.
∴ HCF of 6 and 25 = 1
Example 5. What will be the HCF of (3 x 5 x 11 × 13), (5 × 11 x 17 × 21) and (5 x 11 x 7 × 13)
Solution. Given prime factorisations are
(3 x 5 x 11 x 13), (5 x 11 x 17 x 21) and (5 x 11 x 7 x 13)
In the above prime factorisations, 5 and 11 each occurs as a common factor atleast once.
Hence, HCF of given factorisation = 5×11=55
The Lowest Common Multiple (LCM) of two or more numbers is the lowest (or smallest or least) multiple out of their common multiples.
Example 1. Find the LCM of the following numbers.
(1) 3 and 4
(2) 28 and 42
Solution. (1) Multiples of 3=3, 6, 9, 12, 15, 18, 21, 24, …
Multiples of 4 = 4, 8, 12, 16, 20, 24, …
Common multiples of 3 and 4 = 12, 24
∴ LCM of 3 and 4 is 12.
(2) Multiples of 28= 28, 56, 84, 112, 140, 168,…
Multiples of 42=42, 84, 126, 168, 210, …
Common multiples of 28 and 42= 84, 168,…
∴ LCM of 28 and 42 is 84.
LCM by Prime Factorisation Method
In this method, first we find the prime factorisation of each of the given numbers. Now, LCM is the product of all the different prime factors of the given numbers, using each common prime factor the greatest number of times it appears in the prime factorisation of any of the given numbers.
Example 2. Find the LCM by prime factorisation method:
(1) 20 and 24
(2) 10,15 and 25
Solution. (1) Here, the given numbers are 20 and 24.
Now, prime factorisation of given numbers are
20 = 2 x 2 x 5 and 24 = 2 x 2 x 2 x 3
In these prime factorisations, the maximum number of times the prime factor 2 occurs is three, this happens for 24. Similarly, the prime factor 5 occurs only once is 20 and the prime factor 3 occurs only once is 24.
∴ LCM of 20 and 24 = 2 x 2 x 2 x 3 x 5 = 120
(2) Here, the given numbers are 10, 15 and 25.
Now, prime factorisation of given numbers are
10 = 2 x 5,15 = 3 x 5 and 25 = 5 × 5
In these prime factorisation, the maximum number of times the prime factor 5 occur is two, this happens for 25. Similarly the prime factor 2 occurs only once in 10 and the prime factor 3 occurs only once is 15.
∴ LCM of 10, 15 and 25 = 2 x 3 x 5 x 5 = 150
LCM by Division Method
In this method, we arrange the given numbers in a line in any order. Now, we divide by a lowest prime number which divides any one of the given numbers and carry forward the other numbers which are not divisible. This process is repeated till we get all the number in the row is 1.
HCF and LCM for Class 6
Example 3. Find the LCM by division method.
(1) 36, 40 and 126
(2) 12, 15, 20 and 27
Solution. (1) LCM of 36, 40 and 126

∴ LCM = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520
(2) LCM of 12, 15, 20 and 27

∴ LCM = 2 x 2 x 3 x 3 x 3 x 5 = 540
Example 4. Find the LCM of the following numbers in which one number is the factor of the other.
(1) 5 and 15
(2) 4 and 12
(3) 6 and 24
What do you observe in the results so obtained?
Solution. (1) LCM of 5 and 15

∴ LCM = 3 x 5 = 15
(2) LCM of 4 and 12
∴ LCM = 2 x 2 x 3 = 12
(3) LCM of 6 and 24

∴ LCM = 2 x 2 x 2 x 3 = 24
Here, we observe that in all parts, LCM of the given numbers is the larger of two numbers because one number is factor of the other number.
Note It If one number is the factor of the other, then the LCM of the two numbers will be equal to the greater number.
Example 5. Find the LCM of the following numbers. Observe a common property from the obtained LCM. Is LCM the product of two numbers In each case?
(1) 21 and 4
(2) 6 and 7
(3) 16 and 9
Solution. (1) LCM of 21 and 4

∴ LCM = 2 x 2 x 3 x 7 = 84
(2) LCM of 6 and 7
∴ LCM = 2 x 3 x 7 = 42
(3) LCM of 16 and 9
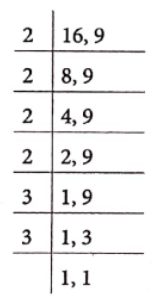
∴ LCM = 2 × 2 × 2 × 2 × 3 × 3 = 144
Here, we see that in each case,
LCM of given numbers is a multiple of 3 and 2.
Yes, in each case LCM is equal to the product of given two numbers.
Note it The LCM of two co-prime numbers is always equal to the product of two numbers.
Applications of HCF and LCM
We come across a number of situations in which we have to use of the concepts of HCF and LCM. Some application-based examples are given below:
HCF and LCM for Class 6
Example 6. The HCF of three numbers is 23. If they are in the ratio of 1 : 2 : 3, then find the numbers.
Solution. Let the numbers x, 2x and 3x.
∴ Their HCF is x.
But given HCF = 23
∴ x = 23
2x = 2 x 23 = 46
and 3x = 3 x 23 = 69
Hence, the numbers are 23, 46 and 69.
Example 7. If three numbers are 2a, 3a and 5a, then what will be their LCM?
Solution. The LCM of 2a, 3a and 5a is 30a because 30a is the smallest or lowest number which is divisible by 2a, 3a and 5a.
Example 8. Find the greatest number which divides 285 and 1249, leaving remainder 9 and 7, respectively.
Solution. Here, we have to find the greatest number which divides (285 – 9) and (1249 – 7) exactly.
∴ The required number is HCF of 276 and 1242.
Prime factorisation of 276=2 x 2 x 3 x 23
Prime factorisation of 1242 = 2 x 3 x 3 x 3 x 23
∴ HCF of 276 and 1242 = 2 × 3 × 23 = 138
Hence, the required number is 138.
Example 9. Find the smallest 3-digit number which is exactly divisible by 4, 6 and 8?
Solution. Firstly, we have to find out the LCM of 4, 6 and 8.

∴ LCM = 2 x 2 x 2 x 3 = 24
We know that smallest 3-digit number is 100.
On dividing 100 by 24, we get remainder 4.
Now, required 3-digit number which is exactly divisible by 24
= Smallest 3 – digit number + Divisor – Remainder
= 100 + 24 – 4 = 120
HCF and LCM for Class 6
Example 10. Find the greatest 3-digit number which is exactly divisible by 6, 8 and 10?
Solution. Firstly, we have to find out the LCM of 6, 8 and 10.

∴ LCM = 2 x 2 x 2 x 3 x 5 = 120
We know that largest 3-digit number = 999
On dividing 999 by 120, we get remainder 39.
Now, required 3-digit number which is exactly divisible by 120
= Greatest 3 – digit number – Remainder
= 999 – 39 = 960
Example 11. Find the least number which when divided by 12, 16 and 18 leave remainder 5 in each case.
Solution. First, we have to find out the LCM of 12, 16 and 18.

∴ LCM = 2 x 2 x 2 x 2 x 3 x 3 = 144
Now, required number = LCM + Remainder
= 144 + 5 = 149
Hence, the required number is 149.
Example 12. Dolly purchases two bags of sugar of weight 75 kg and 105 kg. Find the maximum value of weight which can measure the two bags exact number of times.
Solution. For getting the maximum value of weight, we have to find out the HCF of 75 kg and 105 kg.
Now, prime factorisation of 75 = 3 x 5 x 5
and prime factorisation of 105 = 3 x 5 x 7
∴ HCF of 75 and 105 = 3 x 5 = 15
Hence, the required maximum value of weight is 15 kg.
Example 13. Five bells toll at intervals of 12 sec, 15sec, 20 sec, 25sec and 45 sec, respectively. If all of them toll at 7 am, then at what time will they toll together again?
Solution. Firstly, we have to find out the LCM of 12, 15, 20, 25 and 45.

∴ LCM = 2 x 2 x 3 x 3 x 5 x 5 = 900
= \(\frac{900}{60}=15 \mathrm{~min}\)
So, time when they will toll together again
07 : 00 : 00 + 15 : 00 = 07 : 15 : 00
HCF and LCM for Class 6
Example 14. A girl saves * 3.65 daily. Find the least number of days in which she will be able to save an exact number of rupees.
Solution. Here, ₹ 3.65 = 365 paise
The exact number of rupees will be a multiple of 100.
So, we have to find the LCM of 365 and 100.
100 = 2 x 2 x 5 x 5
and 365 = 5 x 73
∴ LCM of 365 and 100 = 2 x 2 x 5 x 5 x 73 = 7300
So, the girl saved 7300 paise.
Hence the least number of days required to save 7300-20 days.
7300 paise = \(\frac{7300}{365}=20 \text { days. }\)
Example 15. On a evening walk, three persons step off together and their steps measures 42 cm, 49 cm and 56 cm, respectively. What is the minimum distance each should walk, so that each can cover the same distance in complete steps?
Solution. Here, the required minimum distance will be equal to LCM of measures of their steps because the minimum distance each persons should walk must be the least common multiple of the measures of their steps. So, we have to find out the LCM of 42, 49 and 56.
i.e.

∴ LCM of 42, 49
and 56 = 2 x 2 x 2 x 3 x 7 x 7 = 1176
Hence, 1176 cm is the required minimum distance.
Question 1. Find the possible factors of 45, 30 and 36.
Solution. (1) Here,
45 = 1 x 45; 45 = 3 x 15; 45 = 5 x 9
∴ Factors of 45 are 1, 3, 5, 9, 15 and 45.
(2) Here,
30 = 1 x 30; 30 = 2 x 15; 30 = 3 x 10; 30 = 5 × 6
∴ Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.
(3) Here,
36 = 1 x 36; 36 = 2 x 18; 36 = 3 x 12; 36 = 4 x 9; 36 = 6 X 6
∴ Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.
Question 2. Match the items in column A with the items in column B.
Solution.
(1) Factors of 35 are 5 and 7 and we know that a number is a multiple of each of its factor. Hence, 35 is a multiple of 7.
(2) We know that a factor of a number is an exact divisor of that number.
Here, 30 is divided by 15. So, 15 is a factor of 30.
(3) Factors of 16 are 2 and 8 and we know that, a number is a multiple of each of its factor. Hence, 16 is a multiple of 8.
(4) We know that every number is a factor of itself. So, 20 is a factor of itself i.e. 20.
(5) We know that a factor of a number is an exact divisor of that number. Here, 50 is divided by 25. So, 25 is a factor of 50.
Now, matching of these items is as follows
(1) → (b) (2) → (d) (3) → (a) (4) → (f) (5) → (e)
Question 3. Find all the multiples of 9 upto 100.
Solution. All the multiples of 9 up to 100 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90 and 99.
Question 4. Observe that 2 x 3+1 = 7 is a prime number. Here, 1 has been added to a multiple of 2 to get a prime number. Can you find some more numbers of this type?
Solution. Some more numbers of this type are as follows
2 x 2 + 1 = 5, 2 x 5 + 1 = 11, 2 x 6 + 1 = 13
2 x 8 + 1 = 17, 2 x 9 + 1 = 19, 2 x 11 + 1 = 23
Here, all numbers 5, 11, 13, 17, 19 and 23 are prime numbers and 1 has been added to a multiple of 2 to get these prime numbers.
HCF and LCM for Class 6
Question 5. What is the sum of any two
(1) odd numbers?
(2) even numbers?
Solution.
(1) Let the two odd numbers be 5 and 7.
Their sum = 5 + 7 = 12 (even number)
Taking one more example.
Let the two odd numbers be 3 and 7
Their sum = 3 + 7 = 10 (even number)
Hence, we can say that sum of any two odd numbers is an even number.
(2) Let the two even numbers be 4 and 8.
Their sum = 4 + 8 = 12 (even number)
Taking one more example.
Let the two even numbers be 6 and 20.
Their sum = 6 + 20 = 26 (even number)
Hence, we can say that sum of any two even numbers is an even number.
Question 6. The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers upto 100.
Solution. All prime numbers upto 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97. Out of these prime numbers, pairs of prime numbers having same digits are
(1) 13,31
(2) 17,71
(3) 37, 73
(4) 79,97
Hence, there are 4 pairs of such types.
Question 7. Write down separately the prime and composite numbers less than 20.
Solution. Prime numbers are those numbers whose only factors are 1 and the number itself.
So, prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.
Composite numbers are those numbers which have more than two factors.
So, composite numbers less than 20 are 4, 6, 8, 9, 10, 12, 14, 15, 16 and 18.
Question 8. What is the greatest prime number between 1 and 10?
Solution. Prime numbers between 1 and 10 are 2, 3, 5 and 7. Therefore, the greatest prime number between 1 and 10 is 7.
Question 9. Give three pairs of prime numbers whose difference is 2.
[Remark Two prime numbers whose difference is 2 are called twin primes].
Solution. Three pairs of prime numbers whose difference is 2 are
(1) (5,7) i.e.7 – 5 = 2
(2) (11, 13) i.e.13 – 11 = 2
(3) (17, 19) i.e. 19 – 17 = 2
Question 10. Which of the following numbers are prime?
(1) 23
(2) 51
(3) 37
(4) 26
Solution.
(1) We find that 23 is not exactly divisible by any of the prime numbers 2, 3, 5, 7, 11, 17 and 19. So, it is a prime number.
(2) We find that 51 is divisible by 3. So, it is not a prime number.
(3) We find that 37 is not exactly divisible by any of the prime numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 and 31. So, it is a prime number.
(4) We find that 26 is exactly divisible by 2 and 13. So, it is not a prime number.
HCF and LCM for Class 6
Question 11. Write seven consecutive composite numbers less than 100, so that there is no prime number between them.
Solution. Seven composite numbers of such type are as follows 90, 91, 92, 93, 94, 95, and 96.
Question 12. Express each of the following numbers as the sum of three odd primes.
(1) 21
(2) 31
(3) 53
(4) 61
Solution. (1) We have, 21
⇒ 21 = 3 + 5 + 13
where 3, 5 and 13 are odd prime numbers.
(2) We have, 31
⇒ 31 = 3 + 5 + 23
where 3, 5 and 23 are odd prime numbers.
(3) We have, 53
⇒ 53 = 13 + 17 + 23
where 13, 17 and 23 are odd prime numbers.
(4) We have, 61
⇒ 61 = 7 + 13 + 41
where 7, 13 and 41 are odd prime numbers.
Question 13. Write five pairs of prime numbers less than 20 whose sum is divisible by 5. [Hint 3+7=10]
Solution. Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.
Here,
2 + 3 = 5 (divisible by 5)
2 + 13 = 15 (divisible by 5)
3 + 7 = 10 (divisible by 5)
3 + 17 = 20 (divisible by 5)
7 + 13 = 20 (divisible by 5)
Hence, five pairs of prime numbers whose sum is divisible by 5 are (2, 3), (2, 13), (3, 7), (3, 17) and (7, 13).
Question 13. Find the common factors of
(1) 8 and 20
(2) 9 and 15
Solution. (1) Factors of 8 = 1, 2,4,8
Factors of 20 = 1, 2,4,5,10, 20
Hence, the common factors of 8 and 20 are 1, 2 and 4.
(2) Factors of 9 = 1,3,9
Factors of 15 = 1,3,5,15
Hence, the common factors of 9 and 15 are 1 and 3.
Question 14. Find first three common multiples of
(1) 6 and 8
(2) 12 and 18
Solution. (1) Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72,…
Multiples of 88, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96,…
Hence, first three common multiples are 24, 48 and 72.
(2) Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132,…
Multiples of 1818, 36, 54, 72, 90, 108, 126, 144,…
Hence, first three common multiples are 36, 72 and 108.
HCF and LCM for Class 6
Question 15. Write all the numbers less than 100, which are common multiples of 3 and 4.
Solution. Multiples of 3 which are less than 100 are as follows:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99
Multiples of 4 which are less than 100 are as follows:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96
Hence, the common multiples of 3 and 4 are 12, 24, 36, 48, 60, 72, 84 and 96.
Question 16. A number is divisible by both 5 and 12. By which other number will that number be always divisible?
Solution. The given number will be divisible by the product of 5 and 12 i.e. it is always divisible by 5 x 12 = 60.
Note If a number is divisible by two co-prime numbers, then it is divisible by their product also.
Question 17. A number is divisible by 12. By what other numbers will that number be divisible?
Solution. If any number is divisible by 12, then this number will also be divisible by the factors of 12
i.e. 12 = 1 x 12; 12 = 2 × 6;12 = 3 x 4
Factors of 12 are 1, 2, 3, 4, 6 and 12.
∴ Number will be also divisible by 1, 2, 3, 4, 6 and 12.
Factors and Multiples Class 6
Question 18. Here are two different factor trees for 60. Write the missing numbers.
Solution. (1) 6 = 2 x 3 and 10 = 5 x 2
Hence, the missing numbers are 3 and 2.
(2) 60 = 30 x 2
30 = 10 x 3
and 10 = 5 x 2
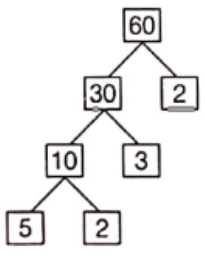
Hence, the missing numbers are 2, 3, 5 and 2.
Question 19. Which factors are not included in the prime factorisation of a composite number?
Solution. Factor 1 and that number itself are not included in the prime factorisation of a composite number.
Factors and Multiples Class 6
Question 20. Write the greatest 4-digit number and express it in terms of its prime factors.
Solution. The greatest 4-digit number = 9999
Now,

Prime factors of 9999 = 3 x 3 x 11 x 101
Question 21. Write the smallest 5-digit number and express it in the form of its prime factors.
Solution. The smallest 5-digit number = 10000
Now,

Prime factors of 10000 = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5
Factors and Multiples Class 6
Question 22. The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Solution. We know that a number is divisible by 6, if the number is divisible by 2 and 3 both.
Let the three consecutive numbers are 3, 4 and 5.
Their product = 3 x 4 x 5 = 60
Now, 60 is divisible by 2 and 3 both.
So, 60 is also divisible by 6.
Hence, product of three consecutive numbers 3, 4 and 5 is divisible by 6.
Taking one more example.
Let the three consecutive numbers are 6, 7 and 8.
Their product = 6 x 7 x 8 = 336
Now, 336 is divisible by 2 and 3 both.
So, 336 is also divisible by 6.
Hence, product of three consecutive numbers 6, 7 and 8 is divisible by 6.
Question 23. In which of the following expressions, prime factorisation has been done?
(1) 24 = 2 × 3 × 4
(2) 56 = 7 x 2 x 2 x 2
(3) 70 = 2 x 5 x 7
(4) 54 = 2 x 3 x 9
Solution. (i) We have, 24 = 2 × 3 × 4
Here, 4 is not a prime number.
So, prime factorisation is not done.
(2) We have, 56 = 7 x 2 x 2 x 2
Here, 2 and 7 are prime numbers.
So, number 56 have prime factorisation.
(3) We have, 70 = 2 x 5 x 7,
Here 2, 5 and 7 all are prime numbers.
So, number 70 have prime factorisation.
(4) We have, 54 = 2 x 3 x 9,
Here, 9 is not a prime number.
So, prime factorisation is not done.
Prime Factorization Class 6
Question 24. 18 is divisible by both 2 and 3. It is also divisible by 2 x 3 = 6. Similarly, a number is divisible by both 4 and 6. Can we say that the number must also be divisible by 4 × 6 = 24? If not, give an example to justify your answer.
Solution. We know that if a number is divisible by two co-prime numbers, then it is divisible by their product also.
Here, 2 and 3 are co-prime numbers. So, 18 is divisible by their product i.e. 6 but 4 and 6 are not co-prime numbers, so the number divisible by 4 and 6 will not be divisible by 4 × 6 = 24.
e.g. Take the number 60.
It is divisible by both 4 and 6 but it is not divisible by its product. i.e. 6 × 4 = 24
Question 25. I am the smallest number, having four different prime factors. Can you find me?
Solution. Since, the number is smallest, so different four smallest prime factors are 2, 3, 5 and 7.
∴ Smallest number having four different prime factors = 2 x 3 x 5 x 7 = 210
Question 26. What is the HCF of two consecutive
(1) numbers?
(2) even numbers?
(3) odd numbers?
Solution.
(1) Let the two consecutive numbers be 8 and 9.
Now, prime factorisation of 8 = 2 x 2 x 2
Prime factorisation of 9 = 3 × 3
Common factor of 8 and 9 = 1
Thus, HCF of 8 and 9 is 1.
Note The HCF of two consecutive numbers is 1.
(2) Let the two consecutive even numbers be 10 and 12.
Now, prime factorisation of 10 = 2 x 5
Prime factorisation of 12 = 2 x 2 x 3
Common factor of 10 and 12 = 2
Thus, HCF of 10 and 12 is 2.
Note The HCF of two consecutive even numbers is 2.
(3) Let two consecutive odd numbers be 3 and 5.
Prime factorisation of 3 = 1 x 3
Prime factorisation of 5 = 1 x 5
Common factor of 3 and 5 = 1
Thus, HCF of 3 and 5 is 1.
Note The HCF of two consecutive odd numbers is 1.
Prime Factorization Class 6
Question 27. HCF of co-prime numbers 4 and 15 was found as follows by factorisation. 4 = 2 x 2 and 15 = 3 x 5, since there is no common prime factor, so HCF of 4 and 15 is 0. Is the answer correct? If not, what is the correct HCF?
Solution. No, the answer is not correct. Because 0 (zero) cannot be factor of any number. If there is no common factor, then it means 1 is the common factor.
∴ HCF of 4 and 15=1
Question 28. Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight, which can measure the weight of the fertiliser exact number of times.
Solution. For getting maximum value of weight, we have to find out the HCF of 75 kg and 69 kg.
i.e.
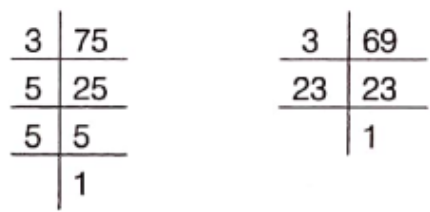
Prime factorisation of 75 = 3 x 5 x 5
Prime factorisation of 69 = 3 x 23
Common factor of 75 and 69 is 3.
Thus, HCF of 75 kg and 69 kg = 3 kg
Hence, the required maximum value of weight is 3 kg.
Question 1. Number of even numbers between 50 and 80, are
Answer. 1. 14
Question 2. The largest number, which always divides the sum of any pair of consecutive odd numbers is
Answer. 2. 4
Question 3. Sum of the number of primes between 16 to 80 and 90 to 100 is
Answer. 3. 17
Question 4. Which of the following pair is not co-prime?
Answer. 3. 84, 94
Question 5. A number is divisible by 5, if it has
Answer. 3. 0 or 5 in its ones place
Question 6. A number is divisible by 5 and 6. It may not be divisible by
Answer. 4. 85
Prime Factorization Class 6
Question 7. If the number 725498 is divisible by 11, the digit at * is
Answer. 3. 6
Question 8. The number of common prime factors of 75, 60, 105 is
Answer. 1. 2
Question 9. The number of distinct prime factors of the largest 4-digit number is
Answer. 2. 3
Question 10. The number of distinct prime factors of the smallest 5-digit number is
Answer. 1. 2
Question 11. The HCF of 144 and 160 is
Answer. 4. None of these
Question 12. The LCM of 12, 24, 32 is
Answer. 4. 96
Question 13. If two numbers are equal, then
Answer. 3. their LCM is equal to their HCF
Question 14. LCM of two numbers is 180. Then, which of the following is not the HCF of the numbers?
Answer. 3. 75
Question 15. The sum of HCF and LCM of two numbers is 1260. If their LCM is 900 more than their HCF, then the product of the two number is
Answer. 1. 194400
Question 16. Photographs are sold in small, medium and large size. The cost of photographs according to their size is given in the table below: Compentency Based Question
Prime Factorization Class 6
150 photographs worth? 10250 were sold. If 75 of them were of small size, find how many larger size photographs were sold?
Answer. 2. 25
Question 1. Assertion (A) The number 9 and 25 are co-prime.
Reason (R) A number is said to be prime, if it has only two factors 1 and the number itself.
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
Question 2. Assertion (A) The HCF of 8, 16 and 24 is 4.
Reason (R) HCF of two or more given numbers is the greatest of their common factors.
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (d) (A) is false but (R) is true.
Prime Factorization Class 6
Question 3. Assertion (A) HCF of 3 and 8 is 1 and LCM of 3 and 8 is 24.
Reason (R) HCF of two co-primes is 1 and the LCM of two co-primes is their product.
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (a) Both (A) and (R) are true and (R) is the correct explanation of (A).
Question 1. 15 is a multiple of………and..
Solution. 3 and 5
Question 2. A number for which the sum of all its factors is equal to twice the number is called a ………. number.
Solution. Perfect
Question 3. The smallest prime number between 80 and 90 is
Solution. 83
Question 4. Numbers having more than two factors are called ……….numbers.
Solution. Composite
Question 5. The LCM of two or more given numbers is the lowest of their common……….
Solution. Multiples
Question 1. If the sum of the digits of a number is divisible by 3, then the number itself is divisible by 9.
Solution. False
Question 2. LCM of two or more numbers is divisible by their HCF.
Solution. Flase
Question 3. Two consecutive even prime numbers are known astwin primes.
Solution. False
Question 4. A number with three or more digits is divisible by 6, if the number formed by its last two digits (i.e. ones and tens) is divisible by 6.
Solution. True
Question 5. The LCM of two co-prime numbers is equal to the product of the numbers.
Solution. True
Question 1. Given below are two columns: Column A and Column B. Match each item of Column A with the corresponding item of Column B.
Solution. (1) → (d), (2) → (f), (3) → (b), (4) → (e), (5) → (c)
Question 2. Match each item of Column A with the corresponding item of Column B.
Solution. (1) → (c), (2) → (f), (3) → (d), (4) → (a), (5) → (b)
Question 1. A photographer is hired to take group photographs of students in each class in a school. He arranges the students along with teachers in rows for the photograph. His arrangement has
A row consists of a minimum of 3 people and a maximum of 8 people.
(1) There are 35 people (students and teachers) in a class for a group photograph. What are the possible arrangements for them?
(2) The photographer arranged some of the students in 6 rows. What can be the maximum number of students in the photograph?
(a) 18
(b) 36
(c) 48
(d) 60
(3) How did the students of Class 7 which are 30 in number want to take a photograph along with 2 teachers. Which of the following is the possible arrangement for them?
(a) 2 rows with 16 students in each.
(b) 4 rows with 8 students/teachers in each.
(c) 5 rows with 6 students in each and 1 row for teachers.
Solution. (1) Total number of people (students and teachers) = 35
∴ Factors of 35 are 1, 5, 7 and 35.
Hence, possible arrangements
= 7 rows and 5 students/teachers per row
or 5 rows and 7 students/teachers per row
(2) (c) The photographer arranged students in 6 rows.
Given, maximum number of people in a row = 8
∴ Maximum number of students = 6 x 8=48
(3) (b) There are 30 students and 2 teachers in class 7.
Thus, in total 32 people.
Let us consider maximum people in a row i.e. 8.
So, divide 32 by 8 to know the number of rows.
32 ÷ 8 = 4
Hence, 4 rows with 8 students/teachers in each.
Question 1. Write the first three multiples of each of the following
(1) 11
(2) 12
Solution. (1) First three multiples of 11 = 11, 22, 33
(2) First three multiples of 12 = 12, 24, 36
Question 2. Write the greatest and the smallest prime number between 10 and 20.
Solution. Greatest prime number = 19
Smallest prime number = 11
Question 3. Write all the prime numbers between
(1) 10 and 15
(2) 20 and 35
Solution. (1) Prime numbers between 10 and 15 = 11, 13
(2) Prime numbers between 20 and 35 = 23, 29, 31
Question 4. Which of the following are composite numbers?
7, 13, 16
Solution. Given numbers are 7, 13, 16.
Factors of 7 = 1,7
Factors of 13 = 1,13
Factors of 16 = 1, 2,4,8,16
∴ 16 is a composite number.
Question 5. Write the common factor of 6 and 10.
Solution. Factors of 6 = 1, 2, 3,6
Factors of 10 = 1, 2, 5,10
Common factors of 6 and 10 = 1, 2
Class 6 Maths Chapter 3 Solutions
Question 6. Write the highest common factor of 6 and 15.
Solution. Factors of 6=1, 2, 3, 6
Factors of 15 = 1, 3, 5, 15
Common factors = 1, 3
Highest common factor = 3
Question 7. Write the first two common multiples of 5 and 15.
Solution. Multiples of 5 = 5, 10, 15, 20, 25, 30,…
Multiples of 15 = 15, 30,…
First two common multiples = 15, 30
Question 8. Find the prime factorisation of 40.
Solution. Here, we have 40
∴ 40 = 2 × 2 × 2 × 5
Question 9. If 3 and 10 are two co-prime numbers, then find their LCM.
Solution. We know that the LCM of two co-prime numbers is equal to their product.
∴ The LCM of 3 and 10 = 3 x 10 = 30
Question 1. Give the factorisation of the following numbers.
(1) 136
(2) 252
Solution.
(1) We have, 136
∴ 136 = 2 x 2 x 2 x 17
(2) We have, 252
∴ 252 = 2 x 2 x 3 x 3 x 7
Question 2. Test the divisibility of the following numbers.
(1) 4834 by 2
(2) 723 by 3
(3) 495 by 3 and 5
(4) 2853 by 3 and 9
Solution. (1) Given number is 4834. Here, unit place is 4. So, it is divisible by 2.
(2) Sum of digits of the number = 7 + 2 + 3 = 12, which is divisible by 3.
Hence, the number 723 is also divisible by 3.
(3) Here, unit place is 5. So, it is divisible by 5 and sum of digits = 4 + 9 + 5 = 18. So, it is divisible by 3.
(4) Sum of digits of the number = 2 + 8 + 5 + 3 = 18, which is divisible by 3 and 9 both.
Question 3. In each of the following numbers, replace * by the smallest number to make it divisible by 3.
(1) 27 * 4
(2) 53 * 46
Solution. For a number to be divisible by 3, the sum of the digits of the given number should be divisible by 3.
(1) Sum of digits of 27 * 4 = 2 + 7 + 4 = 13
∴ Replace * by 2
(2) Sum of digits of 53 * 46 = 5 + 3 + 4 + 6 = 18
∴ Replace * by 0
Class 6 Maths Chapter 3 Solutions
Question 4. Determine the least number, which when divided by 3, 4 and 5 leaves remainder 2 in each case.
Solution. First of all, we find the LCM of 3, 4 and 5.

LCM = 2 x 2 x 3 x 5 = 60
Hence, the required number = 60 + 2 = 62
Question 5. Find the HCF of the following numbers using prime factorisation method.
(1) 84 and 98
Solution. (1) We have, 84 and 98
84 = 2 x 2 x 3 x 7 and 98 = 2 x 7 x 7
∴ HCF = 2 x 7 = 14
Question 6. Find the LCM of 160, 170 and 90.
Solution. We have,

Hence, LCM of given numbers
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 17
= 24480
Question 7. Find the LCM of 112, 168, 266 by prime factorisation method.
Solution. We have, 112, 168 and 266

112 = 2 x 2 x 2 x 2 x 7;
168 = 2 x 2 x 2 x 3 x 7
266 = 2 x 7 x 19
∴ LCM = 2 x 2 x 2 x 2 x 3 x 7 x 19 = 6384
Question 8. Three belss ring at intervals of 48 min, 60 min and 90 min, respectively. If all the three bells ring together at 10:00 am, then at what time will the three bells ring again that day?
Solution. We have to find the LCM of 48, 60 and 90

LCM = 2 x 2 x 2 x 2 x 3 x 3 x 5
= 720 min
= \(\frac{720}{60}=12 \mathrm{~h}\)
∴ Bells ring together again at (10:00 am + 12 hr) at 10:00 pm
Question 9. Five bells begin to toll together at intervals of 9 sec, 6 sec, 10 sec and 8 sec, respectively, how many times will they toll together in the span of 1 h?
Solution. We have to find the LCM of 9, 6, 4, 10 and 8.

LCM = 2 x 2 x 2 x 3 x 3 x 5 = 360
In 1 h, the ring will toll together = \(\frac{3600}{360}\)
= 10 times
Class 6 Maths Chapter 3 Solutions
Question 10. In a colony of 100 blocks of flats numbering 1 to 100, a school van stops at every sixth block while a school bus stops at every tents block. On which stop will both of them stop if they start from the entrance of the colony?
Solution. The common stop at which both van and bus stop is the common multiple of 6 and 10.
Multiples of 6 less than 100 are
6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96.
Multiples of 10 less than 100 are
10, 20, 30, 40, 50, 60, 70, 80, 90.
Common multiples of 6 and 10 are 30, 60 and 90.
So, the school van and bus both will stop together at blocks 30, 60 and 90.
Question 11. For an international school competition, student’s stay is booked in two hotels 148 students in Hotel 1 and 164 students in Hotel 2. An equal number of students are accommodated in each hotel room. What can be the maximum number of students in a room?
Solution. Factors of 148 are 1, 2, 4, 37, 74 and 148.
Factors of 164 are 1, 2, 4, 41, 82 and 164.
The common factors of 148 and 164 are 1, 2 and 4.
The highest common factor of 148 and 164 is 4.
∴ Maximum number of students than can be accommodated in a room is 4.
Question 1. Find a 4-digit odd number using each of digits 1, 2, 4 and 5 only once such that when the first and last digits are interchanged, it is divisible by 4.
Solution. The 4-digit number will be an odd number, if the unit place digit is an odd number (i.e. 1 or 5).
Total such odd numbers are
4125, 4215, 1245, 1425, 2145, 2415, 4251, 4521, 5241, 5421, 2451, 2541.
Also we know that any 4-digit number is divisible by 4, if the last two-digit number is divisible by 4.
Consider a number 4521, if we interchage the first and the last digit, the new number will be 1524. Here, we see that the last two digits (i.e. 24) is divisible by 4. So, the number 1524 is divisible by 4.
Similarly, other numbers when we interchange the first and the last digit, divisible by 4 are 4125, 2415, 2451.
Hence, the required 4-digit numbers are 4521, 4125, 2415 and 2451.
Question 2. Three boys step off together from the same place. If their steps measure 36 cm, 48 cm and 54 cm, then at what distance from the starting point will they again step together?
Solution. Given, their step measures are 36 cm, 48 cm and 54 cm.
We must find the LCM of 36, 48, 54,

LCM of 36, 48 and 54 = 2 x 2 x 2 x 2 x 3 x 3 x 3 = 432
They again step together from the starting point at 432 cm i.e. 4 m 32 cm.
Class 6 Maths Chapter 3 Solutions
Question 3. Three brands A, B and C of biscuits are available in packets of 12, 15 and 21 biscuits, respectively. If a shopkeeper wants to buy an equal number of biscuits of each brand, then what is the minimum number of packets of each brand, he should buy?
Solution. In Brand A, number of biscuits=12
In Brand B, number of biscuits = 15
In Brand C, number of biscuits = 21
First of all, we find the LCM of 12, 15 and 21

Now, number of packets of Brand A = \(\frac{420}{12}=35\)
Number of packets of Brand B = \(\frac{420}{15}=28\)
Number of packets of Brand C = \(\frac{420}{21}=20\)
Question 4, On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 46 cm, respectively. What is the minimum distance each should walk, so that each can cover the same distance in complete steps?
Solution. (1) The step measure of each person is 40 cm, 42 cm and 46 cm.So, the minimum distance each should walk is the LCM of 40, 42 and 46.

LCM of 40, 42 and 46 = 2 x 2 x 2 x 3 x 5 x 7 x 23
= 19320 cm = 193.2 m
Class 6 Maths Chapter 3 Solutions
Question 5. A merchant has 130 L of oil of one kind, 190 L of another kind and 250 L of a third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. What should be the greatest capacity of such a tin?
Solution. The greatest capacity of the required measure will be equal to the HCF of 130, 190 and 250 L.
Prime factorisation of 130, 190 and 250 are
130 = 2 x 5 x 13,190 = 2 x 5 x 19 and 250 = 2 x 5 x 5 x 5
Common factors of 130, 190 and 250 = 2 x 5 = 10
Hence, the greatest capacity of tin should be 10 L.
Question 6. Monica, Heronica and Rajat begin to jog around a circular stadium. They complete their revolution in 42 sec, 56 sec and 63 sec, respectively. How many seconds after will they be together at the starting point?
Solution. Required second of time = LCM of 42, 56 and 63 42, 56, 63

LCM = 2 x 2 x 2 x 3 x 3 x 7 = 504 s
Hence, after 504s, they will be together at starting point.
Question 7. In a school library, there are 780 books of English and 364 books of Science. Ms. Yakang, the librarian of the school wants to store these books in shelves such that each shelf should have the same number of books of each subject. What should be the minimum number of books in each shelf?
Solution. Given, number of English books = 780
and number of Science books = 364
For getting the minimum number of books in each shelf, we have to find the HCF of 780 and 364.
Prime factorisation of 780 and 364.

780 = 2 × 2 × 3 × 5 x 13
and 364 = 2 x 2 x 7 x 13
∴ HCF of 780 and 364 = 2 x 2 x 13 = 52
Hence, the minimum number of books in each shelf is 52.
Question 8. John, Rishi and Feroz participated in track events. During practice sessions, their coach observed that John took 48 sec, Rishi took 72 sec and Feroz took 108 sec to run around a circular track. If they start running together at 6 am for half an hour, how many times will they all come together at a same position?
Solution. John, Rishi and Feroz take 48 sec, 72 sec and 108 sec, respectively to complete round of a circular track. We have to calculate LCM to find the time after which they meet on the starting point for first time.

∴ LCM of 48, 72 and 108 = 2 x 2 x 2 x 2 x 3 x 3 x 3 = 432
So, it means the three persons are in the same position after 432 sec or after 7 min 12 sec.
As it is given that, they start running at 6 am for half an hour.
Hence, John, Rishi and Feroz will all come together at the same position 4 times in half an hour.
Class 6 Maths Chapter 3 Solutions
Question 9. Jaya baked muffins using paper liners and cherries. Some paper liner packets contain 8 liners, while others contain 10 liners. A pacted of cherry contains 6 cherries. Every muffin Jaya baked contained 1 cherry. All cherries and paper liners were used up. What can be the minimum number of muffins baked by her?
Solution. To find the minimum number of muffins Jaya baked, we need to find LCM of the paper liners and cherries.
LCM of paper liners of sizes 8 and 10
= 2 × 2 × 2 × 5 = 40
Hence, we need to find LCM of 40 and 6.
∴ LCM of 40 and 6 = 2 x 2 x 2 x 3 x 5 = 120
Therefore, the minimum number of muffins Jaya baked is 120 muffins.