Class 6 Maths

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers

Natural Numbers

The counting numbers 1, 2, 3, 4, 5, … are called natural numbers. The collection of natural numbers is denoted by Ni.e. N=(1,2,3,4,…)

Predecessor If we subtract 1 from any natural number, then we get the predecessor of that number.

e.g. 16 – 1 = 15 i.e. 15 is the predecessor of 16.

Successor If we add 1 to any natural number, then we get the successor of that number.

e.g. 10 + 1 = 11 i.e. 11 is the successor of 10.

Note it Every natural number has a successor and every natural number except 1 has a predecessor because 1 is the smallest natural number. There is no last number i.e. we have infinite natural numbers.

Example 1. Write predecessor and successor of the following numbers

(1) 9

(2) 43

(3) 297

(4) 2901

Solution.

(1) Predecessor of 9 = 9 – 1 = 8

and successor of 9 = 9 + 1 = 10

(2) Predecessor of 43 = 43 – 1 = 42

and successor of 43 = 43 + 1 = 44

(3) Predecessor of 297 = 297 – 1 = 296

and successor of 297 = 297 + 1 = 298

(4) Predecessor of 2901 = 2901 – 1 = 2900

and successor of 2901 = 2901 + 1 = 2902

Read and Learn More MP Board Class 6 Maths Solutions

Example 2. Write

(1) a single-digit predecessor of a two-digit number.

(2) a three-digit successor of a two-digit number.

Solution.

(1) 9, which is a predecessor of 10.

(2) 100, which is a successor of 99.

Example 3. Write the next four natural numbers after 6999.

Solution. The next four natural numbers after 6999 are

6999 + 1 = 7000, 7000 + 1 = 7001,

7001 + 1 = 7002, 7002 + 1 = 7003

i.e. 7000, 7001, 7002 and 7003.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers

The natural numbers along with zero form the collection of whole numbers. The collection of whole numbers is denoted by Wi.e. W = {0,1,2,3,4,…}

All natural numbers are whole numbers but all whole numbers are not natural numbers.

Note it Every whole number has a successor and every whole number except O has a predecessor. There is no last whole number i.e. we have infinite whole numbers.

Example 4. Write the whole number whose successor is 79500.

Solution. The required whole number = Predecessor of

79500 = 79500 – 1 = 79499

Example 5. Write the whole number whose predecessor is 35999.

Solution. The required whole number=Successor of 35999 = 35999 + 1 = 36000

Example 6. Find the number whose successor is 5 more than 364.

Solution. Let the successor be x.

x = 364 + 5 = 369

Hence, the required number is 369-1=368

MP Board Class 6 Maths Solutions

Example 7. Write the four whole numbers occuring just before 1001.

Solution. The four whole numbers just before 1001 are

1001 – 11000, 1000 – 1 = 999,

999 – 1998, 998 – 1 – 997

i.e. 1000, 999, 998 and 997.

Example 8. How many whole numbers are there between 19 and 33?

Solution. Whole numbers between 19 and 33 are

20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32

Hence, the total number of whole numbers between 19 and 33 is 13.

Example 9. How many 3-digit numbers are there between 88 and 702?

Solution. 3-digit numbers between 88 and 702 are

100, 101, 102,…, 701.

Number of these numbers = 701 – 99 = 602

Note it in the above list, 701 is included and 99 is not included.

Example 10. Write the number which is product of successor and predecessor of 1001.

Solution. Successor of 1001 = 1001 + 1 = 1002

Predecessor of 1001 = 1001 – 1 = 1000

∴ Product of successor and predecessor of 1001 = 1002 × 1000 = 1002000

Example 11. Write all the whole numbers between 99 and 199 which do not change if the digits are written in reverse order.

Solution. All the whole numbers between 99 and 199 which do not change, if the digits are written in reverse order, are 101, 111, 121, 131, 141, 151, 161, 171, 181, 191.

Number Line

To represent whole numbers on a number line, draw a line and mark a point on it and label it 0 (zero).

Starting from 0 (zero) on the line, mark out the equal intervals (of unit length) to the right of 0 and label them as 1, 2, 3,…. Thus, the distance between these points labelled as 0, 1,… is called as unit distance.

In this way, you can go to any whole number on the right in this manner. Thus, we represent whole numbers on the number line as shown below

Note it Distance between 16 and 17 is same as distance between 35 and 36 which is one unit.

MP Board Class 6 Maths Solutions

Comparison of Two Whole Numbers

On the number line, the number on the right of the other number is the greater number and the number on the left of the other number is the smaller number.

On the number line, 7 is on the right of 5. So, 7 is greater than 5 i.e. 7 > 5.

The number 6 lies on the left of 9. So, 6 is smaller than 9 i.e. 6 < 9.

Example 12. In each of the following pair of numbers, state which whole number is on the right of the other number on the number line. Also write them with the appropriate sign >,<) between them

(1) 627, 613

(2) 157, 168

(3) 6123, 5674

(4) 113295, 1132956

Solution. (1) On the number line, whole number 627 is on the right of 613 because 627 is greater than 613

i.e. 627 > 613

(2) On the number line, whole number 168 is on the right of 157 because 157 is less than 168

i.e. 157 < 168

(3) On the number line, whole number 6123 is on the right of 5674 because 6123 is greater than 5674

i.e. 6123 > 5674

(4) On the number line, whole number 1132956 is on the right of 113295 because 113295 is less than 1132956

i.e.113295 < 1132956

MP Board Class 6 Maths Solutions

Example 13. Represent the successor and the predecessor of 12 and 7 respectively on the number line.

Solution. Place the successor of 12 on the number line.

12 + 1 = 13

Place the predecessor of 7 on the number line.

So, 7 – 1 = 6

Addition on the Number Line

When we add any number to a given number, we move towards right on the number line.

e.g. Let us add 3 and 5.

We start from 3 on the number line and make 5 jumps to the right by unit distance each. Then, we reach at 8.

So, 3 + 5 = 8

Subtraction on the Number Line

When we subtract any number from a given number, we move towards left on the number line.

e.g. Let us find 6 – 2.

We start from 6 on the number line and make 2 jumps to the left by unit distance each. Then, we reach at 4.

So, 6 – 2 = 4

Multiplication on the Number Line

For multiplication, we make jumps of equal distance starting from origin.

e.g. Let us find 5×3.

We start from 0 (zero) on the number line and move 5 units at a time. After 3 such moves, we reach at 15.

So, 5 x 3 = 15

MP Board Class 6 Maths Solutions

Example 14. Find the value of the following on the number line.

(1) 3 + 6

(2) 8 + 2

(3) 6 – 3

(4) 6 x 3

(5) 2 x 5

Solution. (1) To find 3 + 6

Let us start from 3. Since, we have to add 6 to this number, we make 6 jumps to the right of 3. Each jump being equal to 1 unit. After six jumps, we reach at 9. 1 2 3 4 5 6

So, 3 + 6 = 9

(2) To find 8 + 2

Let us start from 8. Since, we have to add 2 to this number, we make 2 jumps to the right of 8. Each jump being equal to 1 unit. After two jumps, we reach at 10.

So, 8 + 2 = 10

(3) To find 6 – 3

Let us start from 6 and make 3 equal jumps to the left of 6. Each jump is equal to 1 unit. Now, we reach at 3.

so, 6 – 3 = 3

(4) To find 6 x 3

We have to multiply 6 by 3 i.e. 6 units x 3 (or 6 units 3 times).

Let us start from 0, move 6 units to the right of 0, 31 times.

After moving 3 such moves, we reach at 18.

So, 6 x 3 = 18

(5) To find 2 x 5

We have to multiply 2 by 5 i.e. 2 units x5 (or 2 units 5 times).

Let us start from 0, move 2 units to the right of 0, 5 times.

After moving 5 such moves, we reach at 10.

So, 2 × 5 = 10

MP Board Class 6 Maths Solutions

Question 1. Write the predecessor and successor of 19, 1997, 12000, 49 and 100000.

Solution.

Question 2. Is there any natural number that has no predecessor?

Solution. Yes, the smallest natural number I has no predecessor because predecessor of 1 is (1-1=0) zero and zero is not a natural number.

Question 3. Is there any natural number which has no successor? Is there a last natural number?

Solution. No, there is no natural number which has no successor because each natural number has a successor.

e.g. Successor of 4=4+1=5 Successor of 5=5+1=6 and so on.

Also, there is no last natural number because natural number starts from 1 and goes upto infinite.

Question 4. Are all natural numbers also whole numbers?

Solution. Yes, all the natural numbers are also whole numbers.

Question 5. Are all whole numbers also natural numbers?

Solution. No, all whole numbers are not natural numbers because 0 is a whole number but it is not a natural number.

Question 6. Which is the greatest whole number?

Solution. Since, every whole number has a successor. So, there is no greatest whole number.

Question 7. Find the sum, using the number line.

(1) 4+5

Solution. (1) To find 4 + 5

Let us start from 4. Since, we have to add 5 to this number, we make 5 jumps to the right of 4. Each jump being equal to 1 unit. After five jumps, we reach at 9.

∴ 4 + 5 = 9

Question 8. Find the difference, using the number line.

(1)8-3

Solution. (1) To find 8 – 3

Let us start from 8 and make 3 equal jumps to the left of 8. Each jump is equal to 1 unit. Now, we reach at 5.

∴ 8 – 3 = 5

Question 9. Find using the number line.

(1) 2×6

Solution. (1) To find 2×6

We have to multiply 2 by 6

i.e. 2 units x 6 (or 2 units 6 times).

Let us start from 0, move 2 units to the right of 0.

After making 6 such moves, we reach at 12.

∴ 2 × 6 = 12

MP Board Class 6 Maths Solutions Chapter 2 Whole Numbers Exercise 2.1

Question 1. Write the next three natural numbers after 10999.

Solution. 11000, 11001 and 11002.

Question 2. Write the three whole numbers occurring just before 10001.

Solution. 10000, 9999 and 9998.

Question 3. Which is the smallest whole number?

Solution. The smallest whole number is zero (0).

Question 4. How many whole numbers are there between 32 and 53?

Solution. Whole numbers between 32 and 53 are as follows

33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51 and 52.

Hence, the total number of whole numbers between 32 and 53 is 20.

Class 6 Maths Chapter 2 Solutions 

Question 5. Write the successor of

(1) 2440701

(2) 100199

(3) 1099999

(4) 2345670

Solution. The successor of given numbers are as follows

Question 6. Write the predecessor of

(1) 94

(2) 10000

(3) 208090

(4) 7654321

Solution. The predecessor of given numbers are as follows

Question 7. In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line. Also, write them with the appropriate sign (>, <) between them.

(1) 530, 503

(2) 370, 307

(3) 98765, 56789

(4) 9830415, 10023001

Solution.

On the number line, whole number 503 is on the left of 530 because 530 is greater than 503 i.e. 530 > 503.

On the number line, whole number 307 is on the left of 370 because 370 is greater than 307 i.e. 370 > 307.

On the number line, whole number 56789 is on the left of 98765 because 98765 is greater than 56789 i.e. 98765> 56789.

On the number line, whole number 9830415 is on the left of 10023001 because 9830415 is less than 10023001 i.e. 9830415 < 10023001.

Class 6 Maths Chapter 2 Solutions

Question 8. Which of the following statements are true (T) and which are false (F)?

Zero is the smallest natural number.

400 is the predecessor of 399.

Zero is the smallest whole number.

600 is the successor of 599.

All natural numbers are whole numbers.

All whole numbers are natural numbers.

The predecessor of a two-digit number is never a single digit number.

1 is the smallest whole number.

The natural number 1 has no predecessor.

The whole number 1 has no predecessor.

The whole number 13 lies between 11 and 12.

The whole number 0 has no predecessor.

The successor of a two-digit number is always a two-digit number.

Solution.

1. False, because zero is not a natural number. It is a whole number.
2. False, because predecessor of 399 is 399-1=398.
3. True, because whole numbers start with zero (0).
4. True, because successor of 599 is 599 + 1 = 600.
5. True.
6. False, because 0 is not a natural number.
7. False, because predecessor of 10 is 10 – 1 = 9, which is a single digit number.
8. False, because 0 is the smallest whole number.
9. True, because, if we subtract 1 from 1, then we get 0 (1-10), which is not a natural number.
10. False, because predecessor of 1 is 1-1=0 and 0 is a whole number.
11. False, because 13 is greater than 12.
12. True.
13. False, because successor of two-digit number 99 is 99+1=100, which is a three-digit number.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Multiple Choice Questions

Question 1. The product of non-zero whole number and its successor is always

1. an even number
2. an odd number
3. a prime number
4. divisible by 3

Answer. 1. an even number

Question 2. The whole number which has no predecessor is

1. 1
2. 0
3. 2
4. 3

Answer. 2. 0

Question 3. The predecessor of 1 lakh is

1. 99000
2. 99999
3. 999999
4. 100001

Answer. 2. 99999

Class 6 Maths Chapter 2 Solutions

Question 4. The successor of 1 million is Competency Based Question

1. 2 million
2. 1000001
3. 100001
4. 10001

Answer. 2. 1000001

Question 5. The product of two whole numbers is always a

1. natural number
2. even number
3. odd number
4. None of the above

Answer. 4. None of the above

Question 6. The greatest number which always divides the product of the predecessor and successor of an odd natural number other than 1, is

1. 6
2. 4
3. 16
4. 32

Answer. 2. 4

Question 7. Which of the following is right side to 10 on the number line?

1. 8
2. 9
3. 18
4. 0

Answer. 3. 18

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Questions

Question 1. Assertion (A) 1 is a natural number.

Reason (R) Every natural number is a whole number.

(a) A is false but R is true.

(b) A is true but R is false.

(c) Both A and R are true.

(d) Both A and R are false.

Answer. c. Both A and R are true.

Question 2. Assertion (A) 70 is greater than 50.

Reason (R) 70 is the left side to 50 on the number line.

(a) A is false but R is true.

(b) A is true but R is false.

(c) Both A and R are true.

(d) Both A and R are false.

Answer. b. A is true but R is false.

Whole Numbers Class 6 Solutions

Question 3. Assertion (A) 27 is the successor of 26.

Reason (R) Any natural number, you can add 1 to that number and get the next number i.e. you get its successor.

(a) A is false but R is true.

(b) A is true but R is false.

(c) Both A and R are true.

(d) Both A and R are false.

Answer. c. Both A and R are true.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Fill in the Blanks

Question 1. 300 is the predecessor of ……

Solution. 301

Question 2. 450 is the successor of ……

Solution. 449

Question 3. ……… is the successor of the largest 3-digit number.

Solution. 1000

Question 4. The smallest 6-digit natural number ending in 5 is …….

Solution. 100005

Question 5. Addition corresponds to the …… on the number line.

Solution. Right

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers True/False

Question 1. Successor of 1-digit number is always a 1-digit number.

Solution. False

Question 2. Successor of 3-digit number is always a 3-digit number.

Solution. False

Question 3. Every whole number except zero is the successor of another whole number.

Solution. True

Question 4. Sum of two whole numbers is always less than their product.

Solution. False

Question 5. There is a whole number which when added to a whole number, gives the second whole number.

Solution. True

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Match the Columns

1. (1) → (c), (2) → (d), (3) → (e), (4) → (a), (5) → (b)

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Very Short Answer Type Questions

Question 1. How many natural numbers are there between 60 and 72?

Solution. Given numbers are 60 and 72.

Hence, natural numbers between 60 and 72

= (72 – 60) – 1 = 11

Question 2. Write the smallest natural number.

Solution. 1 is the smallest natural number.

Question 3. Write the two immediate predecessors of 2945.

Solution. Given number is 2945.

Immediate predecessors are 2944 and 2943

Question 4. Write the three immediate successors of 3956.

Solution. Given number is 3956.

So, three immediate successors of 3956 are 3957, 3958 and 3959.

Whole Numbers Class 6 Solutions

Question 5. Write a double digit predecessor of three-digit number.

Solution. 99 is a double digit predecessor of 100.

Question 6. Write a triple digit successor of two-digit number.

Solution. 100 is a triple digit successor of 99.

Question 7. Write two whole numbers occuring just before 1001.

Solution. 1000 and 999.

Question 8. Write three whole numbers occuring just after 1000.

Solution. 1001, 1002, 1003

Question 9. Write down the two whole number which are on the right of 3 and on the left of 6.

Solution. 4 and 5 are right of 3 and left of 6.

Question 10. Write the next three consecutive whole numbers of 89.

Solution. The next three consecutive whole numbers of 89 are 90, 91 and 92.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Short Answer Type Questions

Question 1. Write the predecessor of the following

(1) 96

(2) 9998

Solution. (1) Predecessor of 96 = 96 – 1 = 95

(2) Predecessor of 9998 = 9998 – 1 = 9997

Question 2. Determine the sum of the four numbers as given below

• Successor of 32
• Predecessor of 49
• Predecessor of the predecessor of 56
• Successor of the successor of 67

Solution. Successor of 32 = 32 + 1 = 33

Predecessor of 49 = 49 – 1 = 48 Predecessor of 56 is 55

So, predecessor of the predecessor of 56 = 55 – 1 = 54

Successor of 67 is 68

So, successor of the successor of 67 = 68 + 1 = 69

Hence, the sum of four numbers = 33 + 48 + 54 + 69 = 204

Question 3. Write the predecessor of the sum of 345,287 and 368.

Solution. Sum of 645, 287 and 368 is 1300, whose predecessor

= 1300 – 1 = 1299

Question 4. Write the successor of the difference of 145 and 46.

Solution. Difference of 145 and 46 is 99, whose successor

= 99 + 1 = 100

Whole Numbers Class 6 Solutions

Question 5. Find the number whose predecessor is 3 more than 456.

Solution. Let the predecessor be x.

x = 456 + 3 = 459

The required number is 459 + 1 = 460

Question 6. Find the whole number x, when

(1) x – 9 = -9

(2) x – 0 = 1

Solution. (1) x – 9 = -9

⇒ x = -9 + 9

⇒ x = 0

(2) x – 0 = 1

⇒ x = 1

Question 7. Write all the whole numbers between 200 and 300 which do not change if the digits are written in reverse order.

Solution. All the whole numbers between 200 and 300 which do not change, if the digits are written in reverse order are

202, 212, 222, 232, 242, 252, 262, 272, 282, 292

Question 8. Find the number whose successor is 3 more thatn 450.

Solution. Let the number be x.

Then, x + 1 = 450 + 3

x = 452

∴ The number = 452

Whole Numbers Class 6 Solutions

Question 9. In each of the following pairs of numbers, state which whole number is to the left of the other on the number line. Use appropriate symbol (> or <).

(1) 497, 495

(2) 3059, 3096

Solution. We know that the number which lies to the right of other is a greater number.

(1) 495 lies to the left of 497, so, 497 > 495

(2) 3059 lies to the left of 3096, so 3059 <3096

Question 10. There are two whole numbers which when multiplied by itself gives the same number. What are they?

Solution. If we multiply 0 by itself, it gives same number i.e. 0 x 0 = 0, and similarly, 1 x 1 = 1.

∴ The required whole numbers are 0 and 1.

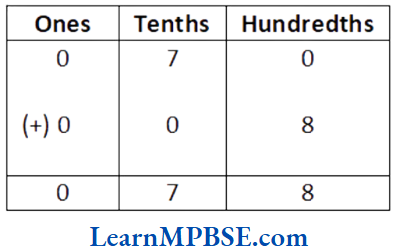
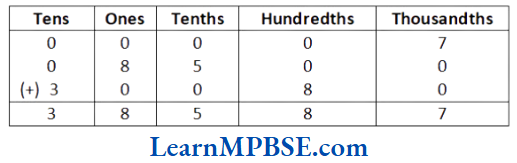
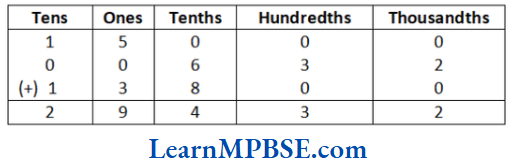
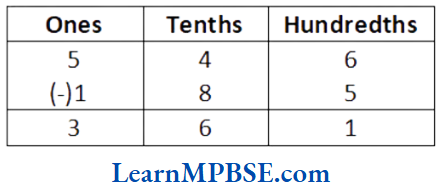
Free downloadable MP Board solutions for Class 6 Maths Chapter 1 Knowing Our Numbers

Class 6 Maths chapter-wise solutions PDF Comparing Numbers

In comparison of two numbers, a number having more number of digits will be greater and a number having less number of digits will be smaller.

e.g. Let 92 and 395 be given numbers. It is clear that number 395 has greater number of digits. Hence, 395 is the greatest number.

If the number of digits in two or more numbers are same, then that number will be larger which has a greater leftmost digit. If this digit also happens to be the same, we look at the next digit and so on.

e.g. Let 395 and 424 be given numbers. Here, both given numbers have same number of digits but 424 has a greater leftmost digit (4 as compared to 3). Hence, 424 is greater number.

Mp Board Class 6 Maths Solutions

Example 1. By instantly looking at the numbers, find which one is the greatest and which one is the smallest in each of the following.

(1) 29, 210, 198, 1234

(2) 19, 311, 218, 4310

(3) 741965, 769, 7064, 8094

(4) 73156, 1369, 18088, 9173231

Solution. (1) Number of digits in 29 = 2

Number of digits in 210 = 3

Number of digits in 198 = 3

Number of digits in 1234 = 4

∴ Greatest number=1234 [maximum number of digits]

Read and Learn More MP Board Class 6 Maths Solutions

and smallest number=29 [minimum number of digits]

(2) Number of digits in 19 = 2

Number of digits in 311 = 3

Number of digits in 218 = 3

Number of digits in 4310 = 4

∴ Greatest number = 4310 [maximum number of digits)

and smallest number=19 [minimum number of digits]

(3) Number of digits in 741965 = 6

Number of digits in 769 = 3

Number of digits in 7064 = 4

Number of digits in 8094 = 4

∴ Greatest number=741965 [maximum number of digits]

and smallest number=769 [minimum number of digits]

(4) Number of digits in 73156 = 5

Number of digits in 1369 = 4

Number of digits in 18088 = 5

Number of digits in 9173231=7

∴ Greatest number=9173231 [maximum number of digits]

and smallest number = 1369 [minimum number of digits]

Mp Board Class 6 Maths Solutions

Example 2. Compare the following number.

(1) 67454 and 78465

(2) 97632 and 96543

(3) 956 and 987

(4) 86545 and 86575

Solution. (1) Both 67454 and 78465 have same number of digits. Now, on comparing first digit from left, we get

6 < 7

∴ 67454 < 78465

(2) Both 956 and 987 have same number of digits and first leftmost digit is also same.

Now, on comparing second digit from left, we get

5 < 8

∴ 956 < 987

(3) Both 97632 and 96543 have same number of digits and first leftmost digit is also same.

Now, on comparing second digit from left, we get

7 > 6

∴ 97632 > 96543

(4) Both 86545 and 86575 have same number of digits and its three digits from left are also same.

Now, on comparing fourth digit from left, we get

4 < 7

∴ 86545 < 86575

MP Board Solutions For Class 6 Maths Chapter 1 Ordering Of Numbers

Ordering of numbers is the arrangements of numbers from smallest to greatest or from greatest to smallest.

Ascending order is the method of arranging the numbers from smallest to greatest.

While descending order is the method of arranging the numbers from greatest to smallest number.

Example 3. Arrange the following numbers in ascending order.

(1) 847, 9754, 8320, 571

(2) 911, 713, 5168, 7431

(3) 3691, 3699, 4312, 4319

(4) 2231, 2291, 2278, 2201

Solution. (1) To convert numbers into ascending order, we arrange numbers from smallest to greatest.

Now, ascending order is

571 < 847 < 8320 < 9754.

(2) To convert numbers into ascending order, we arrange numbers from smallest to greatest.

Now, ascending order is

713 < 911 < 5168 < 7431.

(3) To convert numbers into ascending order, we arrange numbers from smallest to greatest.

Now, arranging them in ascending order

3691 < 3699 < 4312 < 4319.

(4) To convert numbers into ascending order, we arrange numbers from smallest to greatest.

Now, ascending order is

2201 < 2231 < 2278 < 2291.

Class 6 Maths Chapter 1 Solutions

Example 4. Arrange the following numbers in descending order.

(1) 719, 3250, 571, 8256

(2) 819, 5240, 890, 6249

(3) 31093, 31309, 39031, 9391, 31029

(4) 21025, 21206, 29031, 5625, 21029

Solution. (1) To convert number into descending order, we arrange the numbers from greatest to smallest.

Now, descending order of the given numbers is

8256 > 3250 > 719 > 571.

(2) To convert number into descending order, we arrange the numbers from greatest to smallest.

Now, descending order of the given numbers is

6249 > 5240 > 890 > 819.

(3) To convert number into descending order, we arrange the numbers from greatest to smallest.

Now, descending order of the given numbers is

39031 > 31309 > 31093 > 31029 > 9391.

(4) To convert number into descending order, we arrange the numbers from greatest to smallest.

Now, descending order of the given numbers is

29031 > 21206 > 21029 > 21025 > 5625.

MP Board Solutions For Class 6 Maths Chapter 1 Formation Of Smallest And Greatest Numbers

Suppose some digits are given to form greatest number and smallest number.

For greatest number We arrange the given digits in descending order of their values.

For smallest number We arrange the given digits in ascending order of their values.

e.g. The smallest 4-digit number using 5, 3, 4, 2 is 2345 and the greatest 4-digit number using the same digits is 5432.

Example 5. Use the following digits without repetition and make the greatest and smallest 4-digit numbers.

(1) 2, 8, 7, 6

(2) 9, 5, 4, 1

(3) 3, 8, 5, 0

(4) 2, 3, 6, 7

Solution. (1) Descending order of the given digits is 8, 7, 6, 2.

∴ Greatest 4-digit number = 8762

and ascending order of the given digits is 2, 6, 7, 8

∴ Smallest 4-digit number = 2678

(2) Descending order of the given digits is 9, 5, 4, 1.

∴ Greatest 4-digit number = 9541

and ascending order of the given digits is 1,4,5,9

∴ Smallest 4-digit number = 1459

(3) Descending order of the given digits is 8, 5, 3,0

∴ Greatest 4-digit number = 8530

and ascending order of the given digits is 0, 3, 5, 8

∴ The smallest number is 0 which can’t be placed at left most place.

∴ Smallest 4-digit number = 3058

Class 6 Maths Chapter 1 Solutions

Note it While forming a smallest number from given number of digits, zero cannot be placed at leftmost digit. As zero will be meaningless in counting and 4-digit number will become 3-digit number and so on.

(4) Descending order of the given digits is 7, 6, 3, 2.

∴ Greatest 4-digit number = 7632

and ascending order of the given digits is 2, 3, 6, 7

∴ Smallest 4-digit number = 2367

Class 6 Maths Exercises With Answers

Example 6. Make the greatest and the smallest 4-digit numbers using any one digit twice.

(1) 3,6,7

(2) 8, 1, 5

(3) 0, 7, 9

(4) 5, 4, 0

Solution. (1) Descending order of the given digits is 7, 7, 6, 3.

[∵ greatest digit is taken twice]

∴ Greatest 4-digit number = 7763

and ascending order of the given digits is 3, 3, 6, 7. [∵ smallest digit is taken twice]

∴ Smallest 4-digit number = 3367

(2) Descending order of the given digits is 8, 8, 5, 1

[∵ greatest digit is taken twice]

∴ Greatest 4-digit number = 8851

and ascending order of the given digits is 1, 1, 5, 8. [∵ smallest digit is taken twice]

∴ Smallest 4-digit number = 1158

(3) Descending order of the given digits is 9,9,7,0.

[∵ greatest digit is taken twice]

∴ Greatest 4-digit number = 9970

and ascending order of the given digits is 0, 0, 7, 9.

[∵ smallest digit is taken twice]

But 0079 is a 2-digit number. So, keeping 7 (instead of 0) at the left most place and taking the smallest digit twice i.e. 7009.

∴ Smallest 4-digit number = 7009

(4) Descending order of the given digits is 5, 5, 4, 0.

∴ Greatest 4-digit number = 5540

and ascending order of the given digits is 0, 0, 4, 5.

But 0045 is a 2-digit number. So, keeping 4 (instead of 0) at the left most place and taking the smallest digit twice i.e. 4005.

∴ Smallest 4-digit number = 4005

Class 6 Maths Exercises With Answers

Example 7. Make the greatest and the smallest 4-digit numbers using any four different digits if

(1) Digit 5 is always at ones place.

(2) Digit 3 is always at tens place.

(3) Digit 1 is always at thousands place.

Solution. Writing digits written in descending order as 9, 8, 7, 6, 5, 4, 3, 2, 1, 0

(1) According to the question, digit 5 is always at ones place.

∴ Greatest number = 9875

and Smallest number = 1025

(2) According to the question, digit 3 is always at tens place.

∴ Greatest number = 9837

and Smallest number = 1032

(3) According to the question, digit 1 is always at thousands place.

∴ Greatest number = 1987

and Smallest number = 1023

Shifting Digits

Shifting digits means changing the position of the digits in a number.

e.g. Consider two numbers 419 and 941. We observe that both the numbers have same digits but their places are different.

So, if the digits of a number are shifted, then the number also gets change.

MP Board solutions for Class 6 Maths Chapter 1 Greatest Number and Smallest Number

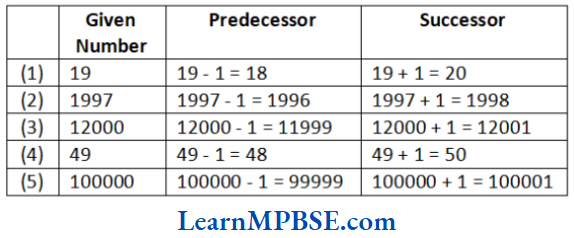
On adding 1 to the greatest n-digit number, we would get the smallest (n+1)-digit number.

e.g. Greatest 2-digit number + 1 = Smallest 3-digit number

i.e. 99 + 1 = 100

(1) Greatest 3-digit number = 999

∴ Smallest 4-digit number = 1000

(2) Greatest 4-digit number = 9999

∴ Smallest 5-digit number = 10000

(3) Greatest 5-digit number = 99999

∴ Smallest 6-digit number = 100000

(4) Greatest 6-digit number = 999999

∴ Smallest 7-digit number = 1000000

(5) Greatest 7-digit number = 9999999

∴ Smallest 8-digit number = 10000000

(6) Greatest 8-digit number = 99999999

∴ Smallest 9-digit number = 100000000

Note it

(1) One hundred = 10 tens

(2) One thousand = 10 hundreds = 100 tens

(3) One lakh 100 thousands = 1000 hundreds

(4) One crore = 100 lakhs = 10000 thousands

(5) One million = 1000 thousands = 10 lakhs

(6) One billion = 1000 millions

Example 8. Starting from the greatest 7-digit number, write the previous 4 numbers in descending order.

Solution. The greatest 7-digit number = 9999999

1st previous number = 9999999 – 1 = 9999998

2nd previous number = 9999999 – 2 = 9999997

3rd previous number = 9999999 – 3 – 9999996

4th previous number = 9999999 – 4 = 9999995

Now, descending order of these number is as follows 9999998 > 9999997 > 9999996 > 9999995

MP Board Solutions For Class 6 Maths Chapter 1 Use Of Commas

Commas help us in reading and writing large numbers. To make reading of large numbers easy, we group various places into periods. This can be done in two different ways:

Indian System of Numeration

In the Indian system of numeration, we use commas after 3 digits starting from the right and there after every 2 digits. The commas after 3, 5 and 7 digits separate thousand, lakh and crore respectively.

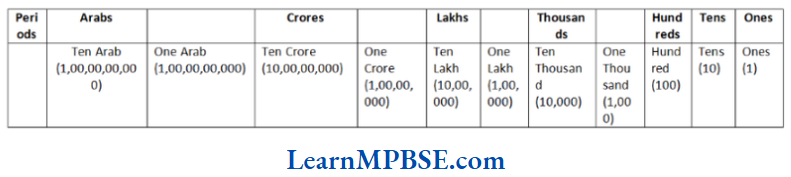
Example 9. Read the numbers and write them using placement boxes.

(1) 475320 (2) 8675964312

Solution. (1) Given number is 475320.

According to the Indian system of numeration,

We read it as, four lakh seventy five thousand three hundred twenty.

Using the commas it is written as 4,75,320.

(2) Given number is 8675964312.

According to the Indian system of numeration,

We read it as eight arab sixty seven crore fifty nine lakh sixty four thousand three hundred twelve. Using commas it written as 8, 67, 59, 64, 312.

Note it While writing number names, we do not use commas.

Mpbse Class 6 Maths Chapter 1

International System of Numeration

In the international system of numeration, commas are placed after every 3 digits starting from the right. The commas after 3 and 6 digits separate thousand and million respectively.

Example 10. Read the numbers and write them using placement boxes.

(1) 9578432

(2) 3572893921

Solution. (1) According to the International system of numeration,

We read it as nine million five hundred seventy eight thousand four hundred thirty two and write as 9, 578, 432.

(2) According to the International system of numeration,

We read it as three billion five hundred seventy two million eight hundred ninety three thousands nine hundred twenty one and write as 3,572, 893, 921.

Mpbse Class 6 Maths Chapter 1

Example 13. Place commas correctly and write numerals.

(1) Fifty three lakh seventy five thousand three hundred seven.

(2) Eight crore five lakh forty one.

(3) Six crore fifty two lakh twenty one thousand three hundred two.

Solution.

MP Board solutions for Class 6 Maths Chapter 1 Place Value and Face Value

Place Value

The place value is the position of each digit in a number which is determined as ones, tens, hundreds, thousands and so on.

e.g. The place value of 1 in 1854 is 1000.

Face Value

The face value is the actual value of the digit in a number. e.g. Face value of 1 in 1854 is 1 only.

The expanded form of the number 1854 is 1 x 1000 + 8 x 100 + 5 x 10 + 4 x 1.

Example 14. Find the place and face values of

(1) 7 in number 97621 (2) 2 in number 25687

Solution. (1) Place value of 7 in 97621 is 7000 and face value of 7 is 7.

(2) Place value of 2 in 25687 is 20000 and face value of 2 is 2.

Example 15. Write the expanded form of the following numbers.

(1) 20000 (2) 38400 (3) 65740 (4) 89324

Solution. (1) 20000 = 2 × 10000

(2) 38400 = 3 x 10000 + 8 x 1000 + 4 x 100

(3) 65740 = 6 x 10000 + 5 x 1000 + 7 x 100 + 4 × 10

(4) 89324 = 8 × 10000 + 9 x 1000 + 3 × 100 + 2 × 10 + 4 × 1

Mpbse Class 6 Maths Chapter 1

Example 16. Write the place value of each digit in the numeral

(1) 369868

(2) 97263480

Solution. (1) Place value of 8 = 8 x 1 = 8

Place value of 6 = 6 x 10 = 60

Place value of 8 = 8 x 100 = 800

Place value of 9 = 9 x 1000 = 9000

Place value of 6 = 6 x 10000 = 60000

Place value of 3 = 3 x 100000 = 300000

(2) Place value of 0 = 0 x 1 = 0

Place value of 8 = 8 x 10 = 80

Place value of 4 = 4 x 100 = 400

Place value of 3 = 3 x 1000 = 3000

Place value of 6 = 6 x 10000 = 60000

Place value of 2 = 2 x 100000 = 200000

Place value of 7 = 7 x 1000000 = 7000000

Place value of 9 = 9 x 10000000 = 90000000

Example 17. Find the sum of place and face values for the following.

(1) 2 in 12456 (2) 5 in 54321

Solution. (1) Place value of 2 = 2000

Face value of 2 = 2

∴ Sum = 2000 + 2 = 2002

(2) Place value of 5 = 50000

Face value of 5 = 5

∴ Sum = 50000 + 5 = 50005

Example 18. Find the differences of place values for the following conditions.

(1) two 7s in 7652713 (2) two 4s in 43810422

Solution. (1) The place value of 7 in ten lakhs place = 70000000

The place value of 7 in hundreds place = 700

Hence, the required difference = 7000000-700 =6999300

(2) The place value of 4 at the crores place = 40000000

The place value of 4 at the hundreds place = 400

Hence, the required difference = 40000000 – 400 = 39999600

Number Comparison Examples Class 6

Example 19. Answer the following questions.

(1) How many 5 – digit numbers are there in all?

(2) How many 7 – digit numbers are there in all?

(3) Write the smallest 8 – digit number having five different digits.

Solution. (1) The largest 5 – digit number = 99999

The smallest 5-digit number = 10000

Number of all 5-digit numbers = (99999 – 10000) +1

= (89999 + 1) = 90000

Hence, there are in all ninety thousand of 5-digit numbers.

(2) The largest 7-digit number = 9999999

The smallest 7 – digit number = 1000000

Number of all 7 – digit numbers

= (9999999 -1 000000) + 1

= (8999999 + 1) = 9000000 = Ninety lakh

Hence, there are in all ninety lakh of 7-digit numbers.

(3) Five smallest digits are 0, 1, 2, 3, 4.

Hence, the required number is 10000234.

MP Board solutions for Class 6 Maths Chapter 1 Large Numbers in Practice

Large numbers are needed is many places in daily life.

e.g. Number of people in a city, money paid or recieved in large transactions etc.

Generally, larger numbers are used to measure length, mass and capacity etc.

The standard unit for measuring length, mass and capacity are metre, grams and litres respectively. The relation between the various units is given by

The units kilo is the greatest and milli is the smallest.

(1) 1 kilometre = 1000 metres

1 metre = 10 decimetre = 100 centimetres

(2) 1 kilogram = 1000 grams

1 gram = 10 decigrams = 100 centigrams = 1000 milligrams

(3) 1 litre 10 decilitres = 100 centilitres = 1000 millilitres

Example 1. A tourist car travelled from different places with a speed 40 km/h. The journey is shown below. 1020 km

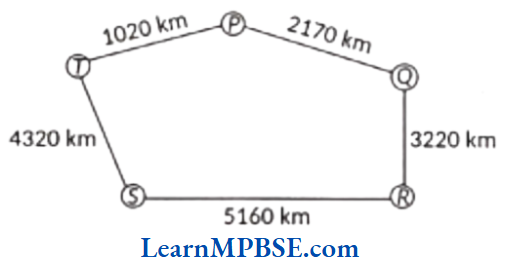
(1) Find the total distance covered from P to R.

(2) Find the total distance covered from R to T.

(3) Find the total distance covered by the car if it starts from P and returns back to P.

(4) Find the difference of distances from Q to R and R to S.

(5) Find out the time taken by the car to reach.

(a) P to Q

(b) R to S

(c) Total journey

Solution. From the given figure,

(1) Total distance covered by car from P to R

= PQ + QR = 2170 + 3220 = 5390 km

(2) Total distance covered by car from R to T

= RS + ST = 5160 + 4320 = 9480 km

(3) Total distance covered by car

= Distance from P to R + Distance from R to T + Distance from T to P

= 5390 + 9480 + 1020 = 15890 km

(4) Distance from Q to R = 3220 km

Distance from R to S = 5160 km

∴ Difference of distances from Q to R and R to S = 5160 – 3220 = 1940 km

(5) We know that Time \(=\frac{\text { Distance }}{\text { Speed }}\)

(a) Time taken by the car to reach P to Q Distance from P to Q

= \(\frac{2170}{40}=\frac{217}{4}=54 \frac{1}{4} \mathrm{~h}\)

(b) Time taken by the car to reach R to S

= \(\frac{5160}{40}=129 \mathrm{~h}\)

(c) Total journey \(=\frac{\text { Total distance covered }}{\text { Speed }}\)

= \(\frac{15890}{40}=\frac{1589}{4}=397 \frac{1}{4} \mathrm{~h}\)

Number Comparison Examples Class 6

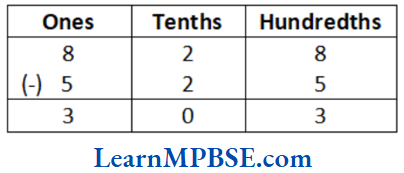
Example 2. The distance between the office and flat of a employee’s house is 2 km 575 m. Everyday she walks both ways. Find the total distance covered by her in 10 days.

Solution. Distance between the office and the flat = 2 km 575 m

= 2 × 1000 + 575 = 2000 + 575

= 2575 m [∴ 1 km = 1000 m]

∴ Distance covered by the employee in one day

= 2 × 2575 = 5150 m

[∴ she walks both ways in one day]

∴ Distance covered in 10 days = 10 x 5150 = 51500 m

= (51 × 1000 + 500) m

= 51 km 500 m

Example 3. If a box contains 400000 medicine tablets each and weight of one tablet is 20 mg. What is the total weight of all tablets in the box in grams and in kilograms both?

Solution. Weight of one tablet = 20 mg

Total weight of 400000 tablets in the box = 400000 x 20 mg =8000000 mg

Now, weight in grams = \(\frac{8000000}{1000} \mathrm{~g}=8000 \mathrm{~g}\)

[∴ \(1 \mathrm{mg}=\frac{1}{1000} \mathrm{~g}\)]

Now, weight in kilograms = \(\frac{8000}{1000} \mathrm{~kg}=8 \mathrm{~kg}\)

[∴ \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)]

Example 4.

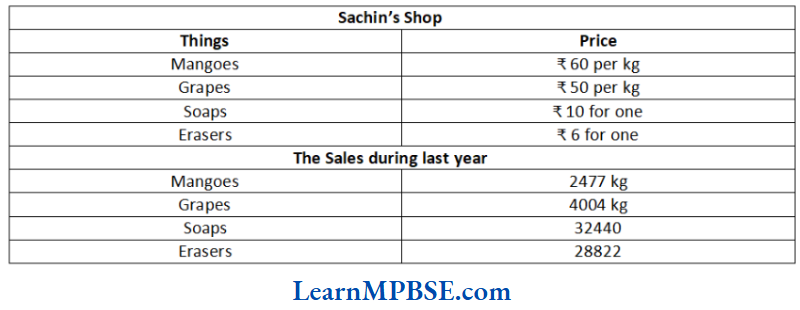
(1) Can you find the total weight of mangoes and grapes Sachin sold last year?

(2) Can you find the total money Sachin got by selling mangoes?

(3) Can you find the total money Sachin got by selling mangoes and grapes together?

(4) Make a table showing how much money Sachin received from selling each item? Arrange the entries of amount of money received in descending order. Find the item which brought him the highest amount.

Solution. (1) Total weight of mangoes and grapes Sachin sold

= 2477 + 4004 = 6481kg

(2) Total money Sachin got by selling mangoes

= Total weight of mangoes in kg x Cost per kg = 2477 x 60 = 148620

(3) Total money Sachin got by selling grapes = 4004 × 50 = 200200

(4) Following table shows the money received from selling items.

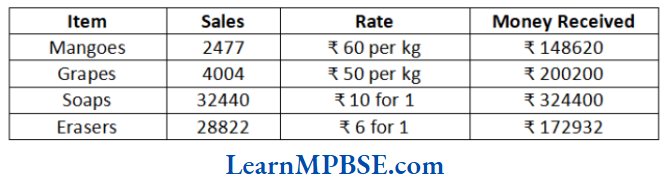
The entries of amount of money received in descending order are as follows

₹ 324400 > 200200 > 172932 > 148620

The item, which brought him the highest amount is Soaps i.e. ₹ 324400.

MPBSE Class 6 Maths Chapter 1

Example 5. A box contains 50 packets of biscuits. Each weights 120 g. How many such boxes be loaded into a van which cannot carry beyond 900 kg?

Solution. Given, total number of packets = 50

Weight of each packets = 120 g

Weight of a box = 50 x 120 g = 6000 g = 6 kg

∴ Required number of boxes = \(\frac{900}{6}=150\)

Hence, only 150 boxes can be loaded in the van.

Example 6. A milk dairy produced 75678 L of milk in a day. It supplied 67689 L of milk to milk depot. Find the milk left in the dairy.

Solution. Production of milk in one day = 75678 L

Supply to milk depot in one day = 67689 L

So, the milk left in the dairy=75678-67689=7989 L

Example 7. A vessel has 2 L and 500 mL of juice. In how many glasses, each of 20 mL capacity, can it be filled?

Solution. Capacity of vessel = 2 L 500 mL = 2 x 1000 + 500 = 2000 + 500 = 2500 mL

[∴ 1 L=1000 mL]

and capacity of one glass = 20 mL

∴ Number of glasses of juice filled out of vessel

Hence, juice can be filled in 125 glasses.

MPBSE Class 6 Maths Chapter 1

Example 8. Population of Bhavnagar was 356213 in the year 1990. In the year 2000, it was found to be increased by 62578. What was the population of the city in 2000?

Solution. Population of the city in year 2000

= Population of the city in year 1990 + Increase in population

= 356213 + 62578 = 418791

Example 9. In a country, the number of electronic cars sold in the year 2020-2021 was 200880. In the year 2021-2022, the number of electronic cars sold was 400100. In which year more cars were sold and how many more?

Solution. Clearly, 400100 is more than 200880. So, more cars were sold in the year 2021-2022 than in 2020-2021.

Now, 400100 – 200880 = 199220

Check the answer by adding

200880 + 199220 = 400100 (the answer is right)

Example 10. Every Friday a small brochure of general knowledge is published with a newspaper. One copy has 10 pages. Every week 12444 copies are printed. How many total pages are printed every Friday?

Solution. Every copy has 10 pages.

∴ 12444 copies will have 12444 x 10 pages.

Now, 12444 × 10 = 124440

Thus, every Friday 124440 pages are printed.

Example 11. If a number 6253 multiplied by 55 instead of multiplying by 46. By how much was the answer greater than the correct answer?

Solution. After multiplying 6253 by 55, we get

= 6253 × 55

= 343915

After multiplying 6253 by 46, we get

= 6253 × 46 = 287638

Difference 343915 – 287638 = 56277

Wrong answer is 56277 greater than the actual answer.

Example 12. The cost of a autograph signed bat is 30222. What is the cost of 25 such bats?

Solution. Cost of 1 autograph signed bat=30222

∴ Cost of 25 autograph signed bat = 30222 x 25 = ₹ 755550

Example 13. Find the difference between the greatest and the least numbers that can be written using the digits 8, 2, 5, 4, 1 each only one.

Solution. Using the digits 8, 2, 5, 4, 1, we get

Greatest number = 85421 and least number = 12458

∴ Difference = 85421 – 12458

= 72963

MP Board solutions for Class 6 Maths Chapter 1

Question 1. Can you instantly find the greatest and the smallest numbers in each row?

(1) 382, 4972, 18, 59785, 750

(2) 1473, 89423, 100, 5000, 310

(3) 1834, 75284, 111, 2333, 450

(4) 2853, 7691, 9999, 12002, 124 Was that easy? Why was it easy?

Solution.

(1) Number of digits in 382 = 3

Number of digits in 4972 = 4

Number of digits in 18 = 2

Number of digits in 59785 = 5

Number of digits in 750 = 3

∴ Greatest number = 59785 [maximum number of digits]

and smallest number = 18 [minimum number of digits]

(2) Number of digits in 1473 = 4

Number of digits in 89423 = 5

Number of digits in 100 = 3

Number of digits in 5000 = 4

Number of digits in 310 = 3

Answer. Greatest number = 89423

Smallest number=100

(3) Number of digits in 1834 = 4

Number of digits in 75284 = 5

Number of digits in 111 = 3

Number of digits in 2333 = 4

Number of digits in 450 = 3

Answer. Greatest number = 75284

Smallest number = 111

(4) Number of digits in 2853 = 4

Number of digits in 7691 = 4

Number of digits in 9999 = 4

Number of digits in 12002 = 5

Number of digits in 124 = 3

Answer. Greatest number = 12002

Smallest number = 124

MPBSE Class 6 Maths Chapter 1

Question 2. Find the greatest and the smallest numbers.

(1) 4536, 4892, 4370, 4452

(2) 15623, 15073, 15189, 15800

(3) 25286, 25245, 25270, 25210

(4) 6895, 23787,24569, 24659

Solution. (1) We have, 4536, 4892, 4370, 4452

Here, each of the given numbers is containing 4-digits and their digits at thousand places are also same. So, we compare the hundreds place digit.

8 > 5 > 4 > 3

∴ The greatest number is 4892 and the smallest number is 4370.

(2) We have, 15623, 15073, 15189, 15800

Here, the two leftmost digits 15 i.e. digits at thousand and ten thousands place are same in each numbers.

So, we compare the hundreds place digit.

∴ The greatest number is 15800 and the smallest number is 15073.

(3) We have, 25286, 25245, 25270, 25210

Here, the three leftmost digits 252 are same in each number.

So, we compare the tens place digit.

∴ The greatest number is 25286 and the smallest number is 25210.

(4) We have, 6895, 23787, 24569, 24659

Here, 6895 is a 4-digit number and other numbers are 5 digits, so it is clear that 6895 is the smallest number.

Now, in remaining three numbers, the digit at ten thousands place is same in each number.

So, we compare the thousands place digit.

∴ 4 > 3

Again, in two numbers, digit at thousands place is same.

So, we compare the hundreds place digit.

∴ 6 > 5

∴ The greatest number is 24659 and smallest number is 6895.

Question 3. Use the given digits without repetition and make the greatest and smallest 4-digit numbers.

(1) 2, 8, 7, 4

(2) 9, 7, 4, 1

(3) 4, 7, 5,0

(4) 1, 7, 6.2

(5) 5, 4, 0, 3

Solution. (1) Here, descending order of the given digits is 8, 7, 4, 2.

∴ Greatest number = 8742

and ascending order of the given digits is 2, 4, 7, 8.

∴ Smallest number=2478

(2) Here, descending order of the given digits is 9, 7, 4, 1.

∴ Greatest number=9741

and ascending order of the given digits is 1, 4, 7, 9.

∴ Smallest number = 1479

(3) Here, descending order of the given digits is 7, 5, 4, 0.

∴ Greatest number = 7540

and ascending order of the given digits is 0, 4, 5, 7.

But 0457 is a 3 digit number, so we have to interchange the place of 4 and 0 i.e. 4057.

∴ Smallest number = 4057

(4) Here, descending order of the given digits is 7, 6, 2, 1.

∴ Greatest number = 7621

and ascending order of the given digits is 1, 2, 6, 7.

∴ Smallest number = 1267

(5) Here, descending order of the given digits is 5, 4, 3,0.

∴ Greatest number = 5430

and ascending order of the given digits is 0, 3, 4, 5.

But 0345 is a 3-digit number. So, we have to interchange the place of 3 and 0 i.e 3045.

∴ Smallest number = 3045

MPBSE Class 6 Maths Chapter 1

Question 4. Make the greatest and the smallest 4-digit numbers by using any one digit twice.

(1) 3, 8, 7

(2) 9, 0,5

(3) 0, 4, 9

(4) 8, 5, 1

Solution. (1) Given digits are 3, 8 and 7.

Here, descending order of the given digits is 8, 8, 7, 3. [greatest digit 8 is taken twice]

∴ Greatest 4-digit number = 8873 and ascending order of the given digits is 3, 3,7,8. [smallest digit 3 is taken twice]

∴ Smallest 4-digit number = 3378

(2) Given digits are 9,0 and 5.

Here, descending order of the given digits is 9, 9, 5, 0.

[greatest digit 9 is taken twice]

∴ Greatest 4-digit number = 9950

and ascending order of the given digits is 0, 0, 5, 9. [smallest digit 0 is taken twice]

But 0059 is a 2-digit number because 0 at first two leftmost places is meaningless.

So, keeping 5 (instead of 0) at the leftmost place and taking the smallest digit 0 twice i.e. 5009.

∴ Smallest 4-digit number = 5009

(3) Given digits are 0, 4 and 9.

Here, descending order of the given digits is 9, 9, 4, 0. [ greatest digit 9 is taken twice]

∴ Greatest 4-digit number = 9940 and ascending order of the given digit is 0, 0, 4, 9. [:smallest digit 0 is taken twice]

But 0049 is a 2-digit number because 0 at first two leftmost places is meaningless.

So, keeping 4 (instead of 0) at the leftmost place and taking the smallest digit 0 twice, we get 4009.

∴ Smallest 4-digit number = 4009

(4) Given digits are 8, 5 and 1.

Here, descending order of the given digits is 8, 8, 5, 1. [ greatest digit 8 is taken twice]

∴ Greatest 4-digit number = 8851

and ascending order of the given digits is 1, 1, 5, 8.

[∴ smallest digit 1 is taken twice]

∴ Smallest 4-digit number=1158

Question 5. Take two digits, say 2 and 3. Make 4-digit numbers using both the digits equal number of times.

(1) Which is the greatest number?

(2) Which is the smallest number?

(3) How many different numbers can you make in all?

Solution. Two given digits are 2 and 3. We want to make 4-digit numbers using both the digit equal number of times.

The possible 4-digit numbers are 2233, 3322, 2332, 3223, 2323 and 3232.

(1) The greatest number is 3322.

(2) The smallest number is 2233.

(3) We can make 6 different numbers in all.

MP Board Class 6 Maths Solutions

Question 6. Who is the tallest? Who is the shortest?

(1) Can you arrange them in the increasing order of their heights?

(2) Can you arrange them in the decreasing order of their heights?

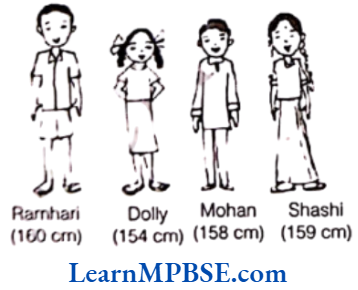
Solution. From the given figure, it is clear that

160 > 159 > 158 > 154

Ramhari is the tallest because he has the height of 160 cm.

From the given figure, it is clear that

154 < 158 < 159 < 160

∴ Dolly is the shortest because she has the height of 154 cm.

(1) Yes, we can arrange their heights in increasing order as follows: Dolly (154 cm) < Mohan (158 cm) < Shashi (159 cm) < Ramhari (160 cm).

(2) Yes, we can arrange their heights in decreasing order as follows: Ramhari (160 cm) > Shashi (159 cm) > Mohan (158 cm) > Dolly (154 cm).

Question 7. Sohan and Rita went to buy an almirah. There were many almirahs available with their price tags.

(1) Can you arrange their prices in increasing order?

(2) Can you arrange their prices in decreasing order?

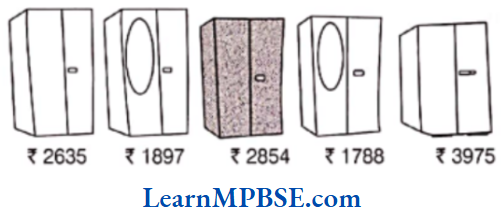
Solution. (1) Yes, prices can be arranged in increasing order as follows:

₹ 1788 < ₹ 1897 < ₹ 2635 < ₹ 2854 < ₹ 3975

(2) Yes, prices can be arranged in decreasing order as follows:

₹ 3975 > ₹ 2854 > ₹ 2635 > ₹ 1897 > ₹ 1788

Question 8 . Think of five situations, where compare three or more quantities.

Solution. Five situations may be

(1) Prices of 4 different kinds of branded shoes are 4225,3835,2620 and 2230, respectively.

(2) The weight of 4 students of Class VI are 33 kg, 38 kg, 35 kg and 37 kg, respectively.

(3) Marks obtained by 4 students in Mathematics out of 100 are 87, 88, 90 and 78, respectively.

(4) The tuition fee paid by 4 students of different classes are 170, 190, 150 and 200, respectively.

(5) The runs scored by 4 players A, B, C and D in an innings are 75, 60, 25 and 82, respectively.

Question 9. (1) Arrange the following numbers in ascending order.

(a) 847, 9754, 8320, 571

(b) 9801, 25751, 36501, 38802

(2) Arrange the following numbers in descending order.

(a) 5000, 7500, 85400, 7861

(b) 1971, 45321, 88715, 92547

Solution. (i) (a) We have, 847, 9754, 8320, 571

Ascending order of given numbers is as follows 571< 847 < 8320 < 9754

Ascending order of given numbers is as follows 9801< 25751 < 36501 < 38802

(b) We have, 9801, 25751, 36501, 38802

(2) (a) We have, 5000, 7500, 85400, 7861

Descending order of given numbers is as follows

85400 > 7861 > 7500 > 5000

(b) We have, 1971, 45321, 88715, 92547

Descending order of given numbers is as follows

92547 > 88715 > 45321 > 1971

MP Board Class 6 Maths Solutions

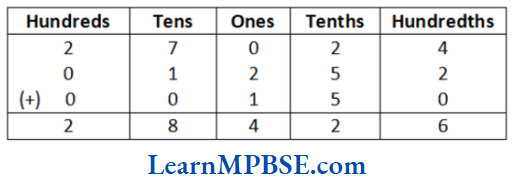
Question 10. Read and expand the numbers wherever there are blanks.

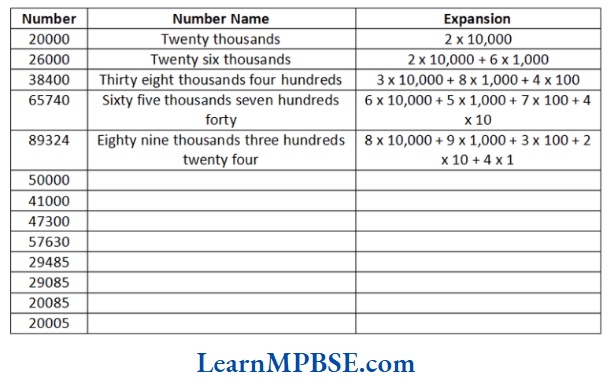
Solution. The remaining blanks are shown as below with appropriate number, name and expansion.

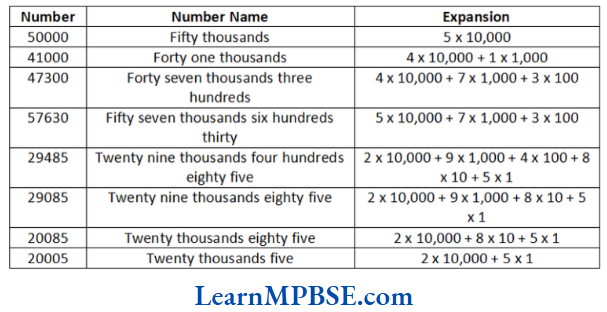
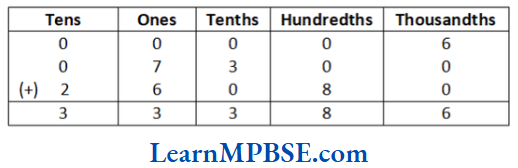
Question 11. Read and expand the numbers wherever there are blanks.

Solution. The remaining blanks are shown as below with appropriate number, name and expansion:

Question 12. (1) What is 10-1=?

(2) What is 100-1=?

(3) What is 10000 -1=?

(4) What is 100000-1 = ?

(5) What is 10000000-1 = ?

Solution.

(1) 10 – 1 = 9

(2) 100 – 1 = 99

(3) 10000 – 1 = 9999

(4) 100000 – 1 = 99999

(5) 10000000 – 1 = 9999999

MP Board Class 6 Maths Solutions

Question 13. Give five examples, where the number of things counted would be more than 6-digit number.

Solution. The least 6-digit number is 100000 (one lakh).

Now, five examples, where the number of things counted would be more than 6-digit number are as follows.

(1) The number of people in a big city.

(2) The number of stars in a clear dark night.

(3) The number of motorcycles in a big town.

(4) The number of grains in a sack full of wheat.

(5) The number of pages of notebooks of all students in a big town.

Question 14. Starting from the greatest 6-digit number, write the previous five numbers in descending order.

Solution. The greatest 6-digit number = 999999

1st previous number = 999999 – 1 = 999998

2nd previous number = 999999 – 2 = 999997

3rd previous number = 999999 – 3 = 999996

4th previous number = 999999 – 4 = 999995

5th previous number = 999999 – 5 = 999994

Now, descending order of these numbers is as follows

999998 > 999997 > 999996 > 999995 > 999994

Question 15. Starting from the smallest 8-digit number, write the next five numbers in ascending order and read them.

Solution. The smallest 8-digit number = 10000000

∴ 1st next number = 10000000 + 1 = 10000001

2nd next number = 10000000 + 2 = 10000002

3rd next number = 10000000 + 3 = 10000003

4th next number = 10000000 + 4 = 10000004

5th next number = 10000000 + 5 = 10000005

Now, ascending order of these numbers is as follows

10000001 < 10000002 < 10000003 < 10000004 < 10000005

MP Board Class 6 Maths Solutions

Question 16. Read these numbers. Write them using placement boxes and then write their expanded forms.

(1) 475320

(2) 9847215

(3) 97645310

(4) 30458094

(a) Which is the smallest number?

(b) Which is the greatest number?

(c) Arrange these numbers in ascending and descending orders.

Solution. After reading these numbers, we have

(1) 475320 Four lakhs seventy five thousands three hundred twenty.

(2) 9847215 Ninety eight lakhs forty seven thousands two hundreds fifteen.

(3) 97645310 Nine crores seventy six lakhs forty five thousands three hundreds ten.

(4) 30458094 Three crores four lakhs fifty eight thousands ninety four.

The placement boxes is shown as below

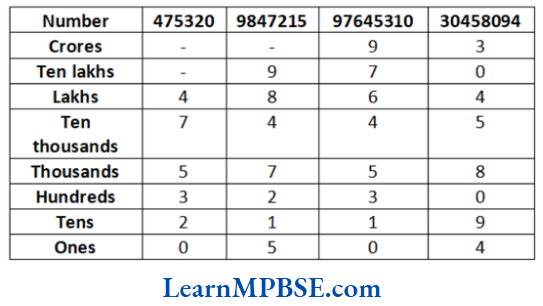
Expanded forms of given numbers are as follow

(1) 475320 = 4 × 100000 + 7 x 10000 + 5 x 1000 + 3 × 100 + 2 x 10 + 0 x 1

(2) 9847215 = 9 × 1000000 + 8 x 100000 + 4 × 10000 + 7 x 1000 + 2 × 100 + 1 x 10 + 5 x 1

(3) 97645310 = 9 x 10000000 + 7 x 1000000 + 6 x 100000 + 4 x 10000 + 5 x 1000 + 3 x 100 + 1 x 10 + 0 x 1

(4) 30458094 = 3 x 10000000 + 4 x 100000 + 5 x 10000 + 8 x 1000 + 0 x 100 + 9 x 10 + 4 × 1

(a) The smallest number = 475320

(b) The greatest number = 97645310

(c) Ascending order of given numbers are as follow

475320 < 9847215 < 30458094 < 97645310

Descending order of given numbers are as follow

97645310 > 30458094 > 9847215 > 475320

MP Board Class 6 Maths Solutions

Question 17.Read these numbers

(1) 527864

(2) 95432

(3) 18950049

(4) 70002509

(a) Write these numbers using placement boxes and then using commas in Indian system of numeration as well as International system of numeration.

(b) Arrange these in ascending and descending orders.

Solution. After reading these number, we have

(1) 527864 Five lakh twenty seven thousand eight hundred sixty four.

(2) 95432 Ninety five thousand four hundred thirty two.

(3) 18950049 One crore eighty nine lakh fifty thousands forty nine.

(4) 70002509 Seven crore two thousand five hundred nine.

(a) Using placement boxes, given number can be

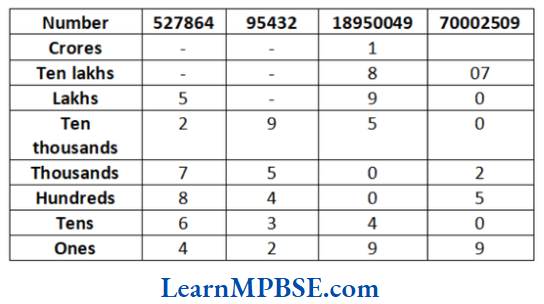
Using the commas, given numbers can be written in Indian system of numeration as

(1) 5,27,864

(2) 95,432

(3) 1,89,50,049

(4) 7,00,02,509

and in International system of numeration, they can be written as,

(1) 527,864

(2) 95,432

(3) 18,950,049

(4) 70,002,509

(b) Ascending order of these numbers are as follow

95432 < 527864 < 18950049 < 70002509

Descending order of these numbers are as follow

70002509 > 18950049 > 527864 > 95432

Question 18. You have the digits 4, 5, 6, 0, 7 and 8. Using them, make five numbers each with 6-digits.

(1) Put commas for easy reading.

(2) Arrange them in ascending and descending orders.

Solution. Given digits are 4, 5, 6, 0, 7 and 8.

We can make many numbers by using these digits, five of them are as follows

876540, 867540, 876450, 876045 and 867405

(1) After putting commas, numbers are as follows

(a) 8,76,540

(b) 8,67,540

(c) 8,76,450

(d) 8,76,045

(e) 8,67,405

(2) Ascending order of numbers is as follows

867405 < 867540 < 876045 < 876450 < 876540

Descending order of numbers is as follows:

876540 > 876450 > 876045 > 867540 > 867405

Question 19. Take the digits 4, 5, 6, 7, 8 and 9. Make any 3 numbers each with 8-digits. Put commas for easy reading.

Solution. Given digits are 4, 5, 6, 7, 8 and 9.

We can make many numbers by using these digits, three of them are as follows

98877456, 98877465 and 98877654

Using commas, numbers can be rewritten as

(1) 9,88,77,456

(2) 9,88,77,465

(3) 9,88,77,654

MP Board Class 6 Maths Solutions

Question 20. From the digits 3, 0 and 4, make five numbers each with 6-digits. Use commas.

Solution. Given digits are 3,0 and 4.

We can make many numbers by using these digits, five of them are as follows

(1) 330443

(2) 343404

(3) 344430

(4) 434043

(5) 344034

Using commas, these numbers can be rewritten as

(1) 3,30,443

(2) 3,43,404

(3) 3,44,430

(4) 4,34,043

(5) 3,44,034

Exercise 1.1

Question 1. Fill in the blanks.

(1) 1 lakh = _________ ten thousands

(2) 1 million = _______ hundred thousands

(3) 1 crore = ________ ten lakhs

(4) 1 crore = _______ millions

(5) 1 million = _______ lakhs

Solution. (1) We know that

1 lakh = 100000 (in digits) = 10 x 10000

= ten x ten thousand (in number name)

1 lakh = ten ten thousand

(2) We know that

1 million = 1000000 (in digits) = 10 x 100000

= ten x hundred thousands (in number name)

∴ 1 million = ten hundred thousands

(3) We know that

1 crore = 10000000 (in digits)

= 10 × 1000000

= ten x ten lakhs (in number name)

∴ 1 crore ten ten lakhs

(4) We know that

1 crore = 10000000 (in digits) = 10 x 1000000

= ten x one million (in number name)

∴ 1 crore = ten millions

(5) We know that

1 million = 1000000 (in digits)

= 10 x 100000 ten x one lakhs

∴ 1 million ten lakhs

Class 6 Maths Chapter 1 Solutions

Question 2. Place commas correctly and write the numerals

(1) Seventy three lakhs seventy five thousands three hundreds seven

(2) Nine crores five lakhs forty one

(3) Seven crores fifty two lakhs twenty one thousands three hundreds two

(4) Fifty eight millions four hundreds twenty three thousands two hundreds two

(5) Twenty three lakhs thirty thousands ten

Solution. Numbers after commas are as follows

(1) 73,75,307

(2) 9,05,00,041

(3) 7,52,21,302

(4) 58,423,202

(5) 23,30,010

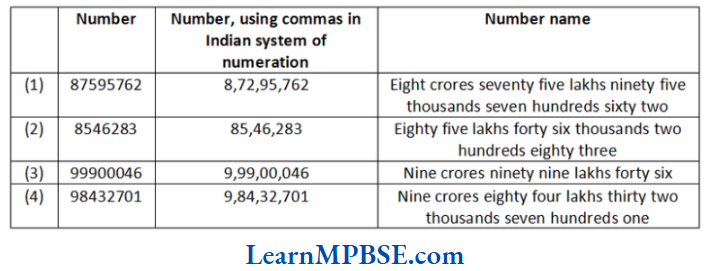
Question 3. Insert commas suitably and write the names according to Indian system of numeration.

(1) 87595762

(2) 8546283

(3) 99900046

(4) 98432701

Solution. We can draw a table to show these operations.

Question 4. Insert commas suitably and write the name according to International system of numeration.

(1) 78921092

(2) 7452283

(3) 99985102

(4) 48049831

Solution. We can draw a table to show these operations

Class 6 Maths Chapter 1 Solutions

Question 5. How many centimetres make a kilometre?

Solution. We know that 1 km = 1000 m = 1000 x 100 cm [1 m = 100 cm]

= 100000 cm

Question 6. How many milligrams make one kilogram?

Solution. We know that 1 kg = 1000 g (1000 x 1000) mg

[1g = 1000 mg]

= 1000000 mg

∴ 1000000 milligrams make one kilogram.

Question 7. A box contains 200000 medicine tablets each weighing 20 mg. What is the total weight of all the tablets in the box in grams and in kilograms?

Solution. Given, weight of one tablet = 20 mg

Total weight of 200000 tablets in the box

= 200000 x 20 mg = 4000000 mg

Now, weight in grams = \(\frac{4000000}{1000} \mathrm{~g}=4000 \mathrm{~g}\)

Now, weight in kilograms = \(\frac{4000}{1000} \mathrm{~kg}=4 \mathrm{~kg}\)

Question 8.

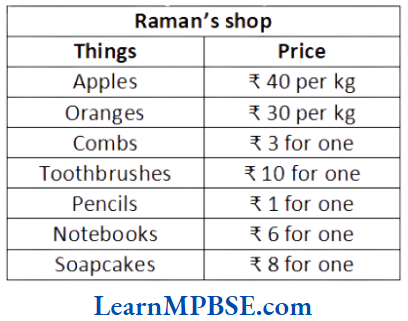
(1) Can you find the total weight of apples and oranges Raman sold last year?

Weight of apples = ______ kg

Weight of oranges = _______ kg

Therefore, total weight = ______ kg + ______ kg = _______ kg

(2) Can you find the total money Raman got by selling apples?

(3) Can you find the total money Raman got by selling apples and oranges together?

(4) Make a table showing how much money Raman received from selling each item? Arrange the entries of amount of money received in descending order. Find the item which brought him the highest amount. How much is this amount?

Solution. (1) Weight of apples sold during the last year = 2457 kg

Weight of oranges sold during the last year = 3004 kg

∴ Total weight of apples and oranges Raman sold, during the last year = 2457+ 3004 = 5461 kg

(2) Total money Raman got by selling apples

= Total weight of apples in kg x Cost per kg

= 2457 x 40 = ₹ 98280

(3) Total money Raman got by selling oranges

= Total weight of oranges in kg x Cost per kg

= 3004 x 30 = ₹ 90120

∴ Total money Raman got by selling apples and oranges together = 98280 + 90120 = ₹ 188400

(4) Following table shows the money received from selling items.

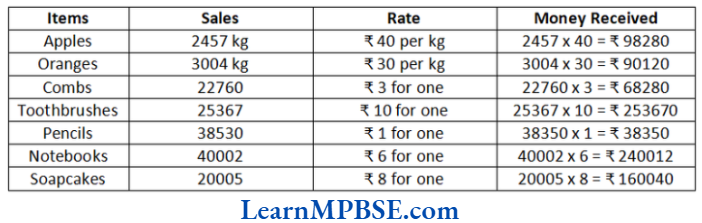
The entries of amount of money received in descending order are as follows:

₹ 253670 > ₹ 240012 > ₹ 160040 > ₹ 98280 > ₹ 90120 > ₹ 68280 > ₹ 38350

The item which brought him the highest amount is toothbrushes. This amount is ₹ 253670.

Exercise 1.2

Question 1. A book exhibition was held for four days in a school. The number of tickets sold at the counter on the first, second, third and final days was respectively 1094, 1812, 2050 and 2751. Find the total number of tickets sold on all the four days.

Solution. Given, number of tickets sold on the first day = 1094

Number of tickets sold on the second day = 1812

Number of tickets sold on the third day = 2050

Number of tickets sold on the fourth day = 2751

∴ Total number of tickets sold on all the four days

= 1094 + 1812 + 2050 + 2751 = 7707

Hence, there are 7707 tickets sold on all the four days.

Class 6 Maths Chapter 1 Solutions

Question 2. Shekhar is a famous cricket player. He has so far scored 6980 runs in test matches. He wishes to complete 10000 runs. How many more runs does he need?

Solution. Given, number of runs scored by Shekhar = 6980

Target of runs to be scored = 10000

∴ Number of runs needed more

= Target of runs – Run scored yet

= 10000 – 6980

= 3020

Question 3. In an election, the successful candidate registered 577500 votes and his nearest rival secured 348700 votes. By what margin did the successful candidate win the election?

Solution. Given, votes registered by the successful candidate = 577500

Votes registered by the nearest rival = 348700

∴ Margin, by which the successful candidate won = Votes of successful candidate – Votes of nearest rival

= 577500 – 348700 = 228800

Question 4. Kirti bookstore sold books worth ₹ 285891 In the first week of June and book worth 400768 in the second week of the month. How much was the sale for the two weeks together? In which week was the sale greater and by how much?

Solution. Given, sale of books in Ist week = ₹ 285891

Sale of books in IInd week = ₹ 400768

Total sales of two weeks = Sale of Ist week + Sale of IInd week

= 285891 + 400768 = ₹ 686659

Since, 400768 > 285891

Thus, sale in the second week is greater.

∴ Difference in the sales amount = 400768 – 285891 = ₹ 114877

Hence, sale in the second week was greater by 114877.

Question 5. Find the difference between the greatest and the least numbers that can be written using the digits 6, 2, 7, 4, 3 each only once.

Solution. Using the digits 6, 2, 7, 4 and 3, we get

Greatest number = 76432 and least number = 23467

∴ Difference = Greatest number – Least number

= 76432 – 23467 = 52965

Note it We can form a greatest number with individual digits by arranging them in descending order from right and similarly, we can form a least number by arranging them in ascending order from right.

Class 6 Maths Chapter 1 Solutions

Question 6. A machine, on an average, manufactures 2825 screws a day. How many screws did it produce in the month of January 2006?

Solution. Number of screws manufactured by the machine in one day = 2825

We know that number of days in the month of January = 31

∴ Number of screws produced by the machine in the month of January, 2006 = 2825 x 31 = 87575

Hence, the number of screws produced by the machine in the month of january, 2006 are 87575.

Question 7. A merchant had 778592 with her. She placed an order for purchasing 40 radio sets at 1200 each. How much money will remain with her after the purchase?

Solution. Given, cost of one radio set = ₹ 1200

Number of radio sets to be purchased = 40

∴ Cost of 40 radio sets = Cost of one radio set x Number of radio sets

= 40 x 1200 = ₹ 748000

∵ Total money with the merchant = ₹ 78592

∴ Money left with the merchant after purchase of 40 radio sets Total money – Cost of 40 radio sets

= 78592 – 48000

= ₹ 30592

Hence, 30592 will remain with her after the purchase.

Question 8. A student multiplied 7236 by 65 instead of multiplying by 56. By how much was his answer greater than the correct answer?

Solution. If a student multiplies 7236 by 65, he will get

= 7236 x 65 = 470340

According to the question,

Student multiplies 7236 by 56 and he will get = 7236 × 56 = 405216

Now, required difference = Actual answer – Wrong answer = 470340 – 405216 = 65124

Class 6 Maths Chapter 1 Solutions

Question 9. To stitch a shirt 2 m 15 cm cloth is needed. Out of 40 m cloth, how many shirts can be stitched and how much cloth will remain?

Solution. Total length of cloth = 40 m = 40 x 100 cm [∵ 1 m = 100 cm]

= 4000 cm

Cloth needed for one shirt = 2 m 15 cm

= (2 × 100) cm + 15 cm

= (200 + 15) cm = 215 cm

∴ Number of shirts stitched out of total cloth

= \(\frac{4000}{215}=18 \frac{130}{215}\)

Hence, 18 shirts can be stitched and cloth left over is 130 cm i.e. 1 m 30 cm.

Question 10. Medicine is packed in boxes, each weighing 4 kg 500 g. How many such boxes can be loaded In a van which cannot carry beyond 800 kg?

Solution.  Given, van can carry a weight of 800 kg = 800 x 1000 g = 800000 g

[∵1 kg = 1000 g]

According to the question,

Weight of one packet = 4 kg 500 g

= 4 × 1000 + 500

= 4000 + 500 = 4500 g

∴ Number of packets that can be loaded in the van

= \(\frac{800000}{4500}=\frac{8000}{45}=177 \frac{35}{45}\)

Hence, only 177 boxes can be loaded in the van.

Question 11. The distance between the school and the house of a student’s house is 1 km 875 m. Everyday she walks both ways. Find the total distance covered by her in six days.

Solution. Given, distance between the school and the house

= 1 km 875 m = 1 x 1000 + 875

= 1000 + 875 = 1875 m

[∵ 1 km = 1000 m]

∴ Distance covered by the student in one day

= 2 x 1875 = 3750 m

[∵ she walks both ways in one day]

∴ Distance covered in 6 days = 6 x 3750 = 22500 m

= (22 × 1000 + 500) m

= 22 km 500 m

[∵ 1 km = 1000 m]

Question 12. A vessel has 4 L and 500 mL of curd. In how many glasses, each of 25 mL capacity, can it be filled?

Solution. Given, capacity of vessel = 4 L 500 mL

= 4 x 1000 + 500 = 4000 + 500 = 4500 mL

[∵ 1 L= 1000 mL]

and capacity of one glass = 25 mL

∴ Number of glasses of curd filled out of vessel Capacity of a vessel

= \(\frac{\text { Capacity of a vessel }}{\text { Capacity of a glass }}=\frac{4500}{25}=180\)

Hence, curd can be filled in 180 glasses.

Review Exercise

Multiple Choice Questions

Question 1. The greatest natural number is

1. 1 crore
2. 10 crores
3. 10 lakhs
4. Not defined

Answer. 4. Not defined

Question 2. The arrangement of 24, 68, 487; 7, 89, 540; 1, 34, 53, 879; 78, 989; 4807 in ascending order is

1. 78, 989 < 4807 < 24, 68, 487 < 7, 89, 540 < 1, 34, 53, 879
2. 7, 89, 540 < 1, 34, 53, 879 < 24, 68, 487 < 78, 989 <4807
3. 4807 <78, 989 <7, 89, 540 < 24, 68, 487 <1, 34, 53, 879
4. None of the above

Answer. 3. 4807 <78, 989 <7, 89, 540 < 24, 68, 487 <1, 34, 53, 879

Question 3. The smallest 5-digit number formed from the digits 5, 3 and 0 is

1. 30500
2. 53000
3. 50355
4. 30005

Answer. 4. 30005

Question 4. The number formed by interchanging the digits 6 and 2 in 465271 is

1. 467521
2. 425671
3. 165274
4. None of these

Answer. 2. 425671

Question 5. How many lakhs make 1 million?

1. one
2. ten
3. hundred
4. thousand

Answer. 2. ten

Question 6. The difference between a million and a thousand is

1. 9990
2. 99900
3. 999000
4. 9990000

Answer. 3. 999000

Question 7. 3691215 with commas as per the Indian system of numeration is

1. 36,91,215
2. 3,69,1215
3. 36,912,15
4. 3,69,12,15

Answer. 1. 36,91,215

Question 8. In Indian system of numeration, the number 58695376 is written as

1. 58,69,53,76
2. 58,695,376
3. 5,86,95,376
4. 586,95,376

Answer. 3. 5,86,95,376

Question 9. The expanded form of the number 9578 is

1. 9 × 10000 + 5 x 1000 + 7 x 10 + 8 × 1
2. 9 × 1000 + 5 x 100 + 7 x 10 + 8 x 1
3. 9 x 1000 + 57 x 10 + 8 x 1.
4. 9 × 100 + 5 x 100 + 7 x 10 + 8 x 1

Answer. 2. 9 × 1000 + 5 x 100 + 7 x 10 + 8 x 1

Question 10. In international system of numeration 59357258 is written as

1. Fifty-nine million three hundred fifty-seven thousand two hundred fifty-eight
2. Five crores ninety four lakh fifty thousand two hundred fifty eight
3. Fifty nine crores three hundred fifty-seven thousand two hundred fifty-eight
4. None of the above

Solution. 1. Fifty-nine million three hundred fifty-seven thousand two hundred fifty-eight

MP Board Class 6 Chapter 1 Maths

Question 11. The expression of 56,83,765 in words is

1. Five crores sixty eight thousand seven hundred sixty five.
2. Fifty six crores eighty three thousand seven hundred sixty five
3. Five crores six hundred eighty three
4. Fifty six lakh eighty three thousand seven hundred sixty five.

Answer. 4. Fifty six lakh eighty three thousand seven hundred sixty five.

Question 12. The place value of 0 in 4,30,976 is

1. 3000
2. 0
3. 6
4. 9

Answer. 2. 0

Question 13. The difference between the face value and the place value of the digit 8 in 38954

1. 4992
2. 6552
3. 7992
4. 5322

Answer. 3. 7992

Question 14. Population of Shivnagar was 458214 in 2001. In year 2004, it was found that the population increased by 123562, then the population in 2004 is

1. 96522
2. 628814
3. 96224
4. 581776

Solution. 4. 581776

Question 15. If a number 4253 multiplied by 44 instead of multiplying by 34, then the answer greater than the correct answer is

1. 5232
2. 42530
3. 8956
4. 7588

Answer. 2. 42530

MP Board solutions for Class 6 Maths Chapter 1 Assertion Reason Type Questions

Question 1. Assertion (A) 59785 is the greatest number among 382, 4972, 18, 59785, 750.

Reason (R) When a number is bigger or larger than the second or rest quantities or number it is known as greatest number.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 2. Assertion (A) 56,500,800 is correct in Indian system of numeration.

Reason (R) 10,00,00,000 is the sequence of comma in Indian system of numeration.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (d) A is false but R is true.

MP Board Class 6 Chapter 1 Maths

Question 3. Assertion (A) 1 crore = 10 million

Reason (R) The smallest number of 8-digit is 1,00,00,000.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (b) Both A and R are true but R is not the correct explanation of A.

MP Board solutions for Class 6 Maths Chapter 1 Fill in the Blanks

Question 1. The smallest 4-digit number with different digits is……..

Answer. 1023

Question 2. In Indian system of numeration, the number 61711682 is written, using commas, as…….

Answer. 6, 17, 11, 682

Question 3. Place value of 5 in 3546 is ……….. .

Answer. 500

Question 4. (1)1 m= …… mm

(2) 1 cm = …… mm

Answer. (1) 1000 (ii) 10

Question 5. By adding 1 to the greatest ………. digit number, we get ten lakh.

Answer. 6

MP Board solutions for Class 6 Maths Chapter 1 True/False

Question 1. 34984 = 3 x 1000 + 49 x 100 + 8 x 10 + 4 x 1

Answer. False

Question 2. 1000000 = 1 crore

Answer. False

Question 3. Face value of 7 in 754612 is 7.

Answer. True

Question 4. Smallest 5-digit number+1 = Greatest 6-digit number.

Answer. False

Question 5. The numbers 4578, 4587, 5478, 5487 are in ascending order.

Answer. True

MP Board Class 6 Chapter 1 Maths

Match the Columns

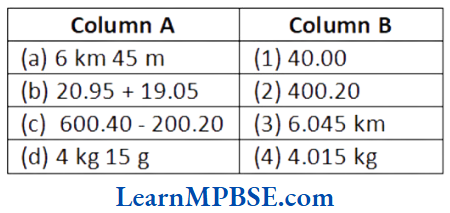
Question 1. Match the Column A with Column B.

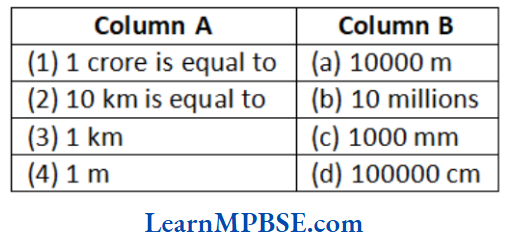
Answer. (1)(b), (2) → (a), (3) → (d), (4) → (c)

MP Board solutions for Class 6 Maths Chapter 1

Question 1. The first and last coach of the metro train are Driving mode cars. The coaches in between are Trailing cars connected through Gangways. Gangways allow passenger movement between cars. This figure shows the dimensions of a Driving mode car and Trailing car along with Gangways.

(1) A train has six coaches. What is the length of the metro train?

(a) 45 m

(b) 133 m

(c) 134 m

(d) 135 m

(2) In the 6 coach metro train, each coach has 50 seats for passengers. The first coach is reserved for women. Sixteen seats are reserved for women and senior citizens in each of the remaining coaches. How many

unreserved passenger seats are in the metro train?

(a) 130

(b) 170

(c) 204

(d) 190

(3) On an average, a metro train completes 4 round trips of 90 km in a day. What is the average distance travelled by the metro?

Solution. (1) (c) Train has two driving coaches of length 23 m and 4 trailing coaches of length 22 m.

∴ Length of metro train = 23 + 23 + 22 + 22 + 22 + 22

= 134 m

(2) (b) Since, first coach is reserved for women.

Therefore, reserved seat=50

Now, there are 5 coaches left and 16 seats are reserved in each coach.

∴ Reserved seats in 5 coach = 16 x 5 = 80 seats

Total reserved seats = 50 + 80 = 130

Total seats in metro = 50 × 6 = 300

∴ Unreserved seats = Total seats – Reserved seats

= 300 – 130 = 170 seats

(3) Metro train completes 4 round trips of 90 km in a day.

∴ Distance travelled in a day = 90 x4 = 360 km

Question 2. Passengers need a metro token to board a train. The cost of the token depends upon the distance travelled in different zones. Different zones represents different metro networks.

The table below shows the cost of tokens for travelling in different zones of a metro.

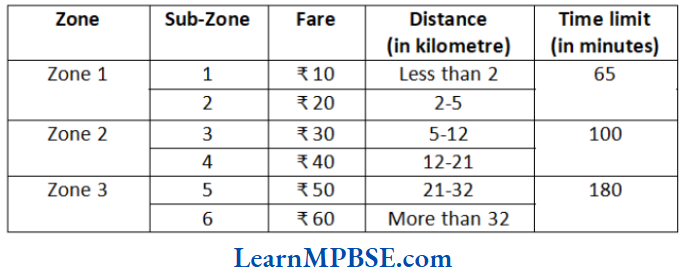
The table below shows the number of passengers travelling on a particular day in different zones.

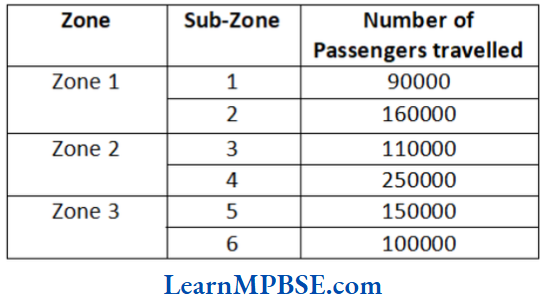
(1) How much revenue was generated on that day in Zone 1?

(2) Which zone generated the highest revenue on that day?

Solution. (1) Revenue generated in zone 1 = Revenue generated in (sub-zone 1+ sub-zone 2 + sub-zones)

Revenue generated in sub-zone 1

= Fare x Number of passenger travelled

= ₹10 × 90000 = ₹ 900000

Revenue generated in sub-zone 2 = ₹ 20 × 160000 = 3200000

Revenue generated in sub-zone 3 = ₹ 30 x 110000 = 3300000

∴ Total revenue generated in zone 1

₹ 900000 + ₹ 3200000 + ₹ 3300000 = ₹ 7400000

(2) Revenue generated in zone 1 = ₹ 7400000

Revenue generated in zone 2 = ₹ 40 x 25000

= ₹ 1000000

Revenue generated in zone 3 = ( 50 x 150000) + (₹60 x 100000)

= 13500000

Clearly, revenue generated in zone 3 is the highest.

Question 3. Siya and Aman are playing with 0-9 number cards. they placed seven cards in a row.

In how many different ways can they place the rest of the cards? 

Solution. Since, we have three place left and 13 cards left has digits 0, 3, 1. We keep changing their place value by shifting digits, thus we get numbers which are 031, 013, 103, 130, 310, 301.

Therefore, there are 6 ways to place the rest of the cards.

Question 4. Siya and Aman reshuffle the cards and divide them equally. Aman makes a 5-digit number using his cards. The picture shows the number formed by Aman.

Siya placed four of her cards as shown in the picture below.

Where should she place the remaining card to form a number greater than the number formed by Aman?

(a) After 9

(b) Before 0

(c) Between 5 and 7

(d) Between 7 and 9

Solution. (b) 5-digit number made by Aman = 31268

4 – digit number made by Siya = 0579

Remaining digit of card = 4

Siya cannot place remaining card anywhere after 0 because it will be a four digit number which is less than digit formed by Aman.

Thus, to form a number greater than the number formed by Aman she should place it before 0.

∴ 40579 > 31268

MP Board Class 6 Chapter 1 Maths

Question 5. In a school, 700 students avail the school’s transport services. The transport manager of the school prints a monthly transport record. The printed record is shown below.

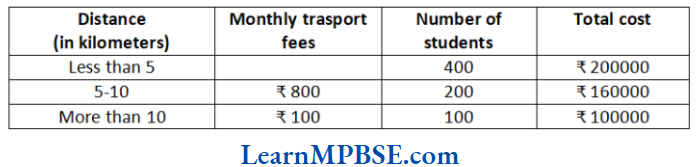
(1) An entry is omitted in the record. What are the monthly transport fees for a distance of less than 5 km? Show your calculation.

(2) In class 6 of a school, 105 students study in different sections. The number of students in each section are between 20 and 40. All sections have equal number of students. How equal number of students can be accommodated in each section?

(3) The school authority plans to install new water coolers. There are 1800 students in the school. A water cooler can serve 100 students. The cost of one water cooler is 40000. How many water coolers are should be installed to serve all the students? What is the cost of installing them?

Solution. (1) Total cost for less than 5 km = 200000

Number of students travelling less than 5 km = 400

∴ Monthly fee for one student = \(\frac{200000}{400}=₹ 500\)

(2) Total number of students = 105

All sections have equal students but the range lies between 20 and 40. Thus, we will do prime factorisation of 105 in required range.

21 x 5 = 105

35 x 3 = 105

∴ 5 sections with 21 students in each section and 3 sections with 35 students in each section.

(3) Total number of students = 1800

1 water cooler serves = 100 students

∴ Required number of water cooler to serve 1800

1800 students = \(\frac{1800}{100}\) = 18

Now, cost of one water cooler = 40000

∴ Cost of 18 water cooler = 18 x 40000 = 720000

MP Board solutions for Class 6 Maths Chapter 1 Very Short Answer Type Questions

Question 1. Which one is the greatest number?

(1) 47645, 48740

(2) 15896, 26760

Solution. (1) Here, ten thousands digit is 4 in both numbers. But thousands digit in 47645 is 7 and thousands digit in 48740 is 8. So, 8>7

Hence, 48740 > 47645

(2) In 15896, ten thousands digit is 1 and ten thousands digit in 26760 is 2. So, 2>1.

Hence, 26760 > 15896.

Question 2. Write the greatest and smallest of the following numbers. 29706, 28706, 39406, 87604

Solution. In the given numbers, we see that 28706 is the smallest and 87604 is the greatest.

Question 3. Using the digits 3, 5, 4, 6 without repetition, write the smallest 4-digit number.

Solution. Here, given digits are 3, 5, 4, 6. For the smallest number, we write the digits in ascending order. So, the smallest four-digit number is 3456.

Question 4. Make the greatest 5-digit number by using the digits 1, 2,7,94, without repetition.

Solution. Given, digits are 1, 2, 7, 9, 4.

For greatest number, we write the digits in descending order.

So, the greatest five-digit number is 97421.

Question 5. Arrange the following numbers in ascending order, 1462, 2605, 3164, 1562.

Solution. The ascending order of the given numbers are as follows

1462 < 1562 < 2605 < 3164

Question 6. Insert the commas in appropriate places according to the Indian system of numeration.

(1) 2464056

(2) 6896462

Solution. According to the Indian system of numeration,

(1) 24,64,056

(2) 68,96,462

Question 7. Insert the commas at appropriate places according to International system of numeration.

(1) 2546726

(2) 7869420

Solution. According to the International system of numeration,

(1) 2,546,726

(2) 7,869,420

Question 8. Write the numeral for the following

Twenty millions five hundreds two thousands and six hundreds thirty two.

Solution. The numeral form is 20,502,632.

Question 9. Write the place value of 6 in 762540.

Solution. The place value of 6 in 762540 = 6 × 10000 = 60000

Question 10. Write the expanded form of the following.

(1) 76496

(2) 986256

Solution. Expanded form of given numbers as

(1) 76496 = 7 x 10000 + 6 x 1000 + 4 x 100 + 9 × 10 + 6

(2) 986256 = 9 × 100000 + 8 x 10000 + 6 × 1000 + 2 × 100 + 5 x 10 + 6

Short Answer Type Questions

Question 1. Make the greatest and smallest five digit numbers by using the following digits (without repetition).

(1) 4, 5, 6, 7, 2

(2) 2, 0, 7, 3, 8

Solution. Here, we have

The greatest five-digit number is 76542. The smallest five-digit number is 24567.

The greatest five-digit number is 87320. The smallest five-digit number is 20378.

Question 2. Write the numeral for the following.

(1) Thirty seven lakhs, forty eight thousands and seven hundreds sixty three.

(2) Thirty two millions, six hundreds sixty thousands and five hundreds five.

(3) Twenty lakhs, four thousands four.

Solution. 37,48,763

32,660,505

20,04,004

Question 3. Find the difference between the place value of two 6’s in 6523689.

Solution. Given, number is 6523689.

Place value of first 6 = 6 x 1000000

= 6000000

Place value of second 6 = 6 x 100 = 600

∴ Difference between the place values of two 6’s

= 6000000 – 600

= 5999400

Question 4. The piece of cloth required for a shirt is 3m 05 cm. How much cloth will be required for 14 shirts?

Solution. Cloth required for 1 shirt = 3 m 05 cm

Cloth required for 14 shirts = (3 m 05 cm) x 14

= 14 x 3 + 14 x 05 = 42 m 70 cm

Question 5. A bus can covers 1126 km in 18 h. At what speed per hour does the bus move?

Solution. Distance covered in 18 h = 1126 km

Distance covered in 1 h = 1126 + 18 = 62 km 555 m

Hence, the speed of the car is 62 km 555 m per hour.

Question 6. The mass of a gas cylinder is 14 kg 250 g. Find the total mass of 20 such cylinder.

Solution. Given, mass of a cylinder = 14 kg 250 g

Mass of 20 cylinders = 20x (14 kg + 250 g)

= 280 kg + 5000 g

= 280 kg + 5 kg = 285 kg

Question 7. A man saves ₹ 250 per month. How much money will save in 2 yr?

Solution. Monthly saving = ₹250

We know that 1 yr = 12 months, 2 yr = 24 months

Total saving in 2 yr = 24 × 250 = ₹ 6000

Question 8. The cost of 20 flats constructed by DDA housing scheme is ₹ 348642060. What is the cost of each flat?

Solution. Total cost of 20 flats = 348642060

Cost of each flat = 348642060 ÷ 20 = 17432103

Question 9. How much money was collected from 1261 students of a school for a charity show, if each student contributed ₹ 520?

Solution. Total number of students in school = 1261

Contribution of money by each student = 520

∴ Total money = 1261 × 520 = 655720

Question 10. Out of 180000 tablets of vitamin A, 18734 are distributed among the students in a district. Find the number of the remaining vitamin tablets.

Solution. Total tablets of vitamin A = 180000

Tablets distributed among children = 18734

Remaining tablets = 180000 -18734

Now, 180000 – 18734 = 161266

∴ Remaining tablets are 161266.

MP Board solutions for Class 6 Maths Chapter 1 Long Answer Type Questions

Question 1. Find the sum of greatest and the smallest 6-digit numbers formed by digits 2, 0, 4, 7, 6, 3 using each digit only once.

Solution. Given digits are 2, 0, 4, 7, 6, 3.

Using each digit only once,

The greatest 6-digit number is 764320.

The smallest 6-digit number is 203467.

Now, sum of these numbers = 764320 + 203467

= 967787

Question 2. In a 5-digit number, digit at tens place is 4, digit at units place is one-fourth of tens place digit, digit at hundreds place is 0, digit at thousands place is 5 times of the digit at units place and ten thousands place digit is double the digit at tens place. Find the number.

Solution. According to the question,

Digit at tens place = 4

Digit at unit place = \(\frac{1}{4}\) of tens place digit = \(\frac{1}{4} \times 4=1\)

Digit at hundreds place = 0

Digit at thousands place = 5 x Digit of unit place

= 5 x 1 = 5

Digit at ten thousands place = 2 x Digit of tens place

= 2 x 4 = 8

∴ Required number = 85041

Question 3. In a 5-digit number, digit at hundreds place is 6, digit at tens place is half of it, digit at unit place is the difference of the digits at hundreds and the tens place. The digit at thousands place is twice the digit at ones place and ten thousands place digit is same as that of tens place. Write the number.

Solution. Digit at hundreds place = 6

Digit at tens place = Half of 6 = 3

Digit at unit place or ones place = Difference of digits at hundreds and tens place

= 6 – 3 = 3

Digit at thousands place = Twice the digit at ones place

i.e. 2 x 3 = 6

Digit at ten thousands place = Digit at tens place = 3

So, the required number is 36633.

Question 4. Reshma’s school is \(\frac{8}{10}\) km away from her house. Daily she walks a distance and then takes a bus to travel \(\frac{1}{2}\) km to reach the school. How far does she walk?

Solution. Distance between her house to the school = \(\frac{8}{10}\) km

Distance covered by bus = \(\frac{1}{2}\) km

She walks distance = \(\left(\frac{8}{10}-\frac{1}{2}\right)=\frac{8-5}{10}=\frac{3}{10} \mathrm{~km}\)

= \(\frac{3 \times 1000}{10}=300 \mathrm{~m}\)

Question 5. There was a stock of 17380200 kg of wheat in a godown of the food corporation of India. Out of this stock, 2756744 kg of wheat was sent to Delhi and 4863108 kg to UP. How much is the balance stock now?

Solution. We have, Total stock of wheat = 17380200 kg

Quantity of wheat sent to Delhi = 2756744 kg

Quantity of wheat sent to UP = 4863108 kg

Total quantity of wheat taken out of the godown

= 2756744 + 4863108 = 7619852 kg

Balance stock of wheat in godown

= 17380200 – 7619852 = 9760348 kg

Hence, 9760348 kg balanced stock wheat in godown.

Question 6. A factory has a container filled with 35874 L of cold drink. In how many bottles of 200 mL capacity each can it be filled?

Solution. Cold drink in the container = 35874 L

= 35874 x 1000 mL = 35874000 mL

Capacity of each bottle= 200 mL

Hence, the number of bottles filled is 35874000 ÷ 200 mL.

Now,

Diagram

Thus, 179370 bottles are filled.

Question 7. Floor of a room measures 4.5m x 3m. Find the minimum number of complete square marble slabs of equal size required to cover the entire floor.

Solution. To find, the minimum number of square slabs to cover the floor, we have to find the greatest size of each such slab.

For this purpose, we have to find the HCF of 450 and 300.

[since, 4.5 m 450 cm and 3 m = 300 cm)

Now, HCF of 450 and 300 = 150

∵ Required size of the slab = 150 cm x 150 cm

∴ \(\text { Number of required slabs }=\frac{\text { Area of the floor }}{\text { Area of one slab }}\)

= \(\frac{450 \times 300}{150 \times 150}=6\)

Hence, the number of slabs is required 6.

Question 8. India’s population has been steadily increasing from 439 millions in 2001. Find the total increase in population from 1961 to 2001. Write the increase in population in Indian system of numeration, using commas suitably.

Solution. Given, population of India in 1961=439 millions

= 439 × 1000000

= 439000000 [∵ 1 million 1000000]

and population of India in 2001 = 1028 millions

= 1028 x 1000000

= 1028000000

[∵ 1 million = 1000000]

∴ Total increase in population from 1961 to 2001

= Population in 2001 – Population in 1961

= 1028000000 – 439000000

= 589000000

= 589 × 1000000

= 589 millions

So, the increase population in Indian system of numeration = 58,90,00,000

Question 9. Chinmay had ₹ 610000. He gave ₹ 87500 to Jyoti, ₹ 126380 to Javed and ₹ 350000 to John. How much money was left with him?

Solution: Given, Chinmay’s total money=610000

Money given to Jyoti by Chinmay=87500

Money given to Javed by Chinmay = 126380

Money given to John by Chinmay = 350000

∴ Money left with Chinmay

= Total money – Distributed money

= 610000-(87500 +126380 + 350000)

= 610000 – 563880

= ₹ 46120

Hence, ₹46120 was left with him.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Comparison of Decimals

For comparing decimals, we follow the steps given below:

(1) We first convert them into like decimals i.e. having a same number of decimal points and then compare the whole part, where the decimal number having a greater whole part will be greater.

e.g. In 1.09 and 2.09, the whole parts are 1 and 2, respectively.

And 2 is greater than 1.

So, 2.09 is greater than 1.09.

(2) If the whole part is the same for both, then compare the tenths part and decimal having greater tenths part will be greater.

In 1.09 and 1.19, the whole part is the same.

But the tenth part of 1.09 is smaller than the enth part of 1.19.

So, 1.19 is greater than 1.09.

(3) If tenth part is also same, then compare the hundredths part and so on.

e.g. In 1.09 and 1.093, converting them into like decimals, we get 1.090 and 1.093.

Here, the whole part, tenths part and hundredths part are same but thousandths part of 1.093 is greater.

So, 1.093 is greater than 1.09.

Read and Learn More MP Board Class 6 Maths Solutions

Note it Without changing the value of a decimal, the number of decimal places can be increased simply by adding zeroes to the extreme right of its decimal parts.

Example 1. Which is greater?

(1) 2.03 or 3.07

(2) 2.09 or 2.19

(3) 3.12 or 3.15

(4) 0.05 or 0.02

(5) 1.7 or 1.72

(6) 2.7 or 2.70

(7) 22.63 or 22.84

(8) 112.316 or 112.314

(9) 6.3 or 3.6

(10) 0.70 or 0.7

Solution. (1) We have, 2.03 and 3.07

On comparing whole parts, we get

2 < 3

∴ Hence, 2.03 < 307

(2) We have, 2.09 and 2.19

Here, whole part of both numbers are same.

So, on comparing the tenths part, we get

0 < 1

Hence, 2.09 < 2.19

(3) We have, 3.12 and 3.15

Here, whole part and tenths part of both numbers are same.

So, on comparing the hundredths part, we get

2 < 5

Hence, 312 < 315

(4) We have, 0.05 and 0.02

Here, whole part and tenths part of both numbers are same.

So, on comparing the hundredths part, we get

5 > 2

Hence, 0.05 > 0.02

(5) We have, 1.7 and 1.72

By converting them into like decimals, we get

1.70 and 1.72

Here, whole part and tenths of both numbers are same.

So, on comparing the hundredths part, we get

0 < 2

Hence, 1.7 < 1.72

(6) We have, 2.7 and 2.70

By converting them into like decimals, we get

2.70 and 2.70

Here, both the given numbers are same.

Hence, 2.7 = 2.70

(7) We have, 22.63 and 22.84

Here, whole part of both numbers are same.

So, on comparing the tenths part, we get

6 < 8

Hence, 22.63 < 22.84

(8) We have, 112.316 and 112.314

Here, whole part, tenths part and hundredth part are same.

So, on comparing the thousandths part, we get

6 > 4

Hence, 112.316 > 112.314

(9) We have, 6.3 and 3.6

On comparing the whole part of 6.3 and 3.6, we get

6 > 3

Hence, 6.3 > 3.6

(10) We have, 0.70 and 0.7

By converting them into like decimals, we get 0.70 and 0.70

Here, both the given numbers are same.

Hence, 0.70 = 0.7

MP Board Class 6 Maths Solutions For Example 2. Arrange the following decimal numbers in ascending order 36.4, 6.02, 6.2, 4.93, 3.793.

Solution. The given decimal numbers are 36.4, 6.02, 6.2, 4.93 and 3.793

By converting them into like decimals, we get 36.400, 6.020, 6.200, 4.930 and 3.793

On comparing these like decimal numbers, we find that 3.793 < 4.930 < 6.020 < 6.200 < 36.400

Thus, 3.793 < 4.93 < 6.02 < 6.2 < 36.4

Hence, the given decimals numbers in ascending order are as follows: 3.793, 4.93, 6.02, 6.2, 36.4.

MP Board Class 6 Maths Solutions

Example 3. Arrange the following decimal numbers in descending order 3.6, 49.26, 0.23, 0.244 and 3.108.

Solution. The given decimal numbers are 3.6, 49.26, 0.23, 0.244 and 3.108

By converting them into like decimals, we get 3.600, 49.260, 0.230, 0.244 and 3.108

On comparing these like decimal numbers, we find that 49.260 > 3.600 > 3.108 > 0.244 > 0.230

Thus, 49.26 > 3.6 > 3.108 > 0.244 > 0.23

Hence, the given decimal numbers in descending order are as follows: 49.26, 3.6, 3.108, 0.244, 0.23.

Example 4. Compare the following figures

Solution. In the figure of left side, we have 12 shaded parts out of 100.

∴ \(\frac{12}{100}=0.12\)

In the right side figure, we have 4 shaded parts out of 10.

∴ \(\frac{4}{10}=0.4\)

Hence, 0.12 < 0.4.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Using Decimals

Decimals are used in numerous ways in our day to day life. e.g. In representing money, length, weight etc.

Money

We know that 100 paise = ₹ 1

∴ \(1 \text { paisa }=₹ \frac{1}{100}=₹ 0.01\)

So, the convert paise (money) into rupee, multiple paise by \(\frac{1}{100}\).

Example 1. Express as rupees using decimal.

(1) 65 paise

(2) 105 paise

(3) 20 rupees 27 paise

(4) 27 rupees and 7 paise in decimal.

Solution.

(1) \(65 \text { paise }=₹ \frac{65}{100}=₹ 0.65\)

(2) \(105 \text { paise }=(100+5) \text { paise }=₹\left(\frac{100}{100}+\frac{5}{100}\right)=₹ 1.05\)

(3) We have, \(₹ 20+27 \text { paise }=₹ 20+₹\left(27 \times \frac{1}{100}\right)\)

= ₹ (20 + 0.27) = ₹ 20.27

(4) We have, \(₹ 27+7 \text { paise }=₹ 27+₹\left(7 \times \frac{1}{100}\right)\)

= ₹ (27 + 0.07) = ₹ 27.07

Example 2. If Sohan gave 950 paise to shopkeeper, then how much money in rupees did he gave to shopkeeper?

Solution. Given, Sohan gave money to shopkeeper = 950 paise

We know that 1 paisa = ₹ \(\frac{1}{100}\)

∴ \(950 \text { paise }=₹ 950 \times \frac{1}{100}=₹ \frac{950}{100}=₹ 9.50\)

Hence, Sohan gave ₹ 9.50 to shopkeeper.

Length

We know that 100 cm = 1m

∴ 1 cm = \(\frac{1}{100} \mathrm{~m}=0.01 \mathrm{~m}\)

So, to convert centimetre into metre, multiply centimetre by \(\frac{1}{100}\).

Also, 1000 m = 1 km

∴ \(1 \mathrm{~m}=\frac{1}{1000} \mathrm{~km}=0.001 \mathrm{~km}\)

So, to convert metre into kilometre, multiply metre by 1/1000

Also, 10 mm = 1 cm

∴ \(1 \mathrm{~mm}=\frac{1}{10} \mathrm{~cm}=0.1 \mathrm{~cm}\)

So, to convert milimetre into centimetre, multiply milimetre by 1/10.

MP Board Class 6 Maths Solutions

Example 3. Express as metres using decimals.

(1) 17 cm

(2) 4 cm

(3) 3 m 48 cm

(4) 309 cm

Solution. (1) We know that 100 cm = 1 m

⇒ \(1 \mathrm{~cm}=\frac{1}{100} \mathrm{~m}\)

∴ \(17 \mathrm{~cm}=17 \times \frac{1}{100} \mathrm{~m}=\frac{17}{100} \mathrm{~m}=0.17 \mathrm{~m}\)

(2) We know that

∴ \(4 \mathrm{~cm}=4 \times \frac{1}{100} \mathrm{~m}=\frac{4}{100} \mathrm{~m}=0.04 \mathrm{~m}\)

(3) We know that 1 cm = \(\frac{1}{100}\) m

∴ 3 m 48 cm = \(3 \mathrm{~m}+48 \mathrm{~cm}=3 \mathrm{~m}+48 \times \frac{1}{100} \mathrm{~m}\)

= \(3 m+\frac{48}{100} m=3 m+0.48 m\)

= (3 + 0.48)m = 3.48 m

(4) We know that

∴ \(309 \mathrm{~cm}=309 \times \frac{1}{100} \mathrm{~m}\)

= \(\frac{309}{100} \mathrm{~m}=3.09 \mathrm{~m}\)

Example 4. Express as centimetres using decimals.

(1) 7 mm

(2) 70 mm

(3) 8 cm 4 mm

(4) 198 mm

Solution. (1) We know that

10 mm = 1cm

⇒ \(1 \mathrm{~mm}=\frac{1}{10} \mathrm{~cm}\)

∴ \(7 \mathrm{~mm}=7 \times \frac{1}{10} \mathrm{~cm}=\frac{7}{10} \mathrm{~cm}=0.7 \mathrm{~cm}\)

(2) We know that

1mm = \(\frac{1}{10}\) cm

∴ \(70 \mathrm{~mm}=70 \times \frac{1}{10} \mathrm{~cm}=\frac{70}{10} \mathrm{~cm}=7 \mathrm{~cm}\)

(3) We know that

1mm = \(\frac{1}{10}\) cm

∴ \(8 \mathrm{~cm} 4 \mathrm{~mm}=8 \mathrm{~cm}+4 \mathrm{~mm}=8 \mathrm{~cm}+\left(4 \times \frac{1}{10}\right) \mathrm{cm}\)

= \(8 \mathrm{~cm}+\frac{4}{10} \mathrm{~cm}=8 \mathrm{~cm}+0.4 \mathrm{~cm}\)

= (8 + 0.4)cm = 8.4 cm

(4) We know that

1mm = \(\frac{1}{10}\) cm

∴ \(198 \mathrm{~mm}=198 \times \frac{1}{10} \mathrm{~cm}=\frac{198}{10} \mathrm{~cm}=19.8 \mathrm{~cm}\)

MP Board Class 6 Maths Solutions

Example 5. Express as kilometers using decimals.

(1) 98 m

(2) 7 m

(3) 6843 m

(4) 15 km 7 m

Solution. (1) We know that

1000 m = 1 km

⇒ \(1 \mathrm{~m}=\frac{1}{1000} \mathrm{~km}\)

∴ \(98 \mathrm{~m}=98 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{98}{1000}=0.098 \mathrm{~km}\)

(2) We know that

l m = \(\frac{1}{1000}\) km

∴ \(7 \mathrm{~m}=7 \times \frac{1}{1000} \mathrm{~km}=\frac{7}{1000} \mathrm{~km}=0.007 \mathrm{~km}\)

(3) We know that

1 m = \(\frac{1}{1000}\) km

∴ \(6843 \mathrm{~m}=6843 \times \frac{1}{1000} \mathrm{~km}=\frac{6843}{1000} \mathrm{~km}\)

= 6.843 km

(4) We know that

1m = \(\frac{1}{1000}\) km

∴ \(15 \mathrm{~km} 7 \mathrm{~m}=15 \mathrm{~km}+7 \mathrm{~m}=15 \mathrm{~km}+7 \times \frac{1}{1000} \mathrm{~km}\)

= \(15 \mathrm{~km}+\frac{7}{1000} \mathrm{~km}=15 \mathrm{~km}+0.007 \mathrm{~km}\)

= (15 + 0.007) km = 15.007 km

Example 6. Express the following using decimals.

1. 6 mm in cm
2. 60 m in km using decimals

Solution. (1) We know that 10 mm = 1 cm

1 mm = \(\frac{1}{10}\) cm

⇒ \(6 \mathrm{~mm}=\frac{6}{10} \mathrm{~cm}=0.6 \mathrm{~cm}\)

(2) We know that 1000 m = 1km

1 m = \(\frac{1}{1000}\) km

⇒ \(60 \mathrm{~m}=\frac{60}{1000} \mathrm{~km}=0.060 \mathrm{~km}\)

Example 7. How can we write 946 mm in metres?

Solution. We know that

1 mm = \(\frac{1}{10}\) cm

and 1 cm = \(\frac{1}{100}\) m

∴ 946 mm = \(946 \times \frac{1}{10} \mathrm{~cm}\)

= \(\frac{946}{10} \mathrm{~cm}=94.6 \mathrm{~cm}\)

= \(94.6 \times \frac{1}{100} \mathrm{~m}=\frac{94.6}{100} \mathrm{~m}=0.946 \mathrm{~m}\)

Weight

We know that 1000 g = 1kg

⇒ 1 g = \(\frac{1}{1000}\) kg

So, to convert gram into kilogram, multiply gram by \(\frac{1}{1000}\)

e.g. \(452 \mathrm{~g}=\frac{452}{1000}=0.452 \mathrm{~kg}\)

MP Board Class 6 Maths Solutions For Example 8. Express as kilograms using decimals.

(1) 6 g

(2) 120 g

(3) 2645 g

(4) 8 kg 9 g

Solution. (1) We know that

1000 g = 1kg

⇒ \(1 \mathrm{~g}=\frac{\mathrm{l}}{1000} \mathrm{~kg}\)

∴ \(6 \mathrm{~g}=6 \times \frac{1}{1000} \mathrm{~kg}=\frac{6}{1000} \mathrm{~kg}=0.006 \mathrm{~kg}\)

(2) We know that

1 g = \(\frac{1}{1000}\) kg

∴ \(120 \mathrm{~g}=120 \times \frac{1}{1000} \mathrm{~kg}\)

= \(\frac{120}{1000} \mathrm{~kg}=0.12 \mathrm{~kg}\)

(3) We know that

1 g = \(\frac{1}{1000}\) kg

∴ \(2645 \mathrm{~g}=2645 \times \frac{1}{1000} \mathrm{~kg}\)

= \(\frac{2645}{1000}\) kg

= 2.645 kg

(4) We know that

1 g = \(\frac{1}{1000}\) kg

∴ 8 kg 9 g = 8 kg + 9 g

= \(8 \mathrm{~kg}+9 \times \frac{1}{1000} \mathrm{~kg}\)

= \(8 \mathrm{~kg}+\frac{9}{1000} \mathrm{~kg}\)

= 8 kg + 0.009 kg

= (8 + 0.009) kg

= 8.009 kg

MP Board Class 6 Maths Solutions

Example 9. Ramesh bought 3 kg 560 g onions that means he bought 3.560 kg onion. State whether the given statement is true or false?

Solution. Weight of onions = 3 kg 560 g

∴ 3 kg 560 g = 3kg + 560 g [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(3 \mathrm{~kg}+560 \times \frac{1}{1000} \mathrm{~kg}\)

= 3 kg + 0.560 kg

= (3 + 0.560) kg

= 3.560 kg

Hence, the given statement is true.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Addition of Numbers with Decimals

To add the numbers with decimals, we follow the steps given below

(1) Firstly, convert the given decimals into like decimals.

(2) Write the numbers according to the place value chart or arrange in columns in such a way that the digits of same place are arranged in same columns.

(3) Now, add the numbers in column from the right, the same way as we carry the regular addition.

Example 1. Find the sum in each of the following

(1) 0.37 +0.46

(2) 0.6+0.09

(3) 0.79+0.65

(4) 2.34+161

Solution. (1) We have, 0.37 + 0.46

∴ 0.37 + 0.46 = 0.83

(2) We have, 0.6 + 0.09

∴ 0.6 + 0.09 = 1.44

(3) We have, 0.79 + 0.65

∴ 0.79 + 0.65 = 1.44

(4) We have, 2.34 + 1.61

∴ 2.34 + 1.61 = 3.95

Class 6 Maths Chapter 8 Solutions 

Example 2. Find the sum in each of the following

(1) 280.64 + 25.5 + 28

(2) 270.24 + 12.52 + 1.5

(3) 0.006 + 7.3 + 26.08

(4) 0.61 + 19.314 + 7

Solution. (1) Here, 280.64 + 255 + 28 can be written as

∴ 280.64 + 25.5 + 28 = 334.14

(2) Here, 270.24 +12.52 +1.5 can be written as Hundreds

∴ 270.24 + 12.52 + 1.50 = 284.26

(3) We have, 0.006 + 7.3 + 26.08

∴ 0.006 + 7.3 + 26.08 = 33.386

(4) We have, 0.61 + 19.314 + 7

∴ 0.61 + 19.314 + 7 = 26924

Class 6 Maths Chapter 8 Solutions 

Example 3. Mahesh spent 30.55 for the Mathematics book and 20.54 for the Science book. Find the total amount spent by Mahesh.

Solution. Money spent for Mathematics book = ₹ 30.55

and money spent for Science book = ₹ 20.54

∴ Total amount spent = ₹ 30.55 + ₹ 20.54

= 30.55 + 20.54 = 51.09

Hence, the total amount spent by Mahesh is * 51.09.

Class 6 Maths Chapter 8 Solutions 

Example 4. Sohan’s grandmother gave him? 15.50 and his grandfather gave him 23.60, then find the total amount given to Sohan from his grandmother and grandfather.

Solution. Money given to Sohan by his grandmother = ₹ 15.50

and money given to Sohan by his grandfather = ₹ 23.60

∴ Total money = ₹ 15.50 + ₹ 23.60

= 15.50 + 23.60 = 39.10

Hence, the total money given to Sohan by his grandmother and grandfather is ₹ 39.10.

Example 5. Shobhit bought 3 m 20 cm cloth for his shirt and 1 m 50 cm for his pant. Then, find the total length of cloth bought by him.

Solution. Shobhit bought cloth for his shirt = 3m 20 cm

= \(3 \mathrm{~m}+20 \mathrm{~cm}=3 \mathrm{~m}+20 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= 3m + 0.20 m = (3 + 0.20) m = 3.20 m

Shobhit bought cloth for his pants=1 m 50 cm

= \(1 \mathrm{~m}+50 \mathrm{~cm}=1 \mathrm{~m}+50 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= 1m + 0.50 m = (1 + 0.50) m = 1.50 m

∴ The total length of cloth bought by Shobhit is

= 3.20 + 1.50 = 4.70 m

Hence, the total length of cloth brought by Shobit is 4.70 m.

Decimals Class 6 Maths Solutions

Example 6. Seema travelled 16 km 475 m by train, 5 km 70 m by bus and 700 m by rickshaw in order to reach a hill station. How much distance travelled by her to reach the hill station?

Solution. Distance travelled by train = 16 km 475 m

= 16 km + 475 m

= \(16 \mathrm{~km}+475 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(16 \mathrm{~km}+\frac{475}{1000} \mathrm{~km}\)

= 16 km + 0.475 km

= (16 + 0.475) km = 16.475 km

Distance travelled by bus = 5 km 70 m = 5 km + 70 m

= \(5 \mathrm{~km}+70 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(5 \mathrm{~km}+\frac{70}{1000} \mathrm{~km}=5 \mathrm{~km}+0.070 \mathrm{~km}\)

= (5 + 0.070) km = 5.070 km

Distance travelled by rickshaw = \(700 \mathrm{~m}=700 \times \frac{1}{1000} \mathrm{~km}\)

[∴ 1 m = \(\frac{1}{1000}\) km]

= \(\frac{700}{1000} \mathrm{~km}=0.700 \mathrm{~km}\)

∴ Total distance travelled by Seema

= 16.475 + 5.070 + 0.700 = 22.245

Hence, the total distance travelled by Seema is 22.245 km.

Example 7. Shaurya bought 5 kg 80 g apples, 8 kg 400 g grapes and 3 kg 340 g mangoes. Find the total weight of all the fruits he bought.

Solution. Weight of apples purchased by Shaurya

= 5 kg 80 g = 5 kg + 80 g

= \(5 \mathrm{~kg}+80 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(5 \mathrm{~kg}+\frac{80}{1000} \mathrm{~kg}=5 \mathrm{~kg}+0.080 \mathrm{~kg}\)

= (5 + 0.080) kg = 5.080 kg

Weight of grapes purchased by Shaurya

= 8 kg 400 g = 8 kg + 400 g

= \(8 \mathrm{~kg}+400 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(8 \mathrm{~kg}+\frac{400}{1000} \mathrm{~kg}=8 \mathrm{~kg}+0.400 \mathrm{~kg}\)

= (8 + 0.400) kg = 8.400 kg

Weight of mangoes purchased by Shaurya

= 3 kg 340 g = 3 kg + 340 g

= \(3 \mathrm{~kg}+340 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(3 \mathrm{~kg}+\frac{340}{1000} \mathrm{~kg}=3 \mathrm{~kg}+0.340 \mathrm{~kg}\)

= (3 + 0.340) kg = 3.340 kg

∴ Total weight of his purchases

= 5.080 + 8.400 + 3.340 = 16.820

Hence, the total weight of all of his purchases is 16.820 kg.

Decimals Class 6 Maths Solutions

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Subtraction of Decimals

To subtract the decimal number, we follow the steps given below

(1) Firstly, convert the given decimals into like decimals.

(2) Write the smaller number below the larger number in column form in such a way that the decimal points of both the numbers are in the same column and the digits of the same place are arranged in same column.

(3) Subtract as we do in case of whole numbers.

(4) Put the decimal point directly under the decimal points of the given numbers.

Note It Sometimes while subtracting decimals, we may need to regroup we did in addition.

Example 1. Subtract

(1) 0.95 from 2.29

(2) 23.75 from 2725

(3) 302.56 m from 416.44 m

(4) 1.416 kg from 3.209 kg

Solution. (1) We have, 2.29 – 0.95

At tenths place subtraction cannot done so grouped it.

∴ 2.29 – 0.95 = 1.34

(2) We have, ₹ 27.25 – ₹ 23.75

At tenths place subtraction cannot done so regrouped it.

∴ ₹ 27.25 – ₹ 23.75 = ₹ (27.25 – 23.75) = ₹ 3.50

(3) We have, 416.44 m – 302.56 m

At tenths place subtraction cannot done so regrouped it.

∴ 416.44 m – 302.56 m = (416.44 – 302.56) m = 113.88 m

(4) We have, 3.209 kg – 1.416 kg

At tenths place subtraction cannot done so regrouped it.

∴ 3.209 kg – 1.416 kg = (3.209 – 1.416) kg

Decimals Class 6 Maths Solutions

Example 2. Find the value of

(1) 8.146 – 5.38

(2) 19.09 – 11.36

(3) 11.5 – 4.49

(4) 13.7 – 9.198

Solution.

(1) We have, 8.146 – 5.38

= 8.146 – 5.380 = 2.766

∴ 8.146 – 5.380 = 2.766

(2) We have, 19.09 – 11.36

= 19.09 – 11.36 = 7.73

∴ 19.09 – 11.36 = 7.73

(3) We have, 11.50 – 4.49

= 11.50 – 4.49 = 7.01

∴ 11.50 – 4.49 = 7.01

(4) We have, 13.7 – 9.198

13.700 – 9.198 = 4.502

∴ 13.7 – 9.198 = 4.502

Example 3. By what amount should 48.76 be increased to get 97?

Solution. We subtract 48.76 from 97 in order to find the number that is to be added to 48.76 to get 97.

Converting into like decimals and then subtracting.

= 97.00 – 48.76 = 48.24

Hence, 48.24 should be increase in 48.76 to get 97.

Decimals Class 6 Maths Solutions

Example 4. What should be added to 29.6 to get 59?

Solution. We subtract 29.6 from 59 in order to find the number that should be added to 29.6 to make it 59.

Converting into like decimals and then subtracting.

= 59.0 – 29.6 = 29.4

Hence, 29.4 should be added to 29.6 to get 59.

Example 5. What should be subtracted from 179 to get 91.94?

Solution. We subtract 91.94 from 179 in order to find the number that should be subtracted from 179 to get 91.94.

Converting into like decimals and then subtracting.

= 179.00 – 91.94 = 87.06

Hence, 87.06 should be subtracted from 179 to get 91.94.

Example 6. Ramesh purchased a book worth ₹ 300.80 from a bookseller and gave him a ₹ 500. How much balance did he get back?

Solution. Total money paid = ₹ 500.00

Cost of the book = ₹ 300.80

∴ Balance = 500.00 – 300.80 = ₹ 199.20

Hence, the balance he will get back from bookseller is ₹ 199.20.

Example 7. Shiva bought a toy for 47.85. He gave ₹50 to the shopkeeper. How much money did he get back from the shopkeeper?

Solution.

Cost of toy bought by Shiva = ₹ 47.85

and money gave to shopkeeper = ₹ 50

∴ Money get back from shopkeeper = ₹ 50 – ₹ 47.85

= ₹ (50 – 47.85) = ₹ 2.15

Hence, the money get back from shopkeeper is ₹ 2.15.

MP Board Class 6 Chapter 8 Maths 

Example 8. Reena had 10 m 5 cm long cloth. She cuts 3 m 65 cm length of cloth from this for making a cover of table. How much cloth is left with her?

Solution. Total length of cloth = 10 m 5 cm = 10m + 5 cm

= \(10 \mathrm{~m}+5 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(10 \mathrm{~m}+\frac{5}{100} \mathrm{~m}\)

= 10 m + 0.05 m

= (10 + 0.05) m

= 10.05 m

Length cut out for cover of table = 3 m 65 cm = 3m + 65 cm

= \(3 \mathrm{~m}+65 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(3 \mathrm{~m}+\frac{65}{100} \mathrm{~m}=3 \mathrm{~m}+0.65 \mathrm{~m}\)

= (3 + 0.65) m = 3.65 m

∴ Length of cloth left with Reena = 10.05 m – 3.65 m = (10.05 – 3.65) m = 6.40 m

Hence, 6.40 m cloth is left with her.

Example 9. Rohan’s school is at a distance of 6 km 450 m from his house. He travels 5 km 225 m by bus and rest on foot. How much distance does he travel on foot?

Solution. Distance of school from Rohan’s house = 6 km 450 m

= 6 km + 450 m

= \(6 \mathrm{~km}+450 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1m = \(\frac{1}{1000}\) km]

= \(6 \mathrm{~km}+\frac{450}{1000} \mathrm{~km}\)

= 6 km + 0.450 km

= (6 + 0.450) km = 6.450 km

and distance travelled by bus = 5 km 225 m

= 5 km + 225 m

= \(5 \mathrm{~km}+225 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1m = \(\frac{1}{1000}\) km]

= \(5 \mathrm{~km}+\frac{225}{1000} \mathrm{~km}\)

= 5 km + 0.225 km

= (5 + 0.225) km = 5.225 km

∴ Distance travelled on foot

= 6.450 km – 5.225 km

=(6.450 – 5.225) km = 1.225 km

Hence, Rohan travels 1.225 km on foot.

Example 10. Ashu bought fruits weight 20 kg. Out of this 6 kg 700 g is apples, 5 kg 25 g is mangoes and rest is grapes. Find the weight of the grapes.

Solution. Given, total weight of fruits = 20 kg

Weight of apples = 6 kg 700 g = 6 kg + 700 g

= \(6 \mathrm{~kg}+700 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(6 \mathrm{~kg}+700 \times \frac{1}{1000} \mathrm{~kg}\)

=6 kg + 0.700 kg

=(6 + 0.700) kg = 6.700 kg

Weight of mangoes = 5 kg 25 g = 5 kg + 25 g

= \(5 \mathrm{~kg}+25 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1g = \(\frac{1}{1000}\) kg]

= \(5 \mathrm{~kg}+\frac{25}{1000} \mathrm{~kg}=5 \mathrm{~kg}+0.025 \mathrm{~kg}\)

= (5 + 0.025) kg = 5.025 kg

∴ Total weight of apples and mangoes

= 6.700 kg + 5.025 kg = 11725 kg

Now, weight of grapes = Total weight of fruits – weight of apples and mangoes

= 20 kg – 11.725 kg = 8.275 kg

Hence, the weight of the grapes is 8.275 kg.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Exercise 8.1

Question 1. Which is greater?

(1) 0.3 or 0.4

(2) 0.07 or 0.02

(3) 1.5 or 1.50

Solution. (1) We have, 0.3 and 0.4

Here, whole part of both numbers are same.

Now, tenths part of 0.3 = 3

and tenths part of 0.4 = 4

Here, 4 is greater than 3.

∴ 0.4 > 0.3

Hence, 0.4 is greater than 0.3.

(2) We have, 0.07 and 0.02

Here, whole parts as well as tenths parts of both numbers are same i.e. 0.

Now, hundredths part of 0.07 = 7

and hundredths part of 0.02 = 2

Here, 7 is greater than 2 i.e.7 > 2

Hence, 0.07 is greater than 0.02.

(3) We have, 1.5 or 1.50

∴ \(1.5=1+\frac{5}{10}+\frac{0}{100} \text { and } 1.50=1+\frac{5}{10}+\frac{0}{100}\)

Here, whole parts, tenths parts as well as hundredths parts of both numbers are same.

∴ 1.5 = 150

Hence, both numbers are equal.

MP Board Class 6 Chapter 8 Maths 

Question 2. Write 2 rupees 5 paise and 2 rupees 50 paise in decimals.

Solution. We have, 2 rupees 5 paise = ₹ 2 + 5 paise

= \(₹ 2+₹\left(5 \times \frac{1}{100}\right)\)

= ₹ (2 + 0.05) = ₹ 2.05

and 2 rupees 50 paise = ₹ 2 + 50 paise

= \(₹ 2+₹\left(50 \times \frac{1}{100}\right)\)

= ₹ (2 + 0.50) = ₹ 2.50

Question 3. Can you write 4 mm in ‘cm’ using decimals?

Solution. Yes, we can write 4 mm in centimetres using decimals as follows

We know that 10 mm = 1 cm

⇒ \(1 \mathrm{~mm}=\frac{1}{10} \mathrm{~cm}\)

∴ \(4 \mathrm{~mm}=4 \times \frac{1}{10} \mathrm{~cm}=\frac{4}{10} \mathrm{~cm}=0.4 \mathrm{~cm}\)

Question 4. How will you write 7 cm 5 mm in ‘cm’ using decimals?

Solution. We know that 10 mm = 1 cm ⇒ 1mm = \(\frac{1}{10}\) cm

∴ \(7 \mathrm{~cm} 5 \mathrm{~mm}=7 \mathrm{~cm}+5 \mathrm{~mm}=7 \mathrm{~cm}+5 \times \frac{1}{10} \mathrm{~cm}\)

= \(7 \mathrm{~cm}+\frac{5}{10} \mathrm{~cm}=\left(7+\frac{5}{10}\right) \mathrm{cm}\)

= (7 + 0.5) cm = 7.5 cm

MP Board Class 6 Chapter 8 Maths 

Question 5. Can you now write 52 m as ‘km’ using decimals? How will you write 340 m as ‘km’ using decimals? How will you write 2008 m in ‘km’?

Solution. Yes, we can write 52 m as ‘km’ using decimals as follows

We know that 1000 m = 1 km ⇒ 1 m = \(\frac{1}{1000}\) km

∴ \(52 \mathrm{~m}=52 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{52}{1000} \mathrm{~km}=0.052 \mathrm{~km}\)

To write 340 m as kilometres.

We know that 1 m = \(\frac{1}{1000}\) km

∴ \(340 \mathrm{~m}=340 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{340}{1000} \mathrm{~km}=0.340 \mathrm{~km}\)

To write 2008 m as kilometers.

We know that 1 m = \(\frac{1}{1000}\) km

∴ \(2008 \mathrm{~m}=2008 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{2008}{1000} \mathrm{~km}=2.008 \mathrm{~km}\)

Question 6. Can you now write 456 g as kg using decimals?

Solution. We know that

1000 g = 1 kg ⇒ \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)

∴ \(456 \mathrm{~g}=456 \times \frac{1}{1000} \mathrm{~kg}=\frac{456}{1000} \mathrm{~kg}=0.456 \mathrm{~kg}\)

Question 7. How will you write 2 kg 9 g in ‘kg’ using decimals?

Solution. We have, 2 kg 9 g = 2kg + 9g

= \(2 \mathrm{~kg}+9 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(2 \mathrm{~kg}+\frac{9}{1000} \mathrm{~kg}=2 \mathrm{~kg}+0.009 \mathrm{~kg}\)

= (2 + 0.009) kg = 2.009 kg

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Exercise 8.2

Question 1. Express as rupees using decimals.

(1) 5 paise

(2) 50 rupees 90 paise

Solution.

(1) We know that 1 paise = ₹ \(\frac{1}{100}\)

∴ \(5 \text { paise }=₹ 5 \times \frac{1}{100}=₹ \frac{5}{100}=₹ 0.05\)

(2) We know that 1 paise = ₹ \(\frac{1}{100}\)

∴ 50 rupees 90 paise = ₹ 50 + 90 paise

= \(₹ 50+₹ 90 \times \frac{1}{100}=₹ 50+₹ \frac{90}{100}\)

= ₹ 50 + ₹ 0.90 = ₹(50 + 0.90) = ₹ 50.90

Question 2. Express as metres using decimals.

(1) 15 cm

(2) 2 m 45 cm

(3) 419 cm

Solution. (1) We know that 100 cm = 1 m

⇒ 1 cm = \(\frac{1}{100}\) m

∴ \(15 \mathrm{~cm}=15 \times \frac{1}{100} \mathrm{~m}=\frac{15}{100} \mathrm{~m}=0.15 \mathrm{~m}\)

(2) We know that 1 cm = \(\frac{1}{100}\) m

∴ \(2 \mathrm{~m} 45 \mathrm{~cm}=2 \mathrm{~m}+45 \mathrm{~cm}=2 \mathrm{~m}+45 \times \frac{1}{100} \mathrm{~m}\)

= \(2 \mathrm{~m}+\frac{45}{100} \mathrm{~m}=2 \mathrm{~m}+0.45 \mathrm{~m}\)

= (2 + 0.45) m = 2.45 m

(3) We know that 1 cm = \(\frac{1}{100}\) m

∴ \(419 \mathrm{~cm}=419 \times \frac{1}{100} \mathrm{~m}=\frac{419}{100} \mathrm{~m}=4.19 \mathrm{~m}\)

MP Board Class 6 Chapter 8 Maths 

Question 3. Express as centimeters using decimals.

(1) 5 mm

(2) 9 cm 8 mm

Solution. (1) We know that 1 mm = \(\frac{1}{10}\) cm

∴ \(5 \mathrm{~mm}=5 \times \frac{1}{10} \mathrm{~cm}=\frac{5}{10} \mathrm{~cm}=0.5 \mathrm{~cm}\)

(2) We know that 1 mm = \(\frac{1}{10}\) cm

∴ \(9 \mathrm{~cm} 8 \mathrm{~mm}=9 \mathrm{~cm}+8 \mathrm{~mm}=9 \mathrm{~cm}+8 \times \frac{1}{10} \mathrm{~cm}\)

= \(9 \mathrm{~cm}+\frac{8}{10} \mathrm{~cm}=\left(9+\frac{8}{10}\right) \mathrm{cm}\)

= (9 + 0.8) cm = 9.8 cm

Question 4. Express as kilometres using decimals.

(1) 8 m

(2) 88 m

(3) 8888 m

(4) 70 km 5 m

Solution. (1) We know that 1000 m = 1 km

⇒ 1 m = \(\frac{1}{1000}\) km

∴ \(8 \mathrm{~m}=8 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{8}{1000} \mathrm{~km}=0.008 \mathrm{~km}\)

(2) We know that 1 m = \(\frac{1}{1000}\) km

∴ \(88 \mathrm{~m}=88 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{88}{1000} \mathrm{~km}=0.088 \mathrm{~km}\)

(3) We know that 1 m = \(\frac{1}{1000}\) km

∴ \(8888 \mathrm{~m}=8888 \times \frac{1}{1000} \mathrm{~km}\)

= \(\frac{8888}{1000} \mathrm{~km}=8.888 \mathrm{~km}\)

(4) We know that 1m = \(\frac{1}{1000}\) km

∴ 70 km 5 m = 70 km + 5 m

= \(70 \mathrm{~km}+5 \times \frac{1}{1000} \mathrm{~km}\)

= \(70 \mathrm{~km}+\frac{5}{1000} \mathrm{~km}\)

= (70 + 0.005) km = 70.005 km

Question 5. Find

(1) 0.29 + 0.36

(2) 0.7 + 0.08

Solution. (1) We have, 0.29 + 0.36

∴ 0.29 + 0.36 = 0.65

(2) We have, 0.7 + 0.08

∴ 0.7 + 0.08 = 0.78

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Exercise 8.3

Question 1. Find the sum in each of the following.

(1) 0.007 + 8.5 + 30.08

(2) 15 + 0.632 + 13.8

Solution. (1) We have, 0.007 + 8.5 + 30.08

∴ 0.007 + 8.5 + 30.08 = 38.587

(2) We have, 15 + 0.632 + 13.8

∴ 15 + 0.632 + 13.8 = 29.432

MP Board Class 6 Chapter 8 Maths 

Question 2. Rashid spent 35.75 for Maths book and 32.60 for Science book. Find the total amount spent by Rashid.

Solution. Money spent by Rashid for Maths book = 35.75 and money spent by Rashid for Science book = 32.60

∴ Total money spent 35.75 + 32.60 = 68.35

Hence, the total money spent by Rashid is ₹ 68.35.

Question 3. Radhika’s mother gave her 10.50 and her father gave her 15.80. Find the total amount given to Radhika by the parents.

Solution. Money given to Radhika by her mother = 10.50 and money given to Radhika by her father= 15.80

∴ Total money = 10.50 + 15.80 = 26.30

Hence, the total money given to Radhika by her parents is ₹ 26.30.

Question 4. Nasreen bought 3 m 20 cm cloth for her shirt and 2 m 5 cm cloth for her trouser. Find the total length of cloth bought by her.

Solution. Cloth bought by Nasreen for her shirt = 3 m 20 cm

= 3 m + 20 cm

= \(3 \mathrm{~m}+20 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= 3m + 0.20 m = (3 + 0.20) m = 3.20 m

Cloth bought by Nasreen for her trouser

= 2m 5 cm = 2m + 5 cm

= \(2 \mathrm{~m}+5 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= 2m + 0.05 m = (2 + 0.05) m = 2.05 m

Total length of cloth 3.20 + 2.05 = 5.25

Hence, the total length of cloth bought by Nasreen is 5.25 m.

Question 5. Naresh walked 2 km 35 m in the morning and 1 km 7 m in the evening. How much distance did he walk in all?

Solution. Naresh walked in morning

= 2 km 35 m = 2 km + 35 m

= \(2 \mathrm{~km}+35 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(2 \mathrm{~km}+\frac{35}{1000} \mathrm{~km}=(2+0.035) \mathrm{km}=2.035 \mathrm{~km}\)

Naresh walked in evening

= 1 km 7 m = 1 km + 7 m

= \(1 \mathrm{~km}+7 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(1 \mathrm{~km}+\frac{7}{1000} \mathrm{~km}=(1+0.007) \mathrm{km}=1.007 \mathrm{~km}\)

∴ Total distance = 2.035 + 1.007 = 3.042

Hence, the total distance walked by Naresh is 3.042 km.

Decimal Representation on Number Line

Question 6. Sunita travelled 15 km 268 m by bus, 7 km 7 m by car and 500 m on foot in order to reach her school. How far is her school from her residence?

Solution. Distance travelled by bus

= 15 km 268 m = 15 km + 268 m

= \(15 \mathrm{~km}+268 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(15 \mathrm{~km}+\frac{268}{1000} \mathrm{~km}\)

= (15 + 0.268) km

= 15.268 km

Distance travelled by car = 7 km 7 m = 7 km + 7m

= \(7 \mathrm{~km}+7 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(7 \mathrm{~km}+\frac{7}{1000} \mathrm{~km}=7 \mathrm{~km}+0.007 \mathrm{~km}\)

= (7 + 0.007) km = 7.007 km

Distance travelled by foot

= \(500 \mathrm{~m}=500 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(\frac{500}{1000} \mathrm{~km}=0.500 \mathrm{~km}\)

∴ Total distance travelled by Sunita

15.268 + 7.007 +0.500 = 22.775

Hence, the total distance travelled by Sunita is 22.775 km.

Question 7. Ravi purchased 5 kg 400 g rice, 2 kg 20 g sugar and 10 kg 850 g flour. Find the total weight of his purchases.

Solution. Weight of rice purchased by Ravi

= 5 kg 400 g = 5 kg + 400 g

= \(5 \mathrm{~kg}+400 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(5 \mathrm{~kg}+\frac{400}{1000} \mathrm{~kg}=(5+0.400) \mathrm{kg}=5.400 \mathrm{~kg}\)

Weight of sugar purchased by Ravi

= 2 kg 20 g = 2kg + 20 g

= \(2 \mathrm{~kg}+20 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(2 \mathrm{~kg}+\frac{20}{1000} \mathrm{~kg}=(2+0.020) \mathrm{kg}=2.020 \mathrm{~kg}\)

Weight of flour purchased by Ravi

= 10 kg 850 g = 10 kg + 850 g

= \(10 \mathrm{~kg}+850 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(10 \mathrm{~kg}+\frac{850}{1000} \mathrm{~kg}=(10+0.850) \mathrm{kg}=10.850 \mathrm{~kg}\)

∴ Total weight of his purchases

5.400 + 2.020 + 10.850 = 18.270

Hence, the total weight of all his purchases is 18.270 kg.

Question 8. Subtract 1.85 from 5.46.

Solution. We have, 5.46 – 1.85

Now,

∴ 5.46 – 1.85 = 3.61

Decimal Representation on Number Line

Question 9. Subtract 5.25 from 8.28.

Solution. We have, 8.28 – 5.25

Now,

∴ 8.28 – 5.25 = 3.03

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Exercise 8.4

Question 1. Subtract.

(1) 18.25 from 20.75

(2) 202.54 m from 250 m

Solution. (1) We have, ₹ 20.75 – ₹ 18.25

Now,

∴ ₹ 20.75 – ₹ 18.25 = ₹ (20.75 – 18.25) = ₹ 2.50

(2) We have, 250 m – 202.54 m

Now,

∴ 250 m 202.54 m = (250 – 202.54) m = 47.46 m

Question 2. Find the value of: 9.756 – 6.28

Solution. We have, 9.756 – 6.28

9.756 – 6.280 = 3.476

∴ 9.756 – 6.28 = 3.476

Question 3. Raju bought a book for ₹ 35.65. He gave ₹ 50 to the shopkeeper. How much money did he get back from the shopkeeper?

Solution. Cost of book bought by Raju = ₹ 35.65

and money given to shopkeeper = ₹ 50

∴ Money get back from shopkeeper = ₹ (50 – 35.65) = ₹ 14.35

Hence, the money get back from shopkeeper is ₹ 14.35.

Decimal Representation on Number Line

Question 4. Rani had ₹ 18.50. She bought one ice-cream for ₹ 11.75. How much money does she have now?

Solution. Total money Rani had = ₹ 18.50

and cost of ice-cream = ₹ 11.75

∴ Remaining money = ₹ (18.50 – 11.75) = ₹ 6.75

Hence, she have ₹ 6.75.

Question 5. Tina had 20 m 5 cm long cloth. She cuts 4 m 50 cm length of cloth from this for making a curtain. How much cloth is left with her?

Solution. Tina had length of cloth 20 m 5 cm = 20 m + 5 cm

= \(20 m+5 \times \frac{1}{100} m\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(20 \mathrm{~m}+\frac{5}{100} \mathrm{~m}\)

= (20 + 0.05) m = 20.05 m

and length of cloth cut by her = 4 m 50 cm

= 4m + 50 cm

= \(m+50 \times \frac{1}{100} m\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(4 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=(4+0.50) \mathrm{m}=4.50 \mathrm{~m}\)

∴ Length of cloth left with Tina 20.05 m-4.50 m

= (20.05 – 4.50) m = 15.55 m

Hence, 15.55 m cloth is left with her.

Decimal Representation on Number Line

Question 6. Namita travels 20 km 50 m everyday. Out of this she travels 10 km 200 m by bus and the rest by auto. How much distance does she travel by auto?

TIPS Firstly, write the distance travelled by Namita in kilometres using decimals. To find the distance travelled by auto, subtract distance travelled by bus from total distance travelled by Namita.

Solution.

Total distance travelled by Namita

= 20 km 50 m = 20 km + 50 m

= \(20 \mathrm{~km}+50 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(20 \mathrm{~km}+\frac{50}{1000} \mathrm{~km}\)

= (20 + 0.050) km = 20.050 km

and distance travelled by Namita by bus

= 10 km 200 m = 10 km + 200 m

= \(10 \mathrm{~km}+200 \times \frac{1}{1000} \mathrm{~km}\) [∴ 1 m = \(\frac{1}{1000}\) km]

= \(10 \mathrm{~km}+\frac{200}{1000} \mathrm{~km}\)

= 10 km + 0.200 km

= (10 + 0.200) km = 10.200 km

∴ Distance travelled by auto

= 20.050 km – 10.200 km

= (20.050 – 10.200) km

= 9.850 km

Hence, she travels 9.850 km by auto.

Question 7. Aakash bought vegetables weighing 10 kg. Out of this, 3 kg 500 g is onions, 2 kg 75 g is tomatoes and the rest is potatoes. What is the weight of the potatoes?

Tips Firstly, write the weight of all vegetables in kilograms using decimals, then add the weight of onions and tomatoes. To find the weight of potatoes, subtract this sum from total weight of vegetables.

Solution. Given, total weight of vegetables = 10 kg

Weight of onions = 3 kg 500 g = 3 kg + 500 g

= \(3 \mathrm{~kg}+500 \times \frac{1}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= \(3 \mathrm{~kg}+\frac{500}{1000} \mathrm{~kg}\)

= 3 kg +0.500 kg

= (3 + 0.500) kg = 3.500 kg

Weight of tomatoes = 2 kg 75 g = 2 kg + 75 g

= \(2 \mathrm{~kg}+\frac{75}{1000} \mathrm{~kg}\) [∴ 1 g = \(\frac{1}{1000}\) kg]

= 2 kg + 0.075 kg

= (2 + 0.075) kg = 2.075 kg

∴ Total weight of onions and tomatoes

= 3.500 kg + 2.075 kg

= (3.500 + 2.075) kg = 5.575 kg

Now, weight of potatoes = Total weight of vegetables – Weight of onions and tomatoes

= 10 kg – 5.575 kg = (10 – 5.575) kg

= 4.425 kg

Hence, the weight of potatoes is 4.425 kg.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Multiple Choice Questions

Question 1. Which is larger 3.1 or 3.044?

1. 3.044
2. 3.1
3. Both are equal
4. None of these

Answer. 2. 3.1

Question 2. Which of the following decimals is the smallest?

1. 0.37
2. 1.52
3. 0.087
4. 0.105

Solution. 3. 0.087

Question 3. Which of the following decimals is the greatest?

1. 0.182
2. 0.0928
3. 0.29
4. 0.038

Answer. 3. 0.29

Decimal Representation on Number Line

Question 4. 0.024 lies between

1. 0.2 and 0.3
2. 0.02 and 0.03
3. 0.03 and 0.029
4. 0.026 and 0.024

Answer. 2. 0.02 and 0.03

Question 5. To change milimetre in centimetre, we divide by

1. 10
2. 100
3. 1000
4. 10000

Answer. 1. 10

Question 6. 66 kg 15 g is equal to

1. 66.15 kg
2. 66.150 kg
3. 66.015 kg
4. 66.0019 kg

Answer. 3. 66.015 kg

Question 7. 555 m is equal to

1. 5 km
2. 0.555 km
3. 5.55 km
4. 55.5 km

Answer. 2. 0.555 km

Question 8. 2 cm 2 mm is equal to

1. 2.2 cm
2. 0.22 cm
3. 2.1 cm
4. 1.2 cm

Answer. 1. 2.2 cm

Question 9. 0.07 + 0.0008 is equal to

1. 0.15
2. 0.015
3. 0.078
4. 0.78

Answer. 3. 0.078

Question 10. \(1+\frac{1}{10}=\)

1. 0.11
2. 1.1
3. 1.01
4. 1.001

Answer. 2. 1.1

Question 11. 15.8 – 6.73 is equal to

1. 8.07
2. 9.07
3. 9.13
4. 9.25

Answer. 2. 9.07

Decimal Representation on Number Line

Question 12. By what amount should 36.45 be increased to get 87?

1. 36.45
2. 123.45
3. 50.55
4. None of these

Answer. 3. 50.55

Question 13. The value of 4.5 + 7.06 – 6.006 is

1. 5.54
2. 5.554
3. 5.0054
4. 5.054

Answer. 2. 5.554

Question 14. Simplify and mark the correct answer.

71.02 + 4.91 – 49.999

1. 25.931
2. 25.941
3. 20.941
4. 39.964

Answer. 1. 25.931

Question 15. 484.71 + 285.33 – 782.38 + 73.9 = ?

1. 61.56
2. 15.75
3. 19.78
4. 35.54

Answer. 1. 61.56

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Assertion – Reason

Question 1. Assertion (A) 31.47 < 31.478

Reason (R) If the whole part of two decimal numbers are equal, we compare their tenths part. If that too are equal, we move to hundredths and then thousandths.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (a) Both (A) and (R) are true and (R) is the correct explanation of (A).

Question 2. Assertion (A) 6005 m = 6.005 km

Reason (R) \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

Question 3. Assertion (A) 2.34 + 6.54 = 9.88

Reason (R) To add two decimal numbers, first check if they have the same number of digits to the right of the decimal point.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (d) (A) is false but (R) is true.

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Fill in the Blanks

Question 1. 8.0999 is ….. than 8.1

Answer. Smaller

Question 2. The value of 545 g is equal to …. kg.

Answer. 0.545 kg

Question 3. 2 km 590 m is equal to ….. km.

Answer. 2.590 km

Question 4. The value of 50 coins of 50 paise = ₹ …..

Answer. 25

MP Board Class 6 Maths Solutions

Question 5. The value of 3.64 – 1.28 is ……

Answer. 2.36

MP Board Class 6 Maths Solutions For Chapter 8 Decimals True/False

Question 1. 4.51 is greater than 4.051.

Answer. True

Question 2. 36.096 is smaller than 45.064.

Answer. True

Question 3. 180 m 28 cm = 180.028 m

Answer. False

Question 4. 4.03 + 0.016 = 4.046

Answer. True

Question 5. 42.28 – 3.19 = 39.09

Answer. True

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Match the Columns

Question 1. Match the Column A with Column B.

Solution. (a) → (3), (b) → (1), (c) → (2), (d) → (4)

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Case Based Type Questions

Question 1. Suraj provides laundry services to nearby areas. The charges for wash and fold are calculated per kilogram of the weight of the clothes.

The table below shows the weight of the clothes for washing and folding from four houses.

(1) Which house will pay the most?

(a) House number 216

(b) House number 324

(c) House number 159

(d) House number 228

(2) What is the total weight of the clothes collected for washing and folding?

(3) Suraj collected 30.50 kg of clothes on Tuesday and 25.48 kg of clothes on Wednesday.

How many more kilograms of clothes were collected by Suraj on Tuesday than on Wednesday?

Solution. (1) (c) On comparing the whole part of 5.60, 3.95, 7.37 and 6.72, we get 7 > 6 > 5 > 3

∴ 7.37 is greater than the other number.

Hence, house number 159 pays the most.

(2) Weight of clothes collected for washing and folding are 5.60 kg, 3.95 kg, 7.37 kg and 6.72 kg.

∴ Total weight of cloths

= 5.60 kg + 3.95 kg + 7.37 kg + 6.72 kg = 23.64 kg

(3) Weight of clothes collected on Tuesday = 30.50 kg

Weight of clothes collected on Wednesday = 25.48 kg

∴ Difference in weight of clothes

= Weight of clothes collected on Tuesday – Weight of clothes collected on Wednesday

= 30.50 kg – 25.48 kg

= (30.50 – 25.48) kg

= 5.02 kg

Hence, Suraj collected 5.02 kg more clothes on Tuesday than on Wednesday.

MP Board Class 6 Maths Solutions

Question 2. The picture shows the nutritional information on a packet of cookies.

The cookies contain four types of fat.

(1) How much fat (in g) is in 100 g of cookies?

(2) Which fat content is the highest in the cookies?

(a) Saturated Fatty Acids.

(b) Monounsaturated Fatty Acids

(c) Polyunsaturated Fatty Acids

(3) The sugar content in the cookies is more than three times the protein content. Do you agree with this statement? Give reasons.

Solution. (1) To find out how much fat is in 100 g of cookies we need to add up the amount of each type of fat listed in the nutritional information.

∴ Fat Saturated Fatty Acids + Monounsaturated Fatty Acids + Polyunsaturated Fatty Acids + Trans Fatty Acids.

= 9 g + 8.2 g + 2.7 g + 0g = 199 g

(2) (a) We need to compare the amount of each type of fat 0 g < 2.7 g < 8.2 g < 9g

∴ Saturated Fatty acids is the highest type of fat content in the cookies.

(3) (b) From the nutritional, information, we see that the cookies contain 24.5 g of sugar and 7 g of protein per 100 g of cookies.

For compare these values, we have

7 + 7 + 7 = 3 x 7 = 21 < 24.5

(content of sugar in cookies)

This shows that the sugar content is more than 3 times the protein content.

∴ Yes, I agree that sugar content in the cookies is more than three times the protein content.

Question 3. Pulkit sets the car air-conditioner at 18.5° C when he starts the car. After a while, he increases the temperature to 21° C.

(1) How much is the increment in the temperature?

(2) Later, he increase the temperature to 24.5° C. What is the total change in temperature?

(3) 160.3 cm = …..

(a) 160 cm + 3 cm

(b) 160 cm + 3 mm

(c) 160 m + 3 cm

(d) 160 mm + 3 cm

(4) Ritesh’s height is 162.9 cm and Aarav’s height is 163.2 cm. What is the difference between their heights?

Solution. (1) Increment in Temperature = 21° C – 18.5°C = 25°C

(2) Total change in temperature = 24.5° C – 18.5°C = 6°C

(3) (b) We know that, 1 cm = 10 mm

Therefore, 160.3 cm = 160 cm + 0.3 cm

= 160 cm + 0.3 × 10 mm

= 160 cm + 3mm

(4) Given, Ritesh’s height=162.9 cm and Aarav’s height = 163.2 cm

∴ Difference between their heights

= 163.2 cm – 162.9 cm

= (163.2 – 162.9) cm

= 0.3 cm

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Very Short Answer Type Questions

Question 1. Which one is greater 1 or 0.98?

Solution. Here, we have 1 and 0.98

Since, whole of 1 is greater than whole of 0.98.

∴ 1 > 0.98

Question 2. Write ₹ 12 and 80 paise in rupees using decimal.

Solution. Given, 12 rupees and 80 paise = \(₹\left(12+\frac{80}{100}\right)=₹ 12.80\)

Question 3. Convert 5214 g to kg.

Solution. We know that 1 g = \(\frac{1}{1000} \mathrm{~kg}\)

∴ \(5214 \mathrm{~g}=\frac{5214}{1000} \mathrm{~kg}\)

= 5.214 kg

MP Board Class 6 Maths Solutions

Question 4. Convert 12 mm into centimetres using decimals.

Solution. We have, 12 mm

Question 5. Find 0.09 + 0.731.

Solution. Here, 0.09 + 0.731 = 0.821

Question 6. Find 11.7 – 6.213.

Solution. Here, 11.7 – 6.213 = 5.487

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Short Answer Type Questions

Question 1. Arrange the following decimal numbers in ascending order 3.74, 2.791, 6.002, 6.2, 4.91

Solution. Given, decimal numbers are 3.74,2.791,6.002,6.2,491

By converting into like decimals, we get

3.740, 2.791, 6.002, 6.200, 4.910

On comparing these like decimals, we get

2.791 < 3.740 4.910 < 6.002 < 6.200

Thus, 2.791 < 3.74 < 4.91 < 6.002 < 6.2

Question 2. Arrange the following decimal numbers in descending order. 1.93, 4.001, 4.10, 19.21, 6.432

Solution. Given, decimal numbers are 1.93, 4.001, 4.10, 19.21, 6.432

By converting into like decimals, we get

1.930, 4.001, 4.100, 19.210, 6.432

On comparing these like decimals, we get

19.210 > 6.432 > 4.100 > 4.001 > 1.930

Thus, 19.21 > 6.432 > 4.10 > 4.001 > 1.93

MP Board Class 6 Maths Solutions

Question 3. Express in kilometers, using decimals.

(1) 15 km 245 m

(2) 19 km 48 m

Solution. We know that 1000 m = 1 km

⇒ \(1 \mathrm{~m}=\frac{1}{1000} \mathrm{~km}\)

(1) \(15 \mathrm{~km} 245 \mathrm{~m}=15 \mathrm{~km}+\frac{245}{1000} \mathrm{~km}\)

= 15 km + 0.245 km = 15.245 km

(2) \(19 \mathrm{~km} 48 \mathrm{~m}=19 \mathrm{~km}+48 \mathrm{~m}=19 \mathrm{~km}+\frac{48}{1000} \mathrm{~km}\)

= 19 km + 0.048 km = 19.048 km

Question 4. Which one is greater?

1 metre 40 centimeters + 60 centimeters or 2.6 metres.

Solution. We know that

∴ 1 m 40 cm = 1 m + 40 cm = \(1 \mathrm{~m}+40 \times \frac{1}{100} \mathrm{~m}\)

= \(1 \mathrm{~m}+\frac{40}{100} \mathrm{~m}=1 \mathrm{~m}+0.40 \mathrm{~m}=1.40 \mathrm{~m}\)

and \(60 \mathrm{~cm}=60 \times \frac{1}{60} \mathrm{~m}=\frac{60}{100} \mathrm{~m}=0.60 \mathrm{~m}\)

Now, 1 m 40 cm + 60 cm = 1.40 m + 0.60 m = 2.0 m

So, we have to compare 2.0 m and 2.6 m

Here, whole part of both numbers are same.

So, compare the tenths part, we get

0 < 6

Here, 2.6 > 2.0.

Therefore, 2.6 metres is greater than

(1 m + 40 cm + 60 cm).

Question 5. Add 67.25, 249, 8.785, 9.8 and 0.23.

Solution. Converting the given decimals into like decimals, we get 67.250, 249.000, 8.785, 9.800 and 0.230

Here, 67.250 + 249.000 + 8.785 + 9.800 + 0.230 = 335.065

Question 6. During three days of a week, a rickshaw puller earns ₹ 40.20, ₹ 60.10 and ₹ 55, respectively. What is his total earning during these days?

Solution. Earning on 1st day = ₹ 40.20

Earning on 2nd day = ₹ 60.10

Earning on 3rd day = ₹ 55.00

∴ Total earning = ₹ 40.20 + ₹ 60.10 + ₹ 55.00 = ₹ 155.30

Question 7. Subtract

(1) ₹ 5.35 from ₹ 9.48

(2) 0.316 kg from 2.876 kg.

Solution. (1) ₹ 9.48 – ₹ 5.36

i.e. 9.48 – 5.36 = ₹ 4.12

(2) 2.876 kg – 0.316 kg

i.e. 2.876 – 0.316 = 2.560 kg

MP Board Class 6 Maths Solutions

Question 8. What should be added to 25.5 to get 50?

Solution. We subtract 25.5 from 50 to get the required result.

∴ 50.0 – 25.5 = 24.5

So, 24.5 should be added to 25.5 to get 50.

Question 9. What should be subtracted from 117.47 to get 47.95?

Solution. To get the required number, we have

117.47 – 47.95 = 69.52

MP Board Class 6 Maths Solutions For Chapter 8 Decimals Long Answer Type Questions

Question 1. Rajesh covers journey by car in 3 h. He covers a distance 60 km 320 m during first hour, 54 km 70 m during the second hour and 65 km 9 m during the third hour. What is the total distance covered in his journey?

Solution. We know that 1000 m = 1 km

∴ 1m = \(\frac{1}{1000} \mathrm{~km}\)

Now, distance covered during the first hour = 60.320 km

Distance covered during the second hour = 54.070 km

Distance covered during the third hour = 65.009 km

Total distance 60.320 km + 54.070 km + 65.009 km = 179.399 km

Hence, the total length of journey is 179.399 km.

Question 2. Sohan purchased a book, a pen and a notebook for ₹ 165.35, ₹ 70 and ₹ 20.50, respectively. How much money will he have to pay to the shopkeeper for these items?

Solution. Cost of a book = ₹ 165.35

Cost of a pen = ₹ 70.00

Cost of a notebook = ₹ 20.50

∴ Total cost = ₹ 165.35 + ₹ 70.00 + ₹ 20.50 = ₹ 255.85

Hence, the total money to be paid by Ramesh is ₹ 255.85.

Question 3. Reshma went to the market with ₹ 5000 cash. Out of this money she purchased one frock, one toy and one bag costing ₹ 1150.48, ₹ 540.52 and ₹ 2160.70, respectively. How much money is left with her?

Solution. Reshma has cash in hand = ₹ 5000

Cost of one frock = ₹ 1150.48

Cost of one toy = ₹ 540.52

Cost of one bag = ₹ 2160.70

∴ Total cost = ₹ 1150.48 + ₹ 540.52 + ₹ 2160.70

= ₹ 3851.70

∴ Balance = ₹ 5000.00 – ₹ 3851.70 = ₹ 1148.30

Hence, the money left with Reshma is ₹ 1148.30.

Question 4. Seema has ₹ 2000, she bought readymade garments for ₹ 987.50, medicines for ₹ 210.25, groceries for ₹ 530.25. She denoted ₹ 200 for charity. How much money is left with her?

Solution. Total money that Seema has = ₹ 2000.

Cost of readymade garments = ₹ 1987.50

Cost of medicines = ₹ 210.25

Cost of groceries = ₹ 530.25

Total cost = ₹ 987.50 + ₹ 210.25 + ₹ 530.25 = ₹ 1728

Money donate for charity = ₹ 200

Total money spent = ₹ 1728.00 + ₹ 200 = ₹ 1928.00

∴ Balance = ₹ 2000.00 – ₹ 1928.00 = ₹ 72.00

So, 72 are left with her.

MP Board Class 6 Maths Solutions

Question 5. Alok purchased 1 kg 200 g potatoes, 250 g dhanina, 5 kg 300 g onion, 500 g palak and 2 kg 600 g tomatoes. Find the total weight of his purchases in kilograms.

Solution. Firstly, we convert all the weight in the same unit i.e. gram into kilogram and then find the total weight.

Given, weight of potatoes = 1 kg + 200 g = 1 kg + 200 g

= \(1 \mathrm{~kg}+\frac{200}{1000} \mathrm{~kg}\) [∴ \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)]

= 1kg + 0.200 kg = 1.200 kg

Weight of dhania = \(250 \mathrm{~g}=\frac{250}{1000} \mathrm{~kg}=0.250 \mathrm{~kg}\)

Weight of onion = 5 kg 300 g = 5 kg + 300 g

= \(5 \mathrm{~kg}+\frac{300}{1000} \mathrm{~kg}=5 \mathrm{~kg}+0.300 \mathrm{~kg}\)

= 5.300 kg

Weight of palak = 500 g = \(\frac{500}{1000} \mathrm{~kg}=0.500 \mathrm{~kg}\)

Weight of tomatoes = 2 kg 600 g = 2 kg + 600 g

= \(2 \mathrm{~kg}+\frac{600}{1000} \mathrm{~kg}\) [∴ \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)]

= 2kg + 0.600 kg = 2.600 kg

∴ Total weight of his purchases in kilograms = Weight of potatoes + Weight of dhania + Weight of onion + Weight of palak + Weight of tomatoes

= 1.200 kg + 0.250 kg + 5.300 kg + 0.500 kg + 2.600 kg

= [1200 +0.250 +5.300 + 0.500 + 2.600] kg

= 9.850

Hence, the total weight is 9.850 kg.