MP Board Class 6 Maths Solutions For Chapter 10 Mensuration

Chapter 10 Mensuration Perimeter

The distance covered along the boundary forming a closed figure when you go round the figure once is called the perimeter. Thus, we can calculate the perimeter of a plane figure by calculating the sum of measurements of all its sides. Unit of perimeter is same as that of length.

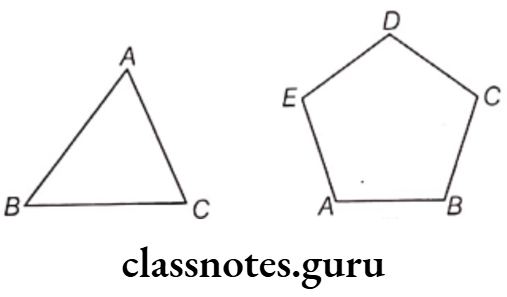
In Diagram (1), perimeter of △ABC = AB + BC + CA

In Diagram (2), perimeter of pentagon ABCDE =AB + BC + CD + DE + EA

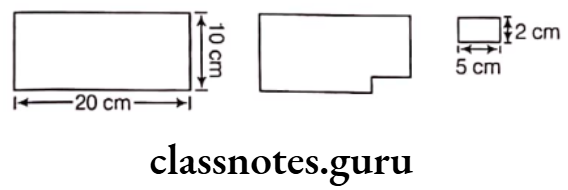
Example 1. Find the perimeter of the given figures.

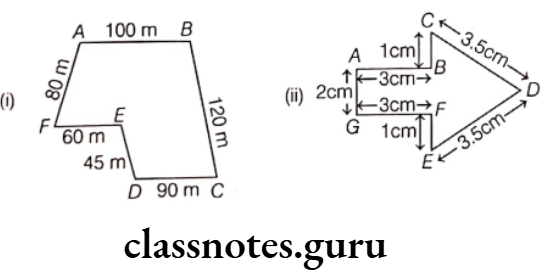
Solution. (1) Perimeter of the figure ABCDEF

Sum of the measurements of all sides

= AB + BC + CD + DE + EF + FA

= 100 + 120 + 90 + 45 + 60 + 80 = 495 m

Hence, the perimeter of the given figure is 495 m.

Read and Learn More MP Board Class 6 Maths Solutions

(2) Perimeter of the figure ABCDEFG

= Sum of the measurements of all sides

= AB + BC + CD + DE + EF + FG + GA

= 3 + 1 + 3.5 + 3.5 + 1 + 3 + 2 = 17 cm

Hence, the perimeter of the given figure is 17 cm.

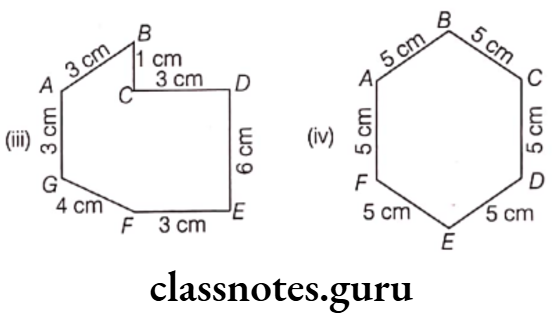
(3) Perimeter of the figure ABCDEFG

= Sum of the measurements of all sides.

= AB + BC + CD + DE + EF + FG + GA

= 4 + 3 + 6 + 3 + 1 + 3 + 3 = 23 cm

Hence, the perimeter of the given figure is 23 cm.

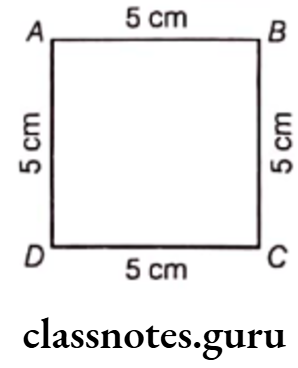
(4) Perimeter of the given figure

= Sum of the measurements of all sides

= AB + BC + CD + DE + EF + FA

= 5 + 5 + 5 + 5 + 5 + 5 = 30 cm

Hence, the perimeter of the given figure is 30 cm.

Perimeter of a Rectangle

The perimeter of a rectangle is the total distance covered by its boundaries or the sides.

In other words, the sum of the measurements of all four sides of a rectangle is called the perimeter of a rectangle.

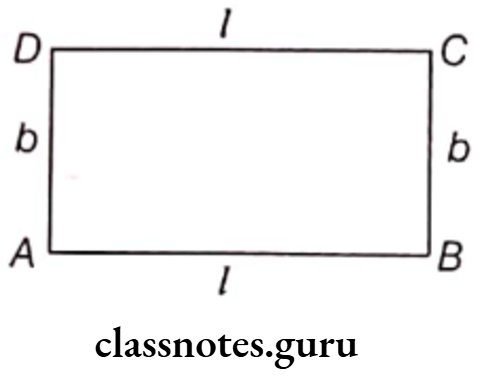
Perimeter of a rectangle ABCD

= Sum of length of its sides

= AB + BC + CD + DA = AB + BC + AB + BC

[∴ opposite sides are equal, CD = AB and DA = BC]

= 2(AB + BC) = 2(1 + b)

where, l = Length of the rectangle

and b = Breadth of the rectangle

Hence, the perimeter of a rectangle is 2 (1+b).

Note it While calculating the perimeter of a rectangle, we must express the length and breadth in the same unit.

Mp Board Class 6 Book Solutions

Example 2. Rohan wants to put a lace border all around a rectangular table cover 5 m long and 3 m wide. Find the length of the lace required by Rohan.

Solution. Given, length of the rectangular table cover = 5 m

and breadth of the rectangular table cover = 3 m

∴ Perimeter of the rectangular table cover = 2 × (length + breadth)

= 2 x (5 + 3) = 2 x 8 = 16m

Hence, the length of the lace required is 16 m.

Example 3. Find the perimeter of a rectangle whose length and breadth are 250 cm and 2 m, respectively.

Solution. Given, length of the rectangle = 250 cm

and breadth of the rectangle = 2 m = 2×100 cm = 200 cm

∴ Perimeter of the rectangle = 2 x (length + breadth)

= 2 × (250 + 200)

= 2 x 450 = 900 cm

Hence, the perimeter of the given rectangle is 900 cm.

Example 4. If the perimeter of a rectangle Is 200 cm and the length is 75 cm, then find Its breadth.

Solution. Given, perimeter of the rectangle = 200 cm

and length of the rectangle = 75 cm

∴ Perimeter of the rectangle = 2 x (length + breadth)

200 = 2(75 + breadth)

= \(\frac{1}{2} \times 200-75\)

= 100 – 75

= 25 cm

Hence, the breadth of the rectangle is 25 cm.

Mp Board Class 6 Book Solutions

Example 5. An athlete takes 10 rounds of a rectangular field which is 30 m long and 20 m wide. Find the total distance covered by him.

Solution. Given, length of rectangular field (l) = 30 m

and breadth of rectangular field (b) = 20 m

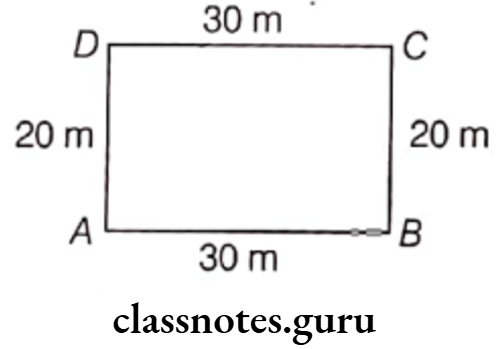
Total distance covered by the athlete in one round

= Perimeter of field (rectangle)

= 2(1 + b)

= 2 (30 + 20)

= 100 m

Since, the distance covered in one round = 100 m

So, the distance covered in 10 rounds = 10 x 100 = 1000 m

Example 6. A man has rectangular piece of land of length and breadth 340 m and 260 m, respectively. If each side is to be fenced with 4 rounds of wires, then what will be the length of wire needed?

Solution. Given, length of rectangular piece of land = 340 m

and breadth of rectangular piece of land = 260 m

Now, perimeter of the field = 2x (length + breadth)

= 2 x (340 + 260)

= 2 × 600

= 1200 m

∴ Each side is to be fenced with 4 rounds of wire.

∴ Total length of the wire required = 4 × 1200 = 4800 m

Example 7. Find the cost of fencing a rectangular park of length 275 m and breadth 125 m at the rate of ₹ 15 per metre.

Solution. Given, length of the rectangular park = 275 m

and breadth of the rectangular park = 125 m

Perimeter of the rectangular park = 2 × (length + breadth)

= 2 x (275 + 125)

= 2 x 400 = 800 m

∴ Cost of fencing of 1 m of park = ₹ 15

∴ Total cost of fencing the park = 15 x 800 = ₹ 12000

Perimeter of Regular Shapes

In regular shapes, all sides are of equal length and all angles are of equal measure.

If a regular polygon has n sides, then

Perimeter = n x Length of a side

where, n = Number of sides

Note it

(1) Perimeter of a regular pentagon = 5 x Length of one side = 5a

(2) Perimeter of a regular hexagon = 6 x Length of one side = 6a

Example 8. Find the perimeter of a regular hexagon with each side measuring 4 cm.

Solution. The given regular hexagon has 6 sides, each with the length of 4 cm.

∴ Perimeter of the regular hexagon = 6 x 4 = 24 cm

Mp Board Class 6 Book Solutions

Example 9. The perimeter of a regular hexagon is 30 cm. How long is its one side?

Solution. Given, perimeter of a regular hexagon = 30 cm

∴ Perimeter of regular hexagon = 6 x Length of a side

⇒ 30 = 6 x Length of a side

∴ Length of a side = \(\frac{30}{6}\) = 5 cm

Hence, the length of each side of a regular hexagon is 5 cm.

Perimeter of a Square

Perimeter of a square ABCD = AB + BC + CD + DA

= AB + AB + AB +AB

= 4AB [∴ AB = BC = CD = AD]

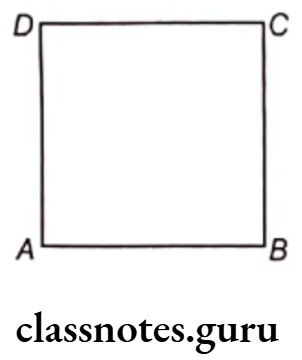
Hence, the perimeter of a square

= 4 x Length of a side of the square

Example 10. Find the distance travelled by Soniya, if she takes three rounds of a square park of side 60 m.

Solution. Given, length of side of square park = 60 cm

Perimeter of a square park = 4 x Length of a side

= 4 × 60 = 240 m

Distance covered in one round = 240 m

Distance covered in three rounds = 3 x 240 = 720 m

Mp Board Class 6 Book Solutions

Example 11. Mohan runs 5 times around a rectangular park with length 140 m and breadth 90 m while Sohan runs 6 times around a square park of side 80 m. Who covers more distance and by how much?

Solution. Distance covered by Mohan in one round

= Perimeter of the rectangular park

= 2x (length + breadth)

= 2 x (140 + 90) = 2 x 230 = 460 m

∴ Distance covered by Mohan is 5 rounds

= 5 × 460 = 2300 m

Distance covered by Sohan in one round

= Perimeter of the square park

= 4 x Length of a side = 4 x 80 = 320 m

∴ Distance covered by Sohan in 6 rounds = 6 x 320 = 1920 m

Difference in the distance covered = 2300-1920 = 380 m

Hence, Mohan covers more distance by 380 m.

Perimeter of an Equilateral Triangle

Perimeter of an equilateral △ABC

= AB + BC + CA = 3AB [∴ AB = BC = CA]

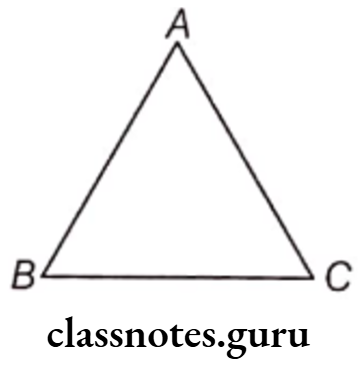
Hence, the perimeter of an equilateral triangle

= 3 x Length of a side of the triangle.

Example 12. If one side of an equilateral triangle is 8 cm, then find its perimeter.

Solution. Perimeter of an equilateral triangle = 3 x Length of a side

[∴in equilateral triangle, all sides are equal, so length of each side will be 8 cm]

= 3 x 8 = 24 cm

Hence, the perimeter of rectangle is 24 cm.

Mp Board Class 6 Maths Solutions

Example 13. How many equilateral triangles of side 4 cm long can be formed with a strip of wire of length 84 cm?

Solution. Given, side of the equilateral triangle = 4 cm

∴ Perimeter of the equilateral triangle

= 3 x Length of a side of the triangle

= 3 x 4 = 12cm

Now, number of equilateral triangles, formed

\(=\frac{\text { Total length of wire }}{\text { Perimeter of triangle }}=\frac{84}{12}=7\)

Hence, the required number of equilateral triangles is 7.

Chapter 10 Mensuration Area of Closed Figures

The amount of surface enclosed by a closed figure is called its area.

To calculate the area of a figure using a square paper, the following conventions are adopted.

(1) Ignore portions of the area that are less than half a square.

(2) If more than half of a square is in a region, just count it as one square.

(3) If exactly half the square is counted, take its area as \(\frac{1}{2}\) sq unit.

Note it The area of one full square is taken as 1 sq unit. If it is a centimetre square sheet, then area of one full square will be 1 cm².

Example 1. Find the area of the figure shown below. (consider area of each square = 1 cm²)

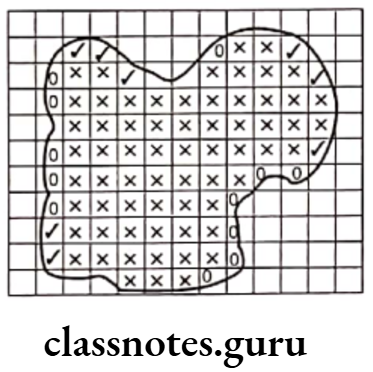
Solution. Area of a square = 1 cm²

Area of figure = Number of (x) squares + Number of (✔) squares + \(\frac{1}{2}\) Number of (0) squares

= \(65+8+\frac{1}{2} \times 12\)

= 65 + 8 + 6 = 79 cm²

[since, x and squares are covered fully by the figure and 0 square are covered half]

Hence, the area of square is 79 cm².

Mp Board Class 6 Maths Solutions

Example 2. Draw any circle on a graph sheet. Count the squares and use them to estimate the area of the circular region.

Solution. First, make a circle of any suitable radius, on the graph paper. Then, count full, half and more than half or less than half squares coming under the circle.

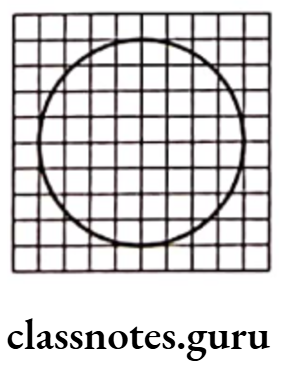
In the figure, fully filled squares = 32

Half filled squares = 0

More than half filled squares = 20

∴ Total area = \(32 \times 1+0 \times \frac{1}{2}+20 \times 1\)

= 32 + 0 + 20 = 52 sq units

Example 3. By counting squares, estimate the area of the given figure.

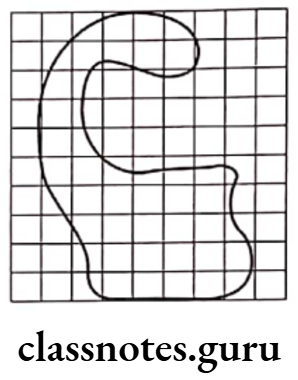
Solution. Let area of one square = 1 cm²

In the figure,

Fully filled squares = 21

Half filled squares = 0

More than half filled squares = 20

∴ Total area = 21 \times 1+0 \times \frac{1}{2}+20 \times 1

= 21 + 0 + 20 = 41 cm²

Chapter 10 Mensuration Area of a Rectangle and Square

Area of a Rectangle

Let length of the rectangle bel and breadth be b.

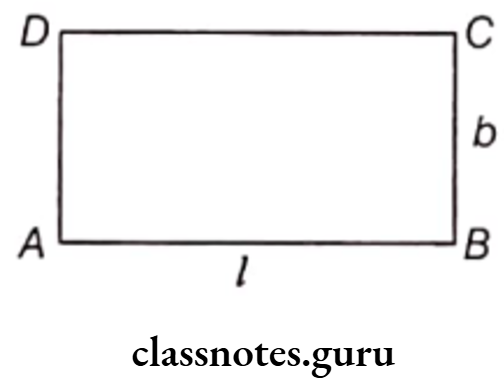
∴ Area of a rectangle (A) = Length x Breath = l x b

Using this formula, l = \(\frac{A}{b}\)

or b = \(\frac{A}{l}\)

Note it The length and breadth of a rectangle must be in the same units.

Mp Board Class 6 Maths Solutions

Example 1. Find the area of a rectangle whose length and breadth are 12 cm and 4 cm, respectively.

Solution. Given, length of the rectangle (1) = 12 cm

and breadth of the rectangle (b) = 4 cm

∴ Area of rectangle = 1 x b = 12 x 4 = 48 cm²

Hence, the area of rectangle is 48 cm².

Example 2. The area of a rectangular piece of cardboard is 48 cm² and its breadth is 6 cm. What is the length of the cardboard?

Solution. Given, area = 48 cm² and breadth (b) = 6 cm

We know that Area = Length x Breadth

∴ \(\text { Length }=\frac{\text { Area }}{\text { Breadth }}=\frac{48}{6}=8 \mathrm{~cm}\)

Hence, the length of cardboard is 8 cm.

Example 3. Find the area in square metre of a piece of land 6 m 75 cm wide and 8 m long.

Solution. Length of the piece of land = 8 m

Breadth of the piece of land = 6 m 75 cm

= 6 + 0.75 = 6.75 m [∴ 1 m = 100 cm]

∴ Area of the piece of land = Length x Breadth

= 8 x 6.75 = 54 m²

Example 4. What is the cost of painting a wall of 500 cm long and 300 cm wide at the rate of 13 per hundred sq m?

Solution. Given, length of a wall = 500 cm

and breadth of a wall = 300 cm

∴ Area of the wall = Length x Breadth

= 500 x 300 = 150000 cm²

∴ Cost of painting per 100 m² = ₹ 13

∴ Cost of 1 m2 = \(₹ \frac{13}{100}\)

Now, cost of 150000 m² = \(150000 \times \frac{13}{100}=₹ 19500\)

Hence, the required cost is ₹ 19500.

Mp Board Class 6 Maths Solutions

Example 5. Meena wants to cover the floor of a rectangular hall 9 m wide and 7 m long by square tiles. If each square tile is of side 1.5 m, then find the number of tiles required to cover the floor of the room.

Solution. Given, length of the rectangular hall = 7m

and breadth of the rectangular hall = 9 m

Area of the floor of the rectangular hall = Length x Breadth = 7 x 9 = 63 m²

Area of one square tile = Side x Side = 1.5 x 1.5 = 2.25 m²

Now, the number of required tiles \(=\frac{\text { Area of the floor }}{\text { Area of one tile }}\)

= \(\frac{63}{2.25}\) = 28 tiles

Hence, 28 tiles are required to cover the floor of the room.

Area of a Square

A four-sided polygon whose all sides are equal in length is called square.

Area of a square = Side x Side = Side²

Example 6. Find the area of a square whose side is 6 cm.

Solution. Given, side = 6 cm

∴ Area of a square Side x Side = 6 x 6 = 36cm²

Hence, the area of square is 36 cm².

Example 7. The perimeter of a square field is 60 m. Find its area.

Solution. Given, perimeter of a square field = 60 m

We know that perimeter of a square = 4 x Side

∴ Side of a square \(=\frac{\text { Perimeter }}{4}=\frac{60}{4}=15 \mathrm{~m}\)

Now, area of the square field = Side x Side

= 15 x 15 = 225 m²

Hence, the required area is 225 m².

Class 6 Maths Chapter 10 Solutions Mp Board

Example 8. What will happen to the area of a square, if its sides are doubled?

Solution. Let the side of a square = a cm

∴ Area of the square = a x a = a² cm² …(1)

Now, when the sides of the square doubled.

Then, the side of the square = 2a cm

∴ Area of the square = 2a x 2a = 4a² cm² …(2)

On comparing Eqs. (1) and (2), we can see, if the sides of a square are doubled, then its area becomes 4 times.

Question 1. Measure and write the length of the four sides of the top of your study table.

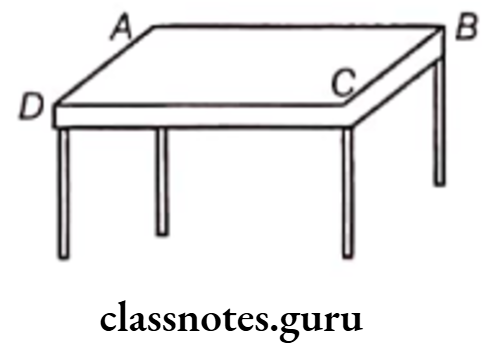
AB = ___cm

BC = ___cm

CD =___cm

DA = ___cm

Now, the sum of the lengths of the four sides

= AB + BC + CD + DA

= ___cm + ___cm + ___cm + ___cm = ___cm

What is the perimeter?

Solution. Let ABCD be the top of study table.

Here, AB and CD are equal and DA and BC are equal.

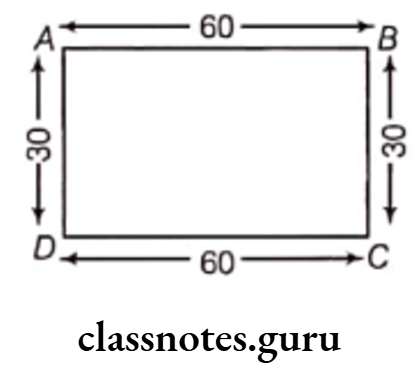
On measuring, we get

AB = CD = 60 cm

and DA = BC = 30 cm

Now, the sum of the lengths of the four sides

= AB + BC + CD + DA

= 60 + 30 + 60 + 30

= 60 + 30 + 60 + 30 = 180 cm

∴ Perimeter of the table

= Sum of the lengths of the four sides

= 180 cm

Hence, the perimeter of the study table is 180 cm.

Class 6 Maths Chapter 10 Solutions Mp Board

Question 2. Measure and write the lengths of the four sides of a page of your notebook. The sum of the lengths of the four sides.

= AB + BC + CD + DA

= ___cm + ___cm + ___cm + ___cm = ___cm

What is the perimeter of the page?

Solution. Let ABCD be the page of a notebook.

On measuring, AB = CD = 15 cm and BC = DA = 20 cm

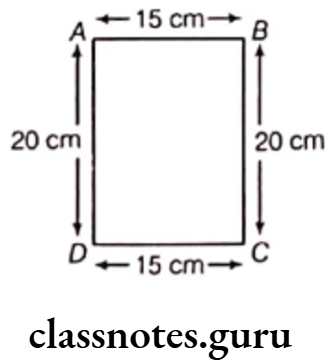
Then, the sum of the lengths of four sides

= AB + BC + CD + DA

= 15 + 20 + 15 + 20

= 15 + 20 + 15 + 20 = 70 cm

Hence, the sum of four sides is 70 cm.

Now, perimeter of the page = Sum of the lengths of four sides = 70 cm

Question 3. Meera went to a park 150 m long and 80 m wide. She took one complete round on its boundary. What is the distance covered by her?

Solution. Let ABCD be a park whose lengths are BC,AD and widths are AB, CD respectively.

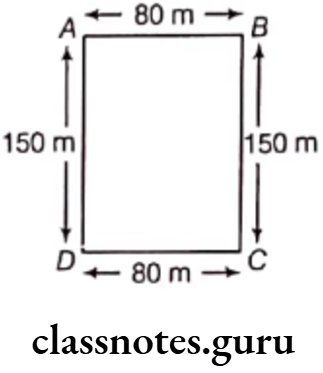
Here, AB = CD = 80 m

and BC = DA = 150 m

Now, sum of the lengths of four sides

= AB + BC + CD + DA

= 80 + 150 + 80 + 150 = 460 m

∴ Perimeter of the park

= Sum of the lengths of four sides of the park

= 460 m

Hence, the distance covered by Meera is 460 m.

Mensuration Class 6 Solutions

Question 4. Find the perimeter of the following figures.

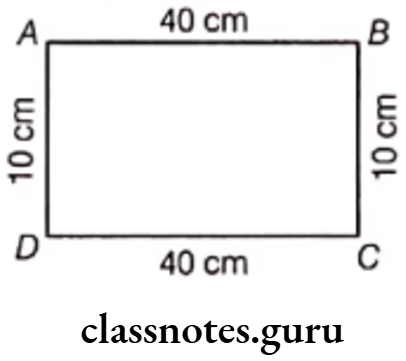
Perimeter AB + BC + CD + DA

Solution. (1) From the given figure, we have

AB= 40 cm, BC = 10 cm,

CD = 40 cm and DA = 10 cm

Now, the sum of the lengths of the four sides

= AB + BC + CD + DA

= 40 + 10 + 40 + 10 = 100 cm

∴ Perimeter of the given figure

= Sum of the lengths of four sides

= 100 cm

Hence, the perimeter of the given figure is 100 cm.

(2) From the given figure, we have

AB = BC = CD = DA = 5 cm

i.e. each side of the given figure is 5 cm.

Now, the sum of the lengths of the four sides

= AB + BC + CD + DA

= 5 + 5 + 5 + 5 = 20 cm

∴ Perimeter of the given figure

= Sum of the lengths of four sides

= 20 cm

Hence, the perimeter of the given figure is 20 cm.

Class 6 Maths Chapter 10 Solutions Mp Board

Question 5. Find various objects from your surrounding which have regular shapes and find their perimeters.

Solution. Let’s take a blackboard which has a regular square shape with side 40 cm each.

Then, the perimeter of square

= 4 x Length side of a square

= 4 × 40

= 160 cm

Let’s take another example of dog’s house which has a pentagon shape with each side 15 m.

Then, the perimeter of dog’s house

= Perimeter of regular pentagon

= 5 x Length of side of pentagon

= 5 x 15 = 75 m

Chapter 10 Mensuration Exercise 10.1

Question 1. Find the perimeter of each of the following figures.

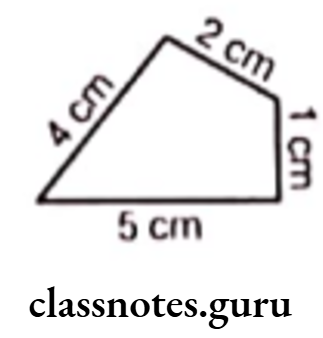
Solution. (1) Let the given figure be ABCD.

Here, AB = 5 cm, BC = 1 cm, CD = 2 cm and DA = 4 cm

Diagram

∴ Perimeter of the given figure

= Sum of the lengths of all sides

= AB + BC + CD + DA

= 5 + 1 + 2 + 4 = 12 cm

Hence, the perimeter of the given figure is 12 cm.

Question 2. A table-top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?

TIPS Firstly, change all the units in same unit and then find perimeter using 2 (length + breadth).

Solution. Given, length of table-top = 2 m 25 cm

= \(2 \mathrm{~m}+25 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(2 m+\frac{25}{100} m\)

= (2 + 0.25) m = 2.25 m

Breadth of table-top = 1 m 50 cm = 1 m + 50 cm

= \(1 m+50 \times \frac{1}{100} m\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(1 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=(1+0.50) \mathrm{m}=1.50 \mathrm{~m}\)

∴ Perimeter of table top = 2x (length + breadth)

= 2 x (2.25 + 1.50)

= 2 x 3.75 = 7.50 m

Hence, the perimeter of the table-top is 7.50 m.

Mp Board Maths Chapter 10 Solutions

Question 3. What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm, respectively?

Solution. Given, length of the wooden strip=32 cm

and breadth of the wooden strip = 21 cm

Now, wooden strip required

= Perimeter of the photograph

=2 x (Length + Breadth)

= 2 x (32 + 21) = 2 x 53 = 106 cm

Hence, the required length of wooden strip is 106 cm.

Question 4. Find the perimeter of each of the following shapes.

(1) A triangle of sides 3 cm, 4 cm and 5 cm.

Solution. (1) Here, AB = 3 cm, BC = 4 cm and CA = 5 cm

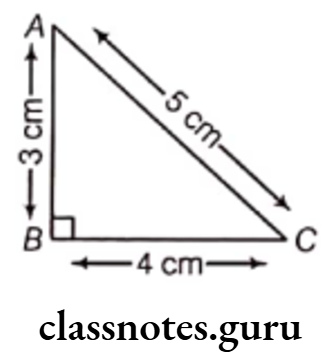
∴ Perimeter of a triangle

= Sum of the lengths of all sides

= AB + BC + CA

= 3 + 4 + 5 = 12 cm

Hence, the perimeter of a triangle is 12 cm.

Question 5. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.

Solution. Given, first side of triangle = 10 cm

Second side of triangle = 14 cm

and third side of triangle = 15 cm

∴ Perimeter of a triangle

= Sum of all sides of triangle

= 10 + 14 + 15 = 39 cm

Hence, the perimeter of a triangle is 39 cm.

Question 6. Find the side of the square whose perimeter is 20 m.

Solution. Given, the perimeter of a square = 20 m

∴ Perimeter of a square = 4 x Length of a side

We know that a square has 4 sides of equal length.

So, we can divide given perimeter by 4, to get the side of a square.

∴ One side of the square \(=\frac{\text { Perimeter of a square }}{4}\)

Hence, the side of a square is 5 m.

Mp Board Maths Chapter 10 Solutions

Question 7. A piece of string is 30 cm long. What will be the length of each side, if the string is used to form

(1) a square?

(2) an equilateral triangle?

(3) a regular hexagon?

Solution. (1) Here, length of string will be the perimeter of square.

∴ Perimeter of square = 30 cm

We know that a square has 4 equal sides.

∴ Perimeter of a square = 4 x Length of a side

Now, length of one side \(=\frac{\text { Perimeter of a square }}{4}\)

= \(\frac{30}{4}\) = 7.5 cm

Hence, the length of each side of a square is 7.5 cm.

(2) Here, length of string will be the perimeter of an equilateral triangle.

∴ Perimeter of equilateral triangle = 30 cm

We know that an equilateral triangle has 3 equal sides.

∴ Perimeter of an equilateral triangle = 3 x Length of a side

∴ Length of a side \(=\frac{\text { Perimeter of an equilateral triangle }}{3}\)

= \(\frac{30}{3}\) = 10 cm

Hence, the length of each side of an equilateral triangle is 10 cm.

(3) Here, length of string will be the perimeter of regular hexagon.

∴ Perimeter of regular hexagon = 30 cm

We know that a regular hexagon has 6 equal sides

Perimeter of a regular hexagon = 6 x Length of a side

∴ Length of a side \(=\frac{\text { Perimeter of a regular hexagon }}{6}\)

= \(\frac{30}{6}\) = 5 cm

Hence, the length of each side of a regular hexagon is 5 cm

Question 8. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle Is 36 cm. What is its third side?

Solution. Let △ABC be the given triangle and its sides AB = 12 cm and BC = 14 cm.

Also, perimeter of triangle = 36 cm We know that,

Perimeter of a triangle = Sum of all its sides

⇒ AB + BC + CA = 36 cm

⇒ 12 + 14 + CA = 36 cm

⇒ 26 + CA = 36 cm

∴ CA = 36 – 26 = 10 cm

Hence, the third side of the triangle is 10 cm.

MP Board Class 6 Chapter 10 Maths

Question 9. Find the cost of fencing a square park of side 250 m at the rate of ₹ 20 per metre.

Solution. Given, side of square park = 250 m

Then, the perimeter of square park

= 4 x Length of side of park

= 4 x 250 = 1000 m

Cost of fencing = ₹ 20 per metre

∴ Cost of fencing = 1000 x 20

= ₹ 20000

Hence, the cost of fencing a square park is ₹ 20000.

Question 10. What is the perimeter of each of the following figures? What do you infer from the answers?

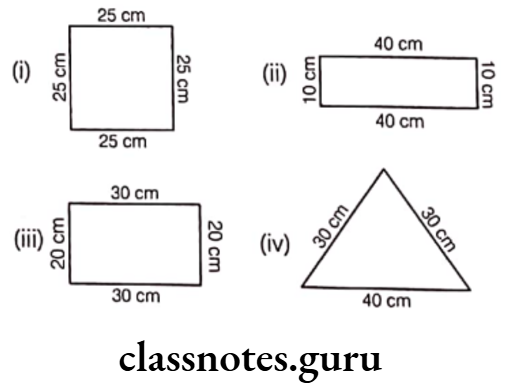
Solution. (1) Given, the figure is a square whose each side is 25 cm.

∴ Perimeter of square = 4 x Length of a side

= 4 × 25 = 100 cm

(2) Given, the figure is a rectangle whose length = 40 cm and breadth = 10 cm

∴ Perimeter of rectangle = 2 x (length + breadth)

= 2 x (40 + 10)

= 2 x 50 = 100 cm

(3) Given, the figure is a rectangle whose length = 30 cm and breadth 20 cm

∴ Perimeter of rectangle = 2 x (length + breadth)

= 2 x (30 + 20) = 2 x 50 = 100 cm

(4) Given, the figure is an isosceles triangle whose sides are 30 cm, 30 cm and 40 cm, respectively.

∴ Perimeter of triangle = Sum of all sides of a triangle

= 30 + 30 + 40 = 100 cm

Here, we observe that the perimeter of each figure is 100 cm i.e. they have equal perimeters.

MP Board Class 6 Chapter 10 Maths

Question 11. Avneet buys 9 square paving slabs, each with a side ofm. He lays them in the form of a square.

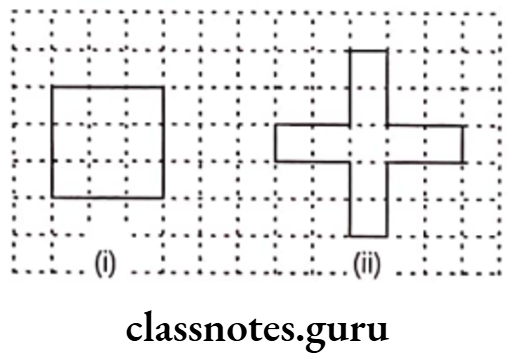
(1) What is the perimeter of his arrangement in the figure(i)?

(2) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement in the figure (ii)?

(3) Which has greater perimeter?

(4) Avneet wonders, if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.)

Solution. (1) Avneet lays 9 squares in the form of a square as shown in the figure, then side of the square

\(=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{1+1+1}{2}=\frac{3}{2} m\)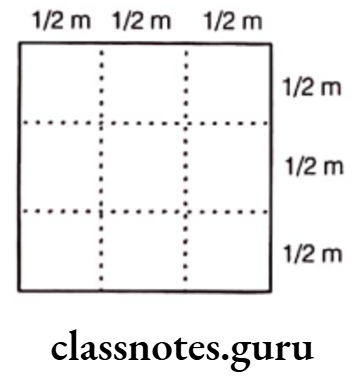

∴ Perimeter of Avneet’s arrangement

= 4 x Length of a side = 4 x \(\frac{3}{2}\) m = 6 m

Hence, the perimeter of Avneet’s arrangement is 6 m.

(2) Shari lays 9 squares in the form of a cross as shown in figure, then

Perimeter of Shari’s arrangement = Sum of all sides

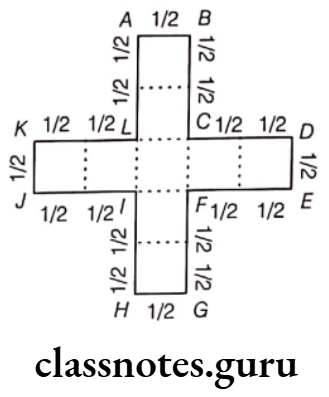
= AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA

= \(\left[\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)+\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)\right.\)

\(\left.+\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)+\frac{1}{2}+\left(\frac{1}{2}+\frac{1}{2}\right)+\left(\frac{1}{2}+\frac{1}{2}\right)\right]\)

= \(\frac{1}{2}+1+1+\frac{1}{2}+1+1+\frac{1}{2}+1+1+\frac{1}{2}+1+1\)

= \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+8=1+1+8=10 \mathrm{~m}\)

Hence, the perimeter of Shari’s arrangement is 10 m.

(3) From above, it is clear that Shari’s arrangement i.e. a cross has greater perimeter.

(4) Yes, there is a way shown along side in which we get a greater perimeter.

Here, we have arrange the 9 squares in the form of a rectangle

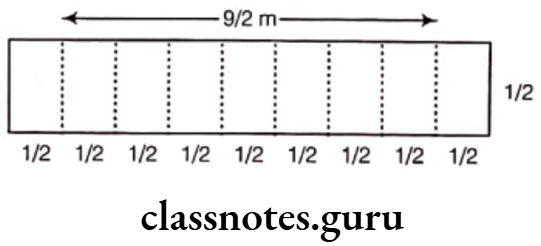
Now, length of rectangle

= \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{9}{2} m\)

and breadth of rectangle = 1/2 m

∴ Perimeter of this rectangle

= 2 x (length + breadth)

= \(2 \times\left(\frac{9}{2}+\frac{1}{2}\right)=2 \times\left(\frac{9+1}{2}\right)\)

= \(2 \times \frac{10}{2}=10 \mathrm{~m}\)

It is clear that it has the perimeter equal to cross. So, we can say that cross has greater perimeter in comparison to square.

Question 12. Draw any circle on a graph sheet. Count the squares and use them to estimate the area of the circular region.

Solution. First, make a circle of any suitable radius, on the graph paper. Then, count full, half and more than half or less than half squares coming under the circle.

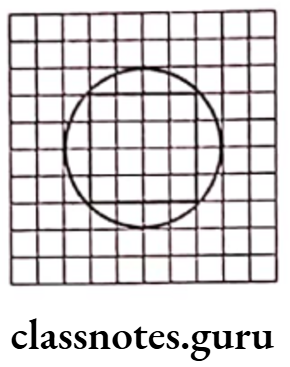
In the figure,

Fully filled squares = 16

Half filled squares = 8

More than half filled squares = 8

∴ Total area = \(16 \times 1+8 \times \frac{1}{2}+8 \times 1\)

= 16 + 4 + 8 = 28 sq units

Chapter 10 Mensuration Exercise 10.2

Question 1. Find the areas of the following figures by counting square

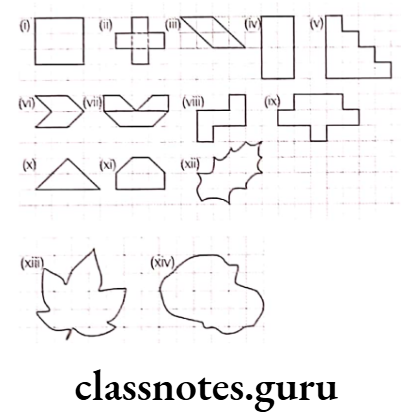
Solution. (1) Given, figure is covered by 9 full squares.

∴ Area = 9 x 1 = 9 sq units

(2) Given, figure is covered by 5 full squares.

∴ Area = 5 x 1 = 5 sq units

(3) Given, figure is covered by 2 full squares and 4 half squares.

∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)

(4) Given, figure is covered by 8 full squares.

∴ Area = 8 x 1 = 8 sq units

(5) Given, figure is covered by 10 full squares.

∴ Area = 10 x 1 = 10 sq units

(6) Given, figure is covered by 2 full squares and 4 half squares.

∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)

(7) Given, figure is covered by 4 full squares and 4 half squares.

∴ Area = \(4 \times 1+4 \times \frac{1}{2}=4+2=6 \text { sq units }\)

(8) Given, figure is covered by 5 full squares.

∴ Area = 5 x 1 = 5 sq units

(9) Given, figure is covered by 9 full squares.

∴ Area = 9 x 1 = 9 sq units

(10) Given, figure is covered by 2 full squares and 4 half squares.

∴ Area = \(2 \times 1+4 \times \frac{1}{2}=2+2=4 \text { sq units }\)

(11) Given, figure is covered by 4 full squares and 2 half squares.

∴ Area = \(4 \times 1+2 \times \frac{1}{2}=4+1=5 \text { sq units }\)

(12) Given, figure is covered by 3 full squares, O half squares, 7 more than half squares and 1 less than half square.

∴ Area = 3 x 1 + 7 x 1 + 1 x 0

= 3 + 7 + 0 = 10 sq units

(13) Given, figure is covered by 7 full squares, 4 half squares, 5 more than half squares and 8 less than half squares.

∴ Area = \(7 \times 1+4 \times \frac{1}{2}+5 \times 1+8 \times 0\)

= 7 + 2 + 5 + 0 = 14 sq units

(14) Given, figure is covered by 9 full squares, 2 half squares, 8 more than half squares and 4 less than half squares.

∴ Area = \(9 \times 1+2 \times \frac{1}{2}+8 \times 1+4 \times 0\)

= 9 + 1 + 8 + 0 = 18 sq units

Chapter 10 Mensuration Exercise 10.3

Question 1. Find the areas of the rectangles whose sides are

(1) 3 cm and 4 cm

(2) 12 m and 21 m

Solution. (1) Here, length of the rectangle = 4 cm

and breadth of the rectangle = 3cm

∴ Area of rectangle = Length x Breadth = 4 x 3 = 12 cm²

Hence, the area of the rectangle is 12 cm².

(2) Here, length of the rectangle = 21 m

and breadth of the rectangle = 12 m

∴ Area of the rectangle = Length x Breadth

= 21 x 12 = 252 m²

Hence, the area of the rectangle is 252 m².

Mp Board Maths Chapter 10 Solutions

Question 2. The length and breadth of three rectangles are as given below.

(1) 9 m and 6 m

(2) 17 m and 3 m

(3) 4 m and 14 m

Which one has the largest area and which one has the smallest?

Solution. (1) Here, length of the rectangle = 9 m

and breadth of the rectangle = 6 m

∴ Area of the rectangle = Length x Breadth = 54 m²

Hence, the area of the rectangle is 54 m².

(2) Here, length of the rectangle = 17 m

and breadth of the rectangle = 3 m

∴ Area of the rectangle = Length x Breadth

= 17 x 3 = 51 m²

Hence, the area of the rectangle is 51 m².

(3) Here, length of the rectangle = 14 m

and breadth of the rectangle = 4 m

∴ Area of the rectangle = Length x Breadth

= 14 x 4 = 56 m²

Hence, the area of the rectangle is 56 m².

Now, we have 56 > 54 > 51

Hence, the rectangle having sides 4 m and 14 m has the largest area and the rectangle having sides 17 m and 3 m has the smallest area.

Question 3. The area of a rectangular garden 50 m long is 300 m². Find the width of the garden.

Solution. Given, area of the rectangular garden = 300 m²

and length of the rectangular garden = 50 m

We know that

Area of the rectangular garden = Length x Breadth

⇒ 300 m² = 50 x Breadth

∴ Breadth = \(\frac{300}{50}\) = 6 m

Hence, the breadth or width of the garden is 6 m.

Question 4. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of 8 per hundred sq m?

Solution. Given, length of a rectangular plot = 500 m

and breadth of a rectangular plot = 200 m

∴ Area of the rectangular plot = Length x Breadth

= 500 x 200 = 100000 m²

∴ Cost of tiling per husband square metres = ₹ 8

∴ Cost of 1 m² = \(₹ \frac{8}{100}\)

Now, cost of 100000 m² = \(100000 \times \frac{8}{100}=₹ 8000\)

Hence, the cost of tiling rectangular plot is ₹ 8000.

Calculating Perimeter for Class 6

Question 5. A table-top measures 2 m by 1m 50 cm. What is its area in square metres?

Solution. Given, length of the table-top = 2 m

and breadth of the table-top

= 1 m 50 cm = 1 m + 50 cm

= \(1 \mathrm{~m}+50 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(1 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=1 \mathrm{~m}+0.50 \mathrm{~m}=150 \mathrm{~m}\)

∴ Area of the table-top = Length x Breadth = 2 x 1.50 = 3

Hence, the area of the table-top is 3 m².

Question 6. A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?

Solution. Given, length of the room = 4 m

and breadth of the room = 3m 50 cm = 3 m + 50 cm

= \(3 \mathrm{~m}+50 \times \frac{1}{100} \mathrm{~m}\) [∴ 1 cm = \(\frac{1}{100}\) m]

= \(3 \mathrm{~m}+\frac{50}{100} \mathrm{~m}=3 \mathrm{~m}+0.50 \mathrm{~m}=3.50 \mathrm{~m}\)

∴ Carpet needed to cover the floor of room

= Area of the floor

= Length x Breadth = 4 m x 3.50 m = 14 m²

Hence, the carpet needed to cover the floor of the room is 14 m².

Question 7. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.

Solution. Given, length of the floor = 5 m

and breadth of the floor = 4 m

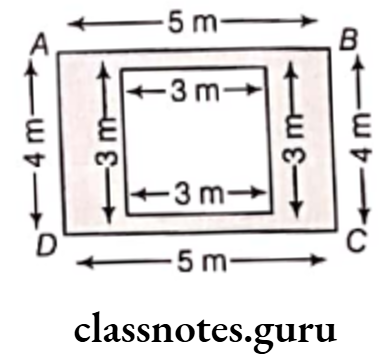
Then, area of the floor

= Length x Breadth

= 5 x 4 = 20 m²

Side of the square carpet = 3 m

∴ Area of the carpet = Side x Side = 3 x 3 = 9m²

Now, area of the floor that is not carpeted

= Area of the floor-Area of the carpet

= 20 – 9 = 11 m²

Hence, 11 m² area of the floor is not carpeted.

Calculating Perimeter for Class 6

Question 8. Five square flower beds each of sides 1 m are dug on a plece of land 5 m long and 4 m wide. What Is the area of the remaining part of the land?

Solution. Given, length of the piece of the land = 5 m

and breadth of the piece of the land = 4 m

Area of the piece of the land = Length x Breadth

= 5 x 4 = 20 m²

Given, side of one square flower bed = 1 m

∴ Area of one square flower bed = Side x Side

= 1 x 1 = 1m²

Then, area of 5 such flower beds

= 5 x Area of one square flower bed

= 5 x 1 = 5m²

Now, area of the remaining part of the land

= Area of the piece of the land – Area of 5 square flower beds

= 20 – 5 = 15 m²

Hence, the area of the remaining part of the land is 15 m².

Question 9. By splitting the following figures into rectangles, find their areas (the measures are given in centimetres).

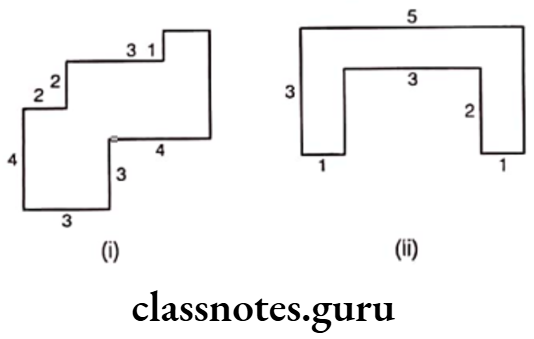
Solution. (1) Let the given figure be divided into rectangles A, B, C and Dand their length and breadth be written on the figure.

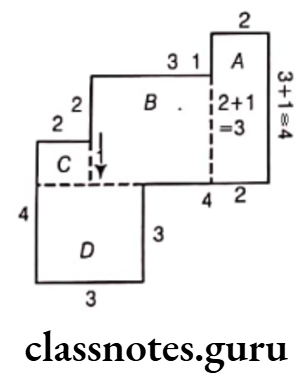
For Rectangle A,.

Length = 4 cm and breadth = 2 cm

Now, area of the Rectangle A = Length x Breadth

= 4 x 2 = 8 cm²

For Rectangle B,

Length = 3 cm and breadth = 3 cm

Area of the Rectangle B = Length x Breadth

= 3 x 3 = 9cm²

For Rectangle C,

Length = 2 cm and breadth = 1 cm

Area of the Rectangle C = Length x Breadth

= 2 x 1 = 2cm²

For Rectangle D, length = 3 cm and breadth = 3 cm

∴ Area of the Rectangle D = Length x Breadth

= 3 x 3 = 9cm²

Now, total area of the given figure

= Area of the Rectangle A + Area of the Rectangle B + Area of the Rectangle C + Area of the Rectangle D

= 8 + 9 + 2 + 9 = 28 cm²

Hence, the required area is 28 cm²

(2) Let the given figure is divided into rectangles A, B and C and their length and breadth are written on the figure.

For Rectangle A,

Length = 2 cm and breadth = 1 cm

∴ Area of the Rectangle A = Length x Breadth

= 2 x 1 = 2 cm²

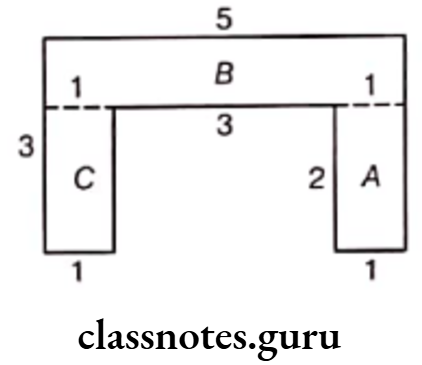
For Rectangle B,

Length = 5 cm and breadth = 1 cm

∴ Area of the Rectangle B = Length x Breadth = 5 x 1 = 5cm²

For Rectangle C,

Length = 2 cm and breadth = 1 cm

∴ Area of the Rectangle C = Length x Breadth

= 2 x 1 = 2cm²

Now, total area of the given figure

= Area of the Rectangle A + Area of the Rectangle B + Area of the Rectangle C

= 2 + 5 + 2 = 9 cm²

Hence, the area of the given figure is 9 cm².

Question 10. On a centimetre squared paper, make as many rectangles as you can, such that the area of the rectangle is 16 cm² (consider only natural number lengths).

(1) Which rectangle has the greatest perimeter?

(2) Which rectangle has the least perimeter?

If you take a rectangle of area 24 cm², what will be your answers? Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter? With the least perimeter? Give example and reason.

Solution. We know that

∴ Area of the rectangle = Length x Breadth

Here, the area of the rectangle is 16 cm².

So, for getting the area 16 cm², there are three cases.

Case 1 When length of the rectangle = 16 cm

and breadth of the rectangle = 1 cm

∴ Area of the rectangle = Length x Breadth

= 16 x 1 = 16cm²

and perimeter of the rectangle

= 2 x (Length + Breadth)

= 2 x (16 + 1) = 2 x 17 = 34 cm

Case 2 When length of the rectangle = 4 cm

and breadth of the rectangle = 4 cm

∴ Area of the rectangle = Length x Breadth

= 4 x 4 = 16cm²

and perimeter of the rectangle

= 2 x (Length + Breadth)

= 2 x (4 + 4) = 2 x 8 = 16 cm

Case 3 When length of the rectangle = 8 cm

and breadth of the rectangle = 2 cm

∴ Area of the rectangle = Length x Breadth

= 8 x 2 = 16 cm²

and perimeter of the rectangle

= 2x (length + breadth)

= 2 x (8 + 2)= 2 x 10 = 20 cm

(1) The rectangle which is made in Case I has the greatest perimeter.

(2) The rectangle which is made in Case II has the least perimeter.

Now, given that the area of the rectangle is 24 cm².

Again, for getting the area 24 cm2, there are four cases

Case 1 When length of the rectangle = 24 cm

and breadth of the rectangle = 1 cm

∴ Area of the rectangle = Length x Breadth

= 24 x 1 = 24 cm²

and perimeter of the rectangle

= 2 x (length + breadth)

= 2 x (24 + 1) = 2 x 25 = 50 cm

Case 2 When length of the rectangle = 12 cm

and breadth of the rectangle = 2 cm

∴ Area of the rectangle

= Length x Breadth = 12 x 2 = 24cm²

and perimeter of the rectangle

= 2 x (length + breadth)

= 2 x (12 + 2) = 2 × 14 = 28 cm

Case 3 When length of the rectangle = 6 cm

and breadth of the rectangle = 4 cm

∴ Area of the rectangle

= Length x Breadth = 6 x 4 = 24 cm²

and perimeter of the rectangle

= 2 x (length + breadth)

= 2 x (6 + 4) = 2 x 10 = 20 cm

Case 4 When length of the rectangle = 8 cm

and breadth of the rectangle = 3 cm

∴ Area of the rectangle

= Length x Breadth = 8 x 3 = 24 cm²

and perimeter of the rectangle

= 2 x (length + breadth)

= 2 x (8 + 3) = 2 x 11 = 22 cm

(1) The rectangle which is made in Case I has the greatest perimeter.

(2) The rectangle which is made in Case III has the least perimeter.

Yes, it is possible to predict the shape of the rectangle with greatest perimeter and with least perimeter.

e.g. A rectangle having area 16 cm² and greatest perimeter 34 cm is of the shape 16 cm x 1 cm

(i.e. length = 16 cm and breadth = 1 cm), also a rectangle having area 24 cm² and least perimeter 20 cm is of the shape 6 cm x 4 cm

(i.e. length = 6 cm and breadth = 4 cm).

The rectangle with the greatest length has the maximum perimeter and the rectangle with the smallest length has the least perimeter.

Chapter 10 Mensuration Multiple Choice Questions

Question 1. Following figures are formed by joining six unit squares. Which figure has the smallest perimeter?

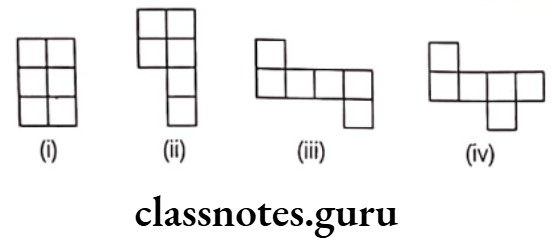
1. 2
2. 3
3. 4
4. 1

Answer. 4. 1

Question 2. A square shaped park ABCD of side 100 m has two equal rectangular flower beds each of size 10 m x 5 m. Length of the boundary of the remaining park is

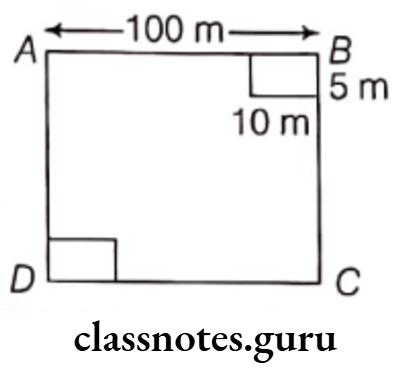
1. 360 m
2. 400 m
3. 340 m
4. 460 m

Answer. 3. 340 m

Question 3. The perimeter of a rectangle whose sides are 1 m 30 cm and 70 cm, is

1. 20 m
2. 4 m
3. 0.2 m
4. 2 m 30 cm

Answer. 2. 4 m

Calculating Perimeter for Class 6

Question 4. Cost of fencing a rectangular park of length 200 m and width 150 m at the rate of ₹ 25 per metre is

1. ₹ 17500
2. ₹ 1750
3. ₹ 1705
4. ₹ 10750

Answer. 1. ₹ 17500

Question 5. Length and breadth of a rectangular sheet of paper are 20 cm and 10 cm, respectively. A rectangular piece is cut from the sheet as shown in figure. Which of the following statements are correct for the remaining sheet?

1. Perimeter remains same but area changes
2. Area remains same but perimeter changes
3. Both area and perimeter are changing
4. Both area and perimeter remain the same

Answer. (c) Both area and perimeter are changing

Question 6. The top of a table is 1 m 20 cm wide and 1 m 50 cm long. The perimeter of this top is

1. 5.30 m
2. 5.40 m
3. 5.50 m
4. 5.60 m

Answer. 2. 5.40 m

Question 7. The ratio of the sides of rectangle is 5:4 and its perimeter is 72 cm. Then, the length of the rectangle is

1. 40 cm
2. 20 cm
3. 30 cm
4. 60 cm

Answer. 2. 20 cm

Question 8. The cost of fencing a rectangular field 24 m long and 18 m wide at ₹ 2.25 per meter is

1. ₹ 243
2. ₹ 234
3. ₹ 189
4. ₹ 198

Answer. 3. ₹ 189

Question 9. The side of a square is 10 cm. How many times will the new perimeter become, if the side of the square is doubled?

1. 2 times
2. 4 times
3. 6 times
4. 8 times

Answer. 2. 4 times

Question 10. The perimeter of a square whose each side is 1 m 30 cm 10 mm, is

1. 5.4 m
2. 5.14 m
3. 5.24 m
4. 5.04 m

Answer. 3. 5.24 m

Examples of Perimeter Problems

Question 11. The side of a square is 6 cm. If its side is doubled, then its new perimeter is

1. 48 cm
2. 36 cm
3. 60 cm
4. 24 cm

Answer. 1. 48 cm

Question 12. The perimeter of a triangle whose sides are 1.2 cm, 3.4 cm and 1.7 cm, is

1. 6.3 cm
2. 6.2 cm
3. 6.5 cm
4. 6.4 cm

Answer. 1. 6.3 cm

Mp Board Maths Chapter 10 Solutions

Question 13. The perimeter of an equilateral triangle of side 5 cm each is

1. \(\frac{\sqrt{3}}{4} \times 15 \mathrm{~cm}\)
2. \(\frac{\sqrt{3}}{4} \times 10 \mathrm{~cm}\)
3. 10 cm
4. 15 cm

Answer. 4. 15 cm

Question 14. The area of rectangle is 630 sq cm and breadth is 15 cm. What is its lenght.

1. 40 cm
2. 60 cm
3. 42 cm
4. 35 cm

Answer. 3. 42 cm

Question 15. Samuel wanted to dig some vertical poles along the boundary of his plot at a distance of 10 m each. If the length of the plot is 30 m and the breadth is 15 m. How many poles are required?

1. 450
2. 45
3. 9
4. 10

Answer. 3. 9

Chapter 10 Mensuration Assertion Reason

Question 1. Assertion (A) Manoj went to a park 20 m long and 10 m wide. He took one complete round of it. The distance covered by him is 60 m.

Reason (R) The amount of surface enclosed by a closed figure is called its area.

(a) Both A and R are true and R is the correct explanation of A

(b) Both A and R are true but R is not the correct explanation of A

(c) A is true but R is false

(d) A is false but R is true

Answer. (b) Both A and R are true but R is not the correct explanation of A

Question 2. Assertion (A) The perimeter of a square of side 1 m is 2 m.

Reason (R) Perimeter is the distance covered along the boundary forming a closed figure when you go around the figure once.

(a) Both A and R are true and R is the correct explanation of A

(b) Both A and R are true but R is not the correct explanation of A

(c) A is true but R is false

(d) A is false but R is true

Answer. (d) A is false but R is true

Examples of Perimeter Problems

Question 3. Assertion (A) The length of wire required to fence the pentagon-shaped park of side 24 cm is 120 cm.

Reason (R) Perimeter of a regular polygon with n sides = n x length of each side

(a) Both A and R are true and R is the correct explanation of A

(b) Both A and R are true but R is not the correct explanation of A

(c) A is true but R is false

(d) A is false but R is true

Answer. (a) Both A and R are true and R is the correct explanation of A

Question 4. Assertion (A) A page is 25 cm long and 20 cm wide. The area of this page is 90 cm.

Reason (R) The amount of surface enclosed by a closed figure is called its area.

(a) Both A and R are true and R is the correct explanation of A

(b) Both A and R are true but R is not the correct explanation of A

(c) A is true but R is false

(d) A is false but R is true

Answer. (d) A is false but R is true

Chapter 10 Mensuration Fill in the Blanks

Question 1. Perimeter of the shaded portion in figure is

AB + … + … + … + … + … + … + HA.

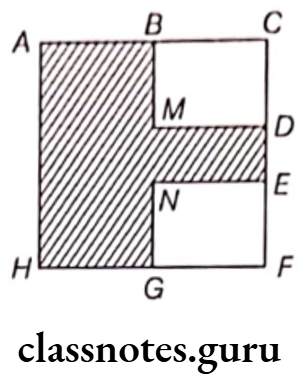
Answer. BM + MD + DE + EN + NG + GH

Mp Board Maths Chapter 10 Solutions

Question 2. Diagonal of a square is side x …..

Answer. √2

Question 3. Standard unit of area is …..

Answer. Square metre (i.e. m²)

Question 4. The amount of region enclosed by a plane closed figure is called its …..

Answer. Area

Question 5. The area of a play ground is 1190 m2. If its length is 35 m, the width is …..

Answer. 34 m

Chapter 10 Mensuration True/False

Question 1. 1 hectare = 100 x 100 m2.

Answer. True

Question 2. Perimeter of rectangle is (l + b).

Answer. False

Question 3. A farmer who wants to fence his field, must find the perimeter of the field.

Answer. True

Question 4. If length of a rectangle is halved and breadth is doubled, then the area of the rectangle obtained remains same.

Answer. True

Question 5. Area of a square is doubled, if the side of the square is doubled.

Answer. False

Chapter 10 Mensuration Match the Columns

Question 1. Mathc the Column I with Column II.

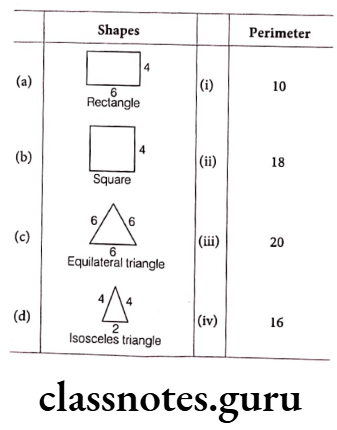
Solution. (a) → (3), (b) → (4), (c) → (2), (d) → (1)

Chapter 10 Mensuration Case Based Questions

Question 1. The figure below shows the football field for a school tournament.

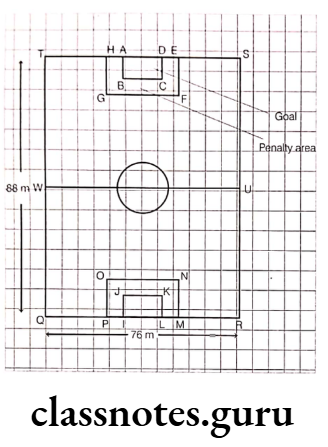
(1) What is the perimeter (in m) of WURQ?

(a) 60 m

(b) 240 m

(c) 960 m

(d) 3344 m

(2) The area enclosed by QRUW is equal to the area enclosed by WUST:

Is the statement true? Give reason.

(3) What is the area (in m²) of the penalty area?

(a) 488 m²

(b) 272 m²

(c) 480 m²

(d) 720 m²

(4) Is the perimeter of the penalty area of the football field double the perimeter of the goal area? Give.

(5) Does the school football field meet the FIFA standards? Give reason.

(6) Find the perimeter of the shape WURMNOPQW.

(a) 280 m

(b) 320 m

(c) 240 m

(d) 420 m

Solution. (1) (b) Given, length of the football field = 88 m

breadth of the football field = 76 m

∴ \(W Q=\frac{1}{2} \times T Q=\frac{1}{2} \times 88=44 \mathrm{~m}\)

Now, perimeter of WURQ = 2x (length + breadth)

= 2 x (44 + 76)

= 2 × 120 = 240 m

Hence, perimeter of WURQ is 240 m.

(2) We have, TW = WQ = 44 m

and QR = WU = 76 m

Now, area enclosed by QRUW = Length x Breadth

= WQ x QR = 44 m x 76 m = 3344 m² ….(1)

Now, area enclosed by WUST = Length x Breadth

= TW x WU = 44 ….(2)

∴ From (1) and (2);

Area enclosed by QRUW = Area enclosed by WUST = 3344 m²

Hence, area enclosed by QRUW is equal to the area enclosed by WUST.

(3) (c) Given, length of the football field = 88 m

and breadth of the football field = 76 m

∴ Side of the small square in the field = \(\frac{88}{22}=4 \mathrm{~m}\)

∴ Area of small square in the field = 4 x 4 = 16 m²

Now, there are 30 small squares lie in the region of penalty area.

∴ Area of the penalty area = 30 x Area of small square

= 30 x 16 m² = 480 m²

Hence, the area of penalty area is 480 m².

(4) We have, side of small square = 4 m

∴ HG = 20 m, GF = 36 m, FE = 20 m, ED = 8 m, DC = 12 m, CB = 20 m, BA = 12 m and AH = 8 m

∴ Perimeter of penalty area

= HG + GF + FE + ED + DC + CB + BA + AH

= 20 + 36 + 20 + 8 + 12 + 20 + 12 + 8

= 136 m …(1)

Now, AB = 12 m, BC = 20 m, CD = 12 m and DA = 20 m

∴ Perimeter of goal area = AB + BC + CD + DA = 12 + 20 + 12 + 20 = 64 m

Hence, perimeter of the penalty area of the football field is not double the perimeter of the goal area.

(5) Yes, the school football field meet the FIFA standards because the areas of WUST and WURQ are the same which is 3344 m.

(a) because the length and the width of TQRS are 88 m and 76 m respectively, which lie with in the standard range which 120 m to 90 m for length and 90 m to 45 m for width.

(b) because the perimeter of TQRS is 328 m which lies with in the standard range which is 420 m to 270 m.

(c) because the area of TQRS is 6688 sq m which lies with in the standard range which 10800 sq m to 4050 sq m.

(6) (a) We have, side of small square=4 m

So, WU = 76 m, UR = 44 m, RM = 20 m, MN = 20 m, No = 36 m, OP = 20 m, PQ = 20 m and QW = 44 m

Now, perimeter of the shape WURMNOPQW

= WU + UR + RM + MN + NO + OP + PQ + QW

= 76 + 44 + 20 + 20 + 36 + 20 + 20 + 44 = 280 m

Hence, perimeter of the shape WURMNOPQW is 280 m

Examples of Perimeter Problems

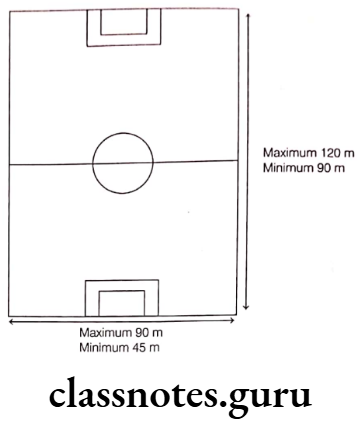
Question 2. International Federation of Association Football (FIFA) is responsible for the organization and promotion of association football’s major international tournaments.

FIFA issues guidelines for the dimensions of football fields. The figure below shows the maximum and minimum lenghts and widths of a football field.

(1) What is the maximum area (in m²) of the football field?

(a) 30 m²

(b) 420 m²

(c) 1080 m²

(d) 10800 m²

(2) What can be the minimum perimeter (in m) of the football field?

(a) 90 m

(b) 135 m

(c) 270 m

(d) 4050 m

Solution. (1) (d) Given, maximum length of the football field

and maximum width of the football field = 90 m

∴ Maximum area of the football field

= Length x Breadth

= 120 m x 90 m = 10800 m²

Hence, the maximum area of the football field is 10800 m².

(2) (c) Given, minimum length of the football field = 90 m

and minimum width of the football field = 45 m

∴ Minimum perimeter of the football field

= 2x (length x breadth)

= 2 x (90 + 45) = 2 x 135 = 270 m

Hence, minimum perimeter of the football field is 270 m

Class 6 Mp Board Maths Question Answers

Question 3. The figure below shows a square wooden frame enclosing a square picture.

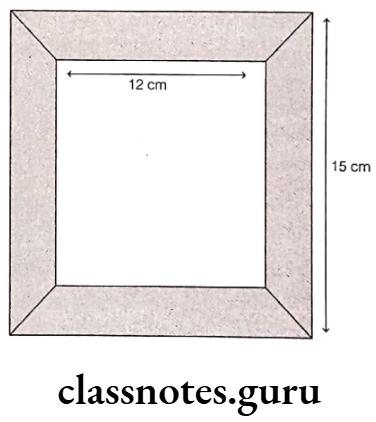
(1) What is the area (in cm²) of the frame?

(a) 81 cm²

(b) 144 cm²

(c) 181 cm²

(d) 225 cm²

(2) What is the perimeter (in cm) of the picture?

(a) 12 cm

(b) 48 cm

(c) 60 cm

(d) 144 cm

Solution. (1) (d) Given, side of square frame = 15 cm

Now, area of square frame = Side x Side

= 15 x 15 = 225 cm²

Hence, area of the frame is 225 cm².

(2) (b) Given, side of the square picture = 12 cm

Now, perimeter of square picture = 4 x Side

= 4 x 12 = 48 cm

Hence, perimeter of the picture is 48 cm.

Chapter 10 Mensuration Very Short Answer Type Questions

Question 1. Length of a rectangle is three times its breadth. Perimeter of the rectangle is 40 cm. Find its length and width.

Solution. Let width of rectangle (b) = x cm

Then, length of rectangle (1) = 3x cm

∴ Perimeter = 2 (1 + b)

⇒ 40 = 2(3x + x) = 8x = 40

⇒ 8x = 40

⇒ \(x=\frac{40}{8}=5 \mathrm{~cm}\)

Hence, the length is 15 cm and width is 5 cm.

Question 2. The perimeter of a regular pentagon is 1240 cm. How long is its each side?

Solution. Given, perimeter = 1240 cm

Perimeter of a regular pentagon = 5 x Length of each side

Length of each side = \(\frac{1240}{5}\) = 248 cm

Hence, its each side is 248 cm.

Class 6 Mp Board Maths Question Answers

Question 3. Find the side of an equilateral triangle, if its perimeter is 30 cm.

Solution. Given that perimeter of an equilateral triangle = 30 cm

∴ Perimeter of an equilateral triangle

= 3 x Side of a triangle

⇒ 30 = 3 x Side of a triangle

⇒ Side = \(\frac{30}{3}\) = 10 cm

Hence, the side of an equilateral triangle is 10 cm.

Question 4. Find the perimeter of a triangle, whose three sides are 5 cm, 6 cm and 7 cm, respectively.

Solution. Perimeter of a triangle = Sum of its all sides

= a + b + c

= (5 + 6 + 7) cm = 18 cm

Question 5. Find the perimeter of an equilateral triangle, whose each side is 5 cm.

Solution. Perimeter of an equilateral triangle = 3 × Side of length

= 3 x 5 cm = 15 cm [given]

Question 6. Perimeter of an isosceles triangle is 50 cm. If one of the two equal sides is 18 cm, find the third side.

Solution. Perimeter = 50 cm

Perimeter of an isosceles triangle = Sum of its all sides

⇒ Perimeter = a + b + c

⇒ 50 = 18 + 18 + Third side

⇒ 50 – 36 = Third side

⇒ Third side = 14 cm

Class 6 Mp Board Maths Question Answers

Question 7. Find the area of a rectangle whose length and width are 10 cm and 6 cm, respectively.

Solution. Given that length (1) = 10 cm

and width (b) = 6 cm

Area of a rectangle = 1 x b = 10 x 6 = 60 cm²

Question 8. If the area of a square is 36 cm², then find its perimeter.

Solution. Given, area of a square = 36 cm²

Area = Side x Side

⇒ 36 = Side x Side

⇒ Side x Side = 6 x 6

⇒ Side = 6 cm

∴ Perimeter of a square = 4 × Side = 4 × 6 = 24 cm

Chapter 10 Mensuration Short Answer Type Questions

Question 1. The length of a rectangular field is twice its breadth. Jamal jogged around it four times and covered a distance of 6 km. What is the length of the field?

Solution. Let breadth of rectangular field = x m

Then, length of rectangular field = 2x m

Distance covered in one round = Perimeter

Distance covered in four rounds = 4 x Perimeter

⇒ 4 × 2 (1 + b) = 6 x 1000 [ perimeter = 2 (1 + b)]

⇒ 8(l + b) = 6000

8(2x + x) = 6000

\(x=\frac{6000}{24}=250 \mathrm{~m}\)

∴ Length of the field = 500 m

Question 2. A room is 9.5 m long and 7.4 m wide. A person wants that the floor of the room to be fitted with tiles of size 20 cm by 10 cm. Find the number of tiles needed.

Solution. Area of room 7.4 x 9.5 m² = 7.4 x 9.5 x 10000 cm²

Area of one tile = 20 x 10 = 200 cm²

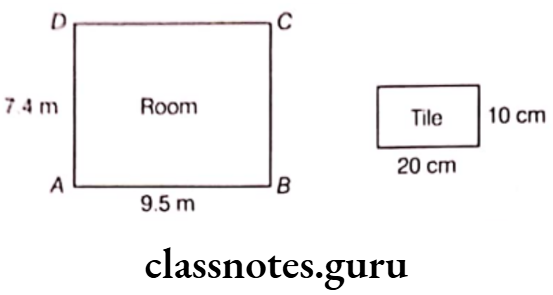
Number of tiles \(=\frac{\text { Area of room }}{\text { Area of a tile }}=\frac{74 \times 95 \times 100}{200}\)

= \(\frac{74 \times 95}{2}=95 \times 37=3515\)

Question 3. Two plots of land having the same perimeter. One is a square with side 70 cm while other is rectangle of length 100 cm. Which plot has the greater area and by how much?

Solution. Area of square Side x Side = 70 x 70 sq cm

= 4900 cm2

Given, length of rectangle = 100 cm

Perimeter of rectangle = Perimeter of square

⇒ 2 (100 + b) = 4 × 70

⇒ 100 + b = 140 ⇒ b = 40 cm

Now, area of rectangle = 1 x b = 40 x 100 = 4000 cm²

Hence, the area of square is more than the area of rectangle by 900 cm².

Class 6 Maths Chapter 10 Solutions Mp Board

Question 4. Three squares are joined together as shown in figure. Their sides are 4 cm, 10 cm and 3 cm. Find the perimeter of the figure.

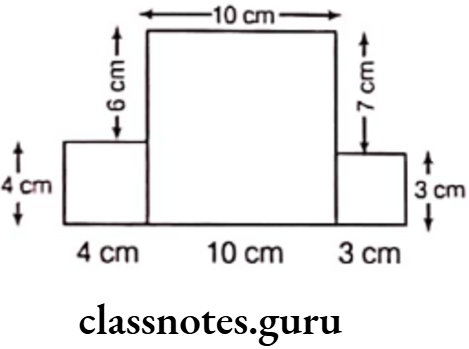
Solution. Given, sides of three squares are 4 cm, 10 cm and 3 cm, respectively.

Total perimeter of given squares

= Sum of all outer sides of the figure

= 4 + 4 + 4 + 6 + 10 + 7 + 3 + 3 + 3 + 10 = 54 cm

Question 5. Tahir measured the distance around a squared field as 200 rods (lathi). Later he found that the length of this rod was 140 cm. Find the side of this field in metres.

Solution. Distance around a square field = 200 rods

Length of this rod = 140 cm

Total distance around a squared field = 200 x 140 = 28000 cm

So, perimeter of this squared field = 28000 cm = 280 m

Sides of this field = \(\frac{280}{4}\) = 70 m

Question 6. The perimeter of rectangle and square are equal. If length of the rectangle is 8 m and breadth is 6 m. Find the area of square.

Solution. Given, length of rectangle (1) = 8 m

and breadth of rectangle (b) = 6 m

Perimeter of rectangle = Perimeter of square

2 (1 + b) = 4x Side of a square

⇒ 2(8 + 6) = 4 × Side of a square

Side of a square = \frac{2(8+6)}{4}=7 \mathrm{~m}

∴ Area of square = 7 x 7 = 49 m²

Question 7. The floor of a room is square in shape. If the side of the floor is 5 m. Find the area of the floor.

Solution. Given, side of the floor = 5 m

Area of the floor = Side x Side = 5 x 5 = 25m²

Hence, the area of the floor is 25 m².

Class 6 Maths Chapter 10 Solutions Mp Board

Question 8. From the following figure, find its

(1) Perimeter

(2) Area of square

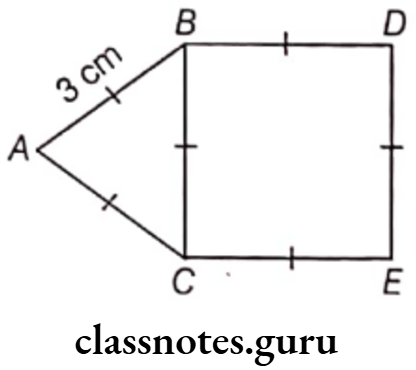
Given, ABC is an equilateral triangle of side 3 cm each and BCED is a square.

Solution. (1) Perimeter = AB + AC + BC + BD + DE + CE

= 3 + 3 + 3 + 3 + 3 + 3 = 18 cm

(2) Area of square BCED = Side2 = 32 = 9 cm²

Chapter 10 Mensuration Long Answer Type Questions

Question 1. Length of a rectangular field is 250 m and width is 150 m. Anuradha runs around this field 3 times. How far did she run? How many times she should run around the field to cover a distance of 4 km?

Solution. Given, length of rectangular field (1) is 250 m and width is 150 m.

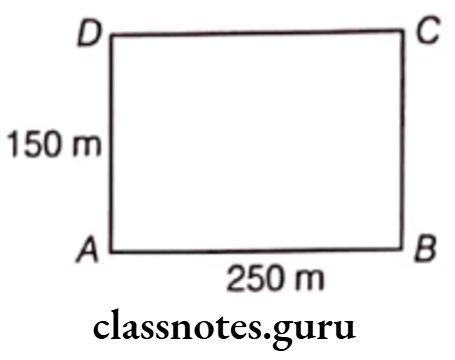
Perimeter of this field = 2(1 + b) = 2(250 + 150) m

= 2 x 400 m = 800 m

Distance covered in one round = Perimeter = 800 m

Distance covered in three rounds = 3 x 800 = 2400 m

Now, number of rounds to cover 4 km i.e. 4000 m.

= \(\frac{4000}{800}\) [∴ 1 km = 1000 m]

Hence, she should run 5 times around the field to cover the distance of 4 km.

Question 2. The lawn in front of Molly’s house is 12 m x 8 m, where as the lawn in front of Dolly’s house is 15 m x 5 m. A bamboo fencing is built around both the lawns. How much fencing is required for both?

Solution. Given, size of lawn in front of Molly’s house = 12 × 8

Perimeter = 2 (12 + 8) = 40 …(1)

Now, size of lawn in front of Dolly’s house = 15 x 5

Perimeter = 2(15 + 5) = 40 …(2)

From Eqs. (1) and (2), we get

40 + 40 = 80 m

Hence, the total length of bamboo fencing is 80 m.

Question 3. A room 9.68 m long and 6.2 m wide. Its floor is to be covered with glazed tiles of 22 cm by 10 cm each. If rate of tiles is ₹ 25 per tile. Find the total cost of tiles.

Solution. Given, length of floor of the room (l) = 9.68 m

and width of floor of the room (b) = 6.2 m

Area of the room = 9.68 x 6.2 m² …(1)

Also, given that length of each tile = 22 cm

and width of each tile = 10 cm

Now, area of each tile = 22 x 10 cm²   …(2)

Number of tiles required to cover the floor of the room

= \(\frac{9.68 \times 6.2 \times 100 \times 100}{22 \times 10}\) [∴ 1m = 100 cm]

= \(\frac{968 \times 62 \times 10}{22 \times 10}=\frac{968 \times 62}{22}=2728\)

∴ Total cost = ₹ 2728 x 25 = ₹ 68200

MP Board Class 6 Maths Solutions

Question 4. There is a rectangular lawn 10 m long and 4 m wide in front of Meena’s house. It is fenced along the two smaller sides and one longer side leaving a gap of 1 m for the entrance. Find the length of fencing.

Solution. Given, width of the lawn, AB = EF = 4 m and length of the lawn, BE = 10 m

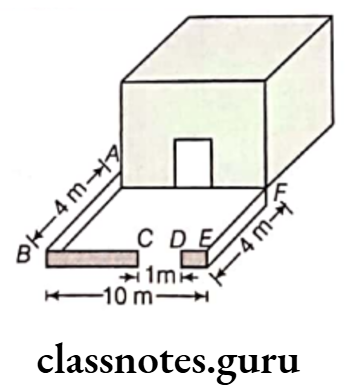
Also, given length of gap, CD = 1 m

Total length of fencing = AB + (BC + DE) + EF

= AB + (BE-CD) + EF

= 4 + (10-1) + 4)

= 4 + 9 + 4 = 17 m

Hence, the length of fencing of the lawn is 17 m.

Question 5. Four regular hexagons are drawn, so as to form the design as shown in figure. If the perimeter of the design is 28 cm. Then, find the length of each side of the hexagon.

Solution. Given, four regular hexagons, as shown in the figure:

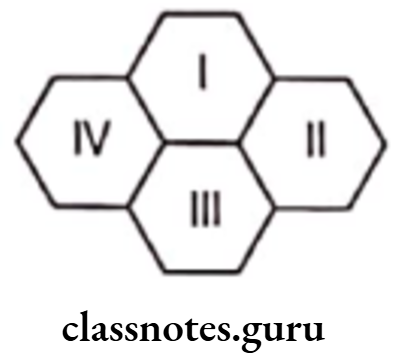
Perimeter of the design = 28 cm

∴ Perimeter of the given design = Sum of all outer sides of the four hexagon.

Here, this figure has 14 outer equal sides.

∴ Perimeter of the design = 14 x Length of one side of hexagon

⇒ 28 = 14 x Length of one side of hexagon

Length of one side of hexagon = \(\frac{28}{14}\) = 2 cm

Hence, the length of each side of the hexagon is 2 cm.

Question 6. In the given figure, all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid-points fo the sides. What is the perimeter of the figure?

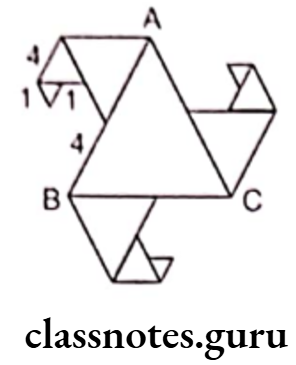
Solution. Given, △ABC is an equilateral triangle.

Here, AB = 8 units

∴ AB = BC = CA = 8 units

Now, △ADE is an equilateral triangle.

Here, E is the mid-point of AB.

∴ \(A E=B E=\frac{A B}{2}=\frac{8}{2}=4 \text { units }\)

Now, in △ADE, AD = DE = EA = 4 units

Similarly, equilateral triangles are △BOT and △UPC, having each sides equal

i.e. BO = OT = BT = UC = PC = PU = 4 units

It is also clear that OC = PA = 4 units

Also, △DIF is an equilateral triangle.

Here, F is the mid-point of DE.

∴ \(D F=F E=\frac{D E}{2}=\frac{4}{2}=2 \text { units }\)

In ADIF, DI = IF = DF = 2 units

Similarly, in △TKN and △RQU,

TK = KN = TN = RQ = UQ = UR = 2 units

It is also clear that NO = RP = 2 units

Also, △HIG is an equilateral triangle.

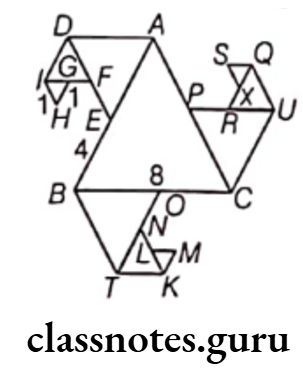
Here, G is the mid-point of IF.

∴ \(I G=G F=\frac{I F}{2}=\frac{2}{2}=1 \text { unit }\)

Now, in △HIG, HG = HI = GI = 1 unit

Similarly, in △MLK and △XQS,

ML = MK = LK = SQ = XS = QX = 1 unit

It is also clear that LN = XR = 1 unit

Now, perimeter of the given figure

= Sum of all outer sides of the given figure

= AD + DI + IH + HG + GF + FE + EB + BT + TK + KM + LM + LN + NO + OC + CU + UQ + QS + XS + XR + PR + PA

= [4 + 2 + 1 + 1 + 1 + 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4]

= 45 units

Hence, the perimeter of the given figure is 45 units.

Class 6 Maths Chapter 10 Solutions Mp Board

Question 7. If length of a rectangle is halved and breadth is doubled, then the area of the rectangle obtained remains same. Is it true?

Solution. True, let the length and breadth of a rectangle bel and b respectively.

We know that

Area of the initial rectangle = Length x Breadth

= 1 x b sq units

If length of a rectangle is halved and breadth is doubled.

i.e. New length = \(\frac{1}{2}\) units

and new breadth = 2b units

Then, the area of new rectangle

= New length x New breadth = \(\frac{1}{2}\) x 2b

= lb sq units

Question 8. In the given figure, each square is of unit length.

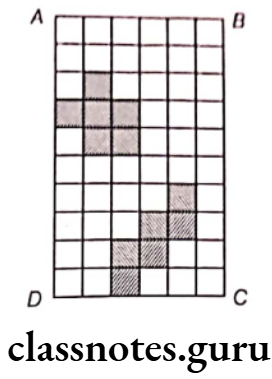
(1) What is the perimeter of the rectangle ABCD?

(2) What is the area of the rectangle ABCD?

(3) Divide this rectangle into ten parts of equal area by shading squares. (Two parts of equal area are shown here)

(4) Find the perimeter of each part which you have divided. Are they all equal?

Solution. Given, each side of square is of unit length. Figure contains length of 10 squares and width of 6 squares. Now, the length of rectangle, AD = BC

= Sum of length of a side of 10 squares

= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

= 10 x 1 = 10 units

and breadth of rectangle, AB = DC = Width of 6 squares = 6 x 1 = 6 units

(1) The perimeter of the rectangle ABCD

= AB + BC + CD + DA

= 6 + 10 + 6 + 10

= 32 units

(2) The area of the rectangle ABCD = Length x Breadth

= AD X AB

= 10 × 6

= 60 sq units

(3) The total area of rectangle = 60 units

Now, we have to divide the rectangle into 10 equal parts i.e. \(\frac{60}{10}\) = 6 squares units

i.e. we have to take a group of 6-6 square blocks, which is shown in the figure.

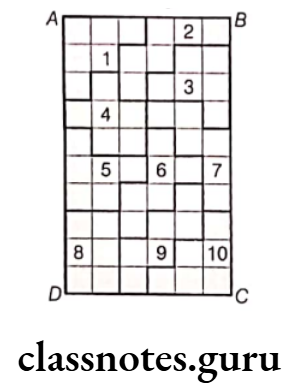
(4) Now, we find the perimeter of Part 1.

We know that perimeter of a figure is the total length of its boundary.

∴ Perimeter of Part 1

= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

= 12 units

Similarly, we can find the perimeters of remaining 9 parts, all the parts have same perimeter i.e. 12 units.

Yes, all the parts have same perimeter.