MP Board Class 6 Maths Solutions For Chapter 11 Algebra

Chapter 11 Algebra Matchstick Patterns

Matchsticks are used to make pattern of letters and other shapes.

Using matchsticks, we can write a general rule regarding the number of matchsticks required for a given shape. We introduce a variable which takes on values 1, 2, 3,…, denoted by letter n.

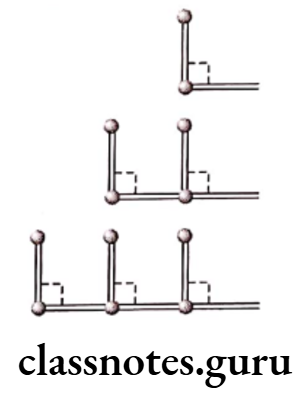
e.g. Let us consider the shape of a right angle.

(1) Number of right angle = 1 Number of matchsticks = 2

(2) Number of right angles = 2 Number of matchsticks = 4

(3) Number of right angles = 3 Number of matchsticks = 6 …… and so on.

Writing the above facts in a table, we have

From the table, we can say that the number of matchsticks required is twice the number of right angled formed.

i.e. Number of matchsticks required = 2 x Number of right angles formed

Read and Learn More MP Board Class 6 Maths Solutions

Hence, we can write as

Number of matchsticks required = 2n,

where n is the number of right angles formed.

Variable

A variable is a number which does not have a fixed value. It can take various values.

To show a variable, we may use any letter as n, m, l, p, x, y, z etc.

In the above example of the shape of right angle.

Number of matchsticks required = 2n

where n is called variable which is the number of right angles formed.

More Matchstick Patterns

We can make many letters of the alphabet and other shapes from matchsticks.

e.g. (1) Patterns of U (L), triangle (A), etc.

Hence, the number of matchsticks required = 3n

(2) Pattern of letter E

To make one E, five matchsticks are used

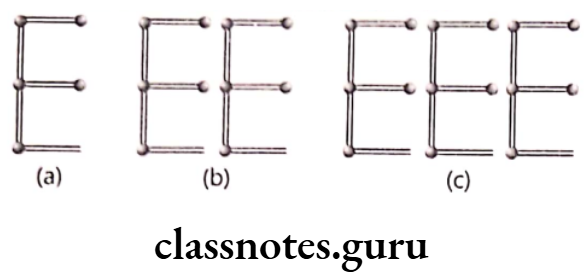
Hence, the number of matchsticks required = 5n

Mp Board Class 6 Maths Solutions

Example 1. Find the rule which gives the numbers of matchsticks required to make the following matchstick pattern. Use a variable to write the rule.

(1) A pattern of letter W

(2) A pattern of letter O

Solution. (1) One W can be formed by 4 matchsticks. Two W can be formed by 8 matchsticks.

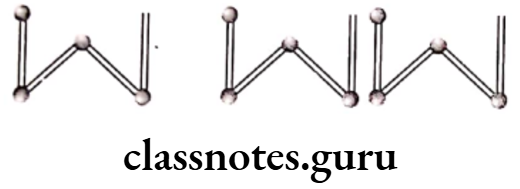
So, let variable n denote the number of W’s.

Now, the number of matchsticks required to make pattern of W are given below.

For n = 1, the number of matchsticks required = 4 x 1 = 4

For n = 2, the number of matchsticks required = 4 x 2 = 8

For n=3, the number of matchsticks required = 4 x 3 = 12

For n = n, the number of matchsticks required = 4 x n = 4n

Hence, the required rule for a pattern of letter W is 4n.

(2). One O can be formed by 4 matchsticks and two O can be formed by 8 matchsticks.

Thus, we get the following pattern of letter O.

So, let variable n denote the number of O’s.

Now, the number of matchsticks required to make pattern of O are given below.

For n = 1, the number of matchsticks required = 4 × 1 = 4

For n = 2, the number of matchsticks required = 4 × 2 = 8

For n = 3, the number of matchsticks required = 4 x 3 = 12

For n = n, the number of matchsticks required = 4 × n = 4n

Hence, the required rule for a pattern of letter O is 4n.

Example 2. Look at the following matchstick pattern of hexagons in the given figures below. The hexagons are not separate. Two neighbouring hexagons have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of hexagons.

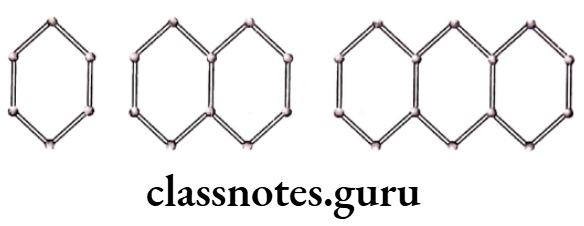
Solution. In figure,

(1) Number of hexagon = 1

and number of matchsticks = 6 = 5 x 1 + 1

(2) Number of hexagons = 2

= 5 x Number of hexagon + 1

and number of matchsticks = 11 = 5 x 2 + 1

(3) Number of hexagons = 3

= 5 x Number of hexagon + 1

and number of matchsticks = 16 = 5 × 3 + 1

= 5x Number of hexagon + 1

Thus, if number of hexagons = x

Then, the number of matchsticks

= 5 x Number of hexagons + 1

= 5x + 1

Hence, the required rule that gives the number of matchsticks is 5x + 1, where x is the number of hexagons.

Examples of Variables

Example 3. The teacher distributes 10 pencils per student. Can you tell how many pencils are needed, considering the number of students? (use x for the number of students).

Solution. Let the number of students be x.

Given, number of pencils distributed per student = 10

Now, number of pencils when

x = 1 is 10 or 10 x 1 = 10 x x

⇒ x = 2 is 20 or 10 x 2 = 10 x x

⇒ x = 3 is 30 or 10 x 3 = 10 x x

∴ Number of pencils for x students are 10x.

Mp Board Class 6 Maths Solutions

Example 4. School children are standing in a ground. There are 10 children in a row. What is the rule which gives the number of children, given the number of rows? (use n for the number of rows.)

Solution. Let the number of rows be n

Given, the number of children in each row = 10

∴ Total number of children = 10n

Here. = 1 child

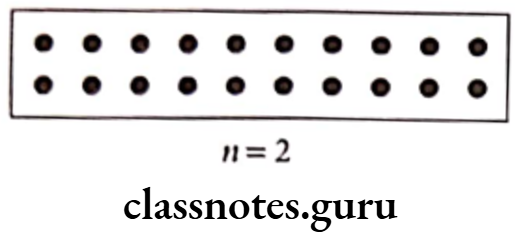
Hence, the rule to find the number of children in row is 10n.

Example 5. If there are 40 apples in a box, how will you write the total number of apples in terms of the number of boxes? (use a for the number of boxes).

Solution. Given, a is the number of boxes and the number of apples in a box = 40

When there is one box

i.e. a = 1, then the number of apples = 40 x 1 = 40 When there are two boxes

i.e. a = 2, then the number of apples = 40 x 2 = 80 When there are three boxes

i.e. a = 3, then the number of apples = 40 x 3 = 120 When there are a boxes

i.e. a = a, then the number of apples = 40 × a = 40a

Hence, the total number of apples in terms of number of boxes can be written as 40a.

Example 6. In her birthday, Radha distributes 5 toffees per student. Can you tell how many toffees are needed, given the number of students? (use letter y for the number of students).

Solution. Let the number of students be y.

Given, the number of toffees distributed to each student = 5

When there is one student i.e. y = 1,

then the number of toffees = 5 x 1 = 5

When there are two students i.e. y = 2,

then the number of toffees = 5 x 2 = 10

When there are three students i.e. y = 3,

then the number of toffees = 5 x 3 = 15

When there are y students i.e. y = y, then the number of toffees = 5 x y = 5y

Hence, 5 y toffees are needed for y students.

Example 7. A drone files 2 km In one minute. Can you express the distance covered by drone in terms of its flying time in minutes? (use z for flying time in minutes).

Solution. Let flying time of drone be z min.

Then, distance covered by drone in one minute = 2 km

∴ Distance covered by drone in 2 min = z x 2 = 2zkm

Hence, the distance covered by the drone in its flying time i.e. in z min is 2z km.

Example 8. Lakhan is Bharat’s younger brother. Lakhan is 5 yr younger than Bharat. Can you write Lakhan’s age in terms of Bharat’s age? Take Bharat’s age to be myr.

Solution. Let Bharat’s age be m yr.

Given, the Lakhan is 5 yr younger than Bharat.

So, age of Lakhan = (Age of Bharat) – 5 yr

⇒ Age of Lakhan (m-5) yr

Thus, we can write Lakhan’s age in terms of Bharat’s age.

Mp Board Class 6 Maths Solutions

Example 9. Hema’s mother made some cookies. She gives some cookies to guests and family members, still 7 cookies remain. If the number of cookies her mother gave away is t, how many cookies did she make?

Solution. Given, the number of cookies was given away by her mother = t

and the number of cookies left over = 7

∴ Total number of cookies made by Hema’s mother

= Number of cookies gave away + Number of cookies left

= t + 7

Hence, the total number of cookies made by her mother is t + 7.

Example 10. Mangoes are to be transferred from larger boxes to smaller boxes. When a large box is emptied, the mangoes from it fill three smaller boxes and still 5 mangoes remain outside.

If the number of mangoes in a small box are taken to be m, what is the number of mangoes in the larger box?

Solution. Given, the number of mangoes in a small box = m

Since, one larger box is emptied to fill three smaller boxes.

So, the number of mangoes in three smaller boxes

= 3 x Number of mangoes in one small box = 3x m = 3m

Also, 5 mangoes remain outside when larger box is emptied to fill three smaller boxes.

So, the number of mangoes in the larger box

= Number of mangoes in three smaller boxes + Mangoes left over

= 3m + 5

Hence, the number of mangoes in the larger box is 3m +5.

Chapter 11 Algebra Exercise 11.1

Question 1. Find the rule which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.

(1) A pattern of letter T as T

(2) A pattern of letter Z as Z

Solution. (1) One T can be formed by 2 matchsticks and 2T can be formed by 4 matchsticks. Thus, we get the following patterns of letter T.

So, let variablen denotes the number of T’s.

Now, the number of matchsticks required to make pattern of T are given below:

For n = 1,

Number of matchsticks required = 2 × 1 = 2

For n=2,

Number of matchsticks required = 2 x 2 = 4

For n = 3,

Number of matchsticks required = 2 × 3 = 6

For n=n,

Number of matchsticks required = 2 x n = 2n

Hence, the required rule for a pattern of letter T is 2n.

(2) One Z can be formed by 3 matchsticks and 2Z can be formed by 6 matchsticks. Thus, we get the following patterns of letter Z.

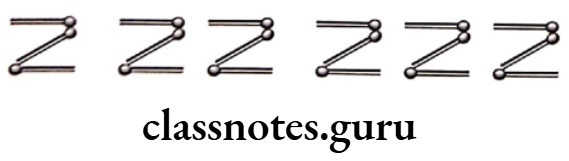
So, let variable n denotes the number of Z’s.

Now, the number of matchsticks required to make pattern of Z are given below:

For n = 1,

Number of matchsticks required = 3 x 1 = 3

For n = 2,

Number of matchsticks required = 3 x 2 = 6

For n = 3,

Number of matchsticks required = 3 × 3 = 9

For n = n,

Number of matchsticks required = 3 x n = 3n

Hence, the required rule for a pattern of letter Z is 3n.

Class 6 Maths Chapter 11 Solutions Mp Board

Question 2. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows?

(use n for the number of rows.)

Solution. Let the number of rows = n

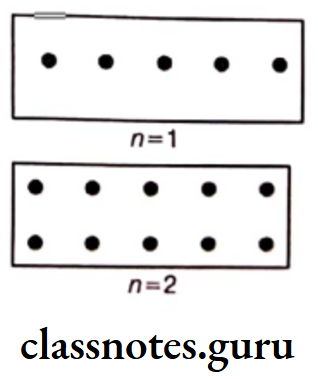
Given, the number of cadets in each row = 5

∴ Total number of cadets = 5n

Here, ⚫ = 1 cadet

Hence, rule to find the number of cadets in n rows is 5n.

Question 3. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (use b for the number of boxes).

Solution. Given, b is the number of boxes and the number of mangoes in a box = 50

When there is one box i.e. b = 1,

then the number of mangoes = 50 x 1 = 50.

When there are two boxes i.e. b = 2,

then the number of mangoes = 50 x 2 = 100

When there are three boxes i.e. b = 3,

then the number of mangoes = 50 x 3 = 150

When there are b boxes i.e. b = b,

then the number of mangoes = 50 x b = 50b

Hence, the total number of mangoes in terms of number of boxes can be written as 50b.

Class 6 Maths Chapter 11 Solutions Mp Board

Question 4. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (use S for the number of students).

Solution. Let the number of students be S.

Given, the number of pencils distributed to each student = 5

When there is one student i.e. S = 1,

then the number of pencils = 5 x 1 = 5

When there are two students i.e. S = 2,

then the number of pencils = 5 x 2 = 10

When there are three students i.e. S = 3,

then the number of pencils = 5 x 3 = 15

When there are S students i.e. S = S,

then the number of pencils = 5 x S = 5S.

Hence, 5$ pencils are needed for S students.

Question 5. A bird flies 1 km in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes? (use t for flying time in minutes).

Solution. Let flying time of bird be t min.

Then, bird flies in one min = 1 km

∴ Bird flies in t min = t x 1 = t km

Hence, the distance covered by the bird in its flying time i.e. int min is t km.

Class 6 Maths Chapter 11 Solutions Mp Board

Question 6. Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots with chalk powder). She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there, if there are 8 rows? If there are 10 rows?

Solution. Given, the number of rows = r

and the number of dots in one row i.e. r = 1 is 9 x 1 = 9

∴ The number of dots in 2 rows i.e. r 2 is 9 x 2 = 18

The number of dots in 3 rows i.e. r = 3 is 9 x 3 = 27

∴ Total number of dots in r rows = 9 x r = 9r

Now, if there are 8 rows i.e. r = 8, then the number of dots

= 9 x 8 = 72 dots

and for r = 10,

The number of dots = 9 x 10 = 90 dots

Question 7. Leela is Radha’s younger sister. Leela is 4 yr younger than Radha. Can you write Leela’s age in terms of Radha’s age? Take Radha’s age to be x years.

Solution. Let Radha’s age be xyr.

Given, the Leela is 4 yr younger than Radha.

So, age of Leela = (Age of Radha) – 4 yr

⇒ Age of Leela = (x-4) yr

Thus, we can write Leela’s age in terms of Radha’s age.

Question 8. Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is I, how many laddus did she make?

Solution. Given, the number of laddus was given away by mother = l

and the number of laddus left over = 5

∴ Total number of laddus made by mother = Number of laddus gave away + Number of laddus left over

= 1 + 5

Hence, the number of laddus made by mother is l + 5.

Mp Board Maths Chapter 11 Solutions

Question 9. Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?

Solution. Given, the number of oranges in a small box = x

Since, one large box is emptied to fill two smaller boxes.

So, the number of oranges in two smaller boxes

= 2 x Number of oranges in one small box = 2 x x = 2x

Also, 10 oranges remain outside when large box is emptied to fill two smaller boxes.

So, the number of oranges in the larger box = Number of oranges in two smaller boxes + Oranges left over

= 2x + 10

Hence, the number of oranges in the large box is 2x + 10.

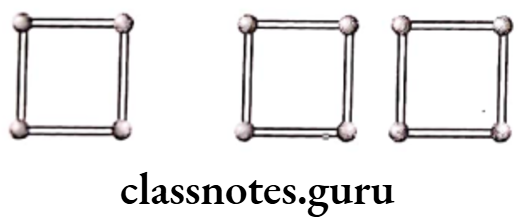
Question 10. Look at the following matchstick pattern of squares. The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares.

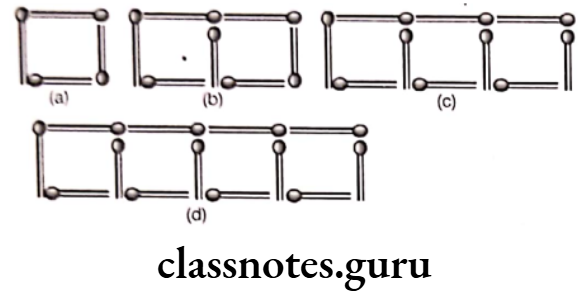
[Hint If you remove the vertical stick at the end, you will get a pattern of C’s.]

Solution.

(a) Number of square = 1

and number of matchsticks = 4 = 3 x 1 + 1 = 3 x Number of square + 1

(b) Number of squares = 2

and number of matchsticks = 7 = 3 x 2 + 1 = 3 x Number of squares + 1

(c) Number of squares = 3

and number of matchsticks = 10 = 3 x 3 + 1 = 3 x Number of squares + 1

(d) Number of squares = 4

and number of matchsticks = 13 = 3 x 4 + 1

= 3 x Number of squares + 1

Thus, if number of squares = x

Then, the number of matchsticks

= 3x Number of squares + 1

= 3x + 1

Hence, the required rule that gives the number of matchsticks is 3x+1, where x is the number of squares.

Chapter 11 Algebra Multiple Choice Questions

Question 1. Six trees are planted in a row. Then, the number of trees planted in n such rows are

1. 6n
2. 6n/5
3. 3n
4. n

Answer. 1. 6n

Question 2. Which of the following represents 6 x X.

1. 6x
2. \(\frac{x}{6}\)
3. 6+x
4. 6-x

Answer. 1. 6x

Question 3. If each matchbox contain 50 matchsticks, then the number of matchsticks required to fill n such boxes is

1. 50+ n
2. 50n
3. 50+ n
4. 50-n

Answer. 2. 50 n

Question 4. A box of fruits contain 60 oranges, the number of oranges required for y such boxes

1. 60+y
2. 60y+5
3. 60 y
4. 60 y-m

Answer. 3. 60 y

Mp Board Maths Chapter 11 Solutions

Question 5. If there are 25 pictures in an album, then the rule which gives total number of pictures in X albums is Competency Based Question

1. 25
2. X
3. 25X/2
4. 25x

Answer. 4. 25 x

Question 6. A train is moving at a speed of x km/h. Then, the rule which gives the distance covered by train in 7h is

1. 7x
2. 7
3. x
4. 7x-h

Answer. 1. 7x

Question 7. Variable means that it

1. has a fixed value
2. can take different values
3. can take only 2 values
4. can take only 3 values

Answer. 1. can take different values

Question 8. Garima puts a handful of seeds into an empty bird feeder. A bird comes and eats 7 of them. Which of the following expression can represent this situation algebraically? Competency Based Question

1. p+7
2. 7p
3. p-7
4. p+7

Answer. 3. p – 7

Question 9. Garima put some more seeds in the feeder. Which of the following expressions can represent this situation algebraically?

1. 2p
2. p + 7
3. p + q
4. p + q – 7

Answer. 4. p + q – 7

Question 10. If x takes the value of 7, then the value of x +13 Is

1. 20
2. 12
3. 21
4. 10

Answer. 1. 20

Question 11. If there are 40 coins in a box and x coins taken out from the box, then the remaining coins in the box can be represented in terms of number of coins taken out by the statement. Competency Based Question

1. 40 is subtracted x times
2. x is subtracted 40 times
3. x is subtracted from 40
4. 40 is subtracted from x

Answer. 3. x is subtracted from 40

Question 12. In algebra, letters may stand for

1. unknown quantities
2. know quantities
3. fixed numbers
4. None of these

Answer. 1. unknown quantities

Mp Board Maths Chapter 11 Solutions

Question 13. Look at the following matchstick pattern of octagons in the given figures below. The octagons are not separate. Two neighbouring octagons have a common matchstick. Then, the rule that gives the number of matchsticks in terms of the number of octagons is 

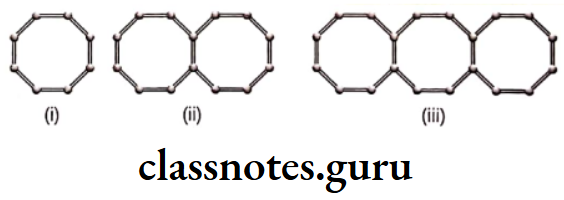
1. 6n+1
2. 7n+1
3. 8n
4. 8n+1

Answer. 2. 7n + 1

Question 14. The difference between Sanjana’s and her mother’s age is 27 yr. Then, the age of Sanjana’s mother is

1. (27-x)
2. (x+27) yr
3. (x-27) yr
4. 27x yr

Answer. 2. (x+27) yr

Question 15. An auto rickshaw charges 20 for the first kilometer, then 7 for each such subsequent kilometres. The total charge (in) for r kilometres is

1. 20+7r
2. 20 + (r-1)7
3. 20 + (r+1)7
4. 27r

Answer. 2. 20 + (r-1)7

Chapter 11 Algebra Assertion-Reason

Question 1. Assertion (A) The rule which gives the number of matchsticks required to make the matchstick pattern L, is 2n.

Reason (R) For n = 1, the number of matchsticks required = 2 x 1 = 2.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 2. Assertion (A) The rule which gives the number of matchsticks required to make the matchstick pattern C, is 3n.

Reason (R) For n = 2, the number of matchsticks required = 3 x 2 = 6

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 3. Assertion (A) n can take different values such as 1, 2, 3, 4, …. .

Reason (R) n is the example of a variable. Its value is not fixed. It can take different values.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Chapter 11 Algebra Fill in the Blanks

Question 1. The variable can take ….. values.

Answer. Different

Question 2. The number of days in w weeks is …. .

Answer. 7w

Question 3. If the present age of Ramandeep is n years, then her age after 7 yr will be ….. .

Answer. n+7

Question 4. The value of ….. is not fixed.

Answer. Variable

Question 5. In 2, 3, 5, l, 10, m and 13, the numbers of variables are …. .

Answer. Two

Class 6 Maths Chapter 11 Solutions

Chapter 11 Algebra True/False

Question 1. The number of matchsticks required to form the letter V is 3.

Answer. False

Question 2. t minutes are equal to 60 t seconds.

Answer. True

Question 3. The difference between the ages of two sisters Lila and Yamini is a variable.

Answer. False

Question 4. Variables can be denoted by any letter as a, b, c, l, m, n, …., x, y, z.

Answer. True

Question 5. 1 kg of potatoes are bought for ₹ 60. Cost of n kg of potatoes is 60 n.

Answer. True

Chapter 11 Algebra Match the Columns

Question 1. Match the Column A with Column B

Answer. (a) → (2), (b) → (3), (c) → (4), (d) → (1)

Chapter 11 Algebra Case Based Questions

Question 1. Sarah buy books from a dealer for her bookstall. She buys 20 comic books, 15 story books and 10 colouring books. A comic book cost ₹ a. A story book costs ₹ 5 more than a comic book and a colouring book costs ₹ 10 more than a story book.

On the basis of the given information, answer the following questions.

(1) Which of the following expression shows the total cost of the comic books?

(a) 20

(b) 20a

(c) 20 + a

(d) 20 – a

(2) Sarah gets a profit of ₹ 2 on the sale of each comic book. Which of the following expression shows the amount Sarah earns by selling 10 comic books?

(a) a + 2

(b) 20a – 20

(c) 10a + 20

(d) 20 + a + 2

Mp Board Class 6 Book Solutions

(3) A colouring book costs ₹ 50. What is the cost of the comic book?

(a) 35

(b) 40

(c) 45

(d) 50

(4) Write an expression to show the total cost of 15 storybooks.

Solution. (1) (b) Since, Sarah bought 20 comic books and cost of 1 comic book is a.

∴ Total cost of comic books = Cost of 1 comic book × Total number of comic books

= a x 20 = 20a

(2) (c) Cost of 1 comic book = a

Cost of 1 comic book with profit of ₹ 2 = a + 2

Number of books she sold = 10

Therefore, the amount Sarah earns by selling 10 comic books = 10 (a + 2) = 10a + 20

(3) (a) Cost of a comic book is ₹ a.

Then, according to the question,

Cost of a story book = Cost of a comic book + ₹ 5

= a + 5

Cost of a colouring book Cost of a story book + ₹ 10 = (a + 5) + 10 = a + 15

Also, it is given that a colouring book costs ₹ 50.

Therefore, equation is a + 15 = 50 ⇒ a = 50 – 15 ⇒ a = 35

Hence, the cost of a comic book is 35.

(4) Cost of 1 story book = a + 5

and total number of story book = 15

Therefore, the total cost of 15 story books = Total number of story books × Cost of one story book

= 15(a + 5) = 15a + 75

Question 2. Sudhir observed the pattern shown below on a cloth. The pattern consists of 4 patches.

The pattern is repeated n number of times in a 4 m long cloth.

(1) Which of the following expressions shows the number of octagon patches on the cloth?

(a) n

(b) 4n

(c) n + 4

(d) n – 4

(2) The cloth is cut into two equal halves. Sudhir observed both cloth parts have an equal number of repeating blocks but the last line is not complete. Which of the following expression shows the number of complete repeating blocks?

(a) n – 1

(b) 2n – 1

(c) \(\frac{n}{2}\)

(d) \(\frac{n}{2}\) – 1

(3) Write an expression which shows the total number of patches on the cloth?

Solution. (1) (a) Since, the pattern is repeated number of times there are n number of octagon patches on the cloth.

(2) (d) Number of repetition of pattern = n

The cloth cut into two equal halves.

∴ Number of repetition of pattern = \(\frac{n}{2}\)

and given last line is not complete.

∴ Number of complete repeating block = \(\frac{n}{2}\) – 1

(3) Total number of patches on cloth = Number of repetition of pattern x Number of patches in each repetition

Since, 4 patches in each pattern and pattern repeated n number of time

∴ Total number of patches on the cloth = 4n

Mp Board Class 6 Book Solutions

Chapter 11 Algebra Very Short Answer Type Questions

Question 1. The cost of one pen is ₹ 15. Find the cost of y pens.

Solution. Cost of one pen = ₹ 15

Cost of y pen = 15 x y = 15y

Question 2. Find the number of matchsticks required to make the pattern of a square.

Solution. The number of matchsticks required to make the pattern of a square is 4.

Question 3. The valye of x pencisl, if cost of 1 pencil is ₹ 10.

Solution. Cost of one pencil = 10.

Cost of x pencil = 10 x x = 10x

Question 4. How many matchsticks will be required to make the pattern of a triangle?

Solution. The number of matchsticks required to make the pattern of a triangle is 3.

Chapter 11 Algebra Short Answer Type Questions

Question 1. The teacher distributes 2 pencils per student. Can you tell how many penciles are needed, given the number of students? (use x for the number of students).

Solution. Teacher distributes pencils per student = 2

Number of students = x

∴ Need of pencils = 2 x x = 2x

Question 2. A dolphin swins 1 km in one minute. Can you express the distance covered by dolphin in terms of its swimming time in minutes? (use t for swimming time in minutes)

Solution. Let the swimming time of dolphin bet min.

Then, dolphin swims in one min = 1 km

∴ Dolphin swims in t min = t x 1 = t km

Hence, the distance covered by dolphin in swimming time i.e. in t min is t km.

Mp Board Class 6 Book Solutions

Question 3. In a village, there are 8 water tanks to collect rain water. On a particular day, x litres of rain water is collected per tank. If 100 L of water was already there in one of the tanks, what is the total amount of water in the tanks on that day?

Solution. Rain water collected on particular day per tank = x L

Number of tanks to collect water = 8

Total water in all tanks = 8x L

Water in one of the tanks = 100 L

∴ Total amount of water = Total water in all tanks + Water in one of the tanks

= (8x + 100) L

Chapter 11 Algebra Long Answer Type Questions

Question 1. Find the rule which gives the number of matchsticks required to make the following matchstick patterns.

A pattern of letter y as Y

Solution. One Y can be formed by 3 matchsticks and 2Y can be formed by 6 matchsticks.

Thus, we get the following patterns of letter Y.

Here, the number of Y’s are increasing.

So, let the variable n denote the number of Y’s.

Now, the number of matchsticks required to make pattern of Y are given below:

For n = 1,

the number of matchsticks required = 3 x 1 = 3 For n = 2,

the number of matchsticks required = 3 x 2 = 6 For n = 3,

the number of matchsticks required = 3 x 3 = 9 For n = n,

the number of matchsticks required = 3 x n = 3n

Hence, the required rule for a pattern of letter Y is 31.

Question 2. Army personnel are standing in an open ground. There are 6 personnel in a row. What is the rule which gives the number of army personnel, given the number of rows? (use n for the number of rows.)

Solution. Let the number of rows = n

Given, the number of army personnel in each row = 6

∴ Total number of army personnel = 6n

Hence, the rule to find the number of army personnel in n rows is бn.

Question 3. If there are 40 oranges in a box, how will you write the total number of oranges in term of the number of boxes? (use b for the number of boxes).

Solution. Given, the number of oranges in box = 40

Let the number of boxes = b

Total number of oranges in term of number of boxes can be written as 40b.

Class 6 Mp Board Maths Question Answers

Question 4. Sakshi is drawing a dot Rongolu (a beautiful pattern of lines joining dots with chalk powder). She has 6 dots in a row. Find,

(1) how many dots will her Rangoli have for r rows?

(2) how many dots are there, if there are 10 rows?

Solution. Given, the number of rows = r

(1) The number of dots in one row

i.e. r = l is 6 x 1 = 6

The number of dots in two rows

i.e. r = 2 is 6 x 2 = 12

∴ Total number of dots in r rows = 6 x r = 6r

(2) If number of rows = 10

∴ The number of dots = 10 x 6 = 60 dots

Question 5. Richa is Madan’s younger sister. Richa is 5 yr younger than Madan. Can you write Richa’s age in terms of Madan’s age? Take Madan’s age to be x yr.

Solution. Let Madan’s age be x yr.

Given, Richa is 5 yr younger than Madan.

So, age of Richa = (Age of Madan) – 5 yr

and age of Richa = (x – 5) yr

Question 6. Mother bought some candy. She gives some candies to guests and family members; still 10 candies to guests and family members; still 10 candies are remain. If the number of candies mother gave away is m, how many candies did she bought?

Solution. Given, the number of candies given to guest and family members = m

and the number of candies left over = 10

∴ Total number of candies she bought = Number of candies gave to guest and family members + Number of candies left over

= m + 10

Hence, the number of candies bought by mother is m + 10.

Question 7. Mangoes are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the mangoes from it fill three smaller boxes and still 20 mangoes remain outside.

If the number of mangoes in a small box are taken to be x, what is the number of mangoes in the larger box?

Solution. Given, the number of mangoes in a small box = x

Since, one large box is emptied to fill three smaller boxes.

So, the number of mangoes in three smaller boxes = 3 x Number of mangoes in one box = 3 x x = 3x

Also, 20 mangoes remain outside when large box is emptied to fill three smaller boxes.

Number of mangoes in the larger box = Number of mangoes in three smaller boxes + Mangoes left over

= 3x + 20

Class 6 Mp Board Maths Question Answers

Question 8. Sunitha is half the age of her mother Geeta. Find their ages

(1) after 4 yr?

(2) before 3 yr?

Solution. Let Sunita’s present age be x.

Given, Sunita is half the age of her mother Geeta.

∴ Geeta’s present age = 2x

(1) Sunita’s age after 4 yr = (x+4) yr

Geeta’s age after 4 yr = (2x+4) yr

(2) Sunita’s age before 3 yr = (x-3) yr

Geeta’s age before 3 yr = (2x-3) yr

Question 9. Look at the following matchstick pattern of pentagons in the figures given below. The pentagons are not separate. Two neighbouring pentagons have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of pentagons.

Solution. From figure,

(1) Number of pentagons = 1

and number of matchsticks = 5 = 4 x 1 + 1

= 4 x Number of pentagons + 1

(2) Number of pentagons = 2

and number of matchsticks = 9 = 4 x 2 + 1

= 4 x Number of pentagons + 1

(3) Number of pentagons = 3

and number of matchsticks = 13 = 4 x 3 + 1

= 4 x Number of pentagons + 1

Thus, if number of pentagons = x

Then, the number of matchsticks

= 4 x Number of pentagons + 1

= 4x + 1

Hence, the required rule that gives the number of matchsticks is 4x+1, where x is the number of pentagons.