Chapter 12 Ratio and Proportion Ratio
The comparison of two numbers or quantities by the method of division is known as the ratio of the numbers and it is denoted by symbol “:”
e.g. Let two numbers be a and b, where b 0, then the ratio of a and b is a:b.
The first term a is called the antecedent and the second term b is called the consequent.
Suppose, we have 5 pens and 9 toys. The ratio of number of pens to number of toys is 5:9 or 5 is to 9.
Ratio in Simplest Form
The ratio a : b is said to be in the simplest form or lowest form if the HCF of a and b is 1. A ratio in the simplest form is also called the ratio in the lowest term.
e.g. The ratio 11:18 is in the simplest form. Since, the HCF of 11 and 18 is 1. To convert a given ratio a: b to its simplest form, we divide each term by the HCF of a and b.
Example 1. Find the ratio of the following
(1) 21 to 84
(2) 30 min to 60 min
(3) 80 cm to 1.2 m
Solution. (1) Here, HCF of 21 and 84 = 21
∴ Ratio = \(\frac{21+21}{84+21}=\frac{1}{4}=1: 4\)
(2) Since, given quantities are in same unit.
∴ HCF of 30 and 60 = 30
∴ Ratio = \(\frac{30 \div 30}{50 \div 30}=\frac{1}{2}=1: 2\)
(3) Since, given quantities are not in the same unit.
Firstly, we have to convert them into same unit.
Read and Learn More MP Board Class 6 Maths Solutions
We know that 1 m = 100 cm
⇒ 1.2 m = 1.2 x 100 cm
= 120 cm
∴ Ratio of 80 cm to 1.2 m i.e. 80 cm to 120 cm = \(\frac{80}{120}\)
∴ HCF of 80 and 120 = 40
∴ Ratio = \(\frac{80 \div 40}{120 \div 40}=\frac{2}{3}\)
Hence, the required ratio is 2 : 3.
Note it Two quantities can be compared if they are expressed in the same unit and ratio has no unit.
Equivalent Ratio
We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.
e.g. 2:3 and 4:6 are equivalent ratios.
Mp Board Class 6 Maths Solutions
Example 2. Give two equivalent ratios of 3 : 5.
Solution. Given, ratio = 3 : 5
Firstly, multiply the numerator and denominator with the same number.
\(\frac{3}{5}=\frac{3 \times 2}{5 \times 2}=\frac{6}{10} \text { and } \frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\)Hence, two equivalent ratios of 3:5 are 6: 10 and 9: 15.
Note it A ratio does not change, if its numerator and denominator are multiplied or divided by the same non-zero number.
Example 3. Consider the statement : Ratio of the breadth to the length of a room is 1 : 2. Complete the following table that shows some possible breadths and lengths of the room.

Solution. Given, the ratio of the breadth to the length of a room = 1 : 1
Also given, breadth of room = 12 m
and length of room = 24 m
Then, the ratio of breadth and length = \(\frac{12}{24}\)
= \(\frac{1}{2}\) = 1 : 2
Now, for missing, we have 24 x 2 = 48
i.e. when we multiply 24 by 2, we get 48.
So to get first missing term, we multiply 12 by 2
∴ 12 x 2 = 24
Thus, the complete table is

Example 4. In a year, there are 55 holidays. What is the ratio of the number of holidays to the number of days in one year?
Solution. Given, number of holidays in one year = 55
We know that number of days in one year = 365
∴ Ratio of the number of holidays to the number of days in one year
\(=\frac{\text { Number of holidays }}{\text { Number of days }}=\frac{55}{365}\)\(= \frac{55 \div 5}{365 \div 5}=\frac{11}{73}\) [∴ HCF of 55 and 365 = 5]
Hence, the required ratio is 11 : 73.
Mp Board Class 6 Maths Solutions
Example 5. Dhoni takes 1 h to reach playground from his house and Sehwag takes 20 min to reach playground from his house. Find the ratio of the time taken by Dhoni to the time taken by Sehwag.
Solution. Here, time taken by Dhoni is in hours and time taken by Sehwag is in minutes.
So, we have to convert time taken by both into the same unit.
∴ Time taken by Dhoni = 1 h = 1 x 60 min = 60 min [∴ 1h = 60 min]
and time taken by Sehwag = 20 min
∴ Ratio of the time taken by Dhoni to the time taken by Sehwag
\(=\frac{\text { Time taken by Dhoni }}{\text { Time taken by Sehwag }}=\frac{60}{20}\)= \(\frac{60+20}{20+20}=\frac{3}{1}=3: 1\) [∴ HCF of 60 and 20 = 20]
Hence, the required ratio is 3 : 1.
Example 6. Out of 40 students in a class, 10 like cricket, 20 like football and remaining like tennis. Find the ratio of
(1) the number of students liking cricket to the number of student liking tennis.
(2) the number of students liking football to the total number of student.
Solution. Given, the total number of students in a class = 40
Number of students who like cricket = 10
Number of students who like football = 20
Then, the number of students who like tennis = Total number of students -(Number of students who like football + Number of students who like cricket)
= 40 – (10 + 20) = 10
(1) Ratio of the number of students liking cricket to the number of student liking tennis
\(=\frac{\text { Number of students who like cricket }}{\text { Number of students who like tennis }}=\frac{10}{10}=1: 1\)(2) Ratio of the number of students liking football to the total number of students
\(=\frac{\text { Number of students who like football }}{\text { Total number of students }}\)\(=\frac{20}{40}=\frac{20 \div 20}{40 \div 20}=\frac{1}{2}\) [HCF of 20 and 40 = 20]
= 1 : 2
Example 7. See the figure and find the ratio of
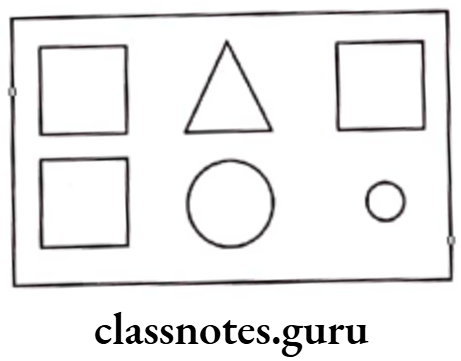
(1) the number of squares to the number of circles Inside the rectangle.
(2) the number of circles to the all shapes inside rectangle.
Solution. In the given figure, number of triangles = 1,
number of squares = 3 and number of circles = 2
∴ Total number of shapes = 1 + 3 + 2 = 6
(1) Required ratio of the number of squares to the number of circles
\(=\frac{\text { Number of squares }}{\text { Number of circles }}=\frac{3}{2}=3: 2\)(2) Required ratio of the number of circles to the all shapes
\(=\frac{\text { Number of circles }}{\text { Total number of shapes }}=\frac{2}{6}=\frac{2+2}{6+2}\) [HCF of 2 and 6 = 6]
= \(\frac{1}{3}\) = 1 : 3
Mp Board Class 6 Maths Solutions
Example 8. Distance travelled by Rakesh and Vishal in an hour are 8 km and 12 km, respectively. Find the ratio of the speed of Rakesh to the speed of Vishal.
Solution. We know that
\(\text { Speed }=\frac{\text { Distance }}{\text { Time }}\)Given, distance travelled by Rakesh in one hour = 8 km Distance 8
∴ Speed of Rakesh \(=\frac{\text { Distance }}{\text { Time }}=\frac{8}{1}=8 \mathrm{~km} / \mathrm{h}\)
and distance travelled by Vishal in one hour = 12 km
∴ Speed of Vishal = \(\frac{12}{1}\) km/h
∴ Ratio of the speed of Rakesh to the speed of Vishal
\(=\frac{\text { Speed of Rakesh }}{\text { Speed of Vishal }}=\frac{8}{12}=\frac{8 \div 4}{12 \div 4}=\frac{2}{3}=2: 3\) [∴ HCF of 8 and 12 = 4]
Example 9. Cost of 8 pens is 160 and cost of 6 pencils is 60. Find the ratio of the cost of a pen to the cost of a pencil.
Solution. Given, cost of 8 pens = ₹ 160
∴ Cost of 1 pen \(=\frac{\text { Total cost of pens }}{\text { Numbers of pens }}=\frac{160}{8}=₹ 20\)
Also given, cost of 6 pencils = ₹ 60
∴ Cost of 1 pencil \(=\frac{\text { Total cost of pencils }}{\text { Number of pencils }}=\frac{60}{6}=₹ 10\)
Hence, the required ratio \(=\frac{\text { Cost of } 1 \text { pen }}{\text { Cost of } 1 \text { pencil }}=\frac{20}{10}=\frac{2}{1}=2: 1\)
Example 10. Father wants to divide ₹ 42 between his sons Ritesh and Raj in the ratio of their ages. If the age of Ritesh is 16 yr and the age of Raj is 12 yr. Find how much Ritesh and Raj will get.
Solution. Given, Ritesh’s age=16 yr and Raj’s age = 12 yr
∴ Ratio of their ages \(=\frac{\text { Ritesh’s age }}{\text { Raj’s age }}=\frac{16}{12}=\frac{16 \div 4}{12 \div 4}=\frac{4}{3}=4: 3\)
[∴ HCF of 16 and 12 = 4]
Now, father wants to divide ₹ 42 between his sons in the ratio of their ages i.e.4 : 3.
∴ Sum of the parts of the ratio = 4 + 3 = 7
Amount which has to be divided = ₹ 42
Here, we can say that Ritesh gets 4 parts and Raj gets 3 parts out of every 7 parts.
∴ Ritesh’s share = \(\frac{4}{7}\) x 42 = ₹ 24
and Raj’s share = \(\frac{3}{7}\) x 42 = ₹ 18
Hence, Ritesh gets ₹ 24 and Raj gets ₹ 18.
Class 6 Maths Chapter 12 Solutions Mp Board
Example 11. Present age of father is 36 yr and that of his son is 6 yr. Find the ratio of the
(1) present age of father to the present age of son.
(2) age of father to the age of son, when son was 4 yr old.
(3) age of father after 10 yr to the age of son after 10 yr.
Solution. Given, present age of father = 36 yr
and present age of son = 6 yr
(1) Required ratio \(=\frac{\text { Present age of father }}{\text { Present age of son }}\)
= \(\frac{36}{6}=\frac{36+6}{6 \div 6}\) [HCF of 36 and 6 = 6]
= \(\frac{6}{1}\) = 6 : 1
(2) When son’s age was 4 yr i.e. 2 yr back (because son’s present age is 6 yr), then father’s age
= 36 – 2 = 34 yr
∴ Required ratio \(=\frac{2 \mathrm{yr} \text { back father’s age }}{2 \mathrm{yr} \text { back son’s age }}\)
\(=\frac{34}{4}=\frac{34+2}{4+2}=\frac{17}{2}=17: 2\)[∴ HCF of 34 and 4 = 2]
(3) After 10 yr, father’s and son’s age will be (36 + 10) yr and (6 + 10) yr, respectively, i.e. 46 yr and 16 yr.
∴ Required ratio \(=\frac{\text { Father’s age after } 10 \mathrm{yr}}{\text { Son’s age after } 10 \mathrm{yr}}\)
= \(\frac{46}{16}=\frac{46 \div 2}{16+2}=\frac{23}{8}=23: 8\)
[∴ HCF of 46 and 16 = 2]
Chapter 12 Ratio And Proportion
If the ratio of the first and second quantities is equal to the ratio of the third and fourth quantities, then the quantities are said to be in proportion and it is denoted by symbol ‘::’ or ‘=’.
Four numbers a, b, c and d are said to be in proportion, if a:bc:d and it is written as a:b::c:d, where a, b, c and d are respectively, known as first, second, third and fourth terms of the proportion.
First and fourth terms are called extreme terms or extremes, whereas second and third terms are called the middle terms or means.
Example 1. Are the ratios in proportion?
(1) 45 : 60 and 36 : 48
(2) 150 : 100 and 135 : 90
Solution. (1) ∴ Ratio of 45 to 60 = \(\frac{45}{60}=\frac{3}{4}=3: 4\)
and ratio of 36 to 48 = \(\frac{36}{48}=\frac{3}{4}=3: 4\)
∴ The ratio of 45 to 60 is equal to 36 to 48
So, 45 : 60 :: 36 : 48
Hence, 45 : 60 and 36 : 48 are in proportion.
(2) ∴ Ratio of 150 to 100 = \(\frac{150}{100}\) = 3 : 2
and ratio of 135 to 90 = \(\frac{135}{90}\) = 3 : 2
∴ The ratio of 150 to 100 is equal to 135 to 90.
So, 150 : 100 :: 135 : 90
Hence, 150, 100, 135 and 90 are in proportion.
Class 6 Maths Chapter 12 Solutions Mp Board
Example 2. If 36 : 81 :: x : 63, then find the value of x.
Solution. Given, 36 : 81 :: x : 63
⇒ \(\frac{36}{81}=\frac{x}{63}\)
⇒ \(\frac{4}{9}=\frac{x}{63}\)
⇒ 9x = 4 x 63
⇒ \(x=\frac{4 \times 63}{9}\)
⇒ x = 4 x 7
Hence, the value of x is 28.
Example 3. Check whether the given ratios are equal i.e. they are in proportion. If yes, then write them in proper form.
(1) 1 : 4 and 5 : 20
(2) 2 : 7 and 8 : 28
(3) 3 : 11 and 4 : 21
(4) ₹ 4 to ₹ 7 and 16 to 28
Solution. (1) We have, 1 : 4 and 5 : 20
Here, \(5: 20=\frac{5}{20}=\frac{5+5}{20+5}=\frac{1}{4}=1: 4\)
[∴ HCF of 5 and 20 = 5]
i.e. 1:4 and 5:20 are in proportion.
Thus, the proper form is 1 : 4 :: 5 : 20.
(2) We have, 2 : 7 and 8 : 28
Here, \(8: 28=\frac{8}{28}=\frac{8 \div 4}{28+4}=\frac{2}{7}=2: 7\)
[∴ HCF of 8 and 28 = 47]
Therefore, 2 : 7 and 8 : 28 are in proportion.
Thus, the proper form is 2 : 7 :: 8 : 28.
(3) We have, 3 : 11 and 4 : 21
Here, \(3: 11=\frac{3}{11} \text { and } 4: 21=\frac{4}{21}\)
Here, 3 : 11 ≠ 4 : 21
Thus, 3:11 and 4:21 are not in proportion.
(4) We have, ₹ 4 : ₹ 7 = 4 : 7 and 16 : 28
Now, \(4: 7=\frac{4}{7} \text { and } 16: 28=\frac{16}{28}=\frac{16 \div 4}{28 \div 4}=\frac{4}{7}\)
[∴ HCF of 16 and 28 = 4]
Hence, 4 : 7 and 16 : 28 are in proportion.
Thus, the proper form is 4 : 7 :: 16 : 28.
Example 4. Determine whether the following are in proportion.
(1) 3, 9, 7,21
(2) 3, 55, 77, 17
Solution. (1) We have, 3, 9, 7, 21
∴ Ratio of 3 to 9 = \(\frac{3}{9}=\frac{3 \div 3}{9+3}\)
[∴ HCF of 3 and 9 = 3]
= \(\frac{1}{3}\) = 1 : 3
and ratio of 7 to 21 = \(\frac{7}{21}=\frac{7 \div 7}{21 \div 7}=\frac{1}{3}=1: 3\)
[∴ HCF of 7 and 21=7]
Therefore, 3, 9,7 and 21 are in proportion.
(2) We have, 3, 55, 77, 17
∴ Ratio of 3 to 55 = \(\frac{3}{55}\) and ratio of 77 to 17 = \(\frac{77}{17}\)
Here, 3 : 55 ≠ 77 : 17
Therefore, 3, 55, 77 and 17 are not in proportion.
Class 6 Maths Chapter 12 Solutions Mp Board
Example 5. Write true (T) and false (F) against each of the following statements:
(1) 0.9 : 0.36 :: 12 : 48
(2) 20 m : 30 m :: 16 s : 24 s
Solution. (1) We have, 0.9 : 0.36 :: 12 : 48
Ratio of 0.9 to 0.36 = \(\frac{0.9}{0.36}=\frac{90}{36}=\frac{90 \div 18}{36+18}=\frac{5}{2}=5: 2\)
[∴ HCF of 90 and 36 = 18]
and ratio of 12 to 48 = \(\frac{12}{48}=\frac{12+12}{48+12}=\frac{1}{4}\)
[∴ HCF of 12 and 48 = 12]
Here, 0.9 : 0.36 ≠ 12 : 48
Hence, the given statement is false.
(2) We have, 20 : 30 :: 16 : 24
Ratio of 20 to 30 = \(\frac{20}{30}=\frac{20+10}{30+10}\)
[∴ HCF of 20 and 30 = 10]
\frac{2}{3} = 2 : 3
and ratio of 16 to 24 = \(\frac{16}{24}=\frac{16 \div 8}{24 \div 8}=\frac{2}{3}=2: 3\)
[∴ HCF of 16 and 24 = 8
Here, 20 : 30 = 16 : 24 = 2 : 3
Hence, the given statement is true.
Example 6. Are the following ratios form a proportion? Also, write the middle terms and extreme terms, where the ratios form a proportion.
(1) 50 cm : 1 m and 80 : 160
(2) 24 L : 60 L and 6 bottles : 15 bottles
Solution. (1) We have, 50 cm : 1 m
= 50 cm : 1 x 100 cm [∴ 1m = 100 cm]
= 50 cm : 100 cm
= \(\frac{50}{100}=\frac{50 \div 50}{100 \div 50}=\frac{1}{2}=1: 2\)
[∴ HCF of 50 and 100 = 50]
and ₹ 80 : ₹ 160 = 80 : 160 = \(\frac{80}{160}=\frac{80 \div 80}{160 \div 80}=\frac{1}{2}=1: 2\)
[∴ HCF of 80 and 160 = 80]
Here, 1 : 2 = 1 : 2
i.e. 50 cm : 1 m = ₹ 80 : ₹ 160
So, the ratios of 50 cm: 1m and 80: 160 are in proportion.
Hence, middle terms are 1 m and 80 and extreme terms are 50 cm and 160.
(2) We have, 24 L : 60 L and 6 bottles : 15 bottles
Now, 24 L to 60 L = \(\frac{24 \mathrm{~L}}{60 \mathrm{~L}}=\frac{24}{60}=\frac{24 \div 12}{60 \div 12}\)
[∴ HCF of 24 and 60 = 12]
= \(\frac{2}{5}\) = 2 : 5
and 6 bottles : 15 bottles = 6 : 15 = \(\frac{6}{15}=\frac{6 \div 3}{15 \div 3}\)
[∴ HCF of 6 and 25 = 3]
= \(\frac{2}{5}\) = 2 : 5
Here, 2:5 = 2:5
i.e. 24 L : 60 L and 6 bottles : 15 bottles are in proportion.
i.e. 24 L : 60 L :: 6 bottles : 15 bottles
Hence, middle terms of ratios are 60 L and 6 bottles and extreme terms of ratios are 24 L and 15 bottles.
Chapter 12 Ratio And Proportion Unitary method
A method in which first we find the value of one unit and then the value of required number of units is called unitary method.
e.g. If the cost of any number of article is given, then the cost of 1 article can be obtained by dividing the cost of given number of articles with the number of articles.
i.e. Cost of 1 article \(=\frac{\text { Cost of the given number of articles }}{\text { Number of articles }}\)
Now, with the help of 1 article, we find the any number of articles. Thus, in this method, the price of 1 article help us, in finding the price of any number of articles.
In unitary method, we follow the following trivial rules of variation:
(1) To get more, we multiply.
(2) To get less, we divide.
Example 1. If the cost of 15 mangoes is ₹90. Find the cost of 17 mangoes.
Solution. Given, the cost of 15 mangoes = ₹ 90
The cost of 1 mango = \(\frac{90}{15}\)
Now, the cost of 17 mangoes = 17 x 6 = ₹ 102
Hence, the cost of 17 mangoes is ₹ 102.
Mp Board Maths Chapter 12 Solutions
Example 2. The yield of wheat from 8 hectares of land is 360 quintals. Find the number of hectares of land required for a yield of 540 quintals.
Solution. Required area of land to yield 360 quintals wheat = 8 hectares
Required area of land to yield 1 quintal wheat = \(\frac{8}{360}\) hectares
Required area of land to yield 540 quintals wheat = \(540 \times \frac{8}{360}=\frac{3 \times 8}{2}=12 \text { hectares }\)
Example 3. If the cost of 5 m of ribbon is 500, then find the cost of 2m of ribbon.
Solution. Given, the cost of 5m of ribbon = ₹ 500
∴ Cost of 1 m of ribbon = \(\frac{500}{5}\) = ₹ 100
∴ Cost of 2m of ribbon = 100 × 2 = ₹ 200
Hence, the cost of 2m of ribbon is ₹ 200.
Example 4. Abhimanyu earns ₹ 2500 in 10 days. How much will he earn in 30 days?
Solution. Here, the number of days is known and money earn is unknown.
Given, Abhimanyu earns in 10 days = ₹ 2500
∴ Abhimanyu earns in 1 day = \(\frac{2500}{10}\) = ₹ 250
∴ Abhimanyu earns in 30 days = 250 x 30 = 7500
Hence, Abhimanyu earns ₹7500 in 30 days.
Example 5. During a rainy season, it has rained 369 mm in last 3 days, how many centimetres of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.
Solution. Here, the number of days is known and rainfall is unknown.
Given, rainfall in 3 days = 369 mm
∴ Rainfall in 1 day = \(\frac{369}{3}\) = 123 mm
∴ Rainfall in one full week i.e. 7 days = 123 × 7 mm = 861 mm
In centimetre, rainfall in one full week
= \(861 \times \frac{1}{10} \mathrm{~cm}=861 \mathrm{~cm}\) [∴ 1 mm = \(\frac{1}{10}\) cm]
Hence, 86.1 cm rain will fall in 7 days or one full week.
Example 6. The cost of 8 kg of sugar is ₹ 48.80.
(1) What will be the cost of 10 kg of sugar?
(2) What quantity of sugar can be purchased in ₹ 81?
Solution. (1) Here, the quantity of sugar is known and cost is unknown.
Given, the cost of 8 kg of sugar = ₹ 48.80
∴ Cost of 1 kg of sugar = \(\frac{48.80}{8}=₹ 6.10\)
∴ Cost of 10 kg of sugar = 6.10 x 10 = ₹ 61.0
Hence, the cost of 10 kg of sugar is ₹ 61.
(2) Here, the cost of sugar is known and quantity of sugar is unknown.
Given, in ₹ 48.80 quantity of sugar that can be purchased = 8 kg
∴ In ₹ 1, quantity of sugar that can be purchased = \(\frac{8}{48.80}=\frac{8 \times 10}{488}=\frac{80}{488} \mathrm{~kg}\)
∴ In ₹ 81, quantity of sugar that can be purchased = \(\frac{80}{188} \times 81=13.28 \mathrm{~kg}\)
Hence, 13.28 kg sugar can be purchased in ₹ 81.
Example 7. Venus pays ₹ 7000 as rent for 2 months. How much does she has to pay for a whole year, if the rent per month remains the same?
Solution. Given, rent paid for 2 months = ₹ 7000
∴ Rent paid for 1 month = \(\frac{7000}{2}=₹ 3500\)
∴ Rent paid for a whole year i.e. 12 months = 3500 × 12 = ₹ 42000
Hence, she has to pay ₹ 42000 for a whole year.
Mp Board Maths Chapter 12 Solutions
Example 8. The cost of 2 dozen bananas is ₹ 80. How many bananas can be purchased for ₹ 20?
Solution. We know that I dozen = 12 units
Given, in 80 the number of bananas that can be purchased = 2 dozen = 2 x 12 = 24
∴ In ₹ 1, the number of bananas that can be purchased
\(=\frac{24}{80}=\frac{24 \div 8}{80 \div 8}=\frac{3}{10}\) [∴ HCF of 24 and 80 = 8]
∴ In ₹ 20, the number of bananas that can be purchased
\(=\frac{3}{10} \times 20=\frac{60}{10}=6\)Example 9. A vehicle requires 120 L of petrol for covering a distance of 720 km. How much petrol will be required by the vehicle to cover a distance of 1850 km?
Solution. Given, petrol required for 720 km = 120 L
∴ Petrol required for 1 km = \(\frac{120}{720}=\frac{120+120}{720+120}=\frac{1}{6} L\)
∴ Petrol required for 1850 km = \(\frac{1}{6} \times 1850=308.33 \mathrm{~L}\)
Hence, 308.33 L petrol will be required by the vehicle to cover 1850 km.
Example 10. Arjun purchases 20 pens for ₹ 260 and Aryan purchases 8 pens for ₹ 96. Can you say who got the pens cheaper?
Solution. For Arjun, the cost of 20 pens = ₹ 260
∴ Cost of 1 pen = \(\frac{260}{20}=₹ 13\)
For Aryan, cost of 8 pens = ₹ 96
∴ Cost of 1 pen = \(\frac{96}{8}=₹ 12\)
Here, ₹ 12 < ₹ 13
Hence, Aryan got the pens cheaper.
Question 1. In a class, there are 20 boys and 40 girls. What is the ratio of the number of boys to the number of girls?
Solution. Here, number of boys = 20 and number of girls = 40
∴ Ratio of the number of boys to the number of girls
\(=\frac{\text { Number of boys }}{\text { Number of girls }}=\frac{20}{40}=\frac{2}{4}=\frac{1}{2}=1: 2\)Hence, the required ratio is 1 : 2.
Question 2. Ravi walks 6 km in an hour while Roshan walks 4 km in an hour. What is the ratio of the distance covered by Ravi to the distance covered by Roshan?
Solution. Given, Ravi walks 6 km in an hour
i.e. distance covered by Ravi in one hour = 6 km
and Roshan walks 4 km in an hour
i.e. distance covered by Roshan in one hour = 4 km
∴ Ratio of the distance covered by Ravi to the distance covered by Roshan
\(=\frac{\text { Distance covered by Ravi in one hour }}{\text { Distance covered by Roshan in one hour }}=\frac{6}{4}=\frac{3}{2}=3: 2\)Hence, the required ratio is 3 : 2.
Mp Board Maths Chapter 12 Solutions
Question 3. Saurabh takes 15 min to reach school from his house and Sachin takes one hour to reach school from his house. Find the ratio of the time taken by Saurabh to the time taken by Sachin.
Solution. Here, time taken by Saurabh is in minutes and time taken by Sachin is in hours. So, we have to convert time taken by both into the same unit.
∴ Time taken by Sachin = 1 h = 1 x 60 min = 60 min
[∴ 1 h = 60 min]
and time taken by Saurabh = 15 min
∴ Ratio of the time taken by Saurabh to the time taken by Sachin
\(=\frac{\text { Time taken by Saurabh }}{\text { Time taken by Sachin }}=\frac{15}{60}=\frac{15 \div 15}{60 \div 15}\)[∴ HCF of 15 and 60 = 15]
= \(\frac{1}{4}\) = 1 : 4
Hence, the required ratio is 1:4.
Question 4. Cost of a toffee is 50 paise and cost of a chocolate is ₹ 10. Find the ratio of the cost of a toffee to the cost of a chocolate.
Solution. Here, cost of a toffee and a chocolate are not in the same unit. So, we have to convert both into the same unit.
∴ Cost of a toffee = 50 paise
and cost of a chocolate = ₹ 10 = 10 x 100 paise
= 1000 paise [∴ ₹ 1 = 100 paise]
∴ Ratio of the cost of a toffee to the cost of a chocolate
\(=\frac{\text { Cost of a toffee }}{\text { Cost of a chocolate }}=\frac{50}{1000}=\frac{50 \div 50}{1000 \div 50}\)[∴ HCF of 50 and 1000 = 50]
= \(\frac{1}{20}\) = 1 : 20
Hence, the required ratio is 1 : 20.
Question 5. In a school, there were 73 holidays in one year. What is the ratio of the number of holidays to the number of days in one year?
Solution. Given, number of holidays in one year = 73
We know that number of days in one year = 365
∴ Ratio of the number of holidays to the number of days in one year
\(=\frac{\text { Number of holidays }}{\text { Total number of days }}=\frac{73}{365}=\frac{73 \div 73}{365 \div 73}\)[∴ HCF of 73 and 365 = 73]
= \(\frac{1}{5}\) = 1 : 5
Hence, the required ratio is 1 : 5.
Chapter 12 Ratio And Proportion Exercise 12.1
Question 1. There are 20 girls and 15 boys in a class.
(1) What is the ratio of number of girls to the number of boys?
(2) What is the ratio of number of girls to the total number of students in the class?
Solution. Given, number of girls = 20 and number of boys = 15
∴ Total number of students in the class = 20 + 15 = 35
(1) Ratio of the number of girls to the number of boys
\(=\frac{\text { Number of girls }}{\text { Number of boys }}=\frac{20}{15}=\frac{20+5}{15+5}=\frac{4}{3}=4: 3\)(2) Ratio of the number of girls to the total number of students in the class
\(=\frac{\text { Number of girls }}{\text { Total number of students }}=\frac{20}{35}\)= \(\frac{20+5}{35 \div 5}=\frac{4}{7}=4: 7\)
Question 2. Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of
(1) number of students liking football to the number of students liking tennis.
(2) number of students liking cricket to total number of students.
Solution. Given, the total number of students in a class = 30
Number of students who like football = 6
Number of students who like cricket = 12
Then, the number of students who like tennis
= Total number of students – (Number of students who like football + Number of students who like cricket)
= 30 – (6 + 12) = 30 – 18 = 12
(1) Ratio of the number of students liking football to the number of students liking tennis
\(=\frac{\text { Number of students who like football }}{\text { Number of students who like tennis }}\)= \(\frac{6}{12}=\frac{6 \div 6}{12 \div 6}=\frac{1}{2}=1: 2\)
(2) Ratio of the number of students liking cricket to the total number of students
\(=\frac{\text { Number of students who like cricket }}{\text { Total number of students }}\) \(=\frac{12}{30}=\frac{12 \div 6}{30 \div 6}=\frac{2}{5}\)MP Board Class 6 Chapter 12 Maths
Question 3. See the figure and find the ratio of
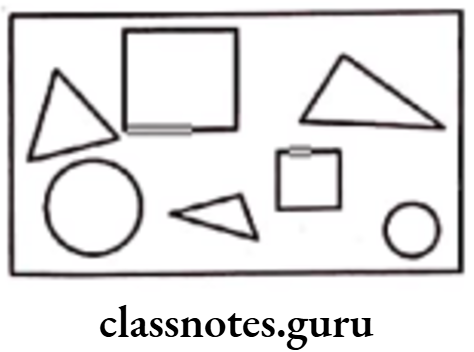
(1) number of triangles to the number of circles inside the rectangle.
(2) number of squares to all the figures inside the rectangle.
(3) number of circles to all the figures inside the rectangle.
Solution. In the given figure,
Number of triangles = 3; Number of squares = 2; Number of circles = 2
∴ Total number of shapes = 3 + 2 + 2 = 7
(1) Required ratio of the number of triangles to the number of circles
\(=\frac{\text { Number of triangles }}{\text { Number of circles }}=\frac{3}{2}=3: 2\)(2) Required ratio of the number of squares to all the shapes
\(=\frac{\text { Number of squares }}{\text { Total number of shapes }}=\frac{2}{7}=2: 7\)(3) Required ratio of the number of circles to all the shapes
\(=\frac{\text { Number of circles }}{\text { Total number of shapes }}=\frac{2}{7}=2: 7\)Question 4. Distances travelled by Hamid and Akhtar in an hour are 9 km and 12 km, respectively. Find the ratio of speed of Hamid to the speed of Akhtar.
Solution. Given, distance travelled by Hamid in one hour = 9 km
∴ Speed of Hamid = \(\frac{\text { Distance }}{\text { Time }}=\frac{9}{1}=9 \mathrm{~km} / \mathrm{h}\)
and distance travelled by Akhtar in one hour = 12 km
∴ Speed of Akhtar = \(\frac{12}{1}\) = 12 km/h
∴ Ratio of the speed of Hamid to the speed of Akhtar \(=\frac{\text { Speed of Hamid }}{\text { Speed of Akhtar }}=\frac{9}{12}=\frac{9 \div 3}{12 \div 3}=\frac{3}{4}=3: 4\)
Mp Board Class 6 Book Solutions
Question 5. Find the ratio of the following.
(1) 81 to 108
Solution.
(1) Required ratio = \(\frac{81}{108}=\frac{81+27}{108+27}=\frac{3}{4}=3: 4\)
Question 6. Find the ratio of the following.
(1) 30 min to 1.5 h
(2) 40 cm to 1.5 m
(3) 55 paise to 1
(4) 500 mL to 2 L
Solution. (1) Here, we have to convert 1.5 h into min.
We know that 1 h = 60 min
∴ 1.5 h = 1.5 x 60 min = 90 min
∴ Required ratio = \(\frac{30}{90}=\frac{30 \div 30}{90 \div 30}=\frac{1}{3}=1: 3\)
(2) Here, we have to convert 1.5 m into cm.
We know that 1 m = 100 cm
∴ 1.5 m = 1.5 x 100 cm = 150 cm
∴ Required ratio = \(\frac{40}{150}=\frac{40 \div 10}{150+10}=\frac{4}{15}=4: 15\)
(3) Here, we have to convert ₹ 1 into paise.
We know that ₹ 1 = 100 paise
∴ Required ratio = \(\frac{55}{100}=\frac{55 \div 5}{100 \div 5}=\frac{11}{20}=11: 20\)
(4) Here, we have to convert L into mL.
We know that 1 L = 1000 mL
∴ 2 L = 2 x 1000 mL = 2000 mL
∴ Required ratio = \(\frac{500}{2000}=\frac{5}{20}=\frac{1}{4}=1: 4\)
Question 7. In a year, Seema earns ₹ 150000 and saves ₹ 50000. Find the ratio of
(1) money that Seema earns to the money she saves.
(2) money that she saves to the money she spends.
Solution. Given, money earned by Seema = ₹ 150000
and money saved by Seema = ₹ 50000
(1) Required ratio \(=\frac{\text { Money earned by Seema }}{\text { Money saved by Seema }}\)
= \(\frac{150000}{50000}=\frac{15000+50000}{50000+50000}=\frac{3}{1}=3: 1\)
(2) ∴ Moeny spend by Seema = Earned money = Saved money
= (150000 – 50000) = ₹ 100000
∴ Required ratio \(=\frac{\text { Money saved by Seema }}{\text { Money spend by Seema }}\)
= \(\frac{50000}{100000}=\frac{50000 \div 50000}{100000 \div 50000}\)
= \(\frac{1}{2}\) = 1 : 2
Question 8. There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students.
Solution. Given, number of teachers = 102
and number of students = 3300
∴ Required ratio of the number of teachers to the number of students
\(=\frac{\text { Number of teachers }}{\text { Number of students }}\)= \(\frac{102}{3300}=\frac{102 \div 6}{3300 \div 6}\) [∴ HCF of 102 and 3300 is 6]
= \(\frac{17}{550}\) = 17 : 550
Mp Board Class 6 Book Solutions
Question 9. In a college, out of 4320 students, 2300 are girls.
Solution. Given, number of girls = 2300
and total number of students = 4320
∴ Number of boys = Total number of students – Number of girls
= 4320 – 2300 = 2020
Question 10. Out of 1800 students in a school, 750 opted basketball, 800 opted cricket and remaining opted table tennis. If a student can opt only one game, find the ratio of
Solution. Given, total number of students = 1800
Number of students who opted basketball = 750
Number of students who opted cricket = 800
∴ Number of students who opted table tennis = Total number of students – (number of students who opted basket ball + number of students who opted cricket)
= 1800 – (150 + 800)
= 1800 – 1550 = 250
Question 11. Cost of a dozen pens is ₹ 180 and cost of 8 ball pens is ₹ 56. Find the ratio of the cost of a pen to the cost of a ball pen.
Solution. Given, cost of 12 pens = 180
∴ Cost of 1 pen \(=\frac{\text { Total cost of pens }}{\text { Number of pens }}\)
= \(\frac{180}{12}\) = ₹ 15
Also given, cost of 8 ball pens = ₹ 56 [∴ 1 dozen = 12 units]
∴ Cost of 1 ball pen \(=\frac{\text { Total cost of ball pens }}{\text { Number of ball pens }}=\frac{56}{8}=₹ 7\)
Hence, the required ratio \(=\frac{\text { Cost of } 1 \text { pen }}{\text { Cost of } 1 \text { ball pen }}\)
= \(\frac{15}{7}\) = 15 : 7
Question 12. Consider the statement: Ratio of breadth and length of a hall is 2:5. Complete the following table that shows some possible breadths and lengths of the hall.

Solution. Given, ratio of breadth and length of a hall = 2 : 5
Also given, breadth of the hall = 10
and length of the hall = 25
Then, the ratio of breadth and length = \(\frac{10}{25}=\frac{2}{5}=2: 5\)
Now, for finding first missing number, we have
25 x 2 = 50
i.e. when we multiply 25 by 2, we get 50.
So, to get first missing term, we multiply 10 by 2.
∴ 10 × 2 = 20
Hence, the second breadth of the hall = 20
and length of the hall = 50
For finding second missing number, we have
40 = 10 x 4
i.e. when we multiply 10 by 4, we get 40.
So, to get second missing term, we multiply 25 by 4.
∴ 25 x 4 = 100
Hence, third breadth of hall = 40 and length = 100
Thus, the complete table is

Class 6 Mp Board Maths Question Answers
Question 13. Divide 20 pens between Sheela and Sangeeta in the ratio of 3: 2.
Solution. Given, ratio is 3: 2, whose two parts are 3 and 2.
∴ Sum of two parts = 3 + 2 = 5
This means, if there are 5 pens, Sheela gets 3 pens and Sangeeta gets 2 pens.
We can say that Sheela gets 3 parts and Sangeeta gets 2 parts out of every 5 parts.
Now, total number of pens = 20
∴ Number of pens for Sheela = \(\frac{3}{5}\) x 20 = 12
and number of pens for Sangeeta = \(\frac{2}{5}\) x 20 = 8
Hence, out of 20 pens Sheela gets 12 pens and Sangeeta gets 8 pens.
Question 14. Mother wants to divide ₹ 36 between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya is 15 yr and age of Bhoomika is 12 yr find how much Shreya and Bhoomika will get.
Solution. Given, Shreya’s age = 15 yr
and Bhoomika’s age = 12 yr
∴ Ratio of their ages \(=\frac{\text { Shreya’s age }}{\text { Bhoomika’s age }}\)
= \(\frac{15}{12}=\frac{15+3}{12+3}=\frac{5}{4}=5: 4\)
Now, mother wants to divide 36 between her daughters in the ratio of their ages.
∴ Sum of the parts of ratios = 5 + 4 = 9
Amount which has to be divided = ₹ 36
Here, we can say that Shreya gets 5 parts and Bhoomika gets 4 parts out of every 9 parts.
∴ Shreya’s share = \(\frac{5}{9}\) x 36 = ₹ 20
and Bhoomika’s share = \(\frac{4}{9}\) x 36 = ₹ 16
Hence, Shreya gets ₹ 20 and Bhoomika gets ₹ 16.
Question 15. Present age of father is 42 yr and that of his son is 14 yr. Find the ratio of
(1) present age of father to the present age of son.
(2) age of the father to the age of son, when son was 12 yr old.
(3) age of father after 10 yr to the age of son after 10 yr.
(4) age of father to the age of son when father was 30 yr old.
Solution. Given, present age of father = 42 yr
and present age of son = 14 yr
(1) Required ratio \(=\frac{\text { Present age of father }}{\text { Present age of son }}\)
= \(\frac{42}{14}=\frac{42+14}{14 \div 14}=\frac{3}{1}=3: 1\)
(2) When son’s age was 12 yr i.e. 2 yr back (because son’s present age is 14 yr).
Then, father’s age = (42 – 2) = 40 yr
∴ Required ratio \(=\frac{2 \mathrm{yr} \text { back father’s age }}{2 \mathrm{yr} \text { back son’s age }}=\frac{40}{12}=\frac{40 \div 4}{12 \div 4}\)
[∴ HCF of 40 and 12 is 4]
= \(\frac{10}{3}\)
(3) After 10 yr, father and son’s age will be (42 + 10) yr and (14 + 10) yr respectively i.e. 52 yr and 24 yr.
∴ Required ratio \(=\frac{\text { After } 10 \mathrm{yr} \text { father’s age }}{\text { After } 10 \mathrm{yr} \text { son’s age }}\)
= \(\frac{52}{24}=\frac{52 \div 4}{24 \div 4}\)
[∴ HCF of 52 and 24 is 4]
= \(\frac{13}{6}\) = 13 : 6
(4) When father’s age was 30 yr i.e. 12 yr back (because father’s present age is 42 yr and (42 – 12) = 30 yr.
Then, son’s age (14 – 12) = 2 yr
∴ Required ratio \(=\frac{12 \mathrm{yr} \text { back father’s age }}{12 \mathrm{yr} \text { back son’s age }}\)
= \(\frac{30}{2}=\frac{30+2}{2+2}=\frac{15}{1}=15: 1\)
Question 16. 1 : 5 and 3 : 15
Solution. We have, 1 : 5 and 3 : 15
Here, \(3: 15=\frac{3}{15}=\frac{3 \div 3}{15+3}=\frac{1}{5}=1: 5\)
i.e. 1 : 5 and 3 : 15 are in proportion.
Thus, the proper form is 1 : 5 :: 3 : 15.
Question 17. 2 : 9 and 18 : 81
Solution. We have, 2 : 9 and 18 : 81
Here, \(18: 81=\frac{18}{81}=\frac{18 \div 9}{81 \div 9}\)
[∴ HCF of 18 and 81 is 9]
= \(\frac{2}{9}\) = 2 : 9
i.e. 2 : 9 and 18 : 81 are in proportion.
Thus, the proper form is 2 : 9 :: 18 : 81.
Question 18. 15 : 45 and 5 : 25
Solution. We have, 15 : 45 and 5 : 25
Here, \(15: 45=\frac{15}{45}=\frac{15 \div 15}{45 \div 15}=\frac{1}{3}=1: 3\)
and \(5: 25=\frac{5}{25}=\frac{5 \div 5}{25 \div 5}=\frac{1}{5}=1: 5\)
Here, 15 : 45 ≠ 5 : 25
Thus, 15 : 45 and 5 : 25 are not in proportion.
Class 6 Mp Board Maths Question Answers
Question 19. 4 : 12 and 9 : 27
Solution. We have, 4 : 12 and 9 : 27
Here, \(4: 12=\frac{4}{12}=\frac{4 \div 4}{12 \div 4}=\frac{1}{3}=1: 3\)
Now, \(9: 27=\frac{9}{27}=\frac{9 \div 9}{27 \div 9}=\frac{1}{3}=1: 3\)
Hence, 4 : 12 = 9 : 27 = 1 : 3 i.e. 4 : 12 and 9 : 27 are in proportion.
Thus, the proper form is 4 : 12 :: 9 : 27.
Question 20. ₹ 10 to ₹ 15 and 4 to 6
Solution. We have, ₹ 10 : ₹ 15 = 10 : 15 and 4 : 6
Now, \(10: 15=\frac{10}{15}=\frac{10 \div 5}{15 \div 5}=\frac{2}{3}=2: 3\)
and \(4: 6=\frac{4}{6}=\frac{4+2}{6+2}=\frac{2}{3}=2: 3\)
Here, 10 : 15 = 4 : 6 = 2 : 3 i.e. 10 : 15 and 4 : 6 are in proportion.
Thus, the proper form is 10 : 15 :: 4 : 6.
Chapter 12 Ratio And Proportion Exercise 12.2
Question 1. Determine, if the following are in proportion.
(1) 15, 45, 40, 120
(2) 33, 121, 9, 96
Solution. (1) We have, 15, 45, 40, 120
∴ Ratio of 15 to 45 = \(\frac{15}{45}=\frac{15 \div 15}{45 \div 15}=\frac{1}{3}=1: 3\)
[∴ HCF of 15 and 45 = 15]
and ratio of 40 to 120 = \(\frac{40}{120}=\frac{40 \div 40}{120 \div 40}=\frac{1}{3}=1: 3\)
[∴ HCF of 40 and 120 = 40]
Here, 15 : 45 = 40 : 120 = 1 : 3
Therefore, 15, 45, 40 and 120 are in proportion.
(2) We have 33, 121, 9, 96
∴ Ratio of 33 to 121 = \(\frac{33}{121}=\frac{33 \div 11}{121 \div 11}=\frac{3}{11}=3: 11\)
and ratio of 9 to 96 = \(\frac{9}{96}=\frac{9 \div 3}{96 \div 3}=\frac{3}{32}=3: 32\)
[∴ HCF of 9 and 96 = 3]
Here, 3 : 11 ≠ 3 : 32 i.e. 33 : 121 ≠ 9 : 96
Therefore, 33, 121, 9 and 96 are not in proportion.
Question 2. Write True (T) or False (F) against each of the following statements:
(1) 16 : 24 : 20 : 30
Solution. (1) We have, 16 : 24 :: 20 : 30
∴ Ratio of 16 to 24 = \(\frac{16}{24}=\frac{16+8}{24+8}=\frac{2}{3}=2: 3\)
and ratio of 20 to 30 = \(\frac{20}{30}=\frac{20+10}{30+10}=\frac{2}{3}=2: 3\)
Here, 16 : 24 = 20 : 30 = 2 : 3,
So, 16 : 24 :: 20 : 30
Hence, given statement is true.
Class 6 Mp Board Maths Question Answers
Question 3. Are the following statements true?
(1) 40 persons: 200 persons = ₹ 15 : ₹ 75
Solution. (1) 40 persons : 200 persons
= \(\frac{40}{200}=\frac{40 \div 10}{200 \div 10}=\frac{4}{20}=\frac{1}{5}=1: 5\)
and \(\text { ₹ } 15: ₹ 75=\frac{15}{75}=\frac{15 \div 15}{75 \div 15}=\frac{1}{5}=1: 5\)
Question 4. Determine, if the following ratios form a proportion. Also, write the middle term and extreme terms, where the ratios form a proportion.
(1) 25 cm : 1 m and ₹ 40 : ₹ 160
(2) 39 L : 65 L and 6 bottles : 10 bottles
(3) 2 kg : 80 kg and 25 g : 625 g
(4) 200 mL : 2.5 L and ₹ 4 : ₹ 50
Solution. (1) Here, 25 cm : 1 m = 25 cm : 1 x 100 cm
[∴ 1 m = 100 cm]
= \(25: 100=\frac{25}{100}=\frac{25 \div 25}{100 \div 25}=\frac{1}{4}=1: 4\)
and \(₹ 40: ₹ 160=40: 160=\frac{40}{160}=\frac{1}{4}=1: 4\)
Here, 1 : 4 = 1 : 4 i.e. 25 cm : 1 m = ₹ 40 : ₹ 160
So, the ratios of 25 cm : 1 m and ₹ 40 : ₹ 160 are in proportion.
i.e. 25 cm : 1m :: ₹ 40 : ₹ 160
Now, middle terms are 1 m and 40 and extreme terms are 25 cm and 160.
(2) Here, \(39 L : 65 L = 39: 65=\frac{39}{65}=\frac{39+13}{65+13}=\frac{3}{5}=3: 5\)
and 6 bottles: 10 bottles 6 : 10 = \(\frac{6}{10}\)
= \(\frac{6+2}{10+2}=\frac{3}{5}=3: 5\)
Here, 3 : 5 = 3 : 5 i.e. 39 L : 65 L
= 6 bottles : 10 bottles.
So, the ratio of 39 L: 65 L and 6 bottles : 10 bottles are in proportion
i.e. 39 L : 65 L :: 6 bottles : 10 bottles
Hence, middle terms of ratios are 65 L and 6 bottles and extreme terms of ratios are 39 L and 10 bottles
(3) Here, \(2 \mathrm{~kg}: 80 \mathrm{~kg}=2: 80=\frac{2}{80}=\frac{2 \div 2}{80 \div 2}=\frac{1}{40}=1: 40\)
and \(25 \mathrm{~g}: 625 \mathrm{~g}=25: 625=\frac{25}{625}=\frac{25 \div 25}{625 \div 25}=\frac{1}{25}=1: 25\)
Since, both ratios are not equal.
∴ 2 kg : 80 kg ≠ 25 g : 625 g
Hence, the given ratios are not in proportion.
(4) Here, \(200 \mathrm{~mL}: 2.5 \mathrm{~L}=200 \times \frac{1}{1000} \mathrm{~L}: 2.5 \mathrm{~L}\)
[∴ 1 mL = \(\frac{1}{1000}\) L]
= \(\frac{200}{1000} \mathrm{~L}: 2.5 \mathrm{~L}=0.200 \mathrm{~L}: 2.5 \mathrm{~L}\)
= \(0.200: 2.5=\frac{0.200}{2.5}=\frac{2}{25}=2: 25\)
and \(₹ 4: ₹ 50=4: 50=\frac{4}{50}=\frac{4 \div 2}{50 \div 2}=\frac{2}{25}=2: 25\)
Here, 2 : 25 = 2 : 25 i.e. 200 mL : 2.5 L = ₹ 4 : ₹ 50
So, the ratios of 200 mL : 2.5 L and ₹ 4 : ₹ 50 are in proportion.
i.e. 200 mL : 2.5 L :: ₹ 4 : ₹ 50
Hence, middle terms of ratios are 2.5 L and ₹ 4 and extreme terms of ratios are 200 mL and ₹ 50.
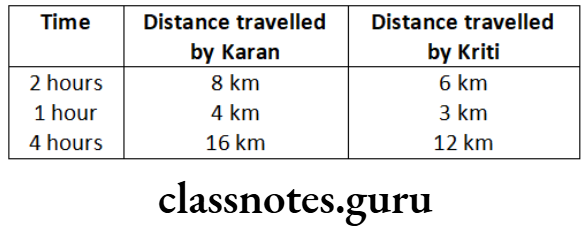
Question 5. Read the table and fill in the boxes.

Solution. From the above table,
Distance travelled by Kriti in 2 h = 6 km
∴ Distance travelled by Kriti in 1 h = \(\frac{6}{2}\) = 3 km
Now, distance travelled by Kriti in 4 h = 3 x 4 = 12 km
Also, distance travelled by Karan in 1 h = 4 km
∴ Distance travelled by Karan in 4 h = 4 x 4 = 16 km
On completing the boxes, we get the following table:
Chapter 12 Ratio And Proportion Exercise 12.3
Question 1. If the cost of 7 m of cloth is ₹ 1470, find the cost of 5 m of cloth.
Solution. Given, cost of 7 m of cloth = 1470
∴ Cost of 1 m of cloth = \(\frac{1470}{7}=₹ 210\)
∴ Cost of 5 m of cloth = 210 x 5 = ₹ 1050
Hence, the cost of 5 m of cloth is ₹ 1050.
Mp Board Class 6 Maths Solutions
Question 2. Ekta earns ₹ 3000 in 10 days. How much will she earn in 30 days?
Solution. Here, the number of days is known and money earns is unknown.
Given, Ekta earns in 10 days = ₹ 3000
∴ Ekta earns in 1 day = \(\frac{3000}{10}=₹ 300\)
∴ Ekta earns in 30 days = 300 x 30 = 9000
Hence, Ekta earns 9000 in 30 days.
Question 3. If it has rained 276 mm in the last 3 days, how many centimetre of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.
Solution. Here, the number of days is known and rain fall is unknown.
Given, rainfall in 3 days = 276 mm
∴ Rainfall in 1 day. = \(\frac{276}{3}\) = 92 mm
∴ Rainfall in one full week i.e. 7 days = 92 x 7 = 644 mm
In centimetre, rainfall in one full week
= \(644 \times \frac{1}{10} \mathrm{~cm}=64.4 \mathrm{~cm}\) [∴ 1 mm = \(\frac{1}{10}\) cm]
Hence, 64.4 cm rain will fall in 7 days or in one full week.
Question 4. Cost of 5 kg of wheat is ₹ 91.50.
(1) What will be the cost of 8 kg of wheat?
(2) What quantity of wheat can be purchased in ₹ 183?
Solution. (1) Here, the quantity of wheat is known and cost is unknown.
Given, cost of 5 kg of wheat = ₹ 91.50
∴ Cost of 1 kg of wheat = \(\frac{91.50}{5}=₹ 18.3\)
∴ Cost of 8 kg of wheat = 18.30 x 8 = ₹ 146.40
Hence, the cost of 8 kg of wheat is ₹ 146.40.
(2) Here, the cost of wheat is known and quantity of wheat is unknown.
Given, in ₹ 91.50 quantity of wheat that can be purchased = 5 kg
∴ In ₹ 1, quantity of wheat that can be purchased
= \(\frac{5}{91.50}=\frac{5 \times 10}{915}=\frac{50}{915} \mathrm{~kg}\)
[multiplying numerator and denominator both by 10]
∴ In ₹ 183, quantity of wheat that can be purchased
= \(\frac{50}{915} \times 183=\frac{50}{5}=10 \mathrm{~kg}\)
Hence, 10 kg wheat can be purchased in ₹ 183.
Mp Board Class 6 Maths Solutions
Question 5. The temperature dropped 15 degree celsius in the last 30 days. If the rate of temperature drop remains the same, how many degrees will the temperature drop in the next ten days?
Solution. Given, in last 30 days, temperature drop = 15 degree
∴ In 1 day, temperature drop = \(\frac{15}{30}=\frac{15+15}{30 \div 15}=\frac{1}{2} \text { degree }\)
∴ In next 10 days, temperature drop
= \(\frac{1}{2} \times 10 \text { degree }=5 \text { degree }\)
Hence, temperature dropped 5 degree in the next 10 days.
Question 6. Shaina pays ₹ 15000 as rent for 3 months. How much does she has to pay for a whole year, if the rent per month remains same?
Solution. Given, rent paid for 3 months = ₹ 15000
∴ Rent paid for 1 month = \(\frac{15000}{3}=₹ 5000\)
∴ Rent paid for a whole year i.e. 12 months
= 5000 × 12 = ₹ 60000
Hence, she has to pay ₹ 60000 for a whole year.
Question 7. Cost of 4 dozens bananas is ₹ 180. How many bananas can be purchased for ₹ 90?
Solution. We know that, I dozen = 12 unit
Given, in ₹ 180, number of bananas that can be purchased = 4 dozen
= 4 x 12 = 48
[∴ 1 dozen = 12 unit]
∴ In ₹ 1, number of bananas that can be purchased
\(=\frac{48}{180}=\frac{48 \div 12}{180+12}=\frac{4}{15}\)∴ In ₹ 90, number of bananas that can be purchased
\(=\frac{4}{15} \times 90=4 \times 6=24\)Hence, 24 bananas can be purchased for ₹ 90.
Class 6 Maths Chapter 12 Solutions Mp Board
Question 8. The weight of 72 books is 9 kg. What is the weight of 40 such books?
Solution. Given, weight of 72 books = 9 kg
∴ Weight of 1 book = \(\frac{9}{72}\)
∴ Weight of 40 books = \(\frac{9}{72} \times 40=\frac{360}{72} \mathrm{~kg}=\frac{360 \div 72}{72 \div 72}=5 \mathrm{~kg}\)
Hence, the weight of 40 books is 5 kg.
Question 9. A truck requires 108 L of diesel for covering a distance of 594 km. How much diesel will be required by the truck to cover a distance of 1650 km?
Solution. Given, diesel required for 594 km = 108 L
∴ Diesel required for 1 km = \(\frac{108}{594}=\frac{108 \div 54}{594 \div 54}=\frac{2}{11} L\)
∴ Diesel required for 1650 km = \(\frac{2}{11} \times 1650=2 \times 150=300 \mathrm{~L}\)
Hence, 300 L diesel required by the truck to cover 1650 km.
Question 10. Raju purchases 10 pens for ₹ 150 and Manish buys 7 pens for ₹ 84. Can you say who got the pens cheaper?
Solution. For Raju, cost of 10 pens=150
∴ Cost of 1 pen = \(\frac{150}{10}\) = ₹ 15
For Manish, cost of 7 pens = ₹ 84
∴ Cost of 1 pen = \(\frac{84}{7}\) ₹ 12
Here, ₹ 12 < ₹ 15
Hence, Manish got the pens cheaper.
Question 11. Anish made 42 runs in 6 overs and Anup made 63 runs in 7 overs. Who made more runs per over?
Solution. Runs made by Anish in 6 overs = 42
∴ Runs made by Anish in 1 over = \(\frac{42}{6}\) = 7
Runs made by Anup in 7 overs = 63
∴ Runs made by Anup in 1 over = \(\frac{63}{7}\) = 9
∴ 9 > 7
Hence, Anup made more runs per over.
Chapter 12 Ratio And Proportion Multiple Choice Questions
Question 1. The ratio of 6 books to 30 books is
- 5 : 1
- 2 : 3
- 1 : 5
- 2 : 5
Answer. 3. 1 : 5
Question 2. The simplest form of the ratio 384 : 480 is
- 2 : 5
- 4 : 5
- 5 : 4
- 3 : 5
Answer. 2. 4 : 5
Question 3. In a box, the ratio of red marbles to blue marbles is 7:4. Which of the following could be the total number of marbles in the box?
- 18
- 19
- 21
- 22
Answer. 4. 22
Question 4. The ratio of the number of sides of a triangle to the number of edges of a cube is
- 4 : 1
- 1 : 4
- 1 : 3
- 2 : 3
Answer. 2. 1 : 4
Class 6 Maths Chapter 12 Solutions Mp Board
Question 5. Margarette works in a factory and earns ₹ 955 per month. She saves 185 per month from her earnings. Then, the ratio of her income to her expenditure is Competency Based Question
- 154 : 37
- 191 : 37
- 191 : 154
- 37 : 191
Answer. 3. 191 : 154
Question 6. Avinash works as a lecturer and earns ₹ 12000 per month. His wife who is a doctor earns ₹ 15000 per month. Then, the ratio of Avinash’s income to their total income is
- 4 : 9
- 9 : 4
- 4 : 5
- 5 : 4
Answer. 1. 4 : 9
Question 7. If a bus travels 160 km in 4 h and a train travels 320 km in 5 h at uniform speeds, then the ratio of the distances travelled by them in one hour is
- 1: 2
- 4: 5
- 5: 8
- 8: 5
Answer. 3. 5: 8
Question 8. A picture is 40 cm wide and 1.6 m long. The ratio of its width to its perimeter in lowest form is
- 1: 5
- 1: 10
- 2: 5
- 1: 8
Answer. 2. 1: 10
Question 9. Which of the following is the equivalent ratio of 7: 11?
- 14: 22
- 14: 121
- 21: 121
- 49: 66
Answer. 1. 14: 22
Question 10. The ratio of number of circles and number of squares inside the following rectangle is

- 12:11
- 10:9
- 11:10
- 13:11
Answer. 3. 11: 10
Class 6 Maths Chapter 12 Solutions Mp Board
Question 11. Mathematics textbook for Class VI has 320 pages. The chapter ‘Symmetry’ runs from page 261 to page 272. The ratio of the number of pages of this chapter to the total number of pages of the book is
- 11:320
- 3:40
- 3:80
- 272: 320
Answer. 3. 3: 80
Question 12. If 66: 72 : x: 96, then x is equal to
- 108
- 78
- 88
- 48
Answer. 3. 88
Question 13. If 7 : 30 :: x : 15, then the value of x is
- \(\frac{7}{2}\)
- \(\frac{2}{7}\)
- 6
- 7
Answer. 1. \(\frac{7}{2}\)
Question 14. Which of the following are in proportion?
- 1, 3, 11, 22
- 2, 5, 40, 80
- 3, 4, 15, 18
- 2, 3, 20, 30
Answer. 4. 2, 3, 30, 20
Question 15. In a school library, the ratio of Mathematics books to Science books is same as the ratio of Science books to Hindi books. If there are 450 books of Science and 300 books of Hindi, then the number of books of Mathematics is Competency Based Question (c) 300 (d) 450
- 720
- 675
- 300
- 450
Answer. 2. 675
Chapter 12 Ratio And Proportion Assertion Reason
Question 1. Assertion (A) The monthly salary of Hari-Kishan is ₹ 80000. The monthly salary of Manish is ₹ 40000.
Reason (R) Two quantities can be compared only if they are in the same unit.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
Question 2. Assertion (A) 1 : 2 is not equivalent to 10 : 5.
Reason (R) We can get equivalent ratios by multiplying or dividing the numerator and denominator by the same number.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (a) Both A and R are true and R is the correct explanation of A.
MP Board Class 6 Maths Solutions
Question 3. Assertion (A) 25 km : 60 km :: ₹ 15 : ₹ 17.
Reason (R) If two ratios are equal, we say that they are in proportion and use the symbol ‘::’ or ‘=’ to equate the two ratios.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (d) A is false but R is true.
Question 4. Assertion (A) 15 : 40 :: 10 : 30.
Reason (R) Proportion says that two ratios (or fractions) are equal.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Answer. (d) A is false but R is true.
Chapter 12 Ratio And Proportion Fill in the Blanks
Question 1. A ratio expressed in lowest form has no common factor other than ….. in its terms.
Answer. 1
Question 2. To find the ratio of two quantities, they must be expressed in ….. unit.
Answer. Same
Question 3. The cost of 4 pens is ₹ 40. The cost of 11 pens is …. .
Answer. 110
Question 4. Maya can walk 6 km in 2 h. In 3 h, she can walk …… .
Answer. 9 km
Question 5. Sleeping time of a python in a 24 h clock is represented by the unshaded portion in figure.
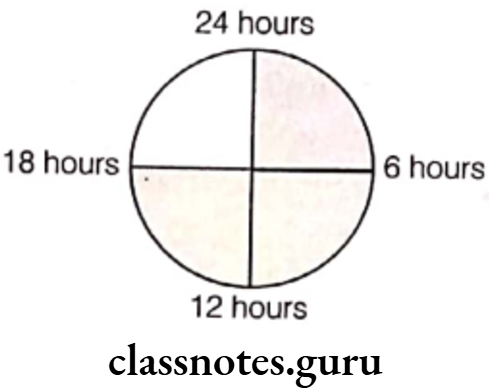
The ratio of sleeping time to the awaking time is …… .
Answer. 1 : 3
Chapter 12 Ratio And Proportion True/False
Question 1. 4 : 7 = 20 : 35
Answer. True
Question 2. 15 m : 40 m = 40 cm : 80 cm
Answer. False
Question 3. The ratio of 20 kg to 200 kg is 1 : 10.
Answer. True
MP Board Class 6 Maths Solutions
Question 4. The ratio 8 : 40 is in its lowest form.
Answer. False
Question 5. If 10 : 30 :: 40 : x, then the value of x is 120.
Answer. True
Chapter 12 Ratio And Proportion Case Based Questions
Question 1. Sam organised a party. He decorated his house and arranged food for guests. He spent ₹ 1600 on decoration and ₹ 8000 on food.
(1) What is the ratio of the money that Sam spent on decoration to the money spent on food?
(a) 1 : 4
(b) 1 : 5
(c) 1 : 6
(d) 5 : 1
(2) Same used paper ribbons to decorate the walls. He made a pattern using groups of four ribbons. Each group has one blue ribbon and the remaining are yellow. What is the ratio of blue ribbons to the total number of ribbons in each pattern?
(3) To decorate one wall, Sam used 18 blue ribbons. How many yellow ribbons were used on that wall?
(a) 3
(b) 6
(c) 36
(d) 54
(4) Sam purchased 40 blue ribbons.

He orders the ribbons shown below.
How many rupees will Sam pay for the 40 ribbons?
Solution. (1) (b) Sam spent the money on decoration = ₹ 1600 and the money he spent on food = 8000
∴ Ratio of money spent on decoration to
money spent on food = \(\frac{1600}{8000}=\frac{1600 \div 1600}{8000 \div 1600}\)
[HCF of 1600 and 8000 = 1600]
= \(\frac{1}{5}\) = 1 : 5
Thus, the ratio of the money spent on decoration to money spent on food is 1:5.
(2) Sam made pattern using four ribbons.
Number of blue ribbons = 1
Number of yellow ribbons = 3
Total number of ribbons = 1 + 3 = 4
∴ Ratio of blue ribbons to the total number of ribbons
\(=\frac{\text { Number of blue ribbons }}{\text { Number of total ribbons }}=\frac{1}{4}\)= 1 : 4
(3) (d) To decorate one wall Sam used 18 blue ribbons. From part (2), we have the ratio of Blue ribbon to yellow ribbon is 1:3.
If one blue ribbon is used, then 3 yellow ribbons will also used.
∴ We have, the number of blue ribbons = 18
∴ The number of yellow ribbons = 18 x 3 = 54
Thus, 54 yellow ribbons were used on the wall.
(4) Sam purchased 40 blue ribbons and 1 pack has 5 rolls with price of ₹ 25.
∴ Price of 5 rolls = ₹ 25
∴ Price of 1 roll of ribbon = \frac{25}{5} = ₹ 5
∴ Price of 40 rolls of ribbon = 5 x 40 = 200
Thus, Sam will pay 200 for 40 ribbons.
Mp Board Maths Chapter 12 Solutions
Question 2. Sam ordered 21 sausages. Of the 15 guests that came to the party, 6 guests had two sausages each, three guests had one sausage each and the remaining guests did not have any sausages.
(1) What is the ratio of the number of sausages left to the number of sausages had by the guests?
(a) 2 : 5
(b) 2 : 7
(c) 5 : 2
(d) 5 : 7
(2) One pack of 3 sausages cost ₹ 120. What is the cost of 21 sausages?
(a) ₹ 40
(b) ₹ 630
(c) ₹ 840
(d) ₹ 140
Solution. (1) (a) Total number of sausages = 21
Out of 15 guests, 6 guests had two sausages each i.e. 6 guests had the number of sausages = 6 x 2 = 12 sausage
and the number of sausages had by 3 guests = 3 x 1 = 3 sausages
Total number of sausages had by guests
= 12 + 3 = 15 sausages
Number of sausages left = 21 – 15 = 6 sausages
Now, ratio of the number of sausages left to the number of sausages had by guests
\(=\frac{\text { Number of sausages left }}{\text { Number of sausages had by guests }}\)= \(\frac{6}{15}=\frac{6 \div 3}{15 \div 3}=\frac{2}{5}=2: 5\)
Thus, the required ratio is 2:5.
(2) (c) Cost of 3 sausages = ₹ 120
Cost of 1 sausage = \(₹ \frac{120}{3}=₹ 40\)
∴ Cost of 21 sausages = 40 × 21 = 840
Thus, cost of 21 sausages is ₹ 840.
Chapter 12 Ratio And Proportion Very Short Answers Type Questions
Question 1. Write the following ratios in the simplest form.
(1) 600 g to 1 kg
(2) 2 cm to 4 m
Solution. (1) Ratio of 600 g to 1 kg = \(\frac{600}{1000}\) [∴ 1 kg = 1000 g]
= \(\frac{3}{5}\) = 3 : 5
(2) 2 cm to 4 m = \(\frac{2}{400}\) [∴ 1m = 100 cm]
Question 2. Give two equivalent ratios of 3 : 8.
Solution. \(3: 8=\frac{3}{8}=\frac{3 \times 2}{8 \times 2}=\frac{6}{16}, 3: 8=\frac{3}{8}=\frac{3 \times 3}{8 \times 3}=\frac{9}{24}\)
Hence, two equivalent ratios of 3 : 8 are 6 : 16 and 9 : 24.
Question 3. Find (1) the ratio of 70 cm to 1 m.
(2) the ratio of 50 paise to ₹ 2.
Solution. (1) We know that 1 m = 100 cm
∴ Required ratio = \(70: 100=\frac{70}{100}=7: 10\)
(2) We know that ₹ 1 = 100 paise
∴ Required ratio = \(\frac{50}{200}=\frac{1}{4}=1: 4\)
Question 4. If the cost of 10 bananas is ₹ 20. What will be the cost of 7 bananas?
Solution. Cost of 10 bananas = ₹ 20
Cost of 1 banana = \(\frac{20}{10}\) = ₹ 2
∴ Cost of 7 bananas = 7 x 2 = ₹ 14
Question 5. Determine whether the given ratios are equal.
30 : 45 and 60 : 100
Solution. We have, 30 : 45 = \(\frac{30}{45}\) = \(\frac{2}{3}\) = 2 : 3
and 60 : 100 = \(\frac{60}{100}\) = \(\frac{3}{5}\) = 3 : 5
So, the ratios 30 : 45 and 60 : 100 are not equal.
Question 6. The cost of 3 dozen pens is ₹ 72. What will be the cost of 7 bananas?
Solution. Cost of 3 dozen pens = ₹ 72
Cost of 1 dozen pens = \(\frac{72}{3}\) = ₹ 24
∴ Cost of 2 dozen pens 24 x 2 = ₹ 48
Question 7. Are the ratios 10 g : 40 g and 25 kg : 100 kg in proportion?
Solution. We have, 10 g : 40 g = \(\frac{10}{40}\) = 1 : 4
and 25 kg : 100 kg = \(\frac{25}{100}\) = 1 : 4
So, they are in proportion.
Mp Board Maths Chapter 12 Solutions
Question 8. Are 10, 15, 20 and 30 in proportion?
Solution. Ratio of 10 to 15 = \(\frac{10}{15}\) = 2 : 3
Ratio of 20 to 30 = \(\frac{20}{30}\) = 2 : 3
Since, 10:15 = 20:30
Hence, 10, 15, 20 and 30 are in proportion.
Question 9. If 15 : 10 :: x : 20, then find the value of x.
Solution. Given, 15 : 10 :: x : 20
⇒ \(\frac{15}{10}=\frac{x}{20}\)
⇒ 10x = 15 x 20
⇒ \(x=\frac{15 \times 20}{10}=30\)
Chapter 12 Ratio And Proportion Short Answer Type Questions
Question 1. Which pair of ratios are equal and why?
(1) \(\frac{2}{3}\), \(\frac{4}{6}\)
(2) \(\frac{8}{4}\), \(\frac{2}{1}\)
(3) \(\frac{4}{5}\), \(\frac{12}{20}\)
Solution. (1) \(\frac{2}{3}=2: 3 \text { and } \frac{4}{6}=2: 3\)
Hence, \(\frac{2}{3}\) and \(\frac{4}{6}\) are equal.
(2) \(\frac{8}{4}=2: 1 \text { and } \frac{2}{1}=2: 1\)
Hence, \(\frac{8}{4}\) and \(\frac{2}{1}\) are equal.
(3) \(\frac{4}{5}=4: 5 \text { and } \frac{12}{20}=\frac{3}{5}=3: 5\)
Hence, \(\frac{4}{5}\) and \(\frac{12}{20}\) are not equal.
Question 2. Reshma prepared 18 kg of burfi by mixing khoya with sugar in the ratio of 7 : 2. How much khoya did she use?
Solution. Quantity of burfi = 18 kg
Given, Khoya : Sugar = 7 : 2
Total = 7 + 2 = 9
Quantity of khoya = \(\frac{7}{9} \times 18=14 \mathrm{~kg}\)
So, Reshma used 14 kg khoya.
Question 3. A line segment 56 cm long is to be divided into two parts in the ratio 2 : 5. Find the length of each part.
Solution. Length of line segment = 56 cm
Ratio of two parts = 2 : 5
Sum of parts = 2 + 5 = 7
∴ Length of first part = \(\frac{2}{7} \times 56=16 \mathrm{~cm}\)
and length of second part = \(\frac{5}{7} \times 56=40 \mathrm{~cm}\)
Mp Board Class 6 Book Solutions
Question 4. Ram and Mohan ran in a race. Ram covered 210 m while during the same time Mohan covered only 180 m. What is the ratio of the distance covered by Mohan to that by Ram?
Solution. Distance covered by Ram = 210 m
Distance covered by Mohan = 180 m
∴ Required ratio = \(\frac{180}{210}=\frac{6}{7}=6: 7\)
Question 5. School starts at 7 : 00 am and gets over at 12 : 30 pm. If the break time is from 9 : 50 am to 10 : 10 am. What is the ratio of the break time to the total time the students spend at school?
Solution. School starts at 7:00 am and gets over at 12:30 pm.
Total time the student spend at shcool
= 5 h 30 min = (5 x 60 + 30) m = 330 min
Break time = 9:50 am to 10 : 10 am = 20 min
∴ Required ratio = \(\frac{20}{330}=2: 33\)
Question 6. There are two rectangles A and B. A has a length of 12 cm and breadth of 6 cm. B has a length of 11 cm and breadth of 9 cm. Find the ratio of their perimeter.
Solution. For Rectangle A,
Length 12 cm and breadth = 6 cm
Perimeter of Rectangle A = 2 x (length + breadth)
= 2 (12 + 6)
= 36 cm
For Rectangle B, Length = 11 cm and breadth = 9 cm
Perimeter of Rectangle B = 2 (11 + 9) = 40 cm
∴ Required ratio = \(\frac{36}{40}=\frac{9}{10}=9: 10\)
Question 7. Line segment AB = 10 cm is divided at C in the ratio 1 : 4, what are the lengths of \(\overline{A C} \text { and } \overline{B C} \text { ? }\)

Solution. Length of line segment AB = 10 cm
and AC : BC = 1 : 4
Sum of parts AC and BC = AC + BC = 1 + 4 = 5
∴ Length of \(\overline{A C}=\frac{1}{5} \times 10=2 \mathrm{~cm}\)
Length of \(\overline{B C}=\frac{4}{5} \times 10=8 \mathrm{~cm}\)
Class 6 Mp Board Maths Question Answers
Question 8. 17 bags of cement costs ₹ 1675.50. How many bags of cement can be bought for ₹ 1182?
Solution. In ₹ 1675.50, number of bags purchased = 17
In ₹ 1, number of bags purchased = \(\frac{17}{1675.50}\)
In ₹ 1182, number of bags purchased = \(\frac{17}{1675.50} \times 1182\)
= 12 (approx.)
Question 9. The sides of a triangle are in the ratio 2 : 3 : 5. If the total perimeter of the triangle is 70 cm, then find the length of the longest side.
Solution. Given, ratio of sides of triangle = 2 : 3 : 5
Total perimeter = 70
Total of the sides = 2 + 3 + 5 = 10
∴ Length of the longest side = \(70 \times \frac{5}{10}=35 \mathrm{~cm}\)
Chapter 12 Ratio And Proportion Long Answer Type Questions
Question 1. Samira sells newspapers at Janpath crossing daily. On a particular day, she had 312 newspapers out of which 216 are in English and remaining in Hindi. Find the ratio of
(1) the number of English newspapers to the number of Hindi newspapers.
(2) the number of Hindi newspapers to the total number of newspapers.
Solution. Total number of newspapers = 312
Number of english newspapers = 216
Hindi newspapers = Total number of newspapers – Number of English newspapers
= 312 – 216 = 96
(1) Ratio of the number of English newspapers to the
number of Hindi newspapers = 216 : 96 = \(\frac{216}{96}=\frac{9}{4}=9: 4\)
(2) Ratio of the number of Hindi newspapers to the
total number of newspapers = \(\frac{96}{312}=\frac{4}{13}=4: 13\)
Class 6 Mp Board Maths Question Answers
Question 2. In a club having 100 members, 20 play carrom, 24 play table tennis, 16 play badminton and the remaining do not play any game (no member plays more than one game). Find the ratio of
(1) the number of members who play carrom to the numbers of those, who play table tennis.
(2) the number of members who play badminton to the number of those, who play carrom.
(3) the number of members who play table tennis to the number of those, who play badminton.
(4) the number of members who play badminton to the number of those, who do not play any game.
Solution. Total number of members = 100
Number of members, who play carrom = 20
Number of members, who play table tennis = 24
Number of members, who play badminton = 16
Number of members, who do not play any game
= 100 – (20 + 24 + 16) = 100 – 60 = 40
(1) Ratio of members who play carrom to the members who play table tennis
= \(20: 24=\frac{20}{24}=5: 6\)
(2) Ratio of members who play badminton to the members who play of carrom
= \(16: 20=\frac{16}{20} \approx \frac{4}{5}=4: 5\)
(3) Ratio of members who play table tennis to the member who play, badminton
= \(24: 16=\frac{24}{16}=\frac{3}{2}=3: 2\)
(4) Ratio of members who play badminton to the number of members, who do not play any game
= \(16: 40=\frac{16}{40}=\frac{2}{5}=2: 5\)
Question 3. Length and breadth of the floor of a room are 5 m and 3 m, respectively. Forty tiles, each with area \(\frac{1}{16}\) m2 are used to cover the floor partially. Find the ratio of the tiled and the non-tiled portion of the floor.
Solution. Given, length of floor of a room = 5 m
and breadth of floor of a room = 3 m
Area of floor = 5 x 3 = 15 m2
Area of one tile = \(\frac{1}{16}\) m2
Area of forty tiles = \(40 \times \frac{1}{16}=\frac{5}{2} \mathrm{~m}^2\)
Tiled portion of the floor = \(\frac{5}{2}\) m2
Now, non-tiled portion of the floor = \(\left(15-\frac{5}{2}\right) \mathrm{m}^2\)
= \(\left(\frac{30-5}{2}\right)=\frac{25}{2} \mathrm{~m}^2\)
So, ratio of tiled to the non-tiled portion of the floor
= \(\frac{5}{2}: \frac{25}{2}=\frac{\frac{5}{2}}{\frac{25}{2}}=\frac{5}{25}=\frac{1}{5}=1: 5\)
Hence, the required ratio is 1 : 5.
Question 4. In a year, Ravi earns ₹ 360000 and paid ₹ 24000 as income tax. Find the ratio of his
(1) income to income tax.
(2) income tax to income after paying income tax.
Solution. Given, Ravi earns in a year = ₹ 360000
and Ravi paid income tax in a year = ₹ 24000
(1) Ratio of income to the income tax paid
= 360000 : 24000
= 360 : 24 [dividing by 1000 in both ratios]
= 15 : 1 [dividing by 24 in both ratios]
Hence, the ratio of income to income tax is 15 : 1.
(2) After paying income tax, remaining income
= Total income – Income tax
= 360000 – 24000
= ₹ 336000
∴ Ratio of income tax to income after paying income tax
= 24000 : 336000
= 24 : 336 [dividing by 1000 in both ratios]
= 1 : 14 [dividing by 24 in both ratios]
Hence, the ratio of income tax to income after paying income tax is 1 : 14.
Question 5. Ramesh earns ₹ 28000 per month. His wife Rama earns ₹ 36000 per month. Find the ratio of
(1) Ramesh’s earnings to their total earnings.
(2) Rama’s earnings to their total earnings.
Solution. Given, Ramesh earns per month = ₹ 28000
and Rama earns per month = ₹ 36000
∴ Total earnings = Ramesh’s earning per month + Rama’s earning per month
= ₹ (28000 + 36000) = ₹ 64000
(1) Ratio of Ramesh’s earnings to their total earnings
= Ramesh’s earnings : Total earnings
= 28000 : 64000
= 28 : 64 [dividing by 1000 in both ratios]
= 7 : 16 [dividing by 4 in both ratios]
Hence, the ratio of Ramesh’s earnings to their total earnings is 7: 16.
(2) Rama’s earnings to their total earnings
= Rama’s earnings : Total earnings
= 36000: 64000
= 36 : 64 [dividing by 1000 in both ratios]
= 9 : 16 [dividing by 4 in both ratios]
Hence, the ratio of Rama’s earnings to income their total earnings is 9 : 16.
Class 6 Mp Board Maths Question Answers
Question 6. A recipe calls for 1 cup of milk for every \(2 \frac{1}{2}\) cups of flour to make a cake that would feed 6 persons. How many cups of both flour and milk will be needed to make a similar cake for 8 people?
Solution. Given, milk needed for making cake = 1 cup
and flour needed for making cake = \(2 \frac{1}{2} \text { cups }=\frac{5}{2} \text { cups }\)
Then, the total amount needed Milk + Flour
= \(\left(1+\frac{5}{2}\right) \text { cups }=\frac{7}{2} \text { cups }\)
So, \(\frac{7}{2}\) cups of milk and flour needed to make cake for 6 persons.
Let the needed amount of cups of milk and flour to make cake for 8 persons = x
[where, x is a multiple of cups]
By ratio and proportion law, \(\frac{2}{6}\) = \(\frac{x}{8}\)
⇒ \(\frac{7}{2} \times 8=6 \times x\)
⇒ x = \(\frac{28}{6}\)
⇒ x = \(\frac{14}{3}\) [dividing by 2]
Hence, the cups needed for 8 persons is \(\frac{14}{3}\).
Question 7. A scooter travels 120 km in 3 h and a car travels 120 km in 2 h. Find the ratio of their speeds. [Hint \(\text { Speed }=\frac{\text { Distance travelled }}{\text { Time taken }}\)]
Solution. Given, distance travelled by a scooter = 120 km
Time taken by a scooter = 3h
∴ \(\text { Speed of scooter }=\frac{\text { Distance travelled }}{\text { Time taken }}=\frac{120 \mathrm{~km}}{3 \mathrm{~h}}\)
= 40 km/h
and distance travelled by car = 120 km
and time taken by a car = 2h
∴ \(\text { Speed of the car }=\frac{\text { Distance travelled }}{\text { Time taken }}\)
= \(\frac{120 \mathrm{~km}}{2 \mathrm{~h}}\)
= 60 km/h
= Speed of the scooter : Speed of the car
= 40:60 = 2:3 [dividing by 20 in both ratios]
Hence, the ratio of their speeds is 2: 3.
