MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Factors and Multiples
A factor of a number is an exact divisor of that number i.e. the factor divides the number completely without leaving any remainder.
e.g. 1, 2, 3 and 6 are exact divisors of 6. So, 1, 2, 3 and 6 are factors of 6.
A number is a multiple of each of its factor.
e.g. When 123 x 4, then we can say that 12 is a multiple of 3 and 4.
Diagram
Let us discuss some points about factors and multiples.
(1) I is a factor of every number.
(2) Every number is a factor of itself.
(3) Every factor is less than or equal to the given number.
(4) Number of factors of a given number are finite.
e.g. The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 and 96 which are finite.
(5) Every multiple of a number is greater than or equal to that number.
e.g. Multiples of 3 are 3, 6, 9, 12, 15, …
(6) The number of multiples of a given number is infinite.
e.g. Multiples of 4 are 4, 8, 12, 16, 20,…
(7) Every number is a multiple of itself.
e.g. 7 = 7 x 1 and 11 = 11 x 1
Read and Learn More MP Board Class 6 Maths Solutions
MP Board Class 6 Maths Solutions
Example 1. Write all the possible factors of the following numbers.
(1) 16
(2) 30
(3) 27
(4) 19
Solution. (1) Here, 16 = 1 x 16,16 = 2 x 8,16 = 4 x 4
∴ Factors of 16 are 1, 2, 4, 8 and 16.
(2) Here, 30 = 1 x 30, 30 = 2 x 15, 30 = 3 x 10, 30 = 5 x 6
∴ Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.
(3) Here, 27 = 1 x 27, 27 = 3 × 9
∴ Factors of 27 are 1, 3, 9 and 27.
(4) Here, 19 = 1 × 19
∴ Factors of 19 are 1 and 19.
Note that 0 is not the factor of any number.
Example 2. Write the first four multiples of the following numbers
(1) 5
(2) 12
(3) 13
Solution. (1) Multiples of 5 are
5 x 1 = 5,5 x 2 = 10,5 x 3 = 15,5 x 4 = 20
Hence, the first four multiples of 5 are 5, 10, 15 and 20.
(2) Multiples of 12 are
12 x 1 = 12,12 x 2 = 24,12 x 3 = 36,12 x 4 = 48
Hence, the first four multiples of 12 are 12, 24, 36 and 48.
(3) Multiples of 13 are
13 x 1 = 13, 13 x 2 = 26, 13 x 3 = 39,13 x 4 = 52
Hence, the first four multiples of 13 are 13, 26, 39 and 52.
Note It We can also write the table of required number to get the multiples of that number.
Example 3. Write all the multiples of
(1) 7 upto 90.
(2) 16 less than 150.
Solution. (1) The multiples of 7 upto 90 are
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
7 × 10 = 70
7 x 11 = 77
7 x 12 = 84
Hence, all the multiples of 7 upto 90 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77 and 84..
(2) The multiples of 16 less than 150 are
16 x 1 = 16
16 x 2 = 32
16 x 3 = 48
16 x 4 = 64
16 x 5 = 80
16 X 6 = 96
16 x 7 = 112
16 x 8 = 128
16 x 9 = 144
Hence, all the multiples of 16 less than 150 are 16, 32, 48, 64, 80, 96, 112, 128 and 144.
Class 6 Maths Chapter 3 Mp Board Solutions
Example 4. Write
(1) the sixth multiple of 19.
(2) the seventh multiple of 23.
Solution. (1) Multiples of 19 are
19, 38, 57, 76, 95, 114, 133, ….
Hence, the sixth multiple of 19 is 114.
(2) Multiples of 23 are
23, 46, 69, 92, 115, 138, 161, 184, 207, 230,….
Hence, the seventh multiple of 23 is 161.
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Prime and Composite Numbers
To understand prime and composite numbers, first of all, we have to study about even and odd numbers.
Even Numbers
The numbers which are multiples of 2 are called even numbers. e.g. 2, 4, 6, …, etc. are even numbers.
Odd Numbers
The numbers which are not completely divided by 2 are known as odd numbers. e.g. 1, 3, 5, 7,…, etc. are odd numbers.
Note It A positive integer equal to the sum of its factors. excluding the number itself is said to be a perfect number. The numbers 6, 28,496 and 8128 are perfect numbers.
Example 1. Write the odd and even numbers between the following numbers
(1) 11 and 23
(2) 101 and 115
Solution.
(1) The odd numbers between 11 and 23 are 13, 15, 17, 19 and 21 and the even numbers between 11 and 23 are 12, 14, 16, 18, 20 and 22.
(2) The odd numbers between 101 and 115 are 103, 105, 107, 109, 111 and 113 and the even numbers between 101 and 115 are 102, 104, 106, 108, 110, 112 and 114.
Class 6 Maths Chapter 3 Mp Board Solutions
Example 2. Show that sum of any two odd or any two even numbers is an even number.
Solution. Let the two odd numbers be 7 and 9.
Their sum = 7 + 9 = 16 (even number)
Hence, the sum of any two odd numbers is an even number.
Again, let the two even numbers be 10 and 12.
Their sum = 10 + 12 = 22 (even number)
Hence, the sum of any two odd or even numbers is an even number.
Note it The sum of any two odd numbers or any two even numbers is always an even number.
Example 3. Write the odd and even multiples of
(1) 9 less than 120
(2) 13 upto 140
Solution. (1) Multiples of 9 less than 120 are
9 x 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 x 5 = 45
9 × 6 = 54
9 x 7 = 63
9 × 8 = 72
9 x 9 = 81
9 × 10 = 90
9 x 11 = 99
9 × 12 = 108
9 × 13 = 117
∴ The odd multiples of 9 less than 120 are 9, 27, 45, 63, 81, 99, 117 and the even multiples of 9 less than 120 are 18, 36, 54, 72, 90, 108.
(2) Multiples of 13 upto 140 are
13 x 1 = 13
13 x 2 = 26
13 × 3 = 39
13 x 4 = 52
13 x 5 = 65
13 × 6 = 78
13 x 7 = 91
13 x 8 = 104
13 x 9 = 117
13 x 10 = 130
∴ The odd multiples of 13 upto 140 are 13, 39, 65, 91, 117 and the even multiples of 13 upto 140 are 26, 52, 78, 104, 130.
Prime Numbers
The numbers other than 1, whose only factors are 1 and the number itself are called prime numbers.
e.g. 2, 3, 5, 7, 11,…, etc. are prime numbers.
2 is the smallest prime number which is even and every prime number except 2 is odd.
Two prime numbers whose difference is 2 are called twin prime numbers.
Method of Finding Prime Numbers
Step 1 List all numbers from 1 to 100.
Step 2 Cross out 1 because it is not a prime number.
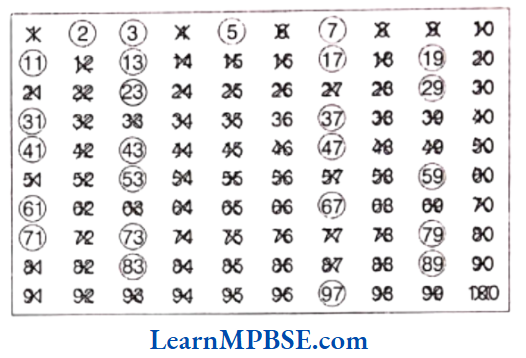
Step 3 Encircle 2, cross out all the multiples of 2, other than 2 itself i.e. 4, 6, 8 and so on.
Step 4 You will find that the next uncrossed number is 3. Encircle 3 and cross out all the multiples of 3, other than 3 itself.
Step 5 The next uncrossed number is 5. Encircle 5 and cross out all the multiples of 5, other than 5 itself.
Step 6 Continue this process till all the numbers in the list are either encircled or crossed out.
All the encircled numbers are prime numbers.
All the crossed out numbers, other than 1 are composite numbers.
This method is called the Sieve of Eratosthenes which is invented by Greek mathematician Eratosthenes.
Example 4. Check whether the following number are prime or not?
(1) 17
(2) 39
(3) 41
(4) 56
Solution.
(1) 17 = 1 x 17, 17 = 17 x 1
Since, 17 has only two factors i.e. 1 and 17.
Therefore, 17 is a prime number.
(2) 39 = 1 x 39, 39 = 3 x 13
Since, 39 has four factors i.e. 1, 3, 13 and 39.
Therefore, 39 is not a prime number.
(3) 41 = 1 x 41, 41 = 41 x 1
Since, 41 has only two factors i.e. 1 and 41. Therefore, 41 is a prime number.
(4) 56 = 1 x 56, 56 = 2 x 28, 56 = 4 x 14, 56 = 7 x 8
Since, 56 has eight factors i.e. 1, 2, 4, 7, 8, 14, 28 and 56.
Therefore, 56 is not a prime number.
Example 5. Give two pairs of prime numbers whose difference is 2.
Solution. Two pairs of prime numbers whose difference is 2 are
(1) 3 and 5 (i.e. 5 – 3 = 2) (2) 29 and 31 (i.e. 31 – 29 = 2)
Mp Board Class 6 Maths Important Questions
Example 6. Observe that 3 x4+1=13 is a prime number. Here, 1 has been added to a multiple of 3 to get a prime number. Give some more examples of this type.
Solution. Some more examples of this type are
3 x 2 + 1 = 7,
3 x 6 + 1 = 19,
3 × 10 + 1 = 31,
3 x 12 + 1 = 37,
3 × 14 + 1 = 43,
3 x 20 + 1 = 61
Here, all numbers 7, 19, 31, 37, 43 and 61 are prime numbers as 1 has been added to the multiples of 3 to get these prime numbers.
Example 7. Find the greatest prime number between 10 and 20.
Solution. Prime numbers between 10 and 20 are 11, 13, 17 and 19. Therefore, the greatest prime number between 10 and 20 is 19.
Example 8. Write four pairs of prime numbers less than 20, whose sum is divisible by 8.
Solution. Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.
Here, 3 + 5 = 8 (divisible by 8) 5 + 11 = 16 (divisible by 8) 11 + 13 = 24 (divisible by 8) 13 + 19 = 32 (divisible by 8)
Hence, four pairs of prime numbers whose sum is divisible by 8 are (3, 5), (5, 11), (11, 13) and (13, 19).
Example 9. The numbers 17 and 71 are prime numbers. Both these numbers have same digits 1 and 7. Find the such pairs of prime numbers upto 100.
Solution. All prime numbers upto 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
Out of these, pairs of prime numbers having same digits are (13, 31), (17,71), (37, 73) and (79,97). Hence, there are 4 pairs of such type.
Class 6 Maths Chapter 3 Exercise Solutions
Example 10. Express the following as the sum of two odd prime numbers.
(1) 32
(2) 40
(3) 34
Solution.
(1) We have, 32 = 29 + 3
(2) We have, 40 = 37 +3
(3) We have, 34 = 31 + 3 or 29+5
Example 11. Express each of the following numbers as the sum of three odd primes.
(1) 41
(2) 25
(3) 27
(4) 71
Solution. (1) We have, 41 ⇒ 41 = 11 + 13 + 17,
where 11, 13 and 17 are odd prime numbers.
(2) We have, 25 ⇒ 25 = 5 + 7 + 13,
where 5, 7 and 13 are odd prime number.
(3) We have, 27 ⇒ 27 = 3 + 5 + 19,
where 3, 5 and 19 are odd prime numbers.
(4) We have, 71 ⇒ 71 = 13 + 17 + 41,
where 13, 17 and 41 are odd prime numbers.
Composite Numbers
The numbers having more than two factors are called composite numbers.
e.g. 4, 6, 8, 9, 10,…, etc. are composite numbers.
Note it 1 is neither a prime number nor a composite number because it has only one factor.
Factors And Multiples Class 6 Questions
Example 12. Write all the prime and composite numbers less than 15.
Solution. Prime numbers less than 15 are 2, 3, 5, 7, 11 and 13.
Composite numbers less than 15 are
4, 6, 8, 9, 10, 12 and 14.
Example 13. Write five consecutive composite numbers less than 100, so that there is no prime number between them.
Solution. Five consecutive composite numbers of such type are 54, 55, 56, 57 and 58.
Example 14. State whether the following statements are true or false.
(1) The sum of three even numbers is even.
(2) The sum of two odd numbers and one even number is odd.
(3) All prime numbers are even.
(4) Sum of two prime numbers is always odd.
(5) The product of two even numbers is always odd.
Solution. (1) True, because the sum of three even numbers is always even.
e.g. 2 + 4 + 6 = 12 (even)
(2) False, because the sum of two odd numbers and one even number is always an even number.
e.g. 1 + 5 + 4 = 10 (even)
(3) False, because 2 is only an even prime number. So, all prime numbers are not even.
(4) False, because the sum of two prime numbers is either odd or even.
e.g. 3 + 5 = 8 (even) and 2 + 3 = 5 (odd)
(5) False, because the product of two even numbers is always even.
e.g. 4 × 6 = 24
Factors And Multiples Class 6 Questions
Example 15. Fill in the blanks
(1) The numbers other than 1 whose only factors are 1 and the number itself are called ……..
(2) The smallest odd prime number is……..
(3) Two prime numbers whose difference is 2 are called…….
(4)……. is the smallest prime number which is even …….
Solution.
(1) The numbers other than 1 whose only factors are 1 and the number itself are called prime numbers.
(2) The smallest odd prime number is 3.
(3) Two prime numbers whose difference is 2 are called twin primes.
(4) 2 is the smallest prime number which is even.
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Test for Divisibility
To check the divisibility of any number by other, we normally perform actual divison and see whether remainder is zero or not.
To check without actual division, some divisibility test of different numbers are given below
Test of Divisibility by 2
A number is divisible by 2, if it has any of the digits 0, 2, 4, 6 or 8 at its ones place.
Example 1. Check whether the number 246 is divisible by 2 or not.
Solution. Here, in 246 the digit at the ones place is 6.
Hence, 246 is divisible by 2.
Test of Divisibility by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
Example 2. Check whether the number 32523 is divisible by 3 or not.
Solution. Given number is 32523.
Sum of the digits = 3 + 2 + 5 + 2 + 3 = 15, which is divisible by 3.
Hence, the number 32523 is divisible by 3.
Test of Divisibility by 4
A number with three or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4.
Class 6 Maths Chapter 3 Solutions
Example 3. Check whether the number 9524624 is divisible by 4 or not.
Solution. Given number is 9524624.
The number formed by last two digits is 24, which is divisible by 4.
Hence, 9524624 is divisible by 4.
Test of Divisibility by 5
A number is divisible by 5 if it has either 0 or 5 at its ones place.
e.g. Each of the number 60, 225, 625 is divisible by 5.
Test of Divisibility by 6
A number is divisible by 6 if the number is divisible by 2 and 3 both.
Example 4. Check whether the number 297144 is divisible by 6 or not.
Solution. Given number is 297144.
We know that a number is divisible by 6 if it is divisible by both 2 and 3.
The number 297144 has an even digit at its ones place. Therefore, it is divisible by 2.
Sum of all the digits in 297144
= 2 + 9 + 7 + 1 + 4 + 4 = 27, which is divisible by 3.
Therefore, the number 297144 is divisible by 6.
Test of Divisibility by 8
A number with 4 or more digits is divisible by 8 if the number formed by the last three digits is divisible by 8.
Example 5. Check whether the number 79152 is divisible by 8 or not.
Solution. Given number is 79152.
The number formed by last three digits is 152 which is divisible by 8.
Hence, 79152 is divisible by 8.
MP Board Class 6 Chapter 3 Maths
Example 6. Which of the following numbers is divisible by both 4 and 8?
(1) 9638
(2) 9640
Solution. (1) We have, 9638
(a) Divisibility by 4
Number formed by last two digits = 38 On dividing 38 by 4, we get
Remainder ≠ 0
∵ 38 is not divisible by 4, so 9638 is also not divisible by 4.
(b) Divisibility by 8
Number formed by last three digits = 638
On dividing 638 by 8, we get
Remainder ≠ 0
∵ 638 is not divisible by 8, so 9638 is also not divisible by 8.
So, 9638 is not divisible by both 4 and 8.
(ii) We have, 9640
(a) Divisibility by 4
Number formed by last two digits=40
On dividing 40 by 4, we get
Remainder = 0
∵ 40 is divisible by 4, so 9640 is also divisible by 4.
(b) Divisibility by 8
Number formed by last three digits=640
On dividing 640 by 8, we get
Remainder = 0
∵ 640 is divisible by 8, so 9640 is also divisible by 8.
Hence, 9640 is divisible by both 4 and 8.
Test of Divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
Example 7. Is 65403 divisible by 9?
Solution. Given number is 65403.
Sum of the digits of the given number = 6 + 5 + 4 + 0 + 3 = 18, which is divisible by 9.
Hence, 65403 is divisible by 9.
Test of Divisibility by 10
A number is divisible by 10 if it has 0 at its ones place.
Example 8. Check whether the number 49600 is divisible by 10 or not?
Solution. Given number is 49600.
Here, the number 49600 has 0 at its ones place.
Therefore, 49600 is divisible by 10.
Test of Divisibility by 11
A number is divisible by 11 if the difference between the sum of the digits at odd places (from the right to left) and the sum of the digits at even places (from the right to left) of the number is either 0 or divisible by 11, then the number is divisible by 11.
MP Board Class 6 Chapter 3 Maths
Example 9. Is 73854 divisible by 11?
Solution. The given number is 73854.
Sum of its digits at odd places = 4 + 8 + 7 = 19
Sum of its digits at even places = 5 + 3 = 8
Difference of these sums = 19 – 8 = 11, which is divisible by 11.
Hence, 73854 is divisible by 11.
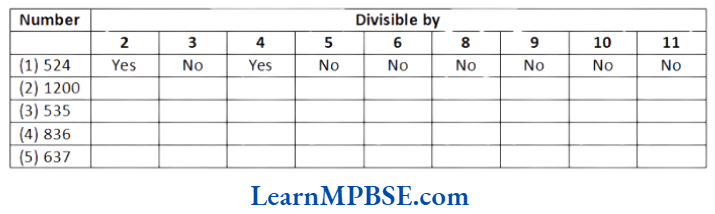
Example 10. Using divisibility tests, determine which of the following numbers are divisible by 2, by 3, by 4, by 5, by 6, by 8, by 9, by 10 and by 11 (say yes or no)?
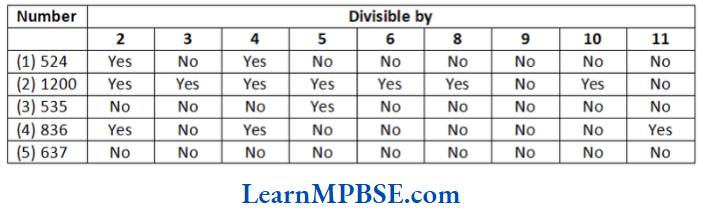
Solution. We know that a number is divisible by
2, if it has digits 0, 2, 4, 6 or 8 at its ones place.
3, if the sum of the digits is a multiple of 3 or it is divisible by 3.
4, if last two digits of the number is completely divisible by 4.
5, if a number has 0 or 5 at its ones place.
6, if it is divisible by 2 and 3 both.
8, if last three digits of the number is completely divisible by 8.
9, if the sum of the digits of the number is divisible by 9.
10, if a number has 0 at its ones place.
11, if the difference of sum of the digits at even place and sum of the digits at odd place is either 0 or multiple of 11. Hence,
Example 11. In each of the following replace by the smallest and the greatest digit, so that the number formed is divisible by 3.
(1) 12525 * 2
(2) 251 * 3373
Solution. (1) We have, 12525 * 2
Sum of the given digits = 1 + 2 + 5 + 2 + 5 + 2 = 17
∵ Multiples of 3 greater than 17 are
18, 21, 24, 27, 30,…
∴ 18 – 17 = 1; 21 – 17 = 4; 24 – 17 = 7; 27 – 17 = 10
But 10 is not a single digit.
∴ Smallest digit = 1 and greatest digit = 7
(2) We have, 251 3373
Sum of the given digits=2+5+1+3+3+7+3=24
∵ 24 is a multiple of 3, so smallest digit = 0
Now, multiples of 3 greater than 24 are
27, 30, 33, 36,…
∴ 27 – 24 = 3; 30 – 24 = 6; 33 – 24 = 9; 36 – 24 = 12
But 12 is not a single digit.
∴ Smallest digit = 0 and greatest digit=9
Example 12. In each of the following replace by a digit so that the number formed is divisible by 11. (II) 866194
(1) 64 * 2456
(2) 86 * 6194
Solution. (1) Let the required unknown digit be x. Then, the number becomes
where, O = odd and E = even
Sum of digits at odd places from right = 6 + 4 + x + 6
= 16 + x
Sum of digits at even places from right = 5 + 2 + 4 = 11
∵ Number is divisible by 11.
∴ Difference of digits will be 0 or 11.
⇒ 16 + x – 11 = 0 or 11 ⇒ x + 5 = 0 or 11
On taking difference 0, x + 5 = 0 ⇒ x = -5 (not possible)
On taking difference 11, x + 5 = 11 ⇒ x = 11 – 5
⇒ x = 6
So, the required digit to write in place of * is 6.
(2) Let the required unknown digit be x.
Then, the number becomes
where, O = odd and E = even
Sum of digits at odd places from right
4 + 1 + x + 8 = 13 + x
Sum of digits at even places from right=9+6+6=21
∵ Number is divisible by 11.
∴ Difference of digits will be 0 or 11.
⇒ 13 + x – 21 = 0 or 11 ⇒ x – 8 = 0 or 11
On taking difference 0, x – 8 = 0 ⇒ x = 8
On taking difference 11, x – 8 = 11
⇒ x = 11 + 8 ⇒ x = 19
[but 19 is not a single digit number, so it is not possible]
So, required digit to write in place of * is 8.
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Common Factors and Common Multiples
In the first topic, we have studied about factors and multiples of numbers. Now, we will study about common factors and common multiples.
Common Factors
The factors which are common of each of the given numbers are called their common factors.
Example 1. Find the common factors of
(1) 8 and 20
(2) 35 and 50
(3) 6, 12 and 18
(4) 8, 16 and 24
Solution. (1) Factors 8 = 1,2,4,8
Factors of 20 = 1, 2, 4, 5, 10, 20
Hence, the common factors of 8 and 20 are 1, 2 and 4.
(2) Factors 35 = 1,5,7,35
Factors of 50 = 1, 2, 5, 10, 25, 50
Hence, the common factors of 35 and 50 are 1 and 5.
(3) Factors of 6 = 1, 2, 3, 6
Factors of 12= 1, 2, 3, 4, 6, 12
Factors of 181, 2, 3, 6, 9, 18
Hence, the common factors of 6, 12 and 18 are 1, 2, 3 and 6.
(4) Factors of 8 = 1, 2, 4, 8
Factors of 16 = 1, 2, 4, 8, 16
Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Hence, the common factors of 8, 16 and 24 are 1, 2, 4 and 8.
Example 2. A number is divisible by 14. By what other numbers will that number be divisible?
Solution. If any number is divisible by 14, then this number will also be divisible by the factors of 14 i.e. by 1, 2 and 7.
Example 3. A number is divisible by 2, 3 and 5. By which other number will that number be always divisible?
Solution. If a number is divisible by 2, 3 and 5, then it is always divisible by their products i.e. 2 × 3 × 5 = 30
Note it If a number is divisible by any two or more numbers, then it is always divisible by their products.
Common Multiples
The multiples which are common to each of the given numbers are called their common multiples.
Mp Board Class 6 Maths Book Pdf
Example 4. Find the first three common multiples of
(1) 2 and 3
(2) 12 and 18
Solution. (1) Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18,…
Multiple of 3 are 3, 6, 9, 12, 15, 18, …
Hence, the first three common multiples of 2 and 3 are 6, 12 and 18.
(2) Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108,…
Multiples of 18 are 18, 36, 54, 72, 90, 108, …
Hence, the first three common multiples of 12 and 18 are 36, 72 and 108.
Example 5. Write all the numbers less than 100 which are common multiples of 4 and 5.
Solution. Multiples of 4 less than 100 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96
Multiples of 5 less than 100 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95
Hence, the common multiples of 4 and 5 less than 100 are 20, 40, 60 and 80.
Co-prime Numbers
Two numbers which have only 1 as their common factor are called co-prime numbers.
Note it Any two prime numbers are always co-primes but two co-prime numbers need not to be prime numbers.
MP Board Class 6 Chapter 3 Maths
Example 6. Which of the following pairs are co-primes?
(1) 8, 25
(2) 4, 10
Solution. (1) Factors of 8 = 1, 2,4,8
Factors of 25 = 1, 5, 25
∴ 8 and 25 have only 1 as common factor.
∴ 8 and 25 are co-prime numbers.
(2) Factors of 4 = 1,2,4
Factors of 10 = 1, 2, 5,10
∴ 4 and 10 have 1, 2 as common factors.
∴ 4 and 10 are not co-prime numbers.
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Prime Factorisation
If a natural number is expressed as the product of prime numbers, then the factorisation of the number is called its prime factorisation.
Example 1. Find the prime factorisation of 630.
Solution. By division method,
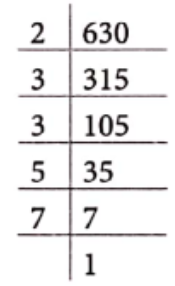
∴ 630 = 2 × 3 × 3 x 5 x 7
which is the required prime factorisation.
Prime Factorisation by Factor Tree Method
Expressing a number with the help of factor tree. Let us factorise 36 in three different ways as given below:
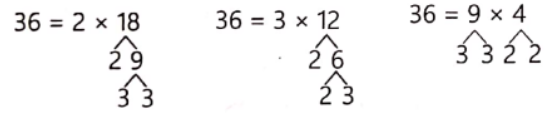
Thus, 36 = 2 x 2 x 3 x 3; 36 = 3 x 2 x 2 x 3; 36 = 3 × 3 × 2 × 2
In all the above factorisations of 36, we ultimately arrive only one factorisation 2 x2 x3x3 and such a factorisation is called a prime factorisation.
Example 2. Find the prime factorisation of 90.
Solution. By factor tree method,
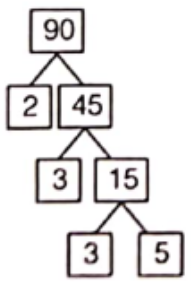
∴ 90 = 2 × 3 × 3 × 5 which is the required prime factorisation.
Hence, the missing numbers are 2, 3 and 3.
Class 6 Maths Prime And Composite Numbers
Example 3. Write down the missing numbers in the below factor trees of 72.
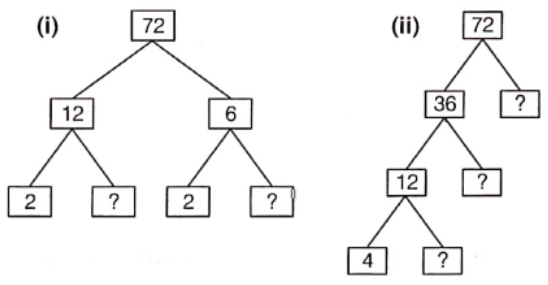
Solution. (1) ∴ 12 = 2 x 6 and 6 = 2 x 3
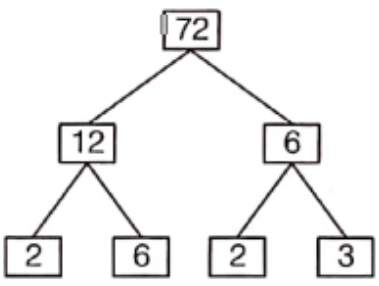
Hence, the missing numbers are 6 and 3.
(2) ∴ 72 = 36 × 2,
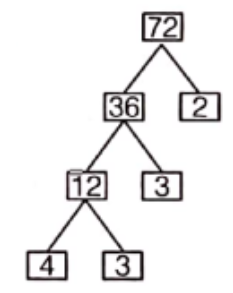
36 12 x 3 and 12=4×3
Example 4. Fill in the given space.
Prime factorisation of 3927 = 3 x 7 x … x 17
Solution. We have, 3927

∴ Prime factorisation of 3927 = 3 x 7 x 11 x 17
So, the required number to write in given space is 11.
Example 5. Write the smallest 4-digit number and all its prime factors.
Solution. Smallest 4-digit number = 1000

∴ Prime factors of 1000 = 2 x 2 x 2 x 5 x 5 x 5
Class 6 Maths Chapter 3 Exercise Solutions
Example 6. Write the greatest 5-digit number and all its prime factors.
Solution. Greatest 5-digit number = 99999

∴ Prime factors of 99999 = 3 x 3 x 41 x 271
Example 7. In which of the following expression, prime factorisation has been done?
(1) 36 = 2 × 3 × 6
(2) 54 = 2 x 3 x 3 x 3
(3) 56 = 2 x 4 x 7
(4) 76 = 2 x 2 x 19
Solution. (1) We have, 36 = 2 × 3 × 6
Here, 6 is not a prime number.
So, it is not the prime factorisation of 36.
(2) We have, 54 = 2 x 3 x 3 x 3
Here, 2 and 3 are prime numbers.
So, it is the prime factorisation of 54.
(3) We have, 56 = 2 x 4 x 7
Here, 4 is not a prime number.
So, it is not the prime factorisation of 56.
(4) We have, 76 = 2 x 2 x 19
Here, 2 and 19 are prime numbers.
So, it is a prime factorisation of 76.
Example 8. I am the smallest number, having four different odd prime factors. Can you find me?
Solution. Since, the number is smallest, so four different smallest odd prime factors are 3, 5, 7 and 11.
∴ Smallest number having four different odd prime factors
= 3 x 5 x 7 x 11 = 1155.
Example 9. Write all the prime factors of 105 and arrange them in ascending order. Is there Is any relation between the two consecutive prime factors?
Solution. Prime factorisation of 105
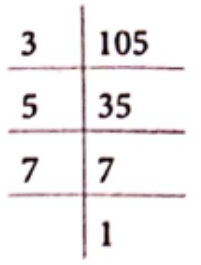
∴ 105 = 3 x 5 x 7
Ascending order of prime factors of 105 is 3, 5, 7.
Here, 5 – 3 = 2 and 7 – 5 = 2
So, the relation between two consecutive
prime factors of 105 is that the difference of two consecutive prime factors is 2.
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Highest Common Factor
The Highest Common Factor (HCF) of two or more numbers is the highest (or greatest) factor out of their common factors. It is also known as Greatest Common Divisor (GCD).
Example 1. Find the HCF of the following numbers.
(1) 24 and 48
(2) 18 and 60
(3) 15, 25 and 30
(4) 12, 16 and 28
Solution. (1) We have, 24 and 48.
Factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.
The common factors of 24 and 48 are 1, 2, 3, 4, 6, 8, 12 and 24.
∴ HCF of 24 and 48 = 24
(2) We have, 18 and 60.
Factors of 18 are 1, 2, 3, 6, 9 and 18.
Factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60.
The common factors of 18 and 60 are 1, 2, 3 and 6.
∴ HCF of 18 and 60=6
(3) We have, 15, 25 and 30.
Factors of 15 are 1, 3, 5 and 15.
Factors of 25 are 1, 5 and 25.
Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.
The common factors of 15, 25 and 30 are 1 and 5.
∴ HCF of 15, 25 and 30=5
(4) We have 12, 16 and 28.
Factors of 12 are 1, 2, 3, 4, 6 and 12.
Factors of 16 are 1, 2, 4, 8 and 16.
Factors of 28 are 1, 2, 4, 7, 14 and 28.
The common factors of 12, 16 and 28 are 1, 2 and 4.
∴ HCF of 12, 16 and 28 = 4
Factors And Multiples Class 6 Questions
Example 2. What is the HCF of
(1) two prime numbers?
(2) two consecutive even numbers?
Solution. (1) Let two prime numbers be 7 and 17.
Factors of 7 are 1 and 7.
Factors of 17 are 1 and 17.
∴ HCF of 7 and 17 is 1.
∴ Hence, HCF of two prime numbers is 1.
(2) Let the two consecutive even numbers be 8 and 10.
Factors of 8 are 1, 2, 4 and 8.
Factors of 10 are 1, 2, 5 and 10
The common factors of 8 and 10 are 1 and 2.
∴ HCF of 8 and 10 is 2.
∴ Hence, HCF of two consecutive even numbers is 2.
HCF by Prime Factorisation Method
In this method, first we find the prime factorisation of each of the given numbers. HCF is the product of all the different common prime factors of the given numbers using each common prime factor the least number of times it appears in the prime factorisation of all of the given numbers.
Example 3. Find the HCF of
(1) 48 and 84
(2) 18 and 60
(3) 15, 25 and 30
(4) 12, 16 and 28
Solution. (1) Here, the given numbers are 48 and 84.
Now, prime factorisation of given numbers are
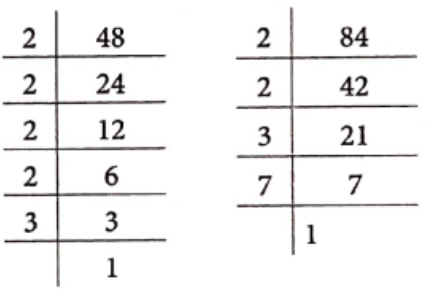
So, 48 = 2 x 2 x 2 x 2 x 3 and 84 = 2 × 2 × 3 × 7
Here, 2 occurs as a common prime factor atleast 2 times and 3 atleast 1 time in both given numbers. Hence, HCF of 48 and 84 = 2×2 x3=12
(2) Here, the given numbers are 18 and 60.
Now, prime factorisation of given numbers are
So, 18 = 2 x 3 x 3 and 60 = 2 x 2 x 3 x 5
Here, 2 and 3 each occurs as a common factor atleast once in both the given numbers.
Hence, HCF of 18 and 60=2×3=6
(3) Here, the given numbers are 15, 25 and 30.
Now, prime factorisation of given numbers are
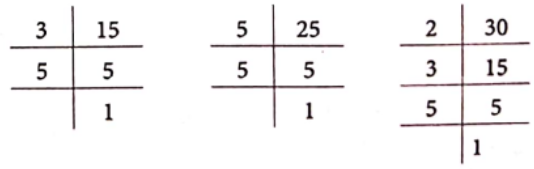
So, 15 = 3 x 5, 25 = 5 x 5, and 30 = 2 x 3 x 5
Here, 5 occurs as a common factor atleast once in each of the given number.
Hence, HCF of 15, 25 and 30=5.
(4) Here, the given numbers are 12, 16 and 28.
Now, prime factorisation of given numbers are
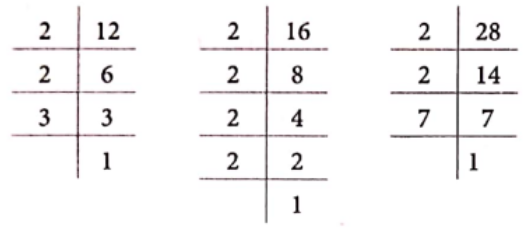
So, 12 = 2 x 2 x 3
16 = 2 × 2 × 2 × 2
and 28 = 2 × 2 x 7
Here, 2 occurs as a common factor atleast 2 times in each of the given number.
Hence, HCF of 12, 16 and 28 = 2 x 2 = 4
Class 6 Maths Prime And Composite Numbers
Example 4. In the factorisation of two co-prime numbers 6 and 25, we found that there is no common prime factor In the prime factorisation of 6 and 25, so HCF of 6 and 25 is 0. Check whether the answer is correct or not and if not correct, then find the correct HCF?
Solution. Prime factorisation of 6 = 2 x 3
Prime factorisation of 25 = 5 x 5
No, the answer is not correct.
Because 0 (zero) cannot be the factor of any number.
If there is no common factor, then it means 1 is the common factor.
∴ HCF of 6 and 25 = 1
Example 5. What will be the HCF of (3 x 5 x 11 × 13), (5 × 11 x 17 × 21) and (5 x 11 x 7 × 13)
Solution. Given prime factorisations are
(3 x 5 x 11 x 13), (5 x 11 x 17 x 21) and (5 x 11 x 7 x 13)
In the above prime factorisations, 5 and 11 each occurs as a common factor atleast once.
Hence, HCF of given factorisation = 5×11=55
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Lowest Common Multiple
The Lowest Common Multiple (LCM) of two or more numbers is the lowest (or smallest or least) multiple out of their common multiples.
Example 1. Find the LCM of the following numbers.
(1) 3 and 4
(2) 28 and 42
Solution. (1) Multiples of 3=3, 6, 9, 12, 15, 18, 21, 24, …
Multiples of 4 = 4, 8, 12, 16, 20, 24, …
Common multiples of 3 and 4 = 12, 24
∴ LCM of 3 and 4 is 12.
(2) Multiples of 28= 28, 56, 84, 112, 140, 168,…
Multiples of 42=42, 84, 126, 168, 210, …
Common multiples of 28 and 42= 84, 168,…
∴ LCM of 28 and 42 is 84.
LCM by Prime Factorisation Method
In this method, first we find the prime factorisation of each of the given numbers. Now, LCM is the product of all the different prime factors of the given numbers, using each common prime factor the greatest number of times it appears in the prime factorisation of any of the given numbers.
Example 2. Find the LCM by prime factorisation method:
(1) 20 and 24
(2) 10,15 and 25
Solution. (1) Here, the given numbers are 20 and 24.
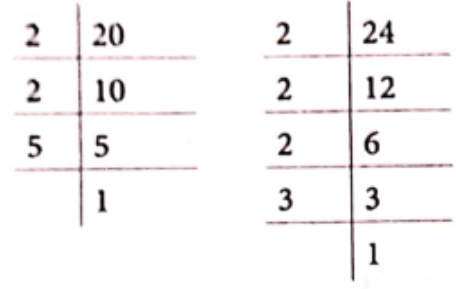
Now, prime factorisation of given numbers are
20 = 2 x 2 x 5 and 24 = 2 x 2 x 2 x 3
In these prime factorisations, the maximum number of times the prime factor 2 occurs is three, this happens for 24. Similarly, the prime factor 5 occurs only once is 20 and the prime factor 3 occurs only once is 24.
∴ LCM of 20 and 24 = 2 x 2 x 2 x 3 x 5 = 120
(2) Here, the given numbers are 10, 15 and 25.
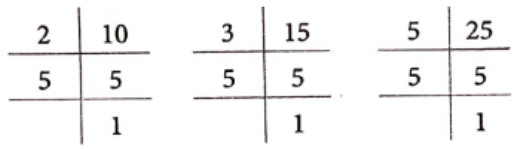
Now, prime factorisation of given numbers are
10 = 2 x 5,15 = 3 x 5 and 25 = 5 × 5
In these prime factorisation, the maximum number of times the prime factor 5 occur is two, this happens for 25. Similarly the prime factor 2 occurs only once in 10 and the prime factor 3 occurs only once is 15.
∴ LCM of 10, 15 and 25 = 2 x 3 x 5 x 5 = 150
LCM by Division Method
In this method, we arrange the given numbers in a line in any order. Now, we divide by a lowest prime number which divides any one of the given numbers and carry forward the other numbers which are not divisible. This process is repeated till we get all the number in the row is 1.
HCF and LCM for Class 6
Example 3. Find the LCM by division method.
(1) 36, 40 and 126
(2) 12, 15, 20 and 27
Solution. (1) LCM of 36, 40 and 126

∴ LCM = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520
(2) LCM of 12, 15, 20 and 27

∴ LCM = 2 x 2 x 3 x 3 x 3 x 5 = 540
Example 4. Find the LCM of the following numbers in which one number is the factor of the other.
(1) 5 and 15
(2) 4 and 12
(3) 6 and 24
What do you observe in the results so obtained?
Solution. (1) LCM of 5 and 15

∴ LCM = 3 x 5 = 15
(2) LCM of 4 and 12
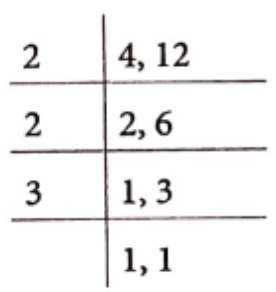
∴ LCM = 2 x 2 x 3 = 12
(3) LCM of 6 and 24

∴ LCM = 2 x 2 x 2 x 3 = 24
Here, we observe that in all parts, LCM of the given numbers is the larger of two numbers because one number is factor of the other number.
Note It If one number is the factor of the other, then the LCM of the two numbers will be equal to the greater number.
Example 5. Find the LCM of the following numbers. Observe a common property from the obtained LCM. Is LCM the product of two numbers In each case?
(1) 21 and 4
(2) 6 and 7
(3) 16 and 9
Solution. (1) LCM of 21 and 4

∴ LCM = 2 x 2 x 3 x 7 = 84
(2) LCM of 6 and 7
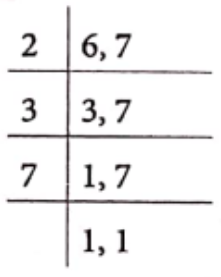
∴ LCM = 2 x 3 x 7 = 42
(3) LCM of 16 and 9
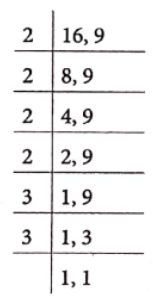
∴ LCM = 2 × 2 × 2 × 2 × 3 × 3 = 144
Here, we see that in each case,
LCM of given numbers is a multiple of 3 and 2.
Yes, in each case LCM is equal to the product of given two numbers.
Note it The LCM of two co-prime numbers is always equal to the product of two numbers.
Applications of HCF and LCM
We come across a number of situations in which we have to use of the concepts of HCF and LCM. Some application-based examples are given below:
HCF and LCM for Class 6
Example 6. The HCF of three numbers is 23. If they are in the ratio of 1 : 2 : 3, then find the numbers.
Solution. Let the numbers x, 2x and 3x.
∴ Their HCF is x.
But given HCF = 23
∴ x = 23
2x = 2 x 23 = 46
and 3x = 3 x 23 = 69
Hence, the numbers are 23, 46 and 69.
Example 7. If three numbers are 2a, 3a and 5a, then what will be their LCM?
Solution. The LCM of 2a, 3a and 5a is 30a because 30a is the smallest or lowest number which is divisible by 2a, 3a and 5a.
Example 8. Find the greatest number which divides 285 and 1249, leaving remainder 9 and 7, respectively.
Solution. Here, we have to find the greatest number which divides (285 – 9) and (1249 – 7) exactly.
∴ The required number is HCF of 276 and 1242.
Prime factorisation of 276=2 x 2 x 3 x 23
Prime factorisation of 1242 = 2 x 3 x 3 x 3 x 23
∴ HCF of 276 and 1242 = 2 × 3 × 23 = 138
Hence, the required number is 138.
Example 9. Find the smallest 3-digit number which is exactly divisible by 4, 6 and 8?
Solution. Firstly, we have to find out the LCM of 4, 6 and 8.

∴ LCM = 2 x 2 x 2 x 3 = 24
We know that smallest 3-digit number is 100.
On dividing 100 by 24, we get remainder 4.
Now, required 3-digit number which is exactly divisible by 24
= Smallest 3 – digit number + Divisor – Remainder
= 100 + 24 – 4 = 120
HCF and LCM for Class 6
Example 10. Find the greatest 3-digit number which is exactly divisible by 6, 8 and 10?
Solution. Firstly, we have to find out the LCM of 6, 8 and 10.

∴ LCM = 2 x 2 x 2 x 3 x 5 = 120
We know that largest 3-digit number = 999
On dividing 999 by 120, we get remainder 39.
Now, required 3-digit number which is exactly divisible by 120
= Greatest 3 – digit number – Remainder
= 999 – 39 = 960
Example 11. Find the least number which when divided by 12, 16 and 18 leave remainder 5 in each case.
Solution. First, we have to find out the LCM of 12, 16 and 18.

∴ LCM = 2 x 2 x 2 x 2 x 3 x 3 = 144
Now, required number = LCM + Remainder
= 144 + 5 = 149
Hence, the required number is 149.
Example 12. Dolly purchases two bags of sugar of weight 75 kg and 105 kg. Find the maximum value of weight which can measure the two bags exact number of times.
Solution. For getting the maximum value of weight, we have to find out the HCF of 75 kg and 105 kg.
Now, prime factorisation of 75 = 3 x 5 x 5
and prime factorisation of 105 = 3 x 5 x 7
∴ HCF of 75 and 105 = 3 x 5 = 15
Hence, the required maximum value of weight is 15 kg.
Example 13. Five bells toll at intervals of 12 sec, 15sec, 20 sec, 25sec and 45 sec, respectively. If all of them toll at 7 am, then at what time will they toll together again?
Solution. Firstly, we have to find out the LCM of 12, 15, 20, 25 and 45.

∴ LCM = 2 x 2 x 3 x 3 x 5 x 5 = 900
= \(\frac{900}{60}=15 \mathrm{~min}\)
So, time when they will toll together again
07 : 00 : 00 + 15 : 00 = 07 : 15 : 00
Factors And Multiples Class 6 Questions
Example 14. A girl saves * 3.65 daily. Find the least number of days in which she will be able to save an exact number of rupees.
Solution. Here, ₹ 3.65 = 365 paise
The exact number of rupees will be a multiple of 100.
So, we have to find the LCM of 365 and 100.
100 = 2 x 2 x 5 x 5
and 365 = 5 x 73
∴ LCM of 365 and 100 = 2 x 2 x 5 x 5 x 73 = 7300
So, the girl saved 7300 paise.
Hence the least number of days required to save 7300-20 days.
7300 paise = \(\frac{7300}{365}=20 \text { days. }\)
Example 15. On a evening walk, three persons step off together and their steps measures 42 cm, 49 cm and 56 cm, respectively. What is the minimum distance each should walk, so that each can cover the same distance in complete steps?
Solution. Here, the required minimum distance will be equal to LCM of measures of their steps because the minimum distance each persons should walk must be the least common multiple of the measures of their steps. So, we have to find out the LCM of 42, 49 and 56.
i.e.

∴ LCM of 42, 49
and 56 = 2 x 2 x 2 x 3 x 7 x 7 = 1176
Hence, 1176 cm is the required minimum distance.
Question 1. Find the possible factors of 45, 30 and 36.
Solution. (1) Here,
45 = 1 x 45; 45 = 3 x 15; 45 = 5 x 9
∴ Factors of 45 are 1, 3, 5, 9, 15 and 45.
(2) Here,
30 = 1 x 30; 30 = 2 x 15; 30 = 3 x 10; 30 = 5 × 6
∴ Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.
(3) Here,
36 = 1 x 36; 36 = 2 x 18; 36 = 3 x 12; 36 = 4 x 9; 36 = 6 X 6
∴ Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.
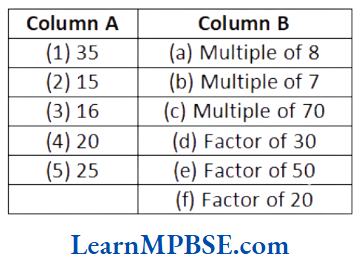
Question 2. Match the items in column A with the items in column B.
Solution.
(1) Factors of 35 are 5 and 7 and we know that a number is a multiple of each of its factor. Hence, 35 is a multiple of 7.
(2) We know that a factor of a number is an exact divisor of that number.
Here, 30 is divided by 15. So, 15 is a factor of 30.
(3) Factors of 16 are 2 and 8 and we know that, a number is a multiple of each of its factor. Hence, 16 is a multiple of 8.
(4) We know that every number is a factor of itself. So, 20 is a factor of itself i.e. 20.
(5) We know that a factor of a number is an exact divisor of that number. Here, 50 is divided by 25. So, 25 is a factor of 50.
Now, matching of these items is as follows
(1) → (b) (2) → (d) (3) → (a) (4) → (f) (5) → (e)
Question 3. Find all the multiples of 9 upto 100.
Solution. All the multiples of 9 up to 100 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90 and 99.
Question 4. Observe that 2 x 3+1 = 7 is a prime number. Here, 1 has been added to a multiple of 2 to get a prime number. Can you find some more numbers of this type?
Solution. Some more numbers of this type are as follows
2 x 2 + 1 = 5, 2 x 5 + 1 = 11, 2 x 6 + 1 = 13
2 x 8 + 1 = 17, 2 x 9 + 1 = 19, 2 x 11 + 1 = 23
Here, all numbers 5, 11, 13, 17, 19 and 23 are prime numbers and 1 has been added to a multiple of 2 to get these prime numbers.
Factors And Multiples Class 6 Questions
Question 5. What is the sum of any two
(1) odd numbers?
(2) even numbers?
Solution.
(1) Let the two odd numbers be 5 and 7.
Their sum = 5 + 7 = 12 (even number)
Taking one more example.
Let the two odd numbers be 3 and 7
Their sum = 3 + 7 = 10 (even number)
Hence, we can say that sum of any two odd numbers is an even number.
(2) Let the two even numbers be 4 and 8.
Their sum = 4 + 8 = 12 (even number)
Taking one more example.
Let the two even numbers be 6 and 20.
Their sum = 6 + 20 = 26 (even number)
Hence, we can say that sum of any two even numbers is an even number.
Question 6. The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers upto 100.
Solution. All prime numbers upto 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97. Out of these prime numbers, pairs of prime numbers having same digits are
(1) 13,31
(2) 17,71
(3) 37, 73
(4) 79,97
Hence, there are 4 pairs of such types.
Question 7. Write down separately the prime and composite numbers less than 20.
Solution. Prime numbers are those numbers whose only factors are 1 and the number itself.
So, prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.
Composite numbers are those numbers which have more than two factors.
So, composite numbers less than 20 are 4, 6, 8, 9, 10, 12, 14, 15, 16 and 18.
Question 8. What is the greatest prime number between 1 and 10?
Solution. Prime numbers between 1 and 10 are 2, 3, 5 and 7. Therefore, the greatest prime number between 1 and 10 is 7.
Question 9. Give three pairs of prime numbers whose difference is 2.
[Remark Two prime numbers whose difference is 2 are called twin primes].
Solution. Three pairs of prime numbers whose difference is 2 are
(1) (5,7) i.e.7 – 5 = 2
(2) (11, 13) i.e.13 – 11 = 2
(3) (17, 19) i.e. 19 – 17 = 2
Question 10. Which of the following numbers are prime?
(1) 23
(2) 51
(3) 37
(4) 26
Solution.
(1) We find that 23 is not exactly divisible by any of the prime numbers 2, 3, 5, 7, 11, 17 and 19. So, it is a prime number.
(2) We find that 51 is divisible by 3. So, it is not a prime number.
(3) We find that 37 is not exactly divisible by any of the prime numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 and 31. So, it is a prime number.
(4) We find that 26 is exactly divisible by 2 and 13. So, it is not a prime number.
Mp Board Class 6 Maths Important Questions
Question 11. Write seven consecutive composite numbers less than 100, so that there is no prime number between them.
Solution. Seven composite numbers of such type are as follows 90, 91, 92, 93, 94, 95, and 96.
Question 12. Express each of the following numbers as the sum of three odd primes.
(1) 21
(2) 31
(3) 53
(4) 61
Solution. (1) We have, 21
⇒ 21 = 3 + 5 + 13
where 3, 5 and 13 are odd prime numbers.
(2) We have, 31
⇒ 31 = 3 + 5 + 23
where 3, 5 and 23 are odd prime numbers.
(3) We have, 53
⇒ 53 = 13 + 17 + 23
where 13, 17 and 23 are odd prime numbers.
(4) We have, 61
⇒ 61 = 7 + 13 + 41
where 7, 13 and 41 are odd prime numbers.
Question 13. Write five pairs of prime numbers less than 20 whose sum is divisible by 5. [Hint 3+7=10]
Solution. Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.
Here,
2 + 3 = 5 (divisible by 5)
2 + 13 = 15 (divisible by 5)
3 + 7 = 10 (divisible by 5)
3 + 17 = 20 (divisible by 5)
7 + 13 = 20 (divisible by 5)
Hence, five pairs of prime numbers whose sum is divisible by 5 are (2, 3), (2, 13), (3, 7), (3, 17) and (7, 13).
Question 13. Find the common factors of
(1) 8 and 20
(2) 9 and 15
Solution. (1) Factors of 8 = 1, 2,4,8
Factors of 20 = 1, 2,4,5,10, 20
Hence, the common factors of 8 and 20 are 1, 2 and 4.
(2) Factors of 9 = 1,3,9
Factors of 15 = 1,3,5,15
Hence, the common factors of 9 and 15 are 1 and 3.
Question 14. Find first three common multiples of
(1) 6 and 8
(2) 12 and 18
Solution. (1) Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72,…
Multiples of 88, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96,…
Hence, first three common multiples are 24, 48 and 72.
(2) Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132,…
Multiples of 1818, 36, 54, 72, 90, 108, 126, 144,…
Hence, first three common multiples are 36, 72 and 108.
Mp Board Class 6 Maths Important Questions
Question 15. Write all the numbers less than 100, which are common multiples of 3 and 4.
Solution. Multiples of 3 which are less than 100 are as follows:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99
Multiples of 4 which are less than 100 are as follows:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96
Hence, the common multiples of 3 and 4 are 12, 24, 36, 48, 60, 72, 84 and 96.
Question 16. A number is divisible by both 5 and 12. By which other number will that number be always divisible?
Solution. The given number will be divisible by the product of 5 and 12 i.e. it is always divisible by 5 x 12 = 60.
Note If a number is divisible by two co-prime numbers, then it is divisible by their product also.
Question 17. A number is divisible by 12. By what other numbers will that number be divisible?
Solution. If any number is divisible by 12, then this number will also be divisible by the factors of 12
i.e. 12 = 1 x 12; 12 = 2 × 6;12 = 3 x 4
Factors of 12 are 1, 2, 3, 4, 6 and 12.
∴ Number will be also divisible by 1, 2, 3, 4, 6 and 12.
Factors and Multiples Class 6
Question 18. Here are two different factor trees for 60. Write the missing numbers.
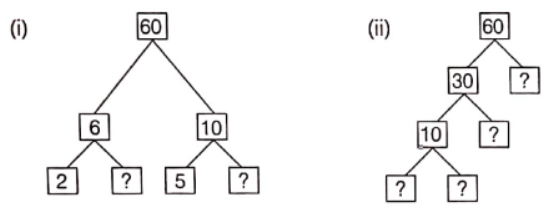
Solution. (1) 6 = 2 x 3 and 10 = 5 x 2
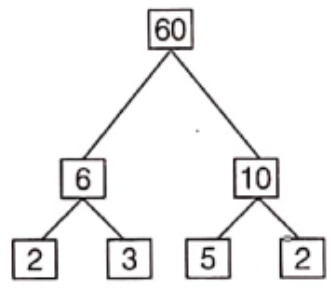
Hence, the missing numbers are 3 and 2.
(2) 60 = 30 x 2
30 = 10 x 3
and 10 = 5 x 2
Hence, the missing numbers are 2, 3, 5 and 2.
Question 19. Which factors are not included in the prime factorisation of a composite number?
Solution. Factor 1 and that number itself are not included in the prime factorisation of a composite number.
Class 6 Maths Chapter 3 Mp Board Solutions
Question 20. Write the greatest 4-digit number and express it in terms of its prime factors.
Solution. The greatest 4-digit number = 9999
Now,

Prime factors of 9999 = 3 x 3 x 11 x 101
Question 21. Write the smallest 5-digit number and express it in the form of its prime factors.
Solution. The smallest 5-digit number = 10000
Now,

Prime factors of 10000 = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5
Class 6 Maths Chapter 3 Mp Board Solutions
Question 22. The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Solution. We know that a number is divisible by 6, if the number is divisible by 2 and 3 both.
Let the three consecutive numbers are 3, 4 and 5.
Their product = 3 x 4 x 5 = 60
Now, 60 is divisible by 2 and 3 both.
So, 60 is also divisible by 6.
Hence, product of three consecutive numbers 3, 4 and 5 is divisible by 6.
Taking one more example.
Let the three consecutive numbers are 6, 7 and 8.
Their product = 6 x 7 x 8 = 336
Now, 336 is divisible by 2 and 3 both.
So, 336 is also divisible by 6.
Hence, product of three consecutive numbers 6, 7 and 8 is divisible by 6.
Question 23. In which of the following expressions, prime factorisation has been done?
(1) 24 = 2 × 3 × 4
(2) 56 = 7 x 2 x 2 x 2
(3) 70 = 2 x 5 x 7
(4) 54 = 2 x 3 x 9
Solution. (i) We have, 24 = 2 × 3 × 4
Here, 4 is not a prime number.
So, prime factorisation is not done.
(2) We have, 56 = 7 x 2 x 2 x 2
Here, 2 and 7 are prime numbers.
So, number 56 have prime factorisation.
(3) We have, 70 = 2 x 5 x 7,
Here 2, 5 and 7 all are prime numbers.
So, number 70 have prime factorisation.
(4) We have, 54 = 2 x 3 x 9,
Here, 9 is not a prime number.
So, prime factorisation is not done.
Prime Factorization Class 6
Question 24. 18 is divisible by both 2 and 3. It is also divisible by 2 x 3 = 6. Similarly, a number is divisible by both 4 and 6. Can we say that the number must also be divisible by 4 × 6 = 24? If not, give an example to justify your answer.
Solution. We know that if a number is divisible by two co-prime numbers, then it is divisible by their product also.
Here, 2 and 3 are co-prime numbers. So, 18 is divisible by their product i.e. 6 but 4 and 6 are not co-prime numbers, so the number divisible by 4 and 6 will not be divisible by 4 × 6 = 24.
e.g. Take the number 60.
It is divisible by both 4 and 6 but it is not divisible by its product. i.e. 6 × 4 = 24
Question 25. I am the smallest number, having four different prime factors. Can you find me?
Solution. Since, the number is smallest, so different four smallest prime factors are 2, 3, 5 and 7.
∴ Smallest number having four different prime factors = 2 x 3 x 5 x 7 = 210
Question 26. What is the HCF of two consecutive
(1) numbers?
(2) even numbers?
(3) odd numbers?
Solution.
(1) Let the two consecutive numbers be 8 and 9.
Now, prime factorisation of 8 = 2 x 2 x 2
Prime factorisation of 9 = 3 × 3
Common factor of 8 and 9 = 1
Thus, HCF of 8 and 9 is 1.
Note The HCF of two consecutive numbers is 1.
(2) Let the two consecutive even numbers be 10 and 12.
Now, prime factorisation of 10 = 2 x 5
Prime factorisation of 12 = 2 x 2 x 3
Common factor of 10 and 12 = 2
Thus, HCF of 10 and 12 is 2.
Note The HCF of two consecutive even numbers is 2.
(3) Let two consecutive odd numbers be 3 and 5.
Prime factorisation of 3 = 1 x 3
Prime factorisation of 5 = 1 x 5
Common factor of 3 and 5 = 1
Thus, HCF of 3 and 5 is 1.
Note The HCF of two consecutive odd numbers is 1.
Prime Factorization Class 6
Question 27. HCF of co-prime numbers 4 and 15 was found as follows by factorisation. 4 = 2 x 2 and 15 = 3 x 5, since there is no common prime factor, so HCF of 4 and 15 is 0. Is the answer correct? If not, what is the correct HCF?
Solution. No, the answer is not correct. Because 0 (zero) cannot be factor of any number. If there is no common factor, then it means 1 is the common factor.
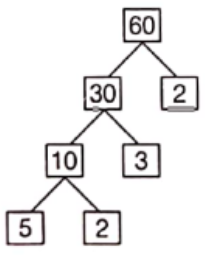
∴ HCF of 4 and 15=1
Question 28. Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight, which can measure the weight of the fertiliser exact number of times.
Solution. For getting maximum value of weight, we have to find out the HCF of 75 kg and 69 kg.
i.e.
Prime factorisation of 75 = 3 x 5 x 5
Prime factorisation of 69 = 3 x 23
Common factor of 75 and 69 is 3.
Thus, HCF of 75 kg and 69 kg = 3 kg
Hence, the required maximum value of weight is 3 kg.
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Multiple Choice Questions
Question 1. Number of even numbers between 50 and 80, are
- 14
- 11
- 12
- 13
Answer. 1. 14
Question 2. The largest number, which always divides the sum of any pair of consecutive odd numbers is
- 2
- 4
- 6
- 8
Answer. 2. 4
Question 3. Sum of the number of primes between 16 to 80 and 90 to 100 is
- 20
- 18
- 17
- 16
Answer. 3. 17
Question 4. Which of the following pair is not co-prime?
- 11, 12
- 73, 74
- 84, 94
- 97, 98
Answer. 3. 84, 94
Question 5. A number is divisible by 5, if it has
- Only 0 in its ones place
- 0 in its tens place
- 0 or 5 in its ones place
- 5 in its ones place
Answer. 3. 0 or 5 in its ones place
Question 6. A number is divisible by 5 and 6. It may not be divisible by
- 10
- 15
- 30
- 85
Answer. 4. 85
Class 6 Maths Chapter 3 Mp Board Solutions
Question 7. If the number 725498 is divisible by 11, the digit at * is
- 1
- 2
- 6
- 0
Answer. 3. 6
Question 8. The number of common prime factors of 75, 60, 105 is
- 2
- 3
- 4
- 5
Answer. 1. 2
Question 9. The number of distinct prime factors of the largest 4-digit number is
- 2
- 3
- 5
- 11
Answer. 2. 3
Question 10. The number of distinct prime factors of the smallest 5-digit number is
- 2
- 4
- 6
- 8
Answer. 1. 2
Question 11. The HCF of 144 and 160 is
- 24
- 15
- 9
- None of these
Answer. 4. None of these
Question 12. The LCM of 12, 24, 32 is
- 92
- 86
- 27
- 96
Answer. 4. 96
Question 13. If two numbers are equal, then
- their LCM is less than their HCF
- their LCM is equal to two times their HCF
- their LCM is equal to their HCF
- None of the above
Answer. 3. their LCM is equal to their HCF
Question 14. LCM of two numbers is 180. Then, which of the following is not the HCF of the numbers?
- 45
- 60
- 75
- 90
Answer. 3. 75
Question 15. The sum of HCF and LCM of two numbers is 1260. If their LCM is 900 more than their HCF, then the product of the two number is
- 194400
- 19440
- 184400
- 126000
Answer. 1. 194400
Question 16. Photographs are sold in small, medium and large size. The cost of photographs according to their size is given in the table below: Compentency Based Question
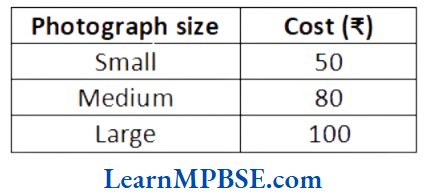
Mp Board Class 6 Maths Important Questions
150 photographs worth? 10250 were sold. If 75 of them were of small size, find how many larger size photographs were sold?
- 14
- 25
- 75
- 130
Answer. 2. 25
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Assertion-Reason Type Questions
Question 1. Assertion (A) The number 9 and 25 are co-prime.
Reason (R) A number is said to be prime, if it has only two factors 1 and the number itself.
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
Question 2. Assertion (A) The HCF of 8, 16 and 24 is 4.
Reason (R) HCF of two or more given numbers is the greatest of their common factors.
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (d) (A) is false but (R) is true.
Prime Factorization Class 6
Question 3. Assertion (A) HCF of 3 and 8 is 1 and LCM of 3 and 8 is 24.
Reason (R) HCF of two co-primes is 1 and the LCM of two co-primes is their product.
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (a) Both (A) and (R) are true and (R) is the correct explanation of (A).
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Fill in the Blanks
Question 1. 15 is a multiple of………and..
Solution. 3 and 5
Question 2. A number for which the sum of all its factors is equal to twice the number is called a ………. number.
Solution. Perfect
Question 3. The smallest prime number between 80 and 90 is
Solution. 83
Question 4. Numbers having more than two factors are called ……….numbers.
Solution. Composite
Question 5. The LCM of two or more given numbers is the lowest of their common……….
Solution. Multiples
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers True/False
Question 1. If the sum of the digits of a number is divisible by 3, then the number itself is divisible by 9.
Solution. False
Question 2. LCM of two or more numbers is divisible by their HCF.
Solution. Flase
Question 3. Two consecutive even prime numbers are known astwin primes.
Solution. False
Question 4. A number with three or more digits is divisible by 6, if the number formed by its last two digits (i.e. ones and tens) is divisible by 6.
Solution. True
Question 5. The LCM of two co-prime numbers is equal to the product of the numbers.
Solution. True
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Match the Columns
Question 1. Given below are two columns: Column A and Column B. Match each item of Column A with the corresponding item of Column B.
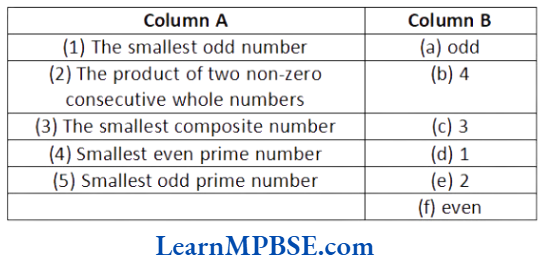
Solution. (1) → (d), (2) → (f), (3) → (b), (4) → (e), (5) → (c)
Question 2. Match each item of Column A with the corresponding item of Column B.
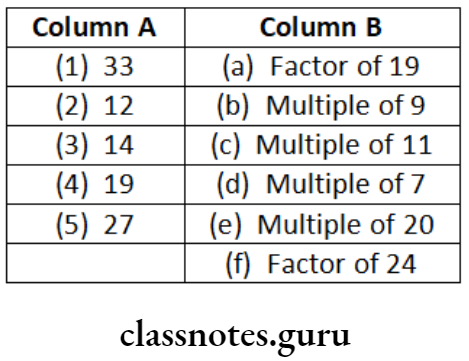
Solution. (1) → (c), (2) → (f), (3) → (d), (4) → (a), (5) → (b)
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Case Based Questions
Question 1. A photographer is hired to take group photographs of students in each class in a school. He arranges the students along with teachers in rows for the photograph. His arrangement has
- atmost 50 people.
- an equal number of people in each row.
A row consists of a minimum of 3 people and a maximum of 8 people.
(1) There are 35 people (students and teachers) in a class for a group photograph. What are the possible arrangements for them?
(2) The photographer arranged some of the students in 6 rows. What can be the maximum number of students in the photograph?
(a) 18
(b) 36
(c) 48
(d) 60
(3) How did the students of Class 7 which are 30 in number want to take a photograph along with 2 teachers. Which of the following is the possible arrangement for them?
(a) 2 rows with 16 students in each.
(b) 4 rows with 8 students/teachers in each.
(c) 5 rows with 6 students in each and 1 row for teachers.
Solution. (1) Total number of people (students and teachers) = 35
∴ Factors of 35 are 1, 5, 7 and 35.
Hence, possible arrangements
= 7 rows and 5 students/teachers per row
or 5 rows and 7 students/teachers per row
(2) (c) The photographer arranged students in 6 rows.
Given, maximum number of people in a row = 8
∴ Maximum number of students = 6 x 8=48
(3) (b) There are 30 students and 2 teachers in class 7.
Thus, in total 32 people.
Let us consider maximum people in a row i.e. 8.
So, divide 32 by 8 to know the number of rows.
32 ÷ 8 = 4
Hence, 4 rows with 8 students/teachers in each.
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Very Short Answer Type Questions
Question 1. Write the first three multiples of each of the following
(1) 11
(2) 12
Solution. (1) First three multiples of 11 = 11, 22, 33
(2) First three multiples of 12 = 12, 24, 36
Question 2. Write the greatest and the smallest prime number between 10 and 20.
Solution. Greatest prime number = 19
Smallest prime number = 11
Question 3. Write all the prime numbers between
(1) 10 and 15
(2) 20 and 35
Solution. (1) Prime numbers between 10 and 15 = 11, 13
(2) Prime numbers between 20 and 35 = 23, 29, 31
Question 4. Which of the following are composite numbers?
7, 13, 16
Solution. Given numbers are 7, 13, 16.
Factors of 7 = 1,7
Factors of 13 = 1,13
Factors of 16 = 1, 2,4,8,16
∴ 16 is a composite number.
Question 5. Write the common factor of 6 and 10.
Solution. Factors of 6 = 1, 2, 3,6
Factors of 10 = 1, 2, 5,10
Common factors of 6 and 10 = 1, 2
Class 6 Maths Chapter 3 Solutions
Question 6. Write the highest common factor of 6 and 15.
Solution. Factors of 6=1, 2, 3, 6
Factors of 15 = 1, 3, 5, 15
Common factors = 1, 3
Highest common factor = 3
Question 7. Write the first two common multiples of 5 and 15.
Solution. Multiples of 5 = 5, 10, 15, 20, 25, 30,…
Multiples of 15 = 15, 30,…
First two common multiples = 15, 30
Question 8. Find the prime factorisation of 40.
Solution. Here, we have 40
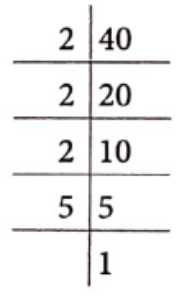
∴ 40 = 2 × 2 × 2 × 5
Question 9. If 3 and 10 are two co-prime numbers, then find their LCM.
Solution. We know that the LCM of two co-prime numbers is equal to their product.
∴ The LCM of 3 and 10 = 3 x 10 = 30
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Short Answer Type Questions
Question 1. Give the factorisation of the following numbers.
(1) 136
(2) 252
Solution.
(1) We have, 136
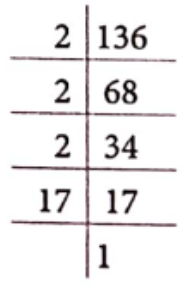
∴ 136 = 2 x 2 x 2 x 17
(2) We have, 252
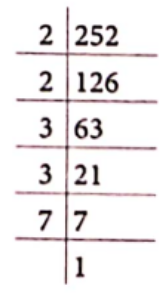
∴ 252 = 2 x 2 x 3 x 3 x 7
Question 2. Test the divisibility of the following numbers.
(1) 4834 by 2
(2) 723 by 3
(3) 495 by 3 and 5
(4) 2853 by 3 and 9
Solution. (1) Given number is 4834. Here, unit place is 4. So, it is divisible by 2.
(2) Sum of digits of the number = 7 + 2 + 3 = 12, which is divisible by 3.
Hence, the number 723 is also divisible by 3.
(3) Here, unit place is 5. So, it is divisible by 5 and sum of digits = 4 + 9 + 5 = 18. So, it is divisible by 3.
(4) Sum of digits of the number = 2 + 8 + 5 + 3 = 18, which is divisible by 3 and 9 both.
Question 3. In each of the following numbers, replace * by the smallest number to make it divisible by 3.
(1) 27 * 4
(2) 53 * 46
Solution. For a number to be divisible by 3, the sum of the digits of the given number should be divisible by 3.
(1) Sum of digits of 27 * 4 = 2 + 7 + 4 = 13
∴ Replace * by 2
(2) Sum of digits of 53 * 46 = 5 + 3 + 4 + 6 = 18
∴ Replace * by 0
Class 6 Maths Chapter 3 Solutions
Question 4. Determine the least number, which when divided by 3, 4 and 5 leaves remainder 2 in each case.
Solution. First of all, we find the LCM of 3, 4 and 5.

LCM = 2 x 2 x 3 x 5 = 60
Hence, the required number = 60 + 2 = 62
Question 5. Find the HCF of the following numbers using prime factorisation method.
(1) 84 and 98
Solution. (1) We have, 84 and 98
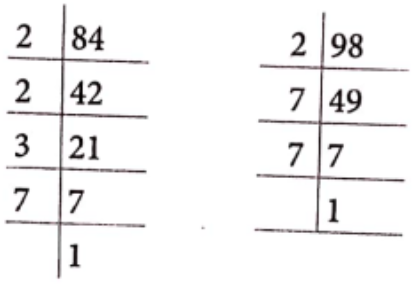
84 = 2 x 2 x 3 x 7 and 98 = 2 x 7 x 7
∴ HCF = 2 x 7 = 14
Question 6. Find the LCM of 160, 170 and 90.
Solution. We have,

Hence, LCM of given numbers
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 17
= 24480
Question 7. Find the LCM of 112, 168, 266 by prime factorisation method.
Solution. We have, 112, 168 and 266

112 = 2 x 2 x 2 x 2 x 7;
168 = 2 x 2 x 2 x 3 x 7
266 = 2 x 7 x 19
∴ LCM = 2 x 2 x 2 x 2 x 3 x 7 x 19 = 6384
Question 8. Three belss ring at intervals of 48 min, 60 min and 90 min, respectively. If all the three bells ring together at 10:00 am, then at what time will the three bells ring again that day?
Solution. We have to find the LCM of 48, 60 and 90

LCM = 2 x 2 x 2 x 2 x 3 x 3 x 5
= 720 min
= \(\frac{720}{60}=12 \mathrm{~h}\)
∴ Bells ring together again at (10:00 am + 12 hr) at 10:00 pm
Question 9. Five bells begin to toll together at intervals of 9 sec, 6 sec, 10 sec and 8 sec, respectively, how many times will they toll together in the span of 1 h?
Solution. We have to find the LCM of 9, 6, 4, 10 and 8.

LCM = 2 x 2 x 2 x 3 x 3 x 5 = 360
In 1 h, the ring will toll together = \(\frac{3600}{360}\)
= 10 times
Mp Board Class 6 Maths Important Questions
Question 10. In a colony of 100 blocks of flats numbering 1 to 100, a school van stops at every sixth block while a school bus stops at every tents block. On which stop will both of them stop if they start from the entrance of the colony?
Solution. The common stop at which both van and bus stop is the common multiple of 6 and 10.
Multiples of 6 less than 100 are
6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96.
Multiples of 10 less than 100 are
10, 20, 30, 40, 50, 60, 70, 80, 90.
Common multiples of 6 and 10 are 30, 60 and 90.
So, the school van and bus both will stop together at blocks 30, 60 and 90.
Question 11. For an international school competition, student’s stay is booked in two hotels 148 students in Hotel 1 and 164 students in Hotel 2. An equal number of students are accommodated in each hotel room. What can be the maximum number of students in a room?
Solution. Factors of 148 are 1, 2, 4, 37, 74 and 148.
Factors of 164 are 1, 2, 4, 41, 82 and 164.
The common factors of 148 and 164 are 1, 2 and 4.
The highest common factor of 148 and 164 is 4.
∴ Maximum number of students than can be accommodated in a room is 4.
MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Long Answer Type Questions
Question 1. Find a 4-digit odd number using each of digits 1, 2, 4 and 5 only once such that when the first and last digits are interchanged, it is divisible by 4.
Solution. The 4-digit number will be an odd number, if the unit place digit is an odd number (i.e. 1 or 5).
Total such odd numbers are
4125, 4215, 1245, 1425, 2145, 2415, 4251, 4521, 5241, 5421, 2451, 2541.
Also we know that any 4-digit number is divisible by 4, if the last two-digit number is divisible by 4.
Consider a number 4521, if we interchage the first and the last digit, the new number will be 1524. Here, we see that the last two digits (i.e. 24) is divisible by 4. So, the number 1524 is divisible by 4.
Similarly, other numbers when we interchange the first and the last digit, divisible by 4 are 4125, 2415, 2451.
Hence, the required 4-digit numbers are 4521, 4125, 2415 and 2451.
Question 2. Three boys step off together from the same place. If their steps measure 36 cm, 48 cm and 54 cm, then at what distance from the starting point will they again step together?
Solution. Given, their step measures are 36 cm, 48 cm and 54 cm.
We must find the LCM of 36, 48, 54,

LCM of 36, 48 and 54 = 2 x 2 x 2 x 2 x 3 x 3 x 3 = 432
They again step together from the starting point at 432 cm i.e. 4 m 32 cm.
Class 6 Maths Chapter 3 Solutions
Question 3. Three brands A, B and C of biscuits are available in packets of 12, 15 and 21 biscuits, respectively. If a shopkeeper wants to buy an equal number of biscuits of each brand, then what is the minimum number of packets of each brand, he should buy?
Solution. In Brand A, number of biscuits=12
In Brand B, number of biscuits = 15
In Brand C, number of biscuits = 21
First of all, we find the LCM of 12, 15 and 21

Now, number of packets of Brand A = \(\frac{420}{12}=35\)
Number of packets of Brand B = \(\frac{420}{15}=28\)
Number of packets of Brand C = \(\frac{420}{21}=20\)
Question 4, On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 46 cm, respectively. What is the minimum distance each should walk, so that each can cover the same distance in complete steps?
Solution. (1) The step measure of each person is 40 cm, 42 cm and 46 cm.So, the minimum distance each should walk is the LCM of 40, 42 and 46.

LCM of 40, 42 and 46 = 2 x 2 x 2 x 3 x 5 x 7 x 23
= 19320 cm = 193.2 m
Class 6 Maths Chapter 3 Solutions
Question 5. A merchant has 130 L of oil of one kind, 190 L of another kind and 250 L of a third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. What should be the greatest capacity of such a tin?
Solution. The greatest capacity of the required measure will be equal to the HCF of 130, 190 and 250 L.
Prime factorisation of 130, 190 and 250 are
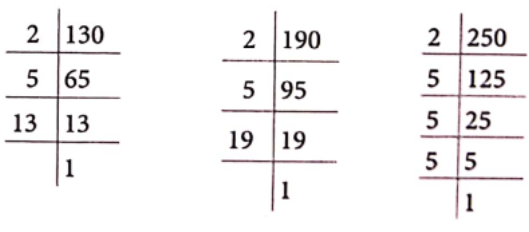
130 = 2 x 5 x 13,190 = 2 x 5 x 19 and 250 = 2 x 5 x 5 x 5
Common factors of 130, 190 and 250 = 2 x 5 = 10
Hence, the greatest capacity of tin should be 10 L.
Question 6. Monica, Heronica and Rajat begin to jog around a circular stadium. They complete their revolution in 42 sec, 56 sec and 63 sec, respectively. How many seconds after will they be together at the starting point?
Solution. Required second of time = LCM of 42, 56 and 63 42, 56, 63

LCM = 2 x 2 x 2 x 3 x 3 x 7 = 504 s
Hence, after 504s, they will be together at starting point.
Question 7. In a school library, there are 780 books of English and 364 books of Science. Ms. Yakang, the librarian of the school wants to store these books in shelves such that each shelf should have the same number of books of each subject. What should be the minimum number of books in each shelf?
Solution. Given, number of English books = 780
and number of Science books = 364
For getting the minimum number of books in each shelf, we have to find the HCF of 780 and 364.
Prime factorisation of 780 and 364.

780 = 2 × 2 × 3 × 5 x 13
and 364 = 2 x 2 x 7 x 13
∴ HCF of 780 and 364 = 2 x 2 x 13 = 52
Hence, the minimum number of books in each shelf is 52.
Question 8. John, Rishi and Feroz participated in track events. During practice sessions, their coach observed that John took 48 sec, Rishi took 72 sec and Feroz took 108 sec to run around a circular track. If they start running together at 6 am for half an hour, how many times will they all come together at a same position?
Solution. John, Rishi and Feroz take 48 sec, 72 sec and 108 sec, respectively to complete round of a circular track. We have to calculate LCM to find the time after which they meet on the starting point for first time.

∴ LCM of 48, 72 and 108 = 2 x 2 x 2 x 2 x 3 x 3 x 3 = 432
So, it means the three persons are in the same position after 432 sec or after 7 min 12 sec.
As it is given that, they start running at 6 am for half an hour.
Hence, John, Rishi and Feroz will all come together at the same position 4 times in half an hour.
Class 6 Maths Chapter 3 Solutions
Question 9. Jaya baked muffins using paper liners and cherries. Some paper liner packets contain 8 liners, while others contain 10 liners. A pacted of cherry contains 6 cherries. Every muffin Jaya baked contained 1 cherry. All cherries and paper liners were used up. What can be the minimum number of muffins baked by her?
Solution. To find the minimum number of muffins Jaya baked, we need to find LCM of the paper liners and cherries.
LCM of paper liners of sizes 8 and 10
= 2 × 2 × 2 × 5 = 40
Hence, we need to find LCM of 40 and 6.
∴ LCM of 40 and 6 = 2 x 2 x 2 x 3 x 5 = 120
Therefore, the minimum number of muffins Jaya baked is 120 muffins.
