MPBSE Class 12 Physics Ohm’s Law Combination Of Cells Notes

Current Electricity

Electric Current and Ohm’s Law Combination Of Cells

A group of cells combined together to increase the circuit current or potential difference is called a battery. Which finds use in torches, radios, tape recorders, etc. Three different combinations of cells are possible

1. Series combination,
2. Parallel combination
3. Mixed combination.

Series Combination of Cells:

Description:

A series combination refers to a configuration of cells where the positive terminal of one cell is linked to the negative terminal of the subsequent cell, and this pattern continues throughout the arrangement.

The positive terminal of the initial cell and the negative terminal of the final cell serve as the two electrodes of the battery assembly.

Calculation of Current:

The Series Combination of Three Cells. Points A and B serve as the positive and negative electrodes of the entire assembly, respectively. Every cell is identical. The electromotive force of each cell is e, while the internal resistance is r. The circuit’s external resistance is R.

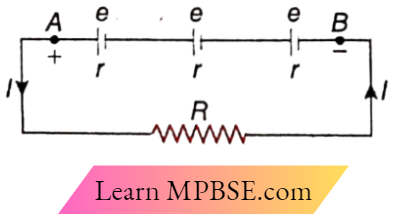
The emf of the whole combination of the cells = e+ e + e = 3e

Total resistance of the circuit = R + r + r + r

= R + 3r.

So, the current through the circuit is,

⇒ \(I=\frac{3 e}{R+3 r}\)

Obviously, if the number of cells by n instead of 3 then the current through the circuit is given by

⇒ \(I=\frac{n e}{R+n r}\)

Ohm’S Law Class 12 Physics Notes

Special cases:

1. When R >> nr, we have

⇒ \(I \approx \frac{n e}{R}\)

i.e., the current through the external circuit becomes n times the current supplied by a single cell. So it can be said that when the internal resistance of each cell is sufficiently small, the current through the circuit increases if we use a series combination of the cells instead of a single cell. For this reason, a series combination of dry cells is used in a torch, radio, etc. instead of a single cell.

2. When R << nr, we have, \(I \approx \frac{n e}{n r}=\frac{e}{r}\) i.e., the current through the external circuit is the same as that supplied by a single cell. So, it can be said that when the internal resistance of each cell is sufficiently high, the current through the circuit remains unchanged even if we use a series combination of the cells instead of a single cell.

3. Out of n number of cells if x cells are connected in reverse order, the number of cells connected correctly is (n-x). The total emf of these (n-x) cells is (n-x)e. As x cells act in the opposite direction the effective emf of the combination of the cells =(n- x)e- xe = (n-2x)e. In this case, the total internal resistance of the combination nr remains unchanged. So, the current through the circuit is

⇒ \(I=\frac{(n-2 x) e}{R+n r}\)

Parallel Combination of Cells:

Description: If all the positive poles of a number of cells are connected to one point and all the negative poles to another point, then this combination of cells is called a parallel combination.

The two points referred to are connected to the main circuit. These two points act as the positive and the negative electrode of the combination.

Calculation of current: The parallel combination of three cells. Points A and B are respectively the positive and the negative electrodes of the whole combination. Each cell is identical. The Entf of each cell is e and internal resistance is r. External resistance of the circuit =R.

The emf of the combination of the cells is e. The internal resistances are arranged in parallel combinations. So if R’ be the equivalent resistance of the internal resistances, then

⇒ \(\frac{1}{R^{\prime}}=\frac{1}{r}+\frac{1}{r}+\frac{1}{r}=\frac{3}{r} \quad \text { or, } R^{\prime}=\frac{r}{3}\)

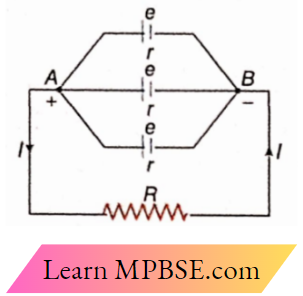
The external resistance R is connected in series with R’. So, the total resistance of the circuit

⇒ \(R+R^{\prime}=R+\frac{r}{3}\)

Therefore, current through the circuit is

⇒ \(I=\frac{\text { emf of the combination of the cells }}{\text { total resistance of the circuit }}=\frac{e}{R+\frac{r}{3}}\)

Obviously, if the number of cells be n instead of 3 then the current through the circuit is given by

⇒ \(I=\frac{e}{R+\frac{r}{n}}=\frac{n e}{n R+r}\)

Mpbse Class 12 Physics Ohm’S Law Solutions

Parallel Combination of Cells Special cases:

1. When nR >> r i.e., \(R \gg \frac{1}{n} r, I \approx \frac{n e}{n R}=\frac{e}{R}\)

i.e., the current in the external resistance is the same as that supplied by a single cell. So it can be said that when \(\frac{1}{n}\) part of the internal resistance of each cell is sufficiently small, the current through the circuit remains unchanged even if we use a parallel combination of the cells instead of a single cell.

2. When nR << r i.e., \(R \ll \frac{1}{n} r, I \approx \frac{n e}{r}\) i.e., the current in the external resistance becomes n times the current supplied by a single cell.

So, it can be said that when \(\frac{1}{n}\) part of the internal resistance of each cell is sufficiently high, the current through the circuit increases if we use a parallel combination of the cells instead of a single cell.

It is evident that if the combination is not connected to an external circuit, then one or more than one closed circuit is formed with the cells between A and B.

So, if the emfs of the cells are different, a local current flows through each cell. As a result, the cells get unnecessarily wasted.

It is to be noted that in series combination if it is not connected with an external circuit, no current flows through the cells.

Combination Of Cells Class 12 Notes

Mixed Combination of Cells:

Description: In a mixed combination, several rows of cells are connected in parallel and each row contains a number of cells in series.

Suppose, a row is made with n number of identical cells in series, m number of such rows are connected in a parallel combination. So, the number of cells in the whole combination = mn. The 3 rows with 4 cells in each row. Total number of cells

= 3 x 4

= 12 [n =-4; m = 3].

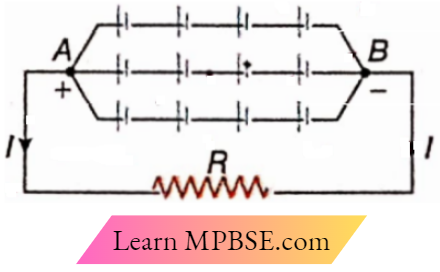
Calculation of current: Suppose, emf of each cell = e internal resistance of each cell = r.

Hence, emf in each row = ne internal resistance of each row = nr. Since, all the rows are connected to two fixed points A and B, the emf of the whole combination of cells =ne. Again, there are m rows each having an internal resistance nr. SoifR’ be the equivalent resistance of the internal resistances, then

⇒ \(\frac{1}{R^{\prime}}=\frac{1}{n r}+\frac{1}{n r}+\cdots \text { up to } m \text { number of terms }=\frac{m}{n r}\)

or, \(R^{\prime}=\frac{n r}{m}\)

The external resistance R is connected in series with this combination of cells. So, the resistance of the whole circuit

⇒ \(R+R^{\prime}=R+\frac{n r}{m}\)

Therefore, current through the circuit is

⇒ \(I=\frac{n e}{R+\frac{n r}{m}}=\frac{m n e}{m R+n r}\)….(1)

Combination Of Cells Class 12 Notes

Condition for maximum current: The given number of cells =mn = constant (m and n may not be constants separately). The cells are to be arranged in such a way, that the current flowing through R becomes maximum. Now, from the equation

1. We can write

⇒ \(I=\frac{m n e}{(\sqrt{m R}-\sqrt{n r})^2+2 \sqrt{m n R r}}\)…(2)

The current will be maximum when \((\sqrt{m R}-\sqrt{n r})^2\) is minimum since the other terms in the right-hand side of the equation

2. Are constants. The minimum value of \((\sqrt{m R}-\sqrt{n r})^2\) is zero, since it is a perfect square of real numbers. Hence, for maximum current in a mixed combination of cells,

⇒ \((\sqrt{m R}-\sqrt{n r})^2=0\)

or, mR = nr…(3)

So, when mR = nr, the maximum current,

⇒ \(I_{\max }=\frac{n e}{2 R}=\frac{m e}{2 r}\)…..(4)

From equation (3) we have,

⇒ \(R=\frac{n r}{m}=R^{\prime}\) = equivalent resistance of the internal resistances of the cells in combination

Hence, to get the maximum current in the circuit the cells are to be arranged in series and parallel combinations in such a way that the equivalent resistance of the internal resistances of the cells equals, the external resistance

Parallel And Series Combination Of Cells Class 12

Comparison among Different Combinations of Cells:

1. Let us take the number of cells. Now if the external resistance is much greater than the total internal resistance of the cells i.e., if R >> mnr, it is advantageous to connect the cells in series.

When \(\frac{1}{mr}\) part of the internal resistance r is much greater than the external resistance R i.e., \(\frac{r}{mr}\) >> R, it is advantageous to connect the cells in parallel. If the difference of R and r is not much, then by obeying the condition mR = nr, the magnitude of the niirreSt increased in a mixed combination.

2. In the case of parallel and mixed combinations the cells form closed circuits among themselves. So, if the connection of the cells with the external circuit remains cut off, the flow of current through the calls continues and the cells decay unnecessarily.

So it is desirable to disconnect the cells when they are not in use. In the series combination of the cells total current is divided among the cells and in the case of mixed combination the total current is divided among the rows.

For this reason, wastage of energy due to internal resistance in series combination is the highest, and In parallel combination, it is the lowest.

4. Appropriate currents and potential differences are to be developed in the external circuit to run different electrical instruments properly. This necessitates suitable connection of the cells in series, in parallel or sometimes in a mixed combination.

Ohm’s Law Combination Of Cells Numerical Examples

Example 1. Two identical cells each of emf 1.5.V are connected in series. If this combination of cells is connected to a resistance and a galvanometer in series, the current that flows through the circuit is 1 A. If the cells are connected in parallel the current becomes 0.6 A. Determine the internal resistance of each cell.
Solution:

Let the internal resistance of each cell = r, the total resistance of the galvanometer, and the external resistance =R. When the cells, are connected in series

emf = 1.5 + 1.5

= 3 V;

internal resistance = r+r

= 2r

So, \(\text { current }=\frac{3}{R+2 r} \quad\)

or, \(1=\frac{3}{R+2 r} \quad\)

or, \(R+2 r=3\)

or, R = 3 – 2r….(1)

When the cells are connected in parallel,

emf = 1.5 V; internal resistance = \(\frac{r \times r}{r+r}=\frac{r}{2}\)

So, \(\text { current }=\frac{1.5}{R+\frac{r}{2}} \quad\)

or, \(0.6=\frac{1.5}{R+\frac{r}{2}}\)

or, \(R+\frac{r}{2}=\frac{1.5}{0.6}=\frac{5}{2} \quad \text { or, } R=\frac{5}{2}-\frac{r}{2}\)…(2)

from (1) and (2) we have,

⇒ \(R+\frac{r}{2}=\frac{1.5}{0.6}=\frac{5}{2} \quad\)

or, \(R=\frac{5}{2}-\frac{r}{2}\)

or, \(3 r=1 \quad \text { or, } r=\frac{1}{3} \Omega\)

Physics Ohm’s Law Combination Of Cells Notes

Example 2. 48 similar cells each of emf 1.5 V and Internal resistance 2Ω are used for sending current through o’ resistance of 6Ω. What will be the current if the cells are connected in the following way:

1. 6 rows and 8 cells in a row,
2. 4 rows and 12 cells in a row.

Solution:

Emf of each cell (e) = 1.5V, internal resistance (r) = 2Ω, external resistance (R) = 6Ω.

1. No. of cells in a row (n) = 8, No.- ofrows (m) = 6. ‘ ‘

So, current,

⇒ \(I=\frac{m n e}{m R+n r}=\frac{6 \times 8 \times 1.5}{6 \times 6+8 \times 2}=\frac{72}{52}=\frac{18}{13}=1.385 \mathrm{~A}\)

2. No of cells in a rovv (n) = 12 ,No. ofrows (m) = 4.

So, current,

⇒ \(I=\frac{m n e}{m R+n r}=\frac{4 \times 12 \times 1.5}{4 \times 6+12 \times 2}=\frac{72}{48}=1.5 \mathrm{~A}\)

Example 3. What is the minimum number of cells each of emf 10V and internal resistance 1Ω to pass a current of 10 A through a resistance R of 3Ω? What is the discharging power of R?
Solution:

By arranging n number of cells in each of. the m number of rows we have,

⇒ \(I=\frac{m n e}{m R+n r}\)

To use the minimum number of cells, we are required to fulfill the condition of maximum current.

In that case,

mR = nr

or, m.3 = n.1

or, n = 3m

Again, maximum current,

⇒ \(I_0=\frac{m n e}{2 m R}=\frac{n e}{2 R} \text { or, } 10=\frac{n \times 10}{2 \times 3} \text { or, } n=6\)

∴ \(m=\frac{n}{3}=\frac{6}{3}=2\)

So, 12 cells need to be arranged in 2 rows and each row will have 6 cells.

Discharging power of R, P = \(I_0^2 R\) =(10)2 X 3 = 300 W

Parallel And Series Combination Of Cells Class 12

Example 4. Electromotive forces of E₁ and E₂ are ‘respectively, 4V and 8V; r₁ = 0.5Ω, r₂ – 1Ω. Determine the current and the terminal potential difference for each cell.

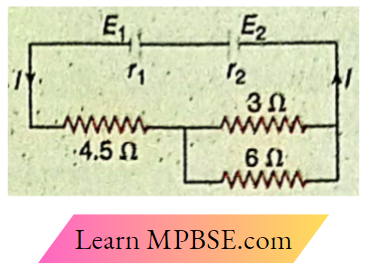
Solution:

The two cells are connected in opposition and E₂ > E₁.

So, current,

⇒ \(I=\frac{E_2-E_1}{r_1+r_2+4.5+\frac{3 \times 6}{3+6}}=\frac{8-4}{0.5+1+4.5+2}=\frac{4}{8}=0.5 \mathrm{~A}\)

Since the two cells are connected in series, current through each cell = 0.5 A.

Potential differences across the terminals of the second cell,

V₂ = E₂-Ir₂

= 8-0.5 x l

= 7.5 V

Since the current is flowing through the first cell in the opposite direction, the potential difference across the terminals of the first cell,

Vl = El + Ir₁

= 4 + 0.5 X 0.5

= 4.25 V