MPBSE Class 12 Physics Ohm’s Law Combination Of Resistances Notes

Electric Current and Ohm’s Law Combination Of Resistances

Several resistances or resistors such as light bulbs, fans, pumps, etc. may bo Joined In a network variously for various purposes.

A combination of resistances can ho of three types:

Aeries combination,

Parallel combination

Mixed combination.

Equivalent resistance:

If a single resistance is used Instead of a combination of resistances, to keep the current unchanged in the circuit, then that single resistance is called the equivalent resistance of the combination.

Ohm’S Law Class 12 Physics Notes

Series Combination of Resistances:

A number of resistances are said to be connected In scries if they are connected end to end consecutively so that the same current flows through each resistance when a potential difference is applied across the combination.

Calculation of equivalent resistance: Three resistances R₁, R₂, and R₃ arc connected in series in between the two points A and D of on electrical circuit.

Let VA, VB, VC, and VD be the potentials at points A, B, C, and D respectively.

If I am the current flowing in the circuit, then according to Ohm’s law

V_A-V_B = IR₁….(1)

V_B – V_C = IR₂…..(2)

V_C – V_D = IR₃….(3)

Adding (1), (2) and (3) we have,

V_A-V_D = I(R₁+ R₂+R₃)…..(4)

If R be the equivalent resistance of the combination and if it is connected between die points A and D, the main current flowing in the circuit will remain die same. So

V_A-V_D = IR…..(5)

From (4) and (5) we have

R = R₁ + R₂ + R₃

Combination Of Resistances Class 12 Notes

Similarly, if n number of resistances are connected in series instead of the three resistances then,

⇒ \(R=R_1+R_2+R_3^{\wedge}+\cdots+R_n=\sum_{i=1}^n R_i\)….(6)

So, the equivalent resistance of a series combination = the sum of the individual resistances.

A few characteristics of the series combination of resistances:

The same current flows through each resistance.

The total potential difference across the combination is equal to the sum of the individual potential difference across each resistance.

Since the current is constant, an individual potential difference is directly proportional to the individual resistance.

Unit 2 Current Electricity Chapter 1 Electric Current and Ohm’s Law Combination Of Resistances Numerical Examples

Example 1. Three resistances of magnitudes 20Ω, 30Ω, and 40Ω, are connected in series,

1. What is the equivalent resistance?
2. If the potential difference across the resistance 20 A is 1 V, calculate the potential difference across the other two resistances and also the total potential difference across the combination.

Solution:

1. Equivalent resistance, R = 20 + 30 + 40

= 90Ω

2. For the resistance of 20Ω

⇒ \(\text { current, } I=\frac{\text { potential difference }}{\text { resistance }}=\frac{1}{20} \mathrm{~A}\)

Since it is a series combination, the current everywhere is \(\frac{1}{20}\)A.

∴ The potential difference across 30Ω resistance

⇒ \(\frac{1}{20} \times 30\)

= 1.5 V

and across the 40Ω resistance = \(\frac{1}{20} \times 40\)

= 2.0 V

⇒ \(\frac{1}{20} \times 90\)

= 4.5 V

Mpbse Class 12 Physics Ohm’S Law Solutions

Example 2. \(\rho_1 \text { and } \rho_2\) are the resistivities of the materials of two wires of the same dimensions. What will be the equivalent resistivity of the series combination of the two wires?
Solution:

Let l be the length and A be the cross-sectional area of each wire.

The equivalent resistance in series combination is

⇒ \(R=R_1+R_2=\rho_1 \frac{l}{A}+\rho_2 \frac{l}{A}=\left(\rho_1+\rho_2\right) \frac{l}{A}\)….(1)

In the series combination, the length of the conductor =21; cross-sectional area = A.

Let the equivalent resistivity be \(\rho\)

∴ \(R=\rho \frac{2 l}{A}\)…..(2)

Comparing (1) and (2) we have,

⇒ \(\rho \frac{2 l}{A}=\left(\rho_1+\rho_2\right) \frac{l}{A} \quad \text { or, } \rho=\frac{\rho_1+\rho_2}{2}\)

Parallel Combination of Resistances:

Two or more resistors are said to be connected in parallel if one end of each is connected to a common point, and the other end to another point.

When this combination is joined in a circuit, the main current is distributed among the resistors, but the potential difference across each is the same

Parallel And Series Combination Of Resistances Class 12

Calculation of equivalent resistance: Three resistances R₁, R₂, and R₃ are connected in parallel in between two common points A and B of an electrical circuit. Let VA and VB be the potentials at points A and B respectively.

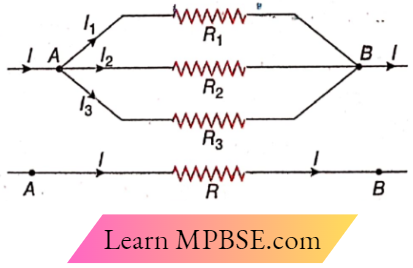
A current I is divided into three parts through these resistances.

I = I₁ +I₂+ I₃…(1)

A and B are the common terminals of each of the three resistances. So according to Ohm’s law,

For the resistance \(R_1, I_1=\frac{V_A-V_B}{R_1}\)….(2)

For the resistance \(R_2, I_2=\frac{V_A-V_B}{R_2}\)…..(3)

For the resistance \(R_3, I_3=\frac{V_A-V_B}{R_3}\)….(4)

Adding (2), (3) and (4) we get,

⇒ \(I_1+I_2+I_3=\left(V_A-V_B\right)\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\right)\)

or, \(I=\left(V_A-V_B\right)\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\right)\)….(5)

If R is the equivalent resistance of the combination and if it is connected between points A and B, the main current flow in the circuit will remain the same. So

⇒ \(I_1+I_2+I_3=\left(V_A-V_B\right)\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\right)\)…(6)

From (5) and (6) we get \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\)

Similarly, if n number of resistances are connected in parallel
instead of the three resistances, we have

⇒ \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\cdots+\frac{1}{R_n}=\sum_{i=1}^n \frac{1}{R_i}\)…(7)

So, the reciprocal of the equivalent resistance of the parallel combination = the sum of the reciprocals of the individual resistances.

Parallel And Series Combination Of Resistances Class 12

Calculation of current in different resistances: If R be the equivalent resistance of a parallel combination connected between two points A and B of the circuit, the main current is given by,

⇒ \(I=\frac{V_A-V_B}{R} \text { or, } V_A-V_B=I R\)

The potential difference of each resistance is ( V_A– V_B).

So, the current flowing through Rl is

⇒ \(I_1=\frac{V_A-V_B}{R_1}=\frac{I \cdot R}{R_1}=I \cdot \frac{R}{R_1}\)

This rule is applicable to each resistance of the parallel combination.

So, the current flowing through any resistance

⇒ \(\text { main current } \times \frac{\text { equivalent resistance }}{\text { corresponding resistance }}\)

A few characteristics of parallel combinations of resistances:

1. The potential difference across each resistance is the same.

2. \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\cdots ; \text { so } \frac{1}{R}\) is greater than each of \(\frac{1}{R_1}+\frac{1}{R_2}+….\) etc. Therefore, the value of R is less than each of R₁, R₂….etc i.e., the equivalent resistance is less than each of the resistances in the combination.

3. Total ament through the parallel combination is the sum of the individual currents through the resistances.

4. Since the potential difference across each resistance Is constant, individual currents are Inversely proportional to the individual resistances.

In domestic electrical circuits, appliances such as bulbs, electric fan, heaters, etc. operate with the same potential difference (220 V), So these are connected in parallel.

Special case (parallel combination of two resistances): Suppose two resistances R₁ and R₂, are connected in parallel. Let their equivalent resistance be R. Then,

⇒ \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2} \quad \text { or, } R=\frac{R_1 R_2}{R_1+R_2}\)

The potential difference across the two ends of the combination,

⇒ \(V=I R=I \frac{R_1 R_2}{R_1+R_2}\)

A potential difference of each resistance = V.

So, current flowing through \(R_1, I_1=\frac{V}{R_1}=I \cdot \frac{R_2}{R_1+R_2}\)

Similarly, current flowing through \(R_2, I_2=I \cdot \frac{R_1}{R_1+R_2}\)

So, current flowing through a resistance

⇒ \(=\text { main current } \times \frac{\text { other resistance }}{\text { sum of the two resistances }}\)

This formula will often be found handy in numerical calculations

Electric Current And Resistance Class 12 Notes

Electric Current and Ohm’s Law Numerical Examples

Example 1. ABC is a triangle formed by wires. The resistances of the sides AB, BC, and CA are respectively 40Ω, 60Ω and 100Ω. What is the equivalent resistance between points A and B?

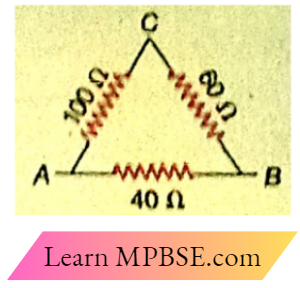
Solution:

Along the path ACD the two resistances 100Ω and 60Ω are connected in series. So the equivalent resistance of the ACD

= 100 + 60

= 160Ω.

Again, the resistance 40Ω of the side All Is connected In parallel with the path ACB, So the equivalent resistance between the two points A and B is

⇒ \(R=\frac{160 \times 40}{160+40}=\frac{160 \times 40}{200}=32 \Omega\)

Example 2. Determine the equivalent resistance between points A and B

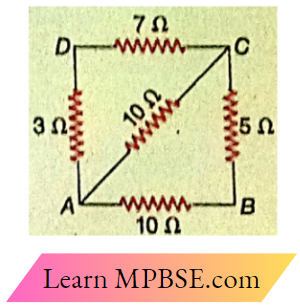
Solution:

The equivalent resistance of the path ADC = 3 + 7 = 10Ω.

With the path ADC, the 10Ω resistance of the diagonal AC Is connected in parallel.

So, the equivalent resistance of AD, DC, and AC

⇒ \(\frac{10 \times 10}{10+10}=5 \Omega \text {. }\)

With this 5Ω resistance, the 5Ω resistance of the side DC Is connected In series. So the equivalent resistance of 5 ft and DC

= 5 + 5

= 10Ω

Now, the 10Ω resistance of AD is also In, parallel with the above equivalent resistance 10Ω.

So, the equivalent resistance between A and B is

⇒ \(R=\frac{10 \times 10}{10+10}=5 \Omega\)

Electric Current And Resistance Class 12 Notes

Example 3. The two circuits draw equal currents from the battery. But the current through the resistance R in the second circuit is \(\frac{1}{10}\)th of that the first circuit. Determine the values of R₁ and R₂.

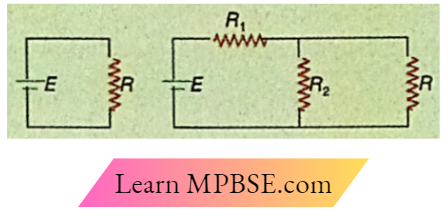
Solution:

Current drawn from the battery in first case,

⇒ \(I_1=\frac{E}{R}\)…..(1)

Current drawn from the battery in the second case,

⇒ \(I_2=\frac{\text { total emf }}{\text { total resistance }}=\frac{E}{R_1+\frac{R R_2}{R+R_2}}\) [∵ R1 is in series with the parallel combination of R and R2 ]

So, \(I_2=\frac{E\left(R+R_2\right)}{R_1 R+R_1 R_2+R R_2}\)….(2)

Accordingly, \(I_1=I_2 \quad \text { or, } \frac{E}{R}=\frac{E\left(R+R_2\right)}{R_1 R+R_1 R_2+R R_2}\)

or, R₁R + R₁R₂ + RR₂ = R₂ + RR₂

or, R₂-R₁R- R₁R₂ = 0 ….(3)

Now, current through the resistance R,

⇒ \(I_R=I_2 \frac{R_2}{R+R_2}\)…(4)

It is given that, \(I_R=\frac{I_1}{10} \quad \text { or, } I_R=\frac{I_2}{10} \quad\left(… I_1=I_2\right)\)

or, \(\frac{I_2 R_2}{R+R_2}=\frac{I_2}{10} \text { [from equation (4)] }\)

or, \(10 R_2=R+R_2 \quad \text { or, } R_2=\frac{R}{9}=0.11 R\)

Putting R2 in equation (3), we get

⇒ \(R^2-R_1 R-R_1 \frac{R}{9}=0 \quad \text { or, } R_1 \frac{10 R}{9}=R^2\)

⇒ \(R_1=\frac{9}{10} R=0.9 R\)

Required resistance, R₂ = 0.117R and 7R₁ = 0.9R

Mpbse Class 12 Physics Ohm’S Law Solutions

Example 4. You are given several identical resistances, each of value R = 10Ω and each capable of carrying a maximum combination of these resistances to obtain a resistance of 5Ω which can carry a current of 4 A. Find the minimum number of resistances of the Type R that will be required.
Solution:

The resistances have to be connected in a series of parallel combinations. Since each resistance can carry a current of 1 A, to pass a 4 A current, we need four paths in parallel. Let r be the resistance of each path.

The equivalent resistance of 4 parallel paths will be \(\frac{r}{4}\).

According to the given problem,

⇒ \(\frac{r}{4}\) = 5

∴ r = 5 x 4

= 20Ω

In order to have 20Ω resistance in each path, two resistances each of resistance 10Ω have to be connected in series.

Since there are four paths, the total number of resistances required

=2 x 4

= 8.

Example 5. A wire of uniform cross-section and length l has a resistance of 16Ω. It is cut into four equal parts. Each part is stretched uniformly to length l and all four stretched parts are connected in parallel. Calculate the total resistance of the combination so formed. Assume that the stretching of the wire does not cause any change in the density of its material.
Solution:

Let the cross-section of the wire change from A to Aj when it is cut into four parts.

As density remains constant, so volume also remains constant.

Volume of each part before stretching = volume of each part after stretching

or, \(\frac{A l}{4}=A_1 l \quad \text { or, } A_1=\frac{A}{4}\)

So resistance of each part, \(R_1=\frac{\rho l}{\frac{A}{4}}=\frac{4 \rho l}{A}\)

Therefore, the equivalent resistance of the parallel combination,

⇒ \(R_{\mathrm{eq}}=\frac{R_1}{4}=\frac{\rho l}{A}=16 \Omega\) [∵ initial resistance = \(\frac{\rho l}{A}=16 \Omega\)]