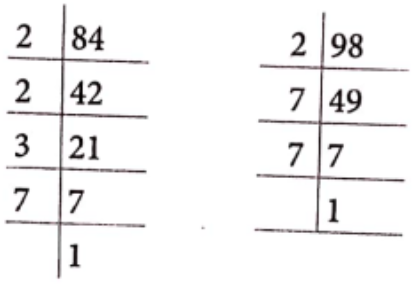
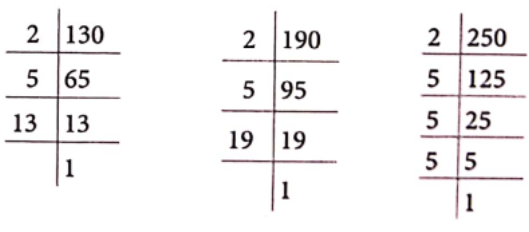
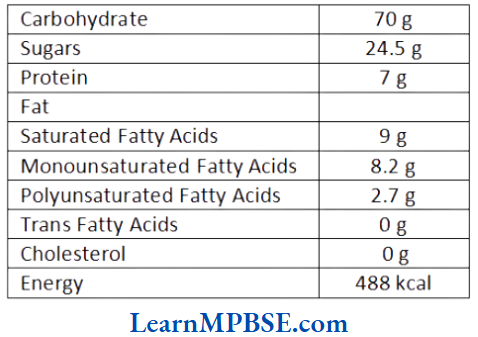
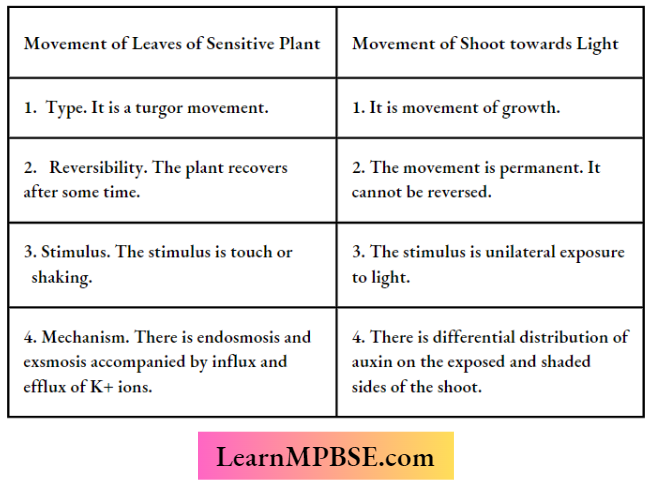
MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes

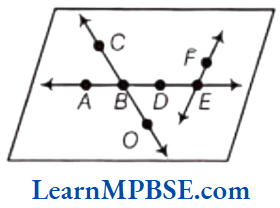
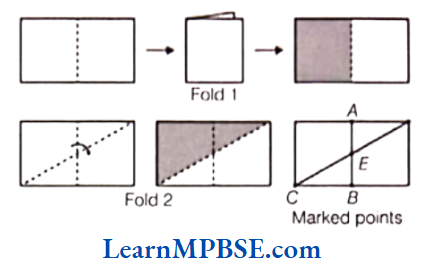
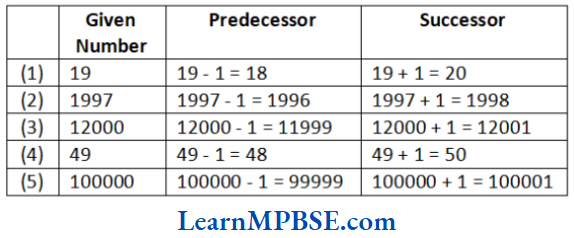
Line Segment

A line segment is a fixed portion of a line. This make it possible to measure a line segment. The distance between the end points of a line segment is called its length. We use the length to compare line segments.

To compare any two line segments, a relationship between their lengths is established.

1. Comparison by Observation

We can compare the line segments by just looking at them.

e.g.

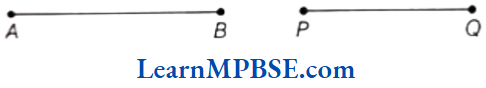
Here, \(\overline{A B}>\overline{P Q}\)

Note it You cannot always be sure about your usual judgement.

2. Comparison by Tracing

In this method, we can compare the line segment using tracing paper. This method depends upon the accuracy in tracing the line segment. If you want to compare the length of a line segment with another line segment, you have to trace another line segment.

e.g.

To compare \(\overline{A B}\) and \(\overline{C D}\), trace CD and place the traced segment on \(\overline{A B}\). As a result, we get

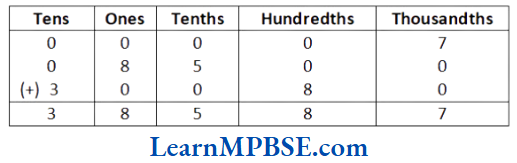
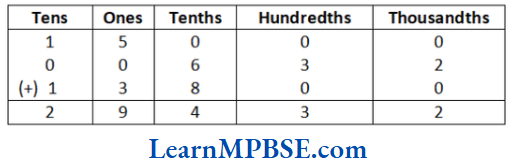
3. Comparison using Ruler and Divider Ruler and Divider

A graduated ruler and the divider are useful to compare lengths of line segments. One side of the ruler is divided into 15 parts.

Each of these 15 parts is of length 1 cm.. Each centimetre is divided into 10 subparts. Each subpart of the division of 1 cm is 10 mm.

MP Board Class 6 Maths Solutions

Read and Learn More MP Board Class 6 Maths Solutions

1 cm = 10 mm

Note it

1 mm = 0.1 cm, 2 mm = 0.2 cm

3.6 cm = 3 cm and 6 mm.

Use of Ruler to Measure Length

For comparison, place the 0 mark of the ruler at A. Read the mark against B. This gives the length of AB.

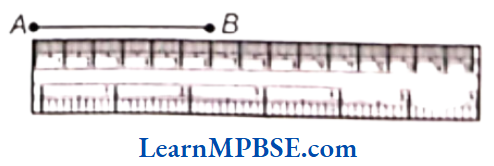
Suppose, the length of AB is 6 cm, we may write Length AB = 6 cm or more simply as \(\overline{A B}\) = 6 cm.

There are chances of errors even in this procedure.

Positioning Error

To get correct measure, the eye should be correctly positioned, just vertically above the mark. Otherwise, errors can happen due to angular viewing.

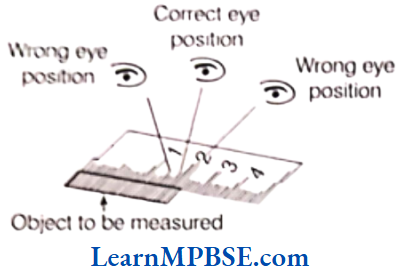
We can avoid this problem using divider.

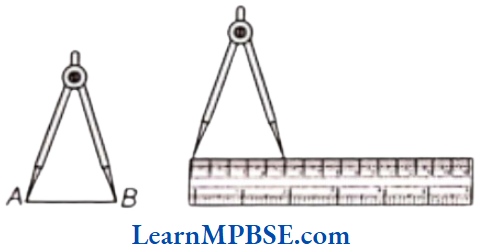
Let us use the divider to measure length.

MP Board Class 6 Book Solutions

Use of Divider to Measure Length

Open the divider. Place the end point of one of its arms at A and the end point of the second arm at B. Taking care that opening of the divider is not disturbed, lift the divider and place it on the ruler. Ensure that one end point is at the zero mark of the ruler. Now, read the mark against the other end point.

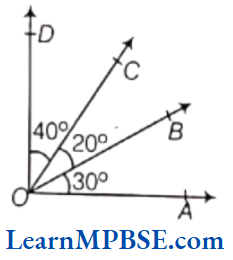
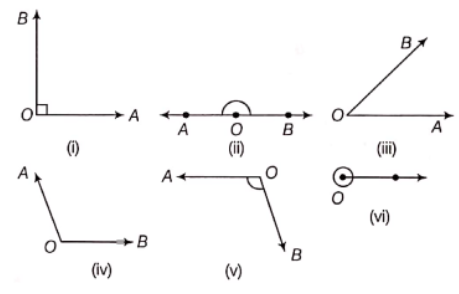
MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Right and Straight Angles

Angle

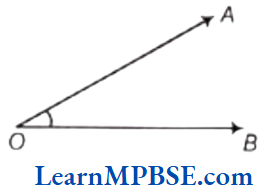
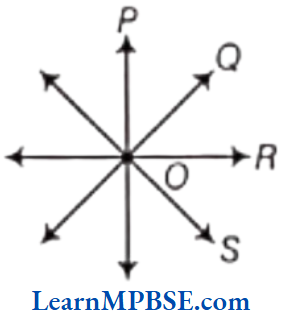
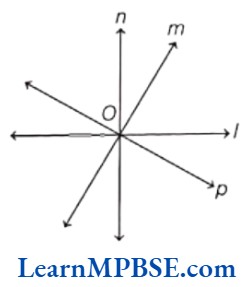
An angle is a figure formed by two rays with the same initial point. It is measured in degrees (°). The common initial point is also known as the vertex of the angle.

Revolution

Turning by a full rotation or a complete 360° angle in the same direction is called a revolution.

e.g. When hour or minute hand of a

clock moves from 12 to 12, it makes one revolution.

We can see such revolutions on clock-faces.

When the hand of a clock moves from one position to another, it turns through an angle.

When the hand of a clock starts at 12 and reaches 3, it has reached quarter past and has made \(\frac{1}{4}\) of a revolution or 1 right angle which is equal to 90°.

When the hand of a clock starts at 12 and reaches 6 1 (half past), the hand has made \(\frac{1}{2}\) of a revolution or 1 straight angle or 2 right angles which equals to 180°.

When the hand of a clock starts at 12 and reaches 9 (quarter to), the hand has made three quarter or \(\frac{3}{4}\) of a revolution or 3 right angles which equals to 270°.

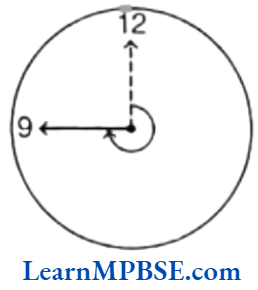
When the hand of a clock starts at 12 and reaches 12 again, it has moved exactly one round of the clock i.e. it has made one complete revolution and the angle for one revolution and the angle for one revolution is called complete angle or 2 straight angles or 4 right angles which equals t 360°.

MP Board Class 6 Maths Solutions

Example 1. What fraction of a clockwise revolution does the hour hand of a clock turn through when it goes from

(1) 8 to 11

(2) 2 to 5

Solution. Moving of hour hand from 8 to 11 on clock is given in the figure.

Hence, from 8 to 11, hour hand turns through \(\frac{1}{4}\) of a revolution, clockwise.

(2) Moving of hour hand from 2 to 5 on clock is given in the figure. Hence, from 2 to 5, hour hand turns through \(\frac{1}{4}\) of a revolution, clockwise.

Example 2. Where will the hand of a clock stop, if it

(1) starts at 1 and makes \(\frac{1}{2}\) of a revolution, clockwise?

(2) starts at 4 and makes \(\frac{3}{4}\) of a revolution, clockwise?

(3) starts at 8 and makes \(\frac{1}{4}\) of a revolution, clockwise?

Solution. (1) If the hand of a clock starts at 1 and makes of a \(\frac{1}{2}\) revolution clockwise, it stops at 7.

(2) If the hand of a clock starts at 4 and makes \(\frac{3}{4}\) of a revolution, clockwise, it stops at 1.

(3) If hand of a clock starts at 8 and makes \(\frac{1}{4}\) of a revolution, clockwise, it stops at 11.

Class 6 Maths Chapter 5 Solutions

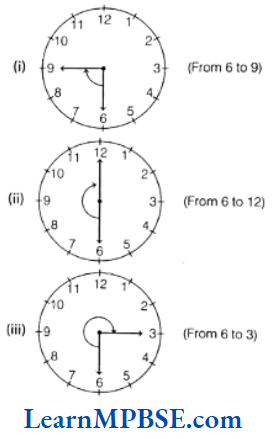
Example 3. Draw a rough diagram of the clock for each of the following

(1) One-fourth revolution

(2) Half revolution

(3) Three-fourth revolution

Solution.

Example 4. How many right angles will hour hand of clock make in half revolution?

Solution. We know that 1 revolution = 4 right angles

Now, dividing by 2 on both sides, we get

\(\frac{1}{2}\) revolution = \(\frac{4}{2}\)right angles

∴ \(\frac{1}{2}\) revolution = 2 right angles

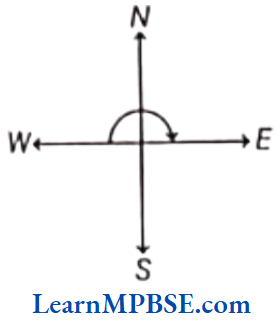
Example 5. Which direction will you face, if you start facing

(1) West and makes \(\frac{1}{2}\) of a revolution, clockwise?

(2) East and make \(\frac{3}{4}\) of revolution, anti-clockwise?

Solution. (1) If we start facing West and \(\frac{1}{2}\) make of a revolution clockwise i.e. two right angles, we will face East.

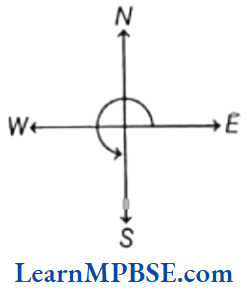
(2) If we start facing East and make \(\frac{3}{4}\) of revolution anti-clockwise i.e. three right angles, we will face south.

Example 6. Write the number of right angles turned through, by the hour hand of clock when it goes from

(1) 4 to 7

(2) 10 to 4

Solution.

(1) Here, the hour hand moves from 4 to 7. It starts from 4 and covers 5, 6 and 7. So, hour hand turned by one right angle.

(2) Here, the hour hand moves from 10 to 4. It starts from 10 and covers 11, 12, 1, 2, 3 and 4. So, hour hand turned by two right angles.

MP Board Class 6 Book Solutions

Example 7. How many right angles do you make, if you start facing

(1) East and turn clockwise to South?

(2) North and turn anti-clockwise to South?

(3) South and turn to South?

Solution.

(1) If we start turning clockwise from East to South, we make one right angle.

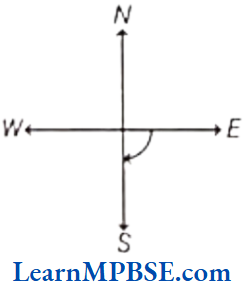
(2) If we start turning anti-clockwise from North to South we make two right angles.

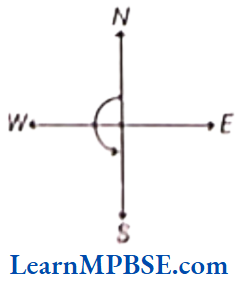
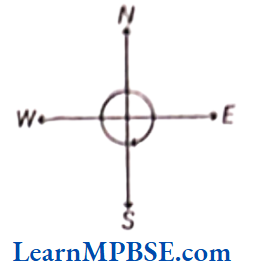
(3) If we start turning clockwise or anti-clockwise from South to South, we make four right angles.

Example 8. Where will the hour hand of a clock stop, if it starts

(1) from 7 and turns through 1 right angle?

(2) from 9 and turns through 2 right angles?

(3) from 11 and turns through 3 right angles?

Solution.

(1) It is clear from the figure that the hour hand starts from 7 and turns through 1 right angle. Hence, it will reach at 10.

(2) It is clear from the figure that the hour hand starts from 9 and turns through 2 right angles. Hence, it will be at 3.

(3) It is clear from the figure that the hour hand starts from 11 and turns through 3 right angles. Hence, it will be at 8.

Example 9. If the hands of clock make one right angle. Then, show it by two different figure.

Solution. Two different figure are

Class 6 Maths Chapter 5 Solutions

Example 10. If a clock hand makes three complete revolution, then how many right angles will be formed?

Solution. We know that there are four right angles in a complete revolution. Therefore, if a clock hand makes three revolution, then the number of right angles

= 3 x 4

= 12 right angles

Example 11. Find the number of straight angles turned by the hour hand of a clock when it goes from 3 to 9.

Solution. When hour hand goes from 3 to 9, it makes one straight angle.

Example 12. Where will the hour hand of a clock stop if it starts

(1) from 6 and turns through 2 straight angles.

(2) from 9 and turns through 1 straight angle.

Solution. (1) It is clear from the figure that the hour hand starts from 6 and turns through 2 straight angles. Hence, it will be reach at 6 because 2 straight angles is equal to 4 right angles.

(2) It is clear from the figure that the hour hand starts from 9 and turns through 1 straight angle. Hence, it will reach at 3 because 1 straight angle is equal to 2 right angles.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Acute, Obtuse and Reflex Angles

Acute Angle

An angle smaller than a right angle is called an acute angle or less than \(\frac{1}{4}\) of a revolution.

e.g. When hour hand moves from 12 to 2, it makes an acute angle.

Class 6 Maths Chapter 5 Solutions

Example 1. How does the angle made by the hour hand of the clock look like when it moves from 6 to 8. Is the angle moved more than 1 right angle?

Solution. It looks like an acute angle.

We know that hour hand of a clock makes a right angle when it covers \(\frac{1}{4}\) of the revolution.

(∵ it covers 7, 8 and 9). Here, hour hand moves from 6 to 8 (covers only two numbers 7 and 8). So, that angle moved by hour hand is less than 1 right angle.

Obtuse Angle

An angle larger than a right angle but less than straight angle is called an obtuse angle.

e.g. When hour hand moves from 12 to 4, it makes an obtuse angle.

Example 2. The hour hand of a clock moves from 3 to 7. Is the revolution of the hour hand more than 1 right angle?

Solution. Yes, it is clear from the figure that hour hand makes one right angle from 3 to 6. So, revolution of the hour hand is more than 1 right angle. It looks like an obtuse angle.

Class 6 Maths Chapter 5 Solutions

Example 3. If a boy facing East and makes \(\frac{1}{4}\) revolution clockwise. Further makes \(\frac{1}{6}\)revolution clockwise. Then, name the angle that he turned totally?

Solution. When boy makes \(\frac{1}{4}\) revolution clockwise.

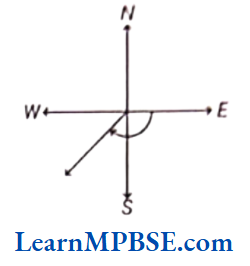
He makes a right angle. Then, he further makes revolution \(\frac{1}{6}\) which is greater than right angle and smaller than straight angle. Therefore, the angle he made is obtuse angle.

Reflex Angle

An angle larger than the straight angle but less than complete angle is called reflex angle.

e.g. When hour hand moves from 12 to 7, it makes a reflex angle.

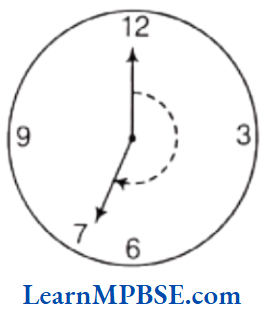
Understanding Elementary Shapes Class 6

Example 4. The hour hand of a clock moves from 3 to 10. Is the revolution of the hour hand more than 2 right angle?

Solution. Yes, it is clear from the figure that hour hand makes 2 right angles from 3 to 9. So, the revolution of the hour hand is more than 2 right angle. It look like a reflex angle.

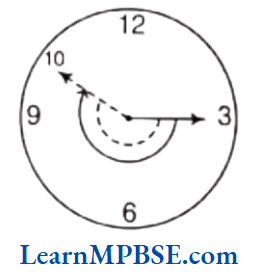
Chapter 5 Understanding Elementary Shapes Measuring Angles

One complete revolution is divided into 360 equal parts. Each part is of one degree (i.e.1°) and we can write one complete revolution as 360° to say ‘three hundred sixty degrees.

Thus, in a clock, 12 divisions = 360°.

To find the measure of an angle, we use an instrument named as protractor.

The Protractor

You can find a protractor in your ‘instrument box’. The curved edge of protractor is divided into 180 equal parts. Each part is equal to one degree.

The markings start from 0° on the right side and ends with 180° on the left side and vice-versa.

Steps of Measuring an Angle

Suppose you want to measure an ZABC, follow the steps given below.

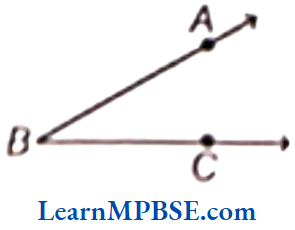
Step 1. Place the protractor, so that the mid-point (M in the figure) of its straight edge lies on the vertex B of the ∠ABC

Step 2. Adjust the protractor, so that ray BC is along the straight-edge of the protractor.

Step 3. There are two ‘scales’ on the protractor, read that scale which has the 0° mark coinciding with the straight-edge (i.e. with ray BC).

Step 4. The mark shown by ray BA on the curved edge gives the degree measure of the angle.

We write m ∠ABC = 40° or simply ∠ABC = 40°.

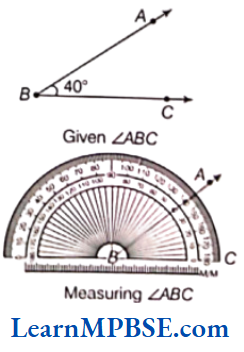
Understanding Elementary Shapes Class 6

Example 1. Measure the angles given below using the protractor and write down the measure.

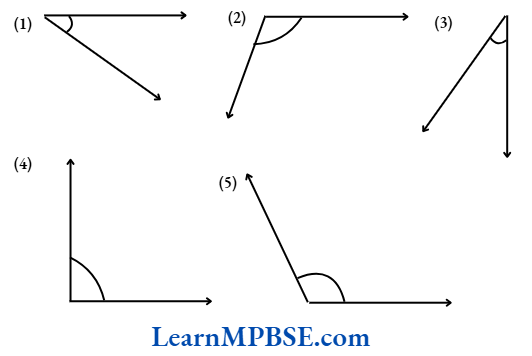
Solution. On measuring the given angles using protractor, we find that

(1) The measure of the given angle is 20°.

(2) The measure of the given angle is 110°.

(3) The measure of the given angle is 45°.

(4) The measure of the given angle is 90°.

(5) The measure of the given angle is 135°.

Example 2. Compare the given angles by their measurement.

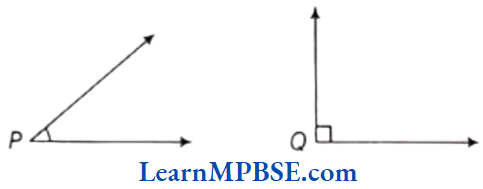
Solution. The measurement of ∠P = 30°

The measurement of ∠Q = 90°,

Hence, ∠Q > ∠P

Example 3. Write down the measure of

(1) some acute angles

(2) some obtuse angles

(give atleast two examples of each)

Solution. We know that the measure of an acute angle is always less than 90°. So, 89°,77°,75°, 60°, 40° all are acute angles.

Also, we know that the measure of an obtuse angle is always greater than 90°. So, 95°, 122°, 111° all are obtuse angles.

Example 4. Which angle has a larger measure?

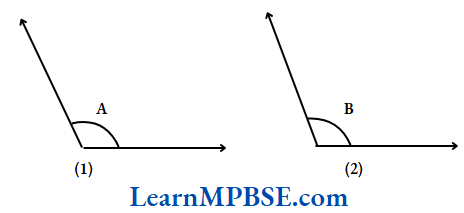
First estimate and then measure ∠A and ∠B

Solution. Observing the given angles, we find that ∠A > ∠B

Measure of ∠A = 120°, Measure of ∠B = 100°

Understanding Elementary Shapes Class 6

Example 5. From these two angles which has larger measure? Estimate and then confirm by measuring them.

Solution. On observing, we find that ∠B > ∠A.

On measuring, we find that ∠A = 30° and ∠B = 60° Thus, ∠B > ∠A

Example 6. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor)

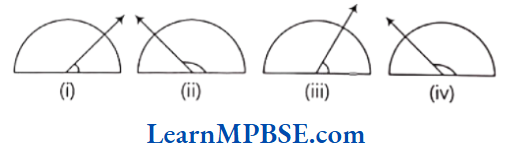
Solution. On estimating with eyes, the measure of angle shown in figure are as follows

(1) 30°

(2) 130°

(3) 80°

Now, on measuring with the protractor, measure of angle shown in figure are as follows:

(1) 35°

(2) 135°

(3) 75°

MP Board Class 6 Chapter 5 Maths

Example 7. Find the angle measure between the hands of the clock in each figure.

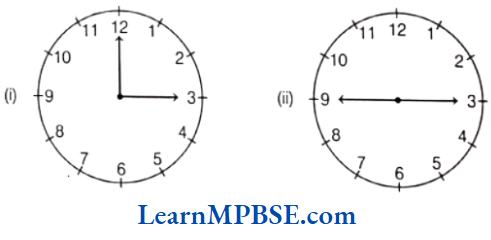
Solution.

(1) Number of divisions between 12 to 3 = 3

We know that 12 divisions = 360°

∴ \(3 \text { divisions }=\frac{360^{\circ}}{12} \times 3=90^{\circ}\)

Hence, the angle between the hands of clock is 90°.

(2) Number of divisions between 9 to 3=6

We know that 12 divisions = 360°

∴ \(6 \text { divisions }=\frac{360^{\circ}}{12} \times 6=180^{\circ}\)

Hence, the angle between the hands of clock 180°.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Perpendicular Lines

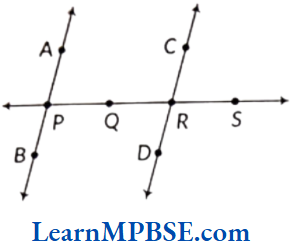
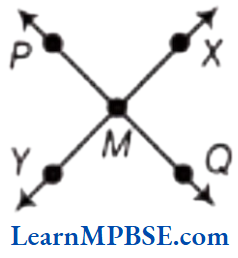
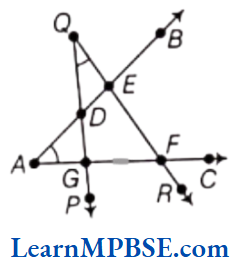
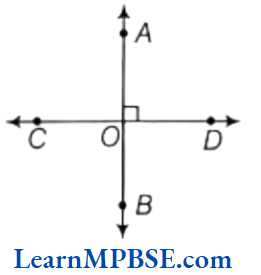
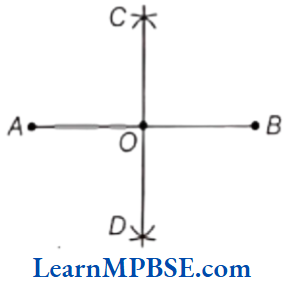
If two lines intersect each other and the angle between them is a right angle, then these lines are said to be perpendicular lines.

e.g. In the following figure, line AB is perpendicular to line CD i.e. AB ⊥ CD

and point O is the point of intersection of line segments AB and CD.

Example 1. Which of the following are models for perpendicular lines?

(1) The opposite edge of a ruler.

(2) The letter Z

(3) Railway lines

(4) The letter L

Solution. (1) No, the opposite edges of a ruler does not make a model of perpendicular lines.

(2) No, the letter Z does not make a model of perpendicular lines.

(3) No, railway lines does not make a model of perpendicular lines.

(4) Yes, the letter L does make a model of perpendicular lines.

MP Board Class 6 Chapter 5 Maths

Example 2. Consider a line AB is perpendicular to the line XY. If AB and XY intersect at the point Q, then find the measure of ∠AOY.

Solution. Given, AB is perpendicular to XY and AB and XY both intersect each other at the point O.

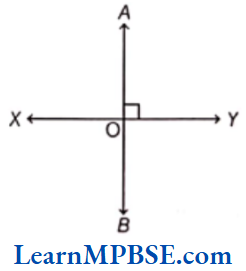
So, it is clear from the adjoining figure that ∠AOY = 90°

Example 3. Find the angle Indicated below and write name of lines which are perpendicular to each other.

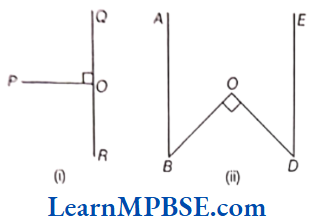
Solution. (1) ∠POQ = 90° and PO ⊥ QR

(2) ∠BOD = 90° and BO ⊥ OD

Perpendicular Bisector

The perpendicular bisector of a line segment is perpendicular to the line segment that divide it into two equal parts.

e.g. In the given figure, CD is perpendicular bisector to line segment AB.

MP Board Class 6 Chapter 5 Maths

Example 4. Study the following diagram. The line / and line mare perpendicular to each others.

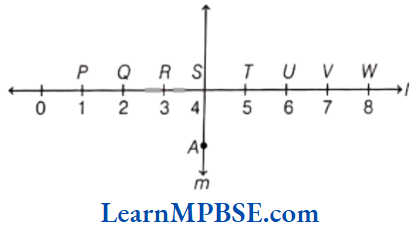
(1) Is RS = ST?

(2) Does AS bisect PV?

(3) Identify any two lines segments for which AS is the perpendicular bisector.

(4) Are these true?

(a) PR > TU

(b) QR = UV

(c) PQ < TW

Solution.

(1) From the given figure,

RS = 1 unit

ST = 1 unit

∴ RS = ST = 1 unit

(2) PS = 3 units

SV = 3 units

∴ PS = SV = 3 units

Now, PS = SV

So, S is the mid-point of PV.

Thus, AS bisects PV.

(3) In the given figure, we can see that AS is the perpendicular to the given line segment.

Since, RS = ST [each = 1 unit]

So, AS is the perpendicular bisector of RT.

Again, QS = SU [each 2 unit]

So, AS is the perpendicular bisector of QU.

(4) (a) Here, PR = PQ + QR

= 1 + 1 = 2 units[PQ = QR = 1 unit]

and TU = 1 unit

∴ PR > TU is true.

(b) Here, QR = 1 unit and UV = 1 unit.

∴ QR = UV = 1 unit

∴ QR = UV is true.

(c) Here, PQ = 1 unit and TW = 3 unit

∴ PQ < TW is true.

Example 5. List out English alphabets which are examples of perpendicular. Write, if any.

Solution. Letter F, L and T are examples of perpendicular lines segments.

Example 6. Observe the following figure, if the line segments PQ and RS are perpendicular bisector of each other and PQ = 6 cm and RS = 8 cm, then find PO and OR?

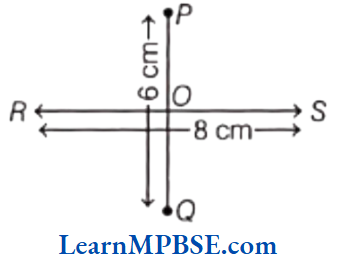
Solution. Since, PQ and RS are perpendicular bisector to each other, therefore they divide each other equally.

Now, PQ = 6 cm

∴ PO + OQ = 6 cm

PO = 3cm

and RS = 8 cm

∴ RO = \(\frac{8}{2}\) = 4 cm

Hence, PO = 3 cm

and RO = 4 cm

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Triangles

A polygon with least number of sides is called a triangle or we can say a plane figure bounded by three lines is called triangle.

Classification Based on Length of the Sides

A triangle is classified according to the measurement of its sides as given below

1. Scalene Triangle

A triangle having all three unequal sides is called a scalene triangle. e.g. ΔABC is a scalene triangle where, AB ≠ BC ≠ CA

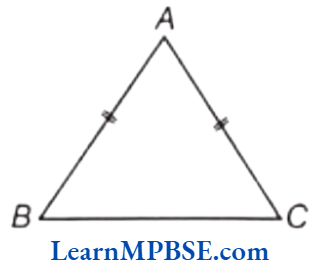
2. Isosceles Triangle

A triangle having two equal sides is called an isosceles triangle.

e.g. ΔABC is an isosceles triangle where, AB = AC

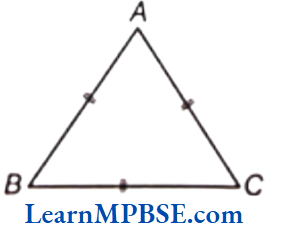
3. Equilateral Triangle

A triangle having three equal sides is called an equilateral triangle.

e.g. ΔABC is an equilateral triangle. where, AB = BC = CA

MP Board Class 6 Chapter 5 Maths

Example 1. Name the triangle with lengths of sides

(1) 9 cm, 10 cm and 11 cm.

(2) 7 cm, 7 cm and 9 cm.

(3) ΔPQR such that PQ = QR = PR = 6 cm.

Solution. (1) Given, first side = 9 cm, second side = 10 cm, and third side = 11 cm

i.e. all the sides are of different length.

So, it is a scalene triangle.

(2) Given, first side = 7 cm, second side = 7 cm and third side = 9 cm

i.e. two sides are equal. So, it is an isosceles triangle.

(3) Given, PQ = QR = PR = 6 cm

i.e. all sides of triangle are equal.

So, it is an equilateral triangle.

Classification Based on Measurement of Angles

A triangle is further classified according to the measurement of its angles as given below

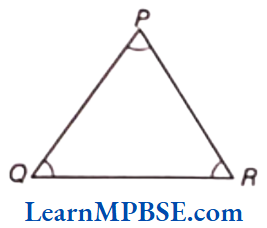
1. Acute Angled Triangle

If each angle of a triangle is less than 90°, then the triangle is called an acute angled triangle.

e.g. ΔPQR is an acute angled triangle where, ∠P, ∠Q and ∠R are acute angles i.e. less than 90°.

2. Right Angled Triangle

If any one angle of a triangle is a right angle, then the triangle is called a right angled triangle.

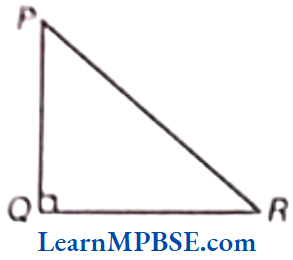
e.g. ΔPQR is a right angled triangle where, ∠Q = 90°.

3. Obtuse Angled Triangle

If any one angle of a triangle is greater than 90° but less than 180°, then the triangle is called an obtuse angled triangle.

e.g. ΔPQR is an obtuse angled triangle, where ∠Q > 90°.

MP Board Class 6 Chapter 5 Maths

Important Properties of Triangles

1. If three sides of a triangle are equal, then the three angles are also equal. Its vice-versa is also true.

2. If two sides of a triangle are equal, then it has two equal angles. Its vice-versa is also true.

3. If three sides of a triangle are unequal, then the three angles are also unequal.

Example 2. Classify the triangles given below.

(1) ΔPQR, m∠P = 40°, m∠Q = 75° and m∠R = 65°.

(2) ΔABC m∠B = 90°.

(3) ΔLMN, m∠M = 90° and LM = MN.

Solution. (1) Given, m∠P = 40°, m∠Q = 75° and m∠R = 65°

Since, all the angles are different and less than 90°. So, it is an acute angled triangle.

(2) Given, m∠B = 90°

i.e. measure of ∠B = 90°.

So, it is a right angled triangle.

(3) Given, m∠M = 90°

i.e. measure of ∠M = 90° and LM = MN

Here, one angle is right angle and two sides are equal.

So, it is an isosceles right angled triangle.

Example 3. In a ΔABC, ∠A = ∠B = ∠C = 60°, then what can you say about the length of sides of ΔABC? Also, write the name of the triangle.

Solution. It is the property of triangle that if all the angles of a triangle are equal, then the three sides of a triangle are also equal.

Thus, the given triangle is an equilateral triangle.

Example 4. In a ΔXYZ, XY = XZ and ZY = 65°. Then, find the value of ∠Z.

Solution. Since, the XY = XZ i.e. two sides of a triangle are equal, therefore it is an isosceles triangle.

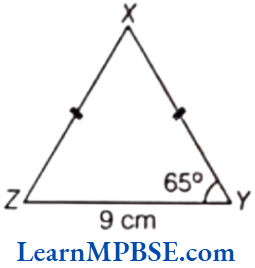
So, ∠Y = ∠Z

∴ ∠Z = 65°

Example 5. Name each of the following triangles in two different ways. (You may judge the nature of the angle by observation)

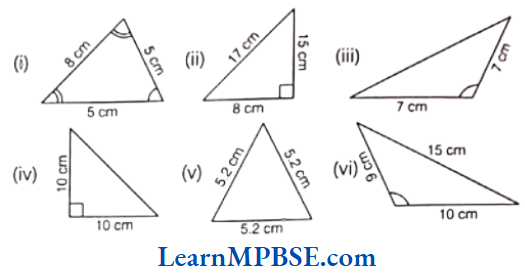
Solution.

1. Here, two sides are equal, so it is an isosceles triangle and all the angles are acute angles. So, it is an acute angled triangle also.
2. In the given figure, all sides are different, so it is a scalene triangle and one angle is right angle. So, it is an right angled triangle also.
3. Here, two sides are equal, so it is an isosceles triangles and one angle is an obtuse angle. So, it is an obtuse angled triangle also.
4. In the given figure, two sides are equal, so it is an isosceles triangle and one angle is right angle. So, it is a right angled triangle also.
5. Here, all the sides are equal, so it is an equilateral triangle and all the angles are acute. So, it is an acute angled triangle also.
6. In the given figure, all the sides are different, so it is a scalene triangle and one angle is an obtuse angle. So, it is an obtuse angled triangle also.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Quadrilaterals

A quadrilateral is a polygon which has four sides, four angles and two diagonals.

Classification of Quadrilaterals

Quadrilaterals can be classified as given below

1. Rectangle

(1) PQ = SR,

PQ || SR

SP = RQ,SP || RQ

(2) ∠P = ∠Q = ∠R = ∠S = 90°

(3) SQ = PR

2. Square

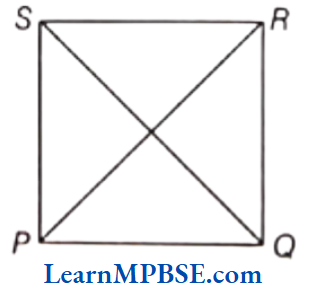
(1) PQ || SR and SP || QR

and PQ = QR = RS = SP

(2) ∠P = ∠Q = ∠R = ∠S = 90°

(3) PR = SQ

3. Parallelogram

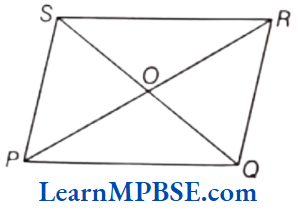
(1) PQ = SR, PQ || SR, SP = QR, SP || QR

(2) ∠P = ∠R, and ∠S = ∠Q

(3) PR ≠ SQ (some times PR=SQ) and OS = OQ, and OR = OP

4. Rhombus

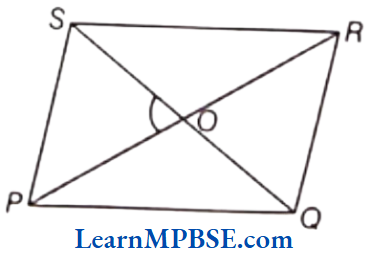
(1) PQ || SR and PS || QR

PQ = QR = RS = SP

(2) ∠P = ∠R and ∠S = ∠Q

(3) PR ≠ SQ (sometimes it may be equal) and

OP = OR, OS = OQ

5. Trapezium

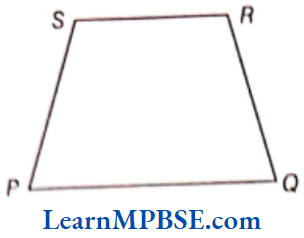
(1) SR || PQ

(2) SR ≠ PQ and SP ≠ RQ

A trapezium is said to be an isosceles trapezium, if its non-parallel sides are equal i.c. SP = RQ

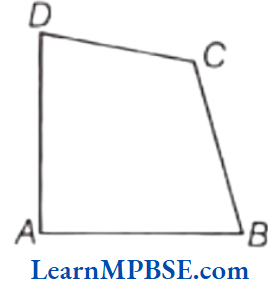
Example 1. Write the number of pairs of opposite sides which are parallel?

Solution. In the adjoining figure, a parallelogram is given.

Here, PQ || SR and PS || QR

Therefore, the number of pairs of opposite sides which are parallel is 2.

MP Board Class 6 Chapter 5 Maths

Example 2. In the given figure PQRS is a quadrilateral, if PR ⊥ SQ, then name all the right angles.

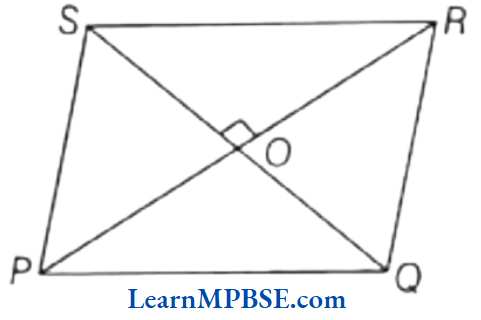
Solution. The right angles in the given figure are ∠POQ, ∠QOR, ∠ROS, ∠SOP.

Example 3. In the adjoining figure, a rectangle is given. Write how many right angles are there.

Solution. According to the property of a rectangle, all the interior angles of a rectangle are right angle (i.e. 90°).

∴ There are four right angles in a rectangle.

Example 4. What is a regular quadrilateral? Draw its figure.

Solution. We know that a square has all its sides and angles equal, so it is said to be a regular quadrilateral

where, PQ = QR = RS = SP

and ∠P = ∠Q = ∠R = ∠S = 90°

Example 5. State the condition under which a rectangle is considered a square.

Solution. A rectangle will be considered as a square if all the sides of a rectangle are equal.

Example 6. Fill in the blanks

(1) The opposite sides of a rectangle are ……. in length.

(2) The diagonals of a square are ……. to one another.

(3) the opposite sides of a trapezium are ……

(4) Each angle of a rectangle is a ……

Solution. (1) equal

(2) perpendicular

(3) parallel

(4) right angle

Example 7. State the reason for the following, if it is true.

(1) A square is the special case of the rectangle.

(2) Parallelogram is a special case of the rectangle.

Solution. (1) Yes, its true. In square, opposite sides are equal and all angles are right angles, so a square is a special case of rectangle.

(2) No, it is not true.

MP Board Class 6 Chapter 5 Maths

Example 8. Write the name of the quadrilaterals in which diagonals are perpendicular to each other?

Solution. In square and rhombus, diagonals are perpendicular to each other.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Polygons

Polygon is a closed shape made of line segments only.

Polygons are classified according to the number of their

These shapes can be seen in everyday life. Windows, doors, walls, almirahs, blackboards, notebooks etc. are usually rectangular in shapes.

Note It

(1) If a polygon has all equal sides, then it is said to be a regular polygon.

(2) The angle determined by two sides meeting at a vertex is called an angle of the polygon.

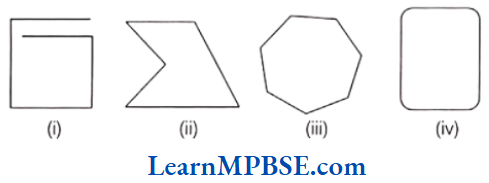
Example 1. Examine whether the following are polygons. If any one among them is not, say why?

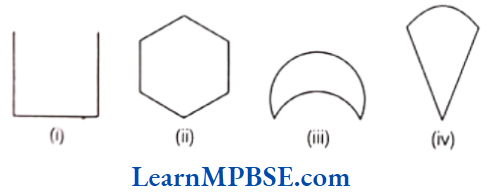
Solution. (1) It is an open figure. So, it is not a polygon.

(2) It is closed figure. So, it is a polygon with six sides i.e. hexagon.

(3) It is not made by line segments. So, it is not a polygon.

(4) It is made by two line segments and curved line. So, it is not a polygon.

Example 2. Name each polygon. Make one more example of each of these.

Solution. (1) This polygon has four sides, so it is quadrilateral. e.g.

(2) This polygon has three sides, so it is a triangle. e.g.

(3) This polygon has five sides, so it is pentagon. e.g.

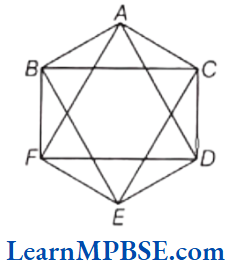
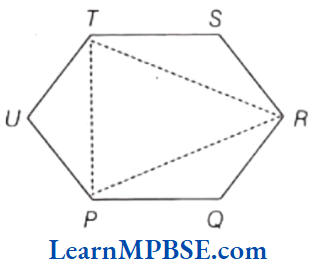
Example 3. Can you draw an equilateral triangle inside a regular hexagon. Show.

Solution. Consider, a regular hexagon ABCDEF.

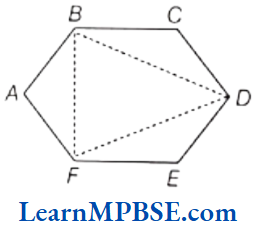
Joining its alternate vertices B, D and F, we get ABDF, which is a regular triangle, (since, all sides are equal).

Thus, the triangle, so formed is an equilateral triangle.

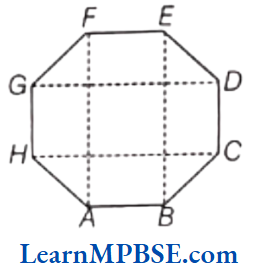
Example 4. Can you make any two rectangle inside a regular octagon. Show.

Solution. Consider, PQRSTUVW is a regular octagon.

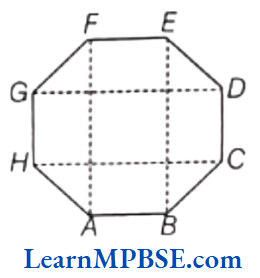
Join vertices P and U, we get \(\overline{P U}\).
Join Q and T, we get \(\overline{Q T}\). Thus, we get a rectangle PQTU.

Again, by joining W, Rand V, S we can get another rectangle WRSV.

Class 6 Maths Chapter 5 Solutions MP Board

Example 5. A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw

(1) pentagon and its diagonals

(2) hexagon and its diagonals

Solution. (1) Here, PQRST is a pentagon.

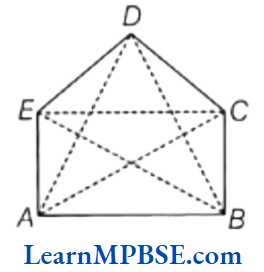
By joining any two vertices, we get diagonals as \(\overline{T R}, \overline{T Q}, \overline{P R}, \overline{P S} \text { and } \overline{S Q} \text {. }\)

(2) Here, ABCDEF is a hexagon

By joining any two vertices, we get diagonals as \(\overline{A D}, \overline{A C}, \overline{A E}, \overline{B F}, \overline{B E}, \overline{F C}, \overline{E C}, \overline{B D}, \overline{F D} .\)

Example 6. What is the condition for a polygon to be considered as a regular polygon? Give any two examples of it.

Solution. When all sides of the polygon are equal in length, the polygon is considered as regular polygon.

e.g. (1) An equilateral triangle

(2) A square

Example 7. Write the number of sides and name of the following figure.

Solution. (1) It is a triangle. The number of sides is 3.

(2) It is a heptagon.

The number of sides is 7.

(3) It is a quadrilateral.

The number of sides is 4.

Example 8. Given a regular pentagon PQRST, where QR = 3 cm, then find the value of x.

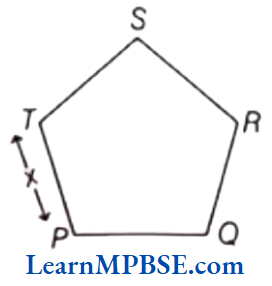
Solution. Since, QR = 3cm

∴ x = PT = 3cm

because in a regular pentagon, all sides are equal.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Exercise 5.1

Question 1. What is the disadvantage in comparing line segments by mere observation?

Solution.

The disadvantage in comparing line segments by mere observation is that sometimes the difference in lengths between Q two line segments may not accurate. So, we cannot always be sure about our usual judgement. e.g. In the given figure, the line segments \(\overline{P Q}\) and \(\overline{R S}\) seems to be equal but actually they are not equal.

Question 2. Why is it better to use a divider than a ruler, while measuring the length of a line segment?

Solution. When we measure the length of a line segment by ruler, there may be some errors due to its thickness and angular viewing. These errors can be removed by measuring a line segment with the help of a divider. Hence, the use of a divider is better than a ruler.

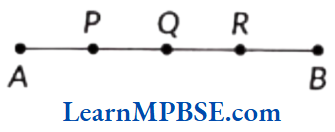
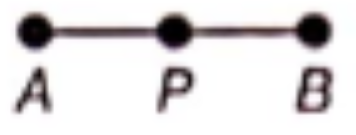
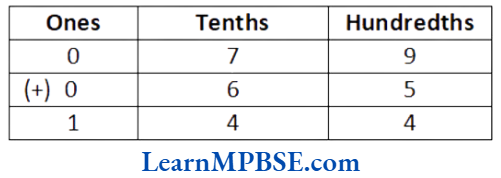
Question 3. Draw any line segment, say \(\overline{A B}\) Take any point Clying in between A and B Measure the lengths of AB, BC and AC. Is AB = AC + CB?

Solution. Let AB be the line segment of length 6 cm and point C lying between A and B.

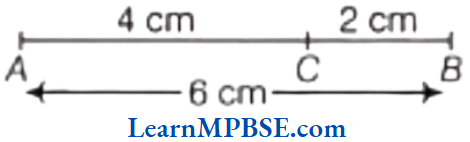
On measuring the lengths of line segments AB, AC and CB using ruler, we find that AB = 6 cm, AC = 4 cm and CB = 2 cm

Now, AC + CB = 4 + 2 = 6 cm = AB

i.e. AC + CB = AB

So, we can say that C lies between A and B.

Note If A. B and C are any three points on a line such that AC + CB = AB, then point C will lie between points A and B. Its converse is also true.

Class 6 Maths Chapter 5 Solutions MP Board

Question 4. If A, B amd C are three points on a line such that AB = 5 cm, BC = 3 cm and AC = 8 cm, which one of them lies between the other two?

Solution. Firstly, draw a line AV of 8 cm. Take a point B on AC such that AB = 5 cm.

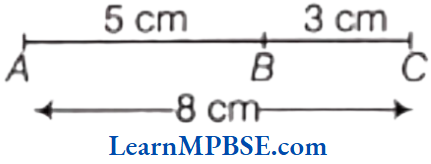
Now, length of BC = AC – AB = 8 – 5 = 3cm

Thus, AB + BC = AC

So, the point B lies between point A and C.

Question 5. Verify whether Dis the mid-point of \(\overline{A G}\).

Solution. From the given figure, it is clear that

AD = AB + BC + CD = 1 + 1 + 1 = 3 units

and DG = DE + EF + FG = 1 + 1 + 1 = 3 units Now,

AG = AD + DG = 3 + 3 = 6 units

and AD = DG 3 units

∴ D lies between A and G.

∴ D is the mid-point of AG.

Question 6. If Bis the mid-point of \(\overline{A C}\) and C is the mid-point of \(\overline{B D}\), where A, B, Cand Dlie on a straight line, say why AB = CD?

Solution. Given, B is the mid-point of \(\overline{A C}\).

∴ AB = BC …(1)

and C is the mid-point of \(\overline{B D}\).

∴ BC = CD …(2)

i.e.

Now, on adding Eqs. (1) and (2), we get

AB + BC = BC + CD

AB = CD

Hence proved

Question 7. Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.

Solution.

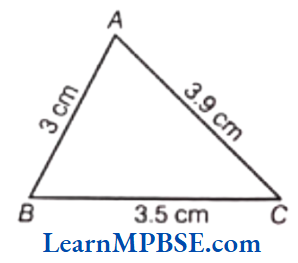
(1) Here, we draw a ΔABC

in which AB = 3 cm,

BC = 35 cm and AC = 39 cm

Now, by adding two sides of ΔABC

i.e. AB + BC = 3 + 3.5 = 6.5 cm Clearly,

AB + BC > AC

(2) Here, we draw a ΔABC in which AB = 3cm, BC = 4 cm and AC = 5 cm

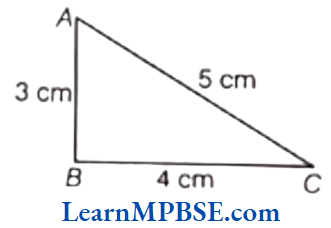
Now, by adding two sides of ΔABC

i.e. AB + BC = 3 + 4 = 7cm

Clearly, AB + BC > AC

(3) Here, we draw a ΔABC in which

AB = BC = AC = 25 cm

Now, by adding two sides of ΔABC

i.e. AB + BC = 2.5 + 2.5 = 5cm

Clearly, AB + BC > AC

(4) Here, we draw a ΔABC in which

AB = 3cm, BC = 35 cm and AC = 4 cm

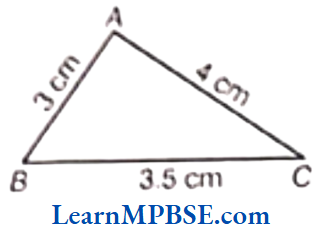
Now, by adding two sides of ΔABC

i.e. AB + BC = 3 + 3.5 = 6.5 cm

Clearly, AB + BC > AC

(5) Here, we draw a ΔABC in which

AB = 2 cm, BC = 4 cm and AC = 45 cm

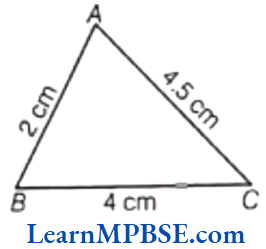
Now, by adding two sides of ΔABC

i.e. AB + BC = 2 + 4 = 6 cm

Clearly, AB + BC > AC

From all these triangles, we observe that in each case, the sum of the lengths of any two sides is greater tahn the third side. So, the sum of the lengths of any two sides can never be less than the third side.

MP Board Class 6 Maths solutions

Question 8. What is the angle name for half a revolution?

Solution. We know that 1 revolution = 2 straight angles

Now, dividing by 2 both sides, we get

\(\frac{1}{4}\) revolution = \(\frac{2}{2}\) straight angle = 1 straight angle

Hence, the angle name for half a revolution is straight angle or two right angles.

Question 9. What is the angle name for one-fourth revolution?

Solution. We know that I revolution = 4 right angles

Now, dividing by 4 on both sides, we get

\(\frac{1}{4}\) revolution = \(\frac{4}{4}\) right angles

\(\frac{1}{4}\) revolution = 1 right angle

Hence, the angle name for one-fourth revolution is one right angle.

Question 10. Draw five other situations of one-fourth, half and three-fourth revolution on a clock.

Solution. (1) One-fourth revolution For one-fourth revolution, the clock hand moves in many individual routes. Some of these situations on a clock are as follows:

(2) Half revolution For half revolution, the clock hand moves in many individual routes. Some of these situations on a clock are as follows

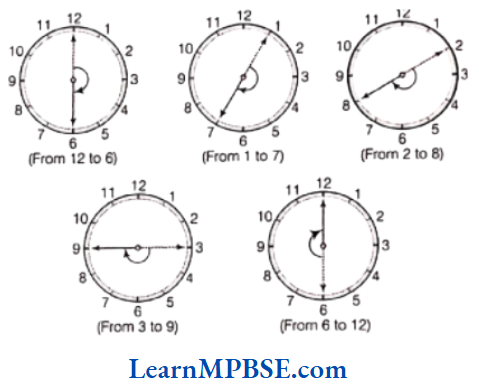
(3) Three-fourth revolution For three-fourth revolution, the clock hand moves in many individual routes. Some of these situations on a clock are as follows:

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Exercise 5.2

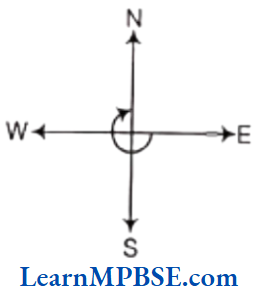
Question 1. What part of a revolution have you turned through, if you stand facing

(1) East and turn clockwise to face North?

(2) South and turn clockwise to face East?

(3) West and turn clockwise to face East?

Solution.

(1) Here, the turn from East to South is one right angle from South to West is one right angle and from West to North is one right angle. So, the turn from East to North is three right angles.

Hence, 3/4 of a revolution is required to turn from East to North.

(2) Here, the turn from South to West is one right angle, from West to North is one right angle and from North to East is one right angle. So, W+ the turn from South to East is three right angles.

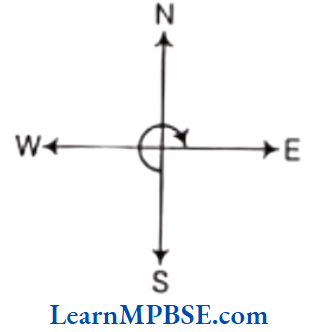
Hence, 3/4 of a revolution is required to turn from South to East.

(3) Here, the turn from West to North is one right angle, from North to East is one right angle. So, the turn from West to East is two right angles.

Hence, 1/2 of a revolution is required to turn from West to East.

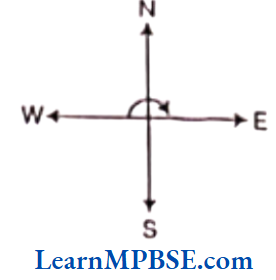
MP Board Class 6 Maths solutions

Question 2. The hour hand of a clock moves from 12 to 5. Is the revolution of the hour hand more than 1 right angle?

Solution. Yes, it is clear from the figure that hour hand makes one right angle from 12 to 3 and since 19 5 lies between 3 and 6. So, revolution of the hour hand is more than 1 right angle.

Question 2. What does the angle made by the hour hand of the clock look like when it moves from 5 to 7. Is the angle moved more than 1 right angle?

Solution. It looks like an acute angle. We know that hour hand of a clock makes a right angle to cover three digits as from 12 to 3, it makes a right angle

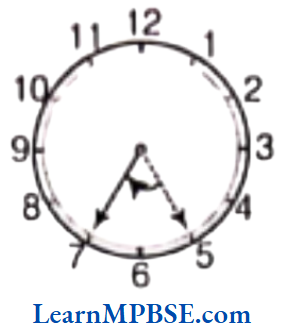
(∴ it covers three digits 1, 2 and 3). Here, hour hand moves from 5 to 7 (covers only two digits 6 and 7). So, the angle moved by hour hand is less than 1 right angle.

Question 3. Draw the following and check the angle with your RA (right angle) tester going

(1) from 12 to 2

(2) from 6 to 7

(3) from 4 to 8

(4) from 2 to 5

Solution.

(1) On checking the angle moved by an hour hand, while going from 12 to 2 by RA (right angle) tester, it is clear that it is less than 1 right angle.

(2) On checking the angle moved by an hour hand, while going from 6 to 7 by RA (right angle) tester, it is clear that it is less than 1 right angle.

(3) On checking the angle moved by an hour hand, while going from 4 to 8 by RA (right angle) tester, it is clear that it is more than 1 right angle.

(4) On checking the angle moved by an hour hand, while going from 2 to 5 by RA (right angle) tester, it is clear that it is equal to 1 right angle.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Exercise 5.3

Question 1. Match the following

Solution. (1) Straight angle is half of a revolution.

(2) Right angle is one-fourth of a revolution.

(3) Acute angle is less than one-fourth of a revolution.

(4) Obtuse angle is between 1/4 and 1/2 of a revolution. (v) Reflex angle is more than half of a revolution.

So, (1) → (c), (2) → (d), (3) → (a), (4) → (e), (5) → (b)

MP Board Class 6 Maths solutions

Question 2. Classify each one of the following angles as right, straight, acute, obtuse or reflex.

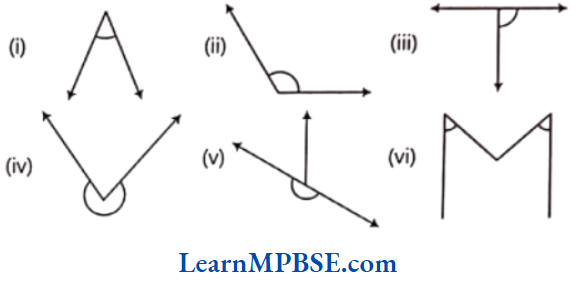
Solution.

(1) Given angle is smaller than a right angle, so it is an acute angle.

(2) Given angle is more than a right angle, so it is an obtuse angle.

(3) Given angle is a right angle.

(4) Given angle is more than a straight angle, so it is a reflex angle.

(5) Given angle is a straight angle.

(6) Both angles are smaller than a right angle, so both these are acute angles.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Exercise 5.4

Question 1. What is the measure of

(1) a right angle?

(2) a straight angle?

Solution.

(1) The measure of a right angle = 90°

(2) The measure of a straight angle

= 2 × right angles = 2 x 90° = 180°

Question 2. Say true or false.

(1) The measure of an acute angle < 90°.

(2) The measure of an obtuse angle < 90°.

(3) The measure of a reflex angle > 180°.

(4) The measure of one complete revolution = 360°.

(5) If m∠A = 53° and m∠B = 35°, then m∠A > m∠B.

Solution.

(1) True, because the measure of an acute angle is always less than 90°.

(2) False, because the measure of an obtuse angle is always greater than 90°.

(3) True, because the measure of a reflex angle is always greater than 180° and less than 360°.

(4) True, because the measure of one complete revolution is equal to 360°.

(5) True, because the measure of ∠A is greater than ∠B.

Question 3. Write down the measures of

(1) some acute angles.

(2) some obtuse angles.

(give atleast two examples of each)

Solution. (1) We know that the measure of an acute angle is always less than 90″.

So, 45, 50, 55°, 60°, 65° all are acute angles.

(2) We know that the measure of an obtuse angle is always greater than 90° but less than 180°.

So, 120, 125, 135°, 140° all are obtuse angles.

Class 6 MP Board Maths question answers

Question 4. Measure the angles given below using the protractor and write down the measure.

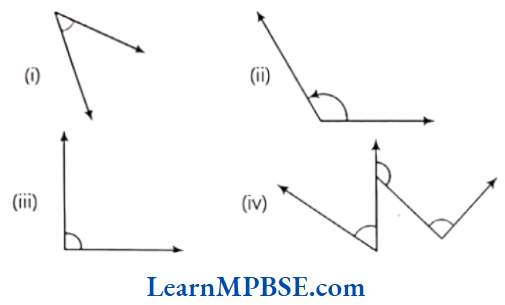
Solution. On measuring the given angles using protractor, we find that

(1) angle is 45°.

(2) angle is 125°.

(3) angle is 90°.

(4) angles are 60°, 125° and 90°, respectively.

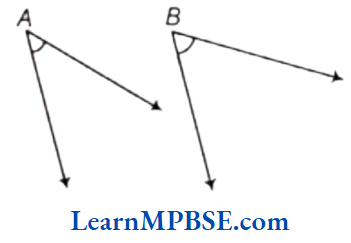
Question 5. Which angle has a larger measure?

First estimate and then measure.

Measure of ∠A =

Measure of ∠B =

Solution. Observing the given angles, we find that ∠B > ∠A.

On measuring, we find that

Measure of ∠A = 40°

Measure of ∠B = 65°

∴ ∠B > ∠A

Question 6. From these two angles which has larger measure? Estimate and then confirm by measuring them.

Solution. On observing, we find that ∠B > ∠A.

On measuring, we find that

∠A = 45° and ∠B = 60°

Thus, ∠B > ∠A

Question 7. Fill in the blanks with acute, obtuse, right or straight angle.

(1) An angle whose measure is less than that of a right angle is.

(2) An angle whose measure is greater than that of a right angle is

(3) An angle whose measure is the sum of the measures of two right angles is

(4) When the sum of the measures of two angles is that of a right angle, then each one of them is

(5) When the sum of the measures of two angles is that of a straight angle and if one of them is acute, then the other should be.

Solution. (1) acute angle

(2) obtuse angle

(3) straight angle

(4) acute angle

(5) obtuse angle

Question 8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor)

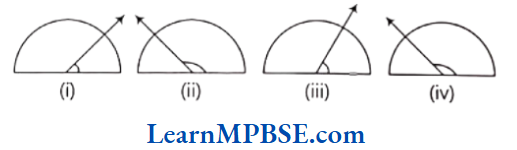
Solution. On estimating with eyes, the measure of angle shown in figure are as follows

(1) 45°

(2) 125°

(3) 60°

(4) 135°

Now, on measuring with the protractor, measure of angle shown in figure are as follows

(1) 40°

(2) 130°

(3) 65°

(4) 135°

Class 6 MP Board Maths Question Answers

Question 9. Investigate In the given figure, the angle measures 30°. Look at the same figure through a magnifying glass. Does the angle becomes larger? Does the size of the angle change?

Solution. No, looking through a magnifying glass does not make the angle larger.

Also, the size of angle does not change.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Exercise 5.5

Question 1. Which of the following are models for perpendicular lines?

(1) The adjacent edges of a table top.

(2) The lines of a railway track.

(3) The line segments forming the letter ‘L’.

(4) The letter ‘V’.

Solution. (1) Yes, the adjacent edges of a table top make a model of perpendicular lines.

(2) No, the lines of a railway track does not make a model of perpendicular lines.

(3) Yes, the line segments forming the letter ‘L’ makes a model of perpendicular lines.

(4) No, the letter ‘V’ does not make a model of perpendicular lines.

Question 2. Let \(\overline{P Q}\) be the perpendicular to the line segment \(\overline{X Y}\). Let \(\overline{P Q}\) and \(\overline{X Y}\) Intersect at the point A. What is the measure of ∠PAY?

Solution. Given, \(\overline{P Q}\) is perpendicular to \(\overline{X Y}\) and \(\overline{P Q}\) and \(\overline{X Y}\) both intersect each other at the point A.

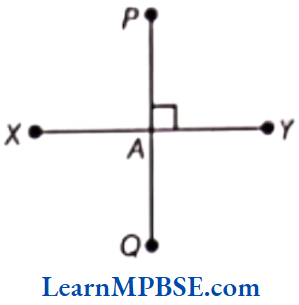
So, it is clear from the adjoining figure that ∠PAY=90°

Class 6 MP Board Maths Question Answers

Question 3. There are two set-squares in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?

Solution. We have two set-squares in our box. In one of them, angles are of 30°, 60°, 90° and in the other, angles are of 45°, 45°, 90°.

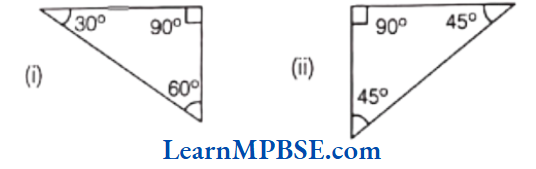
Clearly, they have one angle measure in common, which is

Question 4. Study the following diagram. The line l is perpendicular to line m.

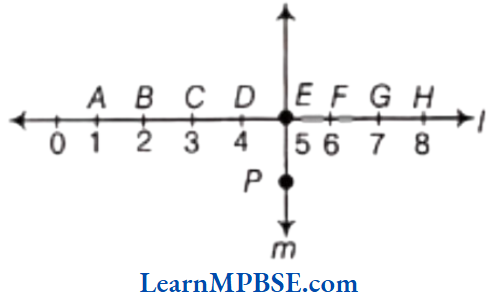
(1) CE = EG?

(2) Does PE bisect CG?

(3) Identify any two line segments for which PE is the perpendicular bisector.

(4) Are these true?

(a) AC > FG (b) CD = GH (c) BC < EH

Solution. (1) From given figure,

CE = CD + DE [CD = DE = 1 unit]

= 1 + 1 = 2 units

and EG = EF + FG [EF = FG = 1 unit]

= 1 + 1 = 2 units

∴ CE = EG 2 units

(2) Since, CE = EG

So, E is the mid-point of CG.

Thus, PE bisects CG.

(3) In the given figure, we can see that PE is perpendicular to the given line segment.

Since, DE = EF [each = 1 unit]

So, PE is the perpendicular bisector of DF.

Again, CE = EG [each = 2 units]

So, PE is the perpendicular bisector of CG.

(4) (a) Here, AC = AB + BC = 1 + 1= 2 units

[AB = BC = l unit]

and FG = 1 unit

∴ AC > FG is true.

(b) Here, CD = 1 unit and GH = 1 unit

∴ CD = GH is true.

(c) Here, BC = 1 unit

and EH = EF + FG + GH

= 1 + 1 + 1 = 3 units

∴ BC < EH is true.

MP Board Class 6 Maths Solutions For Chapter 5 Understanding Elementary Shapes Exercise 5.6

Question 1. Match the following:

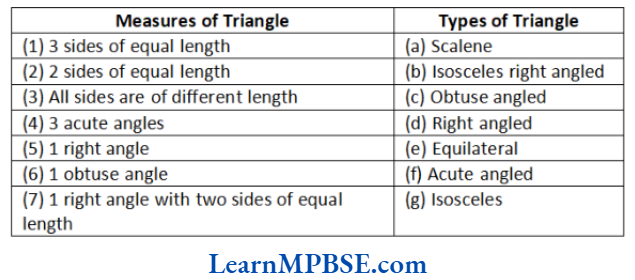
Solution. (1) → (e), (2) → (g), (3) → (a), (4) → (f), (5) → (d), (6) → (c), (7) → (b)

Question 2. Name each of the following triangles in two different ways. (you may judge the nature of the angle by observation)

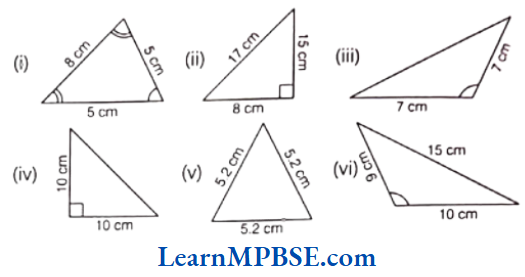
Solution. By observing the given triangles in two different ways, name of each triangle is given below

(1) In the given triangle, two sides are equal, so it is an isosceles triangle and all the angles are acute angles. So, it is an acute angled triangle also.

(2) In the given triangle, all the sides are different, so it is a scalene triangle and one angle is right angle. So, it is a right angled triangle also.

(3) In the given triangle, two sides are equal, so it is an isosceles triangle and one angle is an obtuse angle. So, it is an obtuse angled triangle also.

(4) In the given triangle, two sides are equal, so it is an isosceles triangle and one angle is right angle. So, it is a right angled triangle also.

(5) In the given triangle, all the sides are equal, so it is an equilateral triangle and all the angles are acute. So, it is an acute angled triangle also.

(6) In the given triangle, all the sides are different, so it is a scalene triangle and one angle is an obtuse angle. So, it is an obtuse angled triangle also.

Class 6 MP Board Maths Question Answers

Question 3. Try to construct triangles using matchsticks. Some are shown here.

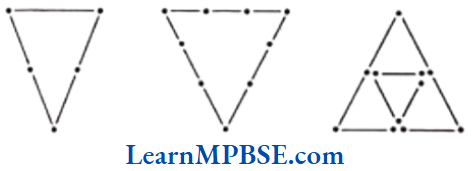
Can you make a triangle with

(1) 3 matchsticks?

(2) 4 matchsticks?

(3) 5 matchsticks?

(4) 6 matchsticks?

(Remember you have to use all the available matchsticks in each case)

Name the type of triangle in each case.

If you cannot make a triangle, think of reason for it.

Solution. (1) With the help of 3 matchsticks, we can make an equilateral triangle. Since, all three matchsticks are of equal length.

(2) With the help of 4 matchsticks, we cannot make any triangle because in this case, sum of two sides is equal to the third side and we know that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.

(3) With the help of 5 matchsticks, we can make an isosceles triangle. Since, we get two sides equal in this case.

(4) With the help of 6 matchsticks, we can make an equilateral triangle. Since, we get three sides equal in this case.

Chapter 5 Understanding Elementary Shapes Exercise 5.7

Question 1. Say true or false.

(1) Each angle of a rectangle is a right angle.

(2) The opposite sides of a rectangle are equal in length.

(3) The diagonals of a square are perpendicular to one another.

(4) All the sides of a rhombus are of equal length.

(5) All the sides of a parallelogram are of equal length.

(6) The opposite sides of a trapezium are parallel.

Solution. (1) True

(2) True

(3) True

(4) True

(5) False, because opposite sides of a parallelogram are of equal length and parallel.

(6) False, because a pair of opposite sides of trapezium are parallel and other pair of opposite sides are non-parallel.

Class 6 Maths Chapter 5 Solutions MP Board

Question 2. Give reason for the following

(1) A square can be thought of as a special rectangle.

(2) A rectangle can be thought of as a special parallelogram.

(3) A square can be thought of as a special rhombus.

(4) Squares, rectangles, parallelograms are all quadrilaterals.

(5) Square is also a parallelogram.

Solution. (1) We know that in a rectangle, opposite sides are equal and each angle is a right angle. If all its sides are equal, then it becomes square.

So, a square can be thought of as a special rectangle.

(2) We know that in a parallelogram, opposite sides are parallel as well as equal and opposite angles are equal. If its opposite angles are right angles, then it becomes a rectangle. So, a rectangle can be thought of as a special parallelogram.

(3) We know that in a rhombus, all four sides are equal and opposite sides are parallel. If its all angles are right angles, then it becomes a square. So, a square can be thought of as a special rhombus.

(4) We know that a polygon, which has four sides is called a quadrilateral. Square, rectangle and parallelogram also have four sides. So, these all are quadrilaterals.

(5) We know that in a parallelogram, opposite sides are parallel as well as equal and opposite angles are equal. In a square, opposite sides are parallel as well as equal and opposite angles are equal to right angle. So, a square is also a parallelogram.

Question 3. A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?

Solution. Yes, a square is a regular quadrilateral because all sides and angles of a square are equal.

Chapter 5 Understanding Elementary Shapes Exercise 5.8

Question 1. Examine whether the following are polygons. If any one among them is not, say why?

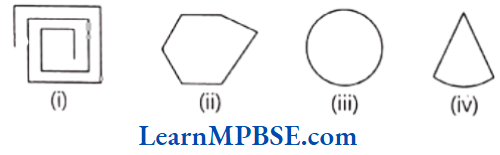
Solution. (1) It is an open figure. So, it is not a polygon.

(2) It is closed figure. So, it is a polygon with six sides i.e. hexagon.

(3) It is not made by line segments. So, it is not a polygon.

(4) It is made by two line segments and a curved line. So, it is not a polygon.

Class 6 Maths Chapter 5 Solutions MP Board

Question 2. Name each polygon.

Make two more examples of each of these.

Solution. (1) This polygon has four sides, so it is a quadrilateral. e.g.

(2) This polygon has three sides, so it is a triangle. e.g.

(3) This polygon has five sides, so it is a pentagon.

e.g.

(4) This polygon has eight sides, so it is an octagon.

e.g.

Question 3. Draw a rough sketch of a regular hexagon. Connecting any three of its vertices, draw a triangle. Identify the type of the triangle you have drawn.

Solution. Here, PQRSTU is a regular hexagon.

Joining its alternate vertices P, Rand T, we get ATPR, which is a regular triangle (since, all sides are equal).

Thus, the triangle so formed is an equilateral triangle.

Question 4. Draw a rough sketch of a regular octagon. (Use squared paper, If you wish).

Draw a rectangle by joining exactly four of the vertices of the octagon.

Solution. Here, ABCDEFGH is a regular octagon. Joining vertices G and D, we get \(\overline{G D}\). Again, joining H and C, we get H\(\overline{H C}\).

Thus, we get a rectangle HCDG.

Again, by joining A, F and B, E, we can get another rectangle ABEF.

Question 5. A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.

Solution. Rough sketch is shown below

Here, ABCDE is a pentagon.

By joining any two vertices, we get diagonals as \(\overline{A C}, \overline{A D}, \overline{B D}, \overline{B E} and \overline{C E}\).

Chapter 5 Understanding Elementary Shapes Multiple Choice Questions

Question 1. Measures of the two angles between hour and minutes hands of a clock at 9 O’ clock are

1. 60°, 300°
2. 270°, 90°
3. 75°, 285°
4. 30°, 330°

Answer. 2. 270°, 90°

Question 2. If a bicycle wheel has 48 spokes, then the angle between a pair of two consecutive spokes is

1. \(\left(5 \frac{1}{2}\right)^{\circ}\)
2. \(\left(7 \frac{1}{2}\right)^{\circ}\)
3. \(\left(\frac{2}{11}\right)^{\circ}\)
4. \(\left(\frac{2}{15}\right)^{\circ}\)

Answer. 2. \(\left(7 \frac{1}{2}\right)^{\circ}\)

Question 3. If figure, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of ∠BPY is

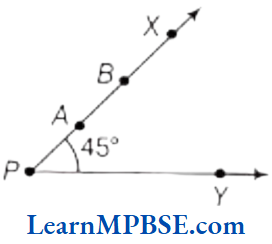
1. greater than 45°
2. 45°
3. less than 45°
4. 90°

Answer. 2. 45°

Class 6 Maths Chapter 5 solutions MP Board

Question 4. Where will the hand of a clock stop if it starts at 5 and makes \(\frac{1}{4}\) revolution clockwise?

1. 7
2. 8
3. 9
4. 10

Answer. 2. 8

Question 5. If you are facing South and turn through a straight angle in which direction will you face now?

1. South
2. North
3. East
4. West

Answer. 2. North

Question 6. Where will the hour hand of a clock stop if it starts at 7 and makes \(\frac{3}{4}\) revolution clockwise?

1. 2
2. 3
3. 4
4. 5

Answer. 3. 4

Question 7. The angle measure of one-fourth revolution is

1. 360°
2. 180°
3. 90°
4. None of these

Answer. 3. 90°

Question 8. How is the measure of an angle expressed?

1. Protractor
2. Compasses
3. Degrees
4. Centimeters

Answer. 3. Degrees

Question 9. If the sum of two angles is greater than 180°, then which of the following is not possible for the two angles?

1. One obtuse angle and one acute angle
2. One reflex angle and one acute angle
3. Two obtuse angles
4. Two right angles

Answer. 4. Two right angles

Question 10. 179° is an example of

1. a straight angle
2. an obtuse angle
3. an acute angle
4. a right angle

Answer. 2. an obtuse angle

Question 11. In figure, AB = BC and AD = BD = DC. Then, the number of isosceles triangles in the figure is

1. 1
2. 2
3. 3
4. 4

Answer. 3. 3

Question 12. The instrument to measure an angle is about

1. ruler
2. protractor
3. divider
4. compasses

Answer. 2. protractor

Question 13. The polygon with the least number of sides is a

1. triangle
2. rectangle
3. pentagon
4. hexagon

Answer. 1. triangle

Question 14. A rhombus with four right angles is known as

1. rectangle
2. square
3. kite
4. None of these

Answer. 2. square

MP Board Class 6 book solutions

Question 15. A polygon has the prime number of sides. Its number of sides is equal to the sum of the two least consecutive primes. The number of diagonals of the polygon is

1. 4
2. 5
3. 7
4. 10

Answer. 2. 5

Chapter 5 Understanding Elementary Shapes Assertion Reason

Question 1. Assertion (A) When we measure the length of a line segment by a ruler, there may be some errors due to angular viewing, these errors can be removed by making a line segment with the help of a divider.

Reason (R) The use of divider is better than a ruler.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (b) Both A and R are true but R is not the correct explanation of A.

Question 2. Assertion (A) When the hand of a clock moves from one position to another, it turns through an angle.

Reason (R) The angle for one revolution is a complete angle.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (b) Both A and R are true but R is not the correct explanation of A.

Chapter 5 Understanding Elementary Shapes Fill in the Blanks

Question 1. The hour hand of a clock stops at ….., if it starts at 12 and makes \(\frac{1}{2}\) revolution clockwise.

Answer. 6

Question 2. The angle formed in half-revolution is ………..

Answer. 180°

Question 3. Angle formed between the hands of a clock, when the time is 3 o’clock ……….

Answer. 90°

Question 4. A pair of opposite sides of a rectangle are ………… and ………….

Answer. Equal, parallel

Question 5. The number of diagonals in a hexagon is.

Answer. Nine

Chapter 5 Understanding Elementary Shapes True/False

Question 1. If the arms of an angle on the paper are increased, the angle increases.

Answer. False

Question 2. If the arms of an angle on the paper are decreased, the angle decreases.

Answer. False

Question 3. A horizontal line and a vertical line always intersect at right angle.

Answer. True

Question 4. Perpendicular bisector of the line segment is perpendicular to the line.

Answer. True

Question 5. A trapezium is a parallelogram.

Answer. False

Chapter 5 Understanding Elementary Shapes Match the Columns

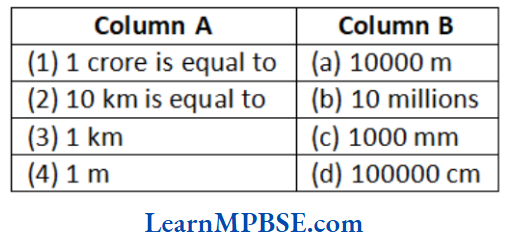
Question 1. Match the Column 1 with Column 2 with their respective values.

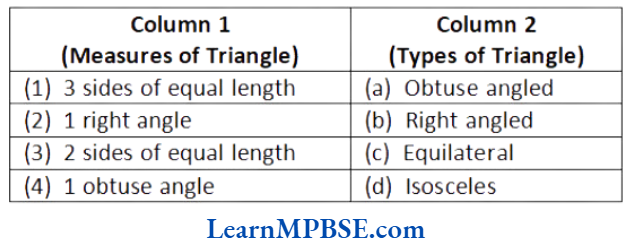
Solution. (1) → (c), (2) → (b), (3) → (d), (4) → (a)

Chapter 5 Understanding Elementary Shapes Case Based Questions

Question 1. A truss is a structural framework of wood or metal arranged in a pattern which is used to support roofs or bridges.

The structure of a truss made of iron rods is shown in the figure below.

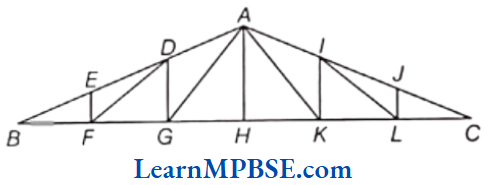
The rods EF, DG, AH, IK and JL are perpendicular to the base BC. A number of triangles are formed by the rods. In ΔABC, side AB = AC. In ΔAGK, all sides are equal and H is the mid-point of GK.

(1) Which type of triangle is ABC?

(a) Scalene

(b) Isosceles

(c) Equilateral

(d) Right-angled triangle

(2) Is ΔDGF a right-angled triangle? Justify your answer.

(3) Is AH the perpendicular bisector of line segment GK? Justify your answer.

(4) The sides of ΔIJL are of length 3 m, 4 m and 5 m. Is ΔIJL an isosceles triangle? Why?

Solution. (1) (b) Since, it given that in ΔABC, AB = AC, which means two sides of this triangle are equal. Therefore, it is an isosceles triangle.

(2) Yes, ADGF is a right-angled triangle because DG is perpendicular to BC, therefore ∠DGF = 90°, making ΔDGF a right-angled triangle.

(3) Yes, AH is the perpendicular bisector of line segment GK.

Since, it is given that H is the mid-point of GK and AH is perpendicular on it.

Therefore, AH is a perpendicular bisector of GK.

(4) If ΔIJL length of sides are 3m, 4m and 5m.

Therefore, ΔIJL is not an isosceles triangle because all the sides of this are unequal or there is no pair of equal sides.

MP Board Class 6 Book Solutions

Question 2. The figure below shows a combination of shapes.

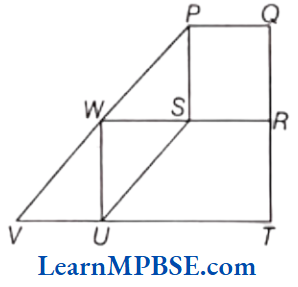
In the figure, US is parallel to WP and UV is parallel to QP.

PQRS is a square. WRTU is a rectangle. PSW and WUV are triangles.

(1) Arun joins Sand Q. SQ is an extension of US Which type of quadrilateral is PQUV? Justify your answer.

(2) Which of the following quadrilaterals is regular?

(a) PQRS

(b) PSUV

(c) RWUT

(d) PQTV

(3) Looking at the figure, Raji claims that, ‘PWUSis rhombus’. Do we have sufficient information to accept her claim? Justify your answer.

Solution. (1) Arun joins S and Q. SQ is an extension of US. PQUV is a parallelogram as its opposite sides are parallel.

(2) PQRS is a regular quadrilateral as its all sides are equal.

(3) No, there is no information on sides lengths of PWUS and opposite angles of PWUS.

Chapter 5 Understanding Elementary Shapes Very Short Answer Type Questions

Question 1. Write the name of triangle whose each angle is acute.

Solution. It is an acute angled triangle.

Question 2. Write the name of triangle whose all three sides are unequal in length.

Solution. A triangle which has all unequal sides is scalene triangle. Here, ΔABC is a scalene triangle.

where, AB ≠ BC ≠ CA

Question 3. Write the name of polygon which has 5 sides.

Solution. A polygon which has 5 sides is pentagon.

Question 4. Find the number of sides in a quadrilateral. What can you say about the number of angles? Is it greater than the number of sides?

Solution. Number of sides in a quadrilateral is 4 and number of angles is also 4

No, the number of angles is same as the number of sides.

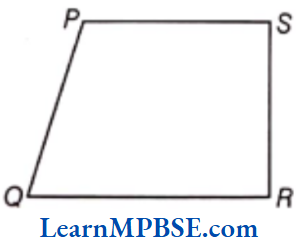
Question 5. If in a quadrilateral, one pair of opposite sides are parallel, then what is the name of such quadrilateral?

Solution. If one pair of opposite sides are parallel, then it is a trapezium. i.e. PS || QR

MP Board Class 6 Maths Solutions

Question 6. What is the difference between a square and a rhombus?

Solution. In a square, all angles are right angle whereas, in rhombus angles may right angle or not.

Question 7. The figure given below shows a tyre of a bicycle.

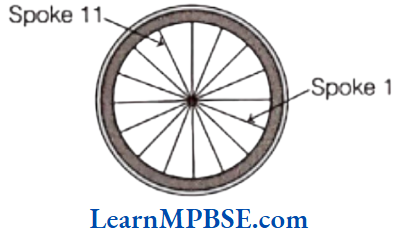
What type of angle does Spoke 1 make with Spoke 11?

Solution. Spoke 1 makes reflex angle and obtuse angle with Spoke 11.

Chapter 5 Understanding Elementary Shapes Short Answer Type Questions

Question 1. Will the lengths of line segment AB and line segment BC make the length of line segment AC in figure?

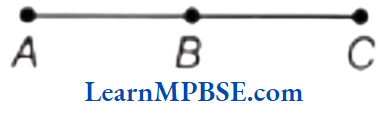
Solution. Here, \(\overline{A B}+\overline{B C}=\overline{A C}\)

Hence, the length of line segment \(\overline{A B}+\overline{B C}\) make the length of line segment \(\overline{A C}\).

Question 2. Will the measure of ∠ABC and ∠CBD make the measure of ∠ABD in figure?

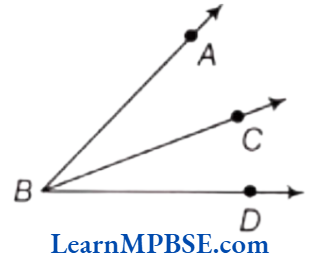
Solution. Here, ∠ABD = ∠ABC + ∠CBD

Hence, the measure of ∠ABC and ∠CBD makes the measure of ∠ABD.

Question 3. By simply looking at the pair of angles given below. State which of the angles in each pair is greater.

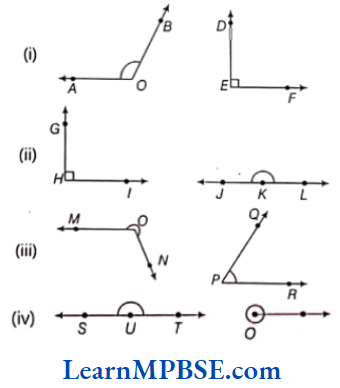
Solution. From the given figures, we can say that

(1) ∠AOB > ∠DEF

(2) ∠JKL > ∠GHI

(3) Reflex angle ∠MON > ∠QPR

(4) ∠0 > ∠SUT

Question 4. Which points in figure, appear to be mid-point of the line segments? When you locate a mid-point, name the two equal line segments formed by it.

Solution. In the figure,

(1) There is no mid-point in \(\overline{A B}\).

(2) O is the mid-point of \(\overline{A B} \text { and } \overline{O A}=\overline{O B}\)

(3) D is the mid-point of \(\overline{B C} \text { and } \overline{B D}=\overline{C D}\)

Question 5. Is it possible for the same

(1) line segment to have two different lengths?

(2) angle to have two different measures?

Solution. (1) No, a line segment cannot have two different lengths.

(2) No, an angle cannot have two different measurements.

Question 6. State the type of angle in the following.

Solution. In the given figures, we have

(1) ∠AOB is a right angle.

(2) ∠AOB is a straight angle.

(3) ∠AOB is an acute angle.

(4) ∠AOB is an obtuse angle.

(5) ∠AOB is an obtuse angle.

(6) ∠O is a complete angle.

MP Board Class 6 Maths Solutions

Question 7. Using a ruler onlu, draw an acute, obtuse and reflex angle.

Solution. (1) Acute ∠AOB

(2) Obtuse ∠POQ

(3) Reflex ∠ROS

Question 8. Convert the following angles (in degrees) into fraction of right angle.

(1) 10°

(2) 20°

(3) 135°

Solution. We know that 1 right angle = 90°

i.e. 1°= \(\frac{1}{90}\) right angle

(1) \(10^{\circ}=\frac{10^{\circ}}{90^{\circ}}=\left(\frac{1}{9}\right) \text { right angle }\)

(2) \(20^{\circ}=\frac{20^{\circ}}{90^{\circ}}=\left(\frac{2}{9}\right) \text { right angle }\)

(3) \(135^{\circ}=\frac{135^{\circ}}{90^{\circ}}=\left(\frac{3}{2}\right) \text { right angle }\)

Question 9. Convert the following into degree.

(1) \(\frac{2}{9}\) right angle

(2) \(\frac{3}{4}\) right angle

Solution. We know that right angle = 90°

(1) \(\frac{2}{9} \text { right angle }=\frac{2}{9} \times 90^{\circ}=20^{\circ}\)

(2) \(\frac{3}{4} \text { right angle } \frac{3}{4} \times 90^{\circ}=675^{\circ}\)

Question 10. In the given figure, PQ ⊥ AB and PO = OQ. Is PQ, the perpendicular bisector of line segment AB? Why or why not?

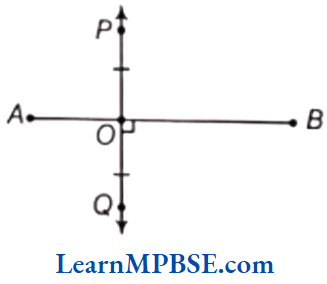
Solution. PQ is not the perpendicular bisector of line segment AB because AO ≠ BO.

[Note AB is the perpendicular bisector of line segment PQ].

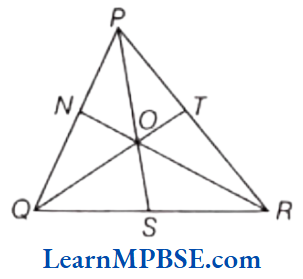
Question 11. Draw any triangle of your choice, then draw all the three medians. Are they passing through one point?

Solution. According to the given information, APQR has medians \(\overline{P S}, \overline{Q T} \text { and } \overline{R N}\). Yes, these medians passing through one point ‘O’.

MP Board Class 6 Maths Solutions

Question 12. Which direction will you face, if you start facing East and make \(\frac{3}{4}\) of a revolution clockwise?

Solution. We face towards North.

Question 13. If each side of a triangle is 6 cm. Name the type of triangle.

Solution. Given that, each side of a triangle is 6 cm.

Hence, it is an equilateral triangle.

Question 14. Find the measure of ∠POQ if PR ⊥ QT.

Solution. Here, ∠POQ = 90°

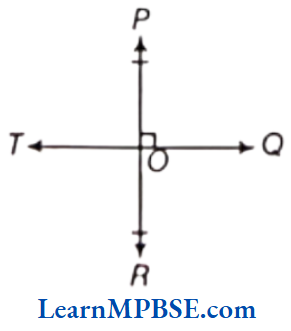
Chapter 5 Understanding Elementary Shapes Long Answer Type Questions

Question 1. Construct two line segments AB and CD of lengths 2.5 cm and 3.2 cm. Construct another segment EF, whose length is the sum of these two line segments. Measure the new length.

Solution. Now, first of all, we draw AB = 2.5 cm and CD = 3.2 cm

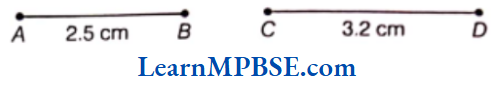
Now, we have to draw a line segment

∴ \(\overline{E F}=\overline{A B}+\overline{C D}\) = 2.5 + 3.2 = 5.7 cm

Hence, new length is 5.7 cm.

Question 2. Name the type of triangle and also draw it rough sketch.

(1) ΔABC; ∠A = ∠B = ∠C = 60°

(2) ΔABC; ∠B = ∠C = 50°

(3) ΔABC; ∠A = 45°, ∠B = 45°, ∠C = 90°

(4) ΔABC; ∠A = 50°, ∠B = 60°, ∠C = 70°

Solution. (1) Given, ∠A = ∠B = ∠C = 60°

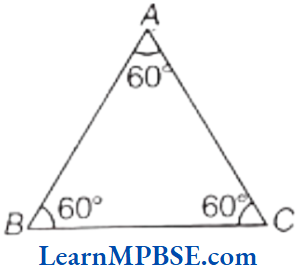
Hence, it is an equilateral triangle.

(2) Given, ∠B = ∠C = 50°

So, AB = AC

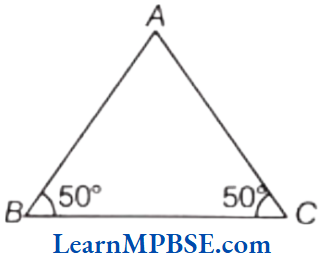
Hence, it is an isosceles triangle.

(3) Given, ∠A = 45°, ∠B = 45°, ∠C = 90°

So, AC = BC

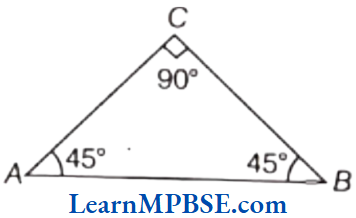
Hence, it is an isosceles right angled triangle.

(4) Given, ∠A = 50°, ∠B = 60°, ∠C = 70°

So, AB ≠ BC ≠ CA

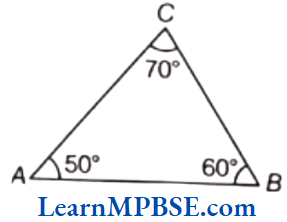
Hence, it is a scalene and acute angled triangle.

MP Board Class 6 book solutions

Question 3. During Maths lab activity, each student was given four broom sticks of length 8 cm, 8 cm, 5 cm, 5 cm to make different types of quadrilaterals.

(1) How many types of quadrilateral can be formed using four broom sticks?

(2) Name the types of quadrilateral formed.

Solution. Given, four broom sticks of length 8 cm, 8 cm, 5 cm and 5 cm.

(1) Three types of quadrilaterals can be formed.

(2) Name of the quadrilaterals are rectangle, parallelogram and kite.

Question 4. Name the following angles of figure using three alphabets

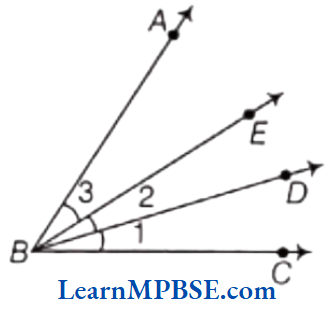
(1) ∠1

(2) ∠2

(3) ∠3

(4) ∠1 + ∠2

(5) ∠2 + ∠3

(6) ∠1 + ∠2 + ∠3

(7) ∠CBA – ∠1

Solution. Name of the angles are as follows:

(1) ∠1 = ∠CBD

(2) ∠2 = ∠DBE

(3) ∠3= ∠EBA

(4) ∠1 + ∠2 = ∠CBE

(5) ∠2 + ∠3 = ∠DBA

(6) ∠1 + ∠2 + ∠3 = ∠CBA

(7) Put the value of ∠CBA [∴ ∠CBA = ∠1 + ∠2 + ∠3]

Now, ∠CBA – ∠1 = ∠1 + ∠2 + ∠3 – ∠1

= ∠2 + ∠3 = ∠DBA [∴ ∠DBA ∠2+ ∠3]

Question 5. In which of the following figures

(1) perpendicular bisector is shown?

(2) bisector is shown?

(3) only bisector is shown?

(4) only perpendicular is shown?

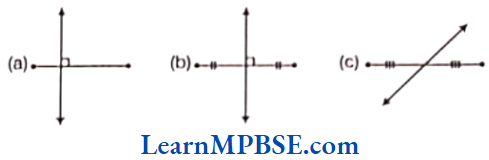
Solution. (1) Perpendicular bisector means, a line is perpendicular to the another line and divides it into two equal parts.

Here, in figure (b), perpendicular bisector is shown.

(2) Bisector means, a line divides the another line in two equal parts.

Here, in figures (b) and (c), bisectors are shown.

(3) Only bisector is shown in figure (c).

(4) Only perpendicular is shown in figure (a).

MP Board Class 6 Maths Solutions

Question 6. Using the given information, name the right angles in the following figures.

(1) AC ⊥ BD

(2) AE ⊥ CE

(3) AC ⊥ CD

(4) OP ⊥ ABC

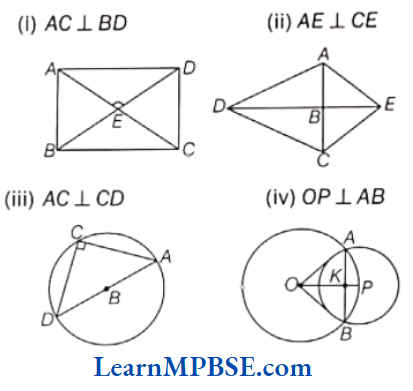
Solution. (1) Since, AC ⊥ BD, it means ∠E = 90°.

∴ ∠AEB, ∠BEC, ∠CED and ∠AED are right angles.

(2) Since, AE ⊥ CE, it means ∠E = 90°

∴ ∠AEC is a right angle.

(3) Since, AC ⊥ CD, it means ∠C = 90°

∴ ∠ACD is a right angle.

(4) Since, OP ⊥ AB, it means ∠K = 90°

∴ ∠AKO, ∠OKB, ∠BKP and ∠AKP are right angles.

MP Board Class 6 book solutions

Question 7. What conclusion can be drawn in each part of figure?

(1) DB is the bisector of ∠ADC.

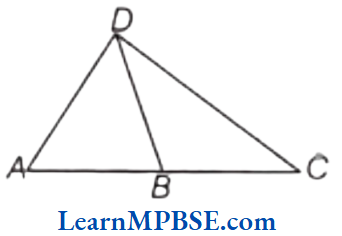
(2) BD bisects ∠ABC.

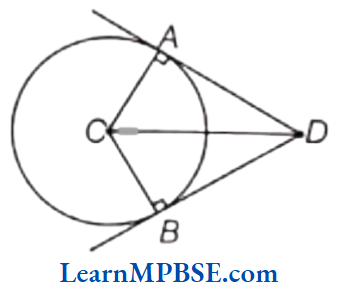
(3) DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB.

Solution. We know that bisector line divides an angle into two equal angles.

(1) Since, BD is the bisector of ∠ADC,

∴ ∠ADB = ∠BDC

(2) Since, BD bisects ∠ABC,

∴ ∠ABD = ∠CBD

(3) Since, DC is the bisector of ∠ADB and CA ⊥ DA and CB ⊥ DB

∴ ∠ADC = ∠BDC and ∠CAD = 90°, ∠CBD = 90°

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas

Point

A point determines a location and has no length, breadth or height. It is denoted by a single capital letter like P, Q, R etc. We can mark unlimited points on a plane.

•P

•Q

•R

The above points will be read as point P, point Q and point R.

e.g.

• The tip of a compass.
• The sharpened end of a pencil etc.

Example 1. Tip of an ice-cream cone gives us an idea of a point. Identify such few situations in your daily life and write them.

Solution. Such few situations in our daily life are as follows:

(1) The corners of a room

(2) Finger tip

(3) The location of a place on map

(4) A satellite in the space

(5) Moon from longer distance

Read and Learn More MP Board Class 6 Maths Solutions

Line Segment

A line segment is the shortest distance between two points which has a definite length.

The line segment joining points A and B is denoted by \(\overline{A B}\) or \(\overline{B A}\). These points A and B are called the end points of the line segment \(\overline{A B}\).

e.g. The edge of a box, a tubelight, the edge of a postcard, etc.

Mp Board Class 6 Maths Chapter 4 Solutions

Example 2. Name any five line segments in the following figure:

Solution. The five line segments in the figure are

\(\overline{A B}\),\(\overline{B C}\),\(\overline{C D}\),\(\overline{D E}\) and \(\overline{F G}\)

Example 3. Name the line segments in the given figure. Is P, the end point of each line segment?

Solution. The line segment in the given figure are as follows: (1) \(\overline{P Q}\) (or \(\overline{Q P}\))

(2) \(\overline{P R}\) (or \(\overline{R P}\))

(iii) \(\overline{P S}\) (or \(\overline{S R}\))

Yes, from the figure, it is clear that point P is the end point of each line segment.

Line

A line is obtained when a line segment \(\overline{A B}\) is extended on both sides indefinitely and denoted by \(\overleftrightarrow{A B}\). Sometimes it is denoted by a single letter as 1, m.

In other words, two points are enough to fix a line.

i.e. Exactly one line can be drawn through the two given points.

A line has length only. It has neither width nor thickness. An endless line can be drawn on a paper by using two arrow heads one at each end of the portion of the line which indicates that it extends in both directions, indefinitely.

Example 4. Name the line given in all possible ways, choosing only two letters at a time from the three given letters.

Solution. Name of lines in all possible ways are as follows:

(1) By taking P, all possible ways are \(\overleftrightarrow{P Q}\) and \(\overleftrightarrow{P S}\).

(2) By taking Q, all possible ways are \(\overleftrightarrow{Q P}\) and \(\overleftrightarrow{Q S}\).

(3) By taking S, all possible ways are \(\overleftrightarrow{S Q}\) and \(\overleftrightarrow{S P}\).

Intersecting Lines

If two lines have one common point, then they are called intersecting lines. The point at which lines meet is called the point of intersection.

In the figure, lines, l1 and l2 are intersecting lines, which intersects at point O.

e.g. Two adjacent edges of a notebook, the english alphabet X, crossing roads etc.

Class 6 Maths Chapter 4 Mp Board Solutions

Example 5. Find

(1) two lines can intersect at how many points ?

(2) how many lines can intersect at one point?

Solution. (1) By the definition of intersecting lines, if two lines have one common point, then they are called intersecting lines. So, two lines can intersect at only one point.

Here, l and m have only one intersecting point i.e. O.

(2) There are infinite number of lines that can intersect at one point.

Here, lines l, m, nand p have one common point O, which is there intersecting point.

Note it The number of lines intersect at one point are infinite.

Parallel Lines

Two lines in a plane which are at equal distance from each other and never meet at any point or cross each other even if extended in any direction, are called parallel lines.

In the above figure, lines \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) does not intersect each other and the common difference between them is always constant. Hence, \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are parallel to each other and are called parallel lines which can be denoted as \(\overleftrightarrow{A B}\) || \(\overleftrightarrow{C D}\)

e.g. The opposite edges of ruler (or scale), the railway lines etc.

Mp Board Class 6 Maths Book Pdf

Example 6. From the following figure, find the

(1) pairs of intersecting lines.

(2) parallel lines.

(3) point of Intersection.

Solution. (1) Pairs of intersecting lines, F and G, F and H, F and I, G and I, H and I, G and H, J and H, J and G, K and G, K and H.

(2) Parallel lines are J ∥ I, J ∥ K, I ∥ K

(3) Point of intersection are A, B, E, C and D.

Ray

A ray is a portion of a line which starts at a point (called as starting point or initial point) and going in one direction endlessly.

In the above figure, \(\overrightarrow{A P}\) is a ray whose starting point is A and P is a point on the path of the ray. Here, the arrow indicates that the ray \(\overrightarrow{A P}\) is endless in the direction from A to P.

e.g. Beam of light from a lighthouse, ray of light from a torch, Sun rays etc.

Example 7. Identify the rays from the following figure.

Solution. The rays are \(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D}, \overrightarrow{B C}, \overrightarrow{B D} \text { and } \overrightarrow{C D}\).

Mp Board Class 6 Maths Important Questions

Example 8. From the given figure answer the following.

(1) Identify the rays and name them.

(2) Is M, a starting point of each of these rays?

Solution. (1) In the given figure, there are four rays namely \(\overrightarrow{M N}\), \(\overrightarrow{M A}\), \(\overrightarrow{N A}\) and \(\overrightarrow{M B}\).

(2) No, M is not the starting point of each of these rays. M is starting point of \(\overrightarrow{M N}\), \(\overrightarrow{M A}\), \(\overrightarrow{M B}\) and for \(\overrightarrow{N A}\), M is not the starting point.

Example 9. In the given figure, name all the rays with initial points as P, Q and R, respectively.

(1) Is ray \(\overrightarrow{P Q}\) different from ray \(\overrightarrow{P R}\)

(2) Is ray \(\overrightarrow{R A}\) different from ray \(\overrightarrow{R B}\).

Solution. \(\overrightarrow{P A}, \overrightarrow{P Q}, \overrightarrow{P R}, \overrightarrow{P B}, \overrightarrow{Q A}, \overrightarrow{Q P}, \overrightarrow{Q R}, \overrightarrow{Q B}, \overrightarrow{R A}, \overrightarrow{R P}, \overrightarrow{R Q}, \overrightarrow{R B}\)

(1) No

(2) Yes

Example 10. By using following figure, write

(1) all the points.

(2) a line.

(3) two rays with initial point Q.

(4) two line segments.

Solution. From the given figure,

(1) all the given points are P, Q, O, R and S.

(2) a line is \(\overleftrightarrow{P R}\)

(3) two rays with initial point Q is \(\overrightarrow{Q P}\) and \(\overrightarrow{Q O}\).

(4) two line segments are \(\overline{O Q} \text { and } \overline{O S}\).

Class 6 Maths Chapter 4 Exercise Solutions

Example 11. Use the following figure to name

(1) Line containing point R.

(2) Line passing through point Q.

(3) Line on which C lies.

(4) Pair of intersecting lines.

Solution. (1) Here, two lines contain point R, one of them is \(\overleftrightarrow{P S}\).

(2) Here, line passing through point Q is \(\overleftrightarrow{P S}\).

(3) C lies on \(\overleftrightarrow{C D}\).

(4) Two pairs of intersecting lines are \(\overleftrightarrow{P S}\), \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P S}\), \(\overleftrightarrow{C D}\).

Example 12. Draw a rough figure and label suitably in each of the following cases.

(1) Point P, Q, R lies on \(\overline{A B}\).

(2) \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P Q}\) intersect at M.

(3) A line \(\overleftrightarrow{A B}\) which does not contain O.

(4) \(\overleftrightarrow{P Q}\) \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{P S}\) meet at P.

Solution. A rough figure in each of the cases is given below.

(1) Point P, Q, R lies on \(\overline{A B}\).

(2) \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{P Q}\) intersect at M.

(3) A line \(\overleftrightarrow{A B}\) which does not contain O.

(4) \(\overleftrightarrow{P Q}\) \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{P S}\) meet at P.

Mp Board Class 6 Maths Chapter 4 Solutions

Example 13. From the figure, name

(1) All pairs of parallel lines.

(2) All pairs of intersecting lines.

(3) Lines whose point of intersection is P.

(4) Lines whose point of intersection is C.

(5) Lines whose point of intersection is R.

Solution. (1) l ∥ m, l ∥ n, m ∥ n

(2) p and q, p and l, p and m, p and n,q and l, q and m,q and n

(3) l and p

(4) q and m

(5) p and n

Example 14. Consider the following figure of line \(\overleftrightarrow{X Y}\). Say whether following statements are true or false in context of the given figure.

(1) Point Y does not lie on \(\overleftrightarrow{A C}\).

(2) A and C are the end points of line segment \(\overleftrightarrow{A Y}\).

(3) X and Y lies on the extended portion of \(\overleftrightarrow{A C}\).

(4) Point B lies outside of \(\overleftrightarrow{X Y}\).

Solution.

(1) False, because Y lies on the extended portion of \(\overleftrightarrow{A C}\).

(2) False, because it is clear from the figure that point C is between A and Y.

(3) True, it is clear from the figure that point X and Y lie on the extended portion of \(\overleftrightarrow{A C}\).

(4) False, point B lies between \(\overleftrightarrow{X Y}\).

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Curves and Polygons

Curve

Any drawing on the paper done without lifting the pencil from the paper and without use of ruler is called a curve. In this sense, a line is also called a curve.

e.g.

There are mainly three types of curves which are given below:

(1) Simple curve If a curve does not cross itself, is called a simple curve.

e.g.

(2) Open curve If a curve does not cut itself, is called an open curve.

In other words, when the end point of a curve are not joined, is called an open curve.

e.g.

(3) Closed curve If a curve cuts itself, is called a closed curve.

In other words, when the end points of a curve are joined, then it is called a closed curve.

e.g.

Position in a Figure

In a closed curve, there are three positions, which are as follows:

• Interior (inside) of the curve
• Boundary (on) of the curve
• Exterior (outside) of the curve

In the figure below, A is in the interior, B is on the curve and C is in the exterior.

The interior of a curve together with its boundary is called its region.

Example 1. Classify the following curves as

(1) Open

(2) Closed

Solution. (1) (a) and (c) are open curves.

(2) (b) and (d) are closed curves.

Example 2. Look at the alphabets given below and answer the questions.

P X S B C D V F

Which of the above letters are made of

(1) straight lines only?

(2) curves only?

(3) both straight line and curves?

Solution. (1) Straight lines only : X V F

(2) Curves only : S C

(3) Both straight line and curves : P B D

Class 6 Maths Chapter 4 Mp Board Solutions

Example 3. Consider the given figure and answer the following questions.

(1) Is it curve ?

(2) Is it closed?

Solution. Since, any drawn figure made without lifting the pencil from the paper is called a curve and if its ends points are joined, it is called a closed curve.

(1) Yes, it is a curve.

(2) Yes, it is closed curve.

Polygon

A simple closed curve made up of line segments is called a polygon.

e.g.

A polygon has finite number of sides.

In the given figure, ABCDE is a polygon.

(1) Sides The line segments, forming a polygon are called its sides. In polygon ABCDE, AB, BC, CD, DE and EA are its sides.

(2) Vertex The meeting point of a pair of sides is called its vertex. In polygon ABCDE, A, B, C, D and E are its vertices.

(3) Adjacent sides Any two sides with a common end point (vertex) are called the adjacent sides of the polygon.

In polygon ABCDE, one pair of adjacent sides is AB and BC (where, B is a common vertex).

(4) Adjacent vertices The end points of the same side of a polygon are called the adjacent vertices.

In polygon ABCDE, A and B, B and C, C and D, D and E, E and A are adjacent vertices.

(5) Diagonals A diagonal is a line segment joining any two non-consecutive vertices.

In polygon ABCDE, AC, AD, BD, BE and CE are diagonals.

Note It No two line segments with a common ends points are coincident.

Example 4. Identify the polygons from the following figures:

Solution. (1) The given figure is not closed. Hence, it is not a polygon.

(2) The given figure is closed. Hence, it is a polygon.

(3) The given figure is closed. Hence, it is a polygon.

(4) In the given figure, two sides are arc. Hence, it is not a polygon.

Mp Board Class 6 Maths Book Pdf

Example 5. Draw a polygon with four line segments and write its

(1) vertices

(2) sides

(3) diagonals

Solution. (1) Vertices of polygon PQRS are P, Q, R and S.

(2) Sides are PQ, QR, RS and SP.

(3) Diagonals are PR and QS.

Example 6. Illustrate, if possible, each one of the following with a rough diagram:

(1) A polygon with five sides.

(2) A polygon with two sides.

Solution. (1) The following figure is shows a polygon with five sides.

(2) It is not possible, because a polygon of two sides cannot be drawn. A minimum of three sides are required to form a polygon.

Example 7. In the given figure, write the

(1) number of sides.

(2) number of vertices.

Solution. (1) The following figure is drawn by joining the sides PQ, QR, RS, ST, TU and UP.

∴ Number of sides = 6

(2) Vertices in the given figure are P, Q, R, S, T and U.

∴ Number of vertices = 6

Mp Board Class 6 Maths Important Questions

Example 8. From the following figure, P answer the following question.

(1) Is PQRTS a polygon ?

(2) Is M lies in the exterior of the polygon?

(3) Is N lies in the interior of the polygon?

Solution. (i) Yes, since PQRTS is a simple closed curve entirely made of line segments, therefore it is a polygon.

(2) No, M lies in the interior of the polygon.

(3) No, N lies in the exterior of the polygon.

Example 9. Name the points which are inside the figure, on the figure and outside the figure.

Solution. Points in the interior of figure: B, M and Q

Points on the figure: A, D, U and S;

Points on the exterior of the figure: C, E and R.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Angles

An angle is made up of two rays starting from a common starting/initial point. The two rays forming the angle are called the arms or sides of the angle and the common initial point is the vertex of the angle.

In the given figure, AOB is an angle and it is denoted by ∠AOB or ∠BOA or ∠O.

Here, OA and OB are arms or sides of angle and O is the vertex of the angle.

(1) In specifying the angle, the vertex is always written as the middle letter.

(2) An angle leads to three divisions of a region i.e. on the angle, the interior of the angle and the exterior of the angle.

In this diagram, point X is in the interior of the angle. Point P, point S and point R are on the angle and point Y is in the exterior of the angle.

Example 1. Write the name of angles in the given figure.

Solution. Here, angles are ∠AOB, ∠BOC and ∠AOC.

Class 6 Maths Chapter 4 Solutions

Example 2. Name the vertex and the arms of ∠PQR, given in the figure below.

Solution. Q is the vertex, PQ and QR are the arms of angle ∠PQR

Example 3. Name the angles in the given figure.

Solution. We know that an angle is made up of two rays starting from a common initial point. So, the angles in given figure are as follow:

(1) ∠A or ∠BAD

(2) ∠B or ∠ABC

(3) ∠C or ∠BCD

(4) ∠D or ∠CDA

Basic Geometrical Ideas Class 6 

Example 4. Draw rough diagrams of two angles for the conditions which are possible.

(1) One point in common.

(2) Three points in common.

(3) Four points in common.

Solution. (1) In the diagram, ∠POQ and ∠ROS have point O in common.

(2) In the diagram, ∠POR and ∠ROS have points O, Q and R in common.

(3) In the diagram, ∠POR and ∠QOR have points O, R, S and T common.

Example 5. Draw rough diagrams of two angles such that they have one ray in common.

Solution. Here, ∠ABC and ∠DBA have ray \(\overrightarrow{B A}\) in common.

Example 6. Write the alternate name of the angle ∠SRQ in the given figure.

Solution. The alternate name for the angle ∠SRQ is ∠R

Basic Geometrical Ideas Class 6 

Example 7. In the following figure, how many angles are there? Name them.

Solution. There are 6 angles i.e. ∠BOA, ∠COA, ∠DOA, ∠BOC, ∠BOD and ∠COD.

Example 8. How many angles does a polygon of six sides has?

Solution. Angles are formed when corners are formed. Following figure is the polygon with six sides.

Here, six corners are formed.

So, the polygon with six sides has 6 angles.

Note it The number of angles in a polygon is equal to the number of sides of the polygon.

Example 9. Name each of the following angles in different ways.

Solution. (1) ∠RQP or ∠PQR or ∠Q or ∠5

(2) ∠ZYX or ∠XYZ or ∠Y or ∠7

(3) ∠CBA or ∠ABC or ∠B or ∠9

Class 6 Maths Chapter 4 Exercise Solutions

Example 10. In figure, write another name for

(1) ∠1

(2) ∠2

(3) ∠3

(4) ∠4

(5) ∠5

Solution.

(1) ∠1 → ∠DAE or ∠EAD

(2) ∠2 → ∠QAC or ∠CAQ

(3) ∠3 → ∠ACD or ∠DCA

(4) ∠4 → ∠ADC or ∠CDA

(5) ∠5 → ∠ARE or ∠ERA

Example 11. In the given diagram, name the point(s).

(1) In the interior of ∠AOB

(2) In the exterior of ∠BOC

(3) On ∠AOB

Solution. (1) In the given figure, point E lies between the sides OA and OB. So, it is in the interior of ∠AOB.

(2) In the given figure, points E, A and G are in the exterior of ∠BOC.

(3) In the given figure, point A, O, D and B lies on the sides OB and OA of ∠AOB, so these points are on ∠AOB.

Question 1. With a sharp tip of the pencil, mark four points on a paper and name them by the letters A, C, P, H. Try to name these points in different ways. One such way could be this

Solution. We can give the name to these given points in different ways as follows:

Question 2. A star in the sky also gives us an idea of a point. Identify atleast five such situations in your daily life.

Solution. Five situations of a point in our daily life are as follow:

(1) Tip of an ice cream cone.

(2) An edge of a table.

(3) Corner of a room.

(4) Corner of a desk.

(5) Corner of a paper.

Question 3. Name the line segments in the figure. Is A, the end point of each line segment?

Solution. We know that the shortest distance between two points is called a line segment.

The line segment joining two points A and B is denoted by \(\overline{A B} \text { or } \overline{B A}\). The line segment in the given figure are as follows:

(1) \(\overline{A B}\) (or \(\overline{B A}\))

(2) \(\overline{A C}\) (or \(\overline{C A}\))

Yes, from the figure, it is clear that point A is the end point of each line segment.

MP Board Class 6 Chapter 4 Maths

Question 4. Take a sheet of paper. Make two folds (and crease them) to represent a pair of intersecting lines and discuss.

(1) Can two lines intersect in more than one point?

(2) Can more than two lines intersect in one point?

Solution. We know that if two lines have one common point, then they are called intersecting lines. By making two folds of a sheet of paper and crease them, we get the following figures.

(1) From figure, it is clear that line l and m intersect at one point O (say) only. So, two lines cannot intersect in more than one point.

(2) Now, we again fold the paper diagonally (i.e. fold the paper three times) and crease them. We get the following figure.

In the figure, four lines l, m, n and o are intersecting at one point O’ (say) only. So, it is clear from the above figure, that more than two lines intersect in one point.

Question 5. (i) Name the rays given in this picture.

(2) Is T a starting point of each of these rays?

Solution. We know that a ray is a part of a line which starts at one point and goes endlessly in a direction.

(1) In the given figure, there are four rays namely \(\overrightarrow{T A}\), \(\overrightarrow{T N}\), \(\overrightarrow{N B}\) and \(\overrightarrow{T B}\).

(2) No, T is not a starting point of each of these rays. T is a starting point of \(\overrightarrow{T A}\), \(\overrightarrow{T B}\) and \(\overrightarrow{T N}\) only but not of \(\overrightarrow{N B}\).

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Exercise 4.1

Question 1. Use the figure to name

(1) five points.

(2) a line.

(3) four rays.

(4) five line segments.

Solution. From the given figure,

(1) Five points are B, C, D, E, and O.

(2) A line is \(\overleftrightarrow{B D}\) (or \(\overleftrightarrow{D B}\)).

(3) Four rays are \(\overrightarrow{O B}\), \(\overrightarrow{O C}\), \(\overrightarrow{O E}\) and \(\overrightarrow{O D}\).

(4) Five line segments in the given figure are \(\overline{O B}\), \(\overline{O C}\), \(\overline{O E}\), \(\overline{O D}\) and \(\overline{D E}\)

Note Two points are enough to fix a line. Hence, we can say that two points determine a line.

Question 2. Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given letters.

Solution. We know that a line is a line segment which can extend indefinitely in both directions. Name of lines in all possible ways are as follow:

(1) By taking A, all possible ways are \(\overleftrightarrow{A B}\), \(\overleftrightarrow{A C}\) and \(\overleftrightarrow{A D}\).

(2) By taking B, all possible ways are \(\overleftrightarrow{B C}\), \(\overleftrightarrow{B D}\) and \(\overleftrightarrow{B A}\).

(3) By taking C, all possible ways are \(\overleftrightarrow{C D}\), \(\overleftrightarrow{C A}\) and \(\overleftrightarrow{C B}\).

(4) By taking D, all possible ways are \(\overleftrightarrow{D A}\), \(\overleftrightarrow{D B}\) and \(\overleftrightarrow{D C}\).

Class 6 Maths Chapter 4 Mp Board Solutions

Question 3. Use the figure to name

(1) line containing point E

(2) line passing through A.

(3) line on which O lies.

(4) two pairs of intersecting lines.

Solution. (1) Here, two lines contain point E, one of them is \(\overleftrightarrow{A E}\).

(2) Here, one line is passing through A, i.e. \(\overleftrightarrow{A E}\).

(3) Line on which O lies, is \(\overleftrightarrow{C O}\) or \(\overleftrightarrow{O C}\).

(4) There are two pairs of intersecting lines i.e. \(\overleftrightarrow{C O}\), \(\overleftrightarrow{A E}\) and \(\overleftrightarrow{A E}\), \(\overleftrightarrow{E F}\).

Question 4. How many lines can pass through

(1) one given point?

(2) two given points?

Solution. (1) Infinite number of lines can pass through one given point.

Let there be a point O on a surface. Now, we can draw infinite lines through it.

(2) Exactly one and only one line can pass through two given points (say A and B)

i.e

Question 5. Draw a rough figure and label suitably in each of the following cases.

(1) Point P lies on \(\overline{A B}\).

(2) \(\overleftrightarrow{X Y}\) and \(\overleftrightarrow{P Q}\) intersect at M.

(3) Line l contains E and F but not D.

(4) \(\overleftrightarrow{O P}\) and \(\overleftrightarrow{O Q}\) meet at 0.

Solution. A rough figure in each of the cases is given below

(1) Point P lies on \(\overline{A B}\).

(2) \(\overleftrightarrow{X Y}\) and \(\overleftrightarrow{P Q}\) intersect at M.

(3) Line l contains E and F but not D.

(4) \(\overleftrightarrow{O P}\) and \(\overleftrightarrow{O Q}\) meet at O.

Class 6 Maths Chapter 4 Mp Board Solutions

Question 6. Consider the following figure of line \(\overleftrightarrow{M N}\). Say whether following statements are true or false in context of the given figure.

(1) Q, M, O, N, Pare points on the line \(\overleftrightarrow{M N}\).

(2) M, O, N are points on a line segment \(\overline{M N}\).

(3) M and N are end points of line segment \(\overline{M N}\).

(4) O and N are end points of line segment \(\overline{O P}\).

(5) M is one of the end points of line segment \(\overline{Q O}\).

(6) M is point on ray \(\overrightarrow{O P}\).

(7) Ray \(\overrightarrow{O P}\) is different from ray \(\overrightarrow{Q P}\).

(8) Ray \(\overrightarrow{O P}\) is same as ray \(\overrightarrow{O M}\).

(9) Ray OM is not opposite to ray \(\overrightarrow{O P}\).

(10) O is not an initial point of \(\overrightarrow{O P}\).

(11) N is the initial point of \(\overrightarrow{N P}\) and \(\overrightarrow{N M}\).

Solution.

(1) True, because points M, O and N lie on the line \(\overleftrightarrow{M N}\) and points Q, Plie on the extended portion of \(\overleftrightarrow{M N}\) on both sides.

(2) True, because points M, O, N lie on the line segment \(\overline{M N}\).

(3) True, because M to N is the shortest route of line segment \(\overline{M N}\).

(4) False, because it is clear from figure that point Nis between O and P.

(5) False, because it is clear from figure that point Mis between Qand O.

(6) False, because M is outside from ray OP.

(7) True, because all the rays have their own existence.

(8) False, because rays \(\overrightarrow{O P}\) and \(\overrightarrow{O M}\) are in opposite directions.

(9) False, because it is clear from figure that rays OM and OP are opposite.

(10) False, because it is clear from figure that point O is the initial point of \(\overrightarrow{O P}\).

(11) True, because it is clear from figure that ray \(\overrightarrow{N P}\) and \(\overrightarrow{N M}\) start from point N.

Question 7. Try to form a polygon with

(1) Five matchsticks.

(2) Four matchsticks.

(3) Three matchsticks.

(4) Two matchsticks.

In which case was it not possible? Why?

Solution. We know that if a closed simple figure is made up entirely of line segments, then it is called a polygon.

(1) Polygon with five matchsticks

(2) Polygon with four matchsticks.

(3) Polygon with three matchsticks

(4) We know that a polygon is a closed plane figure, bounded by line segments. So, with the help of two matchsticks, it is not possible to make a closed plane figure. Hence, no polygon is formed by two matchsticks.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical ideas Exercise 4.2

Question 1. Classify the following curves as (1) Open or (2) Closed.

TIPS A simple curve is one, that does not cross itself. Besides, when the ends of a curve are joined, it is called a closed curve. If its ends are not joined, it is called an open curve.

Solution. (1) (a) and (c) are open curves.

(2) (b), (d) and (e) are closed curves.

Question 2. Draw rough diagram to illustrate the following:

(1) Open curve

(2) Closed curve

Solution. (1) The curve given below is an open curve, since its ends are not joined

(2) The curve given below is a closed curve, since its ends are joined

Question 3. Draw any polygon and shade its interior.

TIPS We know that a simple closed figure made up entirely of line segments is called a polygon and in a closed curve, the interior is inside of the curve.

Solution. ABCD is a polygon, where interior is shaded as given below:

Question 4. Consider the given figure and answer the questions.

(1) Is it a curve?

(2) Is it closed?

TIPS Any drawing drawn without lifting the pencil from the paper is called a curve. A curve is said to be a closed curve, if its ends are joined.

Solution. (1) Yes, it is a curve.

(2) Yes, it is closed.

Mp Board Class 6 Maths Important Questions

Question 5. Illustrate, if possible, each one of the following with a rough diagram:

(1) A closed curve that is not a polygon.

(2) An open curve made up entirely of line segments.

(3) A polygon with two sides.

Solution. (1) The following figure shows a closed curve, but not a polygon, because a polygon is made by line segments only.

(2) The following figure shows an open curve made up entirely of line segments.

(3) It is not possible, because a polygon of two sides cannot be drawn.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Exercise 4.3

Question 1. Name the angles in the given figure.

Solution. We know that an angle is made up of two rays starting from a common initial point. So, the angles in given figure are as follow:

(1) ∠A or ∠DAB

(2) ∠B or ∠ABC

(3) ∠C or ∠DCB

(4) ∠D or ∠ADC

Question 2 In the given diagram, name the point(s).

(1) In the interior of ∠DOE

(2) In the exterior of ∠EOF.

(3) On ∠EOF.

Solution. (1) In given figure, point A lies between the sides OD and OE.

So, it is in the interior of ∠DOE.

(2) In given figure, points C, A and D are in the exterior of ∠EOF.

(3) In given figure, point E, B, O and Flie on the sides OE and OF of ∠EOF.

So, these points are on ZEOF

Mp Board Class 6 Maths Important Questions

Question 3. Draw rough diagrams of two angles such that they have

(1) One point in common.

(2) Two points in common.

(3) Three points in common.

(4) Four points in common.

(5) One ray in common.

Solution. (1) The diagram is shown as below:

Here, ∠ROQ and ∠QOP have one point O in common.

(2) The diagram is shown as below:

Here, ∠MON and ∠ONR have two points O and N in common.

(3) The diagram is shown as below:

Here, ∠AOB and ∠BOC have three points B, E and D in common.

(4) The diagram is shown as below:

Here, ∠AOP and ∠AOQ have four points O, A, B and C in common.

(5) In the figure given below, ZSOT and ZPOT have one ray \(\overrightarrow{O T}\) in common.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Multiple Choice Questions

Question 1. How many points are marked in the following figure?

1. 1
2. 2
3. 3
4. 4

Answer. 4. 4

Question 2. Number of line segments in figure is

1. 5
2. 10
3. 15
4. 20

Answer. 2. 10

Question 3. Which of the following has two end points?

1. Ray
2. Line
3. Line segment
4. None of these

Answer. 3. Line segment

Question 4. A line segment has two end points and a line has …. end points.

1. 1
2. 2
3. 0
4. None of these

Answer. 3. 0

Question 5. Number of lines which can be drawn from one point

1. One
2. Two
3. Infinite
4. Five

Answer. 3. Infinite

Class 6 Maths Chapter 4 Exercise Solutions

Question 6. If two lines intersect each other, then the common point between them is known as ……

1. contact
2. collinear points
3. intersection point
4. concurrence

Answer. 3. intersection point

Question 7. Which of these is an example for a pair of the parallel lines?

1. Corner of a room
2. Railway track
3. Sides of a triangle
4. Surface of a ball

Answer. 2. Railway track

Question 8. A curve which does not cut itself called

1. Open Curve
2. Closed Curve
3. Both (a) and (b)
4. None of these

Answer. 1. Open Curve

Question 9. The number of interior points of the following figure is

1. 5
2. 3
3. 2
4. 4

Answer. 2. 3

Question 10. The least number of line segment required to make a polygon is

1. 1
2. 2
3. 3
4. 5

Answer. 3. 3

Question 11. In the given figure, JLKM is polygon.

Which of the following is true for the polygon JLKM?

1. ∠J is adjacent to ∠K.
2. ∠J is opposite to ∠M.
3. Side JL is opposite to side MK.
4. Side KL is adjacent to side JM.

Answer. 3. Side JL is opposite to side MK.

Class 6 Geometry Concepts

Question 12. The number of diagonals of the following figure is

5

2

6

9

Answer. 3. 6

Question 13. Which of the following are the diagonals of the given polygon?

1. AD and BE
2. AF and FE
3. BC and ED
4. AB and ED

Answer. 1. AD and BE

Question 14. In the given figure, ∠XYZ cannot be written as

1. ∠Y
2. ∠ZXY
3. ∠ZYX
4. ∠XYP

Answer. 2. ∠ZXY

Question 15. The number of angles in the given figure are

1. 3
2. 4
3. 5
4. 6

Answer. 4.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Assertion-Reason Type Question

Question 1. Assertion (A) Sharper the tip, thinner will be the dot.

Reason (R) A point determines a location.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 2. Assertion (A) A line contains a countless number of points.

Reason (R) Line extends indefinitely in both directions.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 3. Assertion (A) A ray PQ can be written as PQ.

Reason (R) A ray has one end point and extends without limit in one direction only.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Fill in the Blanks

Question 1. Two lines intersect at ……….point.

Solution. One

Question 2. In the given figure, points lying in the interior of the polygon are……….., that in the exterior of the polygon are……….and that on the polygon itself are………….

Solution. O and S, T and N; P, Q, R, M

Class 6 Maths Chapter 4 Exercise Solutions

Question 3. The number of common points in the two angles marked in the given figure is …..

Solution. Two

Question 4. The common part between the two angles BAC and DAB in figure is ……

Solution. AB

Question 5. The number of common points in the two angles marked in the given figure is

Solution. Four

Chapter 4 Basic Geometrical Ideas True/False

Question 1. A curve is said to be closed, if its end are not joined.

Solution. False

Question 2. Two parallel lines meet each other at some point.

Solution. False

Question 3. Two non-parallel line segments will always intersect.

Solution. False

Question 4. An angle is made up of two rays starting from a common initial point.

Solution. True

Question 5. Two adjacent angles have exactly one common arm.

Solution. True

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Match the Columns

Question 1. Match the item of Column A in Column B with their respective value.

Solution. (a) → (2), (b) → (1), (c) → (4), (d) → (3)

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Case Based Questions

Question 1. Joy learns the art of knitting from his grandmother.

On the basis of the given information, answer the following questions.

(1) Which of the following pictures can be an example of a line segment?

(2) Which of the following is an open curve?

(3) Why is the below figure not considered a polygon?

(4) How many lines can pass through a point?

Solution. (1) (b) Option (b) is the example of a line segment.

(2) (b) An open curve does not cut itself.

(3) Since, a polygon is entirely made up of line segments. Therefore, the following figure is not considered a polygon because it is formed by two line segment and an arc.

(4) By observing the following figure we can say that many lines or infinite number of lines can pass through a point.

Question 2. Ankit marks five points by folding a rectangular paper sheet as shown below.

On the basis of the given information, answer the following questions.

(1) Choose the right word and fill in the blank. CE is an example of

(a) A ray

(b) An angle

(c) A point

(d) A line segment

(2) Which of the following is not true for both a ray and a line?

(a) They have end points.

(b) They have start points.

(c) They have no thickness.

(d) They can have infinite length.

(3) Fill in the blank with the correct word.

A line segment is a ….. of a line.

Solution. (1) (d) A line segment

(2) (a) A ray is a portion of a line, which starts at a point and goes endlessly in one direction, and a line obtained, when a line segment is extended on both sides indefinitely. Therefore, both does not have end points.

(3) A line segment is part or section of a line.

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Very Short Answer Type Questions

Question 1. Use the follwoing figure to name:

(1) all the points.

(2) two rays

Solution. (1) The points are O, A, B and C.

(2) Two rays are \(\overrightarrow{O A} \text { and } \overrightarrow{O C}\)

Question 2. Name all the line segments in given figure.

Solution. All the line segments are \(\overline{P Q}, \overline{P R}, \overline{P S}, \overline{Q R}, \overline{Q S} \text { and } \overline{R S} \text {. }\)

Mp Board Class 6 Maths Chapter 4 Solutions

Question 3. Name the line segments shown in the figure given below.

Solution. The line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E} \text { and } \overline{A E}\)

Question 4. Consider the following figure and write the name of

(1) a ray which contains point A.

(2) a ray which contains point B.

Solution. (1) Ray, which contains point A is \(\overrightarrow{P A}\).

(2) Ray, which contains point B is \(\overrightarrow{Q B}\).

Question 5. Draw two curves that are open.

Solution. The open curves are

Question 6. Draw two curves that are closed.

Solution. The closed curves are

Question 7. Write all exterior and interior points of the given figure.

Solution. Here, interior points are H, I and exterior point is M.

Class 6 Geometry Concepts

Question 8. Name the vertices in given figure.

Solution. The vertices in the above figure are A, B, C and D.

Question 9. Write vertex of opposite side of AB and BC of the given figure.

Solution. Vertex of opposite side of AB is C and of BC is A.

Question 10. Write all vertices of the given figure.

Solution. In the given figure, vertices are A,B,C,D and E.

Question 11. The number of common points in the two angles marked in the given figure is ….

Solution. The common point in ∠BAC and ∠DAE is point A.

Mp Board Class 6 Maths Chapter 4 Solutions

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometrical Ideas Short Answer Type Questions

Question 1. How many lines can pass through

(1) one given point?

(2) two given points?

Solution. (1) Through one given point, infinite number of lines can be drawn.

(2) Through two given points, only one line can be drawn.

Question 2. Identify parallel line segments in each of the figure given below.

Solution. Parallel lines in the above figures are

(1) ST and QR.

(2) PQ and SR, SP and QR.

(3) PQ and SR, QR and SP.

(4) PQ and TS, QR and TN, SR and NP.

Class 6 Geometry Concepts

Question 3. Name the vertices and the line segments in the given figure.

Solution. The vertices of the figure are A, B, C,D, E and the line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{E A}, \overline{A C}, \overline{A D}\)

Question 4. What is common in the following figures (1) and (2)?

Is figure (1) is a triangle? If not, why?

Solution. In the given figures (1) and (2), both have three line segments. Figure (1) is not a triangle, because it is not a closed curve.

Question 5. Is PQRS a figure of polygon?

Solution. Yes, it is a polygon, because it is a simple closed curve made up of line segments only.

Question 6. In the given figure, list the points which

(1) are in the interior of ∠AOB.

(2) are in exterior of ∠AOB.

(3) lie on ∠AOB.

Solution. (1) The interior points of ∠AOB are S and Q.

(2) The exterior points of ∠AOB are P and R.

(3) The points, which lie on ∠AOB are A, O, B, T and N.

Mp Board Class 6 Maths Chapter 4 Solutions

Question 7. In the given figure, name the points, which are

(1) in its exterior.

(2) in its interior.

(3) on the figure

Solution. (1) The points which lie in the exterior are F, G and H.

(2) Interior points are A, O and C.

(3) The points which lie on the figure are B, D and E.

Question 8. In the given figure, write

(1) name of the vertex of ∠3.

(2) name of the common arm of ∠1 and ∠2.

(3) name the vertex of ∠4.

Solution. (1) The vertex of ∠3 is B.

(2) Common arm of ∠1 and ∠2 is AC.

(3) The vertex of ∠4 is C.

Polygons and Curves for Class 6

Question 9. Write down six angles involved in the given figure.

Solution. Six angles involved in the above figure are ∠ABC, ∠BCA, ∠CAB, ∠AEC, ∠ABD and ∠DBC.

Question 10. In the following figure, name the angles using three letters.

(1) ∠1 (2) ∠2 (3) ∠3

Solution. Here, we can write the name of angles with the help of given figure:

(1) ∠1 = ∠AOB (2) ∠2 = ∠BOC (3) ∠3 = ∠COD

MP Board Class 6 Maths Solutions For Chapter 4 Basic Geometric Ideas Long Answer Type Questions

Question 1. Name the points and then the line segments in each of the following figures.

Solution. (1) The points are A, B, C and line segments are \(\overline{P Q}, \overline{R S}, \overline{P S}\).

(2) The points are A, B, C, D and line segments are \(\overline{A B}, \overline{B C}, \overline{C D} \text { and } \overline{A D}\).

(3) The points are A, B, C, D, E and line segments are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{A E}\).

(4) The points are A, B, C, D, E, F and line segments are \(\overline{A B}, \overline{C D}, \overline{E F}\).

Polygons and Curves for Class 6

Question 2. In the given figure, write

(1) parallel lines.

(2) point of intersection of the line l and n.

(3) point of intersection of the line q and r.

(4) point of intersection of the line m and r.

(5) point of intersection of the line p and m.

Solution. (1) The lines / and m are parallel lines.

(2) Point of intersection of the lines / and n is A.

(3) Point of intersection of the lines q and r is B.

(4) Point of intersection of the lines m and r is D.

(5) Point of intersection of the lines p and m is D.

Question 3. Sohan wants to show gratitude toward his teacher by giving a card made by him. He has three pieces of paper pasted one above the other as shown in the figure. These pieces are arranged in a way that AB ∥ HC ∥ GD ∥ FE.

He wants to decorate the card by putting up a coloured paper on non-parallel sides of the card.

(1) Write the non-parallel sides of the card.

(2) which value is depicted by the Sohan?

Solution. (1) Non-parallel sides are AF and BE.

(2) Respect to teacher, happiness, beauty, and knowledge.

Polygons and Curves for Class 6

Question 4. Look at the following figure and answer the following questions.

(1) Name the four sides of figure made by joining PQRS.

(2) Name the four pairs of adjacent sides.

(3) Name two pairs of opposite sides.

(4) Name a pair of diagonal.

Solution. (1) Four sides of figure PQRS are \(\overline{P Q}, \overline{R S}, \overline{P S} \text { and } \overline{Q R}\).

(2) Four pairs of adjacent sides are PQ and QR, QR and RS, RS and SP, SP and PQ.

(3) Two pairs of opposite sides are QR and PS, PQ and SR.

(4) Pair of diagonal is PR and QS.

Circle Basics Class 6 Solutions

Question 5. Look at figure and mark a point

(1) A, which is in the interior of both ∠1 and ∠2.

(2) B, which is in the interior of only ∠1.

(3) C in the interior of ∠1.

Now, state whether points B and C lie in the interior of ∠2 also.

Solution.

Yes, it is clear from the figure, that the points B and C lie in the interior of ∠2 also.

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Factors and Multiples

A factor of a number is an exact divisor of that number i.e. the factor divides the number completely without leaving any remainder.

e.g. 1, 2, 3 and 6 are exact divisors of 6. So, 1, 2, 3 and 6 are factors of 6.

A number is a multiple of each of its factor.

e.g. When 123 x 4, then we can say that 12 is a multiple of 3 and 4.

Diagram

Let us discuss some points about factors and multiples.

(1) I is a factor of every number.

(2) Every number is a factor of itself.

(3) Every factor is less than or equal to the given number.

(4) Number of factors of a given number are finite.

e.g. The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 and 96 which are finite.

(5) Every multiple of a number is greater than or equal to that number.

e.g. Multiples of 3 are 3, 6, 9, 12, 15, …

(6) The number of multiples of a given number is infinite.

e.g. Multiples of 4 are 4, 8, 12, 16, 20,…

(7) Every number is a multiple of itself.

e.g. 7 = 7 x 1 and 11 = 11 x 1

Read and Learn More MP Board Class 6 Maths Solutions

MP Board Class 6 Maths Solutions

Example 1. Write all the possible factors of the following numbers.

(1) 16

(2) 30

(3) 27

(4) 19

Solution. (1) Here, 16 = 1 x 16,16 = 2 x 8,16 = 4 x 4

∴ Factors of 16 are 1, 2, 4, 8 and 16.

(2) Here, 30 = 1 x 30, 30 = 2 x 15, 30 = 3 x 10, 30 = 5 x 6

∴ Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.

(3) Here, 27 = 1 x 27, 27 = 3 × 9

∴ Factors of 27 are 1, 3, 9 and 27.

(4) Here, 19 = 1 × 19

∴ Factors of 19 are 1 and 19.

Note that 0 is not the factor of any number.

Example 2. Write the first four multiples of the following numbers

(1) 5

(2) 12

(3) 13

Solution. (1) Multiples of 5 are

5 x 1 = 5,5 x 2 = 10,5 x 3 = 15,5 x 4 = 20

Hence, the first four multiples of 5 are 5, 10, 15 and 20.

(2) Multiples of 12 are

12 x 1 = 12,12 x 2 = 24,12 x 3 = 36,12 x 4 = 48

Hence, the first four multiples of 12 are 12, 24, 36 and 48.

(3) Multiples of 13 are

13 x 1 = 13, 13 x 2 = 26, 13 x 3 = 39,13 x 4 = 52

Hence, the first four multiples of 13 are 13, 26, 39 and 52.

Note It We can also write the table of required number to get the multiples of that number.

Example 3. Write all the multiples of

(1) 7 upto 90.

(2) 16 less than 150.

Solution. (1) The multiples of 7 upto 90 are

7 x 1 = 7

7 x 2 = 14

7 x 3 = 21

7 x 4 = 28

7 x 5 = 35

7 x 6 = 42

7 x 7 = 49

7 x 8 = 56

7 x 9 = 63

7 × 10 = 70

7 x 11 = 77

7 x 12 = 84

Hence, all the multiples of 7 upto 90 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77 and 84..

(2) The multiples of 16 less than 150 are

16 x 1 = 16

16 x 2 = 32

16 x 3 = 48

16 x 4 = 64

16 x 5 = 80

16 X 6 = 96

16 x 7 = 112

16 x 8 = 128

16 x 9 = 144

Hence, all the multiples of 16 less than 150 are 16, 32, 48, 64, 80, 96, 112, 128 and 144.

Class 6 Maths Chapter 3 Mp Board Solutions

Example 4. Write

(1) the sixth multiple of 19.

(2) the seventh multiple of 23.

Solution. (1) Multiples of 19 are

19, 38, 57, 76, 95, 114, 133, ….

Hence, the sixth multiple of 19 is 114.

(2) Multiples of 23 are

23, 46, 69, 92, 115, 138, 161, 184, 207, 230,….

Hence, the seventh multiple of 23 is 161.

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Prime and Composite Numbers

To understand prime and composite numbers, first of all, we have to study about even and odd numbers.

Even Numbers

The numbers which are multiples of 2 are called even numbers. e.g. 2, 4, 6, …, etc. are even numbers.

Odd Numbers

The numbers which are not completely divided by 2 are known as odd numbers. e.g. 1, 3, 5, 7,…, etc. are odd numbers.

Note It A positive integer equal to the sum of its factors. excluding the number itself is said to be a perfect number. The numbers 6, 28,496 and 8128 are perfect numbers.

Example 1. Write the odd and even numbers between the following numbers

(1) 11 and 23

(2) 101 and 115

Solution.

(1) The odd numbers between 11 and 23 are 13, 15, 17, 19 and 21 and the even numbers between 11 and 23 are 12, 14, 16, 18, 20 and 22.

(2) The odd numbers between 101 and 115 are 103, 105, 107, 109, 111 and 113 and the even numbers between 101 and 115 are 102, 104, 106, 108, 110, 112 and 114.

Class 6 Maths Chapter 3 Mp Board Solutions

Example 2. Show that sum of any two odd or any two even numbers is an even number.

Solution. Let the two odd numbers be 7 and 9.

Their sum = 7 + 9 = 16 (even number)

Hence, the sum of any two odd numbers is an even number.

Again, let the two even numbers be 10 and 12.

Their sum = 10 + 12 = 22 (even number)

Hence, the sum of any two odd or even numbers is an even number.

Note it The sum of any two odd numbers or any two even numbers is always an even number.

Example 3. Write the odd and even multiples of

(1) 9 less than 120

(2) 13 upto 140

Solution. (1) Multiples of 9 less than 120 are

9 x 1 = 9

9 × 2 = 18

9 × 3 = 27

9 × 4 = 36

9 x 5 = 45

9 × 6 = 54

9 x 7 = 63

9 × 8 = 72

9 x 9 = 81

9 × 10 = 90

9 x 11 = 99

9 × 12 = 108

9 × 13 = 117

∴ The odd multiples of 9 less than 120 are 9, 27, 45, 63, 81, 99, 117 and the even multiples of 9 less than 120 are 18, 36, 54, 72, 90, 108.

(2) Multiples of 13 upto 140 are

13 x 1 = 13

13 x 2 = 26

13 × 3 = 39

13 x 4 = 52

13 x 5 = 65

13 × 6 = 78

13 x 7 = 91

13 x 8 = 104

13 x 9 = 117

13 x 10 = 130

∴ The odd multiples of 13 upto 140 are 13, 39, 65, 91, 117 and the even multiples of 13 upto 140 are 26, 52, 78, 104, 130.

Prime Numbers

The numbers other than 1, whose only factors are 1 and the number itself are called prime numbers.

e.g. 2, 3, 5, 7, 11,…, etc. are prime numbers.

2 is the smallest prime number which is even and every prime number except 2 is odd.

Two prime numbers whose difference is 2 are called twin prime numbers.

Method of Finding Prime Numbers

Step 1 List all numbers from 1 to 100.

Step 2 Cross out 1 because it is not a prime number.

Step 3 Encircle 2, cross out all the multiples of 2, other than 2 itself i.e. 4, 6, 8 and so on.

Step 4 You will find that the next uncrossed number is 3. Encircle 3 and cross out all the multiples of 3, other than 3 itself.

Step 5 The next uncrossed number is 5. Encircle 5 and cross out all the multiples of 5, other than 5 itself.

Step 6 Continue this process till all the numbers in the list are either encircled or crossed out.

All the encircled numbers are prime numbers.

All the crossed out numbers, other than 1 are composite numbers.

This method is called the Sieve of Eratosthenes which is invented by Greek mathematician Eratosthenes.

Example 4. Check whether the following number are prime or not?

(1) 17

(2) 39

(3) 41

(4) 56

Solution.

(1) 17 = 1 x 17, 17 = 17 x 1

Since, 17 has only two factors i.e. 1 and 17.

Therefore, 17 is a prime number.

(2) 39 = 1 x 39, 39 = 3 x 13

Since, 39 has four factors i.e. 1, 3, 13 and 39.

Therefore, 39 is not a prime number.

(3) 41 = 1 x 41, 41 = 41 x 1

Since, 41 has only two factors i.e. 1 and 41. Therefore, 41 is a prime number.

(4) 56 = 1 x 56, 56 = 2 x 28, 56 = 4 x 14, 56 = 7 x 8

Since, 56 has eight factors i.e. 1, 2, 4, 7, 8, 14, 28 and 56.

Therefore, 56 is not a prime number.

Example 5. Give two pairs of prime numbers whose difference is 2.

Solution. Two pairs of prime numbers whose difference is 2 are

(1) 3 and 5 (i.e. 5 – 3 = 2) (2) 29 and 31 (i.e. 31 – 29 = 2)

Mp Board Class 6 Maths Important Questions

Example 6. Observe that 3 x4+1=13 is a prime number. Here, 1 has been added to a multiple of 3 to get a prime number. Give some more examples of this type.

Solution. Some more examples of this type are

3 x 2 + 1 = 7,

3 x 6 + 1 = 19,

3 × 10 + 1 = 31,

3 x 12 + 1 = 37,

3 × 14 + 1 = 43,

3 x 20 + 1 = 61

Here, all numbers 7, 19, 31, 37, 43 and 61 are prime numbers as 1 has been added to the multiples of 3 to get these prime numbers.

Example 7. Find the greatest prime number between 10 and 20.

Solution. Prime numbers between 10 and 20 are 11, 13, 17 and 19. Therefore, the greatest prime number between 10 and 20 is 19.

Example 8. Write four pairs of prime numbers less than 20, whose sum is divisible by 8.

Solution. Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.

Here, 3 + 5 = 8 (divisible by 8) 5 + 11 = 16 (divisible by 8) 11 + 13 = 24 (divisible by 8) 13 + 19 = 32 (divisible by 8)

Hence, four pairs of prime numbers whose sum is divisible by 8 are (3, 5), (5, 11), (11, 13) and (13, 19).

Example 9. The numbers 17 and 71 are prime numbers. Both these numbers have same digits 1 and 7. Find the such pairs of prime numbers upto 100.

Solution. All prime numbers upto 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.

Out of these, pairs of prime numbers having same digits are (13, 31), (17,71), (37, 73) and (79,97). Hence, there are 4 pairs of such type.

Class 6 Maths Chapter 3 Exercise Solutions

Example 10. Express the following as the sum of two odd prime numbers.

(1) 32

(2) 40

(3) 34

Solution.

(1) We have, 32 = 29 + 3

(2) We have, 40 = 37 +3

(3) We have, 34 = 31 + 3 or 29+5

Example 11. Express each of the following numbers as the sum of three odd primes.

(1) 41

(2) 25

(3) 27

(4) 71

Solution. (1) We have, 41 ⇒ 41 = 11 + 13 + 17,

where 11, 13 and 17 are odd prime numbers.

(2) We have, 25 ⇒ 25 = 5 + 7 + 13,

where 5, 7 and 13 are odd prime number.

(3) We have, 27 ⇒ 27 = 3 + 5 + 19,

where 3, 5 and 19 are odd prime numbers.

(4) We have, 71 ⇒ 71 = 13 + 17 + 41,

where 13, 17 and 41 are odd prime numbers.

Composite Numbers

The numbers having more than two factors are called composite numbers.

e.g. 4, 6, 8, 9, 10,…, etc. are composite numbers.

Note it 1 is neither a prime number nor a composite number because it has only one factor.

Factors And Multiples Class 6 Questions

Example 12. Write all the prime and composite numbers less than 15.

Solution. Prime numbers less than 15 are 2, 3, 5, 7, 11 and 13.

Composite numbers less than 15 are

4, 6, 8, 9, 10, 12 and 14.

Example 13. Write five consecutive composite numbers less than 100, so that there is no prime number between them.

Solution. Five consecutive composite numbers of such type are 54, 55, 56, 57 and 58.

Example 14. State whether the following statements are true or false.

(1) The sum of three even numbers is even.

(2) The sum of two odd numbers and one even number is odd.

(3) All prime numbers are even.

(4) Sum of two prime numbers is always odd.

(5) The product of two even numbers is always odd.

Solution. (1) True, because the sum of three even numbers is always even.

e.g. 2 + 4 + 6 = 12 (even)

(2) False, because the sum of two odd numbers and one even number is always an even number.

e.g. 1 + 5 + 4 = 10 (even)

(3) False, because 2 is only an even prime number. So, all prime numbers are not even.

(4) False, because the sum of two prime numbers is either odd or even.

e.g. 3 + 5 = 8 (even) and 2 + 3 = 5 (odd)

(5) False, because the product of two even numbers is always even.

e.g. 4 × 6 = 24

Factors And Multiples Class 6 Questions

Example 15. Fill in the blanks

(1) The numbers other than 1 whose only factors are 1 and the number itself are called ……..

(2) The smallest odd prime number is……..

(3) Two prime numbers whose difference is 2 are called…….

(4)……. is the smallest prime number which is even …….

Solution.

(1) The numbers other than 1 whose only factors are 1 and the number itself are called prime numbers.

(2) The smallest odd prime number is 3.

(3) Two prime numbers whose difference is 2 are called twin primes.

(4) 2 is the smallest prime number which is even.

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Test for Divisibility

To check the divisibility of any number by other, we normally perform actual divison and see whether remainder is zero or not.

To check without actual division, some divisibility test of different numbers are given below

Test of Divisibility by 2

A number is divisible by 2, if it has any of the digits 0, 2, 4, 6 or 8 at its ones place.

Example 1. Check whether the number 246 is divisible by 2 or not.

Solution. Here, in 246 the digit at the ones place is 6.

Hence, 246 is divisible by 2.

Test of Divisibility by 3

A number is divisible by 3 if the sum of its digits is divisible by 3.

Example 2. Check whether the number 32523 is divisible by 3 or not.

Solution. Given number is 32523.

Sum of the digits = 3 + 2 + 5 + 2 + 3 = 15, which is divisible by 3.

Hence, the number 32523 is divisible by 3.

Test of Divisibility by 4

A number with three or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4.

Class 6 Maths Chapter 3 Solutions

Example 3. Check whether the number 9524624 is divisible by 4 or not.

Solution. Given number is 9524624.

The number formed by last two digits is 24, which is divisible by 4.

Hence, 9524624 is divisible by 4.

Test of Divisibility by 5

A number is divisible by 5 if it has either 0 or 5 at its ones place.

e.g. Each of the number 60, 225, 625 is divisible by 5.

Test of Divisibility by 6

A number is divisible by 6 if the number is divisible by 2 and 3 both.

Example 4. Check whether the number 297144 is divisible by 6 or not.

Solution. Given number is 297144.

We know that a number is divisible by 6 if it is divisible by both 2 and 3.

The number 297144 has an even digit at its ones place. Therefore, it is divisible by 2.

Sum of all the digits in 297144

= 2 + 9 + 7 + 1 + 4 + 4 = 27, which is divisible by 3.

Therefore, the number 297144 is divisible by 6.

Test of Divisibility by 8

A number with 4 or more digits is divisible by 8 if the number formed by the last three digits is divisible by 8.

Example 5. Check whether the number 79152 is divisible by 8 or not.

Solution. Given number is 79152.

The number formed by last three digits is 152 which is divisible by 8.

Hence, 79152 is divisible by 8.

MP Board Class 6 Chapter 3 Maths

Example 6. Which of the following numbers is divisible by both 4 and 8?

(1) 9638

(2) 9640

Solution. (1) We have, 9638

(a) Divisibility by 4

Number formed by last two digits = 38 On dividing 38 by 4, we get

Remainder ≠ 0

∵ 38 is not divisible by 4, so 9638 is also not divisible by 4.

(b) Divisibility by 8

Number formed by last three digits = 638

On dividing 638 by 8, we get

Remainder ≠ 0

∵ 638 is not divisible by 8, so 9638 is also not divisible by 8.

So, 9638 is not divisible by both 4 and 8.

(ii) We have, 9640

(a) Divisibility by 4

Number formed by last two digits=40

On dividing 40 by 4, we get

Remainder = 0

∵ 40 is divisible by 4, so 9640 is also divisible by 4.

(b) Divisibility by 8

Number formed by last three digits=640

On dividing 640 by 8, we get

Remainder = 0

∵ 640 is divisible by 8, so 9640 is also divisible by 8.

Hence, 9640 is divisible by both 4 and 8.

Test of Divisibility by 9

A number is divisible by 9 if the sum of its digits is divisible by 9.

Example 7. Is 65403 divisible by 9?

Solution. Given number is 65403.

Sum of the digits of the given number = 6 + 5 + 4 + 0 + 3 = 18, which is divisible by 9.

Hence, 65403 is divisible by 9.

Test of Divisibility by 10

A number is divisible by 10 if it has 0 at its ones place.

Example 8. Check whether the number 49600 is divisible by 10 or not?

Solution. Given number is 49600.

Here, the number 49600 has 0 at its ones place.

Therefore, 49600 is divisible by 10.

Test of Divisibility by 11

A number is divisible by 11 if the difference between the sum of the digits at odd places (from the right to left) and the sum of the digits at even places (from the right to left) of the number is either 0 or divisible by 11, then the number is divisible by 11.

MP Board Class 6 Chapter 3 Maths

Example 9. Is 73854 divisible by 11?

Solution. The given number is 73854.

Sum of its digits at odd places = 4 + 8 + 7 = 19

Sum of its digits at even places = 5 + 3 = 8

Difference of these sums = 19 – 8 = 11, which is divisible by 11.

Hence, 73854 is divisible by 11.

Example 10. Using divisibility tests, determine which of the following numbers are divisible by 2, by 3, by 4, by 5, by 6, by 8, by 9, by 10 and by 11 (say yes or no)?

Solution. We know that a number is divisible by

2, if it has digits 0, 2, 4, 6 or 8 at its ones place.

3, if the sum of the digits is a multiple of 3 or it is divisible by 3.

4, if last two digits of the number is completely divisible by 4.

5, if a number has 0 or 5 at its ones place.

6, if it is divisible by 2 and 3 both.

8, if last three digits of the number is completely divisible by 8.

9, if the sum of the digits of the number is divisible by 9.

10, if a number has 0 at its ones place.

11, if the difference of sum of the digits at even place and sum of the digits at odd place is either 0 or multiple of 11. Hence,

Example 11. In each of the following replace by the smallest and the greatest digit, so that the number formed is divisible by 3.

(1) 12525 * 2

(2) 251 * 3373

Solution. (1) We have, 12525 * 2

Sum of the given digits = 1 + 2 + 5 + 2 + 5 + 2 = 17

∵ Multiples of 3 greater than 17 are

18, 21, 24, 27, 30,…

∴ 18 – 17 = 1; 21 – 17 = 4; 24 – 17 = 7; 27 – 17 = 10

But 10 is not a single digit.

∴ Smallest digit = 1 and greatest digit = 7

(2) We have, 251 3373

Sum of the given digits=2+5+1+3+3+7+3=24

∵ 24 is a multiple of 3, so smallest digit = 0

Now, multiples of 3 greater than 24 are

27, 30, 33, 36,…

∴ 27 – 24 = 3; 30 – 24 = 6; 33 – 24 = 9; 36 – 24 = 12

But 12 is not a single digit.

∴ Smallest digit = 0 and greatest digit=9

Example 12. In each of the following replace by a digit so that the number formed is divisible by 11. (II) 866194

(1) 64 * 2456

(2) 86 * 6194

Solution. (1) Let the required unknown digit be x. Then, the number becomes

where, O = odd and E = even

Sum of digits at odd places from right = 6 + 4 + x + 6

= 16 + x

Sum of digits at even places from right = 5 + 2 + 4 = 11

∵ Number is divisible by 11.

∴ Difference of digits will be 0 or 11.

⇒ 16 + x – 11 = 0 or 11 ⇒ x + 5 = 0 or 11

On taking difference 0, x + 5 = 0 ⇒ x = -5 (not possible)

On taking difference 11, x + 5 = 11 ⇒ x = 11 – 5

⇒ x = 6

So, the required digit to write in place of * is 6.

(2) Let the required unknown digit be x.

Then, the number becomes

where, O = odd and E = even

Sum of digits at odd places from right

4 + 1 + x + 8 = 13 + x

Sum of digits at even places from right=9+6+6=21

∵ Number is divisible by 11.

∴ Difference of digits will be 0 or 11.

⇒ 13 + x – 21 = 0 or 11 ⇒ x – 8 = 0 or 11

On taking difference 0, x – 8 = 0 ⇒ x = 8

On taking difference 11, x – 8 = 11

⇒ x = 11 + 8 ⇒ x = 19

[but 19 is not a single digit number, so it is not possible]

So, required digit to write in place of * is 8.

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Common Factors and Common Multiples

In the first topic, we have studied about factors and multiples of numbers. Now, we will study about common factors and common multiples.

Common Factors

The factors which are common of each of the given numbers are called their common factors.

Example 1. Find the common factors of

(1) 8 and 20

(2) 35 and 50

(3) 6, 12 and 18

(4) 8, 16 and 24

Solution. (1) Factors 8 = 1,2,4,8

Factors of 20 = 1, 2, 4, 5, 10, 20

Hence, the common factors of 8 and 20 are 1, 2 and 4.

(2) Factors 35 = 1,5,7,35

Factors of 50 = 1, 2, 5, 10, 25, 50

Hence, the common factors of 35 and 50 are 1 and 5.

(3) Factors of 6 = 1, 2, 3, 6

Factors of 12= 1, 2, 3, 4, 6, 12

Factors of 181, 2, 3, 6, 9, 18

Hence, the common factors of 6, 12 and 18 are 1, 2, 3 and 6.

(4) Factors of 8 = 1, 2, 4, 8

Factors of 16 = 1, 2, 4, 8, 16

Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24

Hence, the common factors of 8, 16 and 24 are 1, 2, 4 and 8.

Example 2. A number is divisible by 14. By what other numbers will that number be divisible?

Solution. If any number is divisible by 14, then this number will also be divisible by the factors of 14 i.e. by 1, 2 and 7.

Example 3. A number is divisible by 2, 3 and 5. By which other number will that number be always divisible?

Solution. If a number is divisible by 2, 3 and 5, then it is always divisible by their products i.e. 2 × 3 × 5 = 30

Note it If a number is divisible by any two or more numbers, then it is always divisible by their products.

Common Multiples

The multiples which are common to each of the given numbers are called their common multiples.

Mp Board Class 6 Maths Book Pdf

Example 4. Find the first three common multiples of

(1) 2 and 3

(2) 12 and 18

Solution. (1) Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18,…

Multiple of 3 are 3, 6, 9, 12, 15, 18, …

Hence, the first three common multiples of 2 and 3 are 6, 12 and 18.

(2) Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108,…

Multiples of 18 are 18, 36, 54, 72, 90, 108, …

Hence, the first three common multiples of 12 and 18 are 36, 72 and 108.

Example 5. Write all the numbers less than 100 which are common multiples of 4 and 5.

Solution. Multiples of 4 less than 100 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96

Multiples of 5 less than 100 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95

Hence, the common multiples of 4 and 5 less than 100 are 20, 40, 60 and 80.

Co-prime Numbers

Two numbers which have only 1 as their common factor are called co-prime numbers.

Note it Any two prime numbers are always co-primes but two co-prime numbers need not to be prime numbers.

MP Board Class 6 Chapter 3 Maths

Example 6. Which of the following pairs are co-primes?

(1) 8, 25

(2) 4, 10

Solution. (1) Factors of 8 = 1, 2,4,8

Factors of 25 = 1, 5, 25

∴ 8 and 25 have only 1 as common factor.

∴ 8 and 25 are co-prime numbers.

(2) Factors of 4 = 1,2,4

Factors of 10 = 1, 2, 5,10

∴ 4 and 10 have 1, 2 as common factors.

∴ 4 and 10 are not co-prime numbers.

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Prime Factorisation

If a natural number is expressed as the product of prime numbers, then the factorisation of the number is called its prime factorisation.

Example 1. Find the prime factorisation of 630.

Solution. By division method,

∴ 630 = 2 × 3 × 3 x 5 x 7

which is the required prime factorisation.

Prime Factorisation by Factor Tree Method

Expressing a number with the help of factor tree. Let us factorise 36 in three different ways as given below:

Thus, 36 = 2 x 2 x 3 x 3; 36 = 3 x 2 x 2 x 3; 36 = 3 × 3 × 2 × 2

In all the above factorisations of 36, we ultimately arrive only one factorisation 2 x2 x3x3 and such a factorisation is called a prime factorisation.

Example 2. Find the prime factorisation of 90.

Solution. By factor tree method,

∴ 90 = 2 × 3 × 3 × 5 which is the required prime factorisation.

Hence, the missing numbers are 2, 3 and 3.

Class 6 Maths Prime And Composite Numbers

Example 3. Write down the missing numbers in the below factor trees of 72.

Solution. (1) ∴ 12 = 2 x 6 and 6 = 2 x 3

Hence, the missing numbers are 6 and 3.

(2) ∴ 72 = 36 × 2,

36 12 x 3 and 12=4×3

Example 4. Fill in the given space.

Prime factorisation of 3927 = 3 x 7 x … x 17

Solution. We have, 3927

∴ Prime factorisation of 3927 = 3 x 7 x 11 x 17

So, the required number to write in given space is 11.

Example 5. Write the smallest 4-digit number and all its prime factors.

Solution. Smallest 4-digit number = 1000

∴ Prime factors of 1000 = 2 x 2 x 2 x 5 x 5 x 5

Class 6 Maths Chapter 3 Exercise Solutions

Example 6. Write the greatest 5-digit number and all its prime factors.

Solution. Greatest 5-digit number = 99999

∴ Prime factors of 99999 = 3 x 3 x 41 x 271

Example 7. In which of the following expression, prime factorisation has been done?

(1) 36 = 2 × 3 × 6

(2) 54 = 2 x 3 x 3 x 3

(3) 56 = 2 x 4 x 7

(4) 76 = 2 x 2 x 19

Solution. (1) We have, 36 = 2 × 3 × 6

Here, 6 is not a prime number.

So, it is not the prime factorisation of 36.

(2) We have, 54 = 2 x 3 x 3 x 3

Here, 2 and 3 are prime numbers.

So, it is the prime factorisation of 54.

(3) We have, 56 = 2 x 4 x 7

Here, 4 is not a prime number.

So, it is not the prime factorisation of 56.

(4) We have, 76 = 2 x 2 x 19

Here, 2 and 19 are prime numbers.

So, it is a prime factorisation of 76.

Example 8. I am the smallest number, having four different odd prime factors. Can you find me?

Solution. Since, the number is smallest, so four different smallest odd prime factors are 3, 5, 7 and 11.

∴ Smallest number having four different odd prime factors

= 3 x 5 x 7 x 11 = 1155.

Example 9. Write all the prime factors of 105 and arrange them in ascending order. Is there Is any relation between the two consecutive prime factors?

Solution. Prime factorisation of 105

∴ 105 = 3 x 5 x 7

Ascending order of prime factors of 105 is 3, 5, 7.

Here, 5 – 3 = 2 and 7 – 5 = 2

So, the relation between two consecutive

prime factors of 105 is that the difference of two consecutive prime factors is 2.

MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Highest Common Factor

The Highest Common Factor (HCF) of two or more numbers is the highest (or greatest) factor out of their common factors. It is also known as Greatest Common Divisor (GCD).

Example 1. Find the HCF of the following numbers.

(1) 24 and 48

(2) 18 and 60

(3) 15, 25 and 30

(4) 12, 16 and 28

Solution. (1) We have, 24 and 48.

Factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.

Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.

The common factors of 24 and 48 are 1, 2, 3, 4, 6, 8, 12 and 24.

∴ HCF of 24 and 48 = 24

(2) We have, 18 and 60.

Factors of 18 are 1, 2, 3, 6, 9 and 18.

Factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60.

The common factors of 18 and 60 are 1, 2, 3 and 6.

∴ HCF of 18 and 60=6

(3) We have, 15, 25 and 30.

Factors of 15 are 1, 3, 5 and 15.

Factors of 25 are 1, 5 and 25.

Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.

The common factors of 15, 25 and 30 are 1 and 5.

∴ HCF of 15, 25 and 30=5

(4) We have 12, 16 and 28.

Factors of 12 are 1, 2, 3, 4, 6 and 12.

Factors of 16 are 1, 2, 4, 8 and 16.

Factors of 28 are 1, 2, 4, 7, 14 and 28.

The common factors of 12, 16 and 28 are 1, 2 and 4.

∴ HCF of 12, 16 and 28 = 4

Factors And Multiples Class 6 Questions

Example 2. What is the HCF of

(1) two prime numbers?

(2) two consecutive even numbers?

Solution. (1) Let two prime numbers be 7 and 17.

Factors of 7 are 1 and 7.

Factors of 17 are 1 and 17.

∴ HCF of 7 and 17 is 1.

∴ Hence, HCF of two prime numbers is 1.

(2) Let the two consecutive even numbers be 8 and 10.

Factors of 8 are 1, 2, 4 and 8.

Factors of 10 are 1, 2, 5 and 10

The common factors of 8 and 10 are 1 and 2.

∴ HCF of 8 and 10 is 2.

∴ Hence, HCF of two consecutive even numbers is 2.

HCF by Prime Factorisation Method

In this method, first we find the prime factorisation of each of the given numbers. HCF is the product of all the different common prime factors of the given numbers using each common prime factor the least number of times it appears in the prime factorisation of all of the given numbers.

Example 3. Find the HCF of

(1) 48 and 84

(2) 18 and 60

(3) 15, 25 and 30

(4) 12, 16 and 28

Solution. (1) Here, the given numbers are 48 and 84.

Now, prime factorisation of given numbers are

So, 48 = 2 x 2 x 2 x 2 x 3 and 84 = 2 × 2 × 3 × 7

Here, 2 occurs as a common prime factor atleast 2 times and 3 atleast 1 time in both given numbers. Hence, HCF of 48 and 84 = 2×2 x3=12

(2) Here, the given numbers are 18 and 60.

Now, prime factorisation of given numbers are

So, 18 = 2 x 3 x 3 and 60 = 2 x 2 x 3 x 5

Here, 2 and 3 each occurs as a common factor atleast once in both the given numbers.

Hence, HCF of 18 and 60=2×3=6

(3) Here, the given numbers are 15, 25 and 30.

Now, prime factorisation of given numbers are

So, 15 = 3 x 5, 25 = 5 x 5, and 30 = 2 x 3 x 5

Here, 5 occurs as a common factor atleast once in each of the given number.

Hence, HCF of 15, 25 and 30=5.

(4) Here, the given numbers are 12, 16 and 28.

Now, prime factorisation of given numbers are

So, 12 = 2 x 2 x 3

16 = 2 × 2 × 2 × 2

and 28 = 2 × 2 x 7

Here, 2 occurs as a common factor atleast 2 times in each of the given number.

Hence, HCF of 12, 16 and 28 = 2 x 2 = 4

Class 6 Maths Prime And Composite Numbers

Example 4. In the factorisation of two co-prime numbers 6 and 25, we found that there is no common prime factor In the prime factorisation of 6 and 25, so HCF of 6 and 25 is 0. Check whether the answer is correct or not and if not correct, then find the correct HCF?

Solution. Prime factorisation of 6 = 2 x 3

Prime factorisation of 25 = 5 x 5

No, the answer is not correct.

Because 0 (zero) cannot be the factor of any number.

If there is no common factor, then it means 1 is the common factor.

∴ HCF of 6 and 25 = 1

Example 5. What will be the HCF of (3 x 5 x 11 × 13), (5 × 11 x 17 × 21) and (5 x 11 x 7 × 13)

Solution. Given prime factorisations are

(3 x 5 x 11 x 13), (5 x 11 x 17 x 21) and (5 x 11 x 7 x 13)

In the above prime factorisations, 5 and 11 each occurs as a common factor atleast once.

Hence, HCF of given factorisation = 5×11=55

MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Lowest Common Multiple

The Lowest Common Multiple (LCM) of two or more numbers is the lowest (or smallest or least) multiple out of their common multiples.

Example 1. Find the LCM of the following numbers.

(1) 3 and 4

(2) 28 and 42

Solution. (1) Multiples of 3=3, 6, 9, 12, 15, 18, 21, 24, …

Multiples of 4 = 4, 8, 12, 16, 20, 24, …

Common multiples of 3 and 4 = 12, 24

∴ LCM of 3 and 4 is 12.

(2) Multiples of 28= 28, 56, 84, 112, 140, 168,…

Multiples of 42=42, 84, 126, 168, 210, …

Common multiples of 28 and 42= 84, 168,…

∴ LCM of 28 and 42 is 84.

LCM by Prime Factorisation Method

In this method, first we find the prime factorisation of each of the given numbers. Now, LCM is the product of all the different prime factors of the given numbers, using each common prime factor the greatest number of times it appears in the prime factorisation of any of the given numbers.

Example 2. Find the LCM by prime factorisation method:

(1) 20 and 24

(2) 10,15 and 25

Solution. (1) Here, the given numbers are 20 and 24.

Now, prime factorisation of given numbers are

20 = 2 x 2 x 5 and 24 = 2 x 2 x 2 x 3

In these prime factorisations, the maximum number of times the prime factor 2 occurs is three, this happens for 24. Similarly, the prime factor 5 occurs only once is 20 and the prime factor 3 occurs only once is 24.

∴ LCM of 20 and 24 = 2 x 2 x 2 x 3 x 5 = 120

(2) Here, the given numbers are 10, 15 and 25.

Now, prime factorisation of given numbers are

10 = 2 x 5,15 = 3 x 5 and 25 = 5 × 5

In these prime factorisation, the maximum number of times the prime factor 5 occur is two, this happens for 25. Similarly the prime factor 2 occurs only once in 10 and the prime factor 3 occurs only once is 15.

∴ LCM of 10, 15 and 25 = 2 x 3 x 5 x 5 = 150

LCM by Division Method

In this method, we arrange the given numbers in a line in any order. Now, we divide by a lowest prime number which divides any one of the given numbers and carry forward the other numbers which are not divisible. This process is repeated till we get all the number in the row is 1.

HCF and LCM for Class 6

Example 3. Find the LCM by division method.

(1) 36, 40 and 126

(2) 12, 15, 20 and 27

Solution. (1) LCM of 36, 40 and 126

∴ LCM = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

(2) LCM of 12, 15, 20 and 27

∴ LCM = 2 x 2 x 3 x 3 x 3 x 5 = 540

Example 4. Find the LCM of the following numbers in which one number is the factor of the other.

(1) 5 and 15

(2) 4 and 12

(3) 6 and 24

What do you observe in the results so obtained?

Solution. (1) LCM of 5 and 15

∴ LCM = 3 x 5 = 15

(2) LCM of 4 and 12

∴ LCM = 2 x 2 x 3 = 12

(3) LCM of 6 and 24

∴ LCM = 2 x 2 x 2 x 3 = 24

Here, we observe that in all parts, LCM of the given numbers is the larger of two numbers because one number is factor of the other number.

Note It If one number is the factor of the other, then the LCM of the two numbers will be equal to the greater number.

Example 5. Find the LCM of the following numbers. Observe a common property from the obtained LCM. Is LCM the product of two numbers In each case?

(1) 21 and 4

(2) 6 and 7

(3) 16 and 9

Solution. (1) LCM of 21 and 4

∴ LCM = 2 x 2 x 3 x 7 = 84

(2) LCM of 6 and 7

∴ LCM = 2 x 3 x 7 = 42

(3) LCM of 16 and 9

∴ LCM = 2 × 2 × 2 × 2 × 3 × 3 = 144

Here, we see that in each case,

LCM of given numbers is a multiple of 3 and 2.

Yes, in each case LCM is equal to the product of given two numbers.

Note it The LCM of two co-prime numbers is always equal to the product of two numbers.

Applications of HCF and LCM

We come across a number of situations in which we have to use of the concepts of HCF and LCM. Some application-based examples are given below:

HCF and LCM for Class 6

Example 6. The HCF of three numbers is 23. If they are in the ratio of 1 : 2 : 3, then find the numbers.

Solution. Let the numbers x, 2x and 3x.

∴ Their HCF is x.

But given HCF = 23

∴ x = 23

2x = 2 x 23 = 46

and 3x = 3 x 23 = 69

Hence, the numbers are 23, 46 and 69.

Example 7. If three numbers are 2a, 3a and 5a, then what will be their LCM?

Solution. The LCM of 2a, 3a and 5a is 30a because 30a is the smallest or lowest number which is divisible by 2a, 3a and 5a.

Example 8. Find the greatest number which divides 285 and 1249, leaving remainder 9 and 7, respectively.

Solution. Here, we have to find the greatest number which divides (285 – 9) and (1249 – 7) exactly.

∴ The required number is HCF of 276 and 1242.

Prime factorisation of 276=2 x 2 x 3 x 23

Prime factorisation of 1242 = 2 x 3 x 3 x 3 x 23

∴ HCF of 276 and 1242 = 2 × 3 × 23 = 138

Hence, the required number is 138.

Example 9. Find the smallest 3-digit number which is exactly divisible by 4, 6 and 8?

Solution. Firstly, we have to find out the LCM of 4, 6 and 8.

∴ LCM = 2 x 2 x 2 x 3 = 24

We know that smallest 3-digit number is 100.

On dividing 100 by 24, we get remainder 4.

Now, required 3-digit number which is exactly divisible by 24

= Smallest 3 – digit number + Divisor – Remainder

= 100 + 24 – 4 = 120

HCF and LCM for Class 6

Example 10. Find the greatest 3-digit number which is exactly divisible by 6, 8 and 10?

Solution. Firstly, we have to find out the LCM of 6, 8 and 10.

∴ LCM = 2 x 2 x 2 x 3 x 5 = 120

We know that largest 3-digit number = 999

On dividing 999 by 120, we get remainder 39.

Now, required 3-digit number which is exactly divisible by 120

= Greatest 3 – digit number – Remainder

= 999 – 39 = 960

Example 11. Find the least number which when divided by 12, 16 and 18 leave remainder 5 in each case.

Solution. First, we have to find out the LCM of 12, 16 and 18.

∴ LCM = 2 x 2 x 2 x 2 x 3 x 3 = 144

Now, required number = LCM + Remainder

= 144 + 5 = 149

Hence, the required number is 149.

Example 12. Dolly purchases two bags of sugar of weight 75 kg and 105 kg. Find the maximum value of weight which can measure the two bags exact number of times.

Solution. For getting the maximum value of weight, we have to find out the HCF of 75 kg and 105 kg.

Now, prime factorisation of 75 = 3 x 5 x 5

and prime factorisation of 105 = 3 x 5 x 7

∴ HCF of 75 and 105 = 3 x 5 = 15

Hence, the required maximum value of weight is 15 kg.

Example 13. Five bells toll at intervals of 12 sec, 15sec, 20 sec, 25sec and 45 sec, respectively. If all of them toll at 7 am, then at what time will they toll together again?

Solution. Firstly, we have to find out the LCM of 12, 15, 20, 25 and 45.

∴ LCM = 2 x 2 x 3 x 3 x 5 x 5 = 900

= \(\frac{900}{60}=15 \mathrm{~min}\)

So, time when they will toll together again

07 : 00 : 00 + 15 : 00 = 07 : 15 : 00

Factors And Multiples Class 6 Questions

Example 14. A girl saves * 3.65 daily. Find the least number of days in which she will be able to save an exact number of rupees.

Solution. Here, ₹ 3.65 = 365 paise

The exact number of rupees will be a multiple of 100.

So, we have to find the LCM of 365 and 100.

100 = 2 x 2 x 5 x 5

and 365 = 5 x 73

∴ LCM of 365 and 100 = 2 x 2 x 5 x 5 x 73 = 7300

So, the girl saved 7300 paise.

Hence the least number of days required to save 7300-20 days.

7300 paise = \(\frac{7300}{365}=20 \text { days. }\)

Example 15. On a evening walk, three persons step off together and their steps measures 42 cm, 49 cm and 56 cm, respectively. What is the minimum distance each should walk, so that each can cover the same distance in complete steps?

Solution. Here, the required minimum distance will be equal to LCM of measures of their steps because the minimum distance each persons should walk must be the least common multiple of the measures of their steps. So, we have to find out the LCM of 42, 49 and 56.

i.e.

∴ LCM of 42, 49

and 56 = 2 x 2 x 2 x 3 x 7 x 7 = 1176

Hence, 1176 cm is the required minimum distance.

Question 1. Find the possible factors of 45, 30 and 36.

Solution. (1) Here,

45 = 1 x 45; 45 = 3 x 15; 45 = 5 x 9

∴ Factors of 45 are 1, 3, 5, 9, 15 and 45.

(2) Here,

30 = 1 x 30; 30 = 2 x 15; 30 = 3 x 10; 30 = 5 × 6

∴ Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.

(3) Here,

36 = 1 x 36; 36 = 2 x 18; 36 = 3 x 12; 36 = 4 x 9; 36 = 6 X 6

∴ Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.

Question 2. Match the items in column A with the items in column B.

Solution.

(1) Factors of 35 are 5 and 7 and we know that a number is a multiple of each of its factor. Hence, 35 is a multiple of 7.

(2) We know that a factor of a number is an exact divisor of that number.

Here, 30 is divided by 15. So, 15 is a factor of 30.

(3) Factors of 16 are 2 and 8 and we know that, a number is a multiple of each of its factor. Hence, 16 is a multiple of 8.

(4) We know that every number is a factor of itself. So, 20 is a factor of itself i.e. 20.

(5) We know that a factor of a number is an exact divisor of that number. Here, 50 is divided by 25. So, 25 is a factor of 50.

Now, matching of these items is as follows

(1) → (b) (2) → (d) (3) → (a) (4) → (f) (5) → (e)

Question 3. Find all the multiples of 9 upto 100.

Solution. All the multiples of 9 up to 100 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90 and 99.

Question 4. Observe that 2 x 3+1 = 7 is a prime number. Here, 1 has been added to a multiple of 2 to get a prime number. Can you find some more numbers of this type?

Solution. Some more numbers of this type are as follows

2 x 2 + 1 = 5, 2 x 5 + 1 = 11, 2 x 6 + 1 = 13

2 x 8 + 1 = 17, 2 x 9 + 1 = 19, 2 x 11 + 1 = 23

Here, all numbers 5, 11, 13, 17, 19 and 23 are prime numbers and 1 has been added to a multiple of 2 to get these prime numbers.

Factors And Multiples Class 6 Questions

Question 5. What is the sum of any two

(1) odd numbers?

(2) even numbers?

Solution.

(1) Let the two odd numbers be 5 and 7.

Their sum = 5 + 7 = 12 (even number)

Taking one more example.

Let the two odd numbers be 3 and 7

Their sum = 3 + 7 = 10 (even number)

Hence, we can say that sum of any two odd numbers is an even number.

(2) Let the two even numbers be 4 and 8.

Their sum = 4 + 8 = 12 (even number)

Taking one more example.

Let the two even numbers be 6 and 20.

Their sum = 6 + 20 = 26 (even number)

Hence, we can say that sum of any two even numbers is an even number.

Question 6. The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers upto 100.

Solution. All prime numbers upto 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97. Out of these prime numbers, pairs of prime numbers having same digits are

(1) 13,31

(2) 17,71

(3) 37, 73

(4) 79,97

Hence, there are 4 pairs of such types.

Question 7. Write down separately the prime and composite numbers less than 20.

Solution. Prime numbers are those numbers whose only factors are 1 and the number itself.

So, prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.

Composite numbers are those numbers which have more than two factors.

So, composite numbers less than 20 are 4, 6, 8, 9, 10, 12, 14, 15, 16 and 18.

Question 8. What is the greatest prime number between 1 and 10?

Solution. Prime numbers between 1 and 10 are 2, 3, 5 and 7. Therefore, the greatest prime number between 1 and 10 is 7.

Question 9. Give three pairs of prime numbers whose difference is 2.

[Remark Two prime numbers whose difference is 2 are called twin primes].

Solution. Three pairs of prime numbers whose difference is 2 are

(1) (5,7) i.e.7 – 5 = 2

(2) (11, 13) i.e.13 – 11 = 2

(3) (17, 19) i.e. 19 – 17 = 2

Question 10. Which of the following numbers are prime?

(1) 23

(2) 51

(3) 37

(4) 26

Solution.

(1) We find that 23 is not exactly divisible by any of the prime numbers 2, 3, 5, 7, 11, 17 and 19. So, it is a prime number.

(2) We find that 51 is divisible by 3. So, it is not a prime number.

(3) We find that 37 is not exactly divisible by any of the prime numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 and 31. So, it is a prime number.

(4) We find that 26 is exactly divisible by 2 and 13. So, it is not a prime number.

Mp Board Class 6 Maths Important Questions

Question 11. Write seven consecutive composite numbers less than 100, so that there is no prime number between them.

Solution. Seven composite numbers of such type are as follows 90, 91, 92, 93, 94, 95, and 96.

Question 12. Express each of the following numbers as the sum of three odd primes.

(1) 21

(2) 31

(3) 53

(4) 61

Solution. (1) We have, 21

⇒ 21 = 3 + 5 + 13

where 3, 5 and 13 are odd prime numbers.

(2) We have, 31

⇒ 31 = 3 + 5 + 23

where 3, 5 and 23 are odd prime numbers.

(3) We have, 53

⇒ 53 = 13 + 17 + 23

where 13, 17 and 23 are odd prime numbers.

(4) We have, 61

⇒ 61 = 7 + 13 + 41

where 7, 13 and 41 are odd prime numbers.

Question 13. Write five pairs of prime numbers less than 20 whose sum is divisible by 5. [Hint 3+7=10]

Solution. Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.

Here,

2 + 3 = 5 (divisible by 5)

2 + 13 = 15 (divisible by 5)

3 + 7 = 10 (divisible by 5)

3 + 17 = 20 (divisible by 5)

7 + 13 = 20 (divisible by 5)

Hence, five pairs of prime numbers whose sum is divisible by 5 are (2, 3), (2, 13), (3, 7), (3, 17) and (7, 13).

Question 13. Find the common factors of

(1) 8 and 20

(2) 9 and 15

Solution. (1) Factors of 8 = 1, 2,4,8

Factors of 20 = 1, 2,4,5,10, 20

Hence, the common factors of 8 and 20 are 1, 2 and 4.

(2) Factors of 9 = 1,3,9

Factors of 15 = 1,3,5,15

Hence, the common factors of 9 and 15 are 1 and 3.

Question 14. Find first three common multiples of

(1) 6 and 8

(2) 12 and 18

Solution. (1) Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72,…

Multiples of 88, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96,…

Hence, first three common multiples are 24, 48 and 72.

(2) Multiples of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132,…

Multiples of 1818, 36, 54, 72, 90, 108, 126, 144,…

Hence, first three common multiples are 36, 72 and 108.

Mp Board Class 6 Maths Important Questions

Question 15. Write all the numbers less than 100, which are common multiples of 3 and 4.

Solution. Multiples of 3 which are less than 100 are as follows:

3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99

Multiples of 4 which are less than 100 are as follows:

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96

Hence, the common multiples of 3 and 4 are 12, 24, 36, 48, 60, 72, 84 and 96.

Question 16. A number is divisible by both 5 and 12. By which other number will that number be always divisible?

Solution. The given number will be divisible by the product of 5 and 12 i.e. it is always divisible by 5 x 12 = 60.

Note If a number is divisible by two co-prime numbers, then it is divisible by their product also.

Question 17. A number is divisible by 12. By what other numbers will that number be divisible?

Solution. If any number is divisible by 12, then this number will also be divisible by the factors of 12

i.e. 12 = 1 x 12; 12 = 2 × 6;12 = 3 x 4

Factors of 12 are 1, 2, 3, 4, 6 and 12.

∴ Number will be also divisible by 1, 2, 3, 4, 6 and 12.

Factors and Multiples Class 6

Question 18. Here are two different factor trees for 60. Write the missing numbers.

Solution. (1) 6 = 2 x 3 and 10 = 5 x 2

Hence, the missing numbers are 3 and 2.

(2) 60 = 30 x 2

30 = 10 x 3

and 10 = 5 x 2

Hence, the missing numbers are 2, 3, 5 and 2.

Question 19. Which factors are not included in the prime factorisation of a composite number?

Solution. Factor 1 and that number itself are not included in the prime factorisation of a composite number.

Class 6 Maths Chapter 3 Mp Board Solutions

Question 20. Write the greatest 4-digit number and express it in terms of its prime factors.

Solution. The greatest 4-digit number = 9999

Now,

Prime factors of 9999 = 3 x 3 x 11 x 101

Question 21. Write the smallest 5-digit number and express it in the form of its prime factors.

Solution. The smallest 5-digit number = 10000

Now,

Prime factors of 10000 = 2 x 2 x 2 x 2 x 5 x 5 x 5 x 5

Class 6 Maths Chapter 3 Mp Board Solutions

Question 22. The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.

Solution. We know that a number is divisible by 6, if the number is divisible by 2 and 3 both.

Let the three consecutive numbers are 3, 4 and 5.

Their product = 3 x 4 x 5 = 60

Now, 60 is divisible by 2 and 3 both.

So, 60 is also divisible by 6.

Hence, product of three consecutive numbers 3, 4 and 5 is divisible by 6.

Taking one more example.

Let the three consecutive numbers are 6, 7 and 8.

Their product = 6 x 7 x 8 = 336

Now, 336 is divisible by 2 and 3 both.

So, 336 is also divisible by 6.

Hence, product of three consecutive numbers 6, 7 and 8 is divisible by 6.

Question 23. In which of the following expressions, prime factorisation has been done?

(1) 24 = 2 × 3 × 4

(2) 56 = 7 x 2 x 2 x 2

(3) 70 = 2 x 5 x 7

(4) 54 = 2 x 3 x 9

Solution. (i) We have, 24 = 2 × 3 × 4

Here, 4 is not a prime number.

So, prime factorisation is not done.

(2) We have, 56 = 7 x 2 x 2 x 2

Here, 2 and 7 are prime numbers.

So, number 56 have prime factorisation.

(3) We have, 70 = 2 x 5 x 7,

Here 2, 5 and 7 all are prime numbers.

So, number 70 have prime factorisation.

(4) We have, 54 = 2 x 3 x 9,

Here, 9 is not a prime number.

So, prime factorisation is not done.

Prime Factorization Class 6

Question 24. 18 is divisible by both 2 and 3. It is also divisible by 2 x 3 = 6. Similarly, a number is divisible by both 4 and 6. Can we say that the number must also be divisible by 4 × 6 = 24? If not, give an example to justify your answer.

Solution. We know that if a number is divisible by two co-prime numbers, then it is divisible by their product also.

Here, 2 and 3 are co-prime numbers. So, 18 is divisible by their product i.e. 6 but 4 and 6 are not co-prime numbers, so the number divisible by 4 and 6 will not be divisible by 4 × 6 = 24.

e.g. Take the number 60.

It is divisible by both 4 and 6 but it is not divisible by its product. i.e. 6 × 4 = 24

Question 25. I am the smallest number, having four different prime factors. Can you find me?

Solution. Since, the number is smallest, so different four smallest prime factors are 2, 3, 5 and 7.

∴ Smallest number having four different prime factors = 2 x 3 x 5 x 7 = 210

Question 26. What is the HCF of two consecutive

(1) numbers?

(2) even numbers?

(3) odd numbers?

Solution.

(1) Let the two consecutive numbers be 8 and 9.

Now, prime factorisation of 8 = 2 x 2 x 2

Prime factorisation of 9 = 3 × 3

Common factor of 8 and 9 = 1

Thus, HCF of 8 and 9 is 1.

Note The HCF of two consecutive numbers is 1.

(2) Let the two consecutive even numbers be 10 and 12.

Now, prime factorisation of 10 = 2 x 5

Prime factorisation of 12 = 2 x 2 x 3

Common factor of 10 and 12 = 2

Thus, HCF of 10 and 12 is 2.

Note The HCF of two consecutive even numbers is 2.

(3) Let two consecutive odd numbers be 3 and 5.

Prime factorisation of 3 = 1 x 3

Prime factorisation of 5 = 1 x 5

Common factor of 3 and 5 = 1

Thus, HCF of 3 and 5 is 1.

Note The HCF of two consecutive odd numbers is 1.

Prime Factorization Class 6

Question 27. HCF of co-prime numbers 4 and 15 was found as follows by factorisation. 4 = 2 x 2 and 15 = 3 x 5, since there is no common prime factor, so HCF of 4 and 15 is 0. Is the answer correct? If not, what is the correct HCF?

Solution. No, the answer is not correct. Because 0 (zero) cannot be factor of any number. If there is no common factor, then it means 1 is the common factor.

∴ HCF of 4 and 15=1

Question 28. Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight, which can measure the weight of the fertiliser exact number of times.

Solution. For getting maximum value of weight, we have to find out the HCF of 75 kg and 69 kg.

i.e.

Prime factorisation of 75 = 3 x 5 x 5

Prime factorisation of 69 = 3 x 23

Common factor of 75 and 69 is 3.

Thus, HCF of 75 kg and 69 kg = 3 kg

Hence, the required maximum value of weight is 3 kg.

MP Board Class 6 Maths Solutions For Chapter 3 Playing With Numbers Multiple Choice Questions

Question 1. Number of even numbers between 50 and 80, are

1. 14
2. 11
3. 12
4. 13

Answer. 1. 14

Question 2. The largest number, which always divides the sum of any pair of consecutive odd numbers is

1. 2
2. 4
3. 6
4. 8

Answer. 2. 4

Question 3. Sum of the number of primes between 16 to 80 and 90 to 100 is

1. 20
2. 18
3. 17
4. 16

Answer. 3. 17

Question 4. Which of the following pair is not co-prime?

1. 11, 12
2. 73, 74
3. 84, 94
4. 97, 98

Answer. 3. 84, 94

Question 5. A number is divisible by 5, if it has

1. Only 0 in its ones place
2. 0 in its tens place
3. 0 or 5 in its ones place
4. 5 in its ones place

Answer. 3. 0 or 5 in its ones place

Question 6. A number is divisible by 5 and 6. It may not be divisible by

1. 10
2. 15
3. 30
4. 85

Answer. 4. 85

Class 6 Maths Chapter 3 Mp Board Solutions

Question 7. If the number 725498 is divisible by 11, the digit at * is

1. 1
2. 2
3. 6
4. 0

Answer. 3. 6

Question 8. The number of common prime factors of 75, 60, 105 is

1. 2
2. 3
3. 4
4. 5

Answer. 1. 2

Question 9. The number of distinct prime factors of the largest 4-digit number is

1. 2
2. 3
3. 5
4. 11

Answer. 2. 3

Question 10. The number of distinct prime factors of the smallest 5-digit number is

1. 2
2. 4
3. 6
4. 8

Answer. 1. 2

Question 11. The HCF of 144 and 160 is

1. 24
2. 15
3. 9
4. None of these

Answer. 4. None of these

Question 12. The LCM of 12, 24, 32 is

1. 92
2. 86
3. 27
4. 96

Answer. 4. 96

Question 13. If two numbers are equal, then

1. their LCM is less than their HCF
2. their LCM is equal to two times their HCF
3. their LCM is equal to their HCF
4. None of the above

Answer. 3. their LCM is equal to their HCF

Question 14. LCM of two numbers is 180. Then, which of the following is not the HCF of the numbers?

1. 45
2. 60
3. 75
4. 90

Answer. 3. 75

Question 15. The sum of HCF and LCM of two numbers is 1260. If their LCM is 900 more than their HCF, then the product of the two number is

1. 194400
2. 19440
3. 184400
4. 126000

Answer. 1. 194400

Question 16. Photographs are sold in small, medium and large size. The cost of photographs according to their size is given in the table below: Compentency Based Question

Mp Board Class 6 Maths Important Questions

150 photographs worth? 10250 were sold. If 75 of them were of small size, find how many larger size photographs were sold?

1. 14
2. 25
3. 75
4. 130

Answer. 2. 25

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Assertion-Reason Type Questions

Question 1. Assertion (A) The number 9 and 25 are co-prime.

Reason (R) A number is said to be prime, if it has only two factors 1 and the number itself.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

Question 2. Assertion (A) The HCF of 8, 16 and 24 is 4.

Reason (R) HCF of two or more given numbers is the greatest of their common factors.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (d) (A) is false but (R) is true.

Prime Factorization Class 6

Question 3. Assertion (A) HCF of 3 and 8 is 1 and LCM of 3 and 8 is 24.

Reason (R) HCF of two co-primes is 1 and the LCM of two co-primes is their product.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).

(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

(c) (A) is true but (R) is false.

(d) (A) is false but (R) is true.

Answer. (a) Both (A) and (R) are true and (R) is the correct explanation of (A).

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Fill in the Blanks

Question 1. 15 is a multiple of………and..

Solution. 3 and 5

Question 2. A number for which the sum of all its factors is equal to twice the number is called a ………. number.

Solution. Perfect

Question 3. The smallest prime number between 80 and 90 is

Solution. 83

Question 4. Numbers having more than two factors are called ……….numbers.

Solution. Composite

Question 5. The LCM of two or more given numbers is the lowest of their common……….

Solution. Multiples

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers True/False

Question 1. If the sum of the digits of a number is divisible by 3, then the number itself is divisible by 9.

Solution. False

Question 2. LCM of two or more numbers is divisible by their HCF.

Solution. Flase

Question 3. Two consecutive even prime numbers are known astwin primes.

Solution. False

Question 4. A number with three or more digits is divisible by 6, if the number formed by its last two digits (i.e. ones and tens) is divisible by 6.

Solution. True

Question 5. The LCM of two co-prime numbers is equal to the product of the numbers.

Solution. True

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Match the Columns

Question 1. Given below are two columns: Column A and Column B. Match each item of Column A with the corresponding item of Column B.

Solution. (1) → (d), (2) → (f), (3) → (b), (4) → (e), (5) → (c)

Question 2. Match each item of Column A with the corresponding item of Column B.

Solution. (1) → (c), (2) → (f), (3) → (d), (4) → (a), (5) → (b)

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Case Based Questions

Question 1. A photographer is hired to take group photographs of students in each class in a school. He arranges the students along with teachers in rows for the photograph. His arrangement has

• atmost 50 people.
• an equal number of people in each row.

A row consists of a minimum of 3 people and a maximum of 8 people.

(1) There are 35 people (students and teachers) in a class for a group photograph. What are the possible arrangements for them?

(2) The photographer arranged some of the students in 6 rows. What can be the maximum number of students in the photograph?

(a) 18

(b) 36

(c) 48

(d) 60

(3) How did the students of Class 7 which are 30 in number want to take a photograph along with 2 teachers. Which of the following is the possible arrangement for them?

(a) 2 rows with 16 students in each.

(b) 4 rows with 8 students/teachers in each.

(c) 5 rows with 6 students in each and 1 row for teachers.

Solution. (1) Total number of people (students and teachers) = 35

∴ Factors of 35 are 1, 5, 7 and 35.

Hence, possible arrangements

= 7 rows and 5 students/teachers per row

or 5 rows and 7 students/teachers per row

(2) (c) The photographer arranged students in 6 rows.

Given, maximum number of people in a row = 8

∴ Maximum number of students = 6 x 8=48

(3) (b) There are 30 students and 2 teachers in class 7.

Thus, in total 32 people.

Let us consider maximum people in a row i.e. 8.

So, divide 32 by 8 to know the number of rows.

32 ÷ 8 = 4

Hence, 4 rows with 8 students/teachers in each.

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Very Short Answer Type Questions

Question 1. Write the first three multiples of each of the following

(1) 11

(2) 12

Solution. (1) First three multiples of 11 = 11, 22, 33

(2) First three multiples of 12 = 12, 24, 36

Question 2. Write the greatest and the smallest prime number between 10 and 20.

Solution. Greatest prime number = 19

Smallest prime number = 11

Question 3. Write all the prime numbers between

(1) 10 and 15

(2) 20 and 35

Solution. (1) Prime numbers between 10 and 15 = 11, 13

(2) Prime numbers between 20 and 35 = 23, 29, 31

Question 4. Which of the following are composite numbers?

7, 13, 16

Solution. Given numbers are 7, 13, 16.

Factors of 7 = 1,7

Factors of 13 = 1,13

Factors of 16 = 1, 2,4,8,16

∴ 16 is a composite number.

Question 5. Write the common factor of 6 and 10.

Solution. Factors of 6 = 1, 2, 3,6

Factors of 10 = 1, 2, 5,10

Common factors of 6 and 10 = 1, 2

Class 6 Maths Chapter 3 Solutions

Question 6. Write the highest common factor of 6 and 15.

Solution. Factors of 6=1, 2, 3, 6

Factors of 15 = 1, 3, 5, 15

Common factors = 1, 3

Highest common factor = 3

Question 7. Write the first two common multiples of 5 and 15.

Solution. Multiples of 5 = 5, 10, 15, 20, 25, 30,…

Multiples of 15 = 15, 30,…

First two common multiples = 15, 30

Question 8. Find the prime factorisation of 40.

Solution. Here, we have 40

∴ 40 = 2 × 2 × 2 × 5

Question 9. If 3 and 10 are two co-prime numbers, then find their LCM.

Solution. We know that the LCM of two co-prime numbers is equal to their product.

∴ The LCM of 3 and 10 = 3 x 10 = 30

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Short Answer Type Questions

Question 1. Give the factorisation of the following numbers.

(1) 136

(2) 252

Solution.

(1) We have, 136

∴ 136 = 2 x 2 x 2 x 17

(2) We have, 252

∴ 252 = 2 x 2 x 3 x 3 x 7

Question 2. Test the divisibility of the following numbers.

(1) 4834 by 2

(2) 723 by 3

(3) 495 by 3 and 5

(4) 2853 by 3 and 9

Solution. (1) Given number is 4834. Here, unit place is 4. So, it is divisible by 2.

(2) Sum of digits of the number = 7 + 2 + 3 = 12, which is divisible by 3.

Hence, the number 723 is also divisible by 3.

(3) Here, unit place is 5. So, it is divisible by 5 and sum of digits = 4 + 9 + 5 = 18. So, it is divisible by 3.

(4) Sum of digits of the number = 2 + 8 + 5 + 3 = 18, which is divisible by 3 and 9 both.

Question 3. In each of the following numbers, replace * by the smallest number to make it divisible by 3.

(1) 27 * 4

(2) 53 * 46

Solution. For a number to be divisible by 3, the sum of the digits of the given number should be divisible by 3.

(1) Sum of digits of 27 * 4 = 2 + 7 + 4 = 13

∴ Replace * by 2

(2) Sum of digits of 53 * 46 = 5 + 3 + 4 + 6 = 18

∴ Replace * by 0

Class 6 Maths Chapter 3 Solutions

Question 4. Determine the least number, which when divided by 3, 4 and 5 leaves remainder 2 in each case.

Solution. First of all, we find the LCM of 3, 4 and 5.

LCM = 2 x 2 x 3 x 5 = 60

Hence, the required number = 60 + 2 = 62

Question 5. Find the HCF of the following numbers using prime factorisation method.

(1) 84 and 98

Solution. (1) We have, 84 and 98

84 = 2 x 2 x 3 x 7 and 98 = 2 x 7 x 7

∴ HCF = 2 x 7 = 14

Question 6. Find the LCM of 160, 170 and 90.

Solution. We have,

Hence, LCM of given numbers

= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 17

= 24480

Question 7. Find the LCM of 112, 168, 266 by prime factorisation method.

Solution. We have, 112, 168 and 266

112 = 2 x 2 x 2 x 2 x 7;

168 = 2 x 2 x 2 x 3 x 7

266 = 2 x 7 x 19

∴ LCM = 2 x 2 x 2 x 2 x 3 x 7 x 19 = 6384

Question 8. Three belss ring at intervals of 48 min, 60 min and 90 min, respectively. If all the three bells ring together at 10:00 am, then at what time will the three bells ring again that day?

Solution. We have to find the LCM of 48, 60 and 90

LCM = 2 x 2 x 2 x 2 x 3 x 3 x 5

= 720 min

= \(\frac{720}{60}=12 \mathrm{~h}\)

∴ Bells ring together again at (10:00 am + 12 hr) at 10:00 pm

Question 9. Five bells begin to toll together at intervals of 9 sec, 6 sec, 10 sec and 8 sec, respectively, how many times will they toll together in the span of 1 h?

Solution. We have to find the LCM of 9, 6, 4, 10 and 8.

LCM = 2 x 2 x 2 x 3 x 3 x 5 = 360

In 1 h, the ring will toll together = \(\frac{3600}{360}\)

= 10 times

Mp Board Class 6 Maths Important Questions

Question 10. In a colony of 100 blocks of flats numbering 1 to 100, a school van stops at every sixth block while a school bus stops at every tents block. On which stop will both of them stop if they start from the entrance of the colony?

Solution. The common stop at which both van and bus stop is the common multiple of 6 and 10.

Multiples of 6 less than 100 are

6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96.

Multiples of 10 less than 100 are

10, 20, 30, 40, 50, 60, 70, 80, 90.

Common multiples of 6 and 10 are 30, 60 and 90.

So, the school van and bus both will stop together at blocks 30, 60 and 90.

Question 11. For an international school competition, student’s stay is booked in two hotels 148 students in Hotel 1 and 164 students in Hotel 2. An equal number of students are accommodated in each hotel room. What can be the maximum number of students in a room?

Solution. Factors of 148 are 1, 2, 4, 37, 74 and 148.

Factors of 164 are 1, 2, 4, 41, 82 and 164.

The common factors of 148 and 164 are 1, 2 and 4.

The highest common factor of 148 and 164 is 4.

∴ Maximum number of students than can be accommodated in a room is 4.

MP Board Class 6 Maths Solutions For  Chapter 3 Playing With Numbers Long Answer Type Questions

Question 1. Find a 4-digit odd number using each of digits 1, 2, 4 and 5 only once such that when the first and last digits are interchanged, it is divisible by 4.

Solution. The 4-digit number will be an odd number, if the unit place digit is an odd number (i.e. 1 or 5).

Total such odd numbers are

4125, 4215, 1245, 1425, 2145, 2415, 4251, 4521, 5241, 5421, 2451, 2541.

Also we know that any 4-digit number is divisible by 4, if the last two-digit number is divisible by 4.

Consider a number 4521, if we interchage the first and the last digit, the new number will be 1524. Here, we see that the last two digits (i.e. 24) is divisible by 4. So, the number 1524 is divisible by 4.

Similarly, other numbers when we interchange the first and the last digit, divisible by 4 are 4125, 2415, 2451.

Hence, the required 4-digit numbers are 4521, 4125, 2415 and 2451.

Question 2. Three boys step off together from the same place. If their steps measure 36 cm, 48 cm and 54 cm, then at what distance from the starting point will they again step together?

Solution. Given, their step measures are 36 cm, 48 cm and 54 cm.

We must find the LCM of 36, 48, 54,

LCM of 36, 48 and 54 = 2 x 2 x 2 x 2 x 3 x 3 x 3 = 432

They again step together from the starting point at 432 cm i.e. 4 m 32 cm.

Class 6 Maths Chapter 3 Solutions

Question 3. Three brands A, B and C of biscuits are available in packets of 12, 15 and 21 biscuits, respectively. If a shopkeeper wants to buy an equal number of biscuits of each brand, then what is the minimum number of packets of each brand, he should buy?

Solution. In Brand A, number of biscuits=12

In Brand B, number of biscuits = 15

In Brand C, number of biscuits = 21

First of all, we find the LCM of 12, 15 and 21

Now, number of packets of Brand A = \(\frac{420}{12}=35\)

Number of packets of Brand B = \(\frac{420}{15}=28\)

Number of packets of Brand C = \(\frac{420}{21}=20\)

Question 4, On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 46 cm, respectively. What is the minimum distance each should walk, so that each can cover the same distance in complete steps?

Solution. (1) The step measure of each person is 40 cm, 42 cm and 46 cm.So, the minimum distance each should walk is the LCM of 40, 42 and 46.

LCM of 40, 42 and 46 = 2 x 2 x 2 x 3 x 5 x 7 x 23

= 19320 cm = 193.2 m

Class 6 Maths Chapter 3 Solutions

Question 5. A merchant has 130 L of oil of one kind, 190 L of another kind and 250 L of a third kind. He wants to sell the oil by filling the three kinds of oil in tins of equal capacity. What should be the greatest capacity of such a tin?

Solution. The greatest capacity of the required measure will be equal to the HCF of 130, 190 and 250 L.

Prime factorisation of 130, 190 and 250 are

130 = 2 x 5 x 13,190 = 2 x 5 x 19 and 250 = 2 x 5 x 5 x 5

Common factors of 130, 190 and 250 = 2 x 5 = 10

Hence, the greatest capacity of tin should be 10 L.

Question 6. Monica, Heronica and Rajat begin to jog around a circular stadium. They complete their revolution in 42 sec, 56 sec and 63 sec, respectively. How many seconds after will they be together at the starting point?

Solution. Required second of time = LCM of 42, 56 and 63 42, 56, 63

LCM = 2 x 2 x 2 x 3 x 3 x 7 = 504 s

Hence, after 504s, they will be together at starting point.

Question 7. In a school library, there are 780 books of English and 364 books of Science. Ms. Yakang, the librarian of the school wants to store these books in shelves such that each shelf should have the same number of books of each subject. What should be the minimum number of books in each shelf?

Solution. Given, number of English books = 780

and number of Science books = 364

For getting the minimum number of books in each shelf, we have to find the HCF of 780 and 364.

Prime factorisation of 780 and 364.

780 = 2 × 2 × 3 × 5 x 13

and 364 = 2 x 2 x 7 x 13

∴ HCF of 780 and 364 = 2 x 2 x 13 = 52

Hence, the minimum number of books in each shelf is 52.

Question 8. John, Rishi and Feroz participated in track events. During practice sessions, their coach observed that John took 48 sec, Rishi took 72 sec and Feroz took 108 sec to run around a circular track. If they start running together at 6 am for half an hour, how many times will they all come together at a same position?

Solution. John, Rishi and Feroz take 48 sec, 72 sec and 108 sec, respectively to complete round of a circular track. We have to calculate LCM to find the time after which they meet on the starting point for first time.

∴ LCM of 48, 72 and 108 = 2 x 2 x 2 x 2 x 3 x 3 x 3 = 432

So, it means the three persons are in the same position after 432 sec or after 7 min 12 sec.

As it is given that, they start running at 6 am for half an hour.

Hence, John, Rishi and Feroz will all come together at the same position 4 times in half an hour.

Class 6 Maths Chapter 3 Solutions

Question 9. Jaya baked muffins using paper liners and cherries. Some paper liner packets contain 8 liners, while others contain 10 liners. A pacted of cherry contains 6 cherries. Every muffin Jaya baked contained 1 cherry. All cherries and paper liners were used up. What can be the minimum number of muffins baked by her?

Solution. To find the minimum number of muffins Jaya baked, we need to find LCM of the paper liners and cherries.

LCM of paper liners of sizes 8 and 10

= 2 × 2 × 2 × 5 = 40

Hence, we need to find LCM of 40 and 6.

∴ LCM of 40 and 6 = 2 x 2 x 2 x 3 x 5 = 120

Therefore, the minimum number of muffins Jaya baked is 120 muffins.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers

Natural Numbers

The counting numbers 1, 2, 3, 4, 5, … are called natural numbers. The collection of natural numbers is denoted by Ni.e. N=(1,2,3,4,…)

Predecessor If we subtract 1 from any natural number, then we get the predecessor of that number.

e.g. 16 – 1 = 15 i.e. 15 is the predecessor of 16.

Successor If we add 1 to any natural number, then we get the successor of that number.

e.g. 10 + 1 = 11 i.e. 11 is the successor of 10.

Note it Every natural number has a successor and every natural number except 1 has a predecessor because 1 is the smallest natural number. There is no last number i.e. we have infinite natural numbers.

Example 1. Write predecessor and successor of the following numbers

(1) 9

(2) 43

(3) 297

(4) 2901

Solution.

(1) Predecessor of 9 = 9 – 1 = 8

and successor of 9 = 9 + 1 = 10

(2) Predecessor of 43 = 43 – 1 = 42

and successor of 43 = 43 + 1 = 44

(3) Predecessor of 297 = 297 – 1 = 296

and successor of 297 = 297 + 1 = 298

(4) Predecessor of 2901 = 2901 – 1 = 2900

and successor of 2901 = 2901 + 1 = 2902

Read and Learn More MP Board Class 6 Maths Solutions

Example 2. Write

(1) a single-digit predecessor of a two-digit number.

(2) a three-digit successor of a two-digit number.

Solution.

(1) 9, which is a predecessor of 10.

(2) 100, which is a successor of 99.

Example 3. Write the next four natural numbers after 6999.

Solution. The next four natural numbers after 6999 are

6999 + 1 = 7000, 7000 + 1 = 7001,

7001 + 1 = 7002, 7002 + 1 = 7003

i.e. 7000, 7001, 7002 and 7003.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers

The natural numbers along with zero form the collection of whole numbers. The collection of whole numbers is denoted by Wi.e. W = {0,1,2,3,4,…}

All natural numbers are whole numbers but all whole numbers are not natural numbers.

Note it Every whole number has a successor and every whole number except O has a predecessor. There is no last whole number i.e. we have infinite whole numbers.

Example 4. Write the whole number whose successor is 79500.

Solution. The required whole number = Predecessor of

79500 = 79500 – 1 = 79499

Example 5. Write the whole number whose predecessor is 35999.

Solution. The required whole number=Successor of 35999 = 35999 + 1 = 36000

Example 6. Find the number whose successor is 5 more than 364.

Solution. Let the successor be x.

x = 364 + 5 = 369

Hence, the required number is 369-1=368

Class 6 Maths Chapter 2 Whole Numbers Questions

Example 7. Write the four whole numbers occuring just before 1001.

Solution. The four whole numbers just before 1001 are

1001 – 11000, 1000 – 1 = 999,

999 – 1998, 998 – 1 – 997

i.e. 1000, 999, 998 and 997.

Example 8. How many whole numbers are there between 19 and 33?

Solution. Whole numbers between 19 and 33 are

20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32

Hence, the total number of whole numbers between 19 and 33 is 13.

Example 9. How many 3-digit numbers are there between 88 and 702?

Solution. 3-digit numbers between 88 and 702 are

100, 101, 102,…, 701.

Number of these numbers = 701 – 99 = 602

Note it in the above list, 701 is included and 99 is not included.

Example 10. Write the number which is product of successor and predecessor of 1001.

Solution. Successor of 1001 = 1001 + 1 = 1002

Predecessor of 1001 = 1001 – 1 = 1000

∴ Product of successor and predecessor of 1001 = 1002 × 1000 = 1002000

Example 11. Write all the whole numbers between 99 and 199 which do not change if the digits are written in reverse order.

Solution. All the whole numbers between 99 and 199 which do not change, if the digits are written in reverse order, are 101, 111, 121, 131, 141, 151, 161, 171, 181, 191.

Number Line

To represent whole numbers on a number line, draw a line and mark a point on it and label it 0 (zero).

Starting from 0 (zero) on the line, mark out the equal intervals (of unit length) to the right of 0 and label them as 1, 2, 3,…. Thus, the distance between these points labelled as 0, 1,… is called as unit distance.

In this way, you can go to any whole number on the right in this manner. Thus, we represent whole numbers on the number line as shown below

Note it Distance between 16 and 17 is same as distance between 35 and 36 which is one unit.

MP Board Class 6 Maths Solutions

Comparison of Two Whole Numbers

On the number line, the number on the right of the other number is the greater number and the number on the left of the other number is the smaller number.

On the number line, 7 is on the right of 5. So, 7 is greater than 5 i.e. 7 > 5.

The number 6 lies on the left of 9. So, 6 is smaller than 9 i.e. 6 < 9.

Example 12. In each of the following pair of numbers, state which whole number is on the right of the other number on the number line. Also write them with the appropriate sign >,<) between them

(1) 627, 613

(2) 157, 168

(3) 6123, 5674

(4) 113295, 1132956

Solution. (1) On the number line, whole number 627 is on the right of 613 because 627 is greater than 613

i.e. 627 > 613

(2) On the number line, whole number 168 is on the right of 157 because 157 is less than 168

i.e. 157 < 168

(3) On the number line, whole number 6123 is on the right of 5674 because 6123 is greater than 5674

i.e. 6123 > 5674

(4) On the number line, whole number 1132956 is on the right of 113295 because 113295 is less than 1132956

i.e.113295 < 1132956

MP Board Class 6 Maths Solutions

Example 13. Represent the successor and the predecessor of 12 and 7 respectively on the number line.

Solution. Place the successor of 12 on the number line.

12 + 1 = 13

Place the predecessor of 7 on the number line.

So, 7 – 1 = 6

Addition on the Number Line

When we add any number to a given number, we move towards right on the number line.

e.g. Let us add 3 and 5.

We start from 3 on the number line and make 5 jumps to the right by unit distance each. Then, we reach at 8.

So, 3 + 5 = 8

Subtraction on the Number Line

When we subtract any number from a given number, we move towards left on the number line.

e.g. Let us find 6 – 2.

We start from 6 on the number line and make 2 jumps to the left by unit distance each. Then, we reach at 4.

So, 6 – 2 = 4

Multiplication on the Number Line

For multiplication, we make jumps of equal distance starting from origin.

e.g. Let us find 5×3.

We start from 0 (zero) on the number line and move 5 units at a time. After 3 such moves, we reach at 15.

So, 5 x 3 = 15

MP Board Class 6 Maths Solutions

Example 14. Find the value of the following on the number line.

(1) 3 + 6

(2) 8 + 2

(3) 6 – 3

(4) 6 x 3

(5) 2 x 5

Solution. (1) To find 3 + 6

Let us start from 3. Since, we have to add 6 to this number, we make 6 jumps to the right of 3. Each jump being equal to 1 unit. After six jumps, we reach at 9. 1 2 3 4 5 6

So, 3 + 6 = 9

(2) To find 8 + 2

Let us start from 8. Since, we have to add 2 to this number, we make 2 jumps to the right of 8. Each jump being equal to 1 unit. After two jumps, we reach at 10.

So, 8 + 2 = 10

(3) To find 6 – 3

Let us start from 6 and make 3 equal jumps to the left of 6. Each jump is equal to 1 unit. Now, we reach at 3.

so, 6 – 3 = 3

(4) To find 6 x 3

We have to multiply 6 by 3 i.e. 6 units x 3 (or 6 units 3 times).

Let us start from 0, move 6 units to the right of 0, 31 times.

After moving 3 such moves, we reach at 18.

So, 6 x 3 = 18

(5) To find 2 x 5

We have to multiply 2 by 5 i.e. 2 units x5 (or 2 units 5 times).

Let us start from 0, move 2 units to the right of 0, 5 times.

After moving 5 such moves, we reach at 10.

So, 2 × 5 = 10

Class 6 Maths Chapter 2 Whole Numbers Questions

Question 1. Write the predecessor and successor of 19, 1997, 12000, 49 and 100000.

Solution.

Question 2. Is there any natural number that has no predecessor?

Solution. Yes, the smallest natural number I has no predecessor because predecessor of 1 is (1-1=0) zero and zero is not a natural number.

Question 3. Is there any natural number which has no successor? Is there a last natural number?

Solution. No, there is no natural number which has no successor because each natural number has a successor.

e.g. Successor of 4=4+1=5 Successor of 5=5+1=6 and so on.

Also, there is no last natural number because natural number starts from 1 and goes upto infinite.

Question 4. Are all natural numbers also whole numbers?

Solution. Yes, all the natural numbers are also whole numbers.

Question 5. Are all whole numbers also natural numbers?

Solution. No, all whole numbers are not natural numbers because 0 is a whole number but it is not a natural number.

Question 6. Which is the greatest whole number?

Solution. Since, every whole number has a successor. So, there is no greatest whole number.

Question 7. Find the sum, using the number line.

(1) 4+5

Solution. (1) To find 4 + 5

Let us start from 4. Since, we have to add 5 to this number, we make 5 jumps to the right of 4. Each jump being equal to 1 unit. After five jumps, we reach at 9.

∴ 4 + 5 = 9

Question 8. Find the difference, using the number line.

(1)8-3

Solution. (1) To find 8 – 3

Let us start from 8 and make 3 equal jumps to the left of 8. Each jump is equal to 1 unit. Now, we reach at 5.

∴ 8 – 3 = 5

Question 9. Find using the number line.

(1) 2×6

Solution. (1) To find 2×6

We have to multiply 2 by 6

i.e. 2 units x 6 (or 2 units 6 times).

Let us start from 0, move 2 units to the right of 0.

After making 6 such moves, we reach at 12.

∴ 2 × 6 = 12

MP Board Class 6 Maths Solutions Chapter 2 Whole Numbers Exercise 2.1

Question 1. Write the next three natural numbers after 10999.

Solution. 11000, 11001 and 11002.

Question 2. Write the three whole numbers occurring just before 10001.

Solution. 10000, 9999 and 9998.

Question 3. Which is the smallest whole number?

Solution. The smallest whole number is zero (0).

Question 4. How many whole numbers are there between 32 and 53?

Solution. Whole numbers between 32 and 53 are as follows

33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51 and 52.

Hence, the total number of whole numbers between 32 and 53 is 20.

Mp Board Class 6 Maths Important Questions

Question 5. Write the successor of

(1) 2440701

(2) 100199

(3) 1099999

(4) 2345670

Solution. The successor of given numbers are as follows

Question 6. Write the predecessor of

(1) 94

(2) 10000

(3) 208090

(4) 7654321

Solution. The predecessor of given numbers are as follows

Question 7. In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line. Also, write them with the appropriate sign (>, <) between them.

(1) 530, 503

(2) 370, 307

(3) 98765, 56789

(4) 9830415, 10023001

Solution.

On the number line, whole number 503 is on the left of 530 because 530 is greater than 503 i.e. 530 > 503.

On the number line, whole number 307 is on the left of 370 because 370 is greater than 307 i.e. 370 > 307.

On the number line, whole number 56789 is on the left of 98765 because 98765 is greater than 56789 i.e. 98765> 56789.

On the number line, whole number 9830415 is on the left of 10023001 because 9830415 is less than 10023001 i.e. 9830415 < 10023001.

Mp Board Class 6 Maths Book Pdf

Question 8. Which of the following statements are true (T) and which are false (F)?

Zero is the smallest natural number.

400 is the predecessor of 399.

Zero is the smallest whole number.

600 is the successor of 599.

All natural numbers are whole numbers.

All whole numbers are natural numbers.

The predecessor of a two-digit number is never a single digit number.

1 is the smallest whole number.

The natural number 1 has no predecessor.

The whole number 1 has no predecessor.

The whole number 13 lies between 11 and 12.

The whole number 0 has no predecessor.

The successor of a two-digit number is always a two-digit number.

Solution.

1. False, because zero is not a natural number. It is a whole number.
2. False, because predecessor of 399 is 399-1=398.
3. True, because whole numbers start with zero (0).
4. True, because successor of 599 is 599 + 1 = 600.
5. True.
6. False, because 0 is not a natural number.
7. False, because predecessor of 10 is 10 – 1 = 9, which is a single digit number.
8. False, because 0 is the smallest whole number.
9. True, because, if we subtract 1 from 1, then we get 0 (1-10), which is not a natural number.
10. False, because predecessor of 1 is 1-1=0 and 0 is a whole number.
11. False, because 13 is greater than 12.
12. True.
13. False, because successor of two-digit number 99 is 99+1=100, which is a three-digit number.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Multiple Choice Questions

Question 1. The product of non-zero whole number and its successor is always

1. an even number
2. an odd number
3. a prime number
4. divisible by 3

Answer. 1. an even number

Question 2. The whole number which has no predecessor is

1. 1
2. 0
3. 2
4. 3

Answer. 2. 0

Question 3. The predecessor of 1 lakh is

1. 99000
2. 99999
3. 999999
4. 100001

Answer. 2. 99999

Class 6 Maths Chapter 2 Solutions

Question 4. The successor of 1 million is Competency Based Question

1. 2 million
2. 1000001
3. 100001
4. 10001

Answer. 2. 1000001

Question 5. The product of two whole numbers is always a

1. natural number
2. even number
3. odd number
4. None of the above

Answer. 4. None of the above

Question 6. The greatest number which always divides the product of the predecessor and successor of an odd natural number other than 1, is

1. 6
2. 4
3. 16
4. 32

Answer. 2. 4

Question 7. Which of the following is right side to 10 on the number line?

1. 8
2. 9
3. 18
4. 0

Answer. 3. 18

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Questions

Question 1. Assertion (A) 1 is a natural number.

Reason (R) Every natural number is a whole number.

(a) A is false but R is true.

(b) A is true but R is false.

(c) Both A and R are true.

(d) Both A and R are false.

Answer. c. Both A and R are true.

Question 2. Assertion (A) 70 is greater than 50.

Reason (R) 70 is the left side to 50 on the number line.

(a) A is false but R is true.

(b) A is true but R is false.

(c) Both A and R are true.

(d) Both A and R are false.

Answer. b. A is true but R is false.

Class 6 Maths Chapter 2 Mp Board Solutions

Question 3. Assertion (A) 27 is the successor of 26.

Reason (R) Any natural number, you can add 1 to that number and get the next number i.e. you get its successor.

(a) A is false but R is true.

(b) A is true but R is false.

(c) Both A and R are true.

(d) Both A and R are false.

Answer. c. Both A and R are true.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Fill in the Blanks

Question 1. 300 is the predecessor of ……

Solution. 301

Question 2. 450 is the successor of ……

Solution. 449

Question 3. ……… is the successor of the largest 3-digit number.

Solution. 1000

Question 4. The smallest 6-digit natural number ending in 5 is …….

Solution. 100005

Question 5. Addition corresponds to the …… on the number line.

Solution. Right

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers True/False

Question 1. Successor of 1-digit number is always a 1-digit number.

Solution. False

Question 2. Successor of 3-digit number is always a 3-digit number.

Solution. False

Question 3. Every whole number except zero is the successor of another whole number.

Solution. True

Question 4. Sum of two whole numbers is always less than their product.

Solution. False

Question 5. There is a whole number which when added to a whole number, gives the second whole number.

Solution. True

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Match the Columns

1. (1) → (c), (2) → (d), (3) → (e), (4) → (a), (5) → (b)

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Very Short Answer Type Questions

Question 1. How many natural numbers are there between 60 and 72?

Solution. Given numbers are 60 and 72.

Hence, natural numbers between 60 and 72

= (72 – 60) – 1 = 11

Question 2. Write the smallest natural number.

Solution. 1 is the smallest natural number.

Question 3. Write the two immediate predecessors of 2945.

Solution. Given number is 2945.

Immediate predecessors are 2944 and 2943

Question 4. Write the three immediate successors of 3956.

Solution. Given number is 3956.

So, three immediate successors of 3956 are 3957, 3958 and 3959.

Mp Board Class 6 Maths Chapter 2 Solutions

Question 5. Write a double digit predecessor of three-digit number.

Solution. 99 is a double digit predecessor of 100.

Question 6. Write a triple digit successor of two-digit number.

Solution. 100 is a triple digit successor of 99.

Question 7. Write two whole numbers occuring just before 1001.

Solution. 1000 and 999.

Question 8. Write three whole numbers occuring just after 1000.

Solution. 1001, 1002, 1003

Question 9. Write down the two whole number which are on the right of 3 and on the left of 6.

Solution. 4 and 5 are right of 3 and left of 6.

Question 10. Write the next three consecutive whole numbers of 89.

Solution. The next three consecutive whole numbers of 89 are 90, 91 and 92.

MP Board Class 6 Maths Solutions For  Chapter 2 Whole Numbers Short Answer Type Questions

Question 1. Write the predecessor of the following

(1) 96

(2) 9998

Solution. (1) Predecessor of 96 = 96 – 1 = 95

(2) Predecessor of 9998 = 9998 – 1 = 9997

Question 2. Determine the sum of the four numbers as given below

• Successor of 32
• Predecessor of 49
• Predecessor of the predecessor of 56
• Successor of the successor of 67

Solution. Successor of 32 = 32 + 1 = 33

Predecessor of 49 = 49 – 1 = 48 Predecessor of 56 is 55

So, predecessor of the predecessor of 56 = 55 – 1 = 54

Successor of 67 is 68

So, successor of the successor of 67 = 68 + 1 = 69

Hence, the sum of four numbers = 33 + 48 + 54 + 69 = 204

Question 3. Write the predecessor of the sum of 345,287 and 368.

Solution. Sum of 645, 287 and 368 is 1300, whose predecessor

= 1300 – 1 = 1299

Question 4. Write the successor of the difference of 145 and 46.

Solution. Difference of 145 and 46 is 99, whose successor

= 99 + 1 = 100

Mp Board Class 6 Maths Chapter 2 Solutions

Question 5. Find the number whose predecessor is 3 more than 456.

Solution. Let the predecessor be x.

x = 456 + 3 = 459

The required number is 459 + 1 = 460

Question 6. Find the whole number x, when

(1) x – 9 = -9

(2) x – 0 = 1

Solution. (1) x – 9 = -9

⇒ x = -9 + 9

⇒ x = 0

(2) x – 0 = 1

⇒ x = 1

Question 7. Write all the whole numbers between 200 and 300 which do not change if the digits are written in reverse order.

Solution. All the whole numbers between 200 and 300 which do not change, if the digits are written in reverse order are

202, 212, 222, 232, 242, 252, 262, 272, 282, 292

Question 8. Find the number whose successor is 3 more thatn 450.

Solution. Let the number be x.

Then, x + 1 = 450 + 3

x = 452

∴ The number = 452

Class 6 Maths Chapter 2 Whole Numbers Questions

Question 9. In each of the following pairs of numbers, state which whole number is to the left of the other on the number line. Use appropriate symbol (> or <).

(1) 497, 495

(2) 3059, 3096

Solution. We know that the number which lies to the right of other is a greater number.

(1) 495 lies to the left of 497, so, 497 > 495

(2) 3059 lies to the left of 3096, so 3059 <3096

Question 10. There are two whole numbers which when multiplied by itself gives the same number. What are they?

Solution. If we multiply 0 by itself, it gives same number i.e. 0 x 0 = 0, and similarly, 1 x 1 = 1.

∴ The required whole numbers are 0 and 1.

Free downloadable MP Board solutions for Class 6 Maths Chapter 1 Knowing Our Numbers

Class 6 Maths chapter-wise solutions PDF Comparing Numbers

In comparison of two numbers, a number having more number of digits will be greater and a number having less number of digits will be smaller.

e.g. Let 92 and 395 be given numbers. It is clear that number 395 has greater number of digits. Hence, 395 is the greatest number.

If the number of digits in two or more numbers are same, then that number will be larger which has a greater leftmost digit. If this digit also happens to be the same, we look at the next digit and so on.

e.g. Let 395 and 424 be given numbers. Here, both given numbers have same number of digits but 424 has a greater leftmost digit (4 as compared to 3). Hence, 424 is greater number.

Mp Board Class 6 Maths Chapter 1 Solutions

Example 1. By instantly looking at the numbers, find which one is the greatest and which one is the smallest in each of the following.

(1) 29, 210, 198, 1234

(2) 19, 311, 218, 4310

(3) 741965, 769, 7064, 8094

(4) 73156, 1369, 18088, 9173231

Solution. (1) Number of digits in 29 = 2

Number of digits in 210 = 3

Number of digits in 198 = 3

Number of digits in 1234 = 4

∴ Greatest number=1234 [maximum number of digits]

Read and Learn More MP Board Class 6 Maths Solutions

and smallest number=29 [minimum number of digits]

(2) Number of digits in 19 = 2

Number of digits in 311 = 3

Number of digits in 218 = 3

Number of digits in 4310 = 4

∴ Greatest number = 4310 [maximum number of digits)

and smallest number=19 [minimum number of digits]

(3) Number of digits in 741965 = 6

Number of digits in 769 = 3

Number of digits in 7064 = 4

Number of digits in 8094 = 4

∴ Greatest number=741965 [maximum number of digits]

and smallest number=769 [minimum number of digits]

(4) Number of digits in 73156 = 5

Number of digits in 1369 = 4

Number of digits in 18088 = 5

Number of digits in 9173231=7

∴ Greatest number=9173231 [maximum number of digits]

and smallest number = 1369 [minimum number of digits]

Mp Board Class 6 Maths Chapter 1 Solutions

Example 2. Compare the following number.

(1) 67454 and 78465

(2) 97632 and 96543

(3) 956 and 987

(4) 86545 and 86575

Solution. (1) Both 67454 and 78465 have same number of digits. Now, on comparing first digit from left, we get

6 < 7

∴ 67454 < 78465

(2) Both 956 and 987 have same number of digits and first leftmost digit is also same.

Now, on comparing second digit from left, we get

5 < 8

∴ 956 < 987

(3) Both 97632 and 96543 have same number of digits and first leftmost digit is also same.

Now, on comparing second digit from left, we get

7 > 6

∴ 97632 > 96543

(4) Both 86545 and 86575 have same number of digits and its three digits from left are also same.

Now, on comparing fourth digit from left, we get

4 < 7

∴ 86545 < 86575

MP Board Solutions For Class 6 Maths Chapter 1 Ordering Of Numbers

Ordering of numbers is the arrangements of numbers from smallest to greatest or from greatest to smallest.

Ascending order is the method of arranging the numbers from smallest to greatest.

While descending order is the method of arranging the numbers from greatest to smallest number.

Example 3. Arrange the following numbers in ascending order.

(1) 847, 9754, 8320, 571

(2) 911, 713, 5168, 7431

(3) 3691, 3699, 4312, 4319

(4) 2231, 2291, 2278, 2201

Solution. (1) To convert numbers into ascending order, we arrange numbers from smallest to greatest.

Now, ascending order is

571 < 847 < 8320 < 9754.

(2) To convert numbers into ascending order, we arrange numbers from smallest to greatest.

Now, ascending order is

713 < 911 < 5168 < 7431.

(3) To convert numbers into ascending order, we arrange numbers from smallest to greatest.

Now, arranging them in ascending order

3691 < 3699 < 4312 < 4319.

(4) To convert numbers into ascending order, we arrange numbers from smallest to greatest.

Now, ascending order is

2201 < 2231 < 2278 < 2291.

Class 6 Maths Chapter 1 Mp Board Solutions

Example 4. Arrange the following numbers in descending order.

(1) 719, 3250, 571, 8256

(2) 819, 5240, 890, 6249

(3) 31093, 31309, 39031, 9391, 31029

(4) 21025, 21206, 29031, 5625, 21029

Solution. (1) To convert number into descending order, we arrange the numbers from greatest to smallest.

Now, descending order of the given numbers is

8256 > 3250 > 719 > 571.

(2) To convert number into descending order, we arrange the numbers from greatest to smallest.

Now, descending order of the given numbers is

6249 > 5240 > 890 > 819.

(3) To convert number into descending order, we arrange the numbers from greatest to smallest.

Now, descending order of the given numbers is

39031 > 31309 > 31093 > 31029 > 9391.

(4) To convert number into descending order, we arrange the numbers from greatest to smallest.

Now, descending order of the given numbers is

29031 > 21206 > 21029 > 21025 > 5625.

MP Board Solutions For Class 6 Maths Chapter 1 Formation Of Smallest And Greatest Numbers

Suppose some digits are given to form greatest number and smallest number.

For greatest number We arrange the given digits in descending order of their values.

For smallest number We arrange the given digits in ascending order of their values.

e.g. The smallest 4-digit number using 5, 3, 4, 2 is 2345 and the greatest 4-digit number using the same digits is 5432.

Example 5. Use the following digits without repetition and make the greatest and smallest 4-digit numbers.

(1) 2, 8, 7, 6

(2) 9, 5, 4, 1

(3) 3, 8, 5, 0

(4) 2, 3, 6, 7

Solution. (1) Descending order of the given digits is 8, 7, 6, 2.

∴ Greatest 4-digit number = 8762

and ascending order of the given digits is 2, 6, 7, 8

∴ Smallest 4-digit number = 2678

(2) Descending order of the given digits is 9, 5, 4, 1.

∴ Greatest 4-digit number = 9541

and ascending order of the given digits is 1,4,5,9

∴ Smallest 4-digit number = 1459

(3) Descending order of the given digits is 8, 5, 3,0

∴ Greatest 4-digit number = 8530

and ascending order of the given digits is 0, 3, 5, 8

∴ The smallest number is 0 which can’t be placed at left most place.

∴ Smallest 4-digit number = 3058

Mp Board Class 6 Maths Book Pdf

Note it While forming a smallest number from given number of digits, zero cannot be placed at leftmost digit. As zero will be meaningless in counting and 4-digit number will become 3-digit number and so on.

(4) Descending order of the given digits is 7, 6, 3, 2.

∴ Greatest 4-digit number = 7632

and ascending order of the given digits is 2, 3, 6, 7

∴ Smallest 4-digit number = 2367

Mp Board Class 6 Maths Important Questions

Example 6. Make the greatest and the smallest 4-digit numbers using any one digit twice.

(1) 3,6,7

(2) 8, 1, 5

(3) 0, 7, 9

(4) 5, 4, 0

Solution. (1) Descending order of the given digits is 7, 7, 6, 3.

[∵ greatest digit is taken twice]

∴ Greatest 4-digit number = 7763

and ascending order of the given digits is 3, 3, 6, 7. [∵ smallest digit is taken twice]

∴ Smallest 4-digit number = 3367

(2) Descending order of the given digits is 8, 8, 5, 1

[∵ greatest digit is taken twice]

∴ Greatest 4-digit number = 8851

and ascending order of the given digits is 1, 1, 5, 8. [∵ smallest digit is taken twice]

∴ Smallest 4-digit number = 1158

(3) Descending order of the given digits is 9,9,7,0.

[∵ greatest digit is taken twice]

∴ Greatest 4-digit number = 9970

and ascending order of the given digits is 0, 0, 7, 9.

[∵ smallest digit is taken twice]

But 0079 is a 2-digit number. So, keeping 7 (instead of 0) at the left most place and taking the smallest digit twice i.e. 7009.

∴ Smallest 4-digit number = 7009

(4) Descending order of the given digits is 5, 5, 4, 0.

∴ Greatest 4-digit number = 5540

and ascending order of the given digits is 0, 0, 4, 5.

But 0045 is a 2-digit number. So, keeping 4 (instead of 0) at the left most place and taking the smallest digit twice i.e. 4005.

∴ Smallest 4-digit number = 4005

Class 6 Maths Chapter 1 Exercise Solutions

Example 7. Make the greatest and the smallest 4-digit numbers using any four different digits if

(1) Digit 5 is always at ones place.

(2) Digit 3 is always at tens place.

(3) Digit 1 is always at thousands place.

Solution. Writing digits written in descending order as 9, 8, 7, 6, 5, 4, 3, 2, 1, 0

(1) According to the question, digit 5 is always at ones place.

∴ Greatest number = 9875

and Smallest number = 1025

(2) According to the question, digit 3 is always at tens place.

∴ Greatest number = 9837

and Smallest number = 1032

(3) According to the question, digit 1 is always at thousands place.

∴ Greatest number = 1987

and Smallest number = 1023

Shifting Digits

Shifting digits means changing the position of the digits in a number.

e.g. Consider two numbers 419 and 941. We observe that both the numbers have same digits but their places are different.

So, if the digits of a number are shifted, then the number also gets change.

MP Board solutions for Class 6 Maths Chapter 1 Greatest Number and Smallest Number

On adding 1 to the greatest n-digit number, we would get the smallest (n+1)-digit number.

e.g. Greatest 2-digit number + 1 = Smallest 3-digit number

i.e. 99 + 1 = 100

(1) Greatest 3-digit number = 999

∴ Smallest 4-digit number = 1000

(2) Greatest 4-digit number = 9999

∴ Smallest 5-digit number = 10000

(3) Greatest 5-digit number = 99999

∴ Smallest 6-digit number = 100000

(4) Greatest 6-digit number = 999999

∴ Smallest 7-digit number = 1000000

(5) Greatest 7-digit number = 9999999

∴ Smallest 8-digit number = 10000000

(6) Greatest 8-digit number = 99999999

∴ Smallest 9-digit number = 100000000

Note it

(1) One hundred = 10 tens

(2) One thousand = 10 hundreds = 100 tens

(3) One lakh 100 thousands = 1000 hundreds

(4) One crore = 100 lakhs = 10000 thousands

(5) One million = 1000 thousands = 10 lakhs

(6) One billion = 1000 millions

Example 8. Starting from the greatest 7-digit number, write the previous 4 numbers in descending order.

Solution. The greatest 7-digit number = 9999999

1st previous number = 9999999 – 1 = 9999998

2nd previous number = 9999999 – 2 = 9999997

3rd previous number = 9999999 – 3 – 9999996

4th previous number = 9999999 – 4 = 9999995

Now, descending order of these number is as follows 9999998 > 9999997 > 9999996 > 9999995

MP Board Solutions For Class 6 Maths Chapter 1 Use Of Commas

Commas help us in reading and writing large numbers. To make reading of large numbers easy, we group various places into periods. This can be done in two different ways:

Indian System of Numeration

In the Indian system of numeration, we use commas after 3 digits starting from the right and there after every 2 digits. The commas after 3, 5 and 7 digits separate thousand, lakh and crore respectively.

Example 9. Read the numbers and write them using placement boxes.

(1) 475320 (2) 8675964312

Solution. (1) Given number is 475320.

According to the Indian system of numeration,

We read it as, four lakh seventy five thousand three hundred twenty.

Using the commas it is written as 4,75,320.

(2) Given number is 8675964312.

According to the Indian system of numeration,

We read it as eight arab sixty seven crore fifty nine lakh sixty four thousand three hundred twelve. Using commas it written as 8, 67, 59, 64, 312.

Note it While writing number names, we do not use commas.

Class 6 Maths Chapter 1 Exercise Solutions

International System of Numeration

In the international system of numeration, commas are placed after every 3 digits starting from the right. The commas after 3 and 6 digits separate thousand and million respectively.

Example 10. Read the numbers and write them using placement boxes.

(1) 9578432

(2) 3572893921

Solution. (1) According to the International system of numeration,

We read it as nine million five hundred seventy eight thousand four hundred thirty two and write as 9, 578, 432.

(2) According to the International system of numeration,

We read it as three billion five hundred seventy two million eight hundred ninety three thousands nine hundred twenty one and write as 3,572, 893, 921.

Mpbse Class 6 Maths Chapter 1

Example 13. Place commas correctly and write numerals.

(1) Fifty three lakh seventy five thousand three hundred seven.

(2) Eight crore five lakh forty one.

(3) Six crore fifty two lakh twenty one thousand three hundred two.

Solution.

MP Board solutions for Class 6 Maths Chapter 1 Place Value and Face Value

Place Value

The place value is the position of each digit in a number which is determined as ones, tens, hundreds, thousands and so on.

e.g. The place value of 1 in 1854 is 1000.

Face Value

The face value is the actual value of the digit in a number. e.g. Face value of 1 in 1854 is 1 only.

The expanded form of the number 1854 is 1 x 1000 + 8 x 100 + 5 x 10 + 4 x 1.

Example 14. Find the place and face values of

(1) 7 in number 97621 (2) 2 in number 25687

Solution. (1) Place value of 7 in 97621 is 7000 and face value of 7 is 7.

(2) Place value of 2 in 25687 is 20000 and face value of 2 is 2.

Example 15. Write the expanded form of the following numbers.

(1) 20000 (2) 38400 (3) 65740 (4) 89324

Solution. (1) 20000 = 2 × 10000

(2) 38400 = 3 x 10000 + 8 x 1000 + 4 x 100

(3) 65740 = 6 x 10000 + 5 x 1000 + 7 x 100 + 4 × 10

(4) 89324 = 8 × 10000 + 9 x 1000 + 3 × 100 + 2 × 10 + 4 × 1

Class 6 Maths Chapter 1 Mp Board Solutions

Example 16. Write the place value of each digit in the numeral

(1) 369868

(2) 97263480

Solution. (1) Place value of 8 = 8 x 1 = 8

Place value of 6 = 6 x 10 = 60

Place value of 8 = 8 x 100 = 800

Place value of 9 = 9 x 1000 = 9000

Place value of 6 = 6 x 10000 = 60000

Place value of 3 = 3 x 100000 = 300000

(2) Place value of 0 = 0 x 1 = 0

Place value of 8 = 8 x 10 = 80

Place value of 4 = 4 x 100 = 400

Place value of 3 = 3 x 1000 = 3000

Place value of 6 = 6 x 10000 = 60000

Place value of 2 = 2 x 100000 = 200000

Place value of 7 = 7 x 1000000 = 7000000

Place value of 9 = 9 x 10000000 = 90000000

Example 17. Find the sum of place and face values for the following.

(1) 2 in 12456 (2) 5 in 54321

Solution. (1) Place value of 2 = 2000

Face value of 2 = 2

∴ Sum = 2000 + 2 = 2002

(2) Place value of 5 = 50000

Face value of 5 = 5

∴ Sum = 50000 + 5 = 50005

Example 18. Find the differences of place values for the following conditions.

(1) two 7s in 7652713 (2) two 4s in 43810422

Solution. (1) The place value of 7 in ten lakhs place = 70000000

The place value of 7 in hundreds place = 700

Hence, the required difference = 7000000-700 =6999300

(2) The place value of 4 at the crores place = 40000000

The place value of 4 at the hundreds place = 400

Hence, the required difference = 40000000 – 400 = 39999600

Number Comparison Examples Class 6

Example 19. Answer the following questions.

(1) How many 5 – digit numbers are there in all?

(2) How many 7 – digit numbers are there in all?

(3) Write the smallest 8 – digit number having five different digits.

Solution. (1) The largest 5 – digit number = 99999

The smallest 5-digit number = 10000

Number of all 5-digit numbers = (99999 – 10000) +1

= (89999 + 1) = 90000

Hence, there are in all ninety thousand of 5-digit numbers.

(2) The largest 7-digit number = 9999999

The smallest 7 – digit number = 1000000

Number of all 7 – digit numbers

= (9999999 -1 000000) + 1

= (8999999 + 1) = 9000000 = Ninety lakh

Hence, there are in all ninety lakh of 7-digit numbers.

(3) Five smallest digits are 0, 1, 2, 3, 4.

Hence, the required number is 10000234.

MP Board solutions for Class 6 Maths Chapter 1 Large Numbers in Practice

Large numbers are needed is many places in daily life.

e.g. Number of people in a city, money paid or recieved in large transactions etc.

Generally, larger numbers are used to measure length, mass and capacity etc.

The standard unit for measuring length, mass and capacity are metre, grams and litres respectively. The relation between the various units is given by

The units kilo is the greatest and milli is the smallest.

(1) 1 kilometre = 1000 metres

1 metre = 10 decimetre = 100 centimetres

(2) 1 kilogram = 1000 grams

1 gram = 10 decigrams = 100 centigrams = 1000 milligrams

(3) 1 litre 10 decilitres = 100 centilitres = 1000 millilitres

Example 1. A tourist car travelled from different places with a speed 40 km/h. The journey is shown below. 1020 km

(1) Find the total distance covered from P to R.

(2) Find the total distance covered from R to T.

(3) Find the total distance covered by the car if it starts from P and returns back to P.

(4) Find the difference of distances from Q to R and R to S.

(5) Find out the time taken by the car to reach.

(a) P to Q

(b) R to S

(c) Total journey

Solution. From the given figure,

(1) Total distance covered by car from P to R

= PQ + QR = 2170 + 3220 = 5390 km

(2) Total distance covered by car from R to T

= RS + ST = 5160 + 4320 = 9480 km

(3) Total distance covered by car

= Distance from P to R + Distance from R to T + Distance from T to P

= 5390 + 9480 + 1020 = 15890 km

(4) Distance from Q to R = 3220 km

Distance from R to S = 5160 km

∴ Difference of distances from Q to R and R to S = 5160 – 3220 = 1940 km

(5) We know that Time \(=\frac{\text { Distance }}{\text { Speed }}\)

(a) Time taken by the car to reach P to Q Distance from P to Q

= \(\frac{2170}{40}=\frac{217}{4}=54 \frac{1}{4} \mathrm{~h}\)

(b) Time taken by the car to reach R to S

= \(\frac{5160}{40}=129 \mathrm{~h}\)

(c) Total journey \(=\frac{\text { Total distance covered }}{\text { Speed }}\)

= \(\frac{15890}{40}=\frac{1589}{4}=397 \frac{1}{4} \mathrm{~h}\)

Class 6 Maths Chapter 1 Mp Board Solutions

Example 2. The distance between the office and flat of a employee’s house is 2 km 575 m. Everyday she walks both ways. Find the total distance covered by her in 10 days.

Solution. Distance between the office and the flat = 2 km 575 m

= 2 × 1000 + 575 = 2000 + 575

= 2575 m [∴ 1 km = 1000 m]

∴ Distance covered by the employee in one day

= 2 × 2575 = 5150 m

[∴ she walks both ways in one day]

∴ Distance covered in 10 days = 10 x 5150 = 51500 m

= (51 × 1000 + 500) m

= 51 km 500 m

Example 3. If a box contains 400000 medicine tablets each and weight of one tablet is 20 mg. What is the total weight of all tablets in the box in grams and in kilograms both?

Solution. Weight of one tablet = 20 mg

Total weight of 400000 tablets in the box = 400000 x 20 mg =8000000 mg

Now, weight in grams = \(\frac{8000000}{1000} \mathrm{~g}=8000 \mathrm{~g}\)

[∴ \(1 \mathrm{mg}=\frac{1}{1000} \mathrm{~g}\)]

Now, weight in kilograms = \(\frac{8000}{1000} \mathrm{~kg}=8 \mathrm{~kg}\)

[∴ \(1 \mathrm{~g}=\frac{1}{1000} \mathrm{~kg}\)]

Example 4.

(1) Can you find the total weight of mangoes and grapes Sachin sold last year?

(2) Can you find the total money Sachin got by selling mangoes?

(3) Can you find the total money Sachin got by selling mangoes and grapes together?

(4) Make a table showing how much money Sachin received from selling each item? Arrange the entries of amount of money received in descending order. Find the item which brought him the highest amount.

Solution. (1) Total weight of mangoes and grapes Sachin sold

= 2477 + 4004 = 6481kg

(2) Total money Sachin got by selling mangoes

= Total weight of mangoes in kg x Cost per kg = 2477 x 60 = 148620

(3) Total money Sachin got by selling grapes = 4004 × 50 = 200200

(4) Following table shows the money received from selling items.

The entries of amount of money received in descending order are as follows

₹ 324400 > 200200 > 172932 > 148620

The item, which brought him the highest amount is Soaps i.e. ₹ 324400.

Class 6 Maths Chapter 1 Mp Board Solutions

Example 5. A box contains 50 packets of biscuits. Each weights 120 g. How many such boxes be loaded into a van which cannot carry beyond 900 kg?

Solution. Given, total number of packets = 50

Weight of each packets = 120 g

Weight of a box = 50 x 120 g = 6000 g = 6 kg

∴ Required number of boxes = \(\frac{900}{6}=150\)

Hence, only 150 boxes can be loaded in the van.

Example 6. A milk dairy produced 75678 L of milk in a day. It supplied 67689 L of milk to milk depot. Find the milk left in the dairy.

Solution. Production of milk in one day = 75678 L

Supply to milk depot in one day = 67689 L

So, the milk left in the dairy=75678-67689=7989 L

Example 7. A vessel has 2 L and 500 mL of juice. In how many glasses, each of 20 mL capacity, can it be filled?

Solution. Capacity of vessel = 2 L 500 mL = 2 x 1000 + 500 = 2000 + 500 = 2500 mL

[∴ 1 L=1000 mL]

and capacity of one glass = 20 mL

∴ Number of glasses of juice filled out of vessel

Hence, juice can be filled in 125 glasses.

Mp Board Class 6 Maths Book Pdf

Example 8. Population of Bhavnagar was 356213 in the year 1990. In the year 2000, it was found to be increased by 62578. What was the population of the city in 2000?

Solution. Population of the city in year 2000

= Population of the city in year 1990 + Increase in population

= 356213 + 62578 = 418791

Example 9. In a country, the number of electronic cars sold in the year 2020-2021 was 200880. In the year 2021-2022, the number of electronic cars sold was 400100. In which year more cars were sold and how many more?

Solution. Clearly, 400100 is more than 200880. So, more cars were sold in the year 2021-2022 than in 2020-2021.

Now, 400100 – 200880 = 199220

Check the answer by adding

200880 + 199220 = 400100 (the answer is right)

Example 10. Every Friday a small brochure of general knowledge is published with a newspaper. One copy has 10 pages. Every week 12444 copies are printed. How many total pages are printed every Friday?

Solution. Every copy has 10 pages.

∴ 12444 copies will have 12444 x 10 pages.

Now, 12444 × 10 = 124440

Thus, every Friday 124440 pages are printed.

Example 11. If a number 6253 multiplied by 55 instead of multiplying by 46. By how much was the answer greater than the correct answer?

Solution. After multiplying 6253 by 55, we get

= 6253 × 55

= 343915

After multiplying 6253 by 46, we get

= 6253 × 46 = 287638

Difference 343915 – 287638 = 56277

Wrong answer is 56277 greater than the actual answer.

Example 12. The cost of a autograph signed bat is 30222. What is the cost of 25 such bats?

Solution. Cost of 1 autograph signed bat=30222

∴ Cost of 25 autograph signed bat = 30222 x 25 = ₹ 755550

Example 13. Find the difference between the greatest and the least numbers that can be written using the digits 8, 2, 5, 4, 1 each only one.

Solution. Using the digits 8, 2, 5, 4, 1, we get

Greatest number = 85421 and least number = 12458

∴ Difference = 85421 – 12458

= 72963

MP Board solutions for Class 6 Maths Chapter 1

Question 1. Can you instantly find the greatest and the smallest numbers in each row?

(1) 382, 4972, 18, 59785, 750

(2) 1473, 89423, 100, 5000, 310

(3) 1834, 75284, 111, 2333, 450

(4) 2853, 7691, 9999, 12002, 124 Was that easy? Why was it easy?

Solution.

(1) Number of digits in 382 = 3

Number of digits in 4972 = 4

Number of digits in 18 = 2

Number of digits in 59785 = 5

Number of digits in 750 = 3

∴ Greatest number = 59785 [maximum number of digits]

and smallest number = 18 [minimum number of digits]

(2) Number of digits in 1473 = 4

Number of digits in 89423 = 5

Number of digits in 100 = 3

Number of digits in 5000 = 4

Number of digits in 310 = 3

Answer. Greatest number = 89423

Smallest number=100

(3) Number of digits in 1834 = 4

Number of digits in 75284 = 5

Number of digits in 111 = 3

Number of digits in 2333 = 4

Number of digits in 450 = 3

Answer. Greatest number = 75284

Smallest number = 111

(4) Number of digits in 2853 = 4

Number of digits in 7691 = 4

Number of digits in 9999 = 4

Number of digits in 12002 = 5

Number of digits in 124 = 3

Answer. Greatest number = 12002

Smallest number = 124

Mp Board Class 6 Maths Book Pdf

Question 2. Find the greatest and the smallest numbers.

(1) 4536, 4892, 4370, 4452

(2) 15623, 15073, 15189, 15800

(3) 25286, 25245, 25270, 25210

(4) 6895, 23787,24569, 24659

Solution. (1) We have, 4536, 4892, 4370, 4452

Here, each of the given numbers is containing 4-digits and their digits at thousand places are also same. So, we compare the hundreds place digit.

8 > 5 > 4 > 3

∴ The greatest number is 4892 and the smallest number is 4370.

(2) We have, 15623, 15073, 15189, 15800

Here, the two leftmost digits 15 i.e. digits at thousand and ten thousands place are same in each numbers.

So, we compare the hundreds place digit.

∴ The greatest number is 15800 and the smallest number is 15073.

(3) We have, 25286, 25245, 25270, 25210

Here, the three leftmost digits 252 are same in each number.

So, we compare the tens place digit.

∴ The greatest number is 25286 and the smallest number is 25210.

(4) We have, 6895, 23787, 24569, 24659

Here, 6895 is a 4-digit number and other numbers are 5 digits, so it is clear that 6895 is the smallest number.

Now, in remaining three numbers, the digit at ten thousands place is same in each number.

So, we compare the thousands place digit.

∴ 4 > 3

Again, in two numbers, digit at thousands place is same.

So, we compare the hundreds place digit.

∴ 6 > 5

∴ The greatest number is 24659 and smallest number is 6895.

Question 3. Use the given digits without repetition and make the greatest and smallest 4-digit numbers.

(1) 2, 8, 7, 4

(2) 9, 7, 4, 1

(3) 4, 7, 5,0

(4) 1, 7, 6.2

(5) 5, 4, 0, 3

Solution. (1) Here, descending order of the given digits is 8, 7, 4, 2.

∴ Greatest number = 8742

and ascending order of the given digits is 2, 4, 7, 8.

∴ Smallest number=2478

(2) Here, descending order of the given digits is 9, 7, 4, 1.

∴ Greatest number=9741

and ascending order of the given digits is 1, 4, 7, 9.

∴ Smallest number = 1479

(3) Here, descending order of the given digits is 7, 5, 4, 0.

∴ Greatest number = 7540

and ascending order of the given digits is 0, 4, 5, 7.

But 0457 is a 3 digit number, so we have to interchange the place of 4 and 0 i.e. 4057.

∴ Smallest number = 4057

(4) Here, descending order of the given digits is 7, 6, 2, 1.

∴ Greatest number = 7621

and ascending order of the given digits is 1, 2, 6, 7.

∴ Smallest number = 1267

(5) Here, descending order of the given digits is 5, 4, 3,0.

∴ Greatest number = 5430

and ascending order of the given digits is 0, 3, 4, 5.

But 0345 is a 3-digit number. So, we have to interchange the place of 3 and 0 i.e 3045.

∴ Smallest number = 3045

MPBSE Class 6 Maths Chapter 1

Question 4. Make the greatest and the smallest 4-digit numbers by using any one digit twice.

(1) 3, 8, 7

(2) 9, 0,5

(3) 0, 4, 9

(4) 8, 5, 1

Solution. (1) Given digits are 3, 8 and 7.

Here, descending order of the given digits is 8, 8, 7, 3. [greatest digit 8 is taken twice]

∴ Greatest 4-digit number = 8873 and ascending order of the given digits is 3, 3,7,8. [smallest digit 3 is taken twice]

∴ Smallest 4-digit number = 3378

(2) Given digits are 9,0 and 5.

Here, descending order of the given digits is 9, 9, 5, 0.

[greatest digit 9 is taken twice]

∴ Greatest 4-digit number = 9950

and ascending order of the given digits is 0, 0, 5, 9. [smallest digit 0 is taken twice]

But 0059 is a 2-digit number because 0 at first two leftmost places is meaningless.

So, keeping 5 (instead of 0) at the leftmost place and taking the smallest digit 0 twice i.e. 5009.

∴ Smallest 4-digit number = 5009

(3) Given digits are 0, 4 and 9.

Here, descending order of the given digits is 9, 9, 4, 0. [ greatest digit 9 is taken twice]

∴ Greatest 4-digit number = 9940 and ascending order of the given digit is 0, 0, 4, 9. [:smallest digit 0 is taken twice]

But 0049 is a 2-digit number because 0 at first two leftmost places is meaningless.

So, keeping 4 (instead of 0) at the leftmost place and taking the smallest digit 0 twice, we get 4009.

∴ Smallest 4-digit number = 4009

(4) Given digits are 8, 5 and 1.

Here, descending order of the given digits is 8, 8, 5, 1. [ greatest digit 8 is taken twice]

∴ Greatest 4-digit number = 8851

and ascending order of the given digits is 1, 1, 5, 8.

[∴ smallest digit 1 is taken twice]

∴ Smallest 4-digit number=1158

Question 5. Take two digits, say 2 and 3. Make 4-digit numbers using both the digits equal number of times.

(1) Which is the greatest number?

(2) Which is the smallest number?

(3) How many different numbers can you make in all?

Solution. Two given digits are 2 and 3. We want to make 4-digit numbers using both the digit equal number of times.

The possible 4-digit numbers are 2233, 3322, 2332, 3223, 2323 and 3232.

(1) The greatest number is 3322.

(2) The smallest number is 2233.

(3) We can make 6 different numbers in all.

Mp Board Class 6 Maths Important Questions

Question 6. Who is the tallest? Who is the shortest?

(1) Can you arrange them in the increasing order of their heights?

(2) Can you arrange them in the decreasing order of their heights?

Solution. From the given figure, it is clear that

160 > 159 > 158 > 154

Ramhari is the tallest because he has the height of 160 cm.

From the given figure, it is clear that

154 < 158 < 159 < 160

∴ Dolly is the shortest because she has the height of 154 cm.

(1) Yes, we can arrange their heights in increasing order as follows: Dolly (154 cm) < Mohan (158 cm) < Shashi (159 cm) < Ramhari (160 cm).

(2) Yes, we can arrange their heights in decreasing order as follows: Ramhari (160 cm) > Shashi (159 cm) > Mohan (158 cm) > Dolly (154 cm).

Question 7. Sohan and Rita went to buy an almirah. There were many almirahs available with their price tags.

(1) Can you arrange their prices in increasing order?

(2) Can you arrange their prices in decreasing order?

Solution. (1) Yes, prices can be arranged in increasing order as follows:

₹ 1788 < ₹ 1897 < ₹ 2635 < ₹ 2854 < ₹ 3975

(2) Yes, prices can be arranged in decreasing order as follows:

₹ 3975 > ₹ 2854 > ₹ 2635 > ₹ 1897 > ₹ 1788

Question 8. Think of five situations, where compare three or more quantities.

Solution. Five situations may be

(1) Prices of 4 different kinds of branded shoes are 4225,3835,2620 and 2230, respectively.

(2) The weight of 4 students of Class VI are 33 kg, 38 kg, 35 kg and 37 kg, respectively.

(3) Marks obtained by 4 students in Mathematics out of 100 are 87, 88, 90 and 78, respectively.

(4) The tuition fee paid by 4 students of different classes are 170, 190, 150 and 200, respectively.

(5) The runs scored by 4 players A, B, C and D in an innings are 75, 60, 25 and 82, respectively.

Question 9. (1) Arrange the following numbers in ascending order.

(a) 847, 9754, 8320, 571

(b) 9801, 25751, 36501, 38802

(2) Arrange the following numbers in descending order.

(a) 5000, 7500, 85400, 7861

(b) 1971, 45321, 88715, 92547

Solution. (i) (a) We have, 847, 9754, 8320, 571

Ascending order of given numbers is as follows 571< 847 < 8320 < 9754

Ascending order of given numbers is as follows 9801< 25751 < 36501 < 38802

(b) We have, 9801, 25751, 36501, 38802

(2) (a) We have, 5000, 7500, 85400, 7861

Descending order of given numbers is as follows

85400 > 7861 > 7500 > 5000

(b) We have, 1971, 45321, 88715, 92547

Descending order of given numbers is as follows

92547 > 88715 > 45321 > 1971

Mp Board Class 6 Maths Important Questions

Question 10. Read and expand the numbers wherever there are blanks.

Solution. The remaining blanks are shown as below with appropriate number, name and expansion.

Question 11. Read and expand the numbers wherever there are blanks.

Solution. The remaining blanks are shown as below with appropriate number, name and expansion:

Question 12. (1) What is 10-1=?

(2) What is 100-1=?

(3) What is 10000 -1=?

(4) What is 100000-1 = ?

(5) What is 10000000-1 = ?

Solution.

(1) 10 – 1 = 9

(2) 100 – 1 = 99

(3) 10000 – 1 = 9999

(4) 100000 – 1 = 99999

(5) 10000000 – 1 = 9999999

MP Board Class 6 Maths Solutions

Question 13. Give five examples, where the number of things counted would be more than 6-digit number.

Solution. The least 6-digit number is 100000 (one lakh).

Now, five examples, where the number of things counted would be more than 6-digit number are as follows.

(1) The number of people in a big city.

(2) The number of stars in a clear dark night.

(3) The number of motorcycles in a big town.

(4) The number of grains in a sack full of wheat.

(5) The number of pages of notebooks of all students in a big town.

Question 14. Starting from the greatest 6-digit number, write the previous five numbers in descending order.

Solution. The greatest 6-digit number = 999999

1st previous number = 999999 – 1 = 999998

2nd previous number = 999999 – 2 = 999997

3rd previous number = 999999 – 3 = 999996

4th previous number = 999999 – 4 = 999995

5th previous number = 999999 – 5 = 999994

Now, descending order of these numbers is as follows

999998 > 999997 > 999996 > 999995 > 999994

Question 15. Starting from the smallest 8-digit number, write the next five numbers in ascending order and read them.

Solution. The smallest 8-digit number = 10000000

∴ 1st next number = 10000000 + 1 = 10000001

2nd next number = 10000000 + 2 = 10000002

3rd next number = 10000000 + 3 = 10000003

4th next number = 10000000 + 4 = 10000004

5th next number = 10000000 + 5 = 10000005

Now, ascending order of these numbers is as follows

10000001 < 10000002 < 10000003 < 10000004 < 10000005

Class 6 Maths Chapter 1 Exercise Solutions

Question 16. Read these numbers. Write them using placement boxes and then write their expanded forms.

(1) 475320

(2) 9847215

(3) 97645310

(4) 30458094

(a) Which is the smallest number?

(b) Which is the greatest number?

(c) Arrange these numbers in ascending and descending orders.

Solution. After reading these numbers, we have

(1) 475320 Four lakhs seventy five thousands three hundred twenty.

(2) 9847215 Ninety eight lakhs forty seven thousands two hundreds fifteen.

(3) 97645310 Nine crores seventy six lakhs forty five thousands three hundreds ten.

(4) 30458094 Three crores four lakhs fifty eight thousands ninety four.

The placement boxes is shown as below

Expanded forms of given numbers are as follow

(1) 475320 = 4 × 100000 + 7 x 10000 + 5 x 1000 + 3 × 100 + 2 x 10 + 0 x 1

(2) 9847215 = 9 × 1000000 + 8 x 100000 + 4 × 10000 + 7 x 1000 + 2 × 100 + 1 x 10 + 5 x 1

(3) 97645310 = 9 x 10000000 + 7 x 1000000 + 6 x 100000 + 4 x 10000 + 5 x 1000 + 3 x 100 + 1 x 10 + 0 x 1

(4) 30458094 = 3 x 10000000 + 4 x 100000 + 5 x 10000 + 8 x 1000 + 0 x 100 + 9 x 10 + 4 × 1

(a) The smallest number = 475320

(b) The greatest number = 97645310

(c) Ascending order of given numbers are as follow

475320 < 9847215 < 30458094 < 97645310

Descending order of given numbers are as follow

97645310 > 30458094 > 9847215 > 475320

MP Board Class 6 Maths Solutions

Question 17.Read these numbers

(1) 527864

(2) 95432

(3) 18950049

(4) 70002509

(a) Write these numbers using placement boxes and then using commas in Indian system of numeration as well as International system of numeration.

(b) Arrange these in ascending and descending orders.

Solution. After reading these number, we have

(1) 527864 Five lakh twenty seven thousand eight hundred sixty four.

(2) 95432 Ninety five thousand four hundred thirty two.

(3) 18950049 One crore eighty nine lakh fifty thousands forty nine.

(4) 70002509 Seven crore two thousand five hundred nine.

(a) Using placement boxes, given number can be

Using the commas, given numbers can be written in Indian system of numeration as

(1) 5,27,864

(2) 95,432

(3) 1,89,50,049

(4) 7,00,02,509

and in International system of numeration, they can be written as,

(1) 527,864

(2) 95,432

(3) 18,950,049

(4) 70,002,509

(b) Ascending order of these numbers are as follow

95432 < 527864 < 18950049 < 70002509

Descending order of these numbers are as follow

70002509 > 18950049 > 527864 > 95432

Question 18. You have the digits 4, 5, 6, 0, 7 and 8. Using them, make five numbers each with 6-digits.

(1) Put commas for easy reading.

(2) Arrange them in ascending and descending orders.

Solution. Given digits are 4, 5, 6, 0, 7 and 8.

We can make many numbers by using these digits, five of them are as follows

876540, 867540, 876450, 876045 and 867405

(1) After putting commas, numbers are as follows

(a) 8,76,540

(b) 8,67,540

(c) 8,76,450

(d) 8,76,045

(e) 8,67,405

(2) Ascending order of numbers is as follows

867405 < 867540 < 876045 < 876450 < 876540

Descending order of numbers is as follows:

876540 > 876450 > 876045 > 867540 > 867405

Question 19. Take the digits 4, 5, 6, 7, 8 and 9. Make any 3 numbers each with 8-digits. Put commas for easy reading.

Solution. Given digits are 4, 5, 6, 7, 8 and 9.

We can make many numbers by using these digits, three of them are as follows

98877456, 98877465 and 98877654

Using commas, numbers can be rewritten as

(1) 9,88,77,456

(2) 9,88,77,465

(3) 9,88,77,654

Class 6 Maths Chapter 1 Exercise Solutions

Question 20. From the digits 3, 0 and 4, make five numbers each with 6-digits. Use commas.

Solution. Given digits are 3,0 and 4.

We can make many numbers by using these digits, five of them are as follows

(1) 330443

(2) 343404

(3) 344430

(4) 434043

(5) 344034

Using commas, these numbers can be rewritten as

(1) 3,30,443

(2) 3,43,404

(3) 3,44,430

(4) 4,34,043

(5) 3,44,034

Exercise 1.1

Question 1. Fill in the blanks.

(1) 1 lakh = _________ ten thousands

(2) 1 million = _______ hundred thousands

(3) 1 crore = ________ ten lakhs

(4) 1 crore = _______ millions

(5) 1 million = _______ lakhs

Solution. (1) We know that

1 lakh = 100000 (in digits) = 10 x 10000

= ten x ten thousand (in number name)

1 lakh = ten ten thousand

(2) We know that

1 million = 1000000 (in digits) = 10 x 100000

= ten x hundred thousands (in number name)

∴ 1 million = ten hundred thousands

(3) We know that

1 crore = 10000000 (in digits)

= 10 × 1000000

= ten x ten lakhs (in number name)

∴ 1 crore ten ten lakhs

(4) We know that

1 crore = 10000000 (in digits) = 10 x 1000000

= ten x one million (in number name)

∴ 1 crore = ten millions

(5) We know that

1 million = 1000000 (in digits)

= 10 x 100000 ten x one lakhs

∴ 1 million ten lakhs

Class 6 Maths Chapter 1 Solutions

Question 2. Place commas correctly and write the numerals

(1) Seventy three lakhs seventy five thousands three hundreds seven

(2) Nine crores five lakhs forty one

(3) Seven crores fifty two lakhs twenty one thousands three hundreds two

(4) Fifty eight millions four hundreds twenty three thousands two hundreds two

(5) Twenty three lakhs thirty thousands ten

Solution. Numbers after commas are as follows

(1) 73,75,307

(2) 9,05,00,041

(3) 7,52,21,302

(4) 58,423,202

(5) 23,30,010

Question 3. Insert commas suitably and write the names according to Indian system of numeration.

(1) 87595762

(2) 8546283

(3) 99900046

(4) 98432701

Solution. We can draw a table to show these operations.

Question 4. Insert commas suitably and write the name according to International system of numeration.

(1) 78921092

(2) 7452283

(3) 99985102

(4) 48049831

Solution. We can draw a table to show these operations

Class 6 Maths Chapter 1 Exercise Solutions

Question 5. How many centimetres make a kilometre?

Solution. We know that 1 km = 1000 m = 1000 x 100 cm [1 m = 100 cm]

= 100000 cm

Question 6. How many milligrams make one kilogram?

Solution. We know that 1 kg = 1000 g (1000 x 1000) mg

[1g = 1000 mg]

= 1000000 mg

∴ 1000000 milligrams make one kilogram.

Question 7. A box contains 200000 medicine tablets each weighing 20 mg. What is the total weight of all the tablets in the box in grams and in kilograms?

Solution. Given, weight of one tablet = 20 mg

Total weight of 200000 tablets in the box

= 200000 x 20 mg = 4000000 mg

Now, weight in grams = \(\frac{4000000}{1000} \mathrm{~g}=4000 \mathrm{~g}\)

Now, weight in kilograms = \(\frac{4000}{1000} \mathrm{~kg}=4 \mathrm{~kg}\)

Question 8.

(1) Can you find the total weight of apples and oranges Raman sold last year?

Weight of apples = ______ kg

Weight of oranges = _______ kg

Therefore, total weight = ______ kg + ______ kg = _______ kg

(2) Can you find the total money Raman got by selling apples?

(3) Can you find the total money Raman got by selling apples and oranges together?

(4) Make a table showing how much money Raman received from selling each item? Arrange the entries of amount of money received in descending order. Find the item which brought him the highest amount. How much is this amount?

Solution. (1) Weight of apples sold during the last year = 2457 kg

Weight of oranges sold during the last year = 3004 kg

∴ Total weight of apples and oranges Raman sold, during the last year = 2457+ 3004 = 5461 kg

(2) Total money Raman got by selling apples

= Total weight of apples in kg x Cost per kg

= 2457 x 40 = ₹ 98280

(3) Total money Raman got by selling oranges

= Total weight of oranges in kg x Cost per kg

= 3004 x 30 = ₹ 90120

∴ Total money Raman got by selling apples and oranges together = 98280 + 90120 = ₹ 188400

(4) Following table shows the money received from selling items.

The entries of amount of money received in descending order are as follows:

₹ 253670 > ₹ 240012 > ₹ 160040 > ₹ 98280 > ₹ 90120 > ₹ 68280 > ₹ 38350

The item which brought him the highest amount is toothbrushes. This amount is ₹ 253670.

Exercise 1.2

Question 1. A book exhibition was held for four days in a school. The number of tickets sold at the counter on the first, second, third and final days was respectively 1094, 1812, 2050 and 2751. Find the total number of tickets sold on all the four days.

Solution. Given, number of tickets sold on the first day = 1094

Number of tickets sold on the second day = 1812

Number of tickets sold on the third day = 2050

Number of tickets sold on the fourth day = 2751

∴ Total number of tickets sold on all the four days

= 1094 + 1812 + 2050 + 2751 = 7707

Hence, there are 7707 tickets sold on all the four days.

Class 6 Maths Chapter 1 Solutions

Question 2. Shekhar is a famous cricket player. He has so far scored 6980 runs in test matches. He wishes to complete 10000 runs. How many more runs does he need?

Solution. Given, number of runs scored by Shekhar = 6980

Target of runs to be scored = 10000

∴ Number of runs needed more

= Target of runs – Run scored yet

= 10000 – 6980

= 3020

Question 3. In an election, the successful candidate registered 577500 votes and his nearest rival secured 348700 votes. By what margin did the successful candidate win the election?

Solution. Given, votes registered by the successful candidate = 577500

Votes registered by the nearest rival = 348700

∴ Margin, by which the successful candidate won = Votes of successful candidate – Votes of nearest rival

= 577500 – 348700 = 228800

Question 4. Kirti bookstore sold books worth ₹ 285891 In the first week of June and book worth 400768 in the second week of the month. How much was the sale for the two weeks together? In which week was the sale greater and by how much?

Solution. Given, sale of books in Ist week = ₹ 285891

Sale of books in IInd week = ₹ 400768

Total sales of two weeks = Sale of Ist week + Sale of IInd week

= 285891 + 400768 = ₹ 686659

Since, 400768 > 285891

Thus, sale in the second week is greater.

∴ Difference in the sales amount = 400768 – 285891 = ₹ 114877

Hence, sale in the second week was greater by 114877.

Question 5. Find the difference between the greatest and the least numbers that can be written using the digits 6, 2, 7, 4, 3 each only once.

Solution. Using the digits 6, 2, 7, 4 and 3, we get

Greatest number = 76432 and least number = 23467

∴ Difference = Greatest number – Least number

= 76432 – 23467 = 52965

Note it We can form a greatest number with individual digits by arranging them in descending order from right and similarly, we can form a least number by arranging them in ascending order from right.

Class 6 Maths Chapter 1 Solutions

Question 6. A machine, on an average, manufactures 2825 screws a day. How many screws did it produce in the month of January 2006?

Solution. Number of screws manufactured by the machine in one day = 2825

We know that number of days in the month of January = 31

∴ Number of screws produced by the machine in the month of January, 2006 = 2825 x 31 = 87575

Hence, the number of screws produced by the machine in the month of january, 2006 are 87575.

Question 7. A merchant had 778592 with her. She placed an order for purchasing 40 radio sets at 1200 each. How much money will remain with her after the purchase?

Solution. Given, cost of one radio set = ₹ 1200

Number of radio sets to be purchased = 40

∴ Cost of 40 radio sets = Cost of one radio set x Number of radio sets

= 40 x 1200 = ₹ 748000

∵ Total money with the merchant = ₹ 78592

∴ Money left with the merchant after purchase of 40 radio sets Total money – Cost of 40 radio sets

= 78592 – 48000

= ₹ 30592

Hence, 30592 will remain with her after the purchase.

Question 8. A student multiplied 7236 by 65 instead of multiplying by 56. By how much was his answer greater than the correct answer?

Solution. If a student multiplies 7236 by 65, he will get

= 7236 x 65 = 470340

According to the question,

Student multiplies 7236 by 56 and he will get = 7236 × 56 = 405216

Now, required difference = Actual answer – Wrong answer = 470340 – 405216 = 65124

Class 6 Maths Chapter 1 Exercise Solutions

Question 9. To stitch a shirt 2 m 15 cm cloth is needed. Out of 40 m cloth, how many shirts can be stitched and how much cloth will remain?

Solution. Total length of cloth = 40 m = 40 x 100 cm [∵ 1 m = 100 cm]

= 4000 cm

Cloth needed for one shirt = 2 m 15 cm

= (2 × 100) cm + 15 cm

= (200 + 15) cm = 215 cm

∴ Number of shirts stitched out of total cloth

= \(\frac{4000}{215}=18 \frac{130}{215}\)

Hence, 18 shirts can be stitched and cloth left over is 130 cm i.e. 1 m 30 cm.

Question 10. Medicine is packed in boxes, each weighing 4 kg 500 g. How many such boxes can be loaded In a van which cannot carry beyond 800 kg?

Solution.  Given, van can carry a weight of 800 kg = 800 x 1000 g = 800000 g

[∵1 kg = 1000 g]

According to the question,

Weight of one packet = 4 kg 500 g

= 4 × 1000 + 500

= 4000 + 500 = 4500 g

∴ Number of packets that can be loaded in the van

= \(\frac{800000}{4500}=\frac{8000}{45}=177 \frac{35}{45}\)

Hence, only 177 boxes can be loaded in the van.

Question 11. The distance between the school and the house of a student’s house is 1 km 875 m. Everyday she walks both ways. Find the total distance covered by her in six days.

Solution. Given, distance between the school and the house

= 1 km 875 m = 1 x 1000 + 875

= 1000 + 875 = 1875 m

[∵ 1 km = 1000 m]

∴ Distance covered by the student in one day

= 2 x 1875 = 3750 m

[∵ she walks both ways in one day]

∴ Distance covered in 6 days = 6 x 3750 = 22500 m

= (22 × 1000 + 500) m

= 22 km 500 m

[∵ 1 km = 1000 m]

Question 12. A vessel has 4 L and 500 mL of curd. In how many glasses, each of 25 mL capacity, can it be filled?

Solution. Given, capacity of vessel = 4 L 500 mL

= 4 x 1000 + 500 = 4000 + 500 = 4500 mL

[∵ 1 L= 1000 mL]

and capacity of one glass = 25 mL

∴ Number of glasses of curd filled out of vessel Capacity of a vessel

= \(\frac{\text { Capacity of a vessel }}{\text { Capacity of a glass }}=\frac{4500}{25}=180\)

Hence, curd can be filled in 180 glasses.

Review Exercise

Multiple Choice Questions

Question 1. The greatest natural number is

1. 1 crore
2. 10 crores
3. 10 lakhs
4. Not defined

Answer. 4. Not defined

Question 2. The arrangement of 24, 68, 487; 7, 89, 540; 1, 34, 53, 879; 78, 989; 4807 in ascending order is

1. 78, 989 < 4807 < 24, 68, 487 < 7, 89, 540 < 1, 34, 53, 879
2. 7, 89, 540 < 1, 34, 53, 879 < 24, 68, 487 < 78, 989 <4807
3. 4807 <78, 989 <7, 89, 540 < 24, 68, 487 <1, 34, 53, 879
4. None of the above

Answer. 3. 4807 <78, 989 <7, 89, 540 < 24, 68, 487 <1, 34, 53, 879

Question 3. The smallest 5-digit number formed from the digits 5, 3 and 0 is

1. 30500
2. 53000
3. 50355
4. 30005

Answer. 4. 30005

Question 4. The number formed by interchanging the digits 6 and 2 in 465271 is

1. 467521
2. 425671
3. 165274
4. None of these

Answer. 2. 425671

Question 5. How many lakhs make 1 million?

1. one
2. ten
3. hundred
4. thousand

Answer. 2. ten

Question 6. The difference between a million and a thousand is

1. 9990
2. 99900
3. 999000
4. 9990000

Answer. 3. 999000

Question 7. 3691215 with commas as per the Indian system of numeration is

1. 36,91,215
2. 3,69,1215
3. 36,912,15
4. 3,69,12,15

Answer. 1. 36,91,215

Question 8. In Indian system of numeration, the number 58695376 is written as

1. 58,69,53,76
2. 58,695,376
3. 5,86,95,376
4. 586,95,376

Answer. 3. 5,86,95,376

Question 9. The expanded form of the number 9578 is

1. 9 × 10000 + 5 x 1000 + 7 x 10 + 8 × 1
2. 9 × 1000 + 5 x 100 + 7 x 10 + 8 x 1
3. 9 x 1000 + 57 x 10 + 8 x 1.
4. 9 × 100 + 5 x 100 + 7 x 10 + 8 x 1

Answer. 2. 9 × 1000 + 5 x 100 + 7 x 10 + 8 x 1

Question 10. In international system of numeration 59357258 is written as

1. Fifty-nine million three hundred fifty-seven thousand two hundred fifty-eight
2. Five crores ninety four lakh fifty thousand two hundred fifty eight
3. Fifty nine crores three hundred fifty-seven thousand two hundred fifty-eight
4. None of the above

Solution. 1. Fifty-nine million three hundred fifty-seven thousand two hundred fifty-eight

Mp Board Class 6 Maths Chapter 1 SolutionsMp Board Class 6 Maths Chapter 1 SolutionsMp Board Class 6 Maths Chapter 1 Solutions

Question 11. The expression of 56,83,765 in words is

1. Five crores sixty eight thousand seven hundred sixty five.
2. Fifty six crores eighty three thousand seven hundred sixty five
3. Five crores six hundred eighty three
4. Fifty six lakh eighty three thousand seven hundred sixty five.

Answer. 4. Fifty six lakh eighty three thousand seven hundred sixty five.

Question 12. The place value of 0 in 4,30,976 is

1. 3000
2. 0
3. 6
4. 9

Answer. 2. 0

Question 13. The difference between the face value and the place value of the digit 8 in 38954

1. 4992
2. 6552
3. 7992
4. 5322

Answer. 3. 7992

Question 14. Population of Shivnagar was 458214 in 2001. In year 2004, it was found that the population increased by 123562, then the population in 2004 is

1. 96522
2. 628814
3. 96224
4. 581776

Solution. 4. 581776

Question 15. If a number 4253 multiplied by 44 instead of multiplying by 34, then the answer greater than the correct answer is

1. 5232
2. 42530
3. 8956
4. 7588

Answer. 2. 42530

MP Board solutions for Class 6 Maths Chapter 1 Assertion Reason Type Questions

Question 1. Assertion (A) 59785 is the greatest number among 382, 4972, 18, 59785, 750.

Reason (R) When a number is bigger or larger than the second or rest quantities or number it is known as greatest number.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (a) Both A and R are true and R is the correct explanation of A.

Question 2. Assertion (A) 56,500,800 is correct in Indian system of numeration.

Reason (R) 10,00,00,000 is the sequence of comma in Indian system of numeration.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (d) A is false but R is true.

MP Board Class 6 Chapter 1 Maths

Question 3. Assertion (A) 1 crore = 10 million

Reason (R) The smallest number of 8-digit is 1,00,00,000.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false.

(d) A is false but R is true.

Answer. (b) Both A and R are true but R is not the correct explanation of A.

MP Board solutions for Class 6 Maths Chapter 1 Fill in the Blanks

Question 1. The smallest 4-digit number with different digits is……..

Answer. 1023

Question 2. In Indian system of numeration, the number 61711682 is written, using commas, as…….

Answer. 6, 17, 11, 682

Question 3. Place value of 5 in 3546 is ……….. .

Answer. 500

Question 4. (1)1 m= …… mm

(2) 1 cm = …… mm

Answer. (1) 1000 (ii) 10

Question 5. By adding 1 to the greatest ………. digit number, we get ten lakh.

Answer. 6

MP Board solutions for Class 6 Maths Chapter 1 True/False

Question 1. 34984 = 3 x 1000 + 49 x 100 + 8 x 10 + 4 x 1

Answer. False

Question 2. 1000000 = 1 crore

Answer. False

Question 3. Face value of 7 in 754612 is 7.

Answer. True

Question 4. Smallest 5-digit number+1 = Greatest 6-digit number.

Answer. False

Question 5. The numbers 4578, 4587, 5478, 5487 are in ascending order.

Answer. True

MP Board Class 6 Chapter 1 Maths

Match the Columns

Question 1. Match the Column A with Column B.

Answer. (1)(b), (2) → (a), (3) → (d), (4) → (c)

MP Board solutions for Class 6 Maths Chapter 1

Question 1. The first and last coach of the metro train are Driving mode cars. The coaches in between are Trailing cars connected through Gangways. Gangways allow passenger movement between cars. This figure shows the dimensions of a Driving mode car and Trailing car along with Gangways.

(1) A train has six coaches. What is the length of the metro train?

(a) 45 m

(b) 133 m

(c) 134 m

(d) 135 m

(2) In the 6 coach metro train, each coach has 50 seats for passengers. The first coach is reserved for women. Sixteen seats are reserved for women and senior citizens in each of the remaining coaches. How many

unreserved passenger seats are in the metro train?

(a) 130

(b) 170

(c) 204

(d) 190

(3) On an average, a metro train completes 4 round trips of 90 km in a day. What is the average distance travelled by the metro?

Solution. (1) (c) Train has two driving coaches of length 23 m and 4 trailing coaches of length 22 m.

∴ Length of metro train = 23 + 23 + 22 + 22 + 22 + 22

= 134 m

(2) (b) Since, first coach is reserved for women.

Therefore, reserved seat=50

Now, there are 5 coaches left and 16 seats are reserved in each coach.

∴ Reserved seats in 5 coach = 16 x 5 = 80 seats

Total reserved seats = 50 + 80 = 130

Total seats in metro = 50 × 6 = 300

∴ Unreserved seats = Total seats – Reserved seats

= 300 – 130 = 170 seats

(3) Metro train completes 4 round trips of 90 km in a day.

∴ Distance travelled in a day = 90 x4 = 360 km

Question 2. Passengers need a metro token to board a train. The cost of the token depends upon the distance travelled in different zones. Different zones represents different metro networks.

The table below shows the cost of tokens for travelling in different zones of a metro.

The table below shows the number of passengers travelling on a particular day in different zones.

(1) How much revenue was generated on that day in Zone 1?

(2) Which zone generated the highest revenue on that day?

Solution. (1) Revenue generated in zone 1 = Revenue generated in (sub-zone 1+ sub-zone 2 + sub-zones)

Revenue generated in sub-zone 1

= Fare x Number of passenger travelled

= ₹10 × 90000 = ₹ 900000

Revenue generated in sub-zone 2 = ₹ 20 × 160000 = 3200000

Revenue generated in sub-zone 3 = ₹ 30 x 110000 = 3300000

∴ Total revenue generated in zone 1

₹ 900000 + ₹ 3200000 + ₹ 3300000 = ₹ 7400000

(2) Revenue generated in zone 1 = ₹ 7400000

Revenue generated in zone 2 = ₹ 40 x 25000

= ₹ 1000000

Revenue generated in zone 3 = ( 50 x 150000) + (₹60 x 100000)

= 13500000

Clearly, revenue generated in zone 3 is the highest.

Question 3. Siya and Aman are playing with 0-9 number cards. they placed seven cards in a row.

In how many different ways can they place the rest of the cards? 

Solution. Since, we have three place left and 13 cards left has digits 0, 3, 1. We keep changing their place value by shifting digits, thus we get numbers which are 031, 013, 103, 130, 310, 301.

Therefore, there are 6 ways to place the rest of the cards.

Question 4. Siya and Aman reshuffle the cards and divide them equally. Aman makes a 5-digit number using his cards. The picture shows the number formed by Aman.

Siya placed four of her cards as shown in the picture below.

Where should she place the remaining card to form a number greater than the number formed by Aman?

(a) After 9

(b) Before 0